Hierarchical Controlled Joint Remote Implementation of the Partially Unknown Operations of m Qudits via m High-Dimensional Entangled States
Abstract
1. Introduction
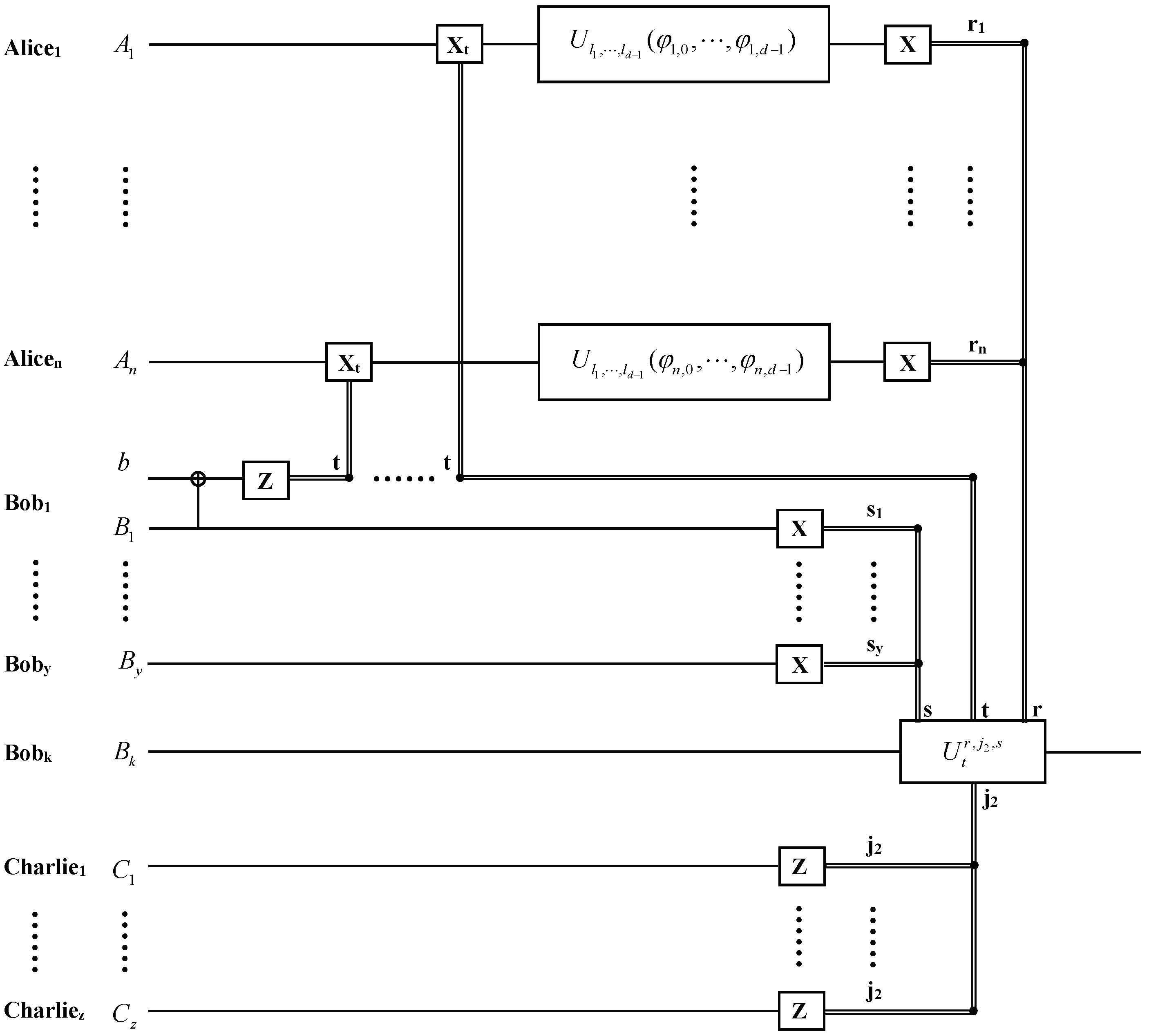
2. Hierarchial Joint Remote Implementation of Partially Unknown Operations of One Qudit via a Multiparticle High-Dimensional Entangled State
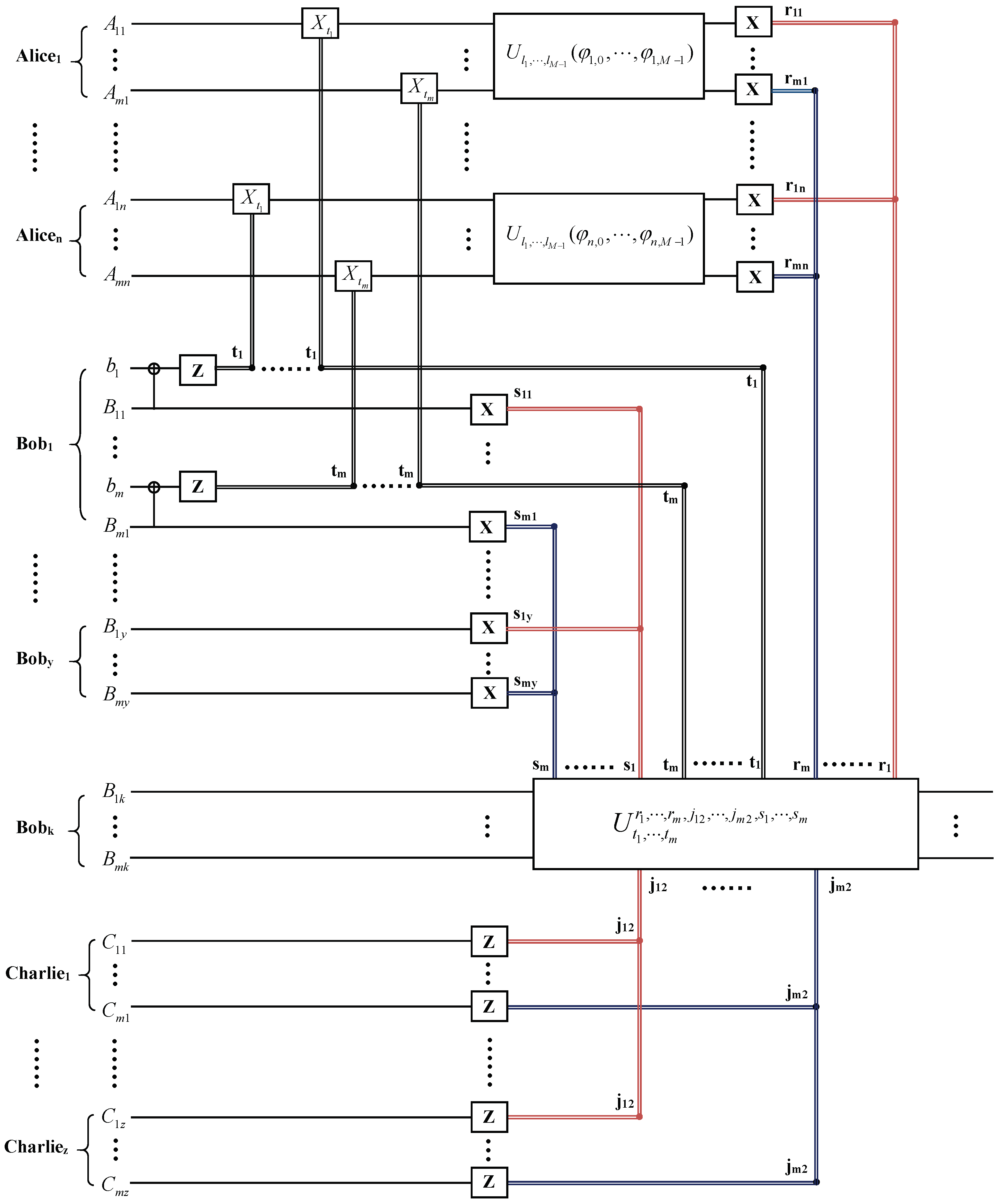
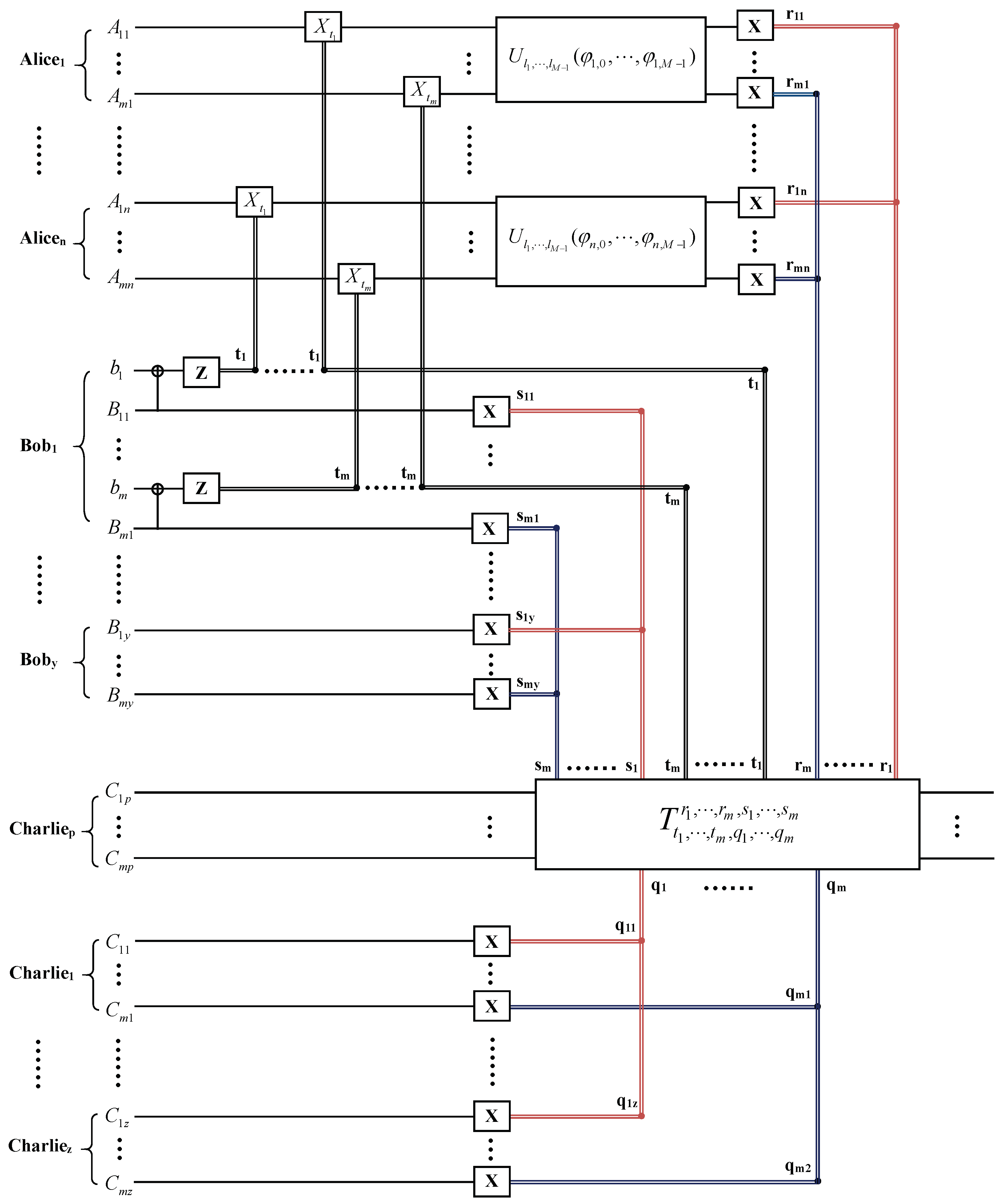
3. Hierarchial Joint Remote Implementation of Partially Unknown Operations of m Qudit via m Multiparticle High-Dimensional Entangled States
4. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassad, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; IEEE: New York, NY, USA, 1984; p. 175. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.L.; Dong, C.; He, Y.; Jing, F.; He, W.T.; Ren, B.C.; Li, C.Y.; Deng, F.G. Efficient quantum key distribution against collective noise using polarization and transverse spatial mode of photons. Opt. Express 2020, 28, 4611. [Google Scholar] [CrossRef] [PubMed]
- Kwek, L.C.; Cao, L.; Luo, W.; Wang, Y.X.; Sun, S.H.; Wang, X.B.; Liu, A.Q. Chip-based quantum key distribution. AAPPS Bull. 2021, 31, 15. [Google Scholar] [CrossRef]
- Liu, B.; Xia, S.; Xiao, D.; Huang, W.; Xu, B.J.; Li, Y. Decoy-state method for quantum-key-distribution-based quantum private query. Sci. China-Phys. Mech. Astron. 2022, 65, 240312. [Google Scholar] [CrossRef]
- Li, Z.J.; Wei, K.J. Improving parameter optimization in decoy-state quantum key distribution. Quantum Eng. 2022, 4, 9717591. [Google Scholar] [CrossRef]
- Wang, W.Y.; Wang, R.; Hu, C.Q.; Zapatero, V.; Qian, L.; Qi, B.; Curty, M.; Lo, H.K. Fully passive quantum key distribution. Phys. Rev. Lett. 2023, 130, 220801. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.K.; Tan, H.; Lu, Y.C.; Liao, S.K.; Huang, J.; Li, H.; Wang, Z.; Mao, H.K.; Yan, B.Z.; et al. High-rate quantum key distribution exceeding 110 Mb s−1. Nat. Photonics 2023, 17, 416. [Google Scholar] [CrossRef]
- Yin, H.L.; Chen, Z.B. Cost-efficient quantum access network boosts practical deployment of quantum key distribution network. Sci. China-Phys. Mech. Astron. 2024, 67, 240332. [Google Scholar] [CrossRef]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Hu, J.Y.; Yu, B.; Jing, M.Y.; Xiao, L.T.; Jia, S.T.; Qin, G.Q.; Long, G.L. Experimental quantum secure direct communication with single photons. Light Sci. Appl. 2016, 5, e16144. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ding, D.S.; Sheng, Y.B.; Zhou, L.; Shi, B.S.; Guo, G.C. Quantum secure direct communication with quantum memory. Phys. Rev. Lett. 2017, 118, 220501. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.G.; Wang, Y.C.; Yang, Y.L.; Chen, X.B.; Li, D.; Zhou, Y.H.; Shi, W.M. Participant attack on the deterministic measurement-device-independent quantum secret sharing protocol. Sci. China-Phys. Mech. Astron. 2021, 64, 260321. [Google Scholar] [CrossRef]
- Qi, Z.; Li, Y.; Huang, Y.; Feng, J.; Zheng, Y.; Chen, X. A 15-user quantum secure direct communication network. Light Sci. Appl. 2021, 10, 183. [Google Scholar] [CrossRef]
- Long, G.L.; Zhang, H.R. Drastic increase of channel capacity in quantum secure direct communication using masking. Sci. Bull. 2021, 66, 1267. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Sheng, Y.B. One-step device-independent quantum secure direct communication. Sci. China-Phys. Mech. Astron. 2022, 65, 250311. [Google Scholar] [CrossRef]
- Liu, X.; Luo, D.; Lin, G.S.; Chen, Z.H.; Huang, C.F.; Li, S.Z.; Zhang, C.X.; Zhang, Z.R.; Wei, K.J. Fiber-based quantum secure direct communication without active polarization compensation. Sci. China-Phys. Mech. Astron. 2022, 65, 120311. [Google Scholar] [CrossRef]
- Sheng, Y.B.; Zhou, L.; Long, G.L. One-step quantum secure direct communication. Sci. Bull. 2022, 67, 367. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Xu, B.W.; Zhong, W.; Sheng, Y.B. Device-independent quantum secure direct communication with single-photon sources. Phys. Rev. Appl. 2023, 19, 014306. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional quantum teleportation. Science 1998, 282, 706. [Google Scholar] [CrossRef]
- Xiao, X.; Yao, Y.; Zhong, W.J.; Li, Y.L.; Xie, Y.M. Enhancing teleportation of quantum Fisher information by partial measurements. Phys. Rev. A 2016, 93, 012307. [Google Scholar] [CrossRef]
- Langenfeld, S.; Welte, S.; Hartung, L.; Daiss, S.; Thomas, P.; Morin, O.; Distante, E.; Rempe, G. Quantum teleportation between remote qubit memories with only a single photon as a resource. Phys. Rev. Lett. 2021, 126, 130502. [Google Scholar] [CrossRef] [PubMed]
- Hermans, S.L.N.; Pompili, M.; Beukers, H.K.C.; Baier, S.; Borregaard, J.; Hanson, R. Qubit teleportation between non-neighbouring nodes in a quantum network. Nature 2022, 605, 663. [Google Scholar] [CrossRef]
- Shen, S.; Yuan, C.Z.; Zhang, Z.C.; Yu, H.; Zhang, R.M.; Yang, C.R.; Li, H.; Wang, Z.; Wang, Y.; Deng, G.W.; et al. Hertz-rate metropolitan quantum teleportation. Light Sci. Appl. 2023, 12, 115. [Google Scholar] [CrossRef]
- Liu, S.S.; Lv, Y.H.; Wang, X.T.; Wang, J.B.; Lou, Y.B.; Jing, J.T. Deterministic all-optical quantum teleportation of four degrees of freedom. Phys. Rev. Lett. 2024, 132, 100801. [Google Scholar] [CrossRef]
- Lo, H.K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar] [CrossRef]
- Pati, A.K. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A 2000, 63, 014302. [Google Scholar] [CrossRef]
- Long, G.L.; Xiao, L. Parallel quantum computing in a single ensemble quantum computer. Phys. Rev. A 2004, 69, 052303. [Google Scholar] [CrossRef]
- Feng, G.R.; Xu, G.F.; Long, G.L. Experimental realization of nonadiabatic holonomic quantum computation. Phys. Rev. Lett. 2013, 110, 190501. [Google Scholar] [CrossRef] [PubMed]
- Ren, B.C.; Wang, G.Y.; Feng, G.R. Universal hyperparallel hybrid photonic quantum gates with dipole-induced transparency in the weak-coupling regime. Phys. Rev. A 2015, 91, 032328. [Google Scholar] [CrossRef]
- Ren, B.C.; Deng, F.G. Robust hyperparallel photonic quantum entangling gate with cavity QED. Opt. Express 2017, 25, 10863. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Long, G.L. Hyperparallel optical quantum computation assisted by atomic ensembles embedded in double-sided optical cavities. Phys. Rev. A 2016, 94, 022343. [Google Scholar] [CrossRef]
- Song, X.K.; Ai, Q.; Qiu, J.; Deng, F.G. Physically feasible three-level transitionless quantum driving with multiple Schrodinger dynamics. Phys. Rev. A 2016, 93, 052324. [Google Scholar] [CrossRef]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75. [Google Scholar] [CrossRef]
- Postler, L.; Heussen, S.; Pogorelov, I.; Rispler, M.; Feldker, T.; Meth, M.; Marciniak, C.D.; Stricker, R.; Ringbauer, M.; Blatt, R.; et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 2022, 605, 675. [Google Scholar] [CrossRef]
- Lu, B.; Liu, L.; Song, J.Y.; Wen, K.; Wang, C. Recent progress on coherent computation based on quantum squeezing. AAPPS Bull. 2023, 33, 7. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X.; Li, X.; Wang, J.W. Chip-based photonic graph states. AAPPS Bull. 2021, 33, 14. [Google Scholar] [CrossRef]
- Gottesman, D.; Chuang, I.L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 1999, 402, 390. [Google Scholar] [CrossRef]
- Huang, Y.F.; Ren, X.F.; Zhang, Y.S.; Duan, L.M.; Guo, G.C. Experimental teleportation of a quantum controlled-not gate. Phys. Rev. Lett. 2004, 93, 240501. [Google Scholar] [CrossRef] [PubMed]
- Daiss, S.; Langenfeld, S.; Welte, S.; Distante, E.; Thomas, P.; Hartung, L.; Morin, O.; Rempe, G. A quantum-logic gate between distant quantum-network modules. Science 2021, 371, 614. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Morvan, A.; Nguyen, L.B.; Naik, R.K.; Jünger, C.; Chen, L.; Kreikebaum, J.M.; Santiago, D.I.; Siddiqi, I. High-fidelity three-qubit iToffoli gate for fixed-frequency superconducting qubits. Nat. Phys. 2022, 18, 783. [Google Scholar] [CrossRef]
- Xu, S.F.; Mao, Y.L.; Feng, L.X.; Chen, H.; Guo, B.X.; Liu, S.; Li, Z.D.; Fan, J.Y. Multiqubit quantum logical gates between distant quantum modules in a network. Phys. Rev. A 2023, 107, L060601. [Google Scholar] [CrossRef]
- Ghosal, P.; Ghosal, A.; Das, D.; Maity, A.G. Quantum superposition of causal structures as a universal resource for local implementation of nonlocal quantum operations. Phys. Rev. A 2023, 107, 022613. [Google Scholar] [CrossRef]
- Huelga, S.F.; Vaccaro, J.A.; Chefles, A.; Plenio, M.B. Quantum remote control: Teleportation of unitary operations. Phys. Rev. A 2001, 63, 042303. [Google Scholar] [CrossRef]
- Huelga, S.F.; Plenio, M.B.; Vaccaro, J.A. Remote control of restricted sets of operations: Teleportation of angles. Phys. Rev. A 2002, 65, 042316. [Google Scholar] [CrossRef]
- Wang, A.M. Remote implementations of partially unknown quantum operations of multiqubits. Phys. Rev. A 2006, 74, 032317. [Google Scholar] [CrossRef]
- Wang, A.M. Combined and controlled remote implementations of partially unknown quantum operations of multiqubits using Greenberger-Horne-Zeilinger states. Phys. Rev. A 2007, 75, 062323. [Google Scholar] [CrossRef]
- Fan, Q.B.; Liu, D.D. Controlled remote implementation of partially unknown quantum operation. Sci. China Ser. G 2008, 51, 1661. [Google Scholar] [CrossRef]
- Qiu, L.; Wang, A.M. Scheme for remote implementation of partially unknown quantum operation of two qubits in cavity QED. Commun. Theor. Phys. 2008, 50, 1233. [Google Scholar]
- Chen, L.B.; Liu, Y.H.; Lu, H. Controlled and remote implementation of a split quantum rotation and sender-encoded secret sharing. Mod. Phys. Lett. B 2010, 24, 431. [Google Scholar] [CrossRef]
- Chen, L.B.; Jin, R.B.; Peng, T.; Lu, H. Realizing open-destination and controlled teleportation of a rotation using partially entangled pairs. Int. J. Mod. Phys. B 2011, 25, 2853. [Google Scholar] [CrossRef]
- Situ, H.; Qiu, D. Investigating the implementation of restricted sets of multiqubit operations on distant qubits: A communication complexity perspective. Quantum Inf. Process. 2011, 10, 609. [Google Scholar] [CrossRef]
- Zhan, Y.B.; Li, X.W.; Ma, P.C.; Shi, J. Controlled remote implementation of quantum operations with high-dimensional systems. Chin. Phys. B 2013, 22, 040306. [Google Scholar] [CrossRef]
- Peng, J.Y.; Bai, M.Q.; Mo, Z.W. Multicharacters remote rotation sharing with five-particle cluster state. Quantum Inf. Process. 2019, 18, 339. [Google Scholar] [CrossRef]
- An, N.B.; Cao, B.T. Controlled remote implementation of operators via hyperentanglement. J. Phys. A 2022, 55, 225307. [Google Scholar] [CrossRef]
- Peng, J.Y.; Tang, L.; Yang, Z.; Lei, H.X.; Bai, M.Q. Many-party controlled remote implementations of multiple partially unknown quantum operations. Quantum Inf. Process. 2023, 22, 2. [Google Scholar] [CrossRef]
- Liu, M.; Maihemuti, N.; Peng, J.Y. Controlled bidirectional remote implementations of partially unknown quantum operations. Phys. Scr. 2024, 99, 045109. [Google Scholar] [CrossRef]
- Shi, W.M.; Bai, M.X.; Zhou, Y.H.; Yang, Y.G. Hierarchical quantum rotation operation sharing with multiparty users. Quantum Inf. Process. 2024, 23, 196. [Google Scholar] [CrossRef]
- Xiang, G.Y.; Li, J.; Guo, G.C. Teleporting a rotation on remote photons. Phys. Rev. A 2005, 71, 044304. [Google Scholar] [CrossRef]
- Muthukrishnan, A.; Stroud, C.R., Jr. Multivalued logic gates for quantum computation. Phys. Rev. A 2000, 65, 052309. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Shor, P.W.; Smolin, J.A.; Terhal, B.M.; Wootters, W.K. Remote state preparation. Phys. Rev. Lett. 2001, 87, 077902. [Google Scholar] [CrossRef]
- Vlasov, A.Y. Noncommutative tori and universal sets of nonbinary quantum gates. J. Meth. Phys. 2002, 65, 2959. [Google Scholar] [CrossRef]
- Zhou, D.L.; Zeng, B.; Xu, Z.; Sun, C.P. Quantum computation based on d-level cluster state. Phys. Rev. A 2003, 68, 062303. [Google Scholar] [CrossRef]
- Wang, C.; Deng, F.G.; Li, Y.S.; Liu, X.S.; Long, G.L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 2005, 71, 044305. [Google Scholar] [CrossRef]
- Li, X.H.; Deng, F.G.; Zhou, H.Y. Controlled teleportation of an arbitrary multi-qudit state in a general form with d-dimensional Greenberger-Horne-Zeilinger states. Chin. Phys. Lett. 2007, 24, 1151. [Google Scholar]
- Luo, M.X.; Wang, X.J. Universal quantum computation with qudits. Sci. China-Phys. Mech. Astron. 2014, 57, 1712. [Google Scholar] [CrossRef]
- Krenn, M.; Huber, M.; Fickler, R.; Lapkiewicz, R.; Ramelow, S.; Zeilinger, A. Generation and confirmation of a (100 × 100)-dimensional entangled quantum system. Proc. Natl. Acad. Sci. USA 2014, 111, 6243. [Google Scholar] [CrossRef]
- Kues, M.; Reimer, C.; Roztocki, P.; Cortés, L.R.; Sciara, S.; Wetzel, B.; Zhang, Y.B.; Cino, A.; Chu, S.T.; Little, B.E.; et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 2017, 7660, 622. [Google Scholar] [CrossRef]
- Bouchard, F.; Fickler, R.; Boyd, R.W.; Karimi, E. High-dimensional quantum cloning and applications to quantum hacking. Sci. Adv. 2017, 3, e1601915. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.M.; Guo, Y.; Liu, B.H.; Huang, Y.F.; Li, C.F.; Guo, G.C. Beating the channel capacity limit for superdense coding with entangled ququarts. Sci. Adv. 2018, 4, eaat9304. [Google Scholar] [CrossRef] [PubMed]
- Reimer, C.; Sciara, S.; Roztocki, P.; Islam, M.; Corts, L.R.; Zhang, Y.B.; Fischer, B.; Loranger, S.; Kashyap, R.; Cino, A.; et al. High-dimensional one-way quantum processing implemented on d-level cluster states. Nat. Phys. 2019, 15, 148. [Google Scholar] [CrossRef]
- Vagniluca, I.; Da Lio, B.; Rusca, D.; Cozzolino, D.; Ding, Y.H.; Zbinden, H.; Zavatta, A.; Oxenløwe, L.K.; Bacco, D. Efficient time-bin encoding for practical high-dimensional quantum key distribution. Phys. Rev. Appl. 2020, 14, 014051. [Google Scholar] [CrossRef]
- Hu, X.M.; Xing, W.B.; Liu, B.H.; Huang, Y.F.; Li, C.F.; Guo, G.C. Efficient generation of highdimensional entanglement through multipath down-conversion. Phys. Rev. Lett. 2020, 125, 090503. [Google Scholar] [CrossRef]
- Hu, X.M.; Xing, W.B.; Liu, B.H.; He, D.Y.; Cao, H.; Guo, Y.; Zhang, C.; Zhang, H.; Huang, Y.F.; Li, C.F.; et al. Distribution of high-dimensional orbital angular momentum entanglement over a 1 km few-mode fiber. Optica 2020, 7, 232. [Google Scholar]
- Hu, X.M.; Zhang, C.; Liu, B.H.; Cai, Y.; Ye, X.J.; Guo, Y.; Xing, W.B.; Huang, C.X.; Huang, Y.F.; Li, C.F.; et al. Experimental high-dimensional quantum teleportation. Phys. Rev. Lett. 2020, 125, 230501. [Google Scholar] [CrossRef]
- Wang, T.J.; Yang, G.Q.; Wang, C. Control power of high-dimensional controlled teleportation. Phys. Rev. A 2020, 101, 012323. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Nikolaeva, A.S.; Xu, P.; Shlyapnikov, G.V.; Fedorov, A.K. Scalable quantum computing with qudits on a graph. Phys. Rev. A 2020, 101, 022304. [Google Scholar] [CrossRef]
- Saha, A.; Majumdar, R.; Saha, D.; Chakrabarti, A.; Sur-Kolay, S. Asymptotically improved circuit for a d-ary Grover’s algorithm with advanced decomposition of the n-qudit Toffoli gate. Phys. Rev. A 2022, 105, 062453. [Google Scholar] [CrossRef]
- Nikolaeva, A.S.; Kiktenko, E.O.; Fedorov, A.K. Decomposing the generalized Toffoli gate with qutrits. Phys. Rev. A 2022, 105, 032621. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Y.; Zhang, F.L. Perfect teleportation with a partially entangled quantum channel. Phys. Rev. A 2022, 106, 032430. [Google Scholar] [CrossRef]
- Hrmo, P.; Wilhelm, B.; Gerster, L.; van Mourik, M.W.; Huber, M.; Blatt, R.; Schindler, P.; Monz, T.; Ringbauer, M. Native qudit entanglement in a trapped ion quantum processor. Nat. Commun. 2023, 14, 2242. [Google Scholar] [CrossRef]
- Luo, K.; Huang, W.H.; Tao, Z.Y.; Zhang, L.B.; Zhou, Y.X.; Chu, J.; Liu, W.X.; Wang, B.Y.; Cui, J.Y.; Liu, S.; et al. Experimental realization of two qutrits gate with tunable coupling in superconducting circuits. Phys. Rev. Lett. 2023, 130, 030603. [Google Scholar] [CrossRef]
- Xing, W.B.; Hu, X.M.; Guo, Y.; Liu, B.H.; Li, C.F.; Guo, G.C. Preparation of multiphoton high-dimensional GHZ states. Opt. Express 2023, 31, 24887. [Google Scholar] [CrossRef] [PubMed]
- Lv, M.Y.; Hu, X.M.; Gong, N.F.; Wang, T.J.; Guo, Y.; Liu, B.H.; Huang, Y.F.; Li, C.F.; Guo, G.C. Demonstration of controlled high-dimensional quantum teleportation. Sci. China-Phys. Mech. Astron. 2024, 67, 230311. [Google Scholar] [CrossRef]
- Xu, Q.; Zhou, L.X.; Feng, T.F.; Qiu, S.F.; Li, S.W.; Zhang, W.J.; Luo, H.; Zhou, X.Q. Experimental quantum state compression from two identical qubits to a qutrit. Sci. China-Phys. Mech. Astron. 2024, 67, 270311. [Google Scholar] [CrossRef]
- Jin, R.H.; Wei, W.S.; Zhou, P. Hierarchical controlled remote preparation of an arbitrary m-qudit state with four-qudit cluster states. Quantum Inf. Process. 2023, 22, 113. [Google Scholar] [CrossRef]
- Wang, Y.C.; Hu, Z.X.; Sanders, B.C.; Kais, S. Qudits and high-dimensional quantum computing. Front. Phys. 2020, 8, 589504. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, R.; Lan, Q.; Zhou, P. Hierarchical Controlled Joint Remote Implementation of the Partially Unknown Operations of m Qudits via m High-Dimensional Entangled States. Entropy 2024, 26, 857. https://doi.org/10.3390/e26100857
Jing R, Lan Q, Zhou P. Hierarchical Controlled Joint Remote Implementation of the Partially Unknown Operations of m Qudits via m High-Dimensional Entangled States. Entropy. 2024; 26(10):857. https://doi.org/10.3390/e26100857
Chicago/Turabian StyleJing, Ruiheng, Qi Lan, and Ping Zhou. 2024. "Hierarchical Controlled Joint Remote Implementation of the Partially Unknown Operations of m Qudits via m High-Dimensional Entangled States" Entropy 26, no. 10: 857. https://doi.org/10.3390/e26100857
APA StyleJing, R., Lan, Q., & Zhou, P. (2024). Hierarchical Controlled Joint Remote Implementation of the Partially Unknown Operations of m Qudits via m High-Dimensional Entangled States. Entropy, 26(10), 857. https://doi.org/10.3390/e26100857






