Maxpro Designs for Experiments with Multiple Types of Branching and Nested Factors
Abstract
1. Introduction
2. Preliminaries
3. Existing Criteria and Limitations
4. Maxpro Criterion for Experiments with Multiple Types of Branching and Nested Factors
5. Optimal Design Construction
5.1. Construction Method
- Start with a beginning design.
- Develop a neighbor design of the current design by using the coordinate exchange algorithm.
- Calculate the -value for the neighbor design, and then decide whether to replace the current design or not.
- 1.
- Randomly generate an U-type design to accommodate the branching factors.
- 2.
- For level z of the lth branching factor, randomly generate a smaller U-type design for , say , and then integrate them based on the levels of the branching factors to accommodate the nested factor , which corresponds to the lth branching factor.
- 3.
- Randomly generate an U-type design to arrange the nested factors.
- 4.
- Letwhich consists of r branching factors, factors nested into the lth branching factors, and t shared factors. Thus, there are factors in total.
- 1.
- Draw a random column number u from
- 2.
- If , the selected factor is a branching factor, then exchange two randomly locations () within the uth column, and also exchange the and rows of the . There are changed elements in total.
- 3.
- If , the selected factor is a nested factor nested into the lth branching factor, then exchange two randomly locations () of the uth column where the associated branching factor has the same level.
- 4.
- If , the selected factor is a shared factor, then exchange two randomly locations () of uth column.
- (a)
- If , turn to Step 2, and suppose ; then, we can obtain . Here, if we only swap the first and second elements of the branching factor and ignore the associated nested factor, the branching–nested structure will be disrupted.
- (b)
- If , go to Step 3. Two selected locations should correspond to the same level of the branching factor (such as level 0), i.e., . Let , and then the resulting design is . In this situation, if two elements come from different levels of the branching factor, then the branching–nested structure should also be broken.
- (c)
- If , proceed to Step 4, and assume ; then, we have .
5.2. Iterative Formulas
- (a)
- If , since the branching factor determines the manner of partitioning, it becomes quite complex, and thus, the iterative formula for the second part of (11) is not considered. The first part of (11) can be updated iteratively. Let , and and correspond to the ith and jth rows of design . Note that is obtained by interchanging the and positions of the uth column of ; then, for and , we haveandwhere and are the th and th rows of . It can be easily derived thatfor which the computational complexity is O.
- (b)
- If , assume the selected locations in the uth column correspond to level of the th branching factor. Clearly, the sub-design for branching and shared factors remains unchanged, and thus, the value for the first part of (11) does not change; that is,As for the second part of (11), among the terms involved, only one of them is subject to change, as follows,where I is a set, collecting row indices where the th branching factor takes level . In addition, can be similarly defined as . The computation will take O, if as well as , and 0 otherwise.
- (c)
- If , can be calculated by (12). In addition, depending on the levels of branching factors at and positions, it can be further divided into the following two cases:
- (i)
- The and runs of the lth branching factor have the same level, say level c, denoting the corresponding run indices such that the lth branching factor takes level c as , then
- (ii)
- The and runs of the lth branching factor take two distinct levels, say level , respectively. Similarly, define , then
In the same fashion, the computational complexity can be given.
- (a)
- If a branching factor is selected, the computational complexity is O.
- (b)
- If a nested factor associated with the th branching factor is selected, the computational complexity is O.
- (c)
- If a shared factor is selected, the computational complexity is O.
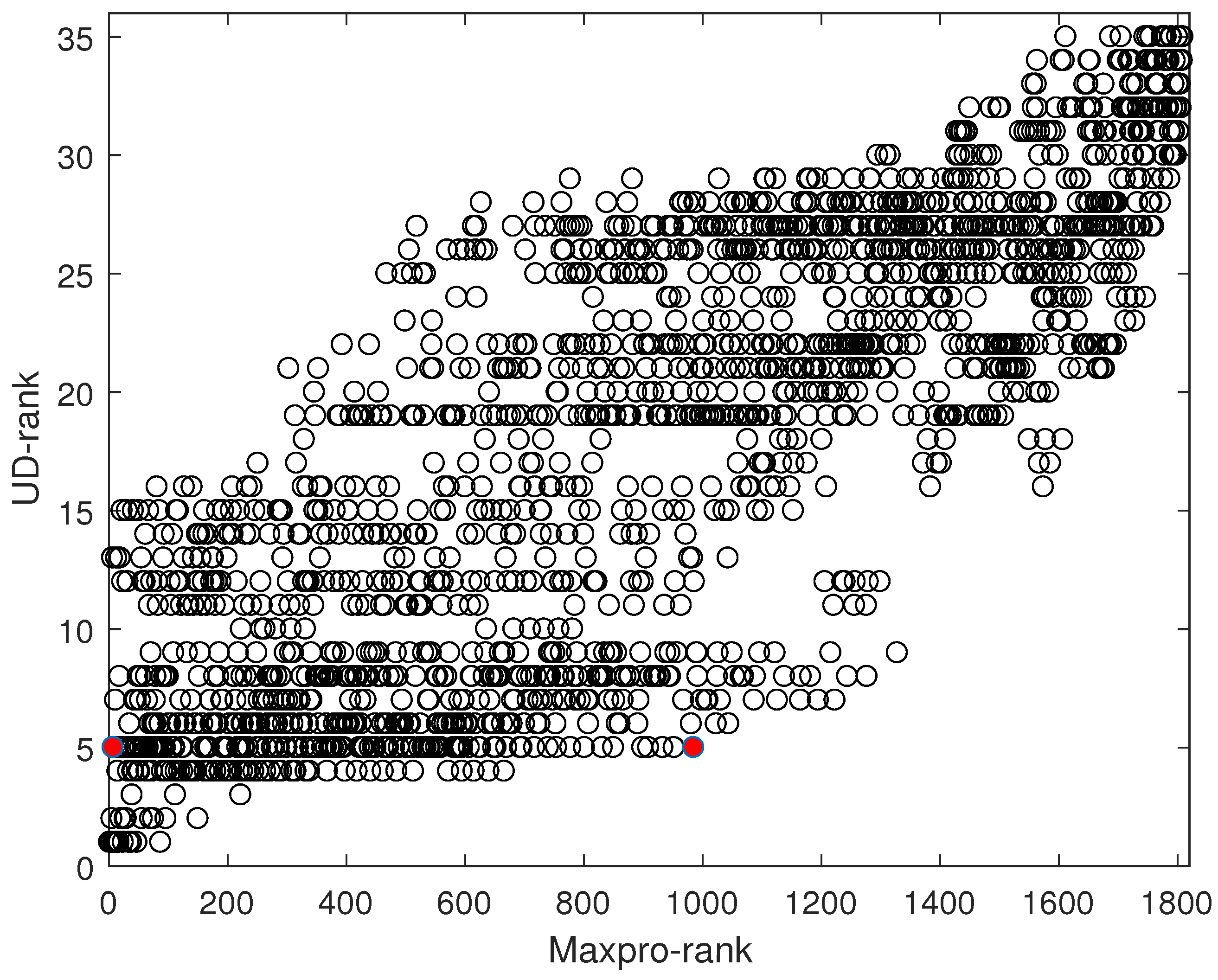
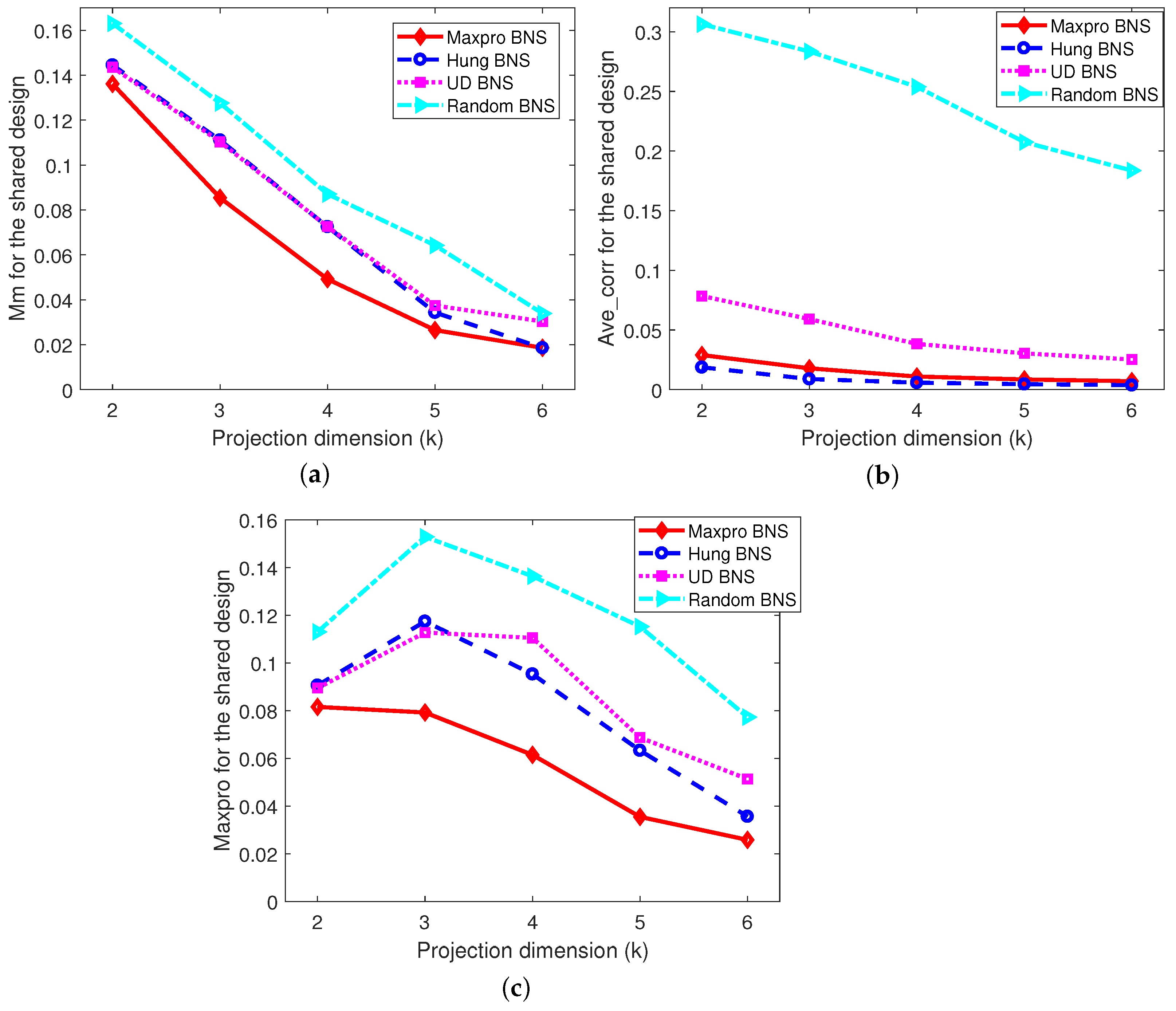
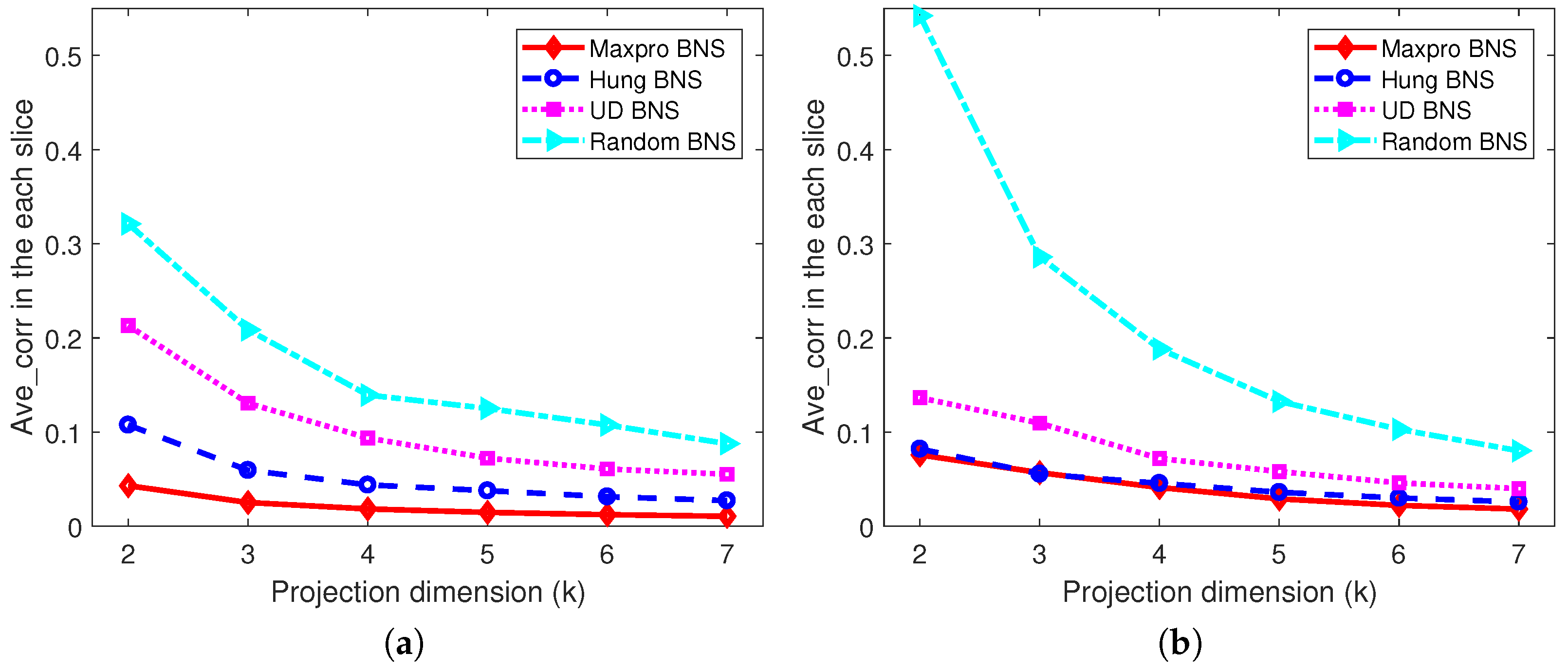
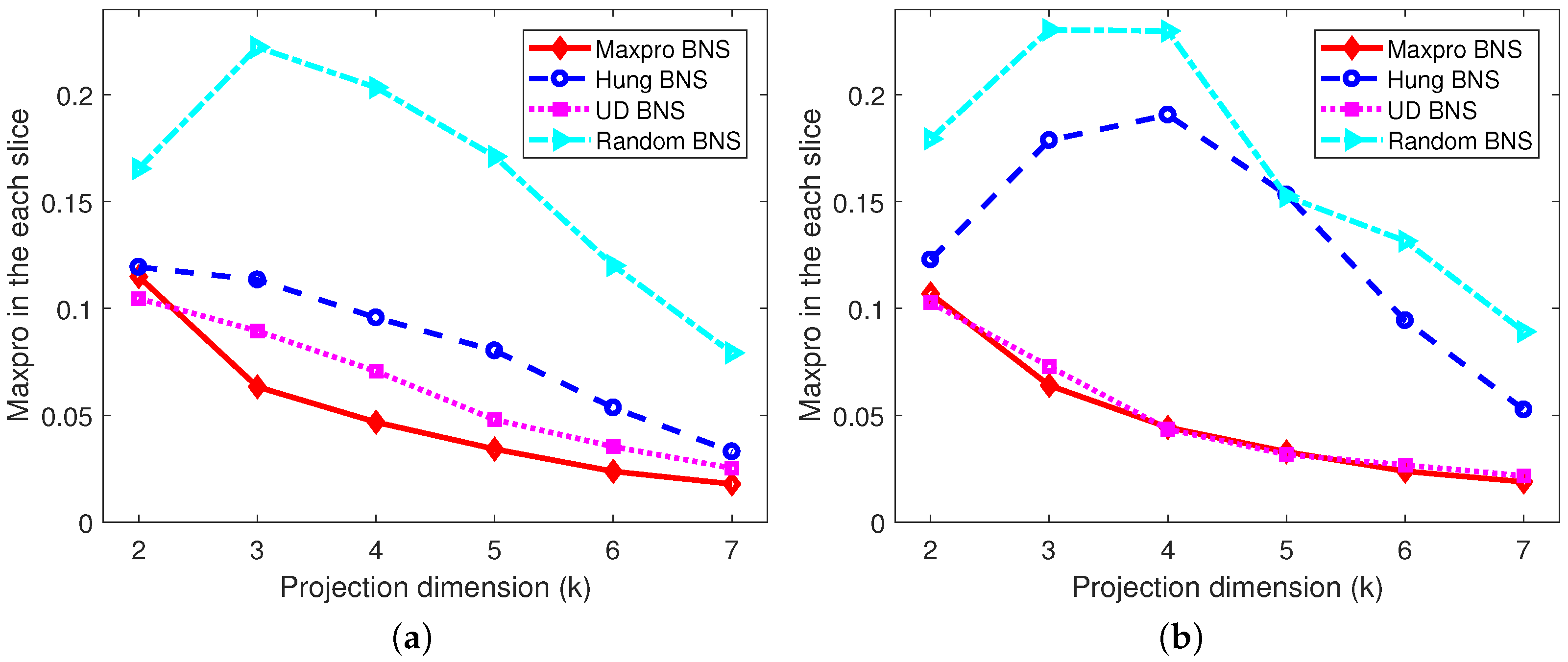
6. Numerical Comparisons
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hung, Y.; Joseph, V.R.; Melkote, S.N. Design and Analysis of Computer Experiments With Branching and Nested Factors. Technometrics 2009, 51, 354–365. [Google Scholar] [CrossRef]
- Decrop, D.; Lammertyn, J.; Goos, P. Optimal experimental design for efficient optical manipulation of magnetic beads seeded in a microwell array. J. Q. Technol. 2017, 49, 402–417. [Google Scholar] [CrossRef]
- Su, H.; Wu, C.J. CME analysis: A new method for unraveling aliased effects in two-level fractional factorial experiments. J. Q. Technol. 2017, 49, 1–10. [Google Scholar] [CrossRef]
- Goos, P.; Jones, B. Optimal Experimental Design in the Presence of Nested Factors. Technometrics 2019, 61, 533–544. [Google Scholar] [CrossRef]
- Yang, F.; Zhou, Z.; Zhou, Y.D. Uniform Designs for Experiments with Branching and Nested Factors. JMVA, 2024; under review. [Google Scholar]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003. [Google Scholar]
- Fang, K.T.; Liu, M.Q.; Qin, H.; Zhou, Y.D. Theory and Application of Uniform Experimental Designs; Springer: Singapore, 2018. [Google Scholar]
- Korobov, N.M. The approximate computation of multiple integrals. Dokl. Akad. Nauk. SSSR 1959, 124, 1207–1210. [Google Scholar]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Fang, K.T.; Li, R.Z.; Sudjianto, A. Design and Modeling for Computer Experiments; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
- Shewry, M.C.; Wynn, H.P. Maximum entropy sampling. J. Appl. Stat. 1987, 14, 165–170. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Scott, D.S. A computer program for the design of group testing experiments. Commun. Stat. Theory Methods 1987, 16, 2943–2955. [Google Scholar] [CrossRef]
- Currin, C.; Mitchell, T.; Morris, M.; Ylvisaker, D. Bayesian prediction of deterministic functions, with applications to the design and analysis of computer experiments. J. Am. Stat. Assoc. 1991, 86, 953–963. [Google Scholar] [CrossRef]
- Koehler, J.R.; Owen, A.B. Computer experiments. In Handbook of Statistics; Ghosh, S., Rao, C.R., Eds.; Elsevier Science: New York, NY, USA, 1996; Volume 13, pp. 261–308. [Google Scholar]
- Lam, C.Q. Sequential Adaptive Designs in Computer Experiments for Response Surface Model Fit. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Morris, M.D.; Mitchell, T.J. Exploratory designs for computational experiments. J. Stat. Plan. Inference 1995, 43, 381–402. [Google Scholar] [CrossRef]
- Johnson, M.E.; Moore, L.M.; Ylvisaker, D. Minimax and maximin distance designs. J. Stat. Plan. Inference 1990, 26, 131–148. [Google Scholar] [CrossRef]
- Joseph, V.R.; Gul, E.; Ba, S. Maximum projection designs for computer experiments. Biometrika 2015, 102, 371–380. [Google Scholar] [CrossRef]
- Joseph, V.R.; Gul, E.; Ba, S. Designing Computer Experiments with Multiple Types of Factors: The MaxPro Approach. J. Q. Technol. 2020, 52, 343–354. [Google Scholar] [CrossRef]
- Owen, A. Controlling correlations in Latin hypercube samples. J. Am. Stat. Assoc. 1994, 89, 1517–1522. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, F.; Zhou, Y.D. Uniformity Criterion for Designs with Both Qualitative and Quantitative Factors. Statistics 2021, 55, 90–109. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.Y.; Lin, D.K.J.; Liu, M.Q. Sliced Latin Hypercube Designs with Both Branching and Nested Factors. Stat. Probab. Lett. 2019, 146, 124–131. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.Y.; Liu, M.Q. Construction of Improved Branching Latin Hypercube Designs. Acta Math. Sci. 2021, 41, 1023–1033. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, M.Q.; Yang, J.F. Orthogonal Designs with Branching and Nested Factors. Stat 2022, 11, e447. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An Efficient Algorithm for Constructing Optimal Design of Computer Experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
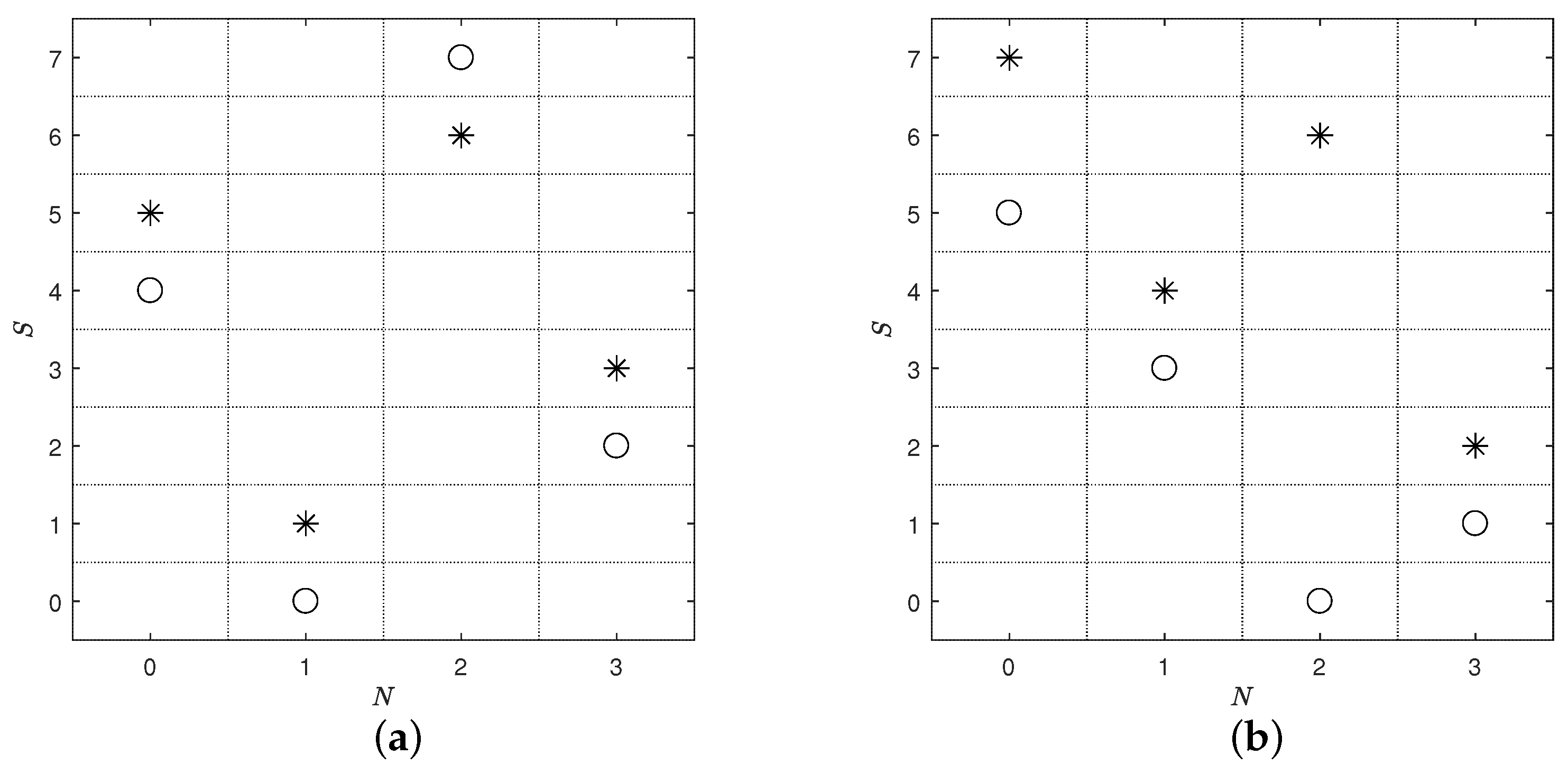


| Run | ||||||
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 5 | 0 | 0 | 7 |
| 2 | 0 | 1 | 1 | 0 | 1 | 4 |
| 3 | 0 | 2 | 6 | 0 | 2 | 6 |
| 4 | 0 | 3 | 3 | 0 | 3 | 2 |
| 5 | 1 | 0 | 4 | 1 | 0 | 5 |
| 6 | 1 | 1 | 0 | 1 | 1 | 3 |
| 7 | 1 | 2 | 7 | 1 | 2 | 0 |
| 8 | 1 | 3 | 2 | 1 | 3 | 1 |
| Run | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | 1 | 10 | 12 | 0 | 0 | 4 | 4 | 2 | 8 |
| 2 | 0 | 0 | 7 | 0 | 3 | 5 | 0 | 0 | 0 | 6 | 6 | 12 |
| 3 | 0 | 0 | 6 | 6 | 6 | 14 | 0 | 0 | 5 | 2 | 14 | 0 |
| 4 | 0 | 0 | 1 | 5 | 13 | 6 | 0 | 0 | 2 | 0 | 10 | 4 |
| 5 | 0 | 1 | 4 | 7 | 8 | 3 | 0 | 1 | 6 | 5 | 8 | 2 |
| 6 | 0 | 1 | 5 | 3 | 15 | 9 | 0 | 1 | 1 | 3 | 12 | 10 |
| 7 | 0 | 1 | 2 | 4 | 0 | 11 | 0 | 1 | 3 | 7 | 0 | 14 |
| 8 | 0 | 1 | 0 | 2 | 5 | 1 | 0 | 1 | 7 | 1 | 4 | 6 |
| 9 | 1 | 0 | 4 | 5 | 14 | 13 | 1 | 0 | 7 | 4 | 11 | 13 |
| 10 | 1 | 0 | 3 | 6 | 2 | 2 | 1 | 0 | 5 | 6 | 15 | 5 |
| 11 | 1 | 0 | 6 | 1 | 11 | 4 | 1 | 0 | 1 | 2 | 3 | 1 |
| 12 | 1 | 0 | 0 | 7 | 9 | 8 | 1 | 0 | 3 | 0 | 7 | 9 |
| 13 | 1 | 1 | 1 | 0 | 4 | 10 | 1 | 1 | 0 | 1 | 13 | 7 |
| 14 | 1 | 1 | 2 | 3 | 12 | 0 | 1 | 1 | 6 | 7 | 5 | 15 |
| 15 | 1 | 1 | 5 | 2 | 1 | 15 | 1 | 1 | 2 | 5 | 1 | 11 |
| 16 | 1 | 1 | 7 | 4 | 7 | 7 | 1 | 1 | 4 | 3 | 9 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Zhou, Z. Maxpro Designs for Experiments with Multiple Types of Branching and Nested Factors. Entropy 2024, 26, 856. https://doi.org/10.3390/e26100856
Yang F, Zhou Z. Maxpro Designs for Experiments with Multiple Types of Branching and Nested Factors. Entropy. 2024; 26(10):856. https://doi.org/10.3390/e26100856
Chicago/Turabian StyleYang, Feng, and Zheng Zhou. 2024. "Maxpro Designs for Experiments with Multiple Types of Branching and Nested Factors" Entropy 26, no. 10: 856. https://doi.org/10.3390/e26100856
APA StyleYang, F., & Zhou, Z. (2024). Maxpro Designs for Experiments with Multiple Types of Branching and Nested Factors. Entropy, 26(10), 856. https://doi.org/10.3390/e26100856






