Secure Ring Signature Scheme for Privacy-Preserving Blockchain
Abstract
:1. Introduction
- The algorithm exploits the concept of distributed key generation to create a system master key, which enhances the process of distributing the key by a trusted authorizer (TA) in traditional signature algorithms and eliminates the risk of key leakage when the TA is untrustworthy or subjected to malicious attacks.
- This scheme is a ring signature constructed based on ECC, which provides better security with the same length of key compared to the scheme based on bilinear pairing. This algorithm strengthens the signature’s unforgeability, which reduces the attackers’ probability of succeeding in cracking the key.
- This scheme improves the efficiency of ring signature generation and verification and is more compatible with the environment of blockchain systems.
2. Related Works
3. Preliminaries
3.1. Elliptic Curve
- O is the additive identity element, that is, for any point P of the elliptic curve, .
- Let be a point on an elliptic curve whose additive inverse element is defined as . This is because, when the connection of and is extended to infinity, another point O on the elliptic curve is obtained, that is the three points , and O on the elliptic curve are collinear, so , , that is .
- Let and , then is determined by the following rule:where
- The multiple of a point P is defined as .
3.2. Problem Assumptions
3.3. Ring-Signature-Generation Algorithm
- KeyGen(): This algorithm needs to input a security parameter l and, then, generate a key pair for each user, where is the public key and is the private key.
- Sign(): This algorithm takes the message m, which needs to be encrypted, the private key of a ring member, and the public key set of the selected ring members and generates a signature for the message m. One of the parameters in the signature follows a ring according to certain rules.
- Verify(): This algorithm is a deterministic algorithm, which takes the public key set , the message m, and the signature as the input and outputs “accept” if the verification passes and “reject” otherwise.
3.4. Security Models
3.4.1. Game I Correctness
- Join oracle machine (JO(⊥) →): With this query, a new user is added to the system and the public key of the new user is output.
- Corruption oracle machine (CO() →: The user’s public key is input, and the corresponding private key is output.
- Signed oracle machine (SO() →): Input signed message m, and set of public keys of size n; the signer’s public key returns a valid ring signature .
3.4.2. Game II Unforgeability
- generates the system parameters params and sends them to .
- adaptively queriesoracles JO, CO, and SO and random oracles .
- outputs a signature message , a set consisting of n user public keys, and two forged signature values , .
3.4.3. Game III Unconditional Anonymity
- generates the system parameters params and sends them to .
- can adaptively query join oracle machine JO.
- sends a signature message and a set consisting of public keys of n users to , where all public keys are obtained by the JO query. randomly selects and computes a signature , where is the private key corresponding to . Finally, sends to .
- outputs a guess .
4. Secure Ring Signature Scheme
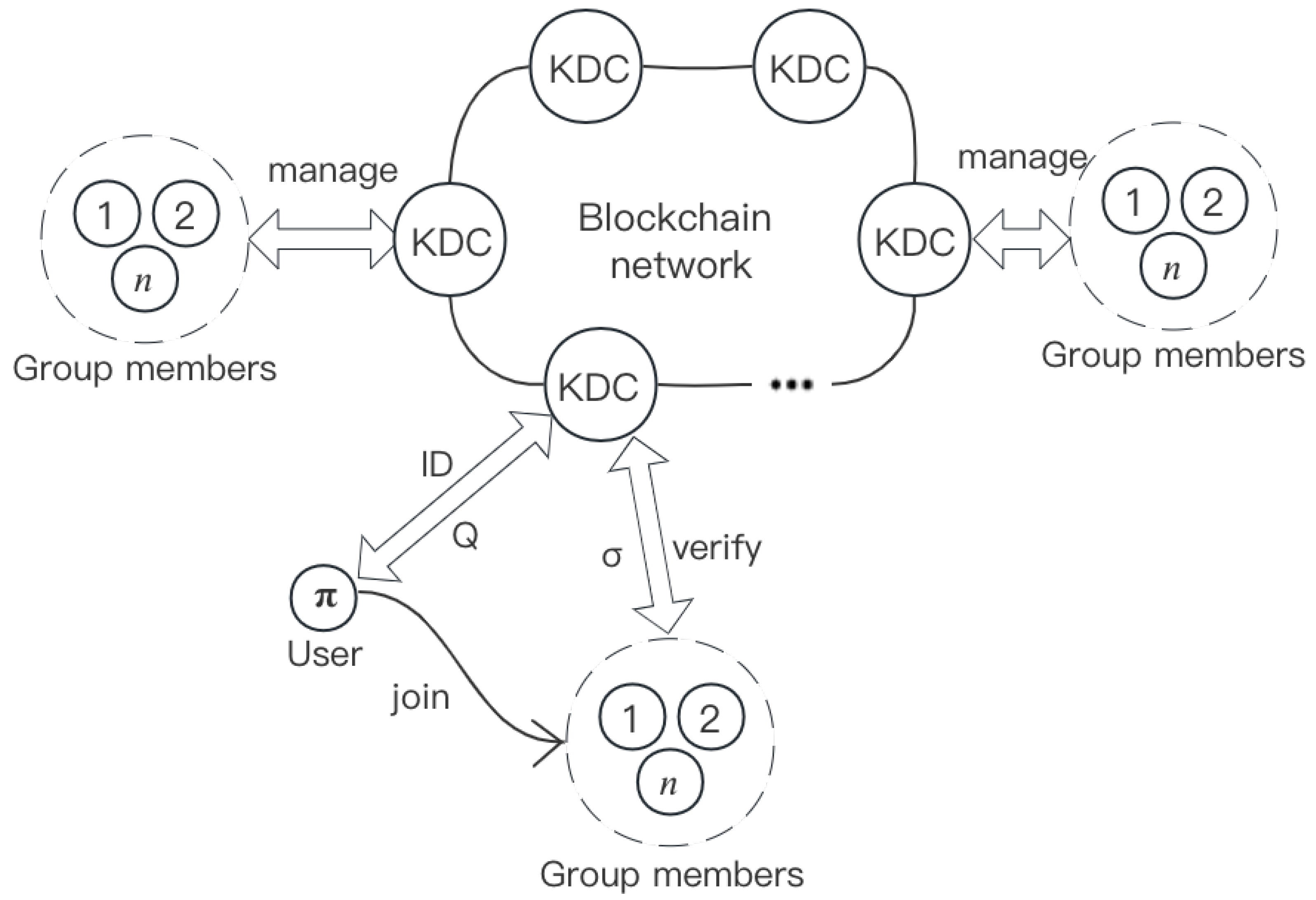
4.1. System Description
4.2. Algorithm Description
4.2.1. Setup Algorithm
4.2.2. Key Generation
4.2.3. Signature Generation
4.2.4. Verify
5. Security Analysis
5.1. Correctness Analysis
5.2. Unforgeability Analysis
- Randomly choose , and compute:
- The ring signature is given as .
5.3. Unconditional Anonymity
6. Performance Evaluation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Decentralized Business Review. 2008, p. 21260. Available online: https://bitcoin.org/en/bitcoin-paper (accessed on 5 August 2023).
- Kano, Y.; Nakajima, T. A novel approach to solve a mining work centralization problem in blockchain technologies. Int. J. Pervasive Comput. Commun. 2018, 14, 15–32. [Google Scholar] [CrossRef]
- Buterin, V. A next-generation smart contract and decentralized application platform. White Pap. 2014, 3, 1–2. [Google Scholar]
- Schollmeier, R. A definition of peer-to-peer networking for the classification of peer-to-peer architectures and applications. In Proceedings of the First International Conference on Peer-to-Peer Computing, Linköping, Sweden, 27–29 August 2001; pp. 101–102. [Google Scholar]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, F.Y. Blockchain: The state of the art and future trends. Acta Autom. Sin. 2016, 42, 481–494. [Google Scholar]
- Burniske, C.; White, A. Bitcoin: Ringing the Bell for a New Asset Class. Ark Invest (January 2017). 2017. Available online: https://research.ark-invest.com/hubfs/1_Download_Files_ARK-Invest/White_Papers/Bitcoin-Ringing-The-Bell-For-A-New-Asset-Class.pdf (accessed on 5 August 2023).
- Agbo, C.C.; Mahmoud, Q.H.; Eklund, J.M. Blockchain technology in healthcare: A systematic review. Healthcare 2019, 7, 56. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Su, M. Integrating blockchain technology into the energy sector—from theory of blockchain to research and application of energy blockchain. Comput. Sci. Rev. 2020, 37, 100275. [Google Scholar] [CrossRef]
- Ron, D.; Shamir, A. Quantitative analysis of the full bitcoin transaction graph. In Proceedings of the Financial Cryptography and Data Security: 17th International Conference, FC 2013, Okinawa, Japan, 1–5 April 2013; pp. 6–24. [Google Scholar]
- Fleder, M.; Kester, M.S.; Pillai, S. Bitcoin transaction graph analysis. arXiv 2015, arXiv:1502.01657. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to leak a secret. In Proceedings of the Advances in Cryptology—ASIACRYPT 2001: 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001; pp. 552–565. [Google Scholar]
- Chaum, D.; Van Heyst, E. Group signatures. In Proceedings of the Advances in Cryptology—EUROCRYPT’91: Workshop on the Theory and Application of Cryptographic Techniques, Brighton, UK, 8–11 April 1991; pp. 257–265. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Feldman, P. A practical scheme for non-interactive verifiable secret sharing. In Proceedings of the 28th Annual Symposium on Foundations of Computer Science, Washington, DC, USA, 12–14 October 1987; pp. 427–438. [Google Scholar]
- Bonneau, J.; Narayanan, A.; Miller, A.; Clark, J.; Kroll, J.A.; Felten, E.W. Mixcoin: Anonymity for bitcoin with accountable mixes. In Proceedings of the Financial Cryptography and Data Security: 18th International Conference, FC 2014, Christ Church, Barbados, 3–7 March 2014; pp. 486–504. [Google Scholar]
- Valenta, L.; Rowan, B. Blindcoin: Blinded, accountable mixes for bitcoin. In Proceedings of the Financial Cryptography and Data Security: FC 2015 International Workshops, BITCOIN, WAHC, and Wearable, San Juan, Puerto Rico, 30 January 2015; pp. 112–126. [Google Scholar]
- Ziegeldorf, J.H.; Matzutt, R.; Henze, M.; Grossmann, F.; Wehrle, K. Secure and anonymous decentralized Bitcoin mixing. Future Gener. Comput. Syst. 2018, 80, 448–466. [Google Scholar] [CrossRef]
- Goldwasser, S.; Micali, S.; Rackoff, C. The knowledge complexity of interactive proof-systems. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali; ACM: New York, NY, USA, 2019; pp. 203–225. [Google Scholar]
- Li, B.; Wang, Y. RZKPB: A privacy-preserving blockchain-based fair transaction method for sharing economy. In Proceedings of the 2018 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/12th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 1164–1169. [Google Scholar]
- Haines, T.; Boyen, X. Votor: Conceptually simple remote voting against tiny tyrants. In Proceedings of the Australasian Computer Science Week Multiconference, Canberra, Australia, 2–5 February 2016; pp. 1–13. [Google Scholar]
- Patil, K.; Wasnik, C.T. An ID-based block ring signature system for secret sharing of data. In Proceedings of the 2017 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 5–7 January 2017; pp. 1–5. [Google Scholar]
- Li, X.; Mei, Y.; Gong, J.; Xiang, F.; Sun, Z. A blockchain privacy protection scheme based on ring signature. IEEE Access 2020, 8, 76765–76772. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, J. Flexible threshold ring signature in chronological order for privacy protection in edge computing. IEEE Trans. Cloud Comput. 2020, 10, 1253–1261. [Google Scholar] [CrossRef]
- Lai, C.; Ma, Z.; Guo, R.; Zheng, D. Secure medical data sharing scheme based on traceable ring signature and blockchain. Peer-Netw. Appl. 2022, 15, 1562–1576. [Google Scholar] [CrossRef]
- Samra, B.; Fouzi, S. New efficient certificateless scheme-based conditional privacy preservation authentication for applications in VANET. Veh. Commun. 2022, 34, 100414. [Google Scholar] [CrossRef]
- Cheng, X.; Guo, R.; Cheng, Y. Construction of efficient ring signature scheme with revocation of anonymity. Commun. Eng. Des. Mag. 2015, 36, 857–861. [Google Scholar]
- Mao, M.; Zhou, Z.X. A forward-secure anonymity signature scheme based on ring signature idea. Microcomput. Inf. 2010, 26, 62–63. [Google Scholar]
| Scheme | Scenario | Techniques | Advantages | Drawbacks |
|---|---|---|---|---|
| [21] | Vote | Bilinear Hash Anonymous- channel | Linkable Practical | Relies on trusted center Lack of efficiency analysis |
| [22] | Cloud computing | Bilinear Hash ID-based | Simplified management High efficiency | Relies on trusted center Does not support key revocation and update |
| [23] | Blockchain | ECC Hash | Improves unforgeability Improves anonymity | Lack of efficiency analysis Relies on trusted center |
| [24] | Edge computing | Bilinear Hash Threshold | Flexible Renewable | Relies on trusted center Lack of efficiency comparison of related schemes |
| [25] | Medical sharing | Bilinear Hash DKG | Traceable Controllable | High computational cost |
| [26] | VANET | Bilinear Hash ECC | Traceable High efficiency | Relies on trusted center |
| Notation | Crypto-Operation |
|---|---|
| ECC-based scalar multiplication operation. | |
| ECC-based point addition operation. | |
| Map-to-point operation. | |
| H | One-way hash function operation, which is negligible. |
| M | Multiplication operation. |
| P | Bilinear pair operation. |
| E | Exponential calculation time. |
| Cryptography Operation | ||||||
|---|---|---|---|---|---|---|
| Execution time (ms) | 1.7090 | 0.0075 | 4.406 | 0.042 | 5.071 | 8.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Peng, C.; Tan, W. Secure Ring Signature Scheme for Privacy-Preserving Blockchain. Entropy 2023, 25, 1334. https://doi.org/10.3390/e25091334
Wang L, Peng C, Tan W. Secure Ring Signature Scheme for Privacy-Preserving Blockchain. Entropy. 2023; 25(9):1334. https://doi.org/10.3390/e25091334
Chicago/Turabian StyleWang, Lin, Changgen Peng, and Weijie Tan. 2023. "Secure Ring Signature Scheme for Privacy-Preserving Blockchain" Entropy 25, no. 9: 1334. https://doi.org/10.3390/e25091334
APA StyleWang, L., Peng, C., & Tan, W. (2023). Secure Ring Signature Scheme for Privacy-Preserving Blockchain. Entropy, 25(9), 1334. https://doi.org/10.3390/e25091334








