Nonequilibrium Thermodynamics of the Majority Vote Model
Abstract
:1. Introduction
2. Majority Vote Model and Phase Transition Behavior
2.1. Entropy Production
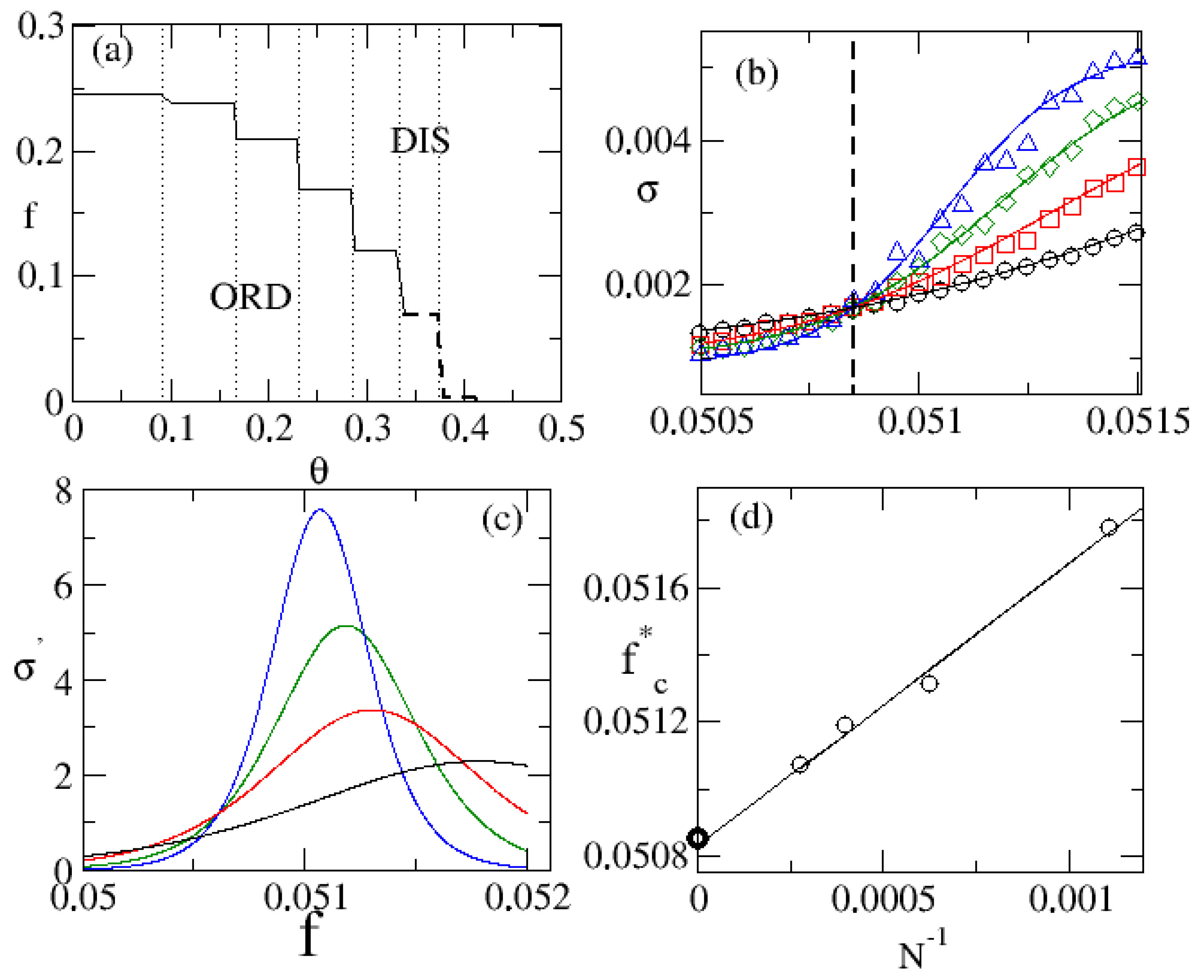
2.2. Overview about Phase Transitions and Finite-Size Scaling
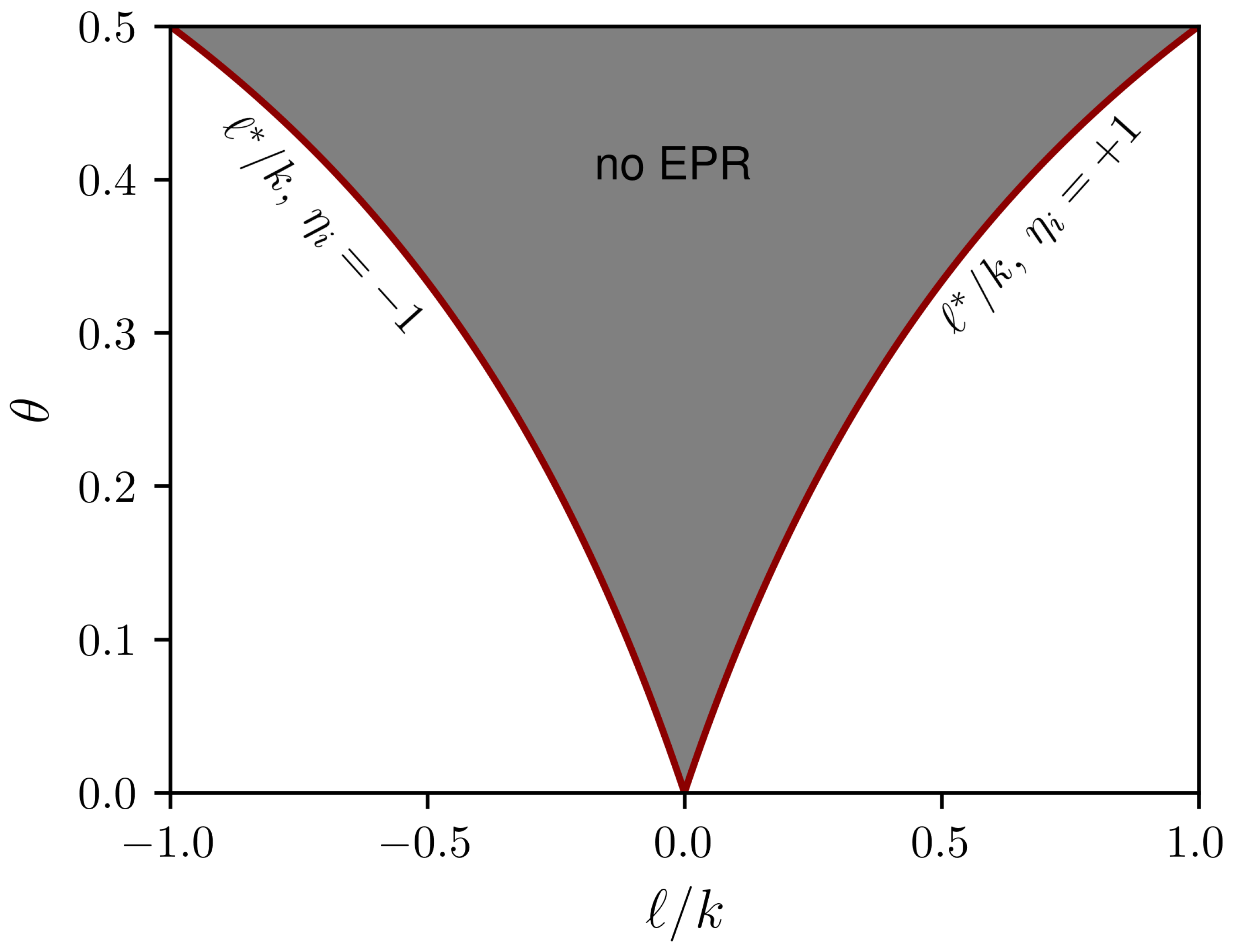
2.3. Discontinuous Phase Transitions in Complex Topologies
3. Thermodynamics of the Majority Vote Model
3.1. General Features
3.2. Fluctuation Theorems
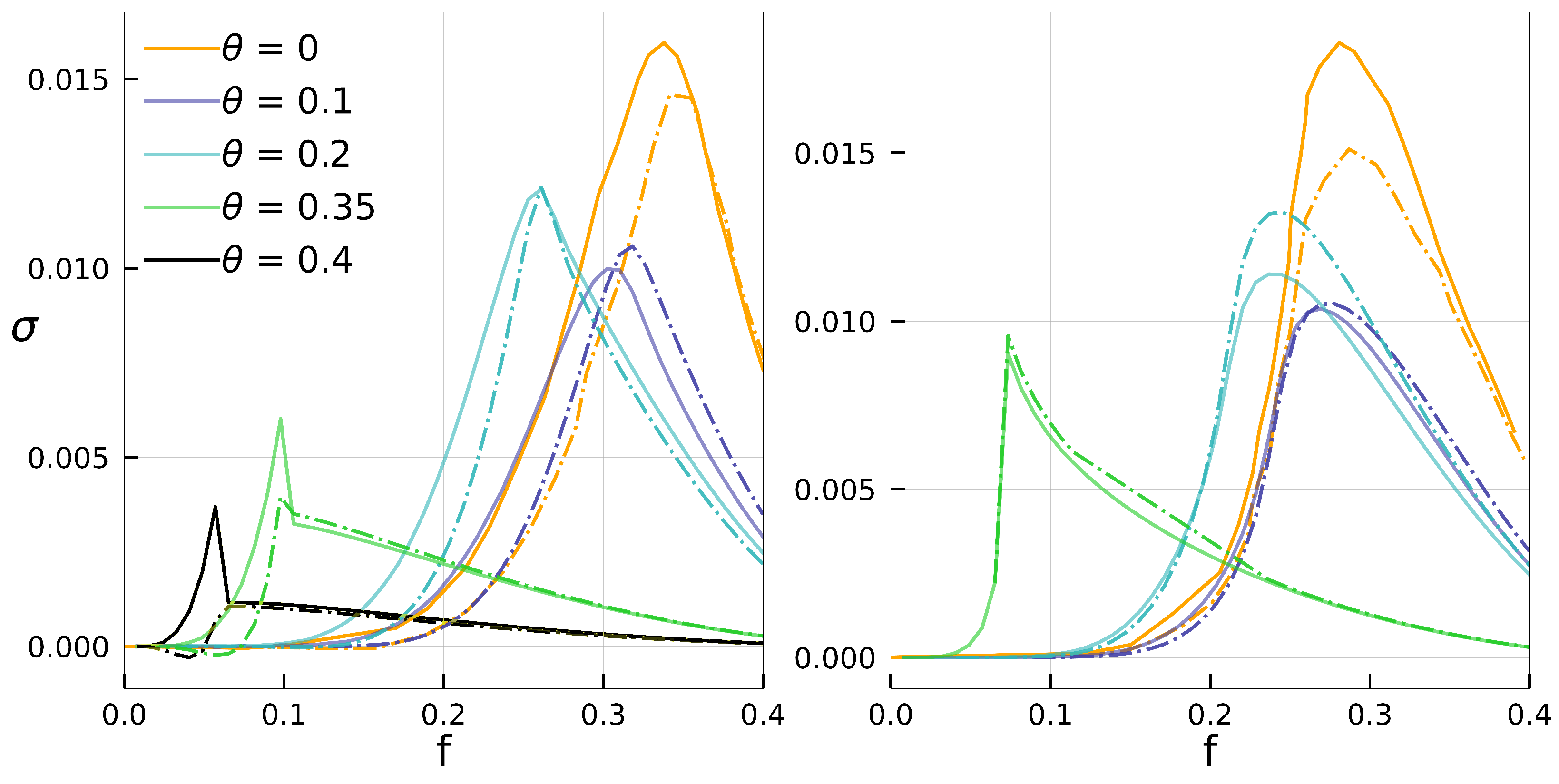
3.3. Heat Fluxes at Phase Transitions
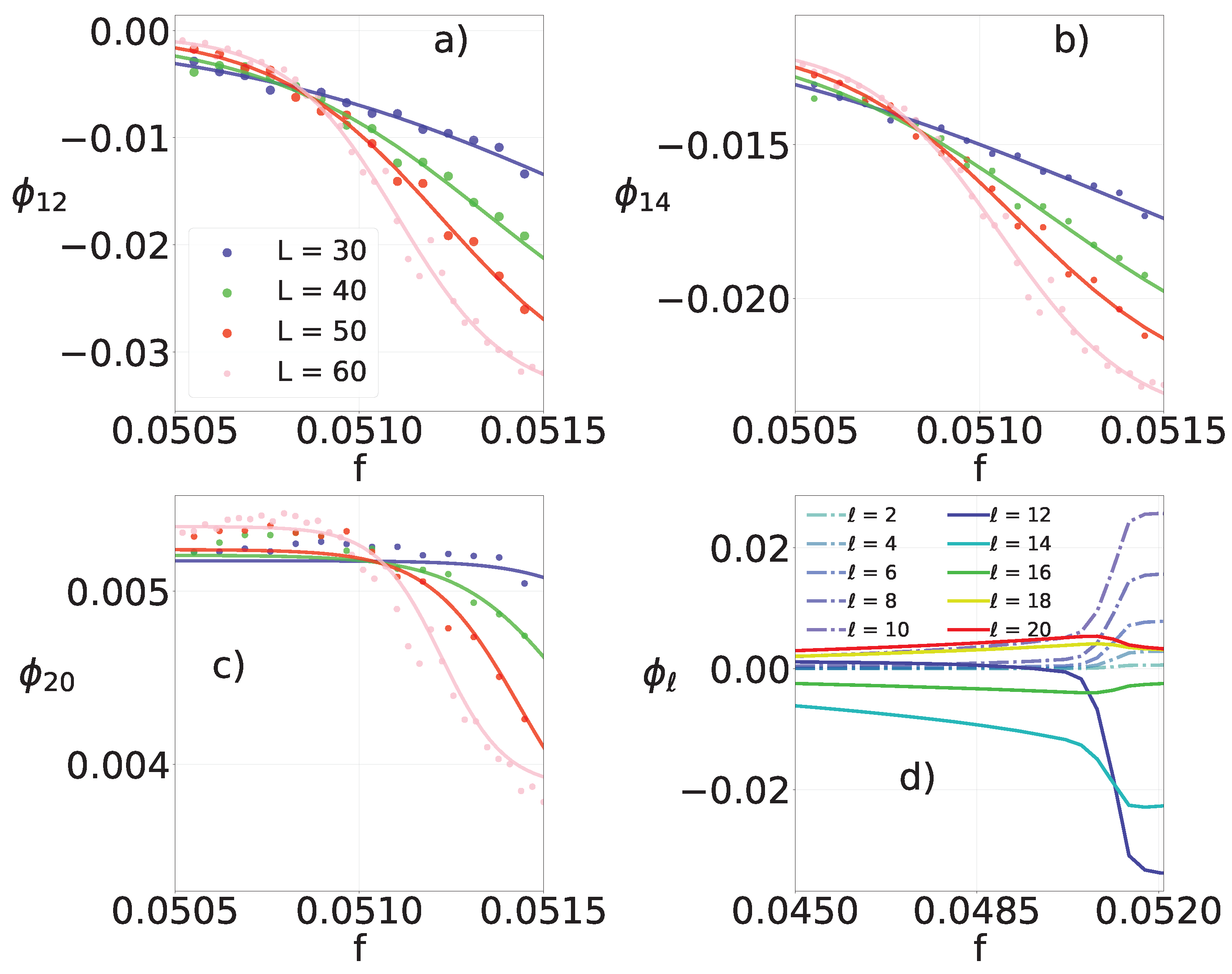
3.4. Contributions to Dissipation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591. [Google Scholar] [CrossRef]
- de Oliveira, M.J. Isotropic majority-vote model on a square lattice. J. Stat. Phys. 1992, 66, 273–281. [Google Scholar] [CrossRef]
- Pereira, L.F.; Moreira, F.B. Majority-vote model on random graphs. Phys. Rev. E 2005, 71, 016123. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Shen, C.; He, G.; Zhang, H.; Hou, Z. Critical noise of majority-vote model on complex networks. Phys. Rev. E 2015, 91, 022816. [Google Scholar] [CrossRef]
- Vieira, A.R.; Crokidakis, N. Phase transitions in the majority-vote model with two types of noises. Phys. A Stat. Mech. Its Appl. 2016, 450, 30–36. [Google Scholar] [CrossRef]
- Encinas, J.; Chen, H.; de Oliveira, M.M.; Fiore, C.E. Majority vote model with ancillary noise in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 516, 563–570. [Google Scholar] [CrossRef]
- Brunstein, A.; Tomé, T. Universal behavior in an irreversible model with C3v symmetry. Phys. Rev. E 1999, 60, 3666–3669. [Google Scholar] [CrossRef]
- Chen, H.; Shen, C.; Zhang, H.; Li, G.; Hou, Z.; Kurths, J. First-order phase transition in a majority-vote model with inertia. Phys. Rev. E 2017, 95, 042304. [Google Scholar] [CrossRef]
- Harunari, P.E.; de Oliveira, M.; Fiore, C.E. Partial inertia induces additional phase transition in the majority vote model. Phys. Rev. E 2017, 96, 042305. [Google Scholar] [CrossRef]
- Encinas, J.M.; Harunari, P.E.; de Oliveira, M.; Fiore, C.E. Fundamental ingredients for discontinuous phase transitions in the inertial majority vote model. Sci. Rep. 2018, 8, 9338. [Google Scholar] [CrossRef]
- Encinas, J.M.; Fiore, C.E. Influence of distinct kinds of temporal disorder in discontinuous phase transitions. Phys. Rev. E 2021, 103, 032124. [Google Scholar] [CrossRef] [PubMed]
- Crochik, L.; Tomé, T. Entropy production in the majority-vote model. Phys. Rev. E 2005, 72, 057103. [Google Scholar] [CrossRef] [PubMed]
- Noa, C.F.; Harunari, P.E.; de Oliveira, M.; Fiore, C. Entropy production as a tool for characterizing nonequilibrium phase transitions. Phys. Rev. E 2019, 100, 012104. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Entropy production in irreversible systems described by a Fokker-Planck equation. Phys. Rev. E 2010, 82, 021120. [Google Scholar] [CrossRef]
- Esposito, M. Stochastic thermodynamics under coarse graining. Phys. Rev. E 2012, 85, 041125. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Tomé, T.; de Oliveira, M.J. Stochastic approach to equilibrium and nonequilibrium thermodynamics. Phys. Rev. E 2015, 91, 042140. [Google Scholar] [CrossRef]
- Schnakenberg, J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys. 1976, 48, 571. [Google Scholar] [CrossRef]
- Tomé, T.; Fiore, C.E.; de Oliveira, M.J. Stochastic thermodynamics of opinion dynamics. Phys. Rev. E 2023, 107, 064135. [Google Scholar] [CrossRef]
- Landau, D.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Fiore, C.E.; Carneiro, C.E.I. Obtaining pressure versus concentration phase diagrams in spin systems from Monte Carlo simulations. Phys. Rev. E 2008, 76, 021118. [Google Scholar] [CrossRef]
- de Oliveira, M.M.; da Luz, M.G.E.; Fiore, C.E. Generic finite size scaling for discontinuous nonequilibrium phase transitions into absorbing states. Phys. Rev. E 2015, 92, 062126. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, M.M.; da Luz, M.G.E.; Fiore, C.E. Finite-size scaling for discontinuous nonequilibrium phase transitions. Phys. Rev. E 2018, 97, 060101. [Google Scholar] [CrossRef] [PubMed]
- Goes, B.O.; Fiore, C.E.; Landi, G.T. Quantum features of entropy production in driven-dissipative transitions. Phys. Rev. Res. 2020, 2, 013136. [Google Scholar] [CrossRef]
- Seara, D.S.; Machta, B.B.; Murrell, M.P. Irreversibility in dynamical phases and transitions. Nat. Commun. 2021, 12, 392. [Google Scholar] [CrossRef] [PubMed]
- Martynec, T.; Klapp, S.H.; Loos, S.A. Entropy production at criticality in a nonequilibrium Potts model. New J. Phys. 2020, 22, 093069. [Google Scholar] [CrossRef]
- Aguilera, M.; Moosavi, S.A.; Shimazaki, H. A unifying framework for mean-field theories of asymmetric kinetic Ising systems. Nat. Commun. 2021, 12, 1197. [Google Scholar] [CrossRef]
- Hanggi, P.; Grabert, H.; Talkner, P.; Thomas, H. Bistable systems: Master equation versus Fokker-Planck modeling. Phys. Rev. A 1984, 29, 371. [Google Scholar] [CrossRef]
- Fiore, C.E.; Harunari, P.E.; Noa, C.E.F.; Landi, G.T. Current fluctuations in nonequilibrium discontinuous phase transitions. Phys. Rev. E 2021, 104, 064123. [Google Scholar] [CrossRef]
- Nguyen, B.; Seifert, U. Exponential volume dependence of entropy-current fluctuations at first-order phase transitions in chemical reaction networks. Phys. Rev. E 2020, 102, 022101. [Google Scholar] [CrossRef]
- Herpich, T.; Thingna, J.; Esposito, M. Collective Power: Minimal Model for Thermodynamics of Nonequilibrium Phase Transitions. Phys. Rev. X 2018, 8, 031056. [Google Scholar] [CrossRef]
- Van den Broeck, C.; Esposito, M. Ensemble and trajectory thermodynamics: A brief introduction. Phys. A Stat. Mech. Its Appl. 2015, 418, 6–16. [Google Scholar] [CrossRef]
- Yeomans, J.M. Statistical Mechanics of Phase Transitions; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hawthorne, F.; Harunari, P.E.; de Oliveira, M.J.; Fiore, C.E. Nonequilibrium Thermodynamics of the Majority Vote Model. Entropy 2023, 25, 1230. https://doi.org/10.3390/e25081230
Hawthorne F, Harunari PE, de Oliveira MJ, Fiore CE. Nonequilibrium Thermodynamics of the Majority Vote Model. Entropy. 2023; 25(8):1230. https://doi.org/10.3390/e25081230
Chicago/Turabian StyleHawthorne, Felipe, Pedro E. Harunari, Mário J. de Oliveira, and Carlos E. Fiore. 2023. "Nonequilibrium Thermodynamics of the Majority Vote Model" Entropy 25, no. 8: 1230. https://doi.org/10.3390/e25081230
APA StyleHawthorne, F., Harunari, P. E., de Oliveira, M. J., & Fiore, C. E. (2023). Nonequilibrium Thermodynamics of the Majority Vote Model. Entropy, 25(8), 1230. https://doi.org/10.3390/e25081230





