Distances in Higher-Order Networks and the Metric Structure of Hypergraphs
Abstract
1. Introduction
- (1)
- If one assigns weights to hyperedges as proper functions of their sizes, then the distance between a couple of nodes is the sum of the weights of all hyperedges in the shortest path, i.e.,where is the set of paths between s and t and is the weight of the hyperedge e of size . The heuristics behind this definition come from social networks: if one assumes that the size of each hyperedge is the size of a company of friends, then when the company size grows, it becomes more difficult for the members of the network to keep in touch with each other. This idea was used in Refs. [7,14], where the authors define hypergraph random walks, arguing that “the walkers may give more or less importance to hyperedges depending on their size”.
- (2)
2. Methods
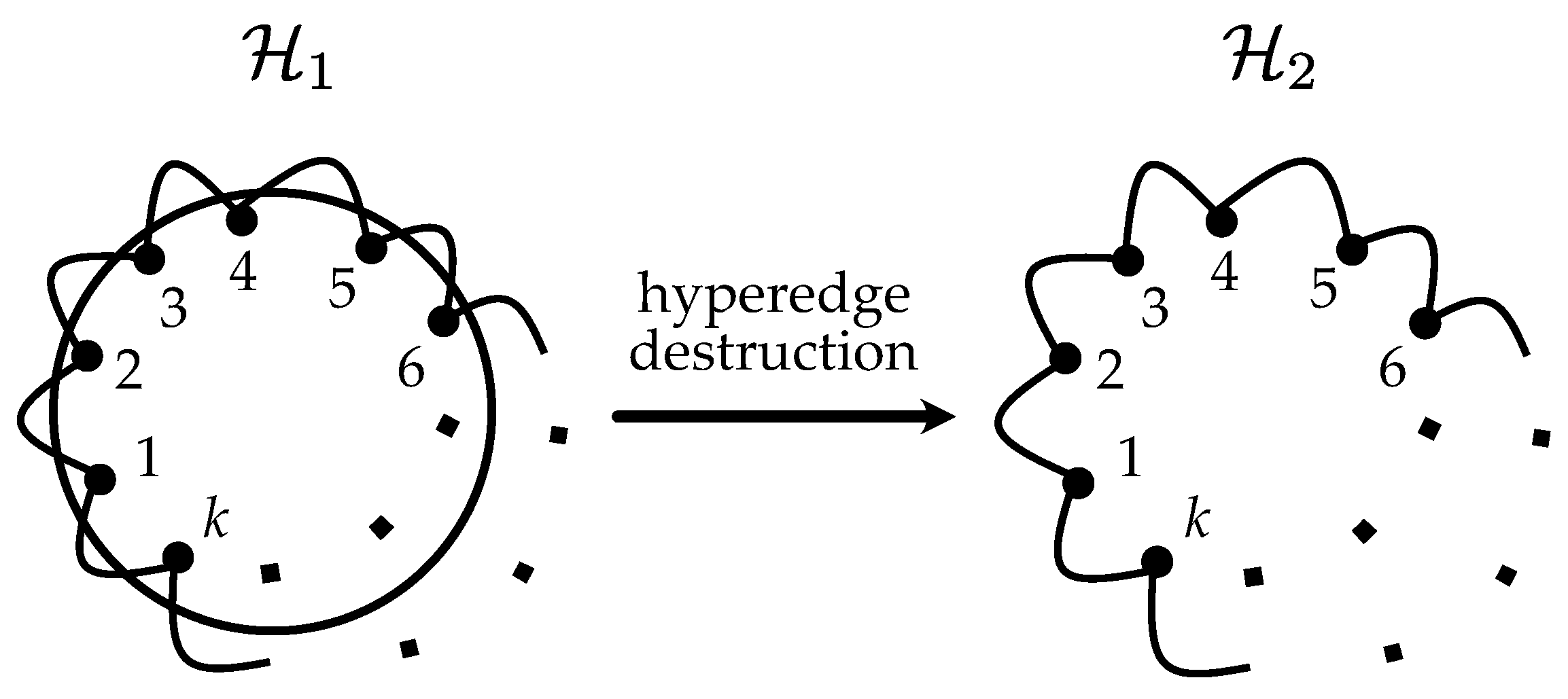
2.1. Weighted Linegraphs
- The distance between the nodes obtained from Formula (2) must be the same as the classic distance in a graph at all times that one considers a (dyadic) complex network as a hypergraph.
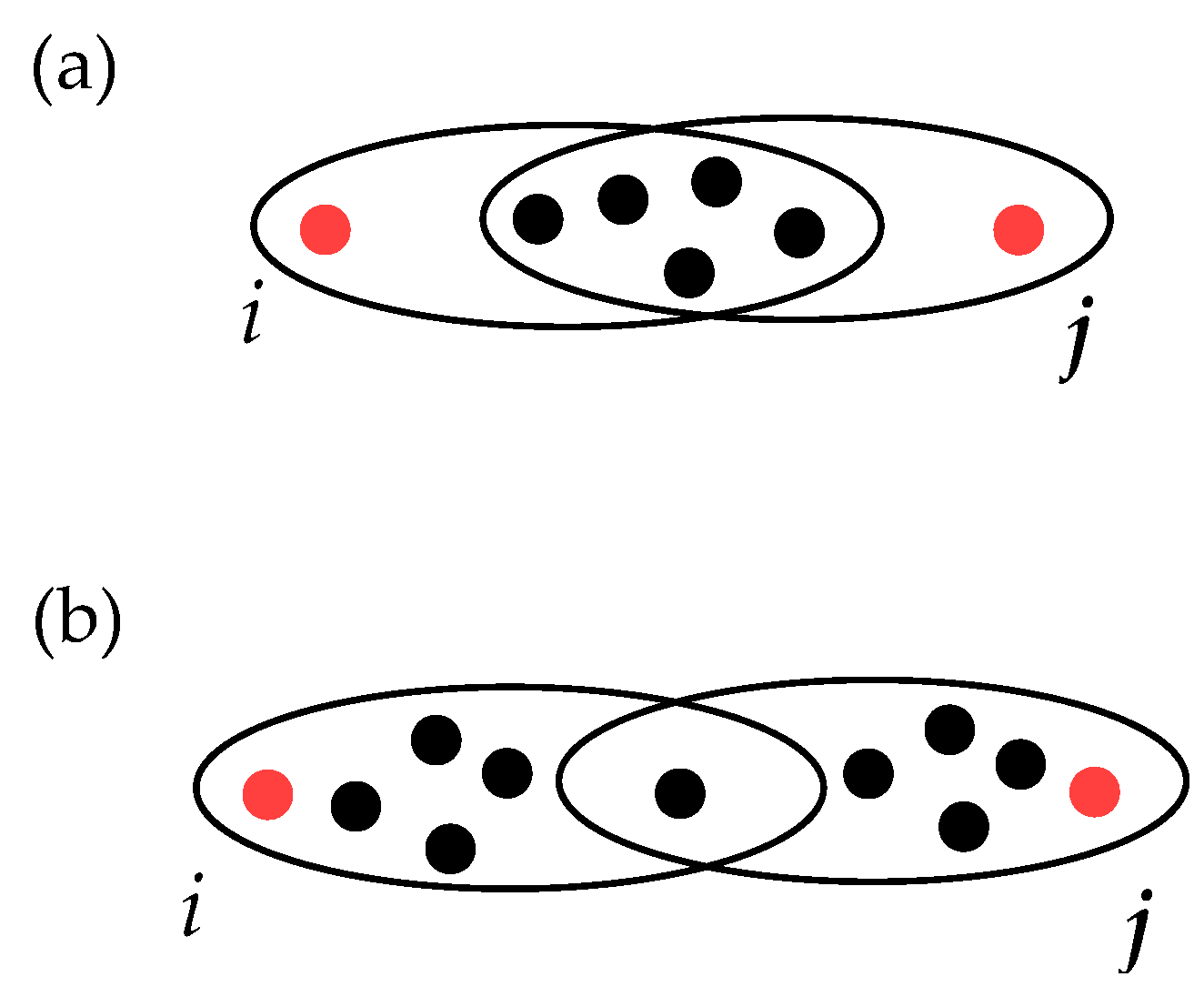
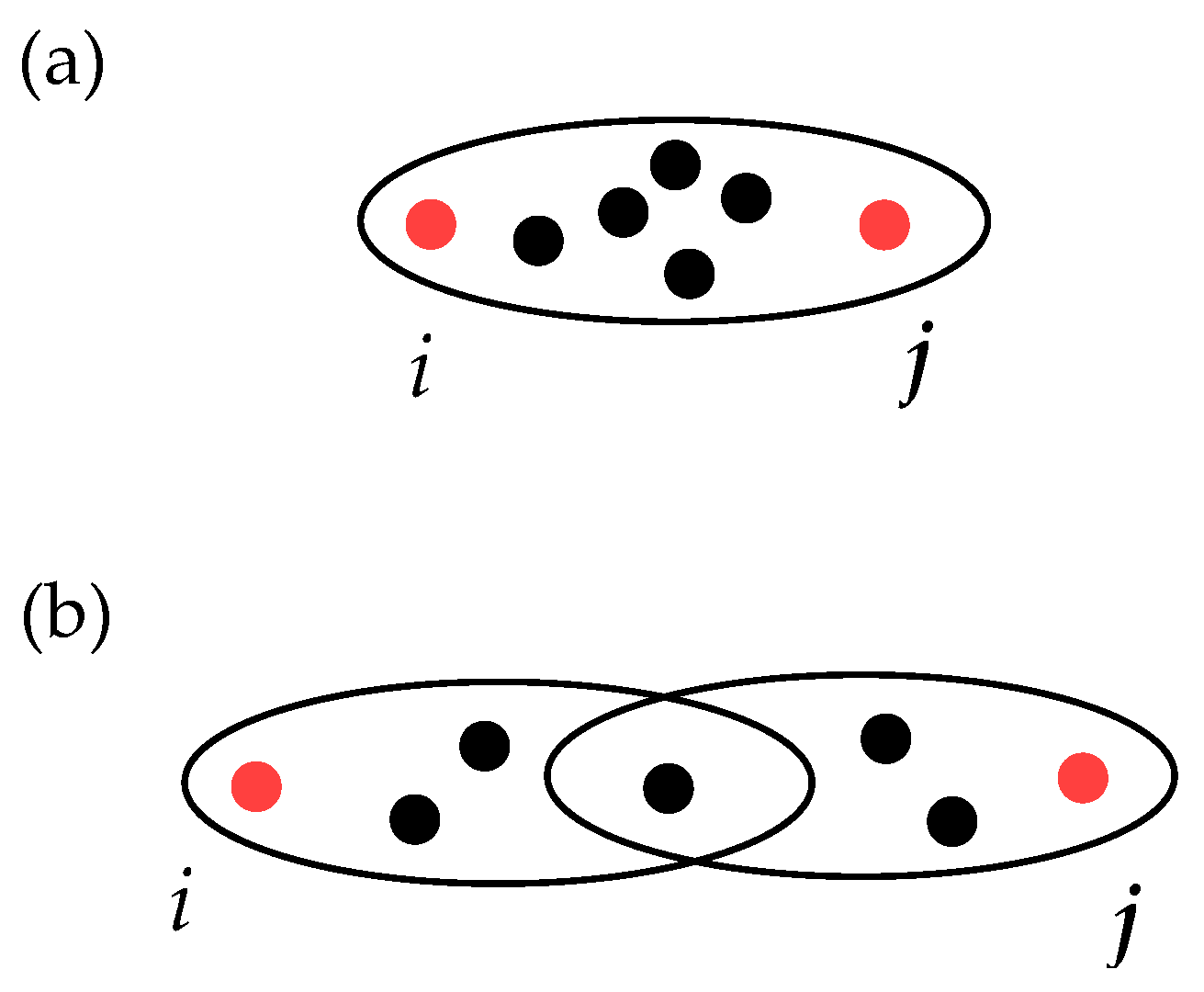
- The bigger the intersection of the hyperedges, the smaller the distance should be. For instance, if one considers the case illustrated in Figure 3, then the weighted distance between i and j in panel (a) should be smaller than that in panel (b). Therefore, the distance should be inversely proportional to the intersection size.
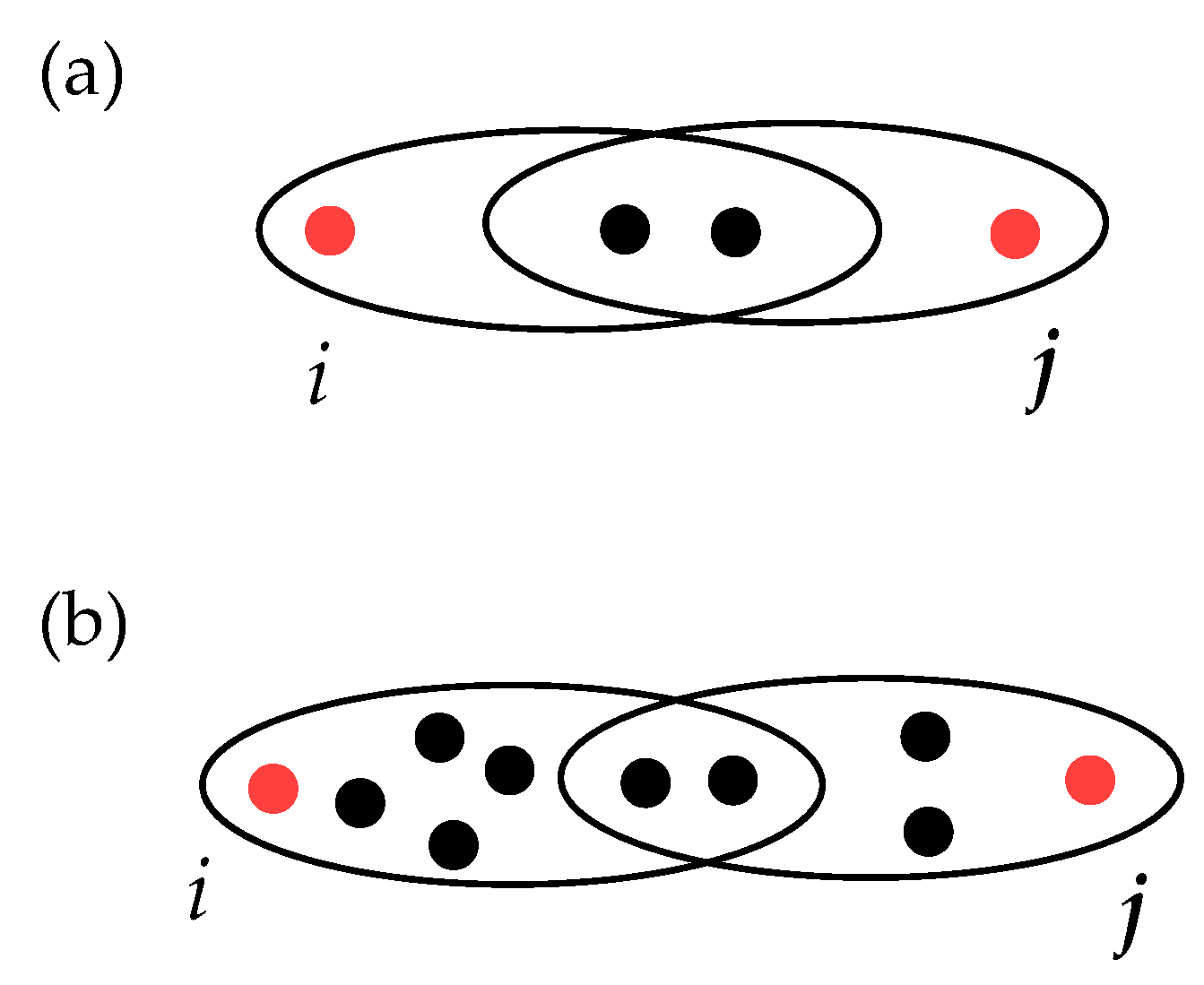
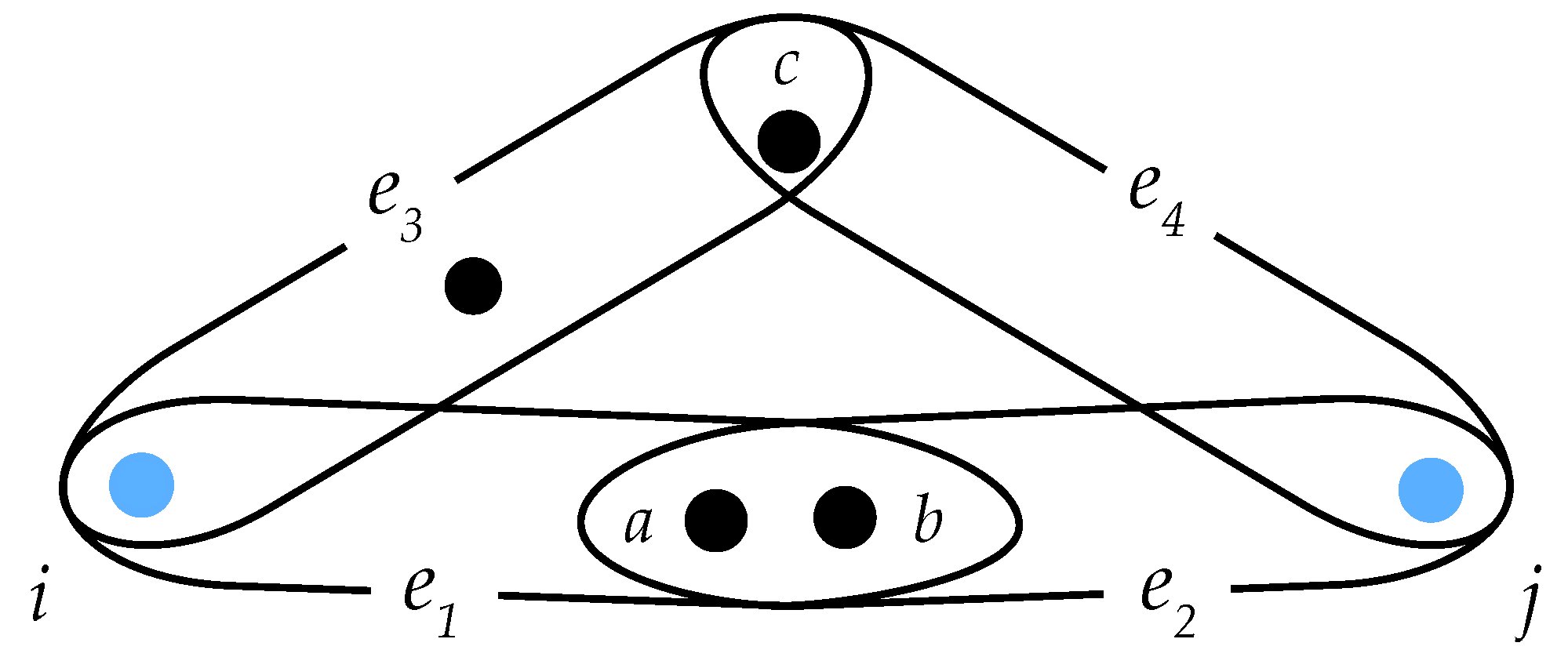
- The bigger the hyperedges involved, the larger the weighted distance should be. In particular, taking as an illustrative example the case of Figure 4, the weighted distance in panel (b) should be larger than that in panel (a) since the sizes of edges are bigger in case (b), while the size of the intersection is the same.
- Finally, the larger is the number of hyperedges involved in the path, the larger weighed distances one should obtain. In other words, the new metric structure should be sensitive to the number of hyperedges in the paths considered. In particular, if one takes two paths, one with only one hyperedge and another with two hyperedges but with the same number of nodes involved in both cases, then the path length should be smaller in the first case (see the illustration in Figure 5, where panel (b) must give a larger distance with respect to the case of panel (a)).
- As the Jaccard index [23] between and is given by , then
- If one takes , then . Furthermore, if one starts from a (dyadic) network , then for every , and if (but connected with in L), then and , which make that . Hence, one has that for this choice of weight function, the distance between the nodes obtained from formula (2) is the same as the classic distance in a graph (first desired property).
- Properties 2–4 also hold for this choice of weight function.
2.2. Some Structural Measures
3. Results
3.1. Synthetic Examples
3.2. Real World Examples
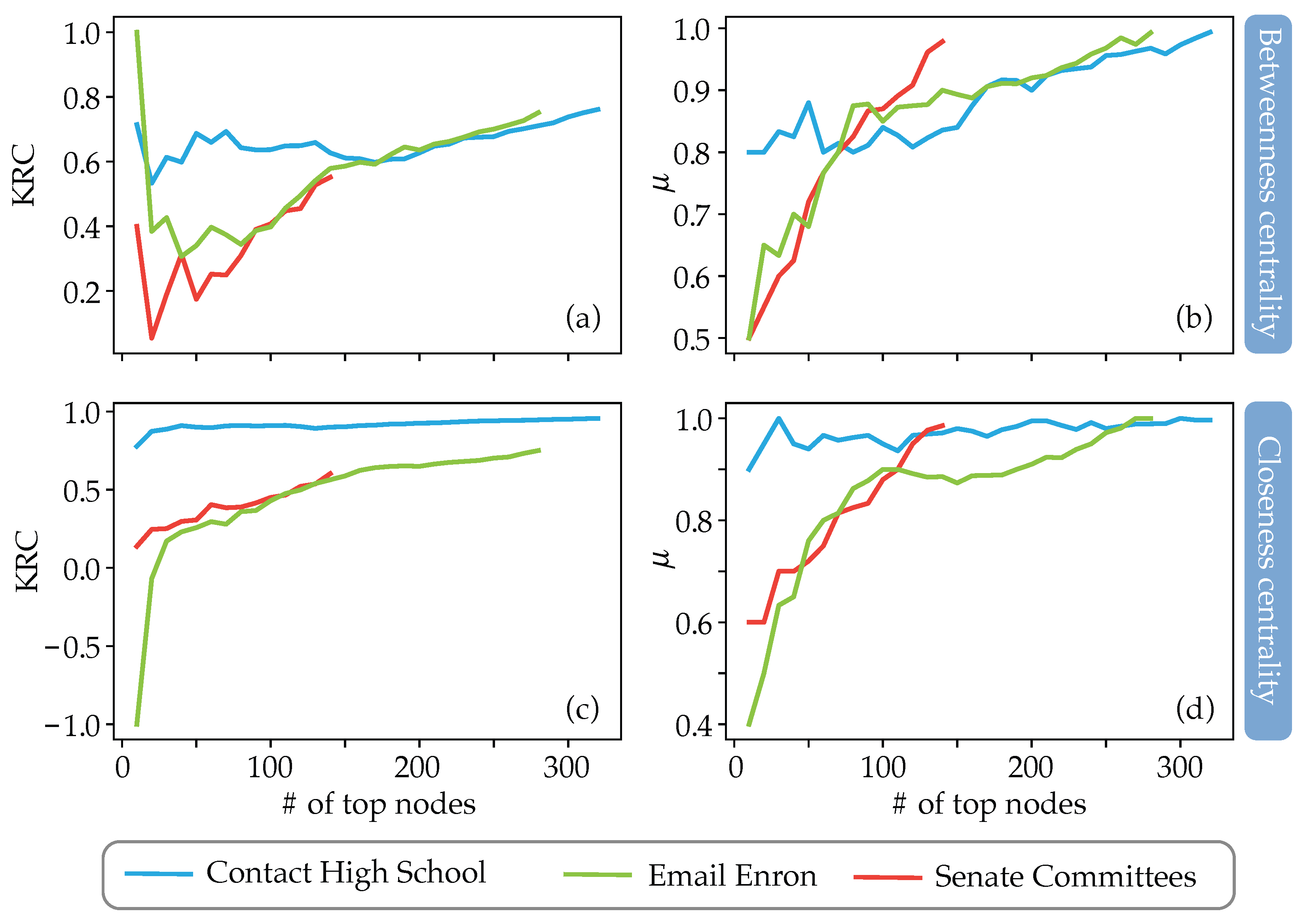
- 1.
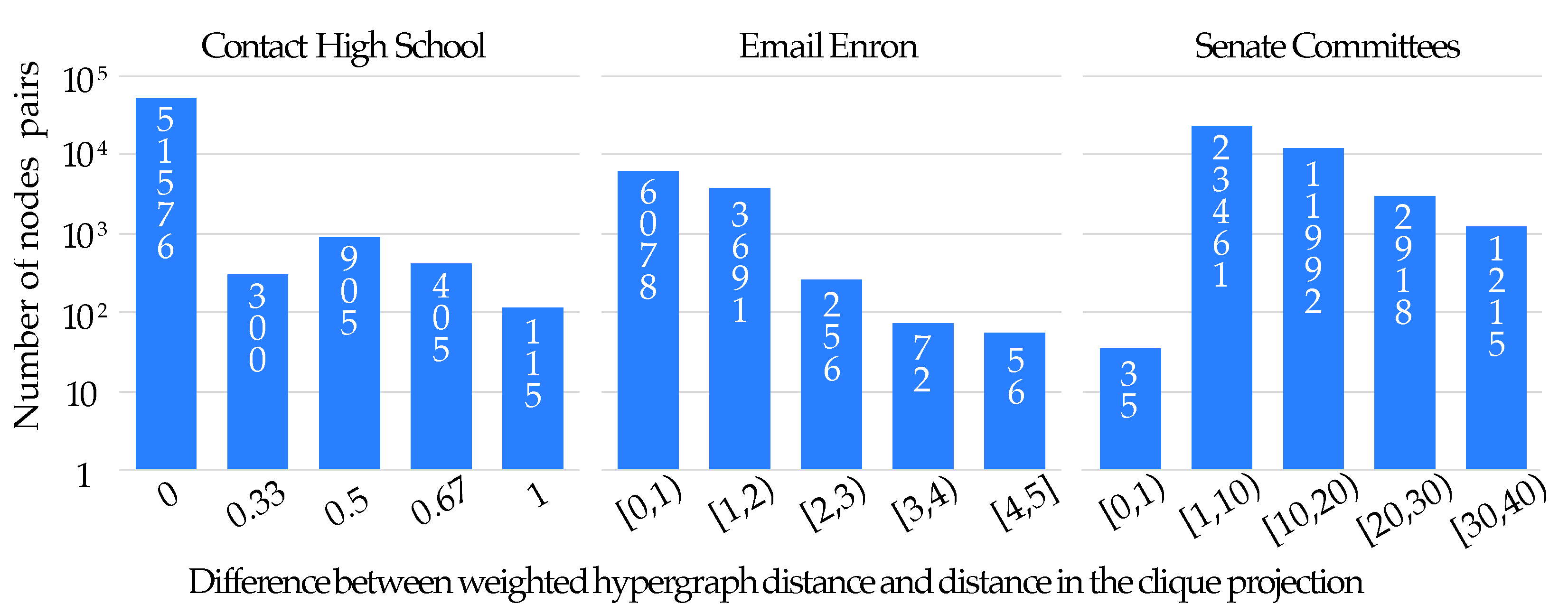
- In the Contact High School hypergraph, the difference in rankings is significantly less considerable than that occurring in the other two hypergraphs, especially for the case of closeness centrality;
- 2.
- The sets of the first 50 top nodes for the cases of the Email Enron and Senate Committees hypergraphs are significantly different when one uses the traditional distance measure and our measure for both betweenness and closeness centralities (see Figure 9b,d);
- 3.
- The KRC coefficient is low in the case of betweenness centralities, even for the case of the Contact High School hypergraph (see Figure 9a);
- 4.
- The KRC coefficient for the case of closeness centrality is low for the Email Enron and Senate Committees hypergraphs (see Figure 9c), being even negative for the case of the Email Enron graph.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Battiston, F.; Cencetti, G.; Iacopini, I.; Latora, V.; Lucas, M.; Patania, A.; Young, J.G.; Petri, G. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 2020, 874, 1–92. [Google Scholar] [CrossRef]
- Boccaletti, S.; De Lellis, P.; del Genio, C.I.; Alfaro-Bittner, K.; Criado, R.; Jalan, S.; Romance, M. The structure and dynamics of networks with higher order interactions. Phys. Rep. 2023, 1018, 1–64. [Google Scholar] [CrossRef]
- Benson, A.R. Three hypergraph eigenvector centralities. SIAM J. Math. Data Sci. 2019, 1, 293–312. [Google Scholar] [CrossRef]
- Carletti, T.; Battiston, F.; Cencetti, G.; Fanelli, D. Random walks on hypergraphs. Phys. Rev. E 2020, 101, 022308. [Google Scholar] [CrossRef] [PubMed]
- Aksoy, S.G.; Joslyn, C.; Marrero, C.O.; Praggastis, B.; Purvine, E. Hypernetwork science via high-order hypergraph walks. EPJ Data Sci. 2020, 9, 16. [Google Scholar] [CrossRef]
- Tudisco, F.; Higham, D.J. Node and edge nonlinear eigenvector centrality for hypergraphs. Commun. Phys. 2021, 4, 201. [Google Scholar] [CrossRef]
- Chodrow, P.S.; Veldt, N.; Benson, A.R. Generative hypergraph clustering: From blockmodels to modularity. Sci. Adv. 2021, 7, eabh1303. [Google Scholar] [CrossRef]
- Kovalenko, K.; Romance, M.; Vasilyeva, E.; Aleja, D.; Criado, R.; Musatov, D.; Raigorodskii, A.M.; Flores, J.; Samoylenko, I.; Alfaro-Bittner, K.; et al. Vector centrality in hypergraphs. Chaos Solitons Fractals 2022, 162, 112397. [Google Scholar] [CrossRef]
- Maletić, S.; Rajković, M.; Vasiljević, D. Simplicial Complexes of Networks and Their Statistical Properties. In Proceedings of the Computational Science—ICCS 2008, Kraków, Poland, 23–25 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 568–575. [Google Scholar]
- Lu, L.; Peng, X. High-ordered random walks and generalized Laplacians on hypergraphs. In Proceedings of the International Workshop on Algorithms and Models for the Web-Graph, Atlanta, GA, USA, 27–29 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 14–25. [Google Scholar]
- Carletti, T.; Fanelli, D.; Lambiotte, R. Random walks and community detection in hypergraphs. J. Phys. Complex. 2021, 2, 015011. [Google Scholar] [CrossRef]
- Konstantinova, E.V.; Skorobogatov, V.A. Application of hypergraph theory in chemistry. Discret. Math. 2001, 235, 365–383. [Google Scholar] [CrossRef]
- Estrada, E.; Rodríguez-Velázquez, J.A. Subgraph centrality and clustering in complex hyper-networks. Phys. A Stat. Mech. Its Appl. 2006, 364, 581–594. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, J.; Schölkopf, B. Learning with hypergraphs: Clustering, classification, and embedding. Adv. Neural Inf. Process. Syst. 2006, 19, 1601–1608. [Google Scholar]
- Puzis, R.; Purohit, M.; Subrahmanian, V. Betweenness computation in the single graph representation of hypergraphs. Soc. Netw. 2013, 35, 561–572. [Google Scholar] [CrossRef]
- Gao, J.; Zhao, Q.; Ren, W.; Swami, A.; Ramanathan, R.; Bar-Noy, A. Dynamic shortest path algorithms for hypergraphs. IEEE/ACM Trans. Netw. 2014, 23, 1805–1817. [Google Scholar] [CrossRef]
- Shun, J. Practical parallel hypergraph algorithms. In Proceedings of the 25th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, San Diego, CA, USA, 22–26 February 2020; pp. 232–249. [Google Scholar]
- Lee, J.; Lee, Y.; Oh, S.M.; Kahng, B. Betweenness centrality of teams in social networks. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 061108. [Google Scholar] [CrossRef]
- Behague, N.C.; Bonato, A.; Huggan, M.A.; Malik, R.; Marbach, T.G. The iterated local transitivity model for hypergraphs. arXiv 2021, arXiv:2101.12560. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone. 1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Fredman, M.L.; Tarjan, R.E. Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms. J. ACM 1987, 34, 596–615. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Casablanca, R.M.; Criado, R.; Mesa, J.A.; Romance, M. A comprehensive approach for discrete resilience of complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 013111. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Benson, A.R.; Abebe, R.; Schaub, M.T.; Jadbabaie, A.; Kleinberg, J. Simplicial closure and higher-order link prediction. Proc. Natl. Acad. Sci. USA 2018, 115, E11221–E11230. [Google Scholar] [CrossRef] [PubMed]
- Mastrandrea, R.; Fournet, J.; Barrat, A. Contact Patterns in a High School: A Comparison between Data Collected Using Wearable Sensors, Contact Diaries and Friendship Surveys. PLoS ONE 2015, 10, e0136497. [Google Scholar] [CrossRef] [PubMed]
- Stewart, C., III; Woon, J. Congressional Committee Assignments, 103rd to 114th Congresses, 1993–2017: Senate. Available online: http://web.mit.edu/17.251/www/data_page.html (accessed on 11 June 2023).
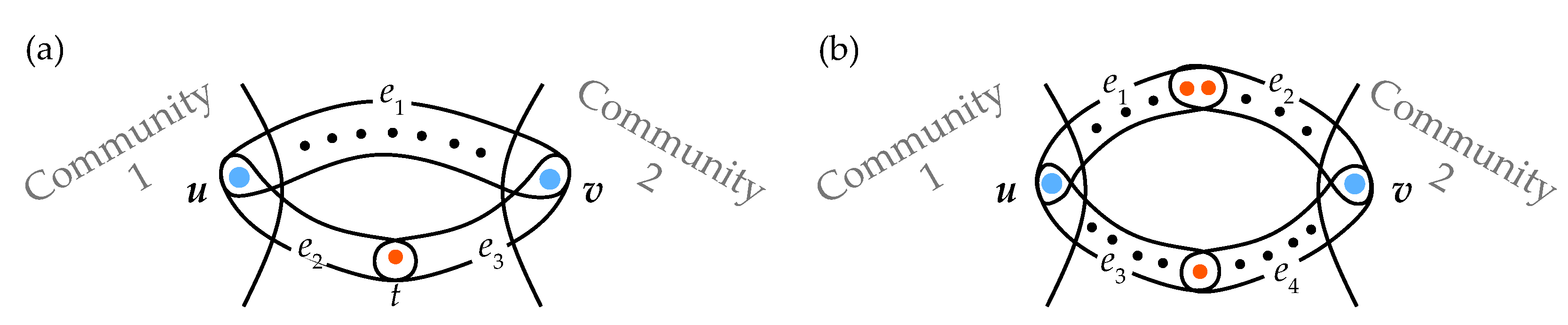
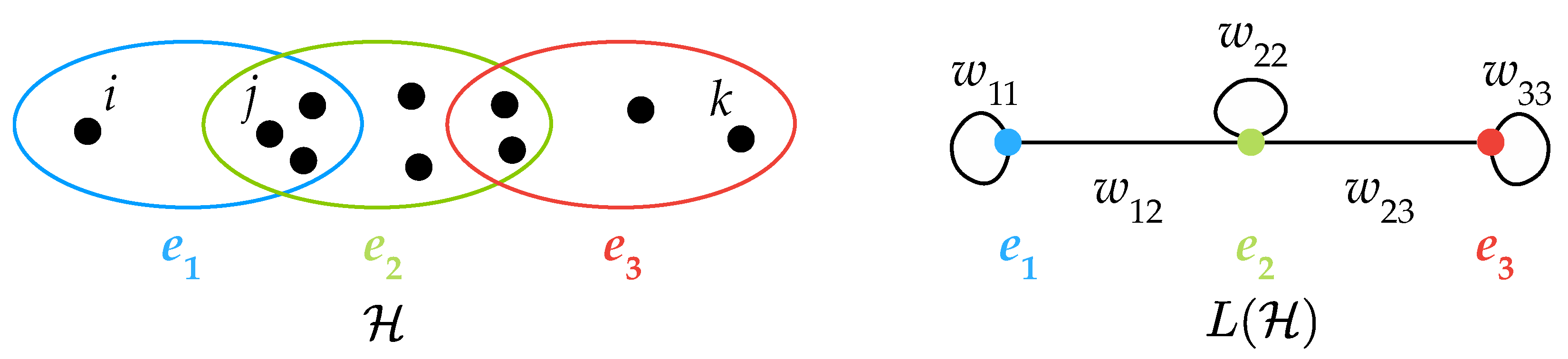
| 0.311 | 1 | |
| 0.303 | 0.303 |
| High School | Email Enron | Senate Committees | |
|---|---|---|---|
| Number of nodes | 327 | 143 | 282 |
| Number of unique hyperedges | 7818 | 1457 | 315 |
| Maximal hyperedge size | 5 | 18 | 31 |
| Minimal hyperedge size | 2 | 2 | 4 |
| Mean hyperedge size | 2.3 | 3.1 | 17.2 |
| Median hyperedge size | 2 | 2 | 19 |
| Contact High School | Email Enron | Senate Committees | |
|---|---|---|---|
| 0.505 | 0.443 | 0.106 | |
| 0.510 | 0.546 | 0.670 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilyeva, E.; Romance, M.; Samoylenko, I.; Kovalenko, K.; Musatov, D.; Raigorodskii, A.M.; Boccaletti, S. Distances in Higher-Order Networks and the Metric Structure of Hypergraphs. Entropy 2023, 25, 923. https://doi.org/10.3390/e25060923
Vasilyeva E, Romance M, Samoylenko I, Kovalenko K, Musatov D, Raigorodskii AM, Boccaletti S. Distances in Higher-Order Networks and the Metric Structure of Hypergraphs. Entropy. 2023; 25(6):923. https://doi.org/10.3390/e25060923
Chicago/Turabian StyleVasilyeva, Ekaterina, Miguel Romance, Ivan Samoylenko, Kirill Kovalenko, Daniil Musatov, Andrey Mihailovich Raigorodskii, and Stefano Boccaletti. 2023. "Distances in Higher-Order Networks and the Metric Structure of Hypergraphs" Entropy 25, no. 6: 923. https://doi.org/10.3390/e25060923
APA StyleVasilyeva, E., Romance, M., Samoylenko, I., Kovalenko, K., Musatov, D., Raigorodskii, A. M., & Boccaletti, S. (2023). Distances in Higher-Order Networks and the Metric Structure of Hypergraphs. Entropy, 25(6), 923. https://doi.org/10.3390/e25060923






