Ancilla-Assisted Generation of Photons from Vacuum via Time-Modulation of Extracavity Qubit
Abstract
1. Introduction
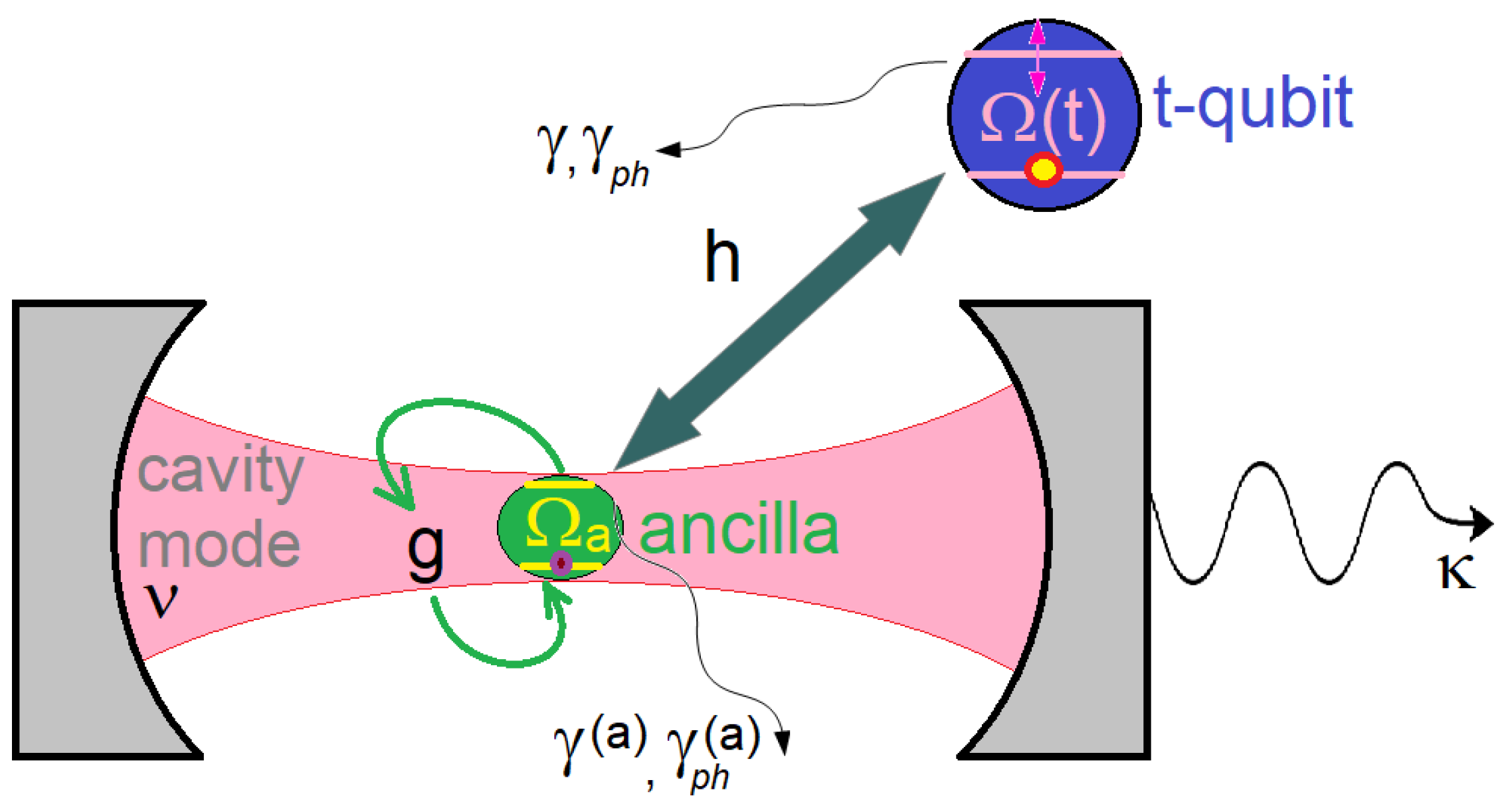
2. Mathematical Formulation
3. Analytic Description
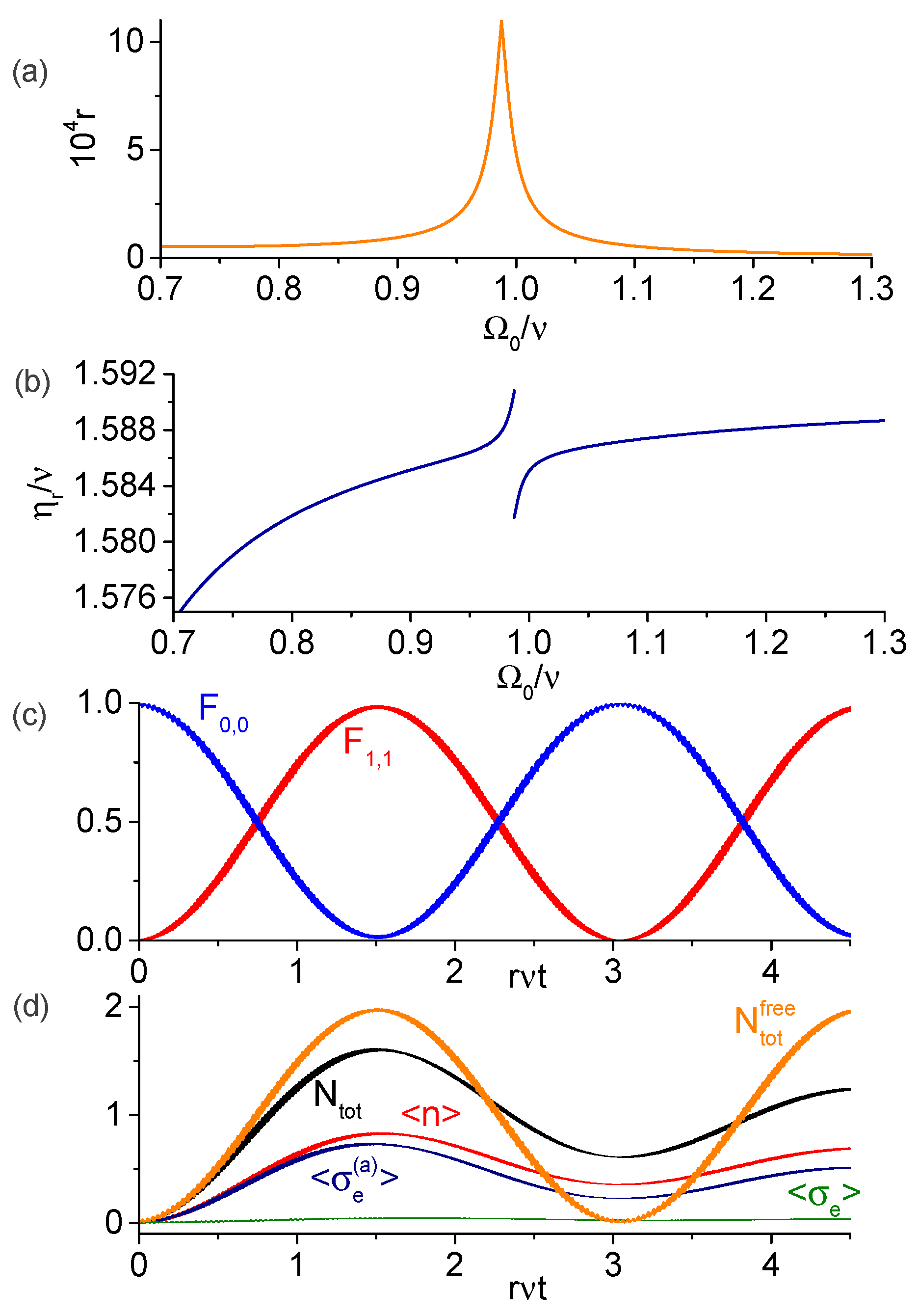
3.1. Spectrum Far from Degeneracies
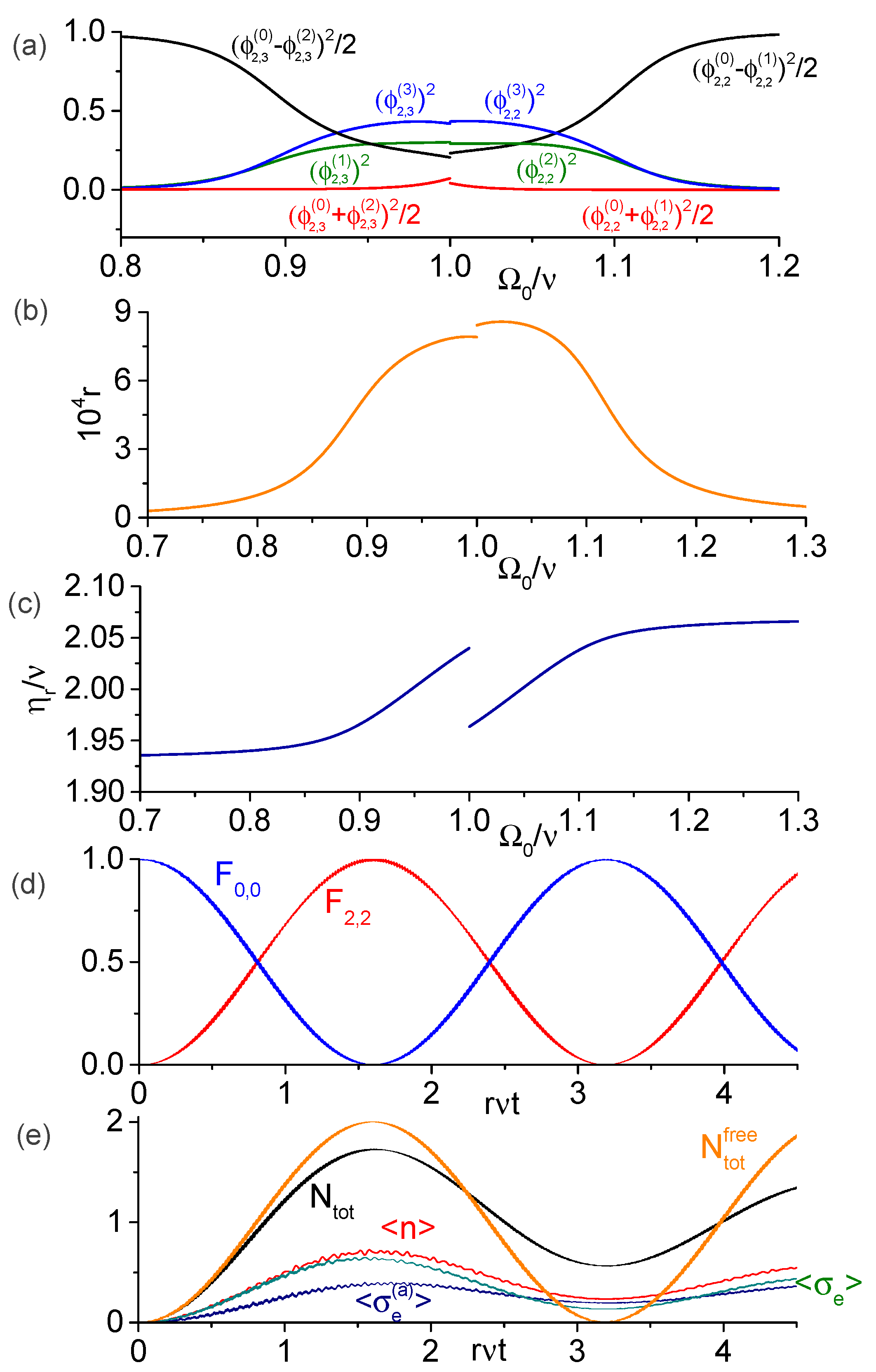
3.2. Spectrum near Degeneracies
3.3. Dynamics in the Dressed-Basis
4. Numeric Results and Discussion
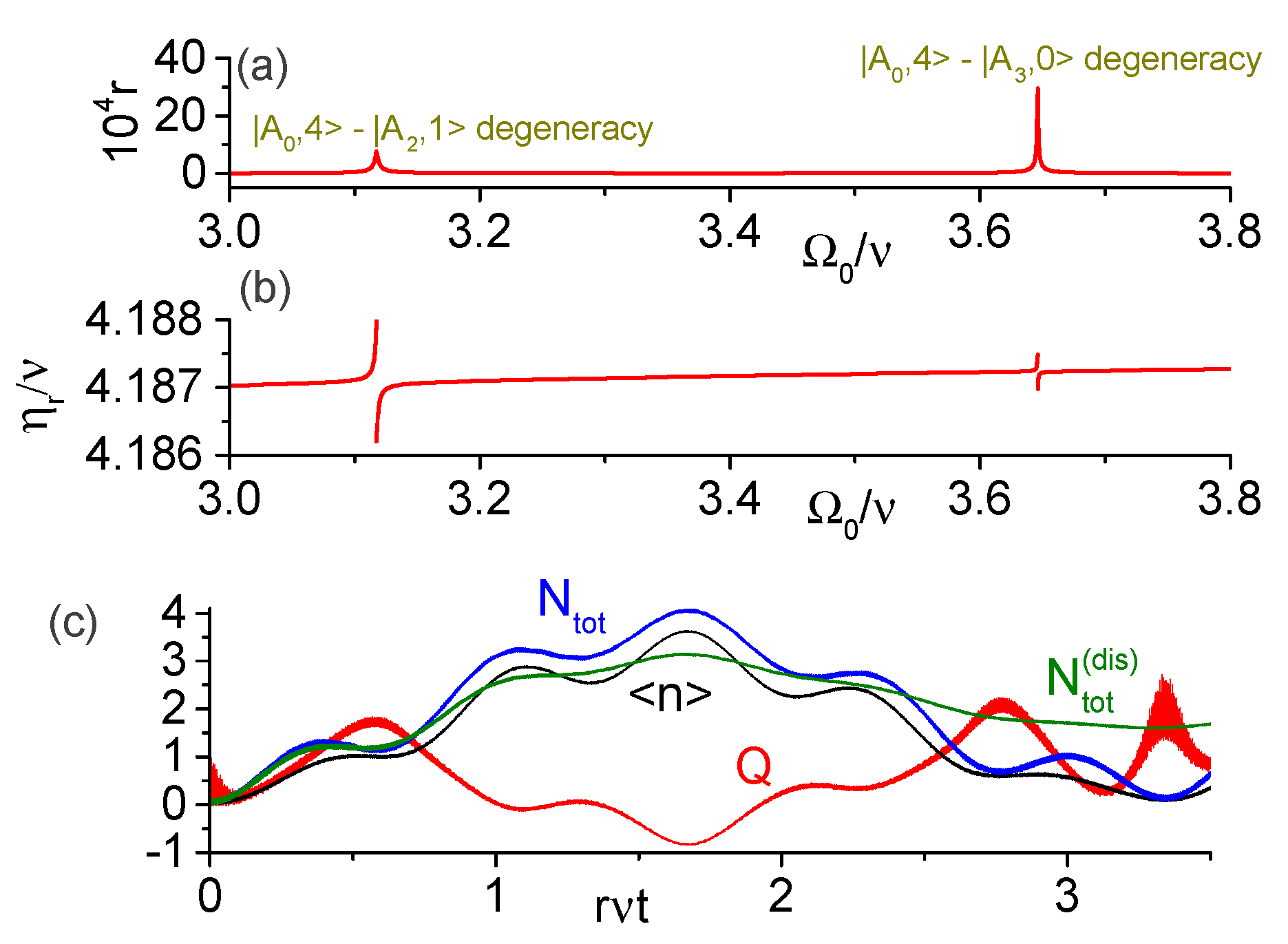
4.1. Multi-Photon Transitions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Auxiliary Expressions
References
- Dodonov, V.V. Nonstationary Casimir effect and analytical solutions for quantum fields in cavities with moving boundaries. In Modern Nonlinear Optics; Advances in Chemical Physics Series, Part 1; Evans, M.W., Ed.; Wiley: New York, NY, USA, 2001; Volume 119, p. 309. [Google Scholar]
- Dodonov, V.V. Current status of the dynamical Casimir effect. Phys. Scr. 2010, 82, 038105. [Google Scholar] [CrossRef]
- Dalvit, D.A.R.; Maia Neto, P.A.; Mazzitelli, F.D. Fluctuations, dissipation and the dynamical Casimir effect. In Casimir Physics; Lecture Notes in Physics; Dalvit, D., Milonni, P., Roberts, D., da Rosa, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 834, p. 419. [Google Scholar]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1. [Google Scholar] [CrossRef]
- Dodonov, V. Fifty Years of the Dynamical Casimir Effect. Physics 2020, 2, 67–104. [Google Scholar] [CrossRef]
- Fulling, S.A.; Davies, P.C.W. Radiation from a moving mirror in two dimensional space-time: Conformal anomaly. Proc. R. Soc. Lond. A 1976, 348, 393. [Google Scholar]
- Maia Neto, P.A.; Machado, L.A.S. Quantum radiation generated by a moving mirror in free space. Phys. Rev. A 1996, 54, 3420. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 1970, 11, 2679. [Google Scholar] [CrossRef]
- Law, C.K. Effective Hamiltonian for the radiation in a cavity with a moving mirror and a time-varying dielectric medium. Phys. Rev. A 1994, 49, 433. [Google Scholar] [CrossRef]
- Lambrecht, A.; Jaekel, M.-T.; Reynaud, S. Motion Induced Radiation from a Vibrating Cavity. Phys. Rev. Lett. 1996, 77, 615. [Google Scholar] [CrossRef]
- Motazedifard, A.; Naderi, M.H.; Roknizadeh, R. Dynamical Casimir effect of phonon excitation in the dispersive regime of cavity optomechanics. J. Opt. Soc. Am. B 2017, 34, 642. [Google Scholar] [CrossRef]
- Wang, X.; Qin, W.; Miranowicz, A.; Savasta, S.; Nori, F. Unconventional cavity optomechanics: Nonlinear control of phonons in the acoustic quantum vacuum. Phys. Rev. A 2019, 100, 063827. [Google Scholar] [CrossRef]
- Carusotto, I.; Balbinot, R.; Fabbri, A.; Recati, A. Density correlations and analog dynamical Casimir emission of Bogoliubov phonons in modulated atomic Bose–Einstein condensates. Eur. Phys. J. D 2010, 56, 391. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Mendonca, J.T. Dynamical Casimir effect in ultra-cold matter with a time-dependent effective charge. Phys. Scr. 2014, T160, 014008. [Google Scholar] [CrossRef]
- Marino, J.; Recati, A.; Carusotto, I. Casimir forces and quantum friction from Ginzburg radiation in atomic Bose–Einstein condensates. Phys. Rev. Lett. 2017, 118, 045301. [Google Scholar] [CrossRef] [PubMed]
- Koghee, S.; Wouters, M. Dynamical Casimir emission from polariton condensates. Phys. Rev. Lett. 2014, 112, 036406. [Google Scholar] [CrossRef] [PubMed]
- Saito, H.; Hyuga, H. Dynamical Casimir effect for magnons in a spinor Bose–Einstein condensate. Phys. Rev. A 2008, 78, 033605. [Google Scholar] [CrossRef]
- Zhao, X.-D.; Zhao, X.; Jing, H.; Zhou, L.; Zhang, W. Squeezed magnons in an optical lattice: Application to simulation of the dynamical Casimir effect at finite temperature. Phys. Rev. A 2013, 87, 053627. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376. [Google Scholar] [CrossRef]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Delsing, P.; Nori, F. Nonclassical microwave radiation from the dynamical Casimir effect. Phys. Rev. A 2013, 87, 043804. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234. [Google Scholar] [CrossRef]
- Svensson, I.-M.; Pierre, M.; Simoen, M.; Wustmann, W.; Krantz, P.; Bengtsson, A.; Johansson, G.; Bylander, J.; Shumeiko, V.; Delsing, P. Microwave photon generation in a doubly tunable superconducting resonator. J. Phys. Conf. Ser. 2018, 969, 012146. [Google Scholar] [CrossRef]
- Jaskula, J.-C.; Partridge, G.B.; Bonneau, M.; Lopes, R.; Ruaudel, J.; Boiron, D.; Westbrook, C.I. Acoustic analog to the dynamical Casimir effect in a Bose–Einstein condensate. Phys. Rev. Lett. 2012, 109, 220401. [Google Scholar] [CrossRef] [PubMed]
- Dodonov, V.V.; Klimov, A.B.; Man’ko, V.I. Generation of squeezed states in a resonator with a moving wall. Phys. Lett. A 1990, 149, 225. [Google Scholar] [CrossRef]
- Aggarwal, N.; Bhattacherjee, A.B.; Banerjee, A.; Mohan, M. Influence of periodically modulated cavity field on the generation of atomic-squeezed states. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 115501. [Google Scholar] [CrossRef]
- You, J.Q.; Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 2011, 474, 589. [Google Scholar] [CrossRef] [PubMed]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169. [Google Scholar] [CrossRef]
- Schmidt, S.; Koch, J. Circuit QED lattices: Towards quantum simulation with superconducting circuits. Ann. Phys. 2013, 525, 395. [Google Scholar] [CrossRef]
- Wendin, G. Quantum information processing with supercon ducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.-x.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar]
- Beaudoin, F.; da Silva, M.P.; Dutton, Z.; Blais, A. First-order sidebands in circuit QED using qubit frequency modulation. Phys. Rev. A 2012, 86, 022305. [Google Scholar] [CrossRef]
- Silveri, M.P.; Tuorila, J.A.; Thuneberg, E.V.; Paraoanu, G.S. Quantum systems under frequency modulation. Rep. Prog. Phys. 2017, 80, 056002. [Google Scholar] [CrossRef]
- Kockum, A.F.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19. [Google Scholar] [CrossRef]
- Dodonov, A.V. Photon creation from vacuum and interactions engineering in nonstationary circuit QED. J. Phys. Conf. Ser. 2009, 161, 012029. [Google Scholar] [CrossRef]
- Dodonov, A.V. Analytical description of nonstationary circuit QED in the dressed-states basis. J. Phys. A Math. Theor. 2014, 47, 285303. [Google Scholar] [CrossRef]
- De Liberato, S.; Ciuti, C.; Carusotto, I. Quantum vacuum radiation spectra from a semiconductor microcavity with a time-modulated vacuum Rabi frequency. Phys. Rev. Lett. 2007, 98, 103602. [Google Scholar] [CrossRef]
- De Liberato, S.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- Sabín, C.; Fuentes, I.; Johansson, G. Quantum discord in the dynamical Casimir effect. Phys. Rev. A 2015, 92, 012314. [Google Scholar] [CrossRef]
- Rossatto, D.Z.; Felicetti, S.; Eneriz, H.; Rico, E.; Sanz, M.; Solano, E. Entangling polaritons via dynamical Casimir effect in circuit quantum electrodynamics. Phys. Rev. B 2016, 93, 094514. [Google Scholar] [CrossRef]
- Felicetti, S.; Sabín, C.; Fuentes, I.; Lamata, L.; Romero, G.; Solano, E. Relativistic motion with superconducting qubits. Phys. Rev. B 2015, 92, 064501. [Google Scholar] [CrossRef]
- Corona-Ugalde, P.; Martín-Martínez, E.; Wilson, C.M.; Mann, R.B. Dynamical Casimir effect in circuit QED for nonuniform trajectories. Phys. Rev. A 2016, 93, 012519. [Google Scholar] [CrossRef]
- Sabín, C.; Peropadre, B.; Lamata, L.; Solano, E. Simulating superluminal physics with superconducting circuit technology. Phys. Rev. A 2017, 96, 032121. [Google Scholar] [CrossRef]
- Di Paolo, A.; Leroux, C.; Hazard, T.M.; Serniak, K.; Gustavsson, S.; Blais, A.; Oliver, W.D. Extensible circuit-QED architecture via amplitude- and frequency-variable microwaves. arXiv 2022, arXiv:2204.08098. [Google Scholar]
- Dodonov, A.V.; Napoli, A.; Militello, B. Emulation of n-photon Jaynes-Cummings and anti-Jaynes-Cummings models via parametric modulation of a cyclic qutrit. Phys. Rev. A 2019, 99, 033823. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Valente, D.; Werlang, T. Antidynamical Casimir effect as a resource for work extraction. Phys. Rev. A 2017, 96, 012501. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Valente, D.; Werlang, T. Quantum power boost in a nonstationary cavity-QED quantum heat engine. J. Phys. A Math. Theor. 2018, 51, 365302. [Google Scholar] [CrossRef]
- Dessano, H.; Dodonov, A.V. One- and three-photon dynamical Casimir effects using a nonstationary cyclic qutrit. Phys. Rev. A 2018, 98, 022520. [Google Scholar] [CrossRef]
- Dodonov, A.V. Dynamical Casimir effect via four- and five-photon transitions using a strongly detuned atom. Phys. Rev. A 2018, 100, 032510. [Google Scholar] [CrossRef]
- de Sousa, I.M.; Dodonov, A.V. Microscopic toy model for the cavity dynamical Casimir effect. J. Phys. A Math. Theor. 2015, 48, 245302. [Google Scholar] [CrossRef]
- Veloso, D.S.; Dodonov, A.V. Prospects for observing dynamical and anti-dynamical Casimir effects in circuit QED due to fast modulation of qubit parameters. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 165503. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Díaz-Guevara, J.J.; Napoli, A.; Militello, B. Speeding up the antidynamical Casimir effect with nonstationary qutrits. Phys. Rev. A 2017, 96, 032509. [Google Scholar] [CrossRef]
- Dodonov, A.V. Novel scheme for anti-dynamical Casimir effect using nonperiodic ultrastrong modulation. Phys. Lett. A 2020, 384, 126685. [Google Scholar] [CrossRef]
- Ma, S.; Miao, H.; Xiang, Y.; Zhang, S. Enhanced dynamic Casimir effect in temporally and spatially modulated Josephson transmission line. Laser Photonics Rev. 2019, 13, 1900164. [Google Scholar] [CrossRef]
- Macrì, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Nonperturbative dynamical Casimir effect in optomechanical systems: Vacuum Casimir–Rabi splittings. Phys. Rev. X 2018, 8, 011031. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Ashhab, S.; Cui, W.; Wu, R.; Nori, F. Two-qubit gate operations in superconducting circuits with strong coupling and weak anharmonicity. New J. Phys. 2012, 14, 073041. [Google Scholar] [CrossRef]
- Ashhab, S.; Nori, F. Switchable coupling for superconducting qubits using double resonance in the presence of crosstalk. Phys. Rev. B 2007, 76, 132513. [Google Scholar] [CrossRef]
- Yamamoto, T.; Watanabe, M.; You, J.Q.; Pashkin, Y.A.; Astafiev, O.; Nakamura, Y.; Nori, F.; Tsai, J.S. Spectroscopy of superconducting charge qubits coupled by a Josephson inductance. Phys. Rev. B 2008, 77, 064505. [Google Scholar] [CrossRef]
- Blais, A.; Grimsmo, A.L.; Girvin, S.M.; Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 2021, 93, 025005. [Google Scholar] [CrossRef]
- Willsch, M.; Willsch, D.; Jin, F.; De Raedt, H.; Michielsen, K. Real-time simulation of flux qubits used for quantum annealing. Phys. Rev. A 2020, 101, 012327. [Google Scholar] [CrossRef]
- Ciani, A.; Terhal, B.M. Stoquasticity in circuit QED. Phys. Rev. A 2021, 103, 042401. [Google Scholar] [CrossRef]
- Dodonov, A.V. Dynamical Casimir effect in cavities with two modes resonantly coupled through a qubit. Phys. Lett. A 2020, 384, 126837. [Google Scholar] [CrossRef]
- Sedov, D.D.; Kozin, V.K.; Iorsh, I.V. Chiral Waveguide Optomechanics: First Order Quantum Phase Transitions with Z3 Symmetry Breaking. Phys. Rev. Lett. 2020, 125, 263606. [Google Scholar] [CrossRef]
- Kozin, V.K.; Iorsh, I.V.; Kibis, O.V.; Shelykh, I.A. Quantum ring with the Rashba spin–orbit interaction in the regime of strong light-matter coupling. Phys. Rev. B 2018, 97, 155434. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Militello, B.; Napoli, A.; Messina, A. Effective Landau-Zener transitions in the circuit dynamical Casimir effect with time-varying modulation frequency. Phys. Rev. A 2016, 93, 052505. [Google Scholar] [CrossRef]
- Vogel, W.; Welsch, D.-G. Quantum Optics; Wiley: Berlin, Germany, 2006. [Google Scholar]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley: Berlin, Germany, 2001. [Google Scholar]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Carmichael, H. An Open System Approach to Quantum Optics; Springer: Berlin, Germany, 1993. [Google Scholar]
- Beaudoin, F.; Gambetta, J.M.; Blais, A. Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 2011, 84, 043832. [Google Scholar] [CrossRef]
- Kirchmair, G.; Vlastakis, B.; Leghtas, Z.; Nigg, S.E.; Paik, H.; Ginossar, E.; Mirrahimi, M.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 2013, 495, 205. [Google Scholar] [CrossRef]
- Riste, D.; Dukalski, M.; Watson, C.A.; de Lange, G.; Tiggelman, M.J.; Blanter, Y.M.; Lehnert, K.W.; Schouten, R.N.; DiCarlo, L. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 2013, 502, 350. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Petrenko, A.; Leghtas, Z.; Vlastakis, B.; Kirchmair, G.; Sliwa, K.M.; Narla, A.; Hatridge, M.; Shankar, S.; Blumoff, J.; et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 2014, 511, 444. [Google Scholar] [CrossRef] [PubMed]
- Silva, E.L.S.; Dodonov, A.V. Analytical comparison of the first- and second-order resonances for implementation of the dynamical Casimir effect in nonstationary circuit QED. J. Phys. A Math. Theor. 2016, 49, 495304. [Google Scholar] [CrossRef]

| t-Qubit Frequency | ||||
|---|---|---|---|---|
| 0.735 | −0.017 | −0.678 | 0.012 | |
| 0.741 | −0.048 | −0.669 | 0.038 | |
| 0.740 | −0.122 | −0.653 | 0.105 | |
| 0.714 | −0.240 | −0.618 | 0.227 | |
| 0.579 | −0.449 | −0.479 | 0.484 | |
| 0.457 | −0.538 | −0.312 | 0.636 | |
| 0.489 | −0.548 | −0.178 | 0.655 |
| t-Qubit Frequency | ||||
|---|---|---|---|---|
| −0.464 | 0.236 | 0.541 | 0.660 | |
| −0.437 | 0.351 | 0.539 | 0.629 | |
| −0.571 | 0.524 | 0.435 | 0.458 | |
| −0.697 | 0.659 | 0.206 | 0.193 | |
| −0.714 | 0.688 | 0.098 | 0.084 | |
| −0.711 | 0.702 | 0.035 | 0.028 | |
| −0.704 | 0.710 | 0.01 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Paula, M.V.S.; Sinesio, W.W.T.; Dodonov, A.V. Ancilla-Assisted Generation of Photons from Vacuum via Time-Modulation of Extracavity Qubit. Entropy 2023, 25, 901. https://doi.org/10.3390/e25060901
de Paula MVS, Sinesio WWT, Dodonov AV. Ancilla-Assisted Generation of Photons from Vacuum via Time-Modulation of Extracavity Qubit. Entropy. 2023; 25(6):901. https://doi.org/10.3390/e25060901
Chicago/Turabian Stylede Paula, Marcos V. S., William W. T. Sinesio, and Alexandre V. Dodonov. 2023. "Ancilla-Assisted Generation of Photons from Vacuum via Time-Modulation of Extracavity Qubit" Entropy 25, no. 6: 901. https://doi.org/10.3390/e25060901
APA Stylede Paula, M. V. S., Sinesio, W. W. T., & Dodonov, A. V. (2023). Ancilla-Assisted Generation of Photons from Vacuum via Time-Modulation of Extracavity Qubit. Entropy, 25(6), 901. https://doi.org/10.3390/e25060901







