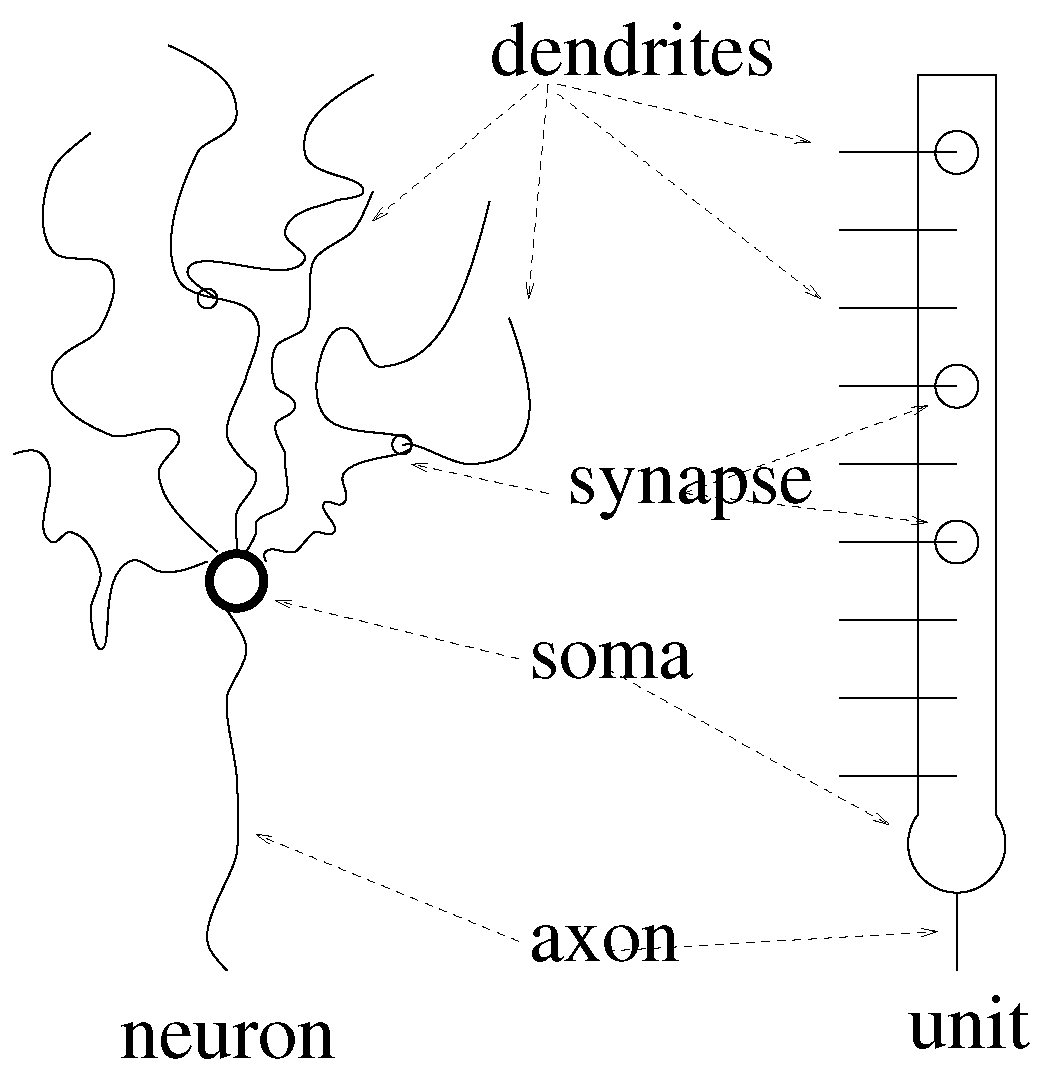
Quantum Lernmatrix
Abstract
1. Introduction
- The input (reading) problem: The amplitude distribution of a quantum state is initialized by reading n data points. Although the existing quantum algorithm requires only steps or and is faster than the classical algorithms, n data points must be read. Hence, the complexity of the algorithm does not improve and is .
- The destruction problem: A quantum associative memory [1,2,3,4,5] for n data points for dimension m requires only or fewer units (quantum bits). An operator, which acts as an oracle [3], indicates the solution. However, this memory can be queried only once because of the collapse during measurement (destruction); hence, quantum associative memory does not have any advantages over classical memory.
- We introduce the Lernmatrix model described by units that model neurons.
- We indicate that Lernmatrix has a tremendous storage capacity, much higher than most other associative memories. This is valid for sparse equally distributed ones in vectors representing the information.
- Quantum counting of ones based on Euler’s formula is described.
- Based on the Lernmatrix model, a quantum Lernmatrix is introduced in which units are represented in superposition and the query operation is based on quantum counting of ones. The measured result is a position of a one or zero in the answer vector.
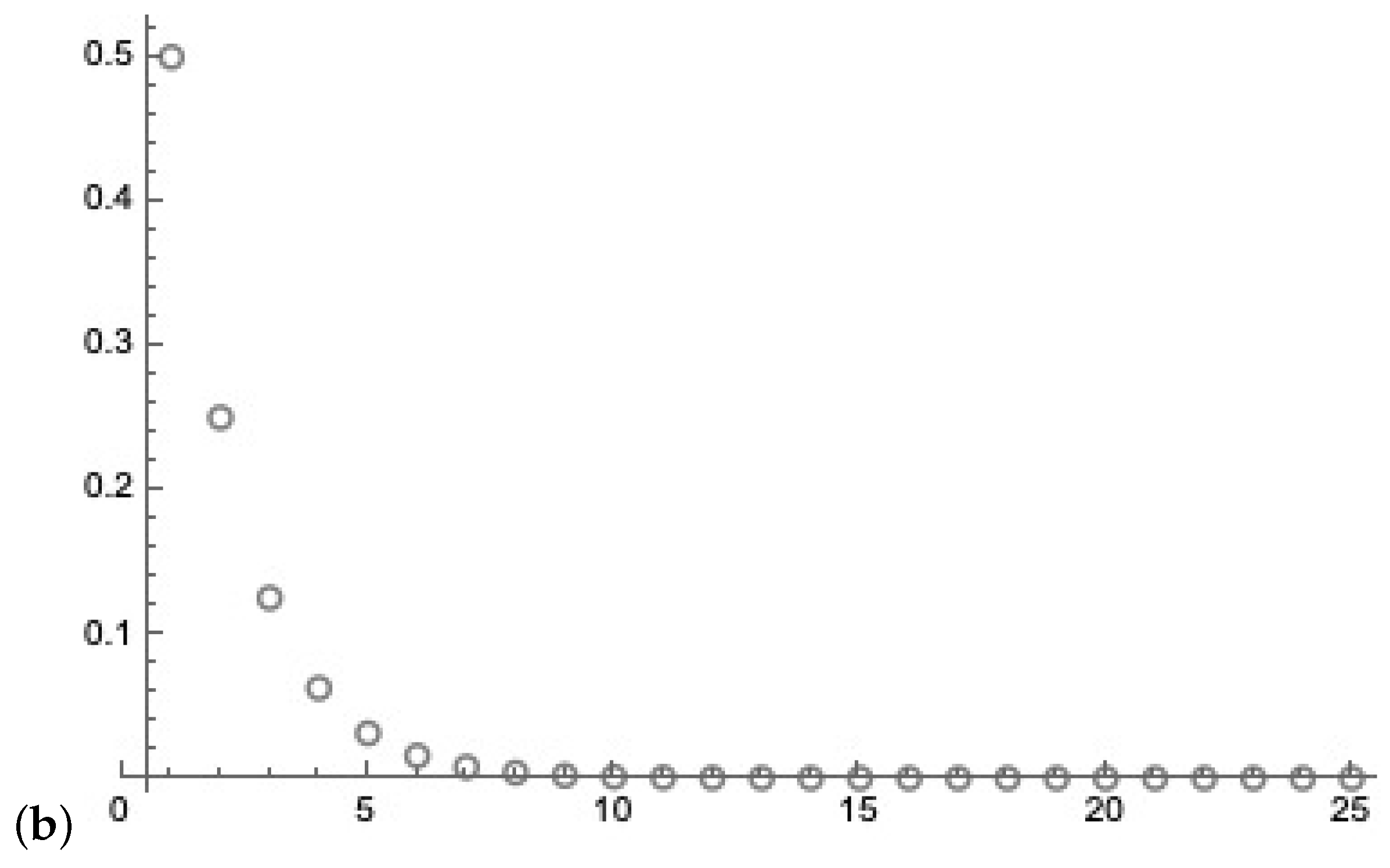
- We analyze the Trugenberger amplification.
- Since a one in the answer vector represents information, we assume in that we can reconstruct the answer vector by measuring several ones, taking for granted that the rest of the vector is zero. In a sparse code with k ones, k measurements of different ones reconstruct the binary answer vector. We can increase the probability of measuring a one by the introduced tree-like structure.
- The Lernmatrix can store much more patterns then the number of units. Because of this, the cost of loading L patterns into quantum states is much lower than storing the patterns individually.
2. Lernmatrix
- The ability to correct faults if false information is given.
- The ability to complete information if some parts are missing.
- The ability to interpolate information. In other words, if a sub-symbol is not currently stored, the most similar stored sub-symbol is determined.
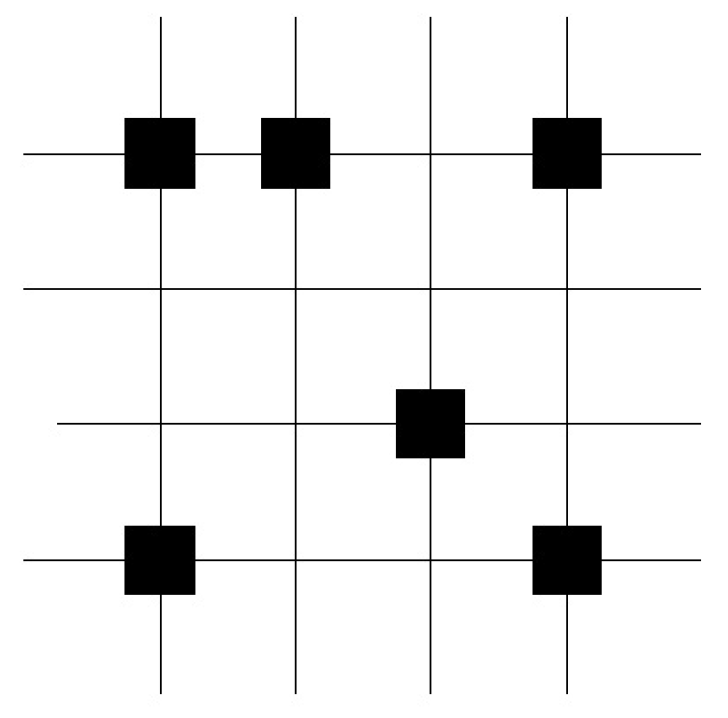
2.1. Learning and Retrieval
- Hetero-association if both vectors are different ,
- Association, if , the answer vector represents the reconstruction of the disturbed query vector.
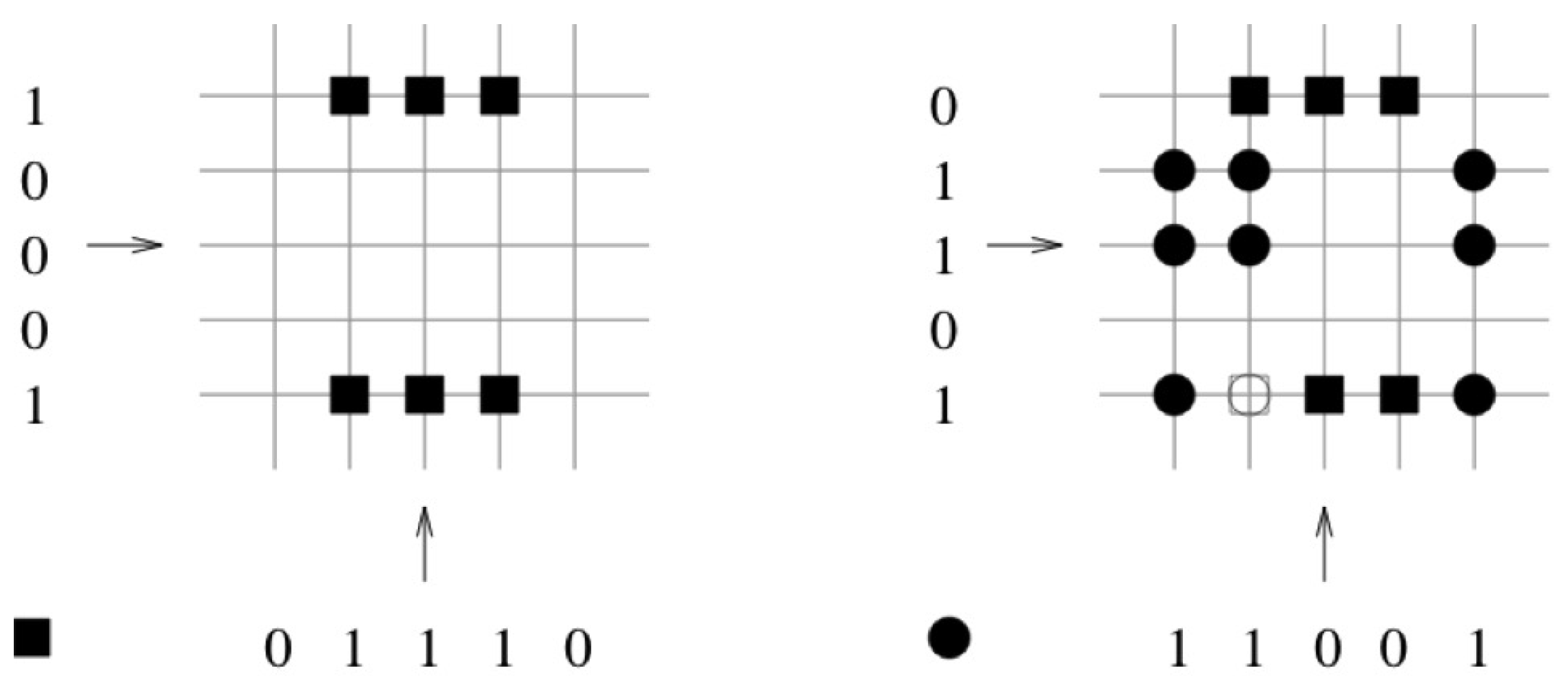
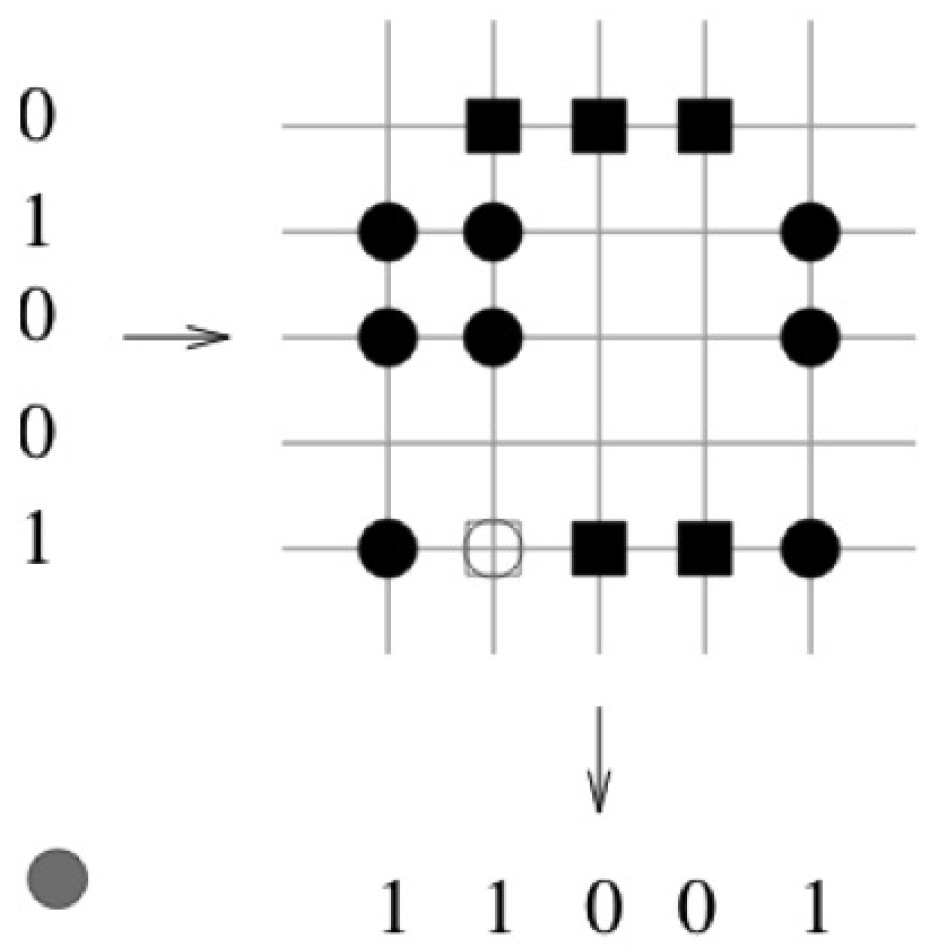
Example
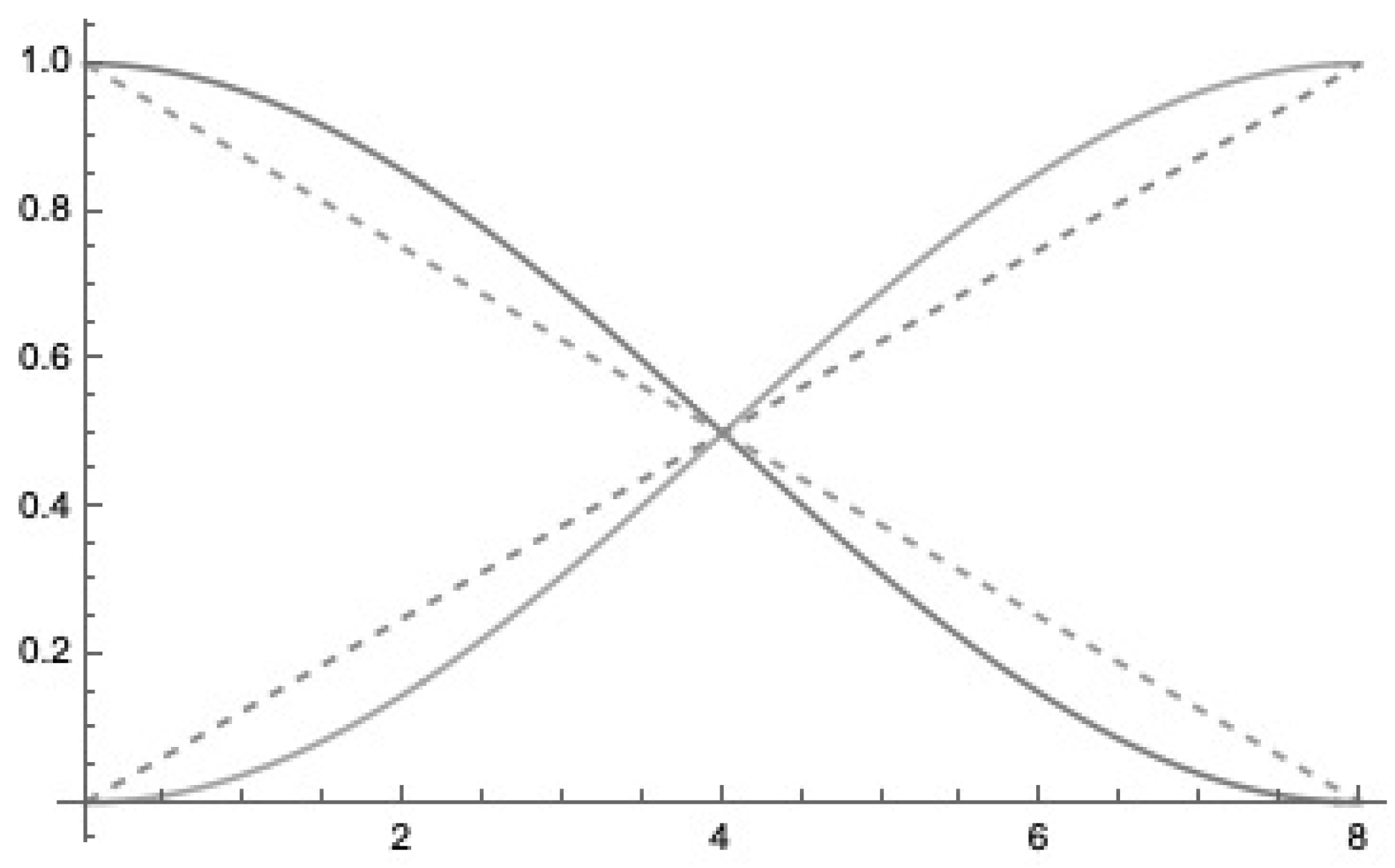
2.2. Storage Capacity
2.3. Large Matrices
3. Monte Carlo Lernmatrix
4. Qiskit Experiments
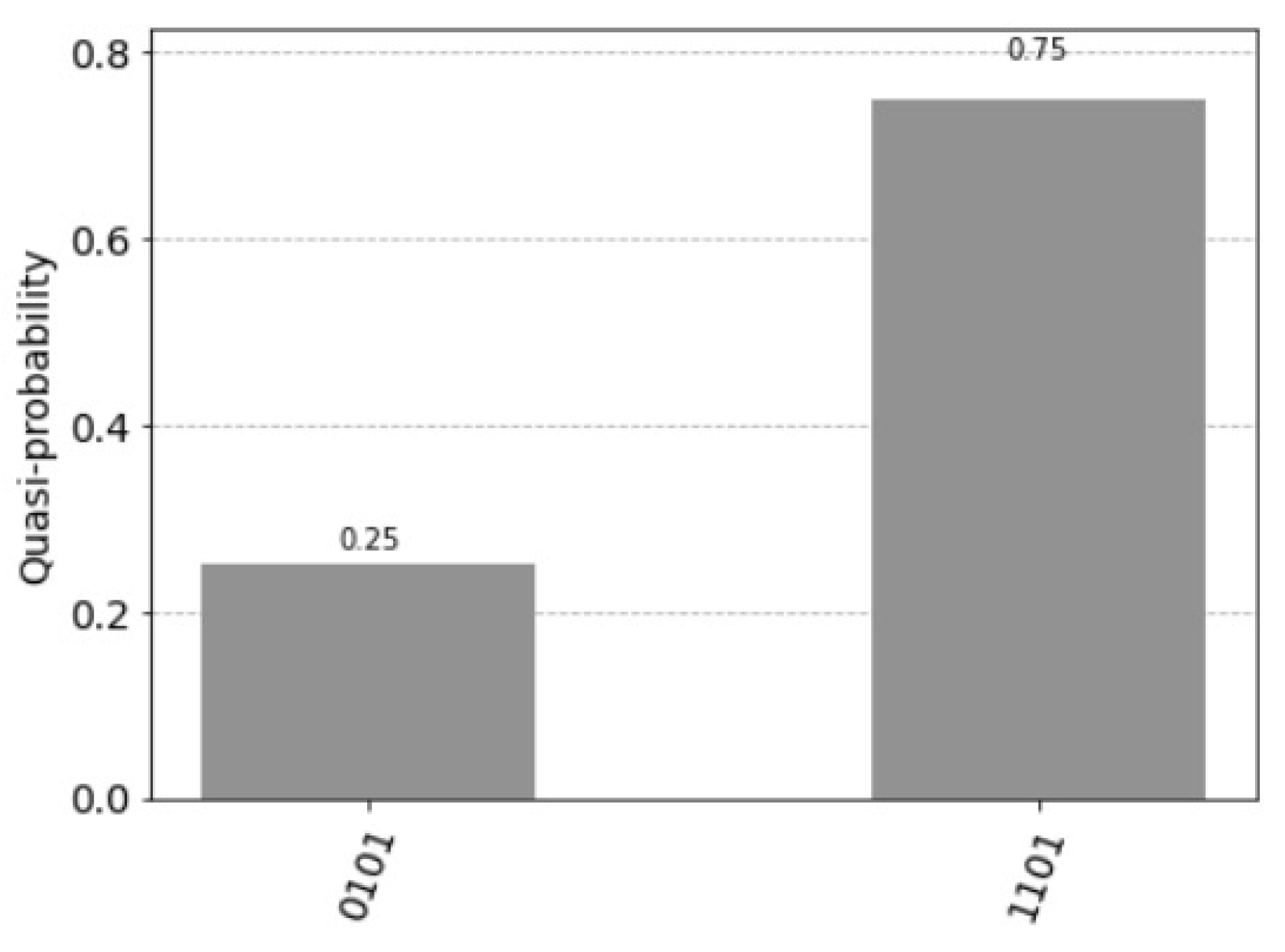
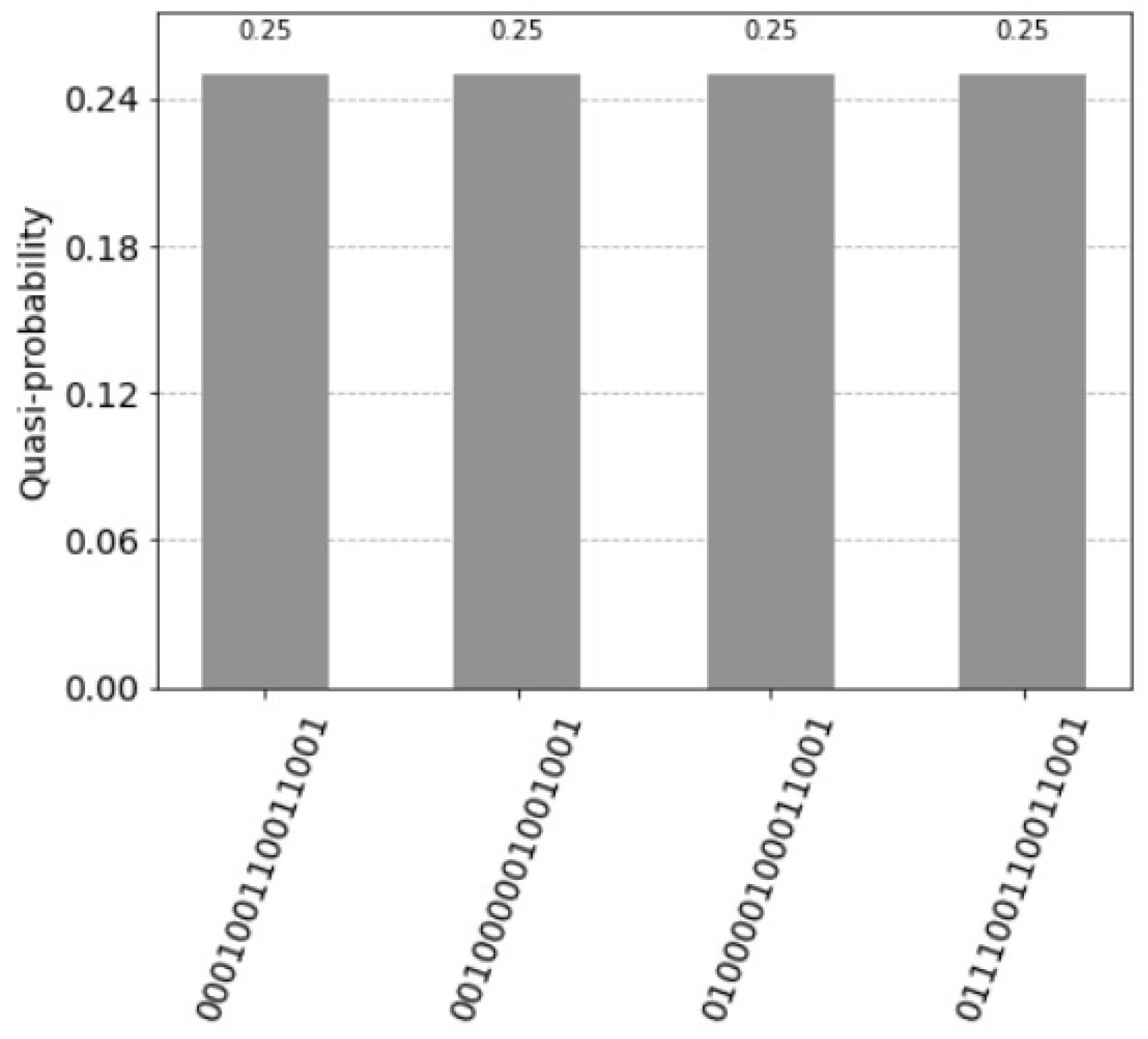
5. Quantum Counting Ones
- from qiskit import QuantumCircuit, Aer, execute
- from qiskit.visualization import plot_histogram
- from math import~pi
- qc = QuantumCircuit(4)
- #Input is |101>
- qc.x(0)
- qc.x(2)
- qc.barrier()
- qc.h(3)
- qc.cp(-pi/6,0,3)
- qc.cp(-pi/6,1,3)
- qc.cp(-pi/6,2,3)
- qc.x(3)
- qc.cp(pi/6,0,3)
- qc.cp(pi/6,1,3)
- qc.cp(pi/6,2,3)
- qc.x(3)
- qc.h(3)
- simulator = Aer.get_backend(’statevector_simulator’)
- # Run and get counts
- result=execute(qc,simulator).result()
- counts = result.get_counts()
- plot_histogram(counts)
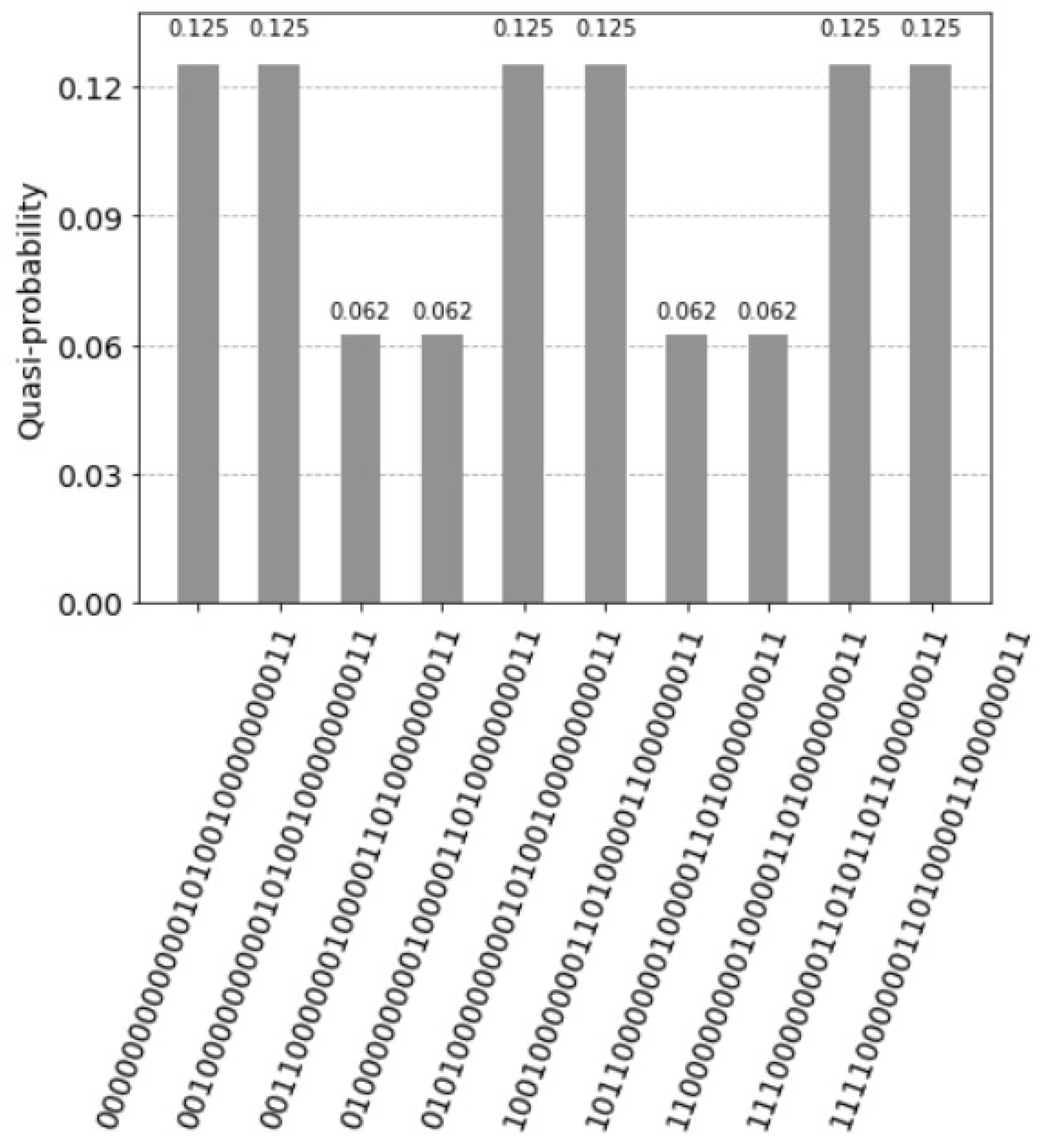
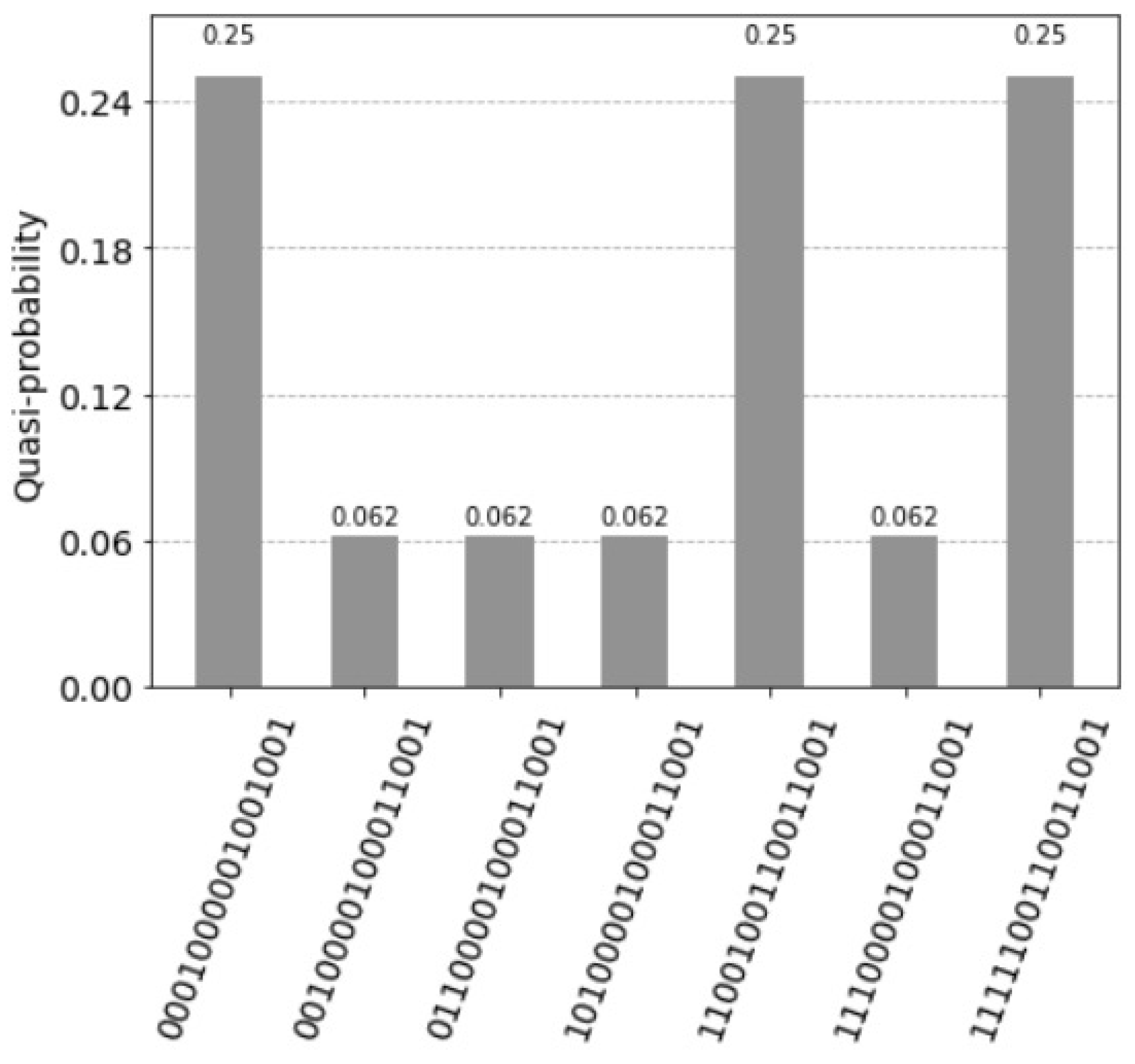
6. Quantum Lernmatrix
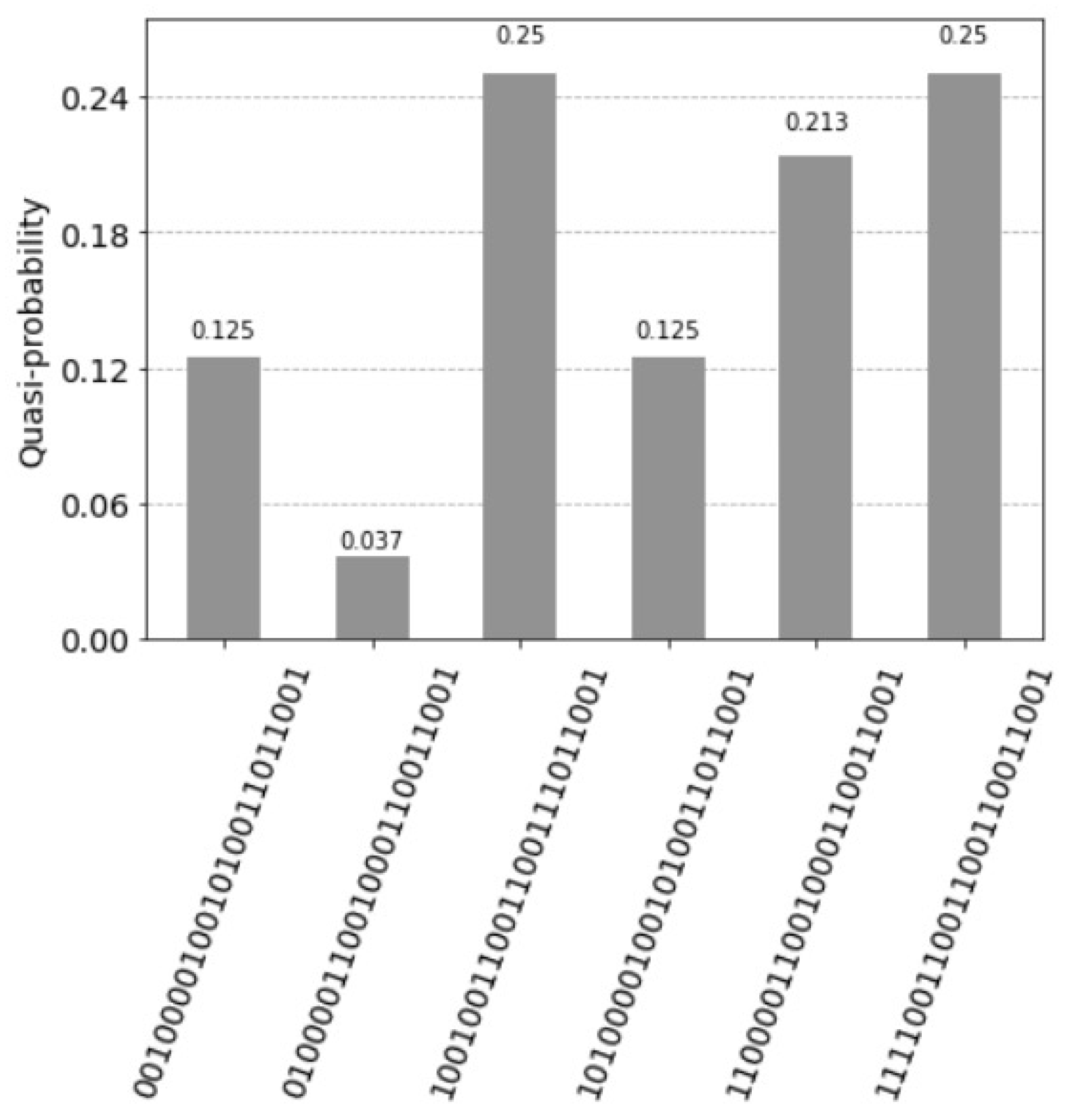
- The first unit has the value and the two corresponding states are: for the control the value is with the measured probability and for the control the value is with the measured probability 0.
- The second unit has the value and the two corresponding states are: for the control the value is with the measured probability and for the control the value is with the measured probability .
- The third unit has the value and the two corresponding states are: for the control the value is with the measured probability = 0 and for the control the value is with the measured probability = 0.
- The fourth unit has the (decimal) value and the two corresponding states are: for the control the value is with the measured probability and for the control the value is with the measured probability 0.
6.1. Generalization
6.2. Example
7. Applying Trugenberger Amplification Several Times
Relation to b
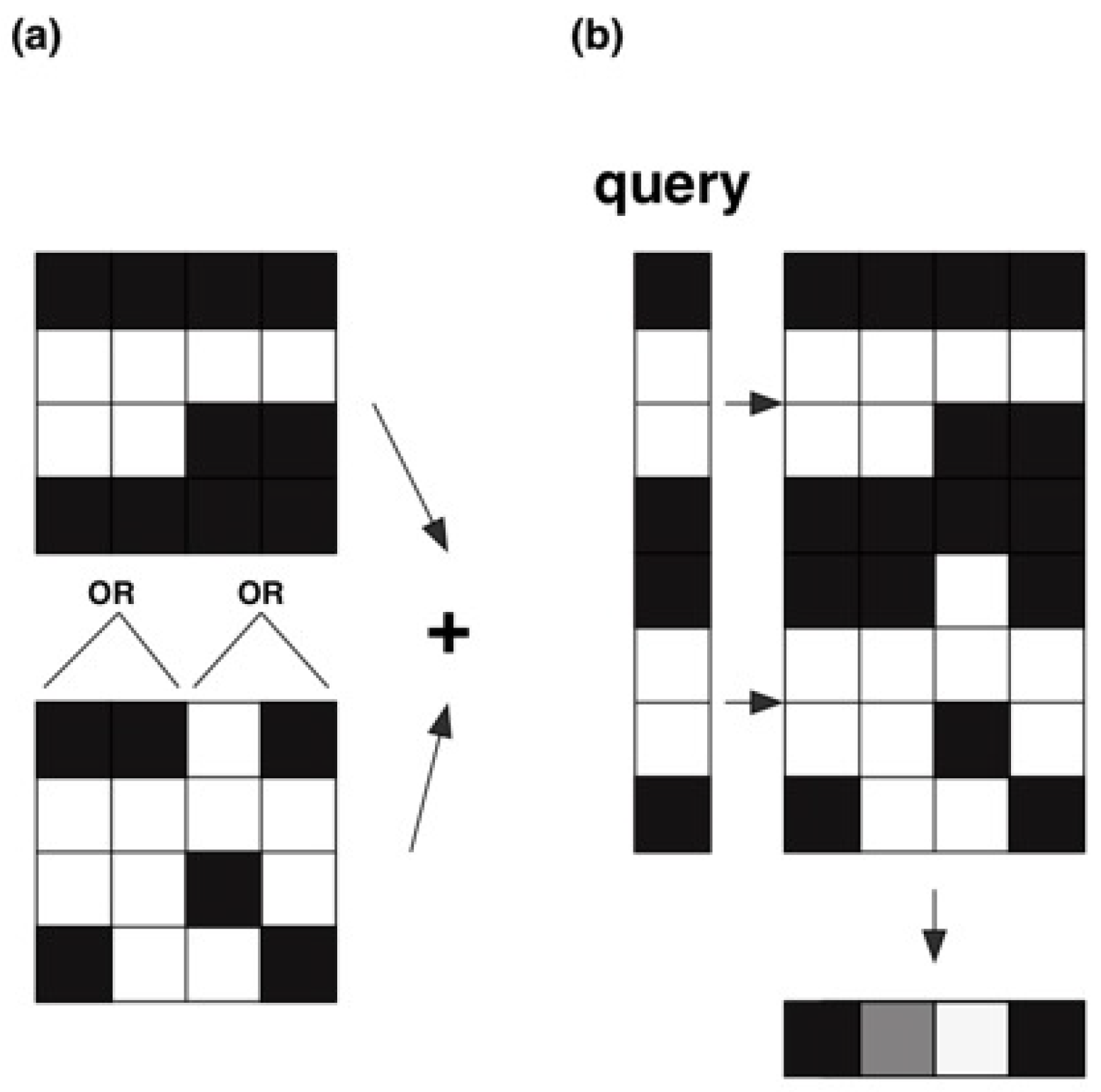
8. Tree-like Structures
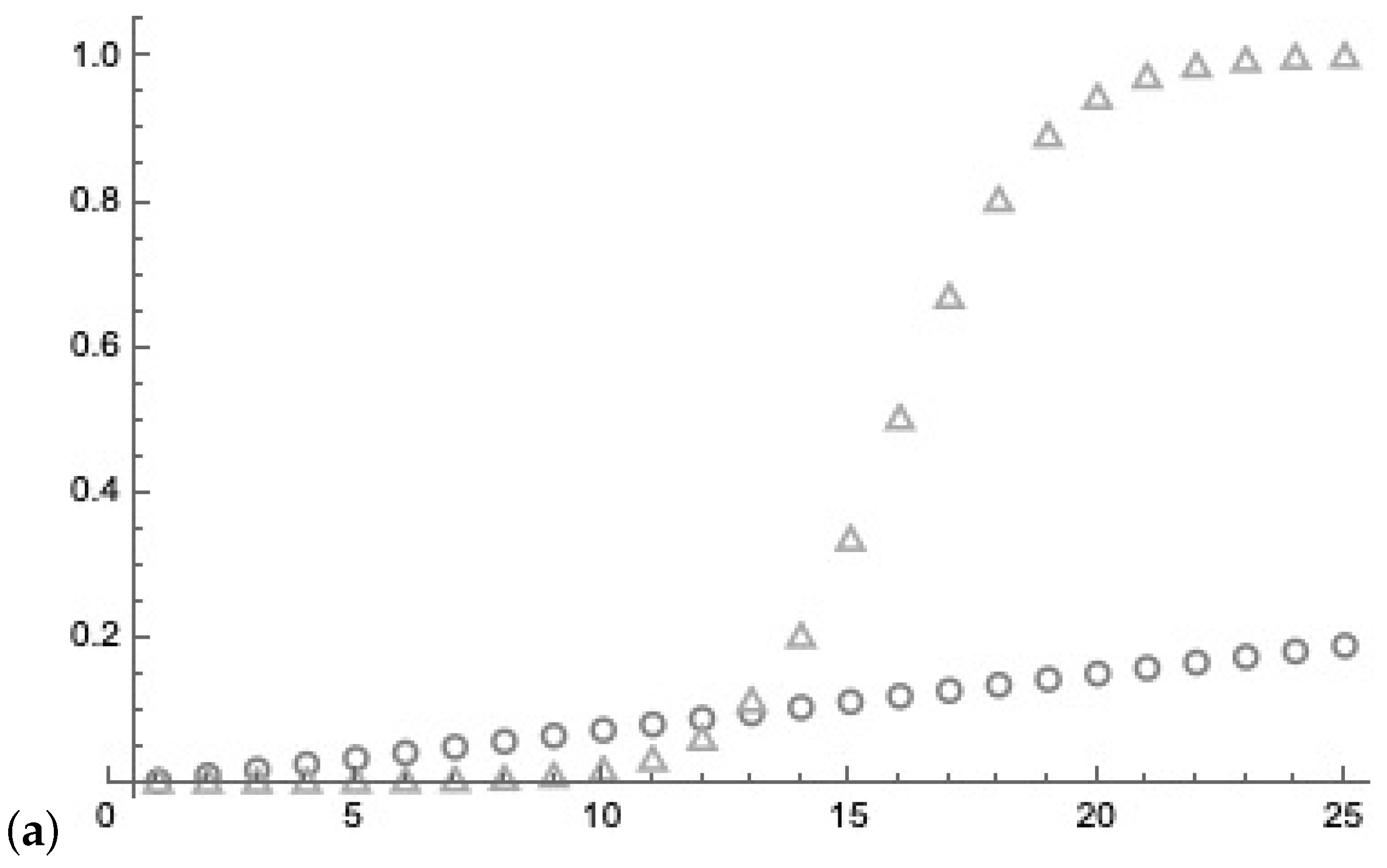
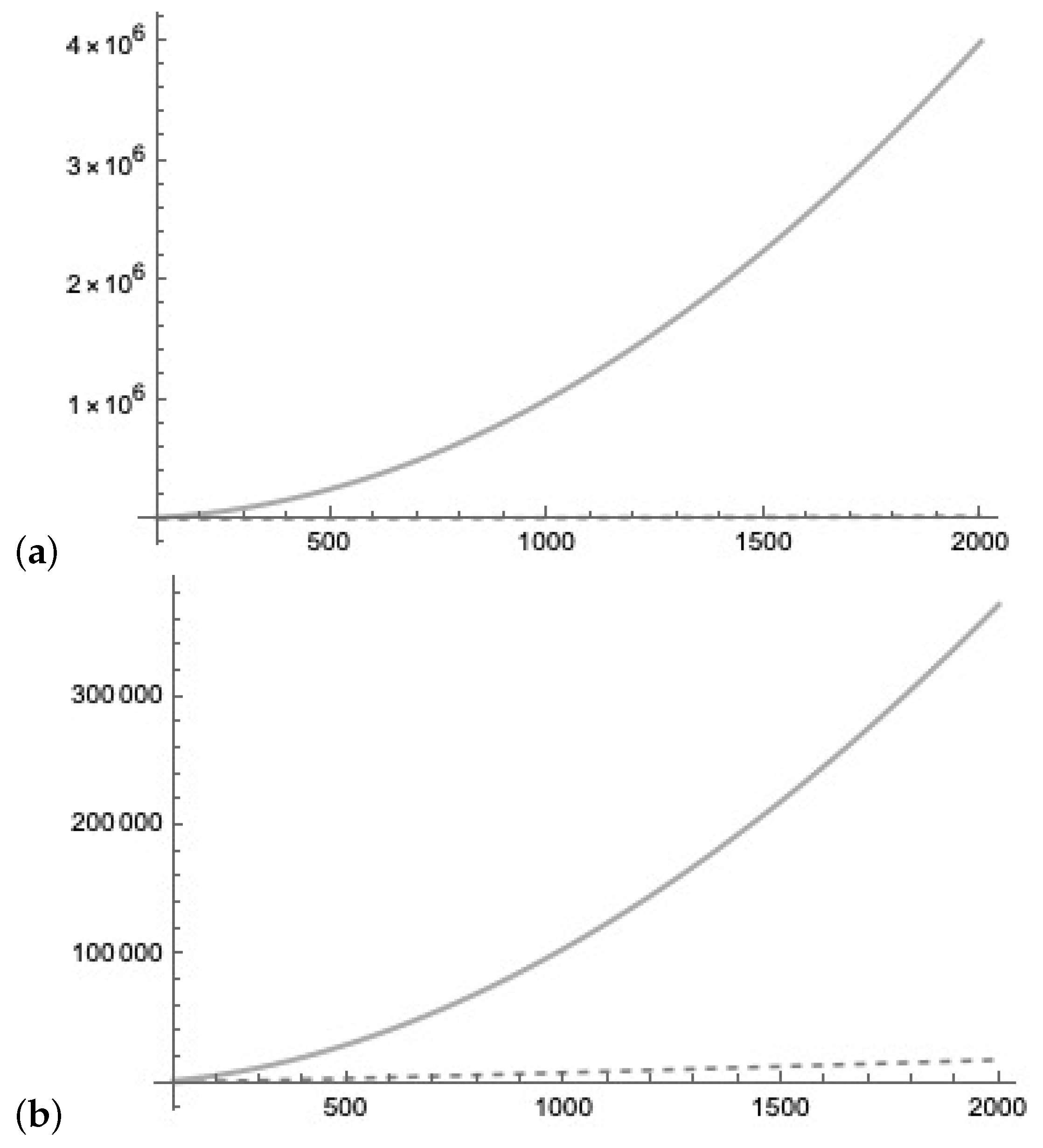
9. Costs
Query Cost of Quantum Lernmatrix
10. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
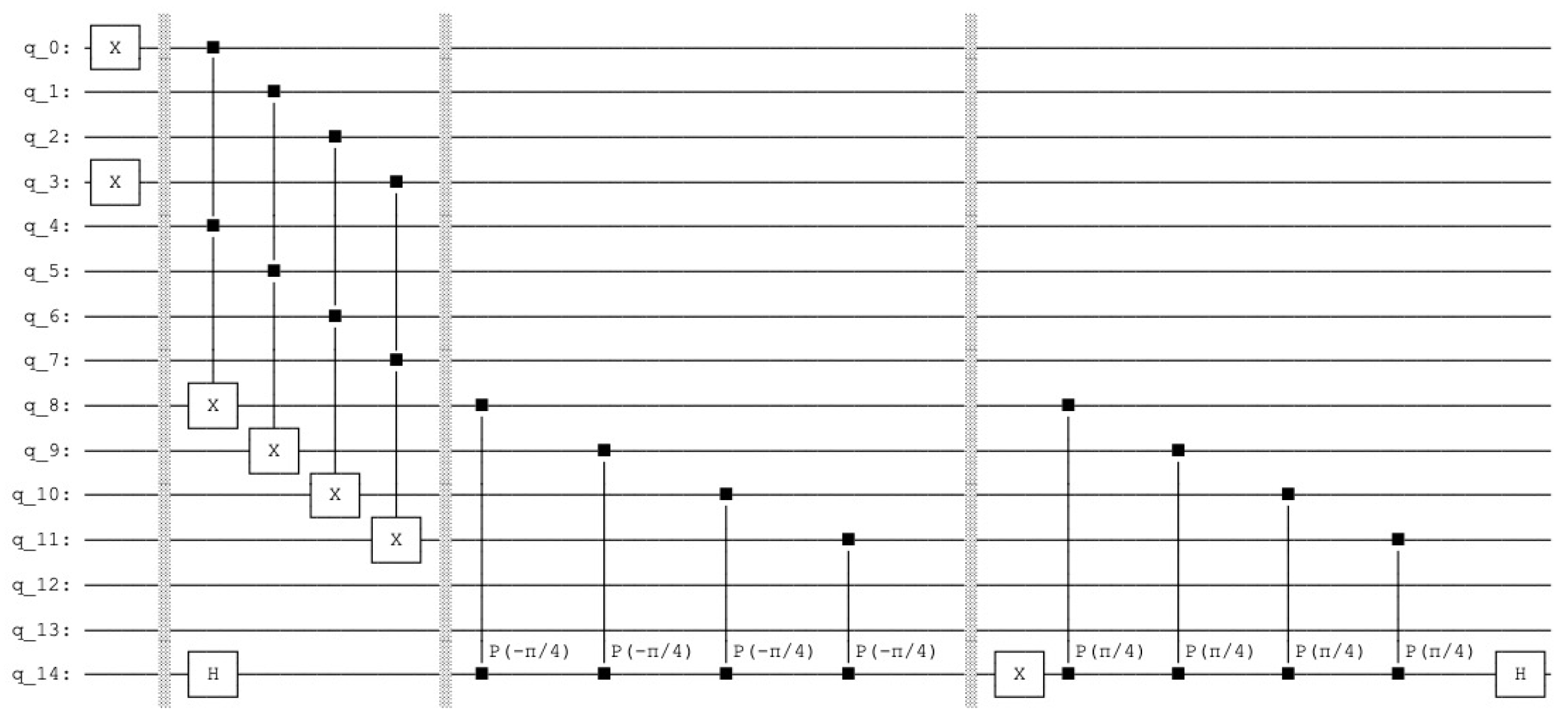
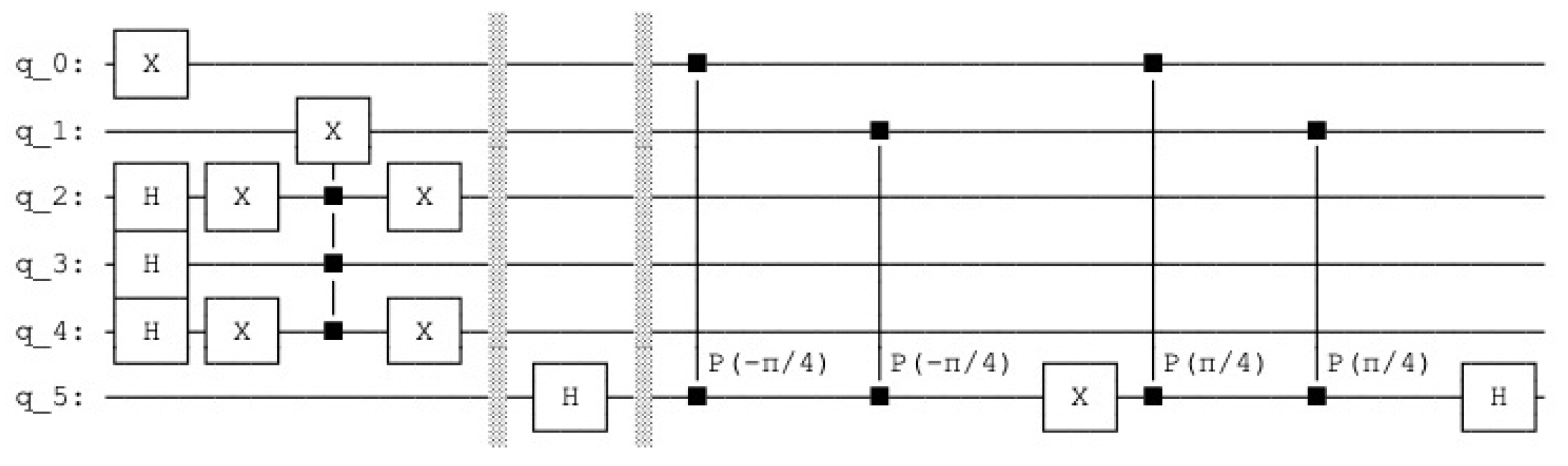
Appendix A. Quantum Lernmatrix
- qc = QuantumCircuit(15)
- #0-3 query
- #4-7 data
- #8-11 count
- #Index Pointer
- #12-13
- #Aux
- #14
- #Sleep Phase
- #Index Pointer
- qc.h(12)
- qc.h(13)
- qc.barrier()
- #1st weights
- qc.ccx(12,13,4)
- qc.ccx(12,13,7)
- qc.barrier()
- #2th weights
- qc.x(12)
- qc.ccx(12,13,4)
- qc.x(12)
- qc.barrier()
- #3th weights
- qc.x(13)
- qc.ccx(12,13,6)
- qc.x(13)
- qc.barrier()
- #4th weights
- qc.x(12)
- qc.x(13)
- qc.ccx(12,13,4)
- qc.ccx(12,13,7)
- qc.x(13)
- qc.x(12)
- qc.barrier()
- #Active Phase
- #query
- qc.x(0)
- qc.x(3)
- qc.barrier()
- qc.ccx(0,4,8)
- qc.ccx(1,5,9)
- qc.ccx(2,6,10)
- qc.ccx(3,7,11)
- #Dividing
- qc.h(14)
- qc.barrier()
- #Marking
- qc.cp(-pi/4,8,14)
- qc.cp(-pi/4,9,14)
- qc.cp(-pi/4,10,14)
- qc.cp(-pi/4,11,14)
- qc.barrier()
- qc.x(14)
- qc.cp(pi/4,8,14)
- qc.cp(pi/4,9,14)
- qc.cp(pi/4,10,14)
- qc.cp(pi/4,11,14)
- qc.h(14)
- qc.draw(fold=110)
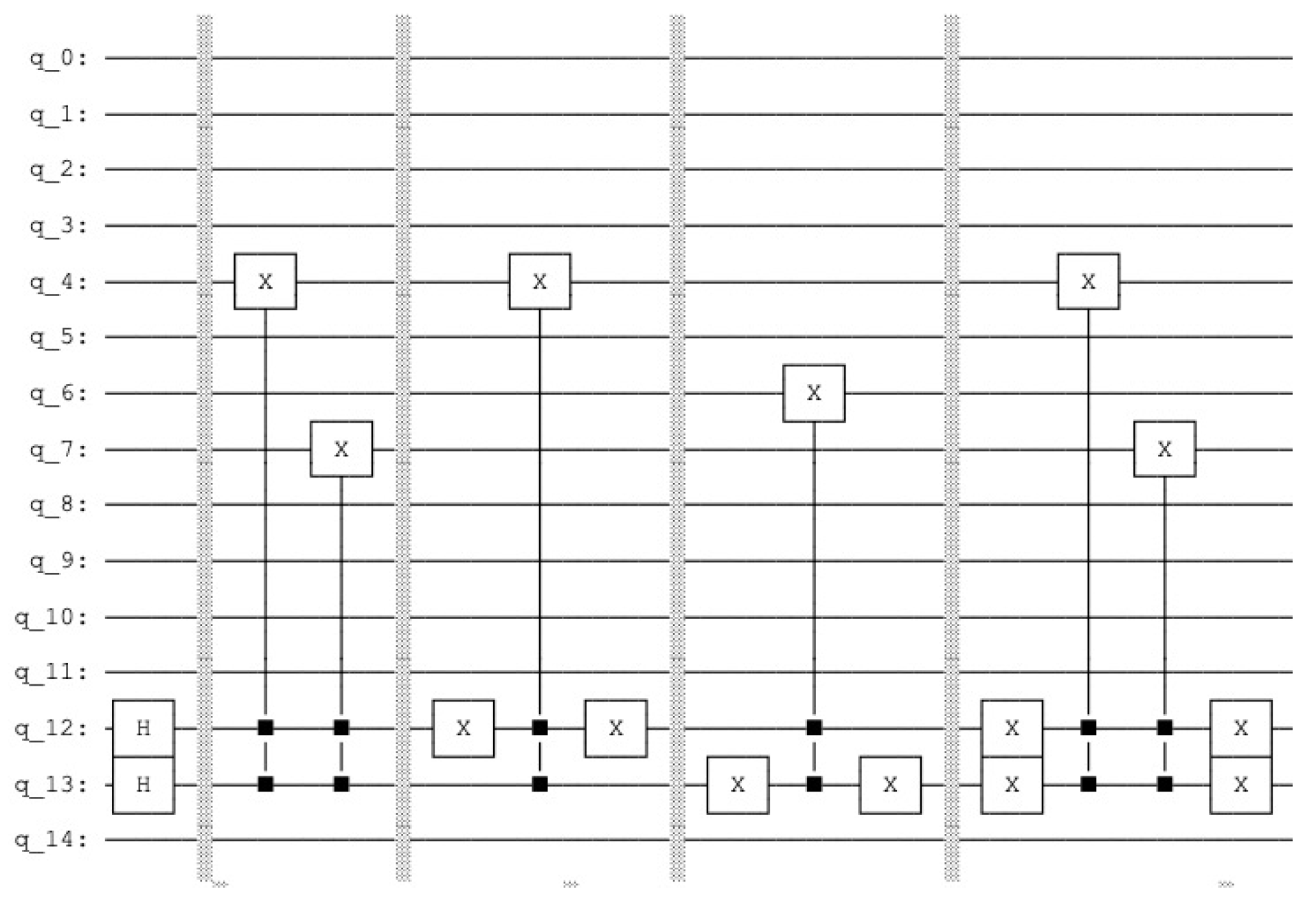
Appendix B. Quantum Tree-like Lernmatrix
- qc = QuantumCircuit(23)
- #0-3 query
- #4-7 data aggregated
- #8-11 data
- #12-19 count
- #Index Pointer
- #20-21
- #Aux
- #22
- #Sleep Phase
- #Index Pointer
- qc.h(20)
- qc.h(21)
- #1st weights
- #OR Aggregated
- qc.barrier()
- qc.ccx(20,21,4)
- qc.ccx(20,21,7)
- #Original
- qc.barrier()
- qc.ccx(20,21,8)
- qc.ccx(20,21,11)
- #2th weights
- qc.x(20)
- #OR Aggregated
- qc.barrier()
- qc.ccx(20,21,4)
- qc.ccx(20,21,7)
- #Original
- qc.barrier()
- qc.ccx(20,21,8)
- qc.x(20)
- #3th weights
- qc.x(21)
- #OR Aggregated
- qc.barrier()
- qc.ccx(20,21,4)
- qc.ccx(20,21,6)
- qc.ccx(20,21,7)
- #Original
- qc.barrier()
- qc.ccx(20,21,10)
- qc.x(21)
- #4th weights
- qc.x(20)
- qc.x(21)
- #OR Aggregated
- qc.barrier()
- qc.ccx(20,21,4)
- qc.ccx(20,21,6)
- qc.ccx(20,21,7)
- #Original
- qc.barrier()
- qc.ccx(20,21,8)
- qc.ccx(20,21,11)
- qc.x(21)
- qc.x(20)
- #Active Phase
- #query
- qc.barrier()
- qc.x(0)
- qc.x(3)
- qc.barrier()
- #query, counting
- #OR Aggregated
- qc.ccx(0,4,12)
- qc.ccx(1,5,13)
- qc.ccx(2,6,14)
- qc.ccx(3,7,15)
- #Original
- qc.ccx(0,8,16)
- qc.ccx(1,9,17)
- qc.ccx(2,10,18)
- qc.ccx(3,11,19)
- #Dividing
- qc.barrier()
- qc.h(22)
- #Marking
- qc.barrier()
- qc.cp(-pi/8,12,22)
- qc.cp(-pi/8,13,22)
- qc.cp(-pi/8,14,22)
- qc.cp(-pi/8,15,22)
- qc.cp(-pi/8,16,22)
- qc.cp(-pi/8,17,22)
- qc.cp(-pi/8,18,22)
- qc.cp(-pi/8,19,22)
- qc.barrier()
- qc.x(22)
- qc.cp(pi/8,12,22)
- qc.cp(pi/8,13,22)
- qc.cp(pi/8,14,22)
- qc.cp(pi/8,15,22)
- qc.cp(pi/8,16,22)
- qc.cp(pi/8,17,22)
- qc.cp(pi/8,18,22)
- qc.cp(pi/8,19,22)
- qc.barrier()
- qc.h(22)
- qc.draw()
References
- Ventura, D.; Martinez, T. Quantum associative memory with exponential capacity. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1988; Volume 1, pp. 509–513. [Google Scholar]
- Ventura, D.; Martinez, T. Quantum associative memory. Inf. Sci. 2000, 124, 273–296. [Google Scholar] [CrossRef]
- Tay, N.; Loo, C.; Perus, M. Face Recognition with Quantum Associative Networks Using Overcomplete Gabor Wavelet. Cogn. Comput. 2010, 2, 297–302. [Google Scholar] [CrossRef]
- Trugenberger, C.A. Probabilistic Quantum Memories. Phys. Rev. Lett. 2001, 87, 067901. [Google Scholar] [CrossRef] [PubMed]
- Trugenberger, C.A. Quantum Pattern Recognition. Quantum Inf. Process. 2003, 1, 471–493. [Google Scholar] [CrossRef]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the STOC’96: Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; ACM: New York, NY, USA, 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 1997, 79, 325. [Google Scholar] [CrossRef]
- Grover, L.K. A framework for fast quantum mechanical algorithms. In Proceedings of the STOC’98: Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; ACM: New York, NY, USA, 1998; pp. 53–62. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Computers Can Search Rapidly by Using Almost Any Transformation. Phys. Rev. Lett. 1998, 80, 4329–4332. [Google Scholar] [CrossRef]
- Aïmeur, E.; Brassard, B.; Gambs, S. Quantum speed-up for unsupervised learning. Mach. Learn. 2013, 90, 261–287. [Google Scholar] [CrossRef]
- Wittek, P. Quantum Machine Learning, What Quantum Computing Means to Data Mining; Elsevier Insights; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Aaronson, S. Quantum Machine Learning Algorithms: Read the Fine Print. Nat. Phys. 2015, 11, 291–293. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A. Mirror modular cloning and fast quantum associative retrieval. arXiv 2022, arXiv:2206.01644. [Google Scholar]
- Brun, T.; Klauck, H.; Nayak, A.; Rotteler, M.; Zalka, C. Comment on “Probabilistic Quantum Memories”. Phys. Rev. Lett. 2003, 91, 209801. [Google Scholar] [CrossRef] [PubMed]
- Harrow, A.; Hassidim, A.; Lloyd, S. Quantum algorithm for solving linear systems of equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum Machine Learning in Feature Hilbert Spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef]
- Palm, G. Neural Assemblies, an Alternative Approach to Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Hecht-Nielsen, R. Neurocomputing; Addison-Wesley: Reading, PA, USA, 1989. [Google Scholar]
- Steinbuch, K. Die Lernmatrix. Kybernetik 1961, 1, 36–45. [Google Scholar] [CrossRef]
- Steinbuch, K. Automat und Mensch, 4th ed.; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Willshaw, D.; Buneman, O.; Longuet-Higgins, H. Nonholgraphic associative memory. Nature 1969, 222, 960–962. [Google Scholar] [CrossRef] [PubMed]
- Contributors, Q. Qiskit: An Open-source Framework for Quantum Computing. Zenodo 2023. [Google Scholar] [CrossRef]
- Palm, G. Assoziatives Gedächtnis und Gehirntheorie. In Gehirn und Kognition; Spektrum der Wissenschaft: Heidelberg, Germany, 1990; pp. 164–174. [Google Scholar]
- Churchland, P.S.; Sejnowski, T.J. The Computational Brain; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Fuster, J. Memory in the Cerebral Cortex; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Squire, L.R.; Kandel, E.R. Memory: From Mind to Moleculus; Scientific American Library: New York, NY, USA, 1999. [Google Scholar]
- Kohonen, T. Self-Organization and Associative Memory, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; Addison-Wesley: Reading, PA, USA, 1991. [Google Scholar]
- Anderson, J.R. Cognitive Psychology and Its Implications, 4th ed.; W. H. Freeman and Company: New York, NY, USA, 1995. [Google Scholar]
- Amari, S. Learning Patterns and Pattern Sequences by Self-Organizing Nets of Threshold Elements. IEEE Trans. Comput. 1972, 100, 1197–1206. [Google Scholar] [CrossRef]
- Anderson, J.A. An Introduction to Neural Networks; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Ballard, D.H. An Introduction to Natural Computation; The MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- McClelland, J.; Kawamoto, A. Mechanisms of Sentence Processing: Assigning Roles to Constituents of Sentences. In Parallel Distributed Processing; McClelland, J., Rumelhart, D., Eds.; The MIT Press: Cambridge, MA, USA, 1986; pp. 272–325. [Google Scholar]
- OFTA. Les Re´seaux de Neurones; Masson: Paris, France, 1991. [Google Scholar]
- Schwenker, F. Küntliche Neuronale Netze: Ein Überblick über die theoretischen Grundlagen. In Finanzmarktanalyse und-Prognose mit Innovativen und Quantitativen Verfahren; Bol, G., Nakhaeizadeh, G., Vollmer, K., Eds.; Physica-Verlag: Heidelberg, Germany, 1996; pp. 1–14. [Google Scholar]
- Sommer, F.T. Theorie Neuronaler Assoziativspeicher. Ph.D. Thesis, Heinrich-Heine-Universität Düsseldorf, Düsseldorf, Germany, 1993. [Google Scholar]
- Wickelgren, W.A. Context-Sensitive Coding, Associative Memory, and Serial Order in (Speech) Behavior. Psychol. Rev. 1969, 76, 1–15. [Google Scholar] [CrossRef]
- Sa-Couto, L.; Wichert, A. “What-Where” sparse distributed invariant representations of visual patterns. Neural Comput. Appl. 2022, 34, 6207–6214. [Google Scholar] [CrossRef]
- Sa-Couto, L.; Wichert, A. Competitive learning to generate sparse representations for associative memory. arXiv 2023, arXiv:2301.02196. [Google Scholar]
- Marcinowski, M. Codierungsprobleme beim Assoziativen Speichern. Master’s Thesis, Fakultät für Physik der Eberhard-Karls-Universität Tübingen, Tübingen, Germany, 1987. [Google Scholar]
- Freeman, J.A. Simulating Neural Networks with Mathematica; Addison-Wesley: Reading, PA, USA, 1994. [Google Scholar]
- Sacramento, J.; Wichert, A. Tree-like hierarchical associative memory structures. Neural Netw. 2011, 24, 143–147. [Google Scholar] [CrossRef] [PubMed]
- Sacramento, J.; Burnay, F.; Wichert, A. Regarding the temporal requirements of a hierarchical Willshaw network. Neural Netw. 2012, 25, 84–93. [Google Scholar] [CrossRef] [PubMed]
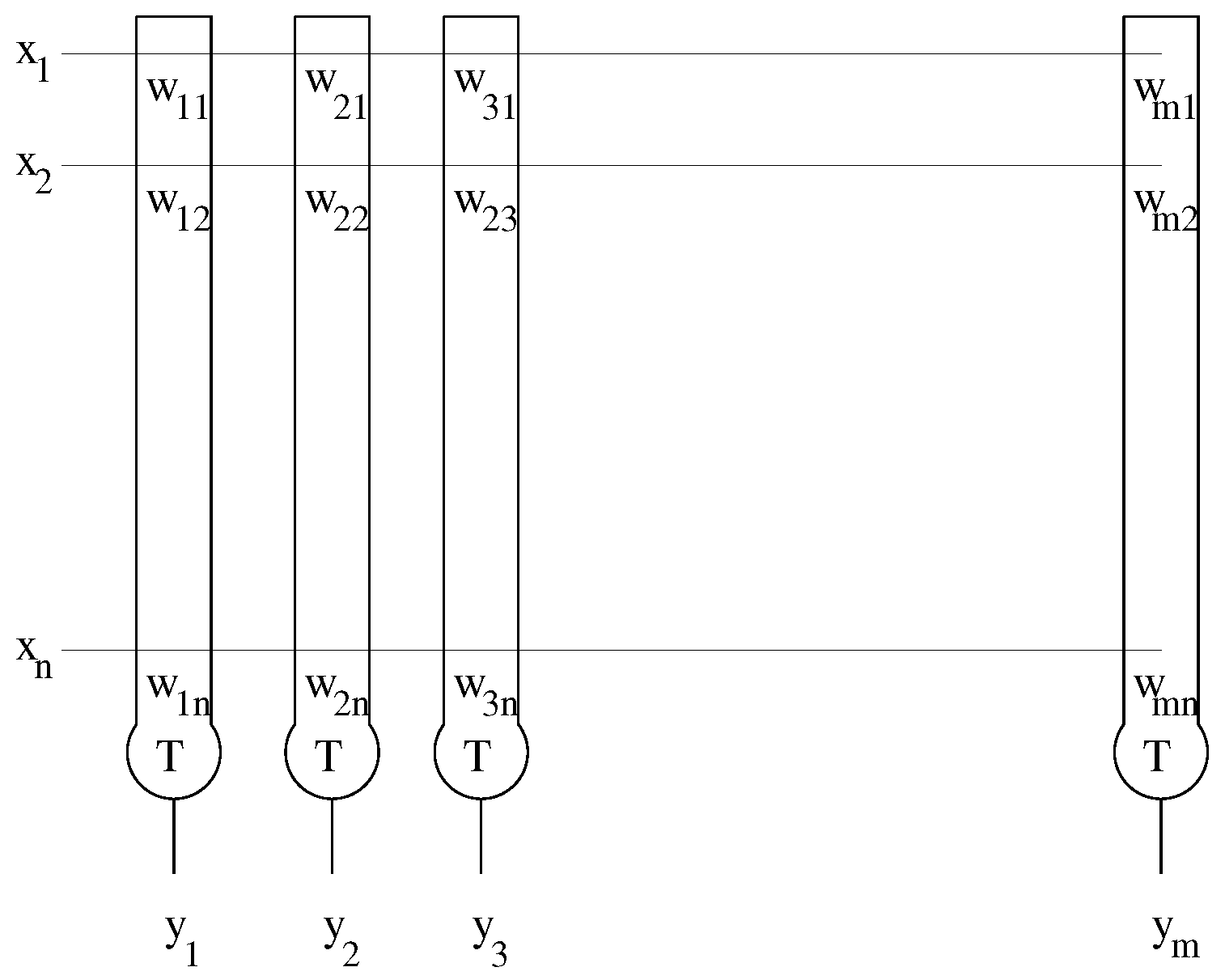







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wichert, A. Quantum Lernmatrix. Entropy 2023, 25, 871. https://doi.org/10.3390/e25060871
Wichert A. Quantum Lernmatrix. Entropy. 2023; 25(6):871. https://doi.org/10.3390/e25060871
Chicago/Turabian StyleWichert, Andreas. 2023. "Quantum Lernmatrix" Entropy 25, no. 6: 871. https://doi.org/10.3390/e25060871
APA StyleWichert, A. (2023). Quantum Lernmatrix. Entropy, 25(6), 871. https://doi.org/10.3390/e25060871