Bandit Algorithm Driven by a Classical Random Walk and a Quantum Walk
Abstract
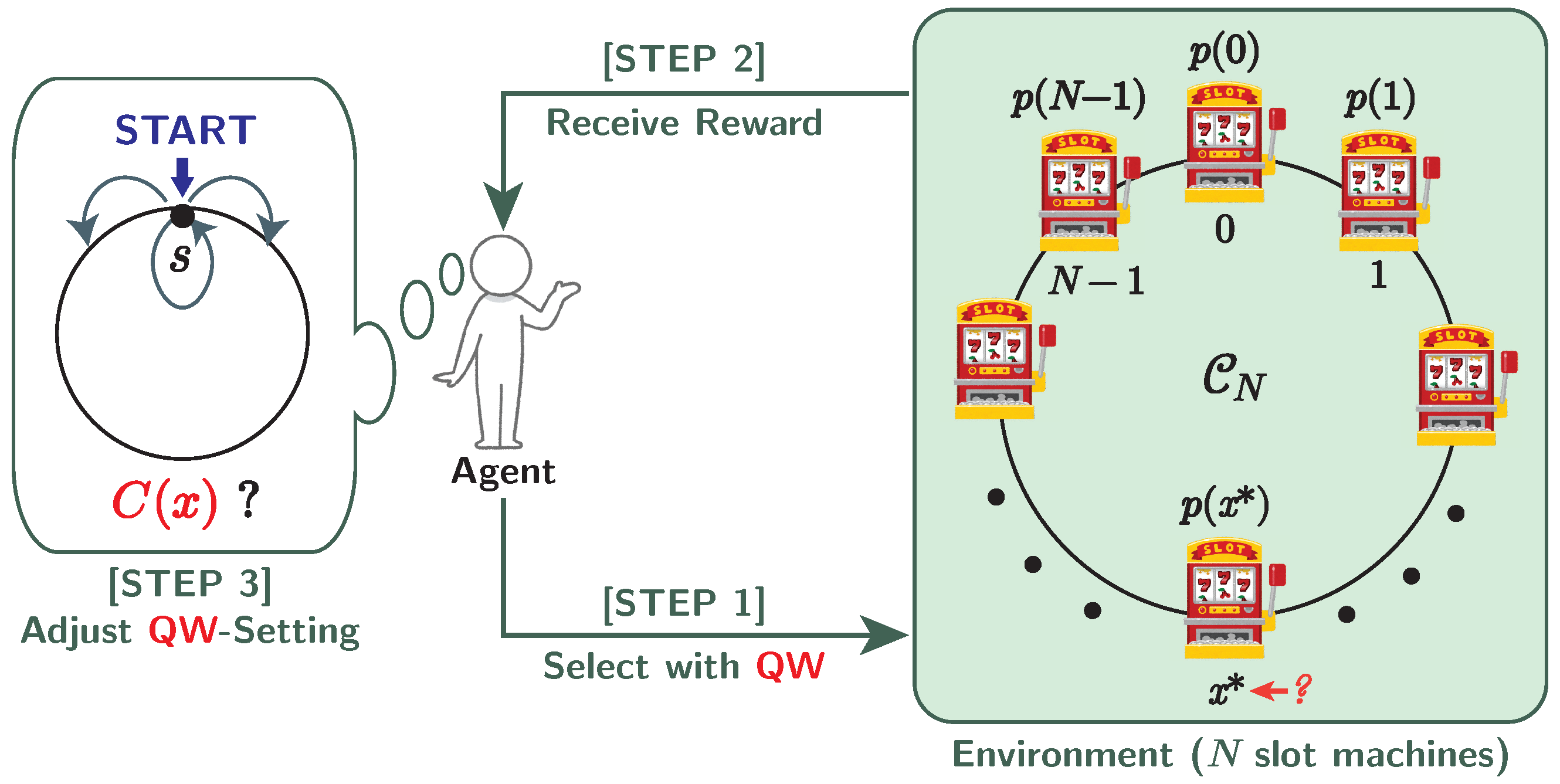
1. Introduction
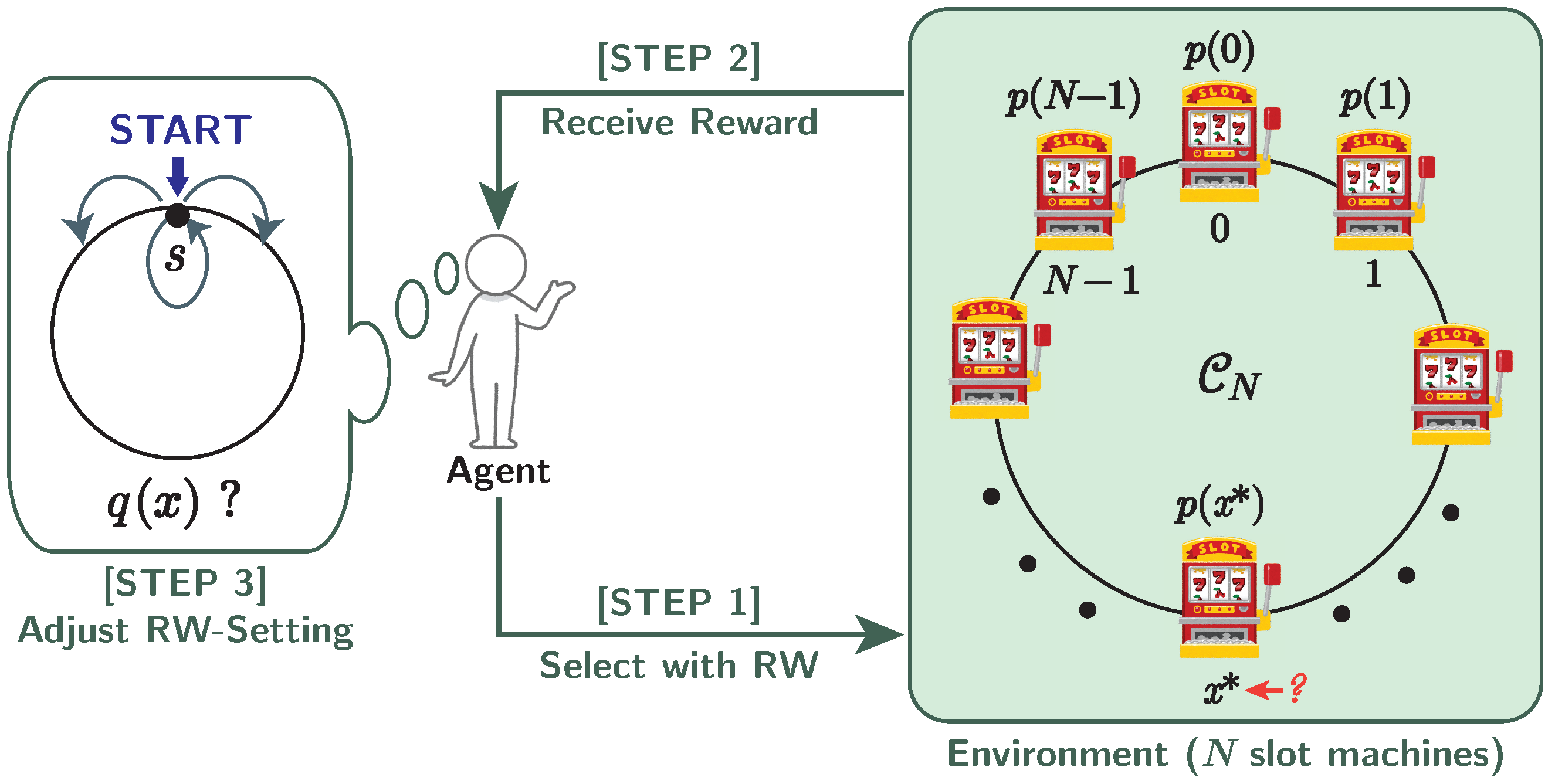
2. Random-Walk-Based Model for MAB Problem
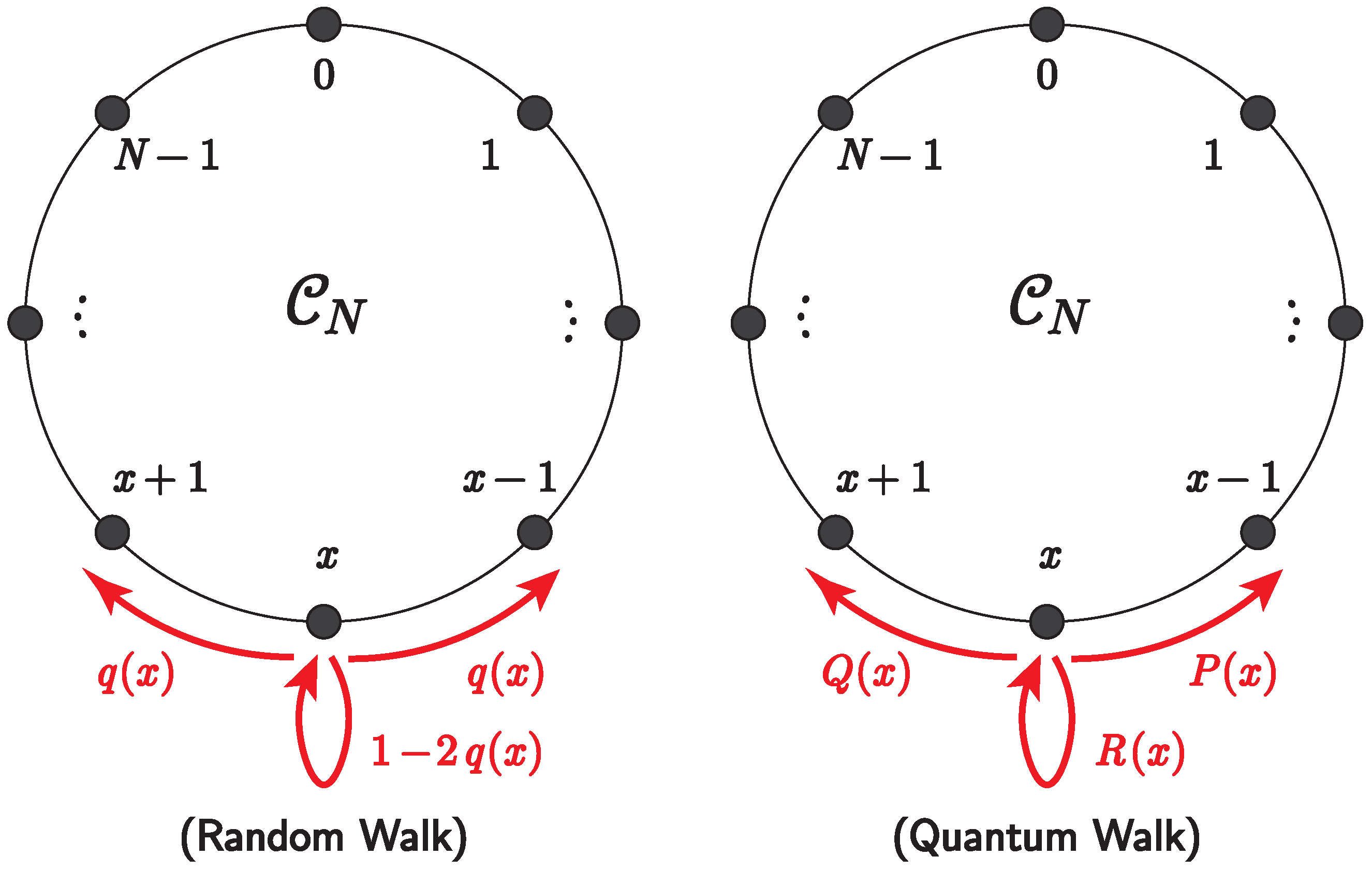
2.1. Random Walk on Cycles
- A walker initially exists at position .
- At each time step, a walker at position x moves one unit clockwise with probability , moves one unit anti-clockwise with probability or stays at the current position with probability .
2.2. Random-Walk-Based Algorithm
- : Initial position of random walk in the j-th decision.
- : Clockwise-transition probability and anti-clockwise-transition probability in the j-th decision.
- : Vertex (slot machine) measured in the j-th decision.
- : Reward on the j-th decision. This value is probabilistically determined by the Bernoulli distribution ; that is,
- : Number of decisions where the slot machine x is selected until the j-th decision.
- : Number of decisions where the slot machine x gives the reward until the j-th decision.
- : Empirical probability that the slot machine x gives the reward on the j-th decision:
- Initial position : Probabilistically determined by the uniform distribution on .
- Transition probability: for all .
3. Quantum-Walk-Based Model for MAB Problem
3.1. Quantum Walk on Cycles
3.2. Quantum-Walk-Based Algorithm
- : Initial state of quantum walk on the j-th decision.
- : Initial position of quantum walk on the j-th decision.
- : Vertex (slot machine) measured on the j-th decision.
- : Reward on the j-th decision, which follows the Bernoulli distribution :
- : Number of decisions in which slot machine x is selected until the j-th decision.
- : Number of decisions in which slot machine x gives the reward until the j-th decision.
- : Empirical probability that slot machine x gives the reward on the j-th decision:
- Initial state: . Here the initial position is probabilistically determined by the uniform distribution on .
- Parameter of coin matrices: for all .
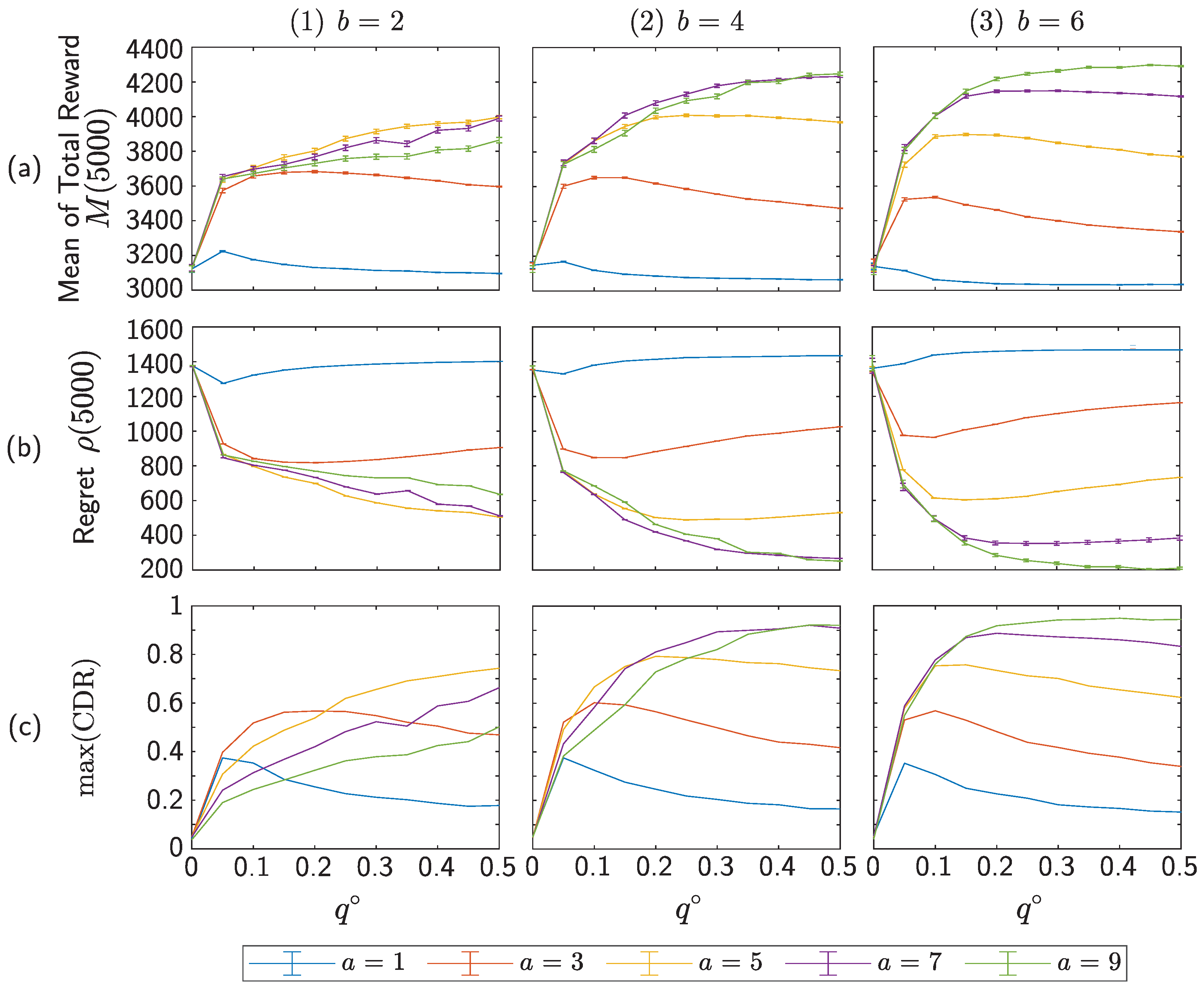
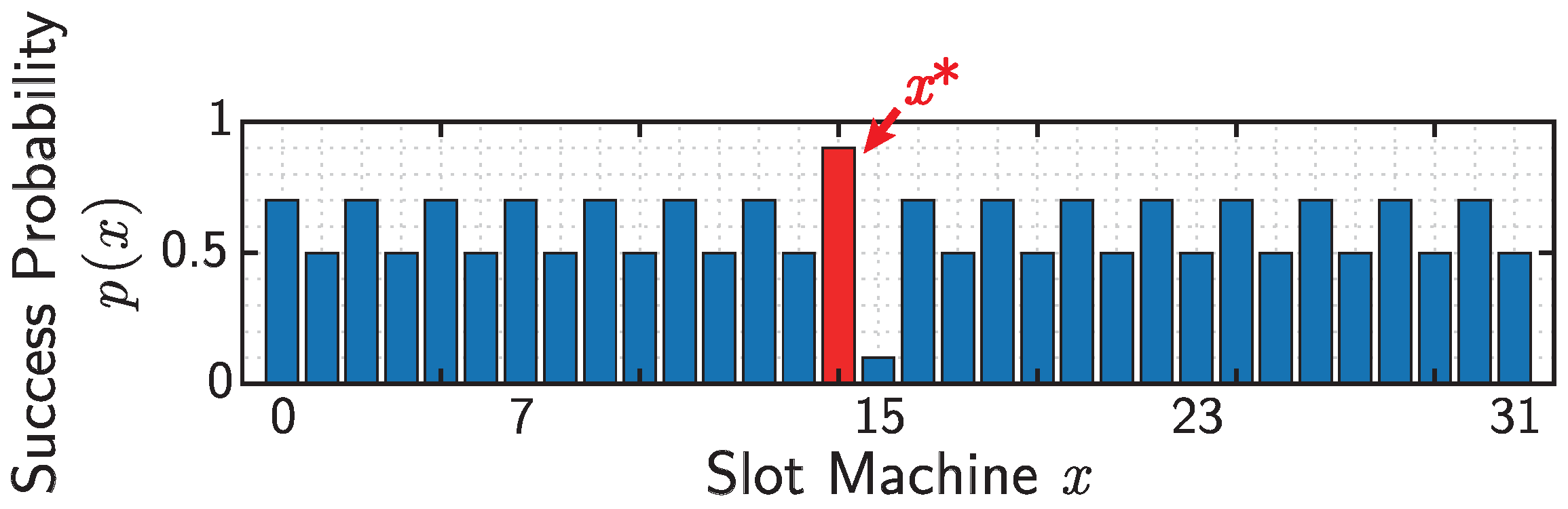
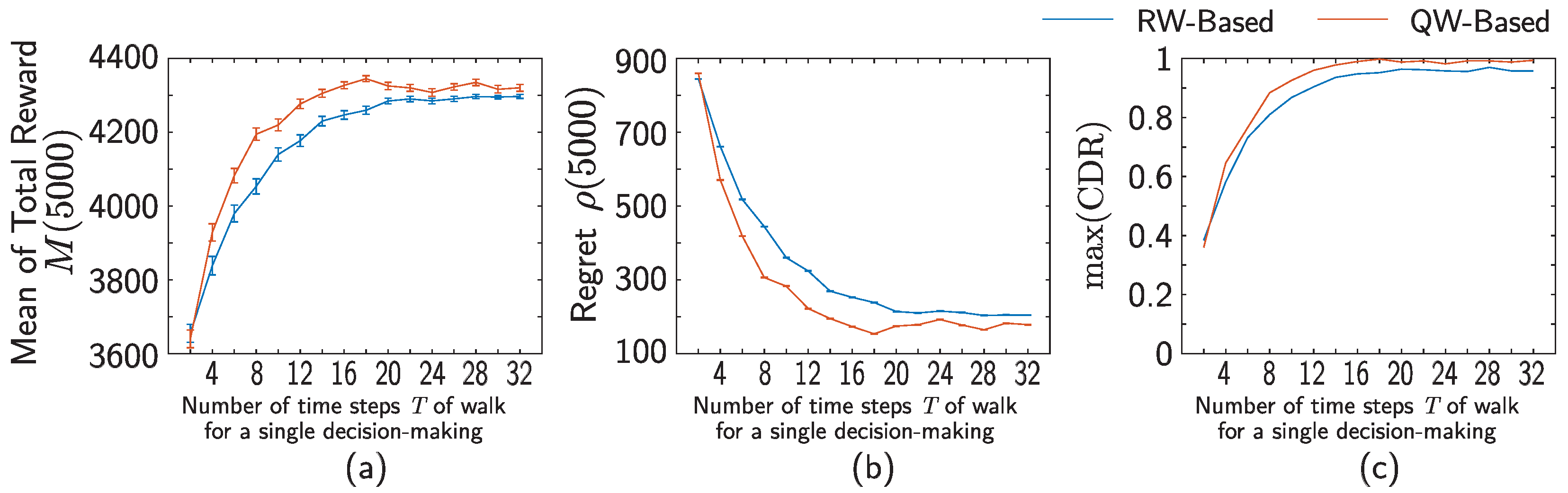
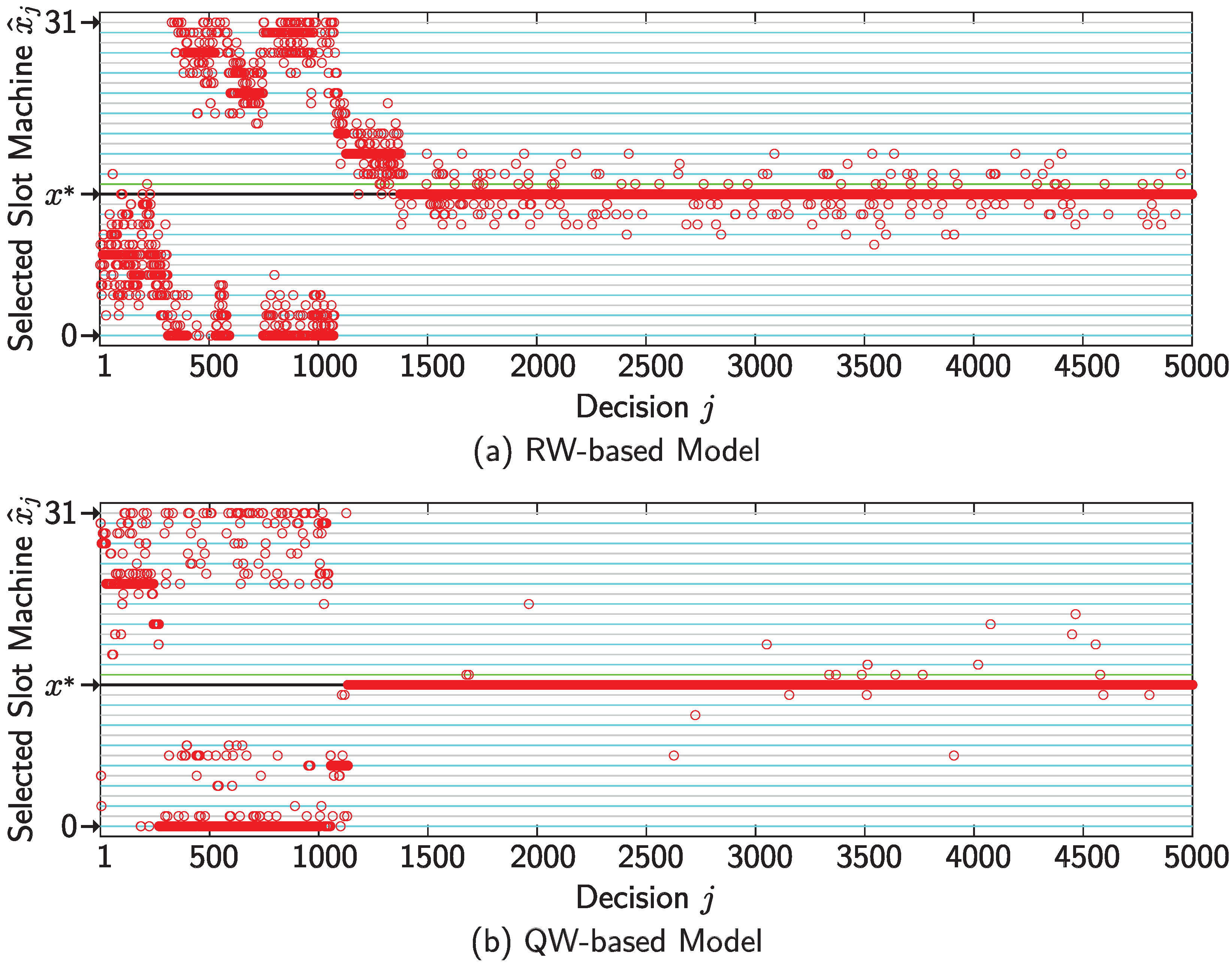
4. Numerical Simulations
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
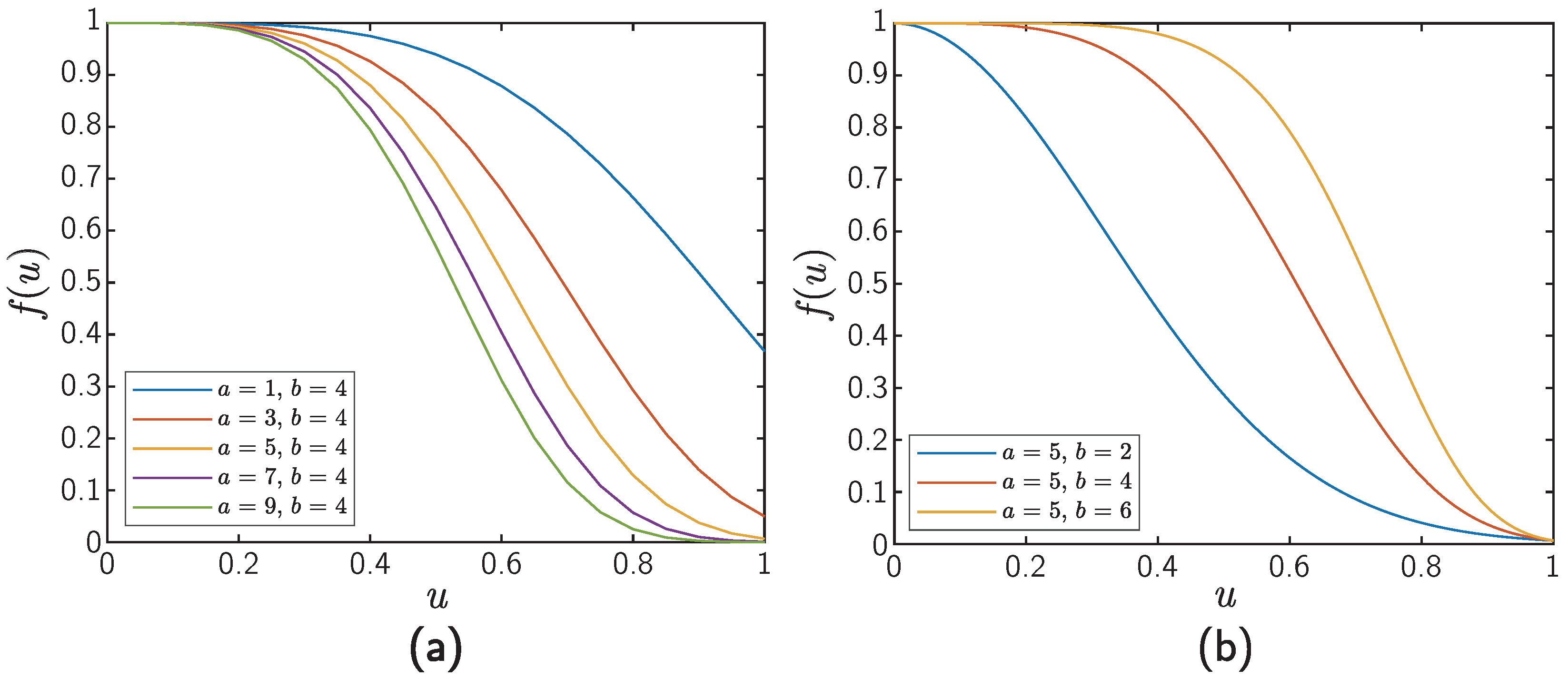
Appendix A. Parameter-Dependencies of RW- and QW-Based Models

References
- Konno, N. Quantum walks. In Quantum Potential Theory; Springer: Berlin/Heidelberg, Germany, 2008; pp. 309–452. [Google Scholar]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Kendon, V. Decoherence in quantum walks—A review. Math. Struct. Comput. Sci. 2007, 17, 1169–1220. [Google Scholar] [CrossRef]
- Inui, N.; Konno, N.; Segawa, E. One-dimensional three-state quantum walk. Phys. Rev. E 2005, 72, 056112. [Google Scholar] [CrossRef]
- Konno, N.; Łuczak, T.; Segawa, E. Limit measures of inhomogeneous discrete-time quantum walks in one dimension. Quantum Inf. Process. 2013, 12, 33–53. [Google Scholar] [CrossRef]
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-dimensional quantum walks. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, Hersonissos, Greece, 6–8 July 2001; pp. 37–49. [Google Scholar]
- Gudder, S.P. Quantum Probability; Elsevier Science: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef]
- Konno, N. Quantum random walks in one dimension. Quantum Inf. Process. 2002, 1, 345–354. [Google Scholar] [CrossRef]
- Konno, N. A new type of limit theorems for the one-dimensional quantum random walk. J. Math. Soc. Jpn. 2005, 57, 1179–1195. [Google Scholar] [CrossRef]
- Linden, N.; Sharam, J. Inhomogeneous quantum walks. Phys. Rev. A 2009, 80, 052327. [Google Scholar] [CrossRef]
- Konno, N. Localization of an inhomogeneous discrete-time quantum walk on the line. Quantum Inf. Process. 2010, 9, 405–418. [Google Scholar] [CrossRef]
- Shikano, Y.; Katsura, H. Localization and fractality in inhomogeneous quantum walks with self-duality. Phys. Rev. E 2010, 82, 031122. [Google Scholar] [CrossRef]
- Sunada, T.; Tate, T. Asymptotic behavior of quantum walks on the line. J. Funct. Anal. 2012, 262, 2608–2645. [Google Scholar] [CrossRef]
- Bourgain, J.; Grünbaum, F.; Velázquez, L.; Wilkening, J. Quantum recurrence of a subspace and operator-valued Schur functions. Commun. Math. Phys. 2014, 329, 1031–1067. [Google Scholar] [CrossRef]
- Suzuki, A. Asymptotic velocity of a position-dependent quantum walk. Quantum Inf. Process. 2016, 15, 103–119. [Google Scholar] [CrossRef]
- Sadowski, P.; Miszczak, J.A.; Ostaszewski, M. Lively quantum walks on cycles. J. Phys. Math. Theor. 2016, 49, 375302. [Google Scholar] [CrossRef]
- Godsil, C.; Zhan, H. Discrete-time quantum walks and graph structures. J. Comb. Theory Ser. A 2019, 167, 181–212. [Google Scholar] [CrossRef]
- Cedzich, C.; Fillman, J.; Geib, T.; Werner, A. Singular continuous Cantor spectrum for magnetic quantum walks. Lett. Math. Phys. 2020, 110, 1141–1158. [Google Scholar] [CrossRef]
- Ahmad, R.; Sajjad, U.; Sajid, M. One-dimensional quantum walks with a position-dependent coin. Commun. Theor. Phys. 2020, 72, 065101. [Google Scholar] [CrossRef]
- Kiumi, C. Localization of space-inhomogeneous three-state quantum walks. J. Phys. A Math. Theor. 2022, 55, 225205. [Google Scholar] [CrossRef]
- Konno, N. A new time-series model based on quantum walk. Quantum Stud. Math. Found. 2019, 6, 61–72. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Obuse, H. Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 2013, 88, 121406. [Google Scholar] [CrossRef]
- Obuse, H.; Asbóth, J.K.; Nishimura, Y.; Kawakami, N. Unveiling hidden topological phases of a one-dimensional Hadamard quantum walk. Phys. Rev. B 2015, 92, 045424. [Google Scholar] [CrossRef]
- Matsuoka, L.; Ichihara, A.; Hashimoto, M.; Yokoyama, K. Theoretical study for laser isotope separation of heavy-element molecules in a thermal distribution. In Proceedings of the International Conference Toward and Over the Fukushima Daiichi Accident (GLOBAL 2011), Chiba, Japan, 11–16 December 2011. No. 392063. [Google Scholar]
- Ichihara, A.; Matsuoka, L.; Segawa, E.; Yokoyama, K. Isotope-selective dissociation of diatomic molecules by terahertz optical pulses. Phys. Rev. A 2015, 91, 043404. [Google Scholar] [CrossRef]
- Wang, J.; Manouchehri, K. Physical Implementation of Quantum Walks; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Ide, Y.; Konno, N.; Matsutani, S.; Mitsuhashi, H. New theory of diffusive and coherent nature of optical wave via a quantum walk. Ann. Phys. 2017, 383, 164–180. [Google Scholar] [CrossRef]
- Yamagami, T.; Segawa, E.; Konno, N. General condition of quantum teleportation by one-dimensional quantum walks. Quantum Inf. Process. 2021, 20, 224. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, Y.; Xue, P. Generalized teleportation by quantum walks. Quantum Inf. Process. 2017, 16, 221. [Google Scholar] [CrossRef]
- Vlachou, C.; Krawec, W.; Mateus, P.; Paunković, N.; Souto, A. Quantum key distribution with quantum walks. Quantum Inf. Process. 2018, 17, 288. [Google Scholar] [CrossRef]
- Childs, A.M. Universal computation by quantum walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef] [PubMed]
- Childs, A.M.; Gosset, D.; Webb, Z. Universal computation by multiparticle quantum walk. Science 2013, 339, 791–794. [Google Scholar] [CrossRef]
- Meyer, D.A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 1996, 85, 551–574. [Google Scholar] [CrossRef]
- Meyer, D.A. On the absence of homogeneous scalar unitary cellular automata. Phys. Lett. A 1996, 223, 337–340. [Google Scholar] [CrossRef]
- Szegedy, M. Quantum speed-up of Markov chain based algorithms. In Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; pp. 32–41. [Google Scholar]
- Patel, A.; Raghunathan, K.; Rungta, P. Quantum random walks do not need a coin toss. Phys. Rev. A 2005, 71, 032347. [Google Scholar] [CrossRef]
- Portugal, R.; Santos, R.A.; Fernandes, T.D.; Gonçalves, D.N. The staggered quantum walk model. Quantum Inf. Process. 2016, 15, 85–101. [Google Scholar] [CrossRef]
- Konno, N.; Portugal, R.; Sato, I.; Segawa, E. Partition-based discrete-time quantum walks. Quantum Inf. Process. 2018, 17, 100. [Google Scholar] [CrossRef]
- Robbins, H. Some aspects of the sequential design of experiments. Bull. Am. Math. Soc. 1952, 58, 527–535. [Google Scholar] [CrossRef]
- Daw, N.D.; O’doherty, J.P.; Dayan, P.; Seymour, B.; Dolan, R.J. Cortical substrates for exploratory decisions in humans. Nature 2006, 441, 876–879. [Google Scholar] [CrossRef]
- Sarkar, R.S.; Mandal, A.; Adhikari, B. Periodicity of lively quantum walks on cycles with generalized Grover coin. Linear Algebra Its Appl. 2020, 604, 399–424. [Google Scholar] [CrossRef]
- Han, Q.; Bai, N.; Kou, Y.; Wang, H. Three-state quantum walks on cycles. Int. J. Mod. Phys. B 2022, 36, 2250075. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Lai, L.; El Gamal, H.; Jiang, H.; Poor, H.V. Cognitive medium access: Exploration, exploitation, and competition. IEEE Trans. Mob. Comput. 2010, 10, 239–253. [Google Scholar]
- Kim, S.J.; Naruse, M.; Aono, M. Harnessing the computational power of fluids for optimization of collective decision making. Philosophies 2016, 1, 245–260. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R.E. Gambling in a rigged casino: The adversarial multi-armed bandit problem. In Proceedings of the IEEE 36th Annual Foundations of Computer Science, Milwaukee, WI, USA, 23–25 October 1995; pp. 322–331. [Google Scholar]

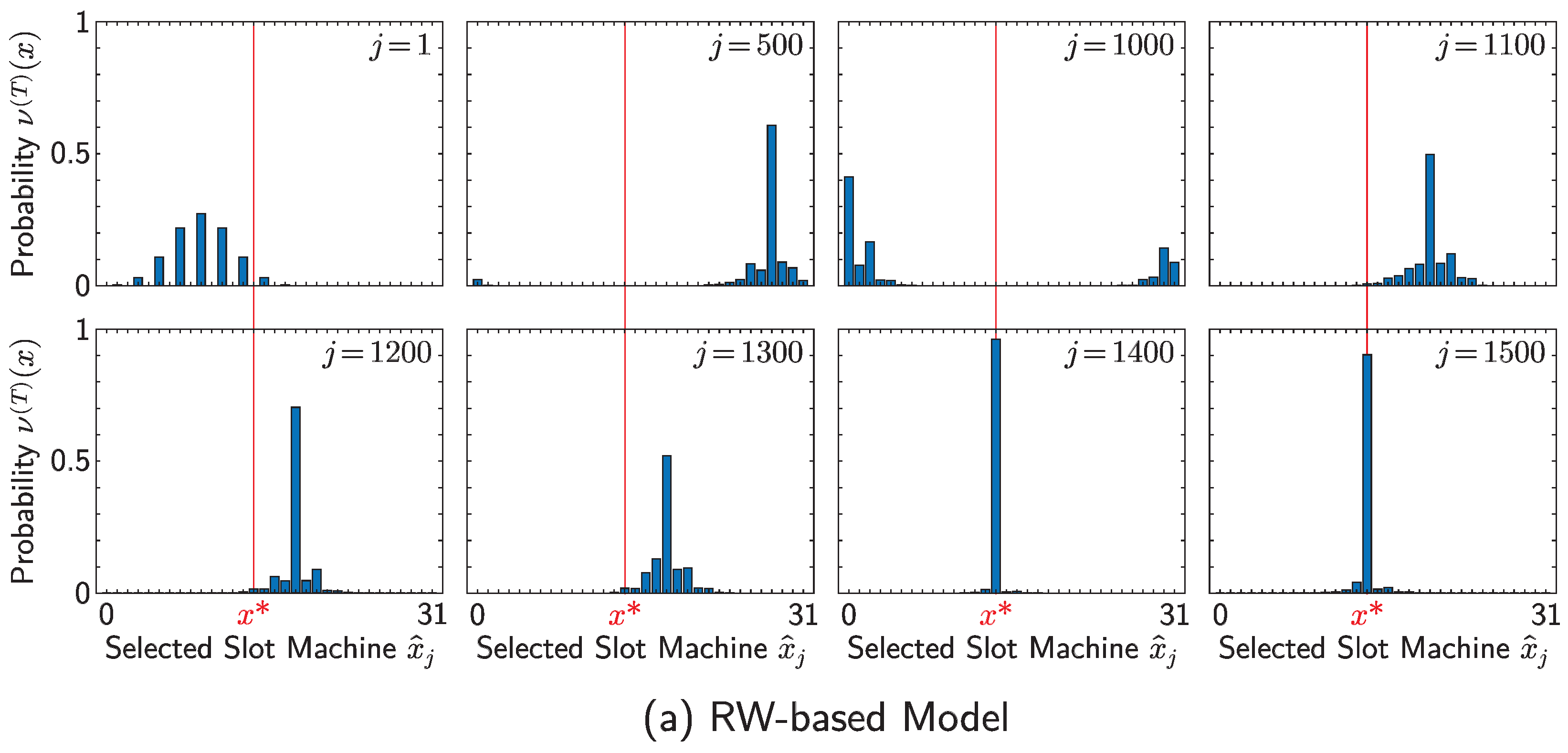
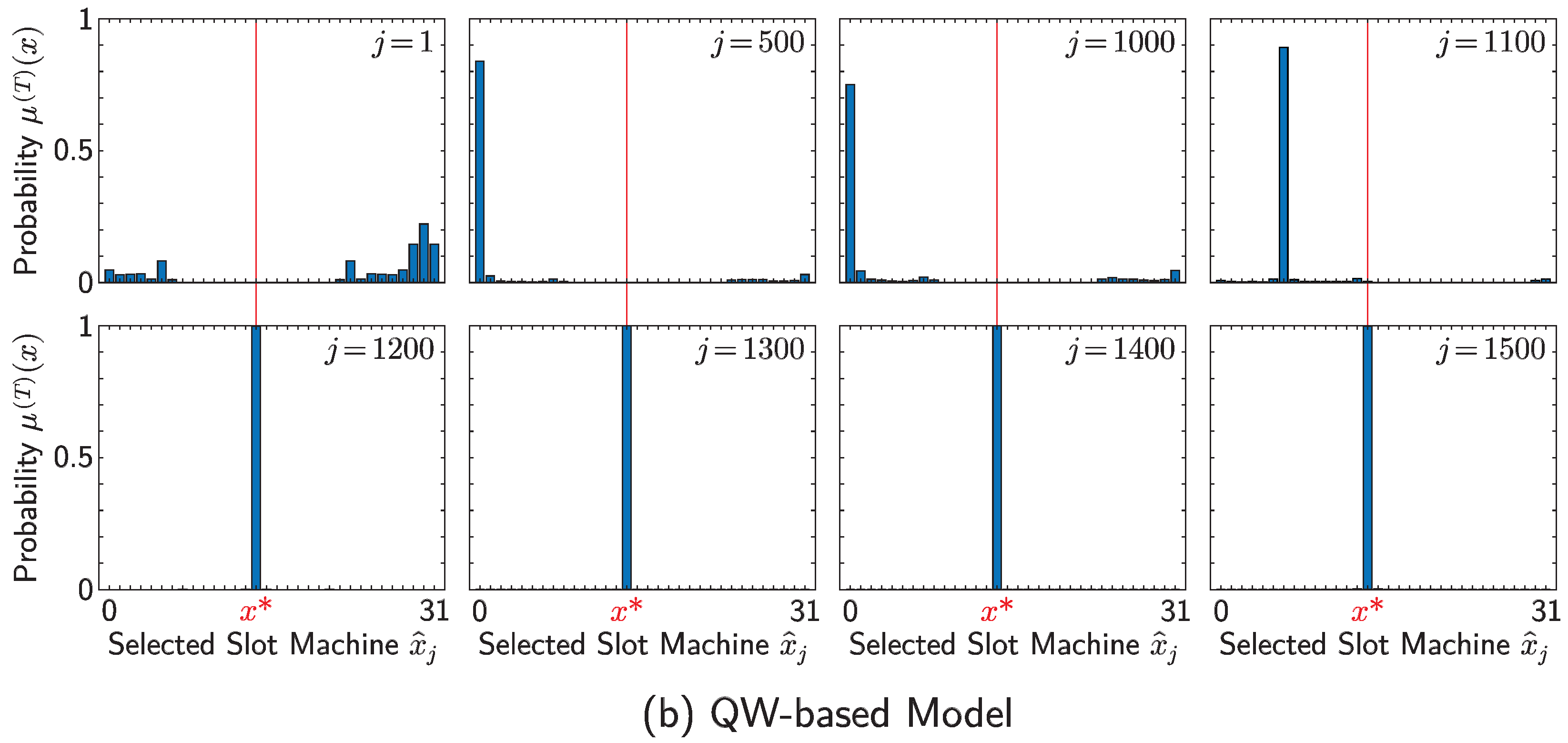
| Parameter | Symbol | Value |
|---|---|---|
| Number of slot machines | N | 32 |
| Number of runs | K | 500 |
| Number of decisions for a single run | J | 5000 |
| Parameters for the QW-based model | ||
| Parameters for the RW-based model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamagami, T.; Segawa, E.; Mihana, T.; Röhm, A.; Horisaki, R.; Naruse, M. Bandit Algorithm Driven by a Classical Random Walk and a Quantum Walk. Entropy 2023, 25, 843. https://doi.org/10.3390/e25060843
Yamagami T, Segawa E, Mihana T, Röhm A, Horisaki R, Naruse M. Bandit Algorithm Driven by a Classical Random Walk and a Quantum Walk. Entropy. 2023; 25(6):843. https://doi.org/10.3390/e25060843
Chicago/Turabian StyleYamagami, Tomoki, Etsuo Segawa, Takatomo Mihana, André Röhm, Ryoichi Horisaki, and Makoto Naruse. 2023. "Bandit Algorithm Driven by a Classical Random Walk and a Quantum Walk" Entropy 25, no. 6: 843. https://doi.org/10.3390/e25060843
APA StyleYamagami, T., Segawa, E., Mihana, T., Röhm, A., Horisaki, R., & Naruse, M. (2023). Bandit Algorithm Driven by a Classical Random Walk and a Quantum Walk. Entropy, 25(6), 843. https://doi.org/10.3390/e25060843





