1. Introduction
This paper is a contribution to the special issue
Quantum Chaos, which is dedicated to the 80th birthday of Giulio Casati who is a leading expert in the fields of classical and quantum chaos. He, actually, already expressed in [
1] the conjecture that the spectral properties of quantum systems with a chaotic classical dynamics coincide with those of random matrices from the Gaussian ensembles (GEs) of corresponding universality class [
2], that is, before Bohigas, Gianoni and Schmit formulated the famous BGS conjecture [
3]. According to the BGS conjecture, they are well described by random marix theory (RMT) [
2,
4,
5,
6,
7], where the appropriate GE for quantum systems with preserved and violated time-reversal invariance are the Gaussian orthogonal ensemble (GOE) and the Gaussian unitary ensemble (GUE), respectively. Criteria for its validity were identified in Ref. [
8] based on the semiclassical periodic orbit (PO) theory, which was pioneered by Gutzwiller [
9,
10]. Casati considered a billiard with the shape of a stadium. Billiards provide a particularly suited model for studies in the context of quantum chaos. The dynamics of classical billiards (CBs), consisting of a point particle which moves freely inside a bounded two-dimensional domain and is reflected specularly at the boundary, can be engineered through the choice of their shape [
11,
12,
13]. The eigenstates of the corresponding nonrelativistic quantum billiard (QB) are determined by solving the Schrödinger equation for a free particle and imposing the Dirichlet boundary condition (BC) on the resulting wave functions. Berry and Tabor showed in [
14] based on action-angle variables that the spectral properties of typical integrable systems [
15] agree well with those of Poissonian random numbers. However, there are numerous examples for ’untypical’ integrable systems, a paradigm one being the harmonic oscillator [
16]. Another example is polygonal billiards [
17,
18,
19], such as triangular billiards, which have been investigated by Casati and his collaborators for nearly three decades [
20,
21,
22,
23] and the rectangular billiard [
24]. Billiards with the shapes of rational polygonals of which the boundary comprises diffractive corners with angles
where
are integers and
[
17,
25,
26,
27,
28,
29,
30,
31,
32] are neither integrable nor chaotic. Therefore, they are referred to as pseudointegrable systems. Their phase space trajectories propagate on invariant surfaces that are topologically equivalent to multihandled, two-dimensional tori with genus
, implying that they are not ergodic in phase space. Yet, the motion in such billiards has a chaotic component arising from the diffractive corners, which are of measure zero in classical phase space. The spectral properties of the corresponding QB differ considerably from those of typical integrable systems [
26,
28,
29,
30,
31]. To be more explicit, they exhibit features that are intermediate between those of Poissonian random numbers and those of random matrices from the GOE in the sense that the levels repel each other linearly like in chaotic systems, and their nearest-neighbor spacing distribution decreases exponentially for large spacings, which is typical for integrable systems [
33]. Depending on the choice of angles of a right-triangle QB, the properties are well described by those of semi-Poissonian numbers, which are obtained by deleting every second one in a sequence of Poissonian ones [
23,
34]. Such cases are considered in the present work.
We present results obtained for the spectral properties, momentum distributions [
35] and Husimi functions [
36,
37] of the rectangular and square-shaped relativistic neutrino billiards (NBs) and their symmetry-projected eigenstates. These are obtained by separating their eigenstates according to their transformation properties under rotation by
and
, respectively. Neutrino billiards were introduced by Berry and Mondragon [
38]. They are governed by the Weyl equation [
39] for a non-interacting, massless spin-1/2 particle—commonly referred to as the Dirac equation in this context [
38]—with the BC that the outward current vanishes. In distinction to QBs, NBs and the relativistic quantum systems considered in Ref. [
40] do not have a well-defined classical counterpart. Insight into their behavior in the semiclassical limit can be obtained based on a semiclassical approximation for the fluctuating part of their spectral density in terms of a trace formula [
41,
42], which is applicable from the ultrarelativistic limit for massless neutrinos to the nonrelativistic limit of large mass
where the energy is close to the rest energy
[
43]. The trace formula is a sum over periodic orbits of the CB of corresponding shape, where in the ultrarelativistic limit, those with an odd number of reflections at the boundary are missing.
An alternative type of billiards exhibiting relativistic features in part of their eigenvalue spectrum are graphene billiards, which are constructed by cutting a honeycomb lattice out of their shape. They are used to model properties of artificial graphene flakes based on a tight-binding model [
44,
45]. Finite-size sheets of graphene [
46,
47,
48,
49], referred to as graphene quantum dots, have the advantage that they can be studied experimentally. The first experiments were presented in [
50,
51,
52]. In the vicinity of the corners of the hexagonal Brillouin zone, where the conduction and valence band touch each other conically, the energy excitations are governed by the Dirac equation for massless spin-1/2 particles [
53]. The occurrence of the conical structure solely originates from the honeycomb structure of graphene, which is formed by two interpenetrating triangular lattices. This led to the realization of numerous experimental ’artificial-graphene’ realizations [
54]. Boundary conditions on the spinor components in a graphene billiard were formulated in [
55,
56,
57]. We modeled rectangular, Africa-shaped and threefold-symmetric graphene billiards experimentally with flat superconducting microwave photonic crystals [
58,
59,
60,
61,
62] and found agreement with the spectral properties of massive neutrino billiards only beyond a certain mass. In addition, theoretical studies of rectangular graphene quantum dots yielded deviations from those of massless neutrino billiards [
63]. Their origin is explained in Ref. [
64] and may be attributed to the presence of the boundary and differing BCs. The extraordinary features presented in this work are only observed in the ultrarelativistic limit for massless neutrino billiards. Similar studies will be performed for graphene billiards for varying BCs in a separate work.
The work was motivated by results obtained in [
65] for the equilateral triangle and in [
66] for sectors of the circle and ellipse NB. The boundary of the equilateral triangle has a
symmetry [
67], that is, threefold rotational symmetry and mirror symmetries with respect to its main axes: that of the circle belongs to the U(1) symmetry class, which comprises all
M-fold rotational symmetries with
, and that of the ellipse has mirror symmetries with respect to its minor and major axes and a twofold rotational symmetry. Generally, the eigenfunctions of a QB with a mirror symmetry are separated into eigenfunctions which are either symmetric or antisymmetric with respect to the symmetry axes, and they fulfill either Neumann or Dirichlet BCs along them. This is not possible for NBs. However, as will be outlined in
Section 2, the eigenstates of NBs whose boundary has a
M-fold rotational symmetry can be separated according to their transformation properties under rotation by
into symmetry-projected eigenstates. Sectors of NBs are constructed by cutting these along the borders of a fundamental domain associated with a discrete rotational symmetry and imposing the same boundary conditions along the cutlines as along the outer boundary, that is, as for the full NB. These NBs are referred to as symmetry-reduced NBs in the following. The circle and ellipse sector CBs have an integrable classical dynamic [
68,
69], and the corresponding QBs exhibit Poissonian statistics. The symmetry-projected eigenstates of the circle and ellipse NBs have been determined analytically in Refs. [
38,
41,
65,
70]. Their spectral properties also exhibit Poissonian statistics, that is, they agree with those of the corresponding QB. The spinor components of the eigenfunctions of an NB are linked through the BCs at the boundary [
38]. Furthermore, for NBs with a discrete rotational symmetry, they transform differently under the associated rotation [
65,
71], implying that the symmetry classes are intermingled when cutting an NB into symmetry-reduced NBs. We demonstrated in [
66] that consequently, the symmetry-reduced and full NBs cannot have any common eigenstates and that the spectral properties of symmetry-reduced circle NBs with an arbitrary inner angle smaller than
and the quarter-ellipse NBs with sufficiently small eccentricity agree with GOE after extracting the contributions from librational modes. This was also attributed to the discontinuity of the BC at the corners, where straight and curved parts are connected.
In [
65], we computed the eigenstates of massive equilateral triangle NBs and their symmetry-projected eigenstates analytically and found that they coincide with those of the corresponding QB. Their short-range correlations exhibit the nontypical behavior expected for rectangular billiards whose side lengths are commensurable; however, otherwise, the spectral properties agree with semi-Poisson statistics. In contrast, those of the massless right-triangle NB, which is obtained by cutting the equilateral triangle NB along a mirror-symmetry axis, agree with Poisson [
66]. These results are in contrast to those for the ellipse and circle NBs and corresponding sector NBs. They are attributed to the fact that the equilateral triangle NB has no curved boundary parts. In the present work, we investigate properties of the symmetry-projected and symmetry-reduced eigenstates of rectangular billiards with commensurable and incommensurable side length. The central question was whether the symmetry-projected eigenstates of rectangular NBs show a similar behavior as those of the equilateral triangle.
2. Review of Characteristic Features of Neutrino Billiards
In the two-dimensional plane
, the Dirac equation for a free spin-1/2 particle with mass
and momentum
reads
Here,
denotes the Dirac Hamiltionian,
,
are the Pauli matrices, and
is the energy of the particle, where
k is the free-space wave vector and
is the ratio of the rest-energy momentum and free-space momentum. The NB was introduced in Ref. [
38] for the ultrarelativistic, i.e., massless case
. It is characterized by the way the particle is confined to the billiard domain
without destroying the self-adjointness of the Hamiltonian. This is ensured by imposing along its boundary
on the solutions of Equation (
1) the BC that the normal component of the local current, which is given by the expectation value of the current operator
,
, vanishes, yielding independently of the mass [
38,
42],
Here, the boundary
or in the complex plane
is parameterized in terms of
t, and
determines the rotational direction of the flow at the boundary, where it is unidirectional [
38]. We chose
. The parameter is defined for rectangular billiards with side lengths
and
in a coordinate system, whose origin is at its center and with the
x-axis parallel to the sides with lengths
where
, while the
y-axis is parallel to those with lengths
where
. Furthermore,
is the angle of the outward-pointing normal vector
at
with respect to the
x-axis. Another choice of parameter which is commonly used is the arc-length
with
denoting the perimeter, which essentially corresponds to
t plus the sum of the lengths of the sides that have been passed when moving along the boundary where we set
at
. In a local coordinate system
which moves counterclockwise along the boundary
and whose coordinate axes are in the directions of the tangential vector
to
at
and the normal vector
, respectively, the combination of the Dirac Equation (
1) at the boundary and Equation (
2) yields with
BCs in terms of separate equations for the wave-function components [
42],
Here,
with
. Note that when introducing
the Dirac equation Equation (
1) takes the form of that for massless neutrinos with modified BCs,
The nonrelativistic limit is reached when the energy is close to the rest energy,
[
43], that is, for sufficiently large
, corresponding to
and
. Conversely, in the ultrarelativistic case
, they equal
and
. The BC imposes a phase relation on the wave-function components
at
and provides a quantization condition whose solutions are the eigenstates of the Hamiltonian
associated with the NB. Alternative BCs for the confinement of relativistic particles to a bounded domain are proposed in [
70,
72] and based on the ‘MIT’ bag model [
73].
Exact analytical solutions were derived for the equilateral triangle NB [
65,
70], the circle NB [
38] and the ellipse NB [
41] based on plane wave expansions. In [
74,
75,
76,
77,
78], the eigenenergies of Dirac particles confined to a one- and a three-dimensional box were computed based on a plane-wave ansatz employing the MIT bag model. However, even though the BCs depend either on
x or on
y, a complete quantization of the rectangular NB with such an ansatz is not possible, because the
x and
y parts of the kinetic energy term do not commute [
38]. A plane wave expansion
with
and BC Equation (
2) or, equivalently, Equation (
3) yields only one-dimensional solutions corresponding to eigenmodes propagating parallel to the
x or
y axis, for which either
or
. Therefore, we employed an extension of the boundary-integral equations (BIEs) derived in Ref. [
38] for massless NBs to massive ones [
42,
79].
The derivation is based on Green’s theorem, which provides exact integral equations for the eigenvalues and the spinor components in the interior of the billiard in terms of those on the boundary. An advantage of the boundary integral approach is that the eigenvalue problem is reduced from a two-dimensional differential equation to a one-dimensional boundary integral. The BIE is given by
where the integration variable
is related to
s by
and
with
Here,
is the Hankel function of the first kind of order
m. At
, i.e.,
,
and
have a logarithmic and a
singularity. The integral over these singularities leads to the
term on the left-hand side [
79]. Accordingly, an interval
, where
is arbitrarily small, is excluded from the integration range on the right-hand side. The corresponding BIE for
is obtained by employing in Equation (
10) the BC in Equation (
6) and those for the spinor components
are obtained with Equation (
4). In the nonrelativistic limit
, the left-hand side approaches zero, implying that the evaluation of the BIE becomes a numerical challenge. We would like to note that for
, the BIE in Equation (
10) does not provide a suitable quantization procedure since the spinor components decouple,
becomes vanishingly small and the BC for
turns into Robin BCs, which become Dirichlet BCs for
. For that reason, the BIEs are replaced in the nonrelativistic limit by one for its normal derivative [
80].
We are interested in the spectral properties and properties of the wave functions of the associated symmetry-projected eigenstates of rectangular NBs which have mirror symmtries with respect to the
x and
y axes and a twofold rotational symmetry—for the square NB, (
) even a fourfold symmetry. Yet, in this respect, there is a crucial difference between QBs and NBs, which has its origin in the fact that the BCs for NBs connect the spinor components
and
at
and may lead to distinct spectral properties, as outlined in [
66,
71,
81]. The characteristics of NBs under a reflection or a rotation operator can be summarized as follows.
Applying on the coordinate vector an orthogonal transformation,
corresponds to applying a unitary transformation
to the Dirac Hamiltonian
. If
is a solution of the Dirac equation in Equation (
1), then the eigenfunction of the transformed Dirac Hamiltonian
is given by
. The unitary operators for a mirror reflection
at the
x-axis or
at the
y-axis are
or
, respectively. However, application of the reflection operator
with
or
on a spinor eigenfunction
of
does not yield an eigenfunction of
[
82], because
does not fulfill the BC in Equation (
2).
The unitary operator
corresponding to a counterclockwise rotation by
,
with
reads
The eigenfunctions of the transformed Dirac Hamiltonian are
. For NBs whose boundary has an
M-fold rotational symmetry
and
, the BC in Equation (
2) is fulfilled for
if
is an eigenfunction of
. Thus, the Hamiltonian
can be brought to a block diagonal form according to the
M one-dimensional irreducible representations labeled by
; that is, its eigenstates can be grouped into
M subspaces defined by their transformation properties under a rotation by
[
83,
84,
85,
86], yielding the symmetry-projected eigenstates
The wave-function components corresponding to
are invariant under rotation by
, whereas for
, a rotation by
is needed to recover the original ones. The Dirac equation in Equation (
1) and the BC in Equation (
6) relate components of the spinor eigenfunction with different transformation properties under rotation by
[
65,
71]. Namely, if the first component belongs to the subspace labeled by
l,
where
, then inserting this property into the Dirac equation yields for the second one
where
corresponds to
. Similarly, using the
M-fold symmetry of the boundary of the NB, i.e.,
and inserting Equation (
15) into the BC in Equation (
6) implies that [
65,
71]
Thus, the spinor components cannot be simultaneously rotationally invariant, implying that the spinor eigenfunctions cannot be rotationally invariant. This intermingling of symmetry properties has its origin in the additional spin degree of freedom [
65,
71].
For a billiard whose boundary has an
M-fold rotational symmetry, the corresponding symmetry-reduced one is constructed by cutting it along the sides of a fundamental domain into sectors with inner angle
. The corresponding symmetry-reduced QB and NB are obtained by imposing the same BCs along the cutlines as along the outer bondary, i.e., as for the full QB, respectively, NB. These are Dirichlet BCs for the QB. Accordingly, their eigenstates coincide with rotationally invariant ones of the full QB. For the corresponding symmetry-reduced NB, the BCs in Equation (
2) are imposed along the cutlines on the outgoing current, which is in the opposite direction to the current in the full NB at one of the cutlines [
66]. Thus, the intermingling of symmetries in Equations (
15) and (
16) of the wave-function components implies that the eigenstates of an NB with a rotationally symmetric boundary cannot be eigenstates of the corresponding symmetry-reduced NB. Accordingly, their spectral properties do not necessarily coincide as demonstrated for circle and ellipse sectors in [
66]. In the following, we will refer to the symmetry class of the spinor component
when specifying the value for
l.
We would like to remark that the symmetry-projected eigenfunctions of a QB with
M-fold rotational symmetry are complex for
, implying that they are not invariant under application of the time-reversal operator
[
83]. Indeed, the eigenfunctions with symmetry class
l are transformed by
into eigenstates with
. Time-reversal invariance of the QB implies that the corresponding eigenvalues are doubly degenerate. It was demonstrated in [
83] that the spectral properties of the states with
typically show GUE statistics, whereas those of the states with
are well described by the GOE if the shape of the QB generates chaotic classical dynamics. On the other hand, the Dirac Hamiltonian in Equation (
1) itself does not commute with the time-reversal operator
. Consequently, if the shape has no mirror symmetry, for all
l, the eigenvalues of the corresponding NB are not degenerate, and the spectral properties of massless NBs typically coincide with those of the GUE.
In the present work, we investigate the spectral properties of symmetry-projected and symmetry-reduced rectangular NBs. To compute the eigenstates, we applied the BIE. It can be separated into individual BIEs for each symmetry class. To take into account the
M-fold symmetry of the boundary
of an NB, we use the periodicity properties
with
. Restricting the range of
to one fundamental domain,
, the BIEs are given as
with
and
where
3. Tools Employed for the Analysis of Properties of the Eigenstates
We analyzed the spectral properties in terms of the nearest-neighbor spacing distribution
, the integrated nearest-neighbor spacing distribution
, the number variance
and the Dyson–Mehta statistic
, which provides a measure for the rigidity of a spectrum [
2]. For this, the ordered eigenvalues
with
were unfolded to mean spacing unity by replacing them with the smooth part of the integrated spectral density,
, which is given for QBs by Weyl’s formula [
87]
, with
denoting the area of the billiard, whereas for massless NBs, the perimeter contribution cancels out [
38]. Furthermore, we analyzed distributions of the ratios [
88,
89] of consecutive spacings between nearest neighbors,
, which are dimensionless so that unfolding is not needed [
88,
89,
90].
We also computed Husimi functions which are defined in classical phase space [
5,
36]. The classical dynamics of a CB is determined by the shape of its boundary
. Similarly, the eigenstates of the corresponding QB or NB are obtained by employing the BIEs originating from Green’s theorem and thus are fully determined by their values along
. Therefore, an appropriate choice of the Poincaré surface of section (PSOS) is obtained by restricting the phase space to
, which commonly is defined in terms of Poincaré–Birkhoff coordinates
, where
with
denoting the angle of the particle trajectory with respect to the normal vector
. In Ref. [
37], Poincaré–Husimi functions are defined for nonrelativistic QBs as the projection of the normal derivative of the associated wave function
at the boundary onto a coherent state [
37], which is localized at
and periodic with period
,
Here,
and
The parameter
controls the resolution of the Husimi plots. The Poincaré–Husimi function provides a probability density of the eigenstates on the Poincaré surface of section [
37] and accordingly is commonly referred to as a quantum Poincaré surface of section. We computed Husimi functions for the NB by replacing
by the symmetry-projected spinor eigenfunctions
, where we employed Equation (
3) to determine their normal derivatives.
We, furthermore, computed momentum distributions [
35], i.e., the Fourier transform of the spinor eigenfunctions
from coordinate space
to momentum space
,
They are localized on the energy shell, that is, at values , and provide information on the directions of the plane waves that form the eigenmode, which is especially useful when it is scarred along periodic orbits or localized.
4. Numerical Results for the Symmetry-Projected Eigenstates of Rectangular NBs
In this section, we present numerical results for the spectral properties and properties of the wave functions, Husimi functions and momentum distributions of the symmetry-projected eigenstates of rectangular NBs with different side-length ratios,
and their symmetry-reduced counterparts, namely triangles
, that are obtained by cutting the corresponding rectangle
along its diagonal. The triangles
have in common that their angles have the structure
with
irrational numbers. Furthermore, in [
66], we considered a triangle, named
, which is obtained by cutting the equilataral triangle with side lengths 2 along a mirror axis into two halves. Its inner angles are
, implying that it is integrable like the
and
billiards. We computed 5000 eigenvalues for each symmetry class and NB. These studies were motivated by recent results which we obtained in Ref. [
66] for the semi-circle NB, the quarter-ellipse NB for various values of its eccentricity, and the
triangle NB [
65]. For an ellipse with semimajor and semiminor axes lengths
and
, respectively, the eccentricity is
. The classical dynamics of a particle in an ellipse CB and the semi- and quarter-ellipse CBs, which are obtained by cutting the ellipse along the semiminor and semimajor axes, respectively, is integrable because the product of the angular momenta with respect to the two focal points is a constant of motion. The eigenfunctions of the corresponding QBs are given by products of the radial and the periodic Mathieu functions [
69,
91,
92,
93,
94], and the eigenvalues are the zeroes of the radial Mathieu function at the boundary. Their spectral properties coincide with those of Poissonian random numbers. The orbits of the ellipse CB and the eigenmodes of the ellipse QB can be separated into librational modes and rotational modes. With decreasing
, the ellipse turns into a circle, and the librational modes turn into the diameter orbit, whereas with increasing eccentricity, the modes resemble those in the rectangular billiard. The eigenfunctions of the ellipse NB are given in terms of superpositions of products of the radial and periodic Mathieu functions [
41]. It has a twofold symmetry so that the spinor components
are either symmetric with respect to a rotation by
and the associated second component
is antisymmetric, or vice versa.
We showed in [
66] that the spectral properties of circle-sector NBs and quarter ellipse-sector NBs with small eccentricity, i.e., nearly circular shape, are well described by the GOE after the extraction of contributions from the diameter orbit in the former one and librational modes in the latter one that bounce back and forth parallel to the semiminor axis and have a vanishing support at the corners connecting straight and curved parts. This behavior was attributed to the intermingling of the symmetry properties associated with the rotational symmetry of the corresponding full NBs and the effects of these corners. Indeed, for the
NB, the spectral properties are close to Poisson statistics [
66], whereas we found good agreement with semi-Poissonian statistics for the symmetry-projected eigenstates of the equilateral triangle NB and QB [
65].
In
Figure 1, we present some results for the semi-ellipse NB for different eccentricities. Shown are the spectral properties of the ellipse NB and its symmetry-projected eigenstates for
and for the semi-ellipse NBs with
. Those of the symmetry-projected eigenstates are close to those of the semi-ellipse NB with
, which is close to Poisson, whereas with decreasing
, they approach semi-Poisson statistics, as is clearly visible in the ratio distributions which are shown in the right part of
Figure 1.
In
Figure 2, we show results for the square NB (
in Equation (
25)), its symmetry-projected eigenstates labeled by
and the
triangle (
in Equation (
25)).
The spectral properties of the symmetry-projected eigenstates agree well with semi-Poisson for the short-range correlations up to a certain number of mean spacings
L for the long-range correlations. The size of the deviations is similar to that of a QB with integrable classical dynamics [
20,
24] for a similar number of eigenvalues, such as, e.g., the ellipse and circle QBs and NBs [
41,
66]. The overshooting of those for the square NB with respect to Poisson statistics originates from non-systematic, occasionally occurring degeneracies of eigenvalues associated with different symmetry classes, which have also been observed for the equilateral triangle NB in Ref. [
65]. The ratio distribution of the
QB is shown together with that of the
NB in the right part of
Figure 2 in (c). It exhibits the nongeneric behavior commonly observed for rectangular QBs with rational ratios of side lengths, whereas that of the NB agrees well with Poisson statistics.
In the left part of
Figure 3, we compare length spectra, that is, the modulus of the Fourier transform
of the fluctuating part of the spectral density,
, from wave number
k to length
l for the full square NB, the symmetry-projected ones and the
triangle NB. The length spectra of the QB and NB exhibit peaks at the lengths of its periodic orbits. Generally, in the length spectra of NBs, peaks at lengths, which correspond to periodic orbits with an odd number of reflections, are missing [
42]. Such orbits are absent in rectangular CBs. Those of the symmetry-projected eigenstates show additional peaks at lengths which correspond to pseudo-orbits, that is, orbits that are periodic in the fundamental domains but not in the full system [
85,
86].
In
Figure 4, we show examples for the momentum distributions, real parts of the spinor components
and
, the local current
and Husimi functions for the symmetry-projected eigenstates of the
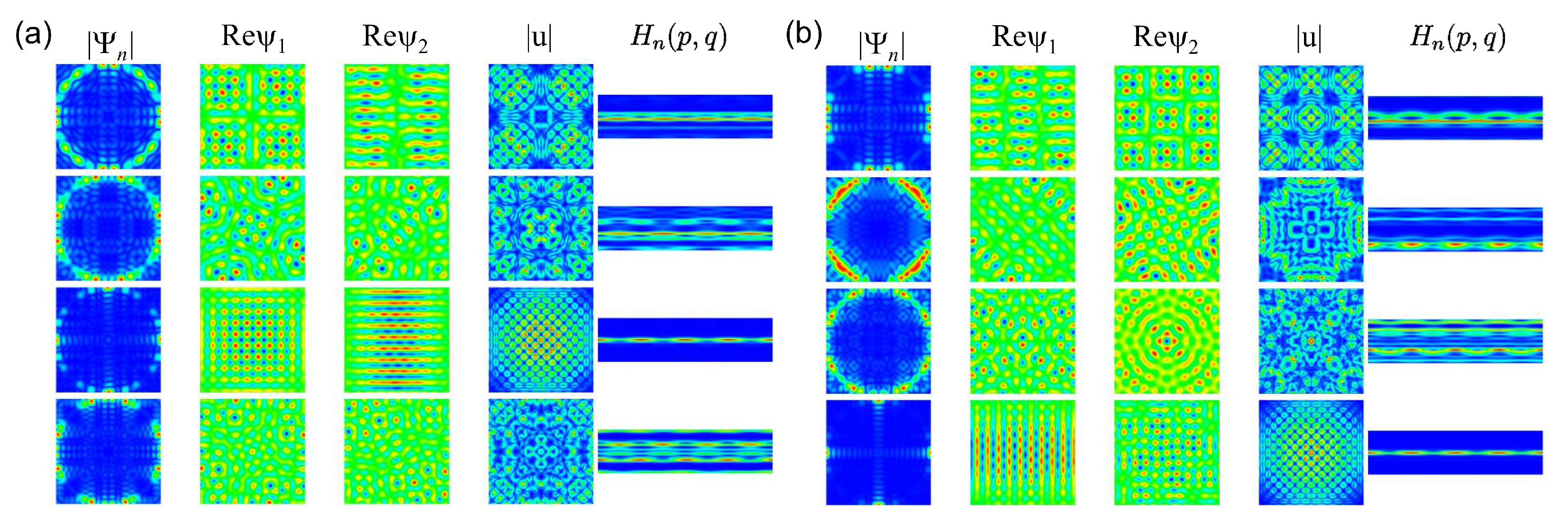
NB with
(a) and
(b). The wave-function patterns are invariant under rotation by
for
and
, and for
and
. For the other components, they need to be rotated by
to recover the original patterns. The momentum distributions are peaked around values
and
along a circle, whose radius is defined by the eigenwavenumber
corresponding to the eigenstate number
n. For
and
or for
and
, it is peaked at
and
and exhibit chessboard structures which resemble those of the square QB, except that their intensities decrease with the distance from the center of the square. Otherwise, the wave-function patterns are distinct and more complex. In addition, from the pattern structure of the local currents, we may conclude that the eigenfunctions are not given by simple superpositions of plane waves. Some of the Husimi functions are localized either in the upper or the lower part of the PSOS, indicating that the corresponding eigenmodes propagate in a preferred direction. This may be attributed to the fact that the BCs in Equation (
2) lead to a unidirectionality of the local current along the boundary. The wave-function patterns are more complex than for the corresponding QB; however, they exhibit a regular structure, so that the GOE-like behavior of the spectral properties is not expected.
Similar results are obtained for the spectral properties of the rectangular
and
NBs and their symmetry-projected eigenstates, shown in the left and right part of
Figure 5, respectively, and in the right part of
Figure 6. The gaps observed in the nearest-neighbor spacing distribution of the
QB are typical for rectangular QBs whose ratios of side lengths are no irrational numbers [
95]. The long-range correlations, on the other hand, approach Poisson statistics with an increasing number of eigenvalues [
24,
96]. The spectral properties of the
NB exhibit Poisson statistics, whereas those of its symmetry-projected eigenstates are well described by semi-Poisson statistics. In the right part of
Figure 3, we show length spectra for the
QB and NB and the symmetry-projected eigenstates of the
NB. The length spectra of the QB and NB exhibit peaks at the same lengths, as there are only periodic orbits with an even number of reflections. The length spectra of the symmetry-projected eigenstates also exhibit peaks at the lengths of the classical periodic orbits and a few additional ones at the lengths of peudo-orbits.
In the right part of
Figure 5 and in
Figure 6, we include the results for the triangular
and
NBs which are constructed by cutting the rectangular
and
NBs along the diagonals. Their spectral properties are close to GOE. We found out that they, actually, agree well with those of a quarter-Poissonian sequence which is obtained by taking from an ordered sequence of Possonian random numbers each fourth number or, equivalently, every second one from a sequence of semi-Poisson numbers, such as those of the corresponding symmetry-projected eigenvalue sequences. The spectral properties of the
and
QBs agree well with semi-Poisson statistics [
34]. This is illustrated in the left part of
Figure 6. Those of the
NB coincide with Poissonian statistics [
66]. Right triangles, that have only one angle which is rational with respect to
, have been studied in detail in Refs. [
21,
23,
34,
97,
98]. It was shown that triangles, whose angles are all irrational with respect to
, exhibit GOE-like spectral properties, whereas those of right triangles are non-Poissonian but differ from GOE. Deviations from GOE were shown to originate from the presence of wave functions that are scarred along bouncing-ball orbits that exhibit a regular pattern, such as the periodic-orbit family consisting of orbits that are reflected perpendicular to the tilted side of the triangle and form a periodic-orbit channel (POC) whose maximum width extends from one diffractive corner to the other one (see below) [
19,
99,
100]. Their contributions, in fact, can be extracted for irrational triangles by proceeding as, e.g., in [
101], whereas for the
and
QBs and NBs, their number is too large. This explains the agreement with semi-Poisson statistics for the
and
QBs [
34], which corresponds to a linear level repulsion and is a special case of intermediate statistics for which analytical expressions exist. These are shown as dashed–dotted lines, e.g., in
Figure 6. For the corresponding NBs, the level repulsion is cubic [
33]. After the extraction of contributions from bouncing-ball orbits, the spectral properties of the
QB are close to GOE behavior, whereas those of the
NB agree well with GUE statistics, as illustrated in
Figure 7, implying that the effect of scarred wave functions is stronger for the QB than it is for the NB. Indeed, scarred wave functions occur more rarely for the
NB than for the
QB. The ratio distributions, shown in the right part of
Figure 7, agree well with GOE and GUE for the
QB and NB, respectively, even though contributions from periodic orbits that lead to scarred wave functions were not extracted, implying that it is insensitive to scarred states. Note that no unfolding is needed for the analysis of ratio distributions. The left part of
Figure 8 shows the fluctuating part of the spectral density (black dots). The contributions from bouncing-ball orbits lead to slow oscillations. To determine them, we used the procedure introduced in [
101], that is, we computed the Fourier transform of the fluctuating part of the spectral density,
, and then the inverse Fourier transform over those parts that correspond to lengths of these orbits. The associated peaks are plotted as orange and turquoise dashed lines for the NB and QB, respectively, in the length spectrum shown in the right part of
Figure 8. The resulting oscillating part of
,
, is shown as red dots connected by a red dashed line in the left part of
Figure 8. To extract the contributions of this part to the spectral properties, the eigenvalues
were unfolded by replacing them with the sum of the smooth and oscillating part of
,
[
102].
In
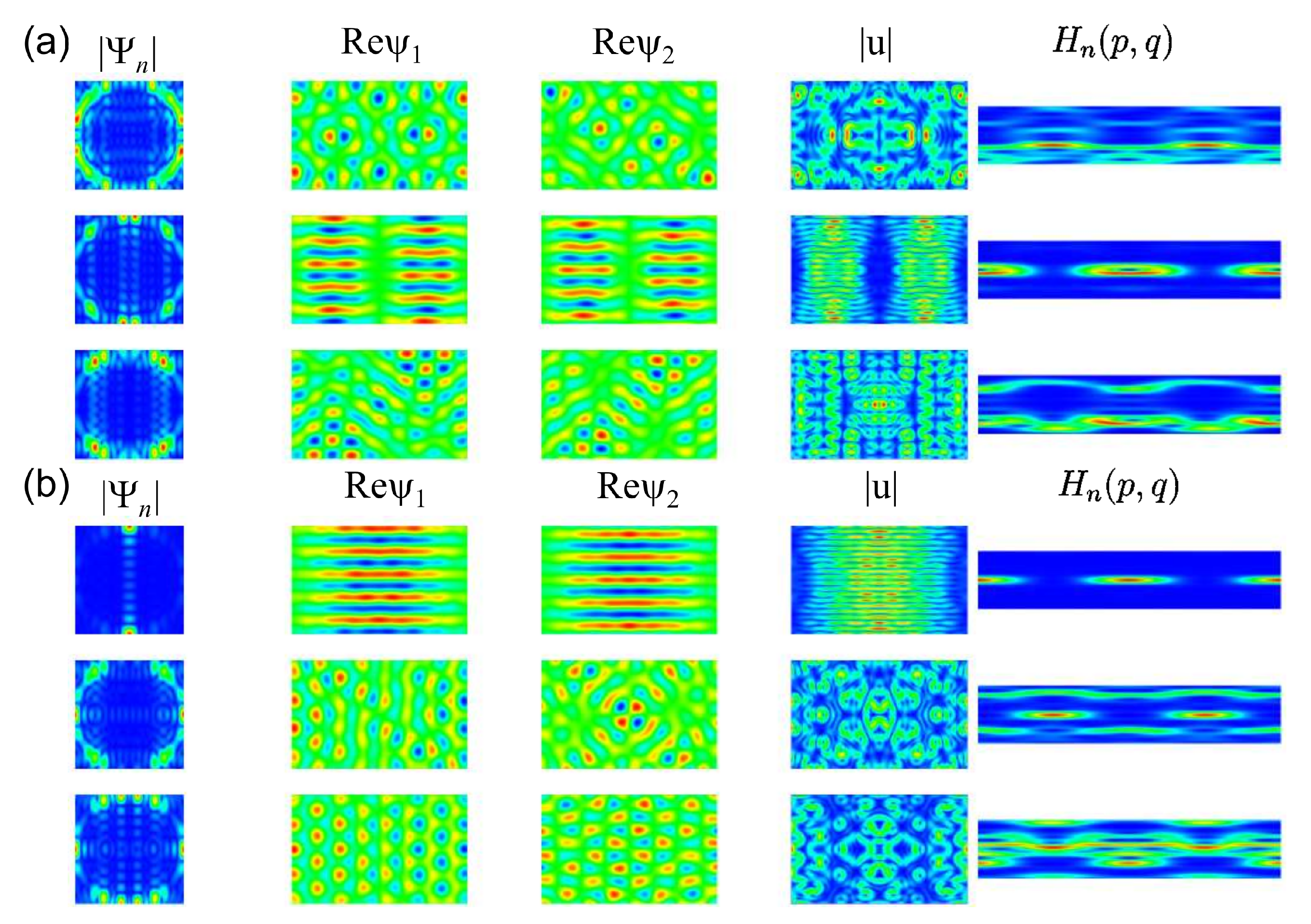
Figure 9, we show momentum distributions, real parts of the spinor components and Husimi functions for a few symmetry-projected eigenstates of the
NB ((a):
; (b):
) and in
Figure 10 for the corresponding right triangle
NB (a) and
QB (b). The momentum distributions are peaked at values
along the circle defined by the eigenwavenumbers
. In the example shown for
and
,
takes the values
. This case, in fact, can be derived based on a plane-wave ansatz, since the propagation of the eigenmodes is one-dimensional [
77]. The wave-function patterns shown for
in the second row are similar to corresponding ones in the
QB. In these examples, the Husimi functions are localized along the
axis. For the other cases, they again exhibit a preferred direction of propagation, but they are distributed over the
plane. Scarred wave functions of the type presented in [
23] are observed in the corresponding symmetry-reduced billiard, i.e., the
QB and NB. The examples shown in
Figure 10 correspond to relatively low-lying states. Here, we chose for the QB eigenstates for which the wave functions and Husimi functions exhibit similar patterns to those of the NB. We show them because for higher excitations, the wave function and local current patterns become complex and are no longer discernible. Still, some of them exhibit scarred eigenstates, such as those shown in the third row. In
Figure 11, we show examples of scarred wave functions for higher-lying eigenstates of the
NB (upper row) and similar ones for the
QB (lower row). They are scarred along bouncing ball orbits from the family of periodic orbits that hit the tilted side perpendicularly and are reflected with constant angles from the sides to the left and right of the
corner.