A Structured Sparse Bayesian Channel Estimation Approach for Orthogonal Time—Frequency Space Modulation
Abstract
1. Introduction
2. System Model
2.1. OTFS Modulation and Demodulation
2.2. Sparse Delay-Doppler Domain Channel Model
3. Structured Sparse Bayesian Approach for Channel Estimation
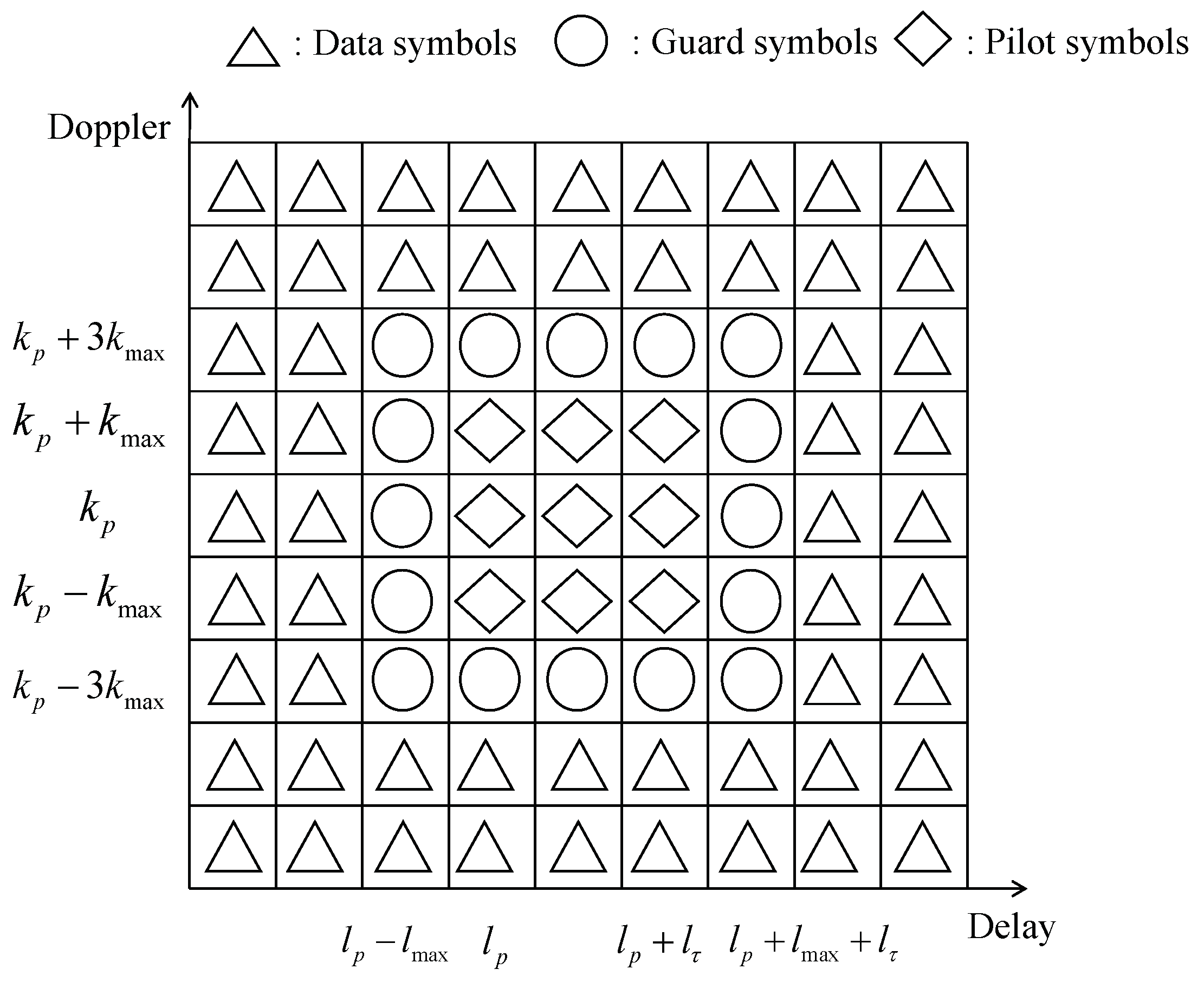
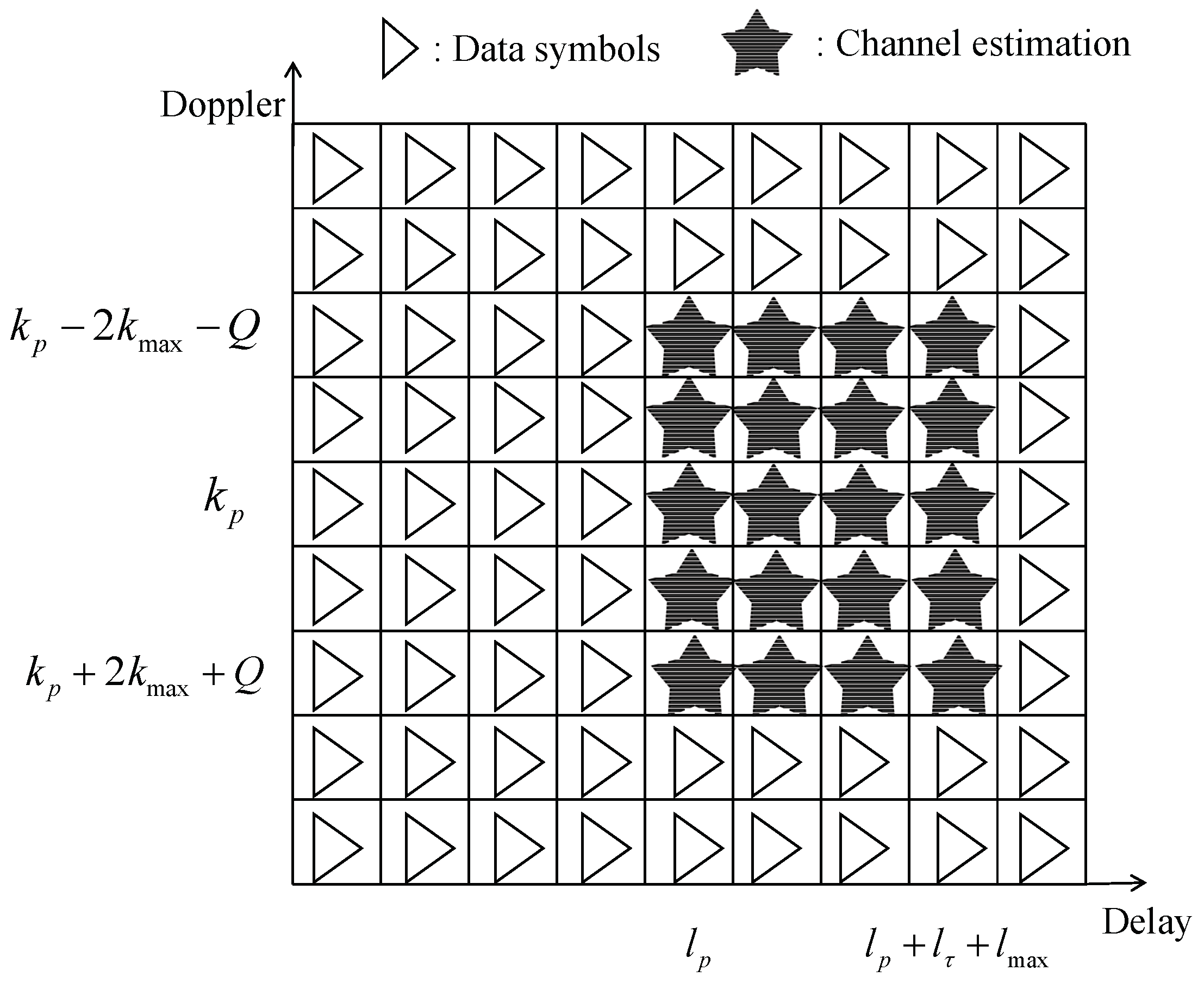
3.1. Pilot Placement and Pattern Design
3.2. Structured Sparse Bayesian Channel Estimation Problem Formulation
SMM Algorithm for Posterior Channel Estimate Evaluation
| Algorithm 1 SMM algorithm for structured SBL |
|
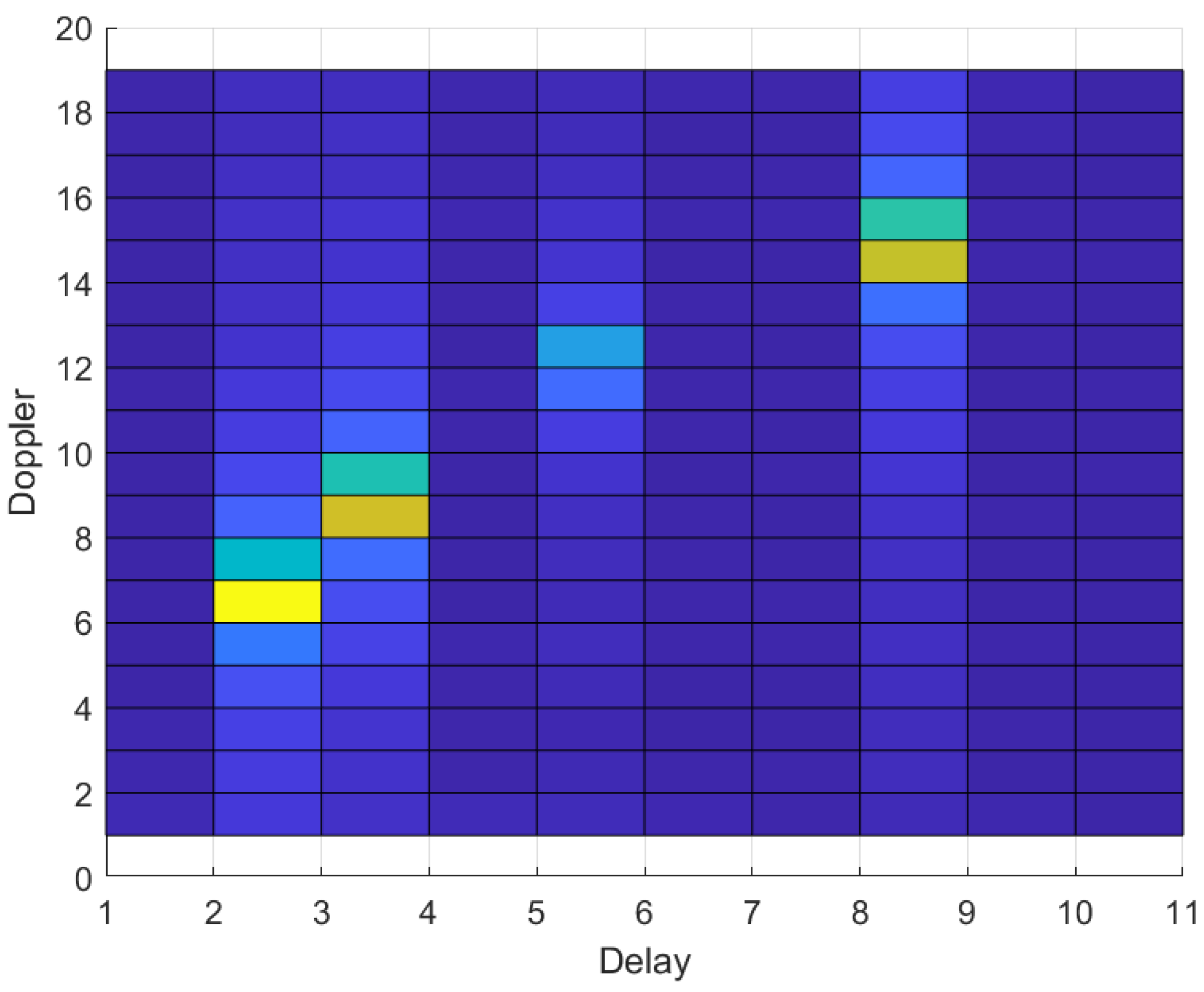
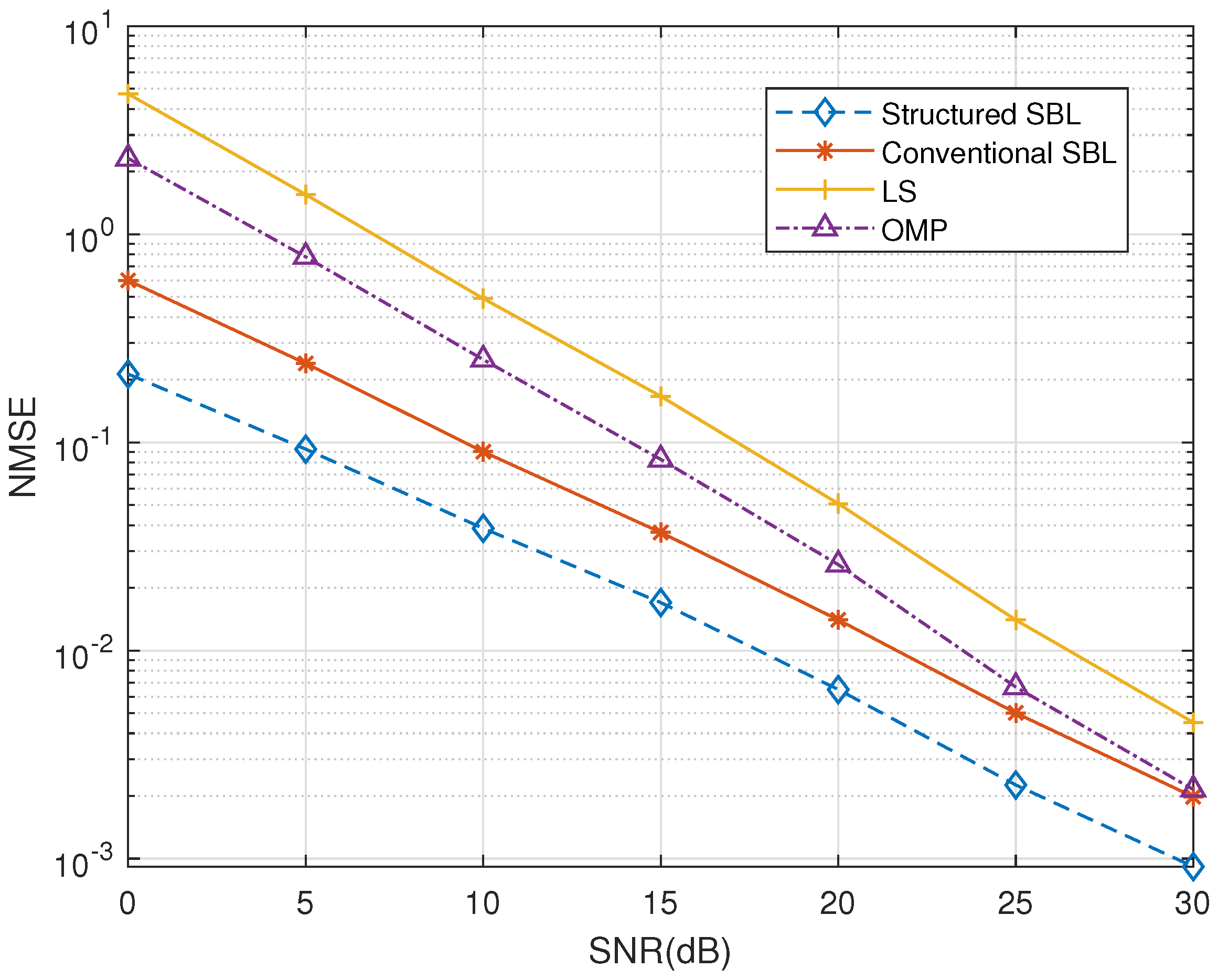
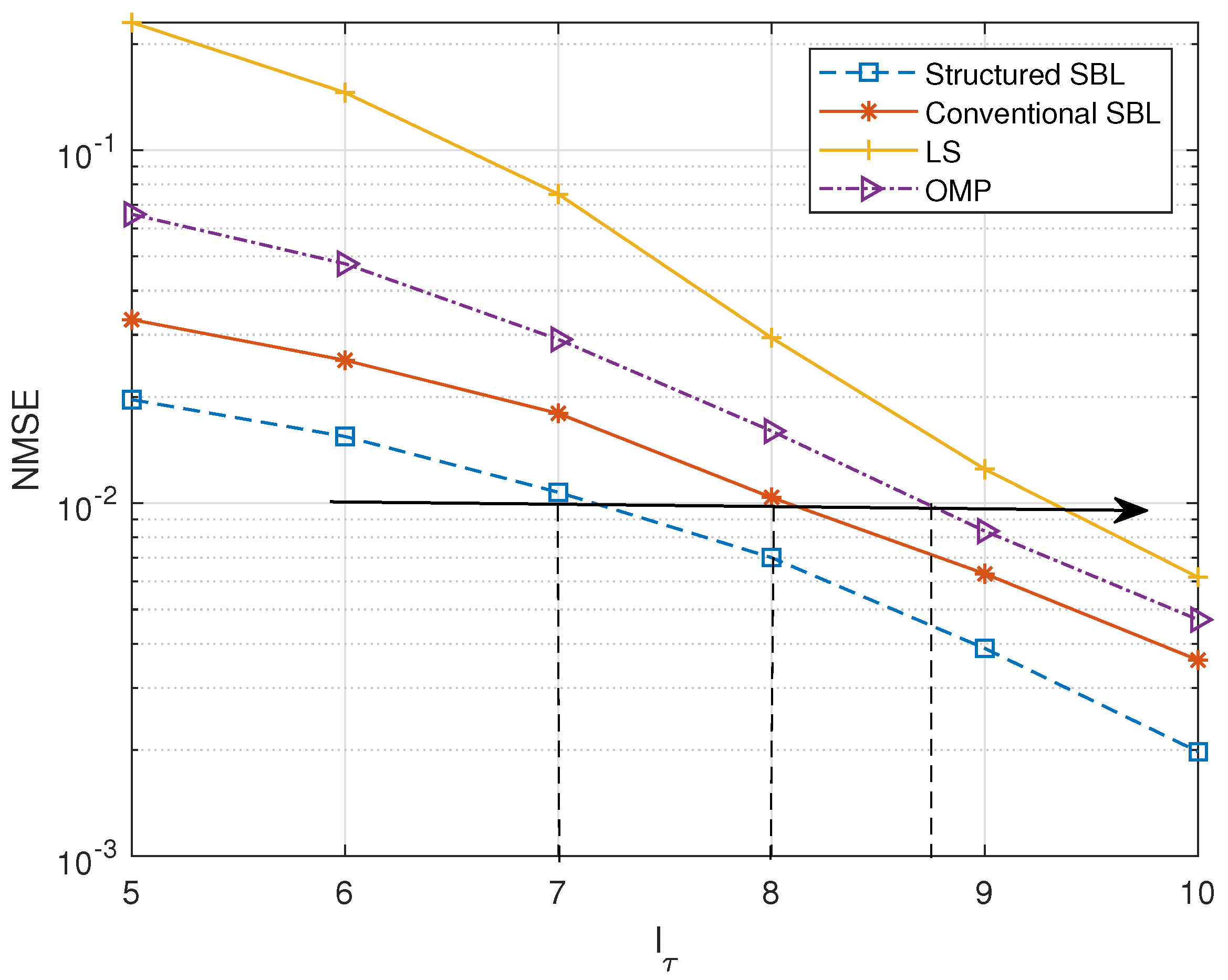
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Joo, C.; Choi, J. Low-delay broadband satellite communications with high-altitude unmanned aerial vehicles. J. Commun. Netw. 2018, 20, 102–108. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, Y.; Mao, S.; Cai, Y.; He, R.; Ai, B.; Zhong, Z.; Liu, Y. Resource Allocation for Millimeter-Wave Train-Ground Communications in High-Speed Railway Scenarios. IEEE Trans. Veh. Technol. 2021, 70, 4823–4838. [Google Scholar] [CrossRef]
- Hui, L.Z.; Yang, G.Q. Uplink User Power Control for Low-Orbit Satellite Communication Systems. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018; pp. 634–639. [Google Scholar]
- Yli-Kaakinen, J.; Loulou, A.; Levanen, T.; Pajukoski, K.; Palin, A.; Renfors, M.; Valkama, M. Frequency-Domain Signal Processing for Spectrally-Enhanced CP-OFDM Waveforms in 5G New Radio. IEEE Trans. Wirel. Commun. 2021, 20, 6867–6883. [Google Scholar] [CrossRef]
- Dong, Y.X.; Jin, W.; Giddings, R.P.; O’Sullivan, M.; Tipper, A.; Durrant, T.; Tang, J.M. Hybrid DFT-Spread OFDM-Digital Filter Multiple Access PONs for Converged 5G Networks. J. Opt. Commun. Netw. 2019, 11, 347–353. [Google Scholar] [CrossRef]
- Wang, S.; Thompson, J.S.; Grant, P.M. Closed-Form Expressions for ICI/ISI in Filtered OFDM Systems for Asynchronous 5G Uplink. IEEE Trans. Commun. 2017, 65, 4886–4898. [Google Scholar] [CrossRef]
- He, L.; Ma, S.; Wu, Y.-C.; Zhou, Y.; Ng, T.-S.; Poor, H.V. Pilot-Aided IQ Imbalance Compensation for OFDM Systems Operating Over Doubly Selective Channels. IEEE Trans. Signal Process. 2011, 59, 2223–2233. [Google Scholar] [CrossRef]
- He, L.; Wu, Y.-C.; Ma, S.; Ng, T.-S.; Poor, H.V. Superimposed Training-Based Channel Estimation and Data Detection for OFDM Amplify-and-Forward Cooperative Systems Under High Mobility. IEEE Trans. Signal Process. 2012, 60, 274–284. [Google Scholar] [CrossRef]
- Wang, T.; Proakis, J.G.; Masry, E.; Zeidler, J.R. Performance degradation of OFDM systems due to Doppler spreading. IEEE Trans. Wirel. Commun. 2006, 5, 1422–1432. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal Time Frequency Space Modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal Time-Frequency Space Modulation: A Promising Next-Generation Waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Farhang, A.; RezazadehReyhani, A.; Doyle, L.E.; Farhang-Boroujeny, B. Low Complexity Modem Structure for OFDM-Based Orthogonal Time Frequency Space Modulation. IEEE Wirel. Commun. Lett. 2018, 7, 344–347. [Google Scholar] [CrossRef]
- RezazadehReyhani, A.; Farhang, A.; Ji, M.; Chen, R.R.; Farhang-Boroujeny, B. Analysis of Discrete-Time MIMO OFDM-Based Orthogonal Time Frequency Space Modulation. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Tiwari, S.; Das, S.S. Circularly pulse-shaped orthogonal time frequency space modulation. Electron. Lett. 2020, 56, 157–160. [Google Scholar] [CrossRef]
- Hossain, M.N.; Sugiura, Y.; Shimamura, T.; Ryu, H.-G. Waveform Design of Low Complexity WR-OTFS System for the OOB Power Reduction. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Seoul, Republic of Korea, 6–9 April 2020; pp. 1–5. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded Pilot-Aided Channel Estimation for OTFS in Delay–Doppler Channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Mishra, H.B.; Singh, P.; Prasad, A.K.; Budhiraja, R. OTFS Channel Estimation and Data Detection Designs With Superimposed Pilots. IEEE Trans. Wirel. Commun. 2022, 21, 2258–2274. [Google Scholar] [CrossRef]
- Gómez-Cuba, F. Compressed Sensing Channel Estimation for OTFS Modulation in Non-Integer Delay-Doppler Domain. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Zhao, L.; Gao, W.-J.; Guo, W. Sparse Bayesian Learning of Delay-Doppler Channel for OTFS System. IEEE Commun. Lett. 2020, 24, 2766–2769. [Google Scholar] [CrossRef]
- Sun, Y.; Babu, P.; Palomar, D.P. Majorization-Minimization Algorithms in Signal Processing, Communications, and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 794–816. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2011, 1, 211–244. [Google Scholar]


| Parameters | Value |
|---|---|
| Symbols N | 64 |
| Subcarries M | 128 |
| Carrier frequency | 15 kHz |
| Subcarrier frequency | Hz |
| The maximum delay | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Xia, X.; Xu, K.; Yang, X.; Xie, W.; Li, Y.; Liu, Y. A Structured Sparse Bayesian Channel Estimation Approach for Orthogonal Time—Frequency Space Modulation. Entropy 2023, 25, 761. https://doi.org/10.3390/e25050761
Zhang M, Xia X, Xu K, Yang X, Xie W, Li Y, Liu Y. A Structured Sparse Bayesian Channel Estimation Approach for Orthogonal Time—Frequency Space Modulation. Entropy. 2023; 25(5):761. https://doi.org/10.3390/e25050761
Chicago/Turabian StyleZhang, Mi, Xiaochen Xia, Kui Xu, Xiaoqin Yang, Wei Xie, Yunkun Li, and Yang Liu. 2023. "A Structured Sparse Bayesian Channel Estimation Approach for Orthogonal Time—Frequency Space Modulation" Entropy 25, no. 5: 761. https://doi.org/10.3390/e25050761
APA StyleZhang, M., Xia, X., Xu, K., Yang, X., Xie, W., Li, Y., & Liu, Y. (2023). A Structured Sparse Bayesian Channel Estimation Approach for Orthogonal Time—Frequency Space Modulation. Entropy, 25(5), 761. https://doi.org/10.3390/e25050761









