Tunable Non-Markovianity for Bosonic Quantum Memristors
Abstract
1. Introduction
2. Model and Methods
3. Results
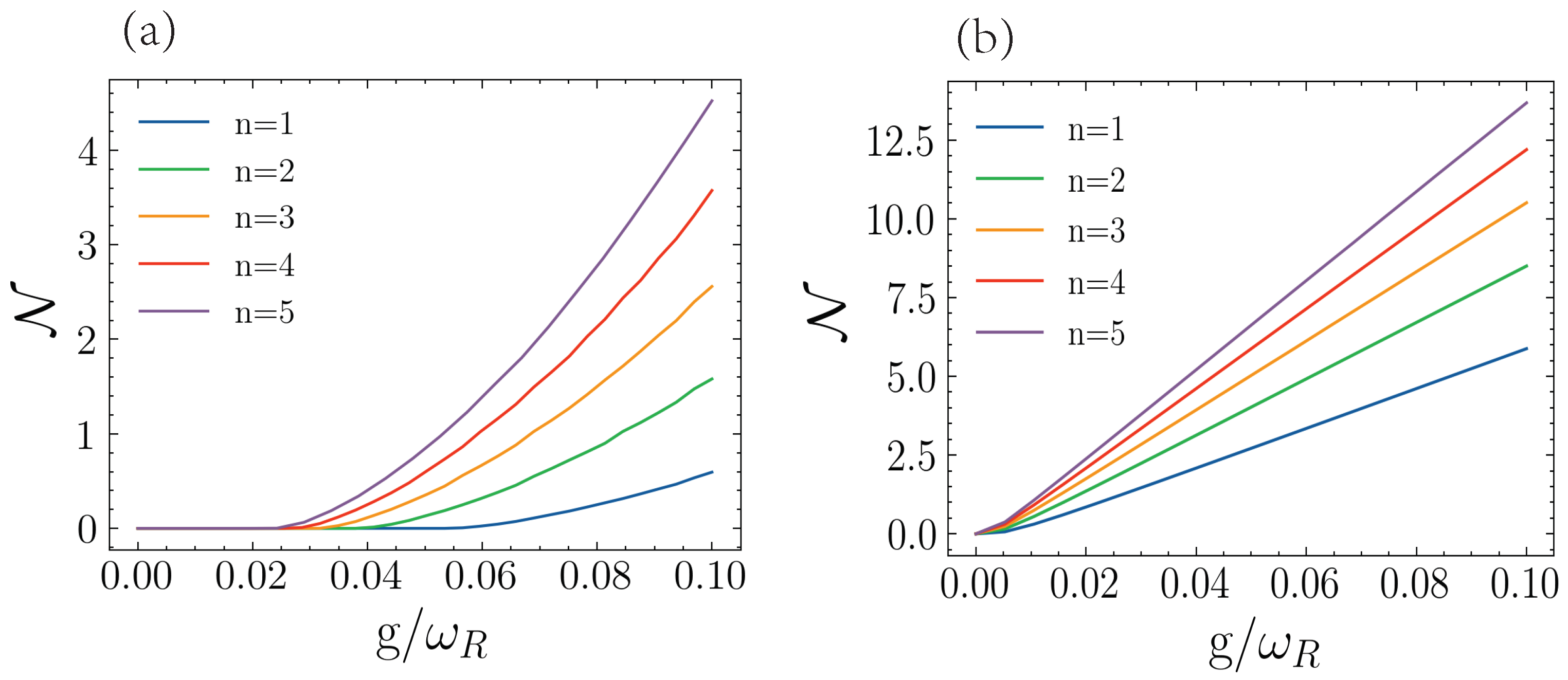
3.1. Dynamical Non-Markovianity (DnM)
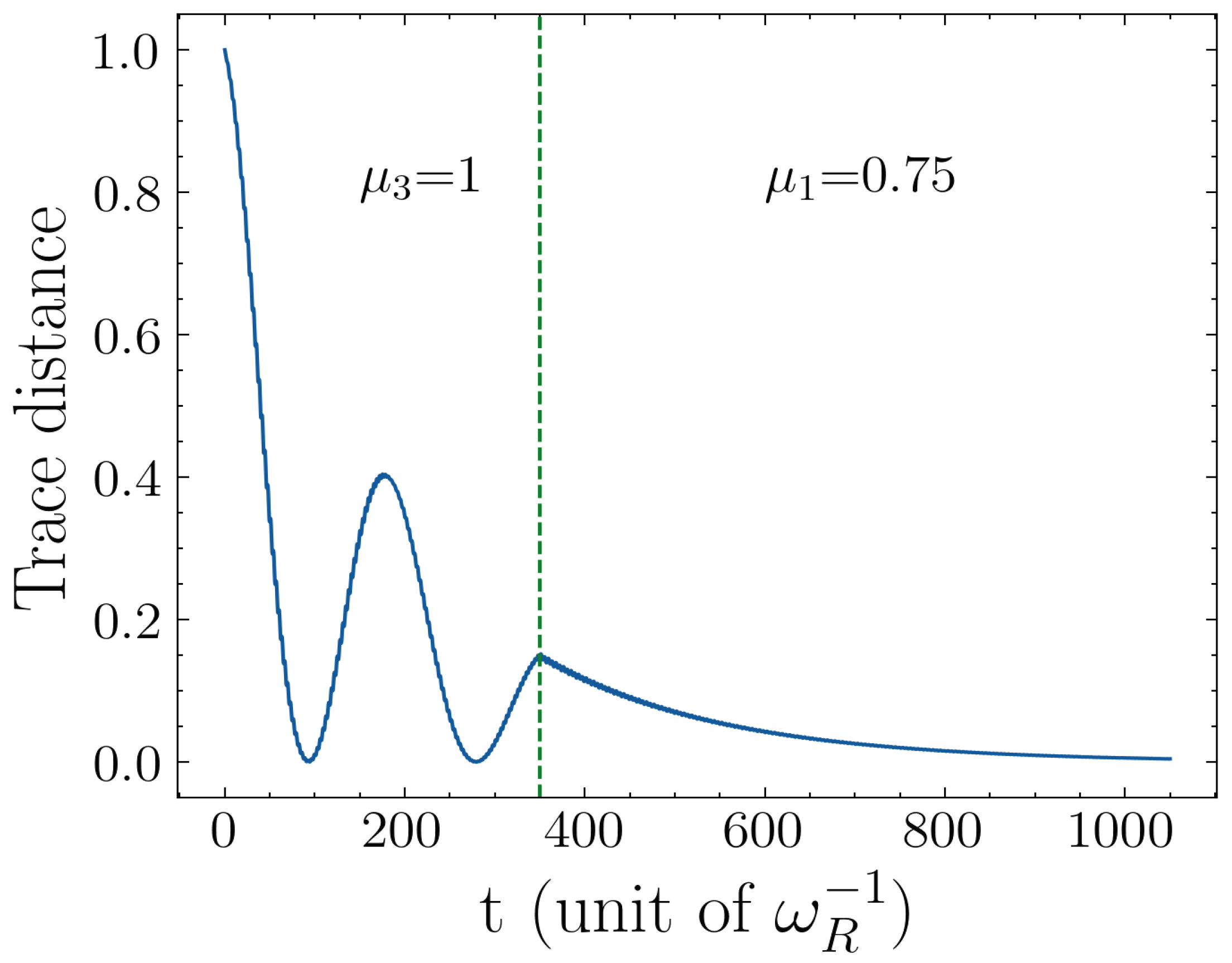
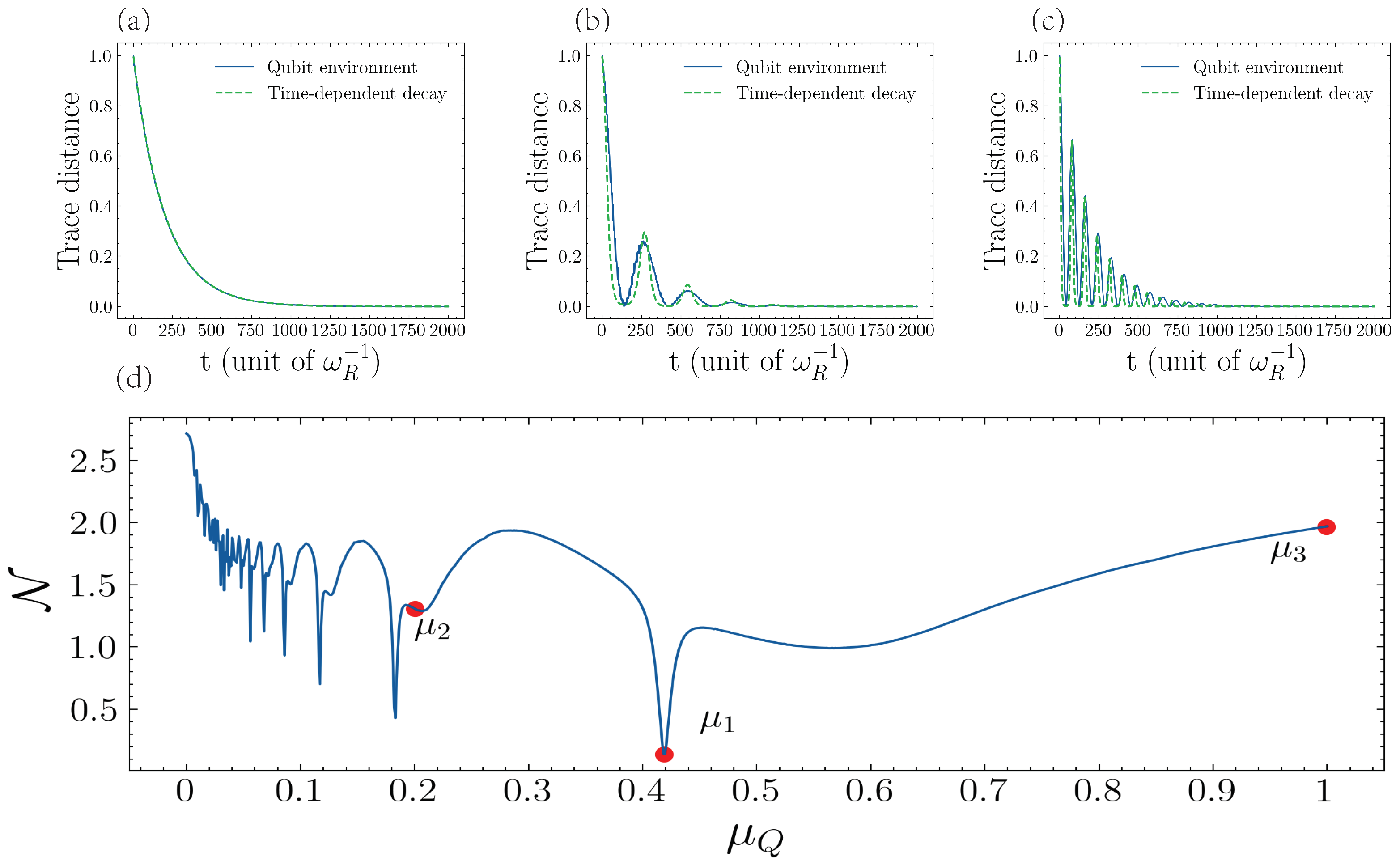
3.2. Time-Dependent Decay Rate
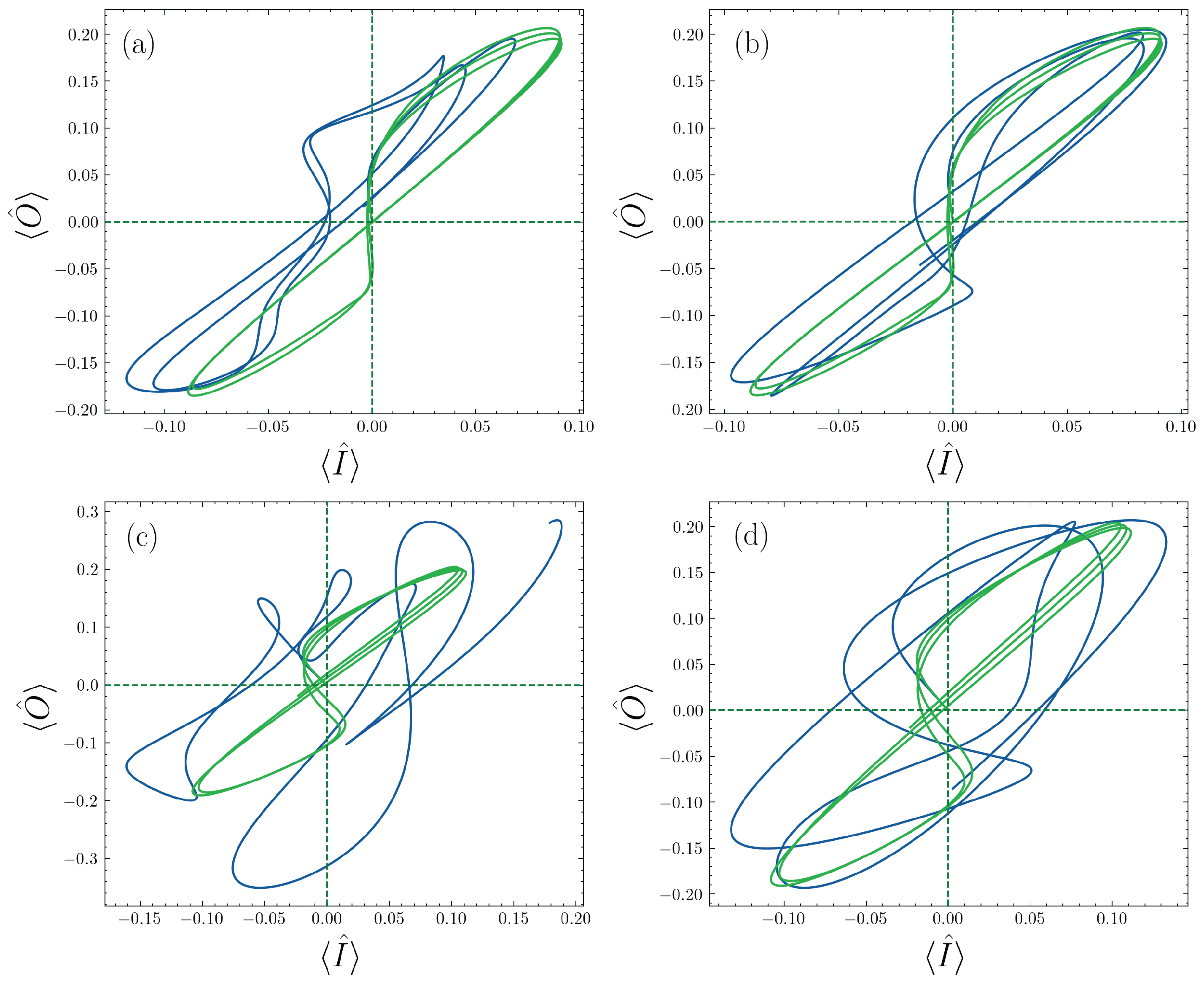
3.3. Bosonic Quantum Memristor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DnM | Dynamical non-Markovianity |
Appendix A
References
- Li, C.-F.; Guo, G.-C.; Pillo, J. Non-Markovian quantum dynamics: What does it mean? EPL 2019, 127, 50001. [Google Scholar] [CrossRef]
- Li, C.-F.; Guo, G.-C.; Pillo, J. Non-Markovian quantum dynamics: What is it good for? EPL 2020, 128, 30001. [Google Scholar] [CrossRef]
- Lee, H.; Cheng, Y.-C.; Fleming, G.R. Coherence Dynamics in Photosynthesis: Protein Protection of Excitonic Coherence. Science 2007, 316, 1462. [Google Scholar] [CrossRef]
- Chin, A.W.; Datta, A.; Caruso, F.; Huelga, S.F.; Plenio, M.B. Noise-assisted energy transfer in quantum networks and light-harvesting complexes? New J. Phys. 2010, 12, 065002. [Google Scholar] [CrossRef]
- Fleming, G.R.; Huelga, S.F.; Plenio, M.B. Focus on quantum effects and noise in biomolecules. New J. Phys. 2011, 13, 115002. [Google Scholar] [CrossRef]
- Alex, W.C.; Susana, F.H.; Martin, B.P. Quantum Metrology in Non-Markovian Environments. Phys. Rev. Lett. 2012, 109, 233601. [Google Scholar]
- Mirkin, N.; Larocca, M.; Wisniacki, D. Quantum metrology in a non-Markovian quantum evolution. Phys. Rev. A 2020, 102, 022618. [Google Scholar] [CrossRef]
- Sweke, R.; Sanz, M.; Sinayskiy, I.; Petruccione, F.; Solano, E. Digital quantum simulation of many-body non-Markovian dynamics. Phys. Rev. A 2016, 94, 022317. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef]
- Pfeiffer, P.; Egusquiza, I.L.; Di Ventra, M.; Sanz, M.; Solano, E. Quantum memristors. Sci. Rep. 2016, 6, 29507. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, M.; Morris, J.; Piacentini, S.; Antesberger, M.; Massa, F.; Crespi, A.; Ceccarelli, F.; Osellame, R.; Walther, P. Experimental photonic quantum memristor. Nat. Photon. 2022, 16, 318–323. [Google Scholar] [CrossRef]
- Sanz, M.; Lamata, L.; Solano, E. Quantum memristors in quantum photonics. APL Photonics 2018, 3, 080801. [Google Scholar] [CrossRef]
- Shevchenko, S.N.; Pershin, Y.V.; Nori, F. Qubit-Based Memcapacitors and Meminductors. Phys. Rev. Appl. 2016, 6, 014006. [Google Scholar] [CrossRef]
- Norambuena, S.; Torres, F.; Di Ventra, M.; Coto, R. Polariton-Based Quantum Memristors. Phys. Rev. Appl. 2022, 17, 024056. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Di Ventra, M. Neuromorphic quantum computing. Proc. IEEE 2012, 100, 2071. [Google Scholar] [CrossRef]
- Pehle, C.; Wetterich, C. Digital quantum simulation of many-body non-Markovian dynamics. Phys. Rev. E 2022, 106, 045311. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Krisn, A.T.; Verstraelen, W.; Liew, T.C.H.; Ghosh, S. Superpolynomial quantum enhancement in polaritonic neuromorphic computing. Phys. Rev. B 2021, 103, 195302. [Google Scholar] [CrossRef]
- De Vega, I.; Aloso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Rivas, Á.; FHuelga, S.; BPlenio, M. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.P. Foundations and measures of quantum non-Markovianity. J. Phys. B: At. Mol. Opt. Phys. 2012, 45, 154001. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef] [PubMed]
- Luchnikov, I.A.; Vintskevich, S.V.; Grigoriev, D.A.; Filippov, S.N. Machine Learning Non-Markovian Quantum Dynamics. Phys. Rev. Lett. 2020, 124, 140502. [Google Scholar] [CrossRef] [PubMed]
- Bastidas, V.M.; Kyaw, T.H.; Tangpanitanon, J.; Romero, G.; Kwek, L.C.; Angelakis, D.G. Floquet stroboscopic divisibility in non-Markovian dynamics. New J. Phys. 2018, 20, 093004. [Google Scholar] [CrossRef]
- Liu, B.-H.; Li, L.; Huang, Y.-F.; Li, C.-F.; Guo, G.-C.; Laine, E.-M.; Breuer, H.-P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931–934. [Google Scholar] [CrossRef]
- Bernardes, N.K.; Cuevas, A.; Orieux, A.; Monken, C.H.; Mataloni, P.; Sciarrino, F.; Santos, M.F. Experimental observation of weak non-Markovianity. Sci. Rep. 2015, 5, 17520. [Google Scholar] [CrossRef]
- Li, B.-W.; Mei, Q.-X.; Wu, Y.-K.; Cai, M.-L.; Wang, L.; Yao, L.; Zhou, Z.-C.; Duan, L.-M. Observation of Non-Markovian Spin Dynamics in a Jaynes-Cummings-Hubbard Model using a Trapped-Ion Quantum Simulator. Phys. Rev. Lett. 2022, 129, 140501. [Google Scholar] [CrossRef] [PubMed]
- García-Pérez, G.; Rossi, M.A.; Maniscalco, S. IBM Q Experience as a versatile experimental testbed for simulating open quantum systems. NPJ Quantum Inf. 2020, 6, 1. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Zhang, N.-N.; He, W.-T.; Kong, X.-Y.; Tao, M.-J.; Deng, F.-G.; Ai, Q.; Long, G.-L. Global correlation and local information flows in controllable non-Markovian open quantum dynamics. NPJ Quantum Inf. 2022, 8, 22. [Google Scholar] [CrossRef]
- Tavis, M.; Cummings, W. Exact Solution for an N-Molecule-radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379. [Google Scholar] [CrossRef]
- Retzker, A.; Solano, E.; Reznik, E. Tavis-Cummings model and collective multiqubit entanglement in trapped ions. Phys. Rev. A 2007, 75, 022312. [Google Scholar] [CrossRef]
- Jäger, S.B.; Schmit, T.; Morigi, G.; Holl, M.J.; Betzholz, R. Lindblad Master Equations for Quantum Systems Coupled to Dissipative Bosonic Modes. Phys. Rev. Lett. 2022, 129, 063601. [Google Scholar] [CrossRef] [PubMed]
- Van Woerkom, D.J.; Scarlino, P.; Ungerer, J.H.; Müller, C.; Koski, J.V.; Landig, A.J.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; et al. Microwave Photon-Mediated Interactions between Semiconductor Qubits. Phys. Rev. X 2018, 8, 041018. [Google Scholar] [CrossRef]
- Casabone, B.; Friebe, K.; Brandstätter, B.; Schüppert, K.; Blatt, R.; Northup, T.E. Enhanced Quantum Interface with Collective Ion-Cavity Coupling. Phys. Rev. Lett. 2020, 114, 023602. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.-K.; Feng, W.; Song, X.-H.; Song, C.; Liu, W.-X.; Guo, Q.-J.; Zhang, X.; Dong, H.; Zheng, D.-N.; et al. Controllable Switching between Superradiant and Subradiant States in a 10-qubit Superconducting Circuit. Phys. Rev. Lett. 2015, 124, 013601. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234. [Google Scholar] [CrossRef]
- Grossmann, F.; Dittrich, T.; Jung, P.; Hänggi, P. Coherent destruction of tunneling. Phys. Rev. Lett. 1991, 67, 516. [Google Scholar] [CrossRef]
- Neu, P.; Silbey, R.J. Tunneling in a cavity. Phys. Rev. A 1996, 54, 5323. [Google Scholar] [CrossRef]
- Luo, X.; Li, L.; You, L.; Wu, B. Coherent destruction of tunneling and dark Floquet state. New J. Phys. 2014, 16, 013007. [Google Scholar] [CrossRef]
- Hu, M.-L.; Lian, H.-L. Geometric quantum discord and non-Markovianity of structured reservoirs. Ann. Phys. 2015, 362, 795. [Google Scholar] [CrossRef]
- Salmiletho, J.; Deppe, F.; Di Ventra, M.; Sanz, M.; Solano, E. Quantum Memristors with Superconducting Circuits. Sci. Rep. 2017, 7, 42044. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.-M.; Albarrán-Arriagada, F.; Alaeian, H.; Solano, E.; Barrios, G.A. Quantum Memristors with Quantum Computers. Phys. Rev. Appl. 2022, 18, 024082. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.-L.; Alvarado Barrios, G.; Solano, E.; Albarrán-Arriagada, F. Tunable Non-Markovianity for Bosonic Quantum Memristors. Entropy 2023, 25, 756. https://doi.org/10.3390/e25050756
Tang J-L, Alvarado Barrios G, Solano E, Albarrán-Arriagada F. Tunable Non-Markovianity for Bosonic Quantum Memristors. Entropy. 2023; 25(5):756. https://doi.org/10.3390/e25050756
Chicago/Turabian StyleTang, Jia-Liang, Gabriel Alvarado Barrios, Enrique Solano, and Francisco Albarrán-Arriagada. 2023. "Tunable Non-Markovianity for Bosonic Quantum Memristors" Entropy 25, no. 5: 756. https://doi.org/10.3390/e25050756
APA StyleTang, J.-L., Alvarado Barrios, G., Solano, E., & Albarrán-Arriagada, F. (2023). Tunable Non-Markovianity for Bosonic Quantum Memristors. Entropy, 25(5), 756. https://doi.org/10.3390/e25050756





