Controlling the Mean Time to Extinction in Populations of Bacteria
Abstract
1. Introduction
2. Model
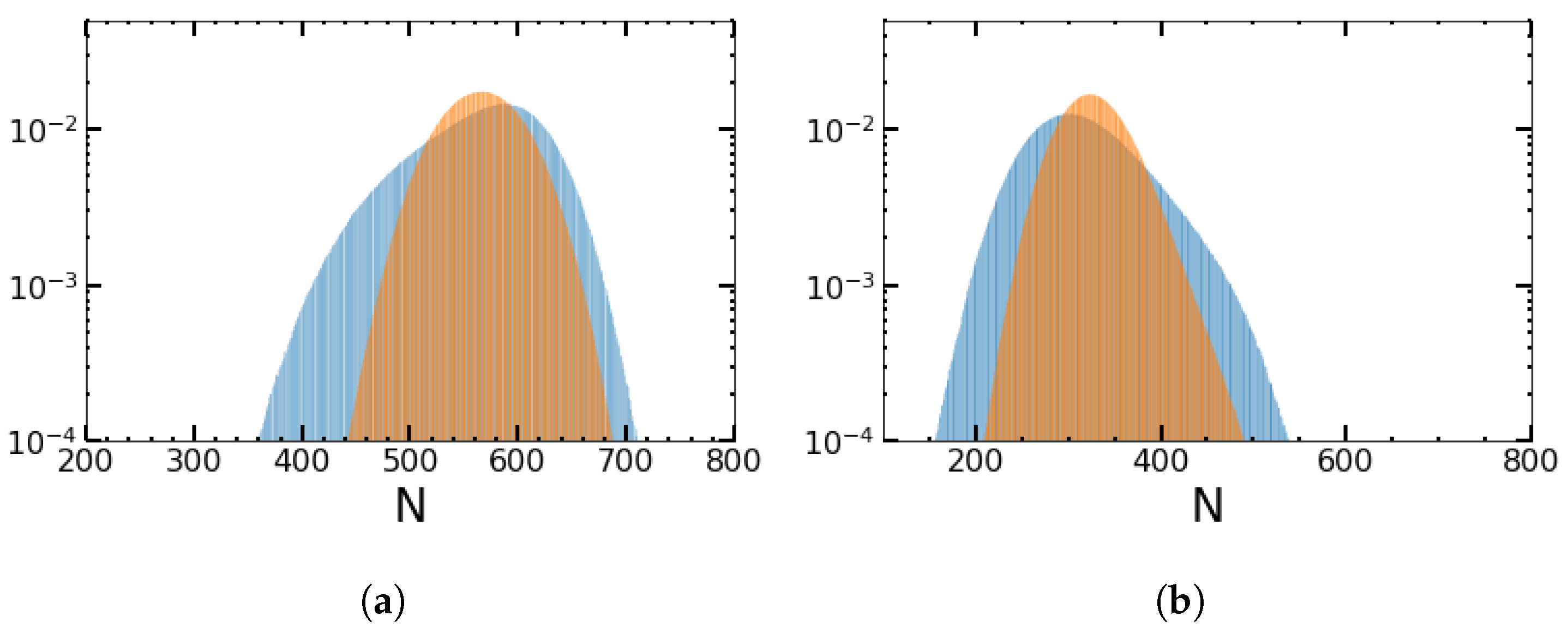
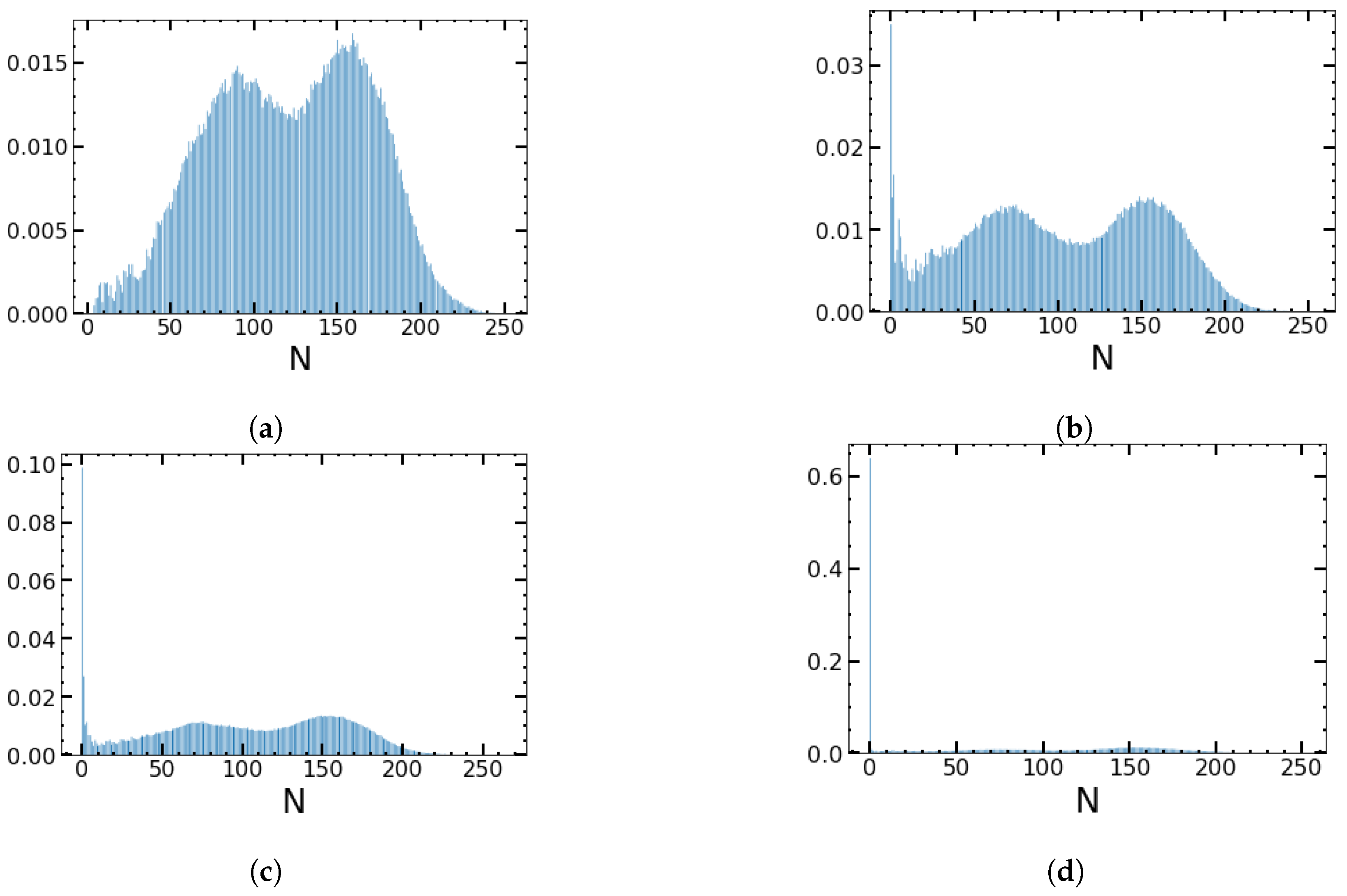
3. Quasi-Stationary Distribution
4. Numerical Simulations
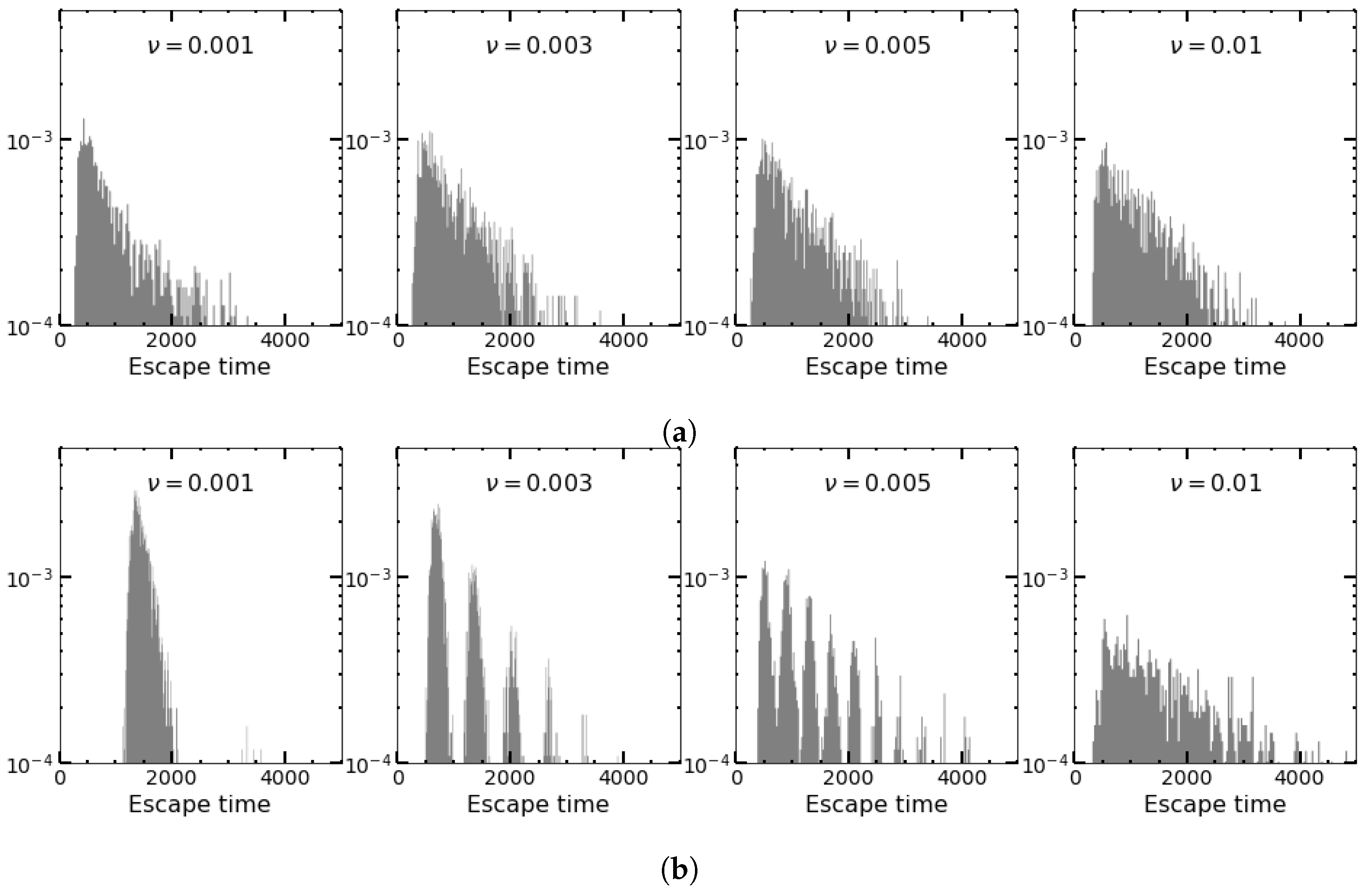
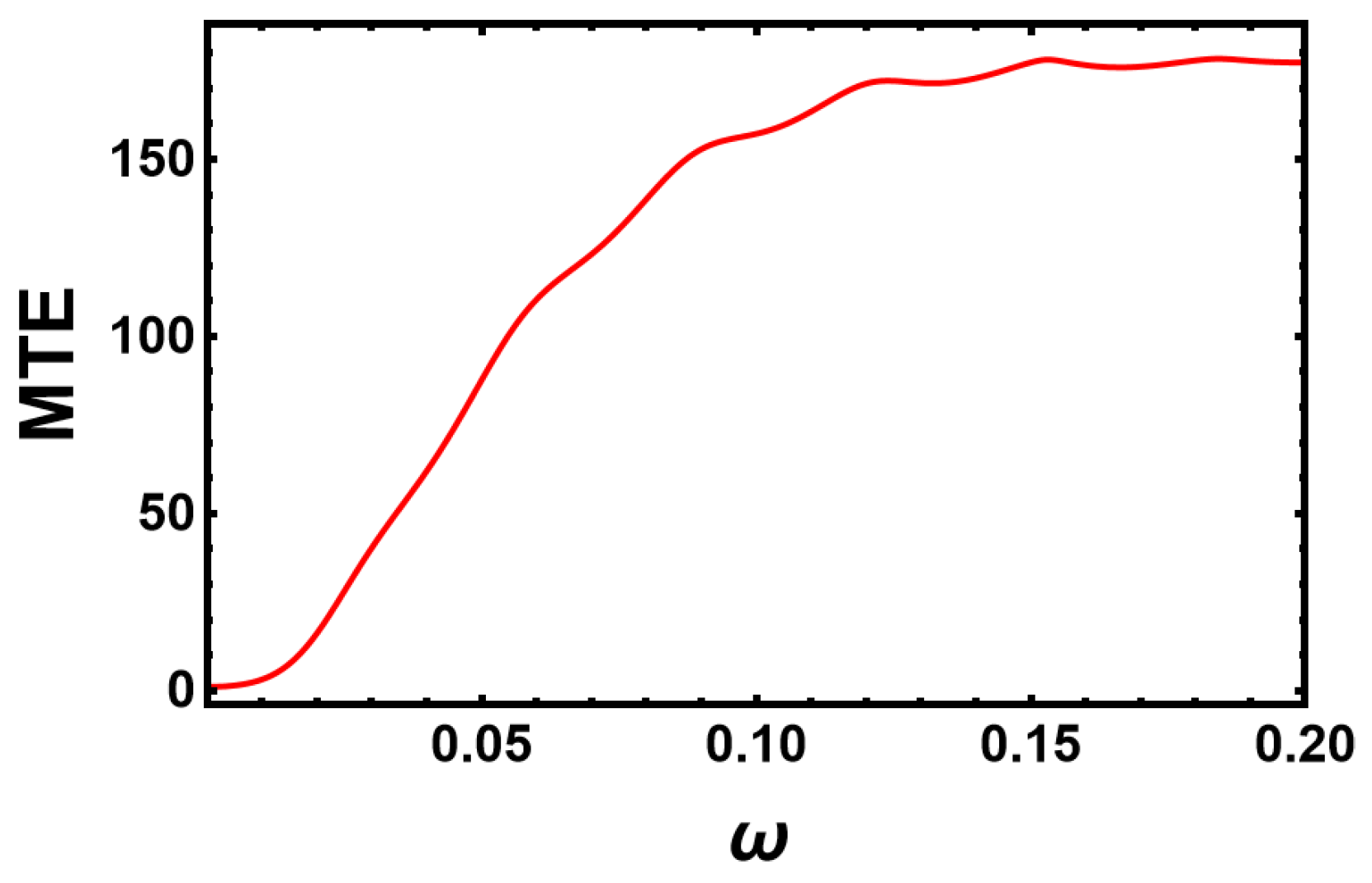
4.1. Numerical Simulations for Sinusoidal Perturbations
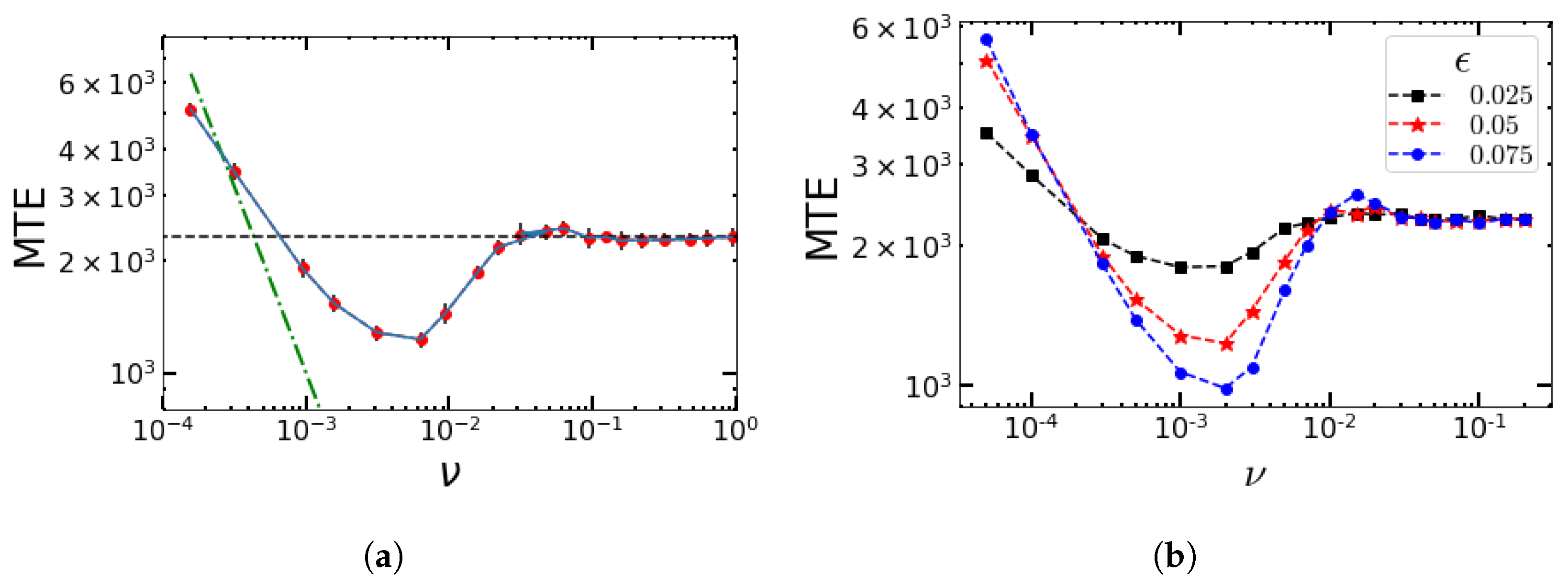
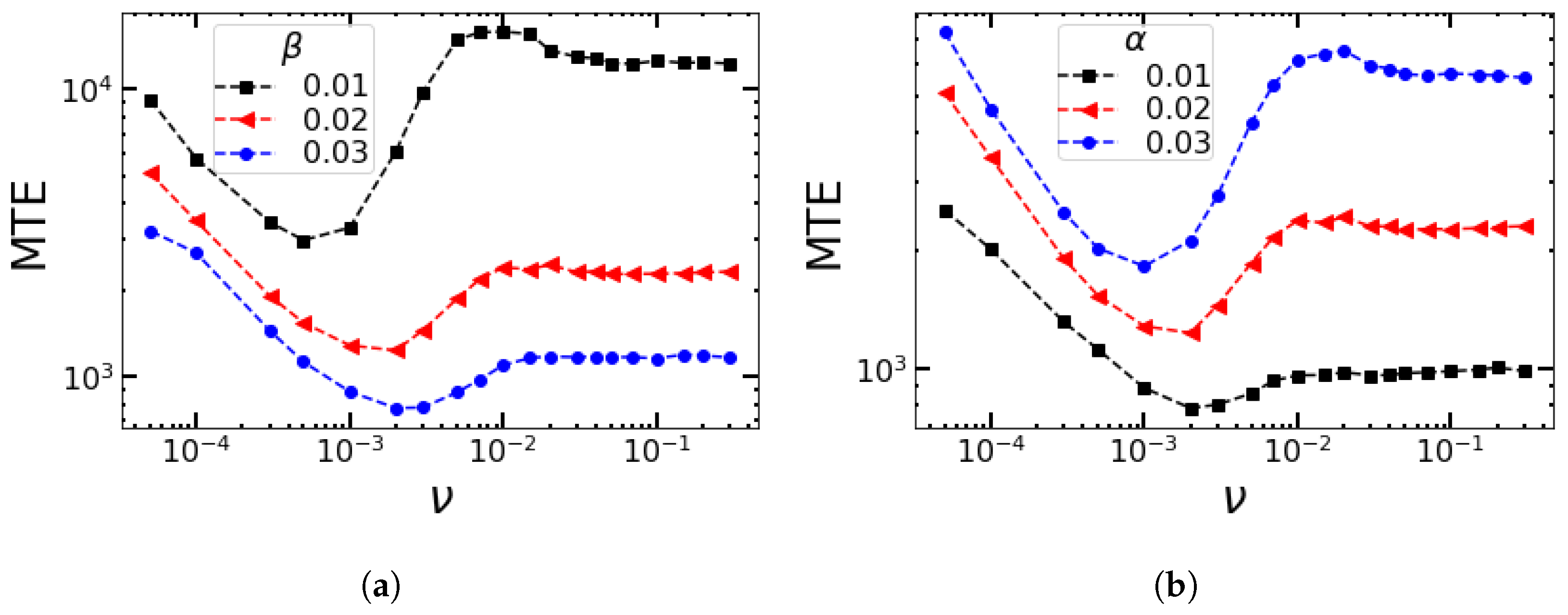
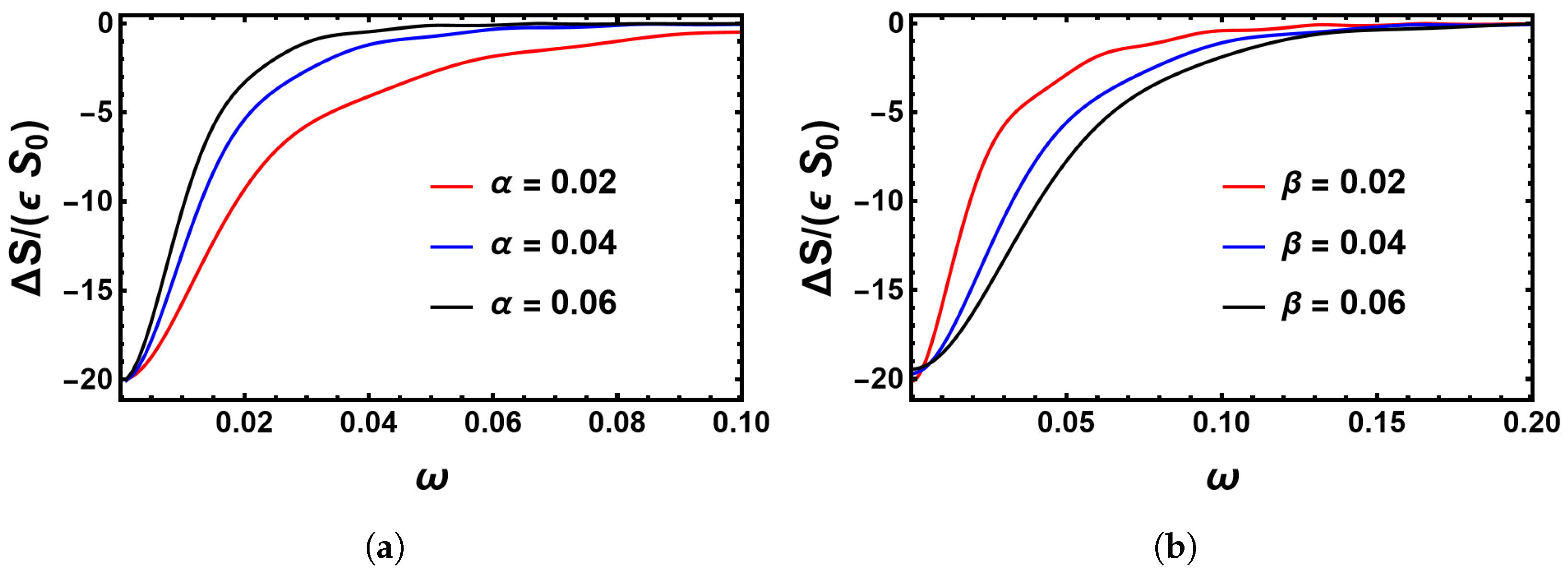
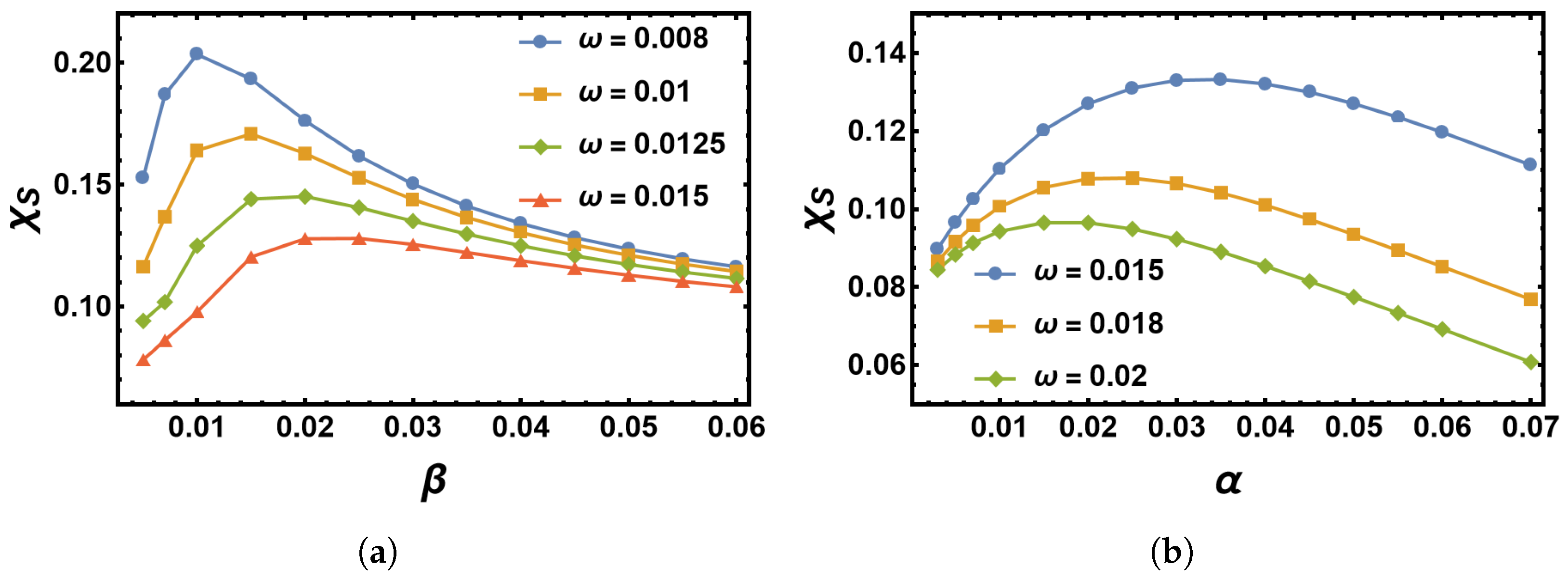
4.2. Impact of the Switching Rates α and β on the MTE’s Frequency Dependence for the Sinusoidal Change
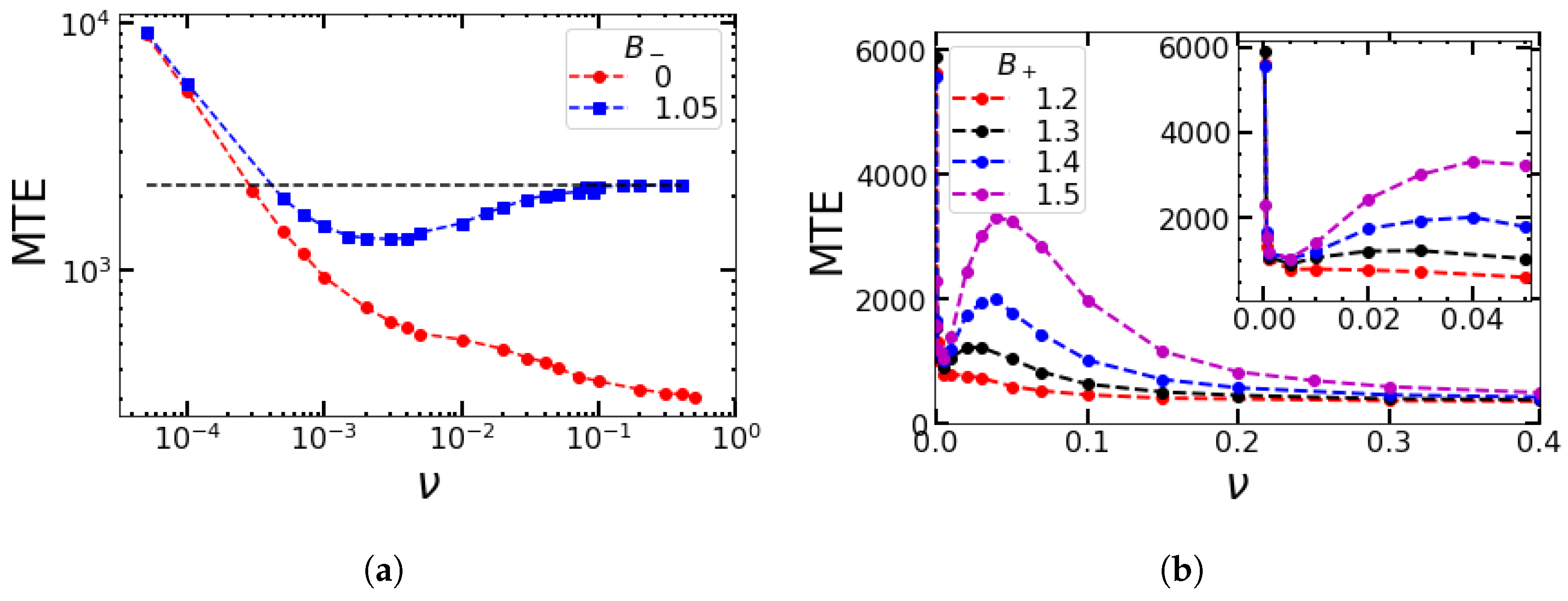
4.3. Impact of the Minimum Value of the Birth Rates
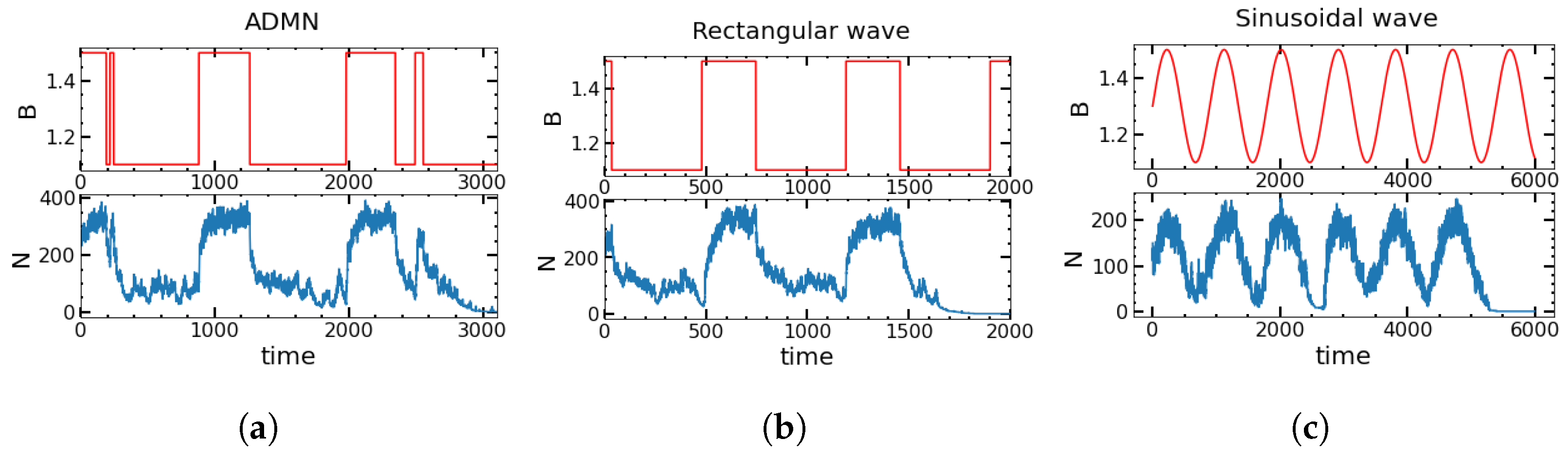
4.4. Deterministic versus Stochastic Changes in the Environment for Square Waves and SDMN
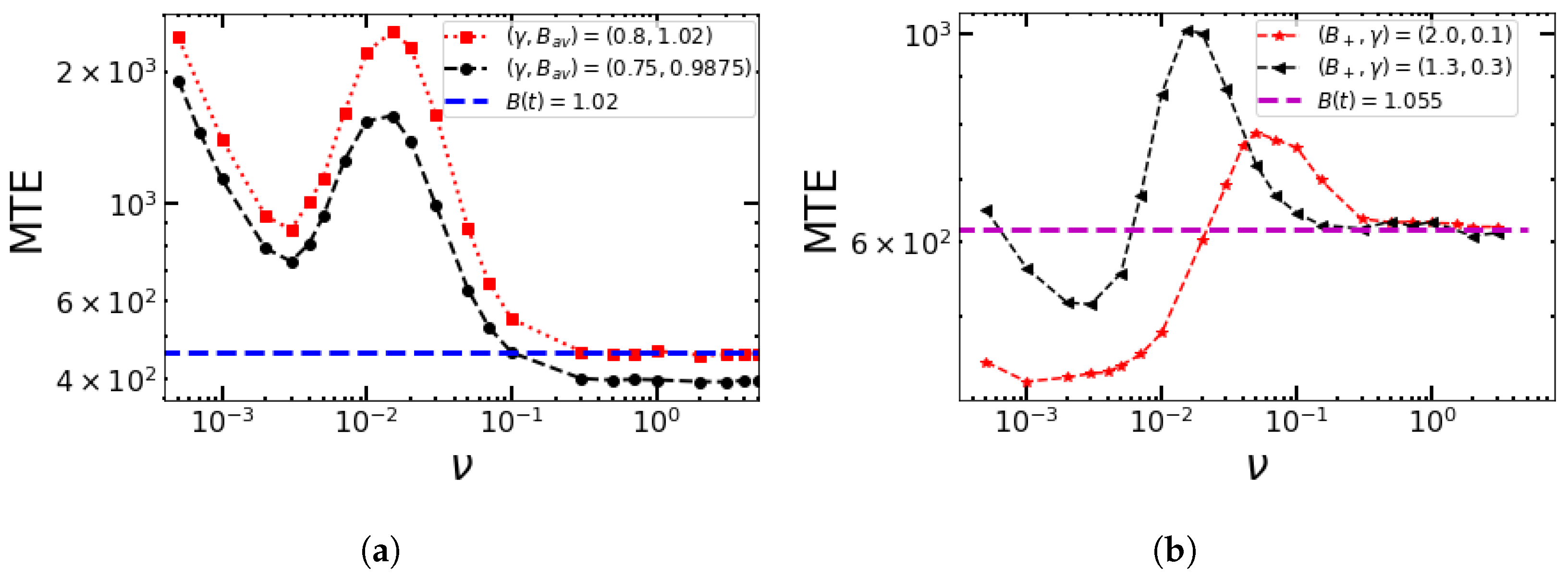
4.5. Duty Cycles with Asymmetric Switching in Competition with Amplitudes
5. WKB Approach for the MTE
5.1. Real-Space WKB
5.2. Momentum-Space WKB
6. Effects of a Changing Environment: Analytical Approaches
6.1. Sinusoidal Changes in the Environment for Weak Perturbations
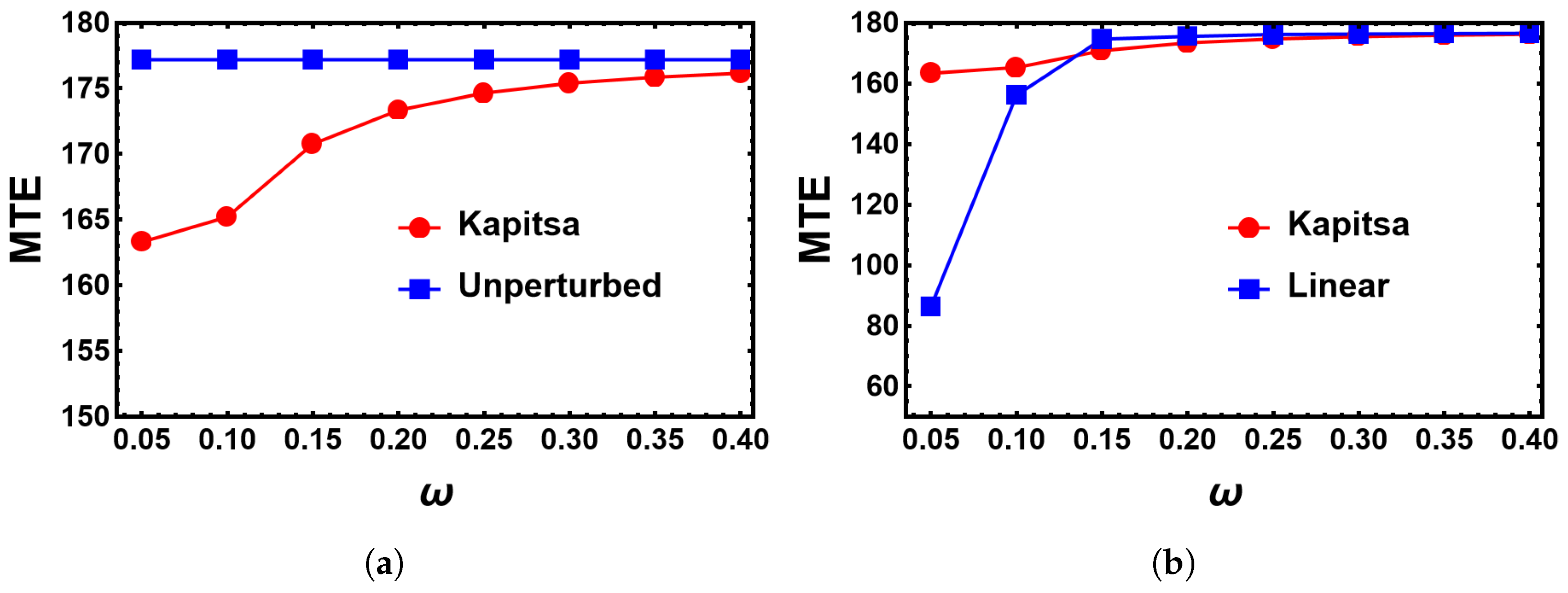
6.2. Sinusoidal Changes of the Environment for High Frequencies
7. Discussion and Summary of the Results
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Methods
Appendix A.1. Stochastic Simulations
Appendix A.1.1. Gillespie Algorithm
Time-Independent Rates
- Initialize the algorithm by setting the initial number of normals (n) and persisters (m) and setting .
- Calculate the propensity function for each reaction. In the absence of any environmental perturbation, we have four stochastic reactions (birth of normals, death of normals, switching from normals to persisters, and switching from persisters to normals), each with a propensity function , respectively. In the presence of ADMN, there are two additional stochastic reactions corresponding to environmental switching .
- Set , where for the unperturbed system and for ADMN.
- Generate two random numbers and from a uniform distribution .
- Find the time until the next reaction should take place, that is, .
- Find the reaction that takes place such that
- Set and update the number of normals (n) and persisters (m) according to the reaction .
- Return to step 2 or quit.
Time-Dependent Rates: Modified Gillespie Algorithm
Appendix A.1.2. Modified Next-Reaction Method
- Initialize the algorithm by setting the initial number of normals (n) and persisters (m) and setting . For each i, set .
- Generate M random numbers from a uniform distribution and set for each i.
- Calculate by solving for .
- Set and let be the time for which the minimum is realized, that is, let be the minimum for the reaction .
- Increase the time by an increment of and update the number of normals and persisters according to the reaction .
- For each i, set .
- For the reaction , let r be a uniform random number , and set .
- Return to step 3 or quit.
Appendix A.2. The Adapted Chernykh-Stepanov Iteration Method
Appendix B. The Kapitsa Method for High Frequencies
References
- Wienand, K.; Frey, E.; Mobilia, M. Evolution of a fluctuating population in a randomly switching environment. Phys. Rev. Lett. 2017, 119, 158301. [Google Scholar] [CrossRef] [PubMed]
- Taitelbaum, A.; West, R.; Assaf, M.; Mobilia, M. Population dynamics in a changing environment: Random versus periodic switching. Phys. Rev. Lett. 2020, 125, 048105. [Google Scholar] [CrossRef] [PubMed]
- Wienand, K.; Frey, E.; Mobilia, M. Eco-evolutionary dynamics of a population with randomly switching carrying capacity. J. R. Soc. Interface 2018, 15, 20180343. [Google Scholar] [CrossRef] [PubMed]
- Hufton, P.G.; Lin, Y.T.; Galla, T.; McKane, A.J. Intrinsic noise in systems with switching environments. Phys. Rev. E 2016, 93, 052119. [Google Scholar] [CrossRef] [PubMed]
- Hufton, P.G.; Lin, Y.T.; Galla, T. Model reduction methods for population dynamics with fast-switching environments: Reduced master equations, stochastic differential equations, and applications. Phys. Rev. E 2019, 99, 032122. [Google Scholar] [CrossRef] [PubMed]
- Israeli, T.; Assaf, M. Population switching under a time-varying environment. Phys. Rev. E 2020, 101, 022109. [Google Scholar] [CrossRef] [PubMed]
- Assaf, M.; Kamenev, A.; Meerson, B. Population extinction in a time-modulated environment. Phys. Rev. E 2008, 78, 041123. [Google Scholar] [CrossRef] [PubMed]
- Lohmar, I.; Meerson, B. Switching between phenotypes and population extinction. Phys. Rev. E 2011, 84, 051901. [Google Scholar] [CrossRef]
- Park, J.I.; Kim, B.J.; Park, H.J. Stochastic resonance of abundance fluctuations and mean time to extinction in an ecological community. Phys. Rev. E 2021, 104, 024133. [Google Scholar] [CrossRef] [PubMed]
- Balaban, N.Q.; Merrin, J.; Chait, R.; Kowalik, L.; Leibler, S. Bacterial persistence as a phenotypic switch. Science 2004, 305, 1622–1625. [Google Scholar] [CrossRef]
- Sousa, A.M.; Machado, I.; Pereira, M.O. Phenotypic Switching: An Opportunity to Bacteria Thrive. In Science against Microbial Pathogens: Communicating Current Research and Technological Advances; Méndez-Vilas, A., Ed.; Formatex Research Center: Basking Ridge, NJ, USA, 2012; pp. 252–262. ISBN 978-84-939843-1-1. [Google Scholar]
- Marrec, L.; Bitbol, A.F. Resist or perish: Fate of a microbial population subjected to a periodic presence of antimicrobial. PLoS Comput. Biol. 2020, 16, e1007798. [Google Scholar] [CrossRef]
- Tepekule, B.; Uecker, H.; Derungs, I.; Frenoy, A.; Bonhoeffer, S. Modeling antibiotic treatment in hospitals: A systematic approach shows benefits of combination therapy over cycling, mixing, and mono-drug therapies. PLoS Comput. Biol. 2017, 13, e1005745. [Google Scholar] [CrossRef] [PubMed]
- Uecker, H.; Bonhoeffer, S. Antibiotic treatment protocols revisited: The challenges of a conclusive assessment by mathematical modelling. J. R. Soc. Interface 2021, 18, 20210308. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Anderson, D.F. A modified next reaction method for simulating chemical systems with time dependent propensities and delays. J. Chem. Phys. 2007, 127, 214107. [Google Scholar] [CrossRef] [PubMed]
- Kussell, E.; Kishony, R.; Balaban, N.Q.; Leibler, S. Bacterial persistence: A model of survival in changing environments. Genetics 2005, 169, 1807–1814. [Google Scholar] [CrossRef] [PubMed]
- Steuernagel, O.; Polani, D. Multiobjective optimization applied to the eradication of persistent pathogens. IEEE Trans. Evol. Comput. 2010, 14, 759–765. [Google Scholar] [CrossRef]
- Assaf, M.; Meerson, B. WKB theory of large deviations in stochastic populations. J. Phys. A Math. Theor. 2017, 50, 263001. [Google Scholar] [CrossRef]
- Smelyanskiy, V.; Dykman, M.; Rabitz, H.; Vugmeister, B. Fluctuations, escape, and nucleation in driven systems: Logarithmic susceptibility. Phys. Rev. Lett. 1997, 79, 3113. [Google Scholar] [CrossRef]
- Gibson, M.A.; Bruck, J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. A 2000, 104, 1876–1889. [Google Scholar] [CrossRef]
- Chernykh, A.; Stepanov, M. Large negative velocity gradients in Burgers turbulence. Phys. Rev. E 2001, 64, 026306. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakur, B.; Meyer-Ortmanns, H. Controlling the Mean Time to Extinction in Populations of Bacteria. Entropy 2023, 25, 755. https://doi.org/10.3390/e25050755
Thakur B, Meyer-Ortmanns H. Controlling the Mean Time to Extinction in Populations of Bacteria. Entropy. 2023; 25(5):755. https://doi.org/10.3390/e25050755
Chicago/Turabian StyleThakur, Bhumika, and Hildegard Meyer-Ortmanns. 2023. "Controlling the Mean Time to Extinction in Populations of Bacteria" Entropy 25, no. 5: 755. https://doi.org/10.3390/e25050755
APA StyleThakur, B., & Meyer-Ortmanns, H. (2023). Controlling the Mean Time to Extinction in Populations of Bacteria. Entropy, 25(5), 755. https://doi.org/10.3390/e25050755





