On Decoder Ties for the Binary Symmetric Channel with Arbitrarily Distributed Input
Abstract
1. Introduction
2. Main Result
3. Proof of Theorem 2
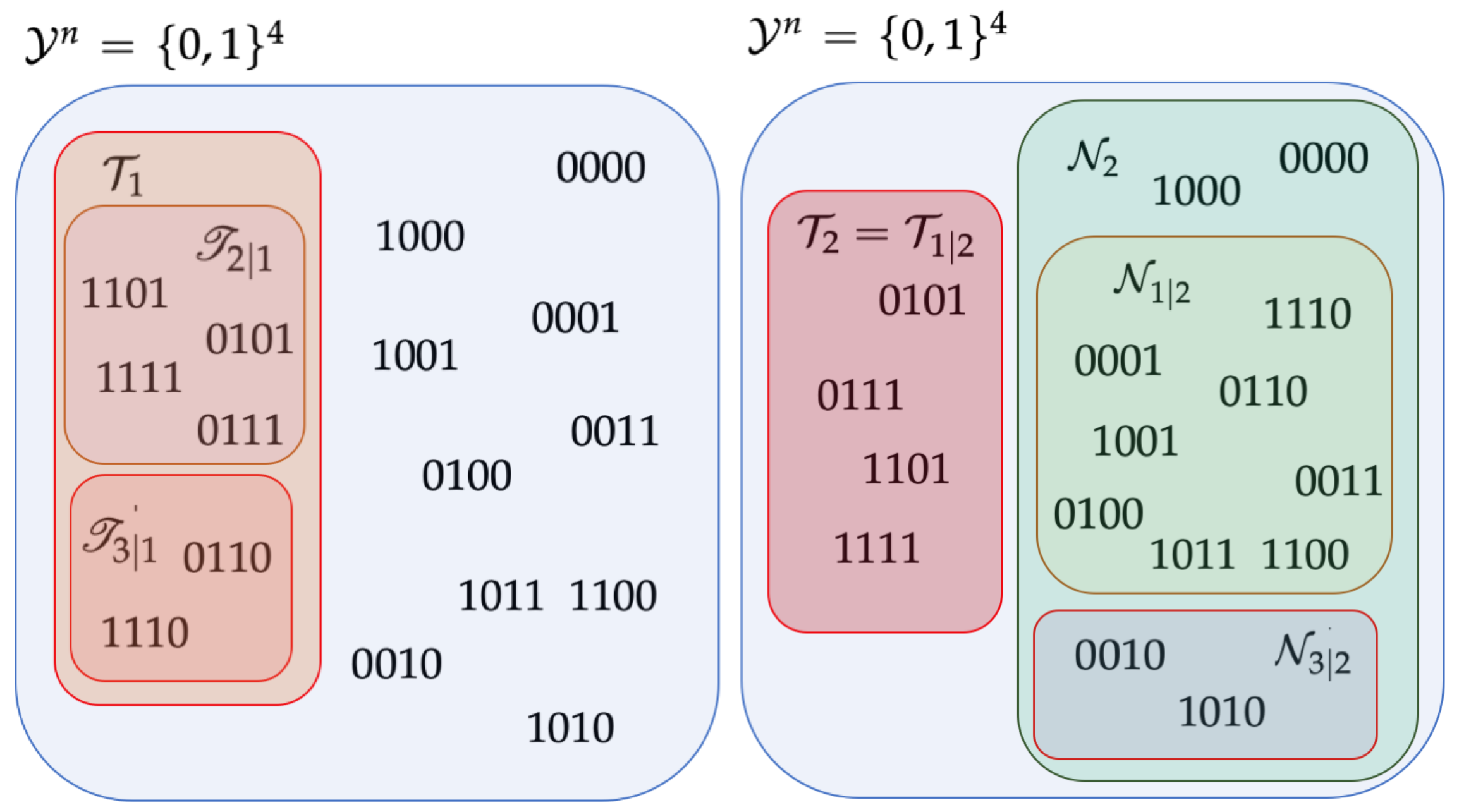
3.1. A Partition of Non-Empty and Corresponding Disjoint Subsets of
- (i)
- The collection forms a (disjoint) partition of .
- (ii)
- is a collection of disjoint subsets of .
3.2. Verification of (32)
3.3. Atomic Decomposition of Non-Empty and the Corresponding Disjoint Subsets of
- (i)
- forms a partition of ;
- (ii)
- is a collection of disjoint subsets of .
- (i)
- forms a (non-empty) partition of ;
- (ii)
- is a collection of (non-empty) disjoint subsets of .
3.4. Characterization of a Linear Upper Bound for
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Supplement to Example 1
| 2 | 2 | 5 | ∅ | ∅ | ∅ | ∅ | ||
| 1 | 3 | 4 | ∅ | ∅ | ∅ | ∅ | ||
| 3 | 1 | 4 | ∅ | ∅ | ∅ | ∅ | ||
| 1 | 1 | 4 | ∅ | ∅ | ∅ | ∅ | ||
| 3 | 3 | 6 | ∅ | ∅ | ∅ | ∅ | ||
| 0 | 2 | 2 | 3 | ∅ | ∅ | ∅ | ∅ | |
| 0 | 0 | 2 | 3 | ∅ | ∅ | |||
| 0 | 2 | 0 | 3 | ∅ | ∅ | |||
| 0 | 2 | 4 | 5 | ∅ | ∅ | ∅ | ∅ | |
| 0 | 4 | 2 | 5 | ∅ | ∅ | ∅ | ∅ | |
| 0 | 2 | 2 | 5 | ∅ | ∅ | ∅ | ∅ | |
| 1 | 1 | 1 | 2 | ∅ | ||||
| 1 | 3 | 3 | 4 | ∅ | ∅ | ∅ | ∅ | |
| 1 | 1 | 3 | 4 | ∅ | ∅ | |||
| 1 | 3 | 1 | 4 | ∅ | ∅ | |||
| 2 | 2 | 2 | 3 | ∅ |
| ∅ | |||||
|---|---|---|---|---|---|
| ∅ | |||||
| ∅ | ∅ | ||||
| ∅ | ∅ | ||||
| ∅ | ∅ | ∅ | |||
| ∅ | |||||
| ∅ | ∅ | ||||
| ∅ | ∅ | ∅ | |||
| ∅ | |||||
| ∅ | ∅ | ||||
| ∅ | ∅ | ∅ | |||
| ∅ | ∅ | ∅ | |||
| ∅ | ∅ | ∅ | |||
| ∅ | ∅ | ∅ | |||
Appendix B. The Proof of the Claim Supporting Proposition 5
- (i)
- : In this case, has no zero components with indices in . Moreover, indicates thatTherefore, we flip arbitrarily a zero component of with its index in to construct a such thatwhich impliesThen, must fulfill (63a), (63c) and (63d) (with replaced by ) as satisfies (61a), (61b) and (61c). We next declare that also fulfills (63b) and will prove this declaration by contradiction.Proof of the declaration: Suppose there exists a satisfyingWe then recall from (45) that is either 0 or . Thus, (A58) can be disproved by differentiating two subcases: , and (Since as can be seen from (50) and (51), we have , i.e., non-empty).In Subcase , that is obtained by flipping a zero component of with index in must satisfy and , which is equivalent toThen, (A58) impliesHence,A contradiction to the fact that satisfies (61a) (with replaced by ) is obtained.In Subcase , we note that implies . Therefore, (A55) leads toThe flipping manipulation on results in and , which is equivalent toTherefore, (A58) implieswhich together with and (A62) result in because . This contradicts . Accordingly, must also fulfill (63b); hence, . This completes the proof of the declaration.With this auxiliary , we are ready to prove that every satisfying (63c) and (63d) also validates (63a) and (63b). Toward this end, we need to proveNote thatwhere (A66a) holds because both and satisfy (63c), implying that all components of and with indices in are equal to one; (A66b) holds because when considering only those portions with indices in (non-empty) , gives either all ones or all zeros according to (45), and both and have exactly ones according to (63c); and (A66c) is valid since both and satisfy (63d). Based on (A66a)–(A66c), we remark that for all , which implies (equivalently, ) for all ).
- (ii)
- : In this case, there is only one zero component of with its index in . Suppose the index of such zero component lie in , where . The flipping manipulation to leads to , which has all one components with respect to . Then, must fulfill (63a), (63c), and (63d) as satisfies (61a), (61b), and (61c). With the components of with respect to (non-empty) being either all zeros or all ones, the same contradiction argument between (A58) and (A64), with replaced by h, can disprove the validity of (A58) for this and for any . Therefore, also fulfills (63b), implying . With this auxiliary , we can again verify (A66a)–(A66c) via the same argument. The claim that satisfying (63c) and (63d) validates (63a) and (63b) is thus confirmed.
References
- Chang, L.H.; Chen, P.N.; Alajaji, F.; Han, Y.S. Decoder Ties Do Not Affect the Error Exponent of the Memoryless Binary Symmetric Channel. IEEE Trans. Inf. Theory 2022, 68, 3501–3510. [Google Scholar] [CrossRef]
- Shannon, C.E.; Gallager, R.G.; Berlekamp, E.R. Lower bounds to error probability for coding on discrete memoryless channels—I. Inf. Control 1967, 10, 65–103. [Google Scholar] [CrossRef]
- Shannon, C.E.; Gallager, R.G.; Berlekamp, E.R. Lower bounds to error probability for coding on discrete memoryless channels—II. Inf. Control 1967, 10, 522–552. [Google Scholar] [CrossRef]
- McEliece, R.J.; Omura, J.K. An improved upper bound on the block coding error exponent for binary-input discrete memoryless channels. IEEE Trans. Inf. Theory 1977, 23, 611–613. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Viterbi, A.J.; Omura, J.K. Principles of Digital Communication and Coding; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Blahut, R. Principles and Practice of Information Theory; Addison-Wesley Longman Publishing Co., Inc.: Albany, NY, USA, 1988. [Google Scholar]
- Barg, A.; McGregor, A. Distance distribution of binary codes and the error probability of decoding. IEEE Trans. Inf. Theory 2005, 51, 4237–4246. [Google Scholar] [CrossRef]
- Haroutunian, E.A.; Haroutunian, M.E.; Harutyunyan, A.N. Reliability Criteria in Information Theory and in Statistical Hypothesis Testing. In Foundations and Trends in Communications and Information Theory; Now Publishers Inc.: Delft, The Netherlands, 2007; Volume 4, pp. 97–263. [Google Scholar]
- Dalai, M. Lower bounds on the probability of error for classical and classical-quantum channels. IEEE Trans. Inf. Theory 2013, 59, 8027–8056. [Google Scholar] [CrossRef]
- Burnashev, M.V. On the BSC reliability function: Expanding the region where it is known exactly. Probl. Inf. Transm. 2015, 51, 307–325. [Google Scholar] [CrossRef]
- Csiszár, I. Joint source-channel error exponent. Probl. Control. Inf. Theory 1980, 9, 315–328. [Google Scholar]
- Zhong, Y.; Alajaji, F.; Campbell, L. On the joint source-channel coding error exponent for discrete memoryless systems. IEEE Trans. Inf. Theory 2006, 52, 1450–1468. [Google Scholar] [CrossRef]
- Alajaji, F.; Phamdo, N.; Fuja, T. Channel codes that exploit the residual redundancy in CELP-encoded speech. IEEE Trans. Speech Audio Process. 1996, 4, 325–336. [Google Scholar] [CrossRef]
- Xu, W.; Hagenauer, J.; Hollmann, J. Joint source-channel decoding using the residual redundancy in compressed images. In Proceedings of the Proceedings of the International Conference on Communications, Washington, DC, USA, 25–28 February 1996; Volume 1, pp. 142–148. [Google Scholar]
- Hagenauer, J. Source-controlled channel decoding. IEEE Trans. Commun. 1995, 43, 2449–2457. [Google Scholar] [CrossRef]
- Goertz, N. Joint Source-Channel Coding of Discrete-Time Signals with Continuous Amplitudes; World Scientific: Singapore, 2007. [Google Scholar]
- Duhamel, P.; Kieffer, M. Joint Source-Channel Decoding: A Cross-Layer Perspective with Applications in Video Broadcasting; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Fresia, M.; Pérez-Cruz, F.; Poor, H.V.; Verdú, S. Joint source and channel coding. IEEE Signal Process. Mag. 2010, 27, 104–113. [Google Scholar] [CrossRef]
- Alajaji, F.; Chen, P.N. An Introduction to Single-User Information Theory; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Chang, L.H.; Chen, P.N.; Alajaji, F.; Han, Y.S. The asymptotic generalized Poor-Verdú bound achieves the BSC error exponent at zero rate. In Proceedings of the IEEE International Symposium on Information Theory, Los Angeles, CA, USA, 21–26 June 2020. [Google Scholar]
- Chen, P.N.; Alajaji, F. A generalized Poor-Verdú error bound for multihypothesis testings. IEEE Trans. Inf. Theory 2012, 58, 311–316. [Google Scholar] [CrossRef]
- Poor, H.V.; Verdú, S. A lower bound on the probability of error in multihypothesis testing. IEEE Trans. Inf. Theory 1995, 41, 1992–1994. [Google Scholar] [CrossRef]
- Chang, L.H.; Chen, P.N.; Alajaji, F.; Han, Y.S. Tightness of the asymptotic generalized Poor-Verdú error bound for the memoryless symmetric channel. arXiv 2020, arXiv:2007.04080v1. [Google Scholar]
| Symbol | Description | Defined in |
|---|---|---|
| A shorthand for | ||
| The code with being the all-zero codeword | ||
| The Hamming distance between the portions of and with indices in | ||
| All terms below are functions of (this dependence is not explicitly shown to simplify notation) | ||
| The set of channel outputs inducing a decoder tie when is sent | (12) | |
| The set of channel outputs leading to a tie-free decoder decision error when is sent | (15) | |
| The set for | (21) | |
| The set of indices for which the components of and differ | ||
| The size of , i.e., | ||
| The subset of consisting of channel outputs such that j is the minimal | (22a) | |
| number r in satisfying | ||
| The subset of consisting of channel outputs that satisfy | (22b) | |
| and that are not included in for | ||
| The subset of consisting of channel outputs | (23) | |
| such that j is the minimal number in | ||
| The subset of defined according to whether each index in is in each | (43) | |
| of , …, , , …, | ||
| The union of , , …, | (48) | |
| The size of , i.e., | ||
| The mapping from to used for partitioning into | (49) | |
| subsets | ||
| The kth partition of for , 1, …, | (52a) | |
| The kth subset of for , 1, …, | (52b) | |
| The set of representative elements in for partitioning | ||
| The subset of associated with | (55a) | |
| The subset of associated with | (55b) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, L.-H.; Chen, P.-N.; Alajaji, F. On Decoder Ties for the Binary Symmetric Channel with Arbitrarily Distributed Input. Entropy 2023, 25, 668. https://doi.org/10.3390/e25040668
Chang L-H, Chen P-N, Alajaji F. On Decoder Ties for the Binary Symmetric Channel with Arbitrarily Distributed Input. Entropy. 2023; 25(4):668. https://doi.org/10.3390/e25040668
Chicago/Turabian StyleChang, Ling-Hua, Po-Ning Chen, and Fady Alajaji. 2023. "On Decoder Ties for the Binary Symmetric Channel with Arbitrarily Distributed Input" Entropy 25, no. 4: 668. https://doi.org/10.3390/e25040668
APA StyleChang, L.-H., Chen, P.-N., & Alajaji, F. (2023). On Decoder Ties for the Binary Symmetric Channel with Arbitrarily Distributed Input. Entropy, 25(4), 668. https://doi.org/10.3390/e25040668







