Entropic Dynamics in a Theoretical Framework for Biosystems
Abstract
1. Introduction
2. Materials and Methods
2.1. Entropic Dynamics
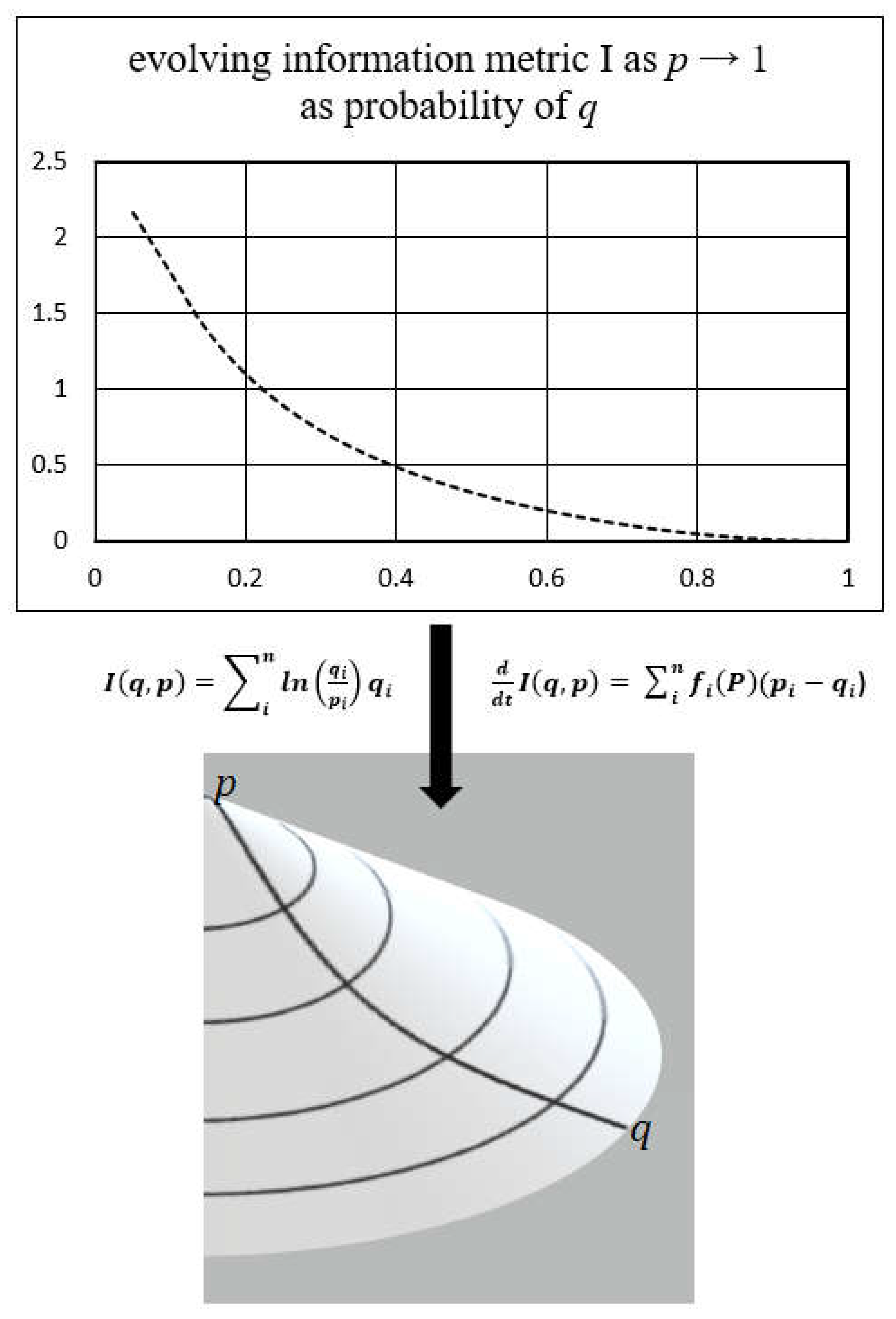
2.2. Kullback Principle of Minimum Information Discrimination
- Uniqueness: the result of the inference should be unique.
- Invariance: the choice of a coordinate system should not matter.
- System independence: it should not matter whether one accounts for independent information about independent systems separately in terms of different densities or together in terms of a joint density.
- Subset independence: it should not matter whether one treats an independent subset of system states in terms of a separate conditional density or in terms of the full system density.
2.3. Biological Continuum (Biocontinuum)
2.4. Information Geometry
2.5. Replicator Dynamics
- is the proportion of type i in the population with the type being any principal attribute category of determined variation and x is the rate of change.
- is the fitness of each type in the population with fitness being a survival likelihood characteristic in the context of the environment.
- is the average population fitness as determined by the weighted average of the fitness of the overall population.
3. Results
3.1. Derivation of Equations of Entropic Dynamics for the Biosystem
3.2. Information Geometry of the Biological Continuum (Biocontinuum)
4. Discussion
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Schrödinger, E. What is Life? Reprint ed.; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Cafaro, C. The Information Geometry of Chaos; VDM Verlag: Saarbrücken, Germany, 2008. [Google Scholar]
- Caticha, A. Entropic Dynamics. Entropy 2015, 17, 6110–6128. [Google Scholar] [CrossRef]
- Prigogine, I.; Stengers, I. Order Out of Chaos; Bantam: Brooklyn, NY, USA, 1984; ISBN 0553343637. [Google Scholar]
- Morowitz, H.J. Energy Flow in Biology: Biological Organization as a Problem in Thermal Physics; Academic Press: Cambridge, MA, USA, 1968. [Google Scholar]
- Leff, H.S.; Rex, A. Maxwell’s Demon: Entropy, Information, Computing; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Hemmo, M.; Shenker, O.R. The Road to Maxwell’s Demon: Conceptual Foundations of Statistical Mechanics; Cambridge University Press: Cambridge, UK, USA, 2012. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Technol. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Summers, R.L. Experiences in the Biocontinuum: A New Foundation for Living Systems; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2020; ISBN 1-5275-5547-X. [Google Scholar]
- Jaynes, E.T.; Rosenkrantz, R.D. (Eds.) Papers on Probability, Statistics and Statistical Physics; Reidel Publishing Company: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Walker, S.I.; Davies, P.C.W. The algorithmic origins of life. J. R. Soc. Interface 2013, 10, 20120869. [Google Scholar] [CrossRef] [PubMed]
- Carlo, R. Meaning = Information + Evolution. arXiv 2016, arXiv:1611.02420. [Google Scholar]
- Ariel, C.; Carlo, C. From Information Geometry to Newtonian Dynamics. arXiv 2007, arXiv:0710.1071. [Google Scholar]
- Ariel, C. From Inference to Physics. In Proceedings of the 28th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Sao Paulo, Brazil, 8–13 July 2008. [Google Scholar]
- Roy, F.B. Science from Fisher Information: A Unification; Cambridge University Press: Cambridge, UK, 2004; ISBN 0-521-00911-1. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Dover: New York, NY, USA, 1968. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Karev, G. Replicator Equations and the Principle of Minimal Production of Information. Bull. Math. Biol. 2010, 72, 1124–1142. [Google Scholar] [CrossRef]
- Karev, G. Principle of Minimum Discrimination Information and Replica Dynamics. Entropy 2010, 12, 1673–1695. [Google Scholar] [CrossRef]
- Summers, R.L. An Action Principle for Biological Systems. J. Phys. Conf. Ser. 2021, 2090, 012109. [Google Scholar] [CrossRef]
- Shore, J.E.; Johnson, R.W. Properties of cross-entropy minimization. IEEE Trans. Inf. Theory 1981, IT-27, 472–482. [Google Scholar] [CrossRef]
- Maturana, H.R.; Varela, F.J. Autopoiesis and Cognition: The Realization of the Living; Springer Science & Business Media: New York, NY, USA, 1991. [Google Scholar]
- Varela, F.; Thompson, E.; Rosch, E. The Embodied Mind: Cognitive Science and Human Experience; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Newby, G.B. 2001. Cognitive space and information space. J. Am. Soc. Inf. Sci. Technol. 2001, 52, 12. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Vol. 191 of Translations of Mathematical Monographs; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Ariel, C. The Basics of Information Geometry. In Proceedings of the 34th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Amboise, France, 21–26 September 2014. [Google Scholar] [CrossRef]
- Fisher, R.A. The Genetical Theory of Natural Selection; Clarendon Press: Oxford, UK, 1930. [Google Scholar]
- Richard, D. The Selfish Gene; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Haldane, J.B.S. A Mathematical Theory of Natural and Artificial Selection, Part V: Selection and Mutation. Math. Proc. Camb. Philos. Soc. 1927, 23, 838–844. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L. Evolutionary Stable Strategies and Game Dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Lotka, A.J. Natural Selection as a Physical Principle. Proc. Natl. Acad. Sci. USA 1922, 8, 151–154. [Google Scholar] [CrossRef]
- Leszek, R. Computational Intelligence. Methods and Techniques; Springer: New York, NY, USA, 2010; ISBN 978-3-540-76287-4. [Google Scholar]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Fujiwara, A.; Shun, A. Gradient Systems in View of Information Geometry. Phys. D Nonlinear Phenom. 1995, 80, 317–327. [Google Scholar] [CrossRef]
- Harper, M. The replicator equation as an inference dynamic. arXiv 2009, arXiv:0911.1763. [Google Scholar]
- Harper, M, Information geometry and evolutionary game theory. arXiv 2009, arXiv:0911.1383.
- Baez, J.C.; Pollard, B.S. Relative Entropy in Biological Systems. Entropy 2016, 18, 46. [Google Scholar] [CrossRef]
- Summers, R.L. Methodology for Quantifying Meaning in Biological Systems. WASET: Int. J. Bioeng. Life Sci. 2023, 17, 1–4. [Google Scholar]
- Summers, R.L. Quantifying the Meaning of Information in Living Systems. Acad. Lett. 2022, 4874, 1–3. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 12738. [Google Scholar] [CrossRef] [PubMed]
- Skarda, C.; Freeman, W. Chaos and the New Science of the Brain. Concepts Neurosci. 1990, 1–2, 275–285. [Google Scholar]
- Skarda, C. The Perceptual Form of Life in Reclaiming Cognition: The Primacy of Action, Intention, and Emotion. J. Conscious. Stud. 1999, 11–12, 79–93. [Google Scholar]
- Vanchurin, V.; Wolf, Y.I.; Koonin, E.V.; Katsnelson, M.I. Thermodynamics of evolution and the origin of life. Proc. Natl. Acad. Sci. USA 2022, 119, e2120042119. [Google Scholar] [CrossRef]
- Summers, R.L. Lyapunov Stability as a Metric for the Meaning of Information in Biological Systems. Biosemiotics 2022, 1–14. [Google Scholar] [CrossRef]
- Ao, P. Laws in Darwinian evolutionary theory. Phys. Life Rev. 2005, 2, 117–156. [Google Scholar] [CrossRef]
- Campbell, J.O. Universal Darwinism As a Process of Bayesian Inference. Front. Syst. Neurosci. 2016, 10, 49. [Google Scholar] [CrossRef]
- Frank, S.A. Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. J. Evol. Biol. 2012, 25, 2377–2396. [Google Scholar] [CrossRef]
- Sella, G.; Hirsh, A.E. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA 2005, 102, 9541–9546. [Google Scholar] [CrossRef]
- Ramirez, J.C.; Marshall, J.A.R. Can natural selection encode Bayesian priors? J. Theor. Biol. 2017, 426, 57–66. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Summers, R.L. Entropic Dynamics in a Theoretical Framework for Biosystems. Entropy 2023, 25, 528. https://doi.org/10.3390/e25030528
Summers RL. Entropic Dynamics in a Theoretical Framework for Biosystems. Entropy. 2023; 25(3):528. https://doi.org/10.3390/e25030528
Chicago/Turabian StyleSummers, Richard L. 2023. "Entropic Dynamics in a Theoretical Framework for Biosystems" Entropy 25, no. 3: 528. https://doi.org/10.3390/e25030528
APA StyleSummers, R. L. (2023). Entropic Dynamics in a Theoretical Framework for Biosystems. Entropy, 25(3), 528. https://doi.org/10.3390/e25030528




