Interplay between Non-Markovianity of Noise and Dynamics in Quantum Systems
Abstract
1. Introduction
2. Model and Non-Markovianity Measures
2.1. Model
2.2. Non-Markovianity Measures
3. Results and Discussion
3.1. Markovian Noise
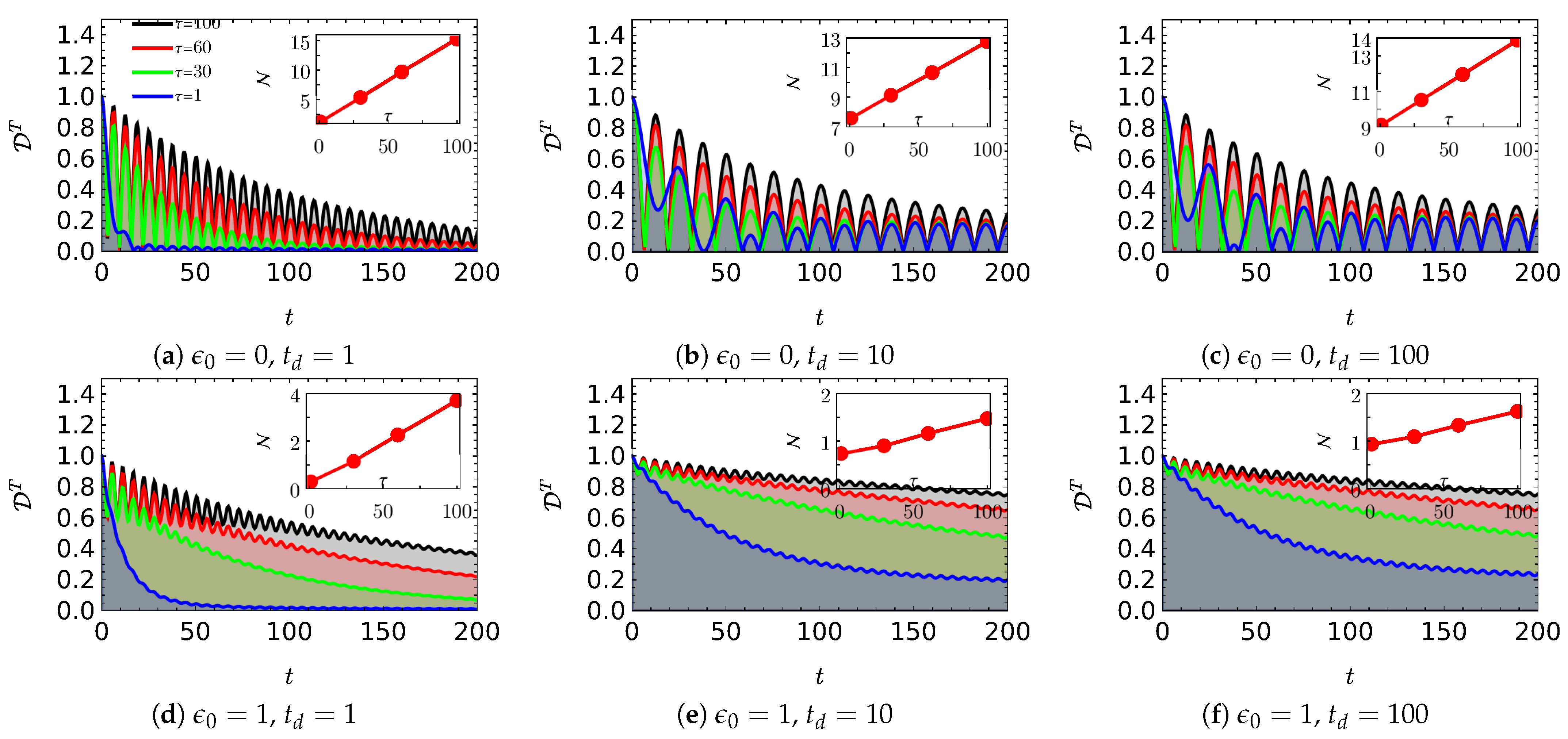
3.2. Biexponentially Distributed Residence Time
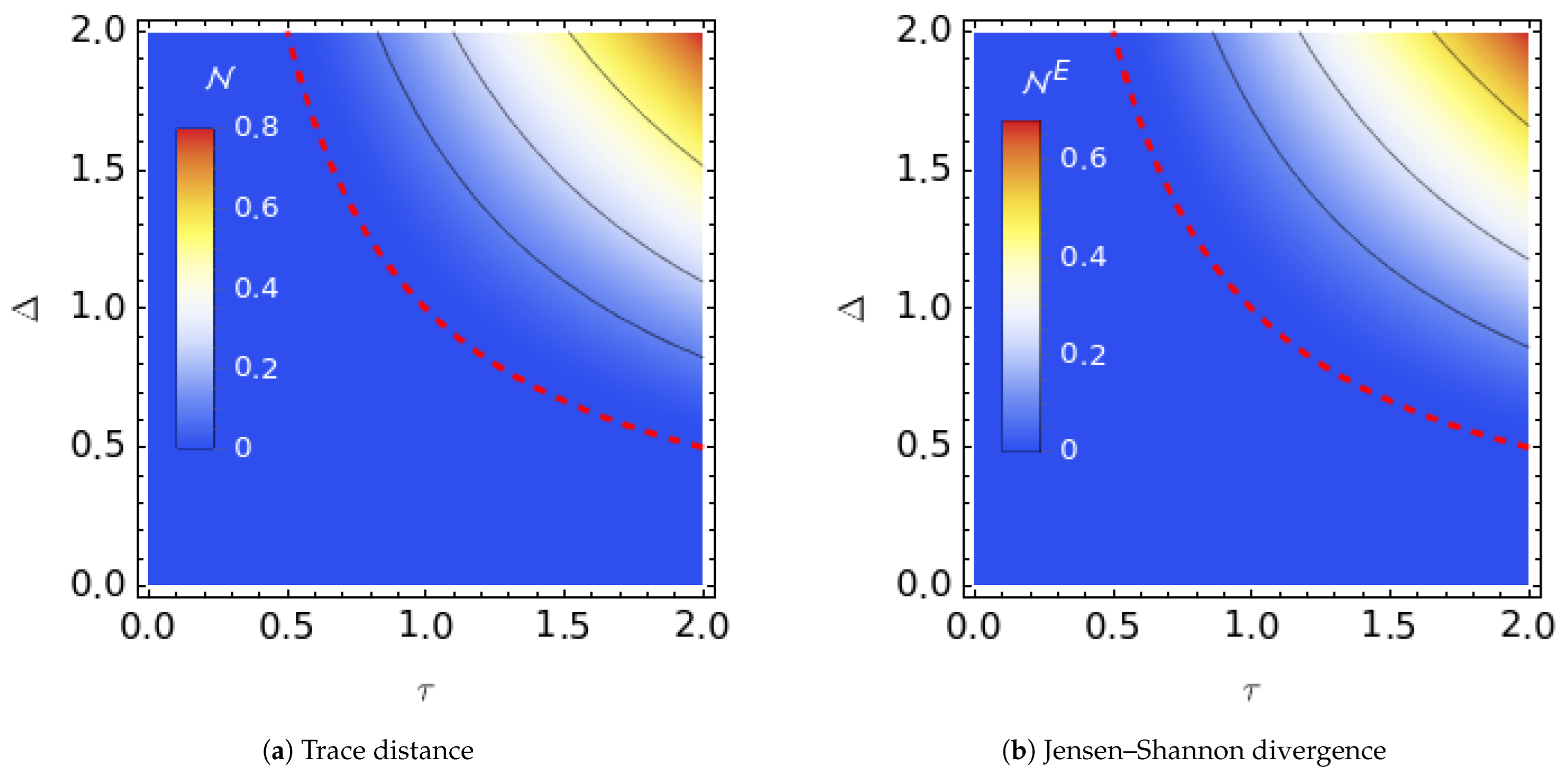
3.3. The Manifest Non-Markovian Noise
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reich, D.M.; Katz, N.; Koch, C.P. Exploiting non-Markovianity for quantum control. Sci. Rep. 2015, 5, 12430. [Google Scholar] [CrossRef]
- Xiang, G.-Y.; Hou, Z.-B.; Li, C.-F.; Guo, G.-C.; Breuer, H.-P.; Laine, E.-M.; Piilo, J. Entanglement distribution in optical fibers assisted by nonlocal memory effects. EPL 2014, 107, 54006. [Google Scholar] [CrossRef]
- Laine, E.-M.; Breuer, H.-P.; Piilo, J. Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 2014, 4, 4620. [Google Scholar] [CrossRef] [PubMed]
- Bylicka, B.; Chruscinski, D.; Maniscalco, S. Non-Markovianity and reservoir memory of quantum channels: A quantum information theory perspective. Sci. Rep. 2014, 4, 5720. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Siddharth, N.; Banerjee, S.; Ghosh, S. Thermodynamics of non-Markovian reservoirs and heat engines. Phys. Rev. E 2018, 97, 062108. [Google Scholar] [CrossRef]
- Miller, M.; Wu, K.-D.; Scalici, M.; Kołodyński, J.; Xiang, G.-Y.; Li, C.-F.; Guo, G.-C.; Streltsov, A. Optimally preserving quantum correlations and coherence with eternally non-Markovian dynamics. New J. Phys. 2022, 24, 053022. [Google Scholar] [CrossRef]
- Pernice, A.; Helm, J.; Strunz, W.T. System–environment correlations and non-Markovian dynamics. J. Phys. B Atom. Mol. Phys. 2012, 45, 154005. [Google Scholar] [CrossRef]
- Megier, N.; Chruscinski, D.; Piilo, J.; Strunz, W. Eternal non-Markovianity: From random unitary to Markov chain realisation. Sci. Rep. 2017, 7, 6379. [Google Scholar] [CrossRef]
- Breuer, H.P.; Amato, G.; Vacchini, B. Mixing-induced quantum non-Markovianity and information flow. New J. Phys. 2018, 20, 043007. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, N.; He, W.E.A. Global correlation and local information flows in controllable non-Markovian open quantum dynamics. Npj Quantum Inf. 2022, 8, 22. [Google Scholar] [CrossRef]
- Haken, H.; Reineker, P. The coupled coherent and incoherent motion of excitons and its influence on the line shape of optical absorption. Z. Phys. 1972, 249, 253–268. [Google Scholar] [CrossRef]
- Haken, H.; Strobl, G. An exactly solvable model for coherent and incoherent exciton motion. Z. Phys. 1973, 262, 135. [Google Scholar] [CrossRef]
- Fox, R.F. Gaussian stochastic processes in physics. Phys. Rep. 1978, 48, 181. [Google Scholar] [CrossRef]
- Kayanuma, Y. Stochastic theory for nonadiabatic level crossing with fluctuating off-diagonal coupling. J. Phys. Soc. Jpn. 1985, 54, 2047. [Google Scholar] [CrossRef]
- Dong, Q.; Torres-Arenas, A.J.; Sun, G.H.; Dong, S.H. Tetrapartite entanglement features of W-Class state in uniform acceleration. Front. Phys. 2020, 15, 11602. [Google Scholar] [CrossRef]
- Shao, J.; Zerbe, C.; Hänggi, P. Suppression of quantum coherence: Noise effect. Chem. Phys. 1998, 235, 81. [Google Scholar] [CrossRef]
- Cialdi, S.; Benedetti, C.; Tamascelli, D.; Olivares, S.; Paris, M.G.A.; Vacchini, B. Experimental investigation of the effect of classical noise on quantum non-Markovian dynamics. Phys. Rev. A 2019, 100, 052104. [Google Scholar] [CrossRef]
- Benedetti, C.; Paris, M.G.A.; Maniscalco, S. Non-markovianity of colored noisy channels. Phys. Rev. A 2014, 89, 012114. [Google Scholar] [CrossRef]
- Benedetti, C.; Buscemi, F.; Bordone, P.; Paris, M.G.A. Non-markovian continuous-time quantum walks on lattices with dynamical noise. Phys. Rev. A 2016, 93, 042313. [Google Scholar] [CrossRef]
- Costa-Filho, J.I.; Lima, R.B.B.; Paiva, R.R.; Soares, P.M.; Morgado, W.A.M.; Franco, R.L.; Soares-Pinto, D.O. Enabling quantum non-Markovian dynamics by injection of classical colored noise. Phys. Rev. A 2017, 95, 052126. [Google Scholar] [CrossRef]
- Bergli, J.; Faoro, L. Exact solution for the dynamical decoupling of a qubit with telegraph noise. Phys. Rev. B 2007, 75, 054515. [Google Scholar] [CrossRef]
- Cywiński, L.; Lutchyn, R.M.; Nave, C.P.; Das Sarma, S. How to enhance dephasing time in superconducting qubits. Phys. Rev. B 2008, 77, 174509. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Decoherence induced by non-Markovian noise in a nonequilibrium environment. Phys. Rev. A 2016, 94, 042110. [Google Scholar] [CrossRef]
- Cheng, B.; Wang, Q.-H.; Joynt, R. Transfer matrix solution of a model of qubit decoherence due to telegraph noise. Phys. Rev. A 2008, 78, 022313. [Google Scholar] [CrossRef]
- Goychuk, I. Quantum dynamics with non-Markovian fluctuating parameters. Phys. Rev. E 2004, 70, 016109. [Google Scholar] [CrossRef]
- Goychuk, I.; Hänggi, P. Quantum two-state dynamics driven by stationary non-Markovian discrete noise: Exact results. Chem. Phys. 2006, 324, 160–171. [Google Scholar] [CrossRef]
- Liu, B.-H.; Li, L.; Huang, Y.-F.; Li, C.-F.; Guo, G.-C.; Laine, E.-M.; Breuer, H.-P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931–934. [Google Scholar] [CrossRef]
- Bernardes, N.; Carvalho, A.; Monken, C.; Santos, M.F. Environmental correlations and markovian to non-markovian transitions in collisional models. Phys. Rev. A 2014, 90, 032111. [Google Scholar] [CrossRef]
- Brito, F.; Werlang, T. A knob for Markovianity. New J. Phys. 2015, 17, 072001. [Google Scholar] [CrossRef]
- Garrido, N.; Gorin, T.; Pineda, C. Transition from non-Markovian to Markovian dynamics for generic environments. Phys. Rev. A 2016, 93, 012113. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mallick, A.; Mandal, D.; Goyal, S.K.; Ghosh, S. Non-Markovianity of qubit evolution under the action of spin environment. Sci. Rep. 2019, 9, 2987. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Heinosaari, T.; Ziman, M. The Mathematical Language of Quantum Theory: From Uncertainty to Entanglement, 1st ed.; Cambridge University Press: Cambridge, UK, 2011; pp. 159–169. [Google Scholar]
- Fuchs, C.A.; Van de Graaf, J. Cryptographic distinguishability measures for quantum-mechanical states. IEEE Trans. Inf. Theory 1999, 45, 1216. [Google Scholar] [CrossRef]
- Majtey, A.P.; Lamberti, P.W.; Prato, D.P. Jensen-Shannon divergence as a measure of distinguishability between mixed quantum states. Phys. Rev. A 2005, 72, 052310. [Google Scholar] [CrossRef]
- Settimo, F.; Breuer, H.-P.; Vacchini, B. Entropic and trace-distance-based measures of non-Markovianity. Phys. Rev. A 2022, 106, 042212. [Google Scholar] [CrossRef]
- Virosztek, D. The metric property of the quantum Jensen-Shannon divergence. Adv. Math. 2021, 380, 107595. [Google Scholar] [CrossRef]
- Wissmann, S.; Karlsson, A.; Laine, E.-M.; Piilo, J.; Breuer, H.-P. Optimal state pairs for non-Markovian quantum dynamics. Phys. Rev. A 2012, 86, 062108. [Google Scholar] [CrossRef]
- Zhou, D.; Lang, A.; Joynt, R. Disentanglement and decoherence from classical non-Markovian noise: Random telegraph noise. Quantum Inf. Process 2010, 9, 727–747. [Google Scholar] [CrossRef]
- Goychuk, I.; Hänggi, P. Theory of non-Markovian stochastic resonance. Phys. Rev. E 2004, 70, 021104. [Google Scholar] [CrossRef]
- Horvath, I.; Horvath, G.; Alamosa, S.A.D.; Telek, M. Numerical inverse Laplace transformation using concentrated matrix exponential distributions. Perform. Eval. 2019, 137, 102067. [Google Scholar] [CrossRef]
- Crump, K.S. Numerical inversion of Laplace transforms using a Fourier series approximation. J. Assoc. Comput. Mach. 1976, 23, 89–96. [Google Scholar] [CrossRef]
- Durbin, F. Numerical inversion of Laplace transforms: An effective improvement of Dubner and Abate’s method. Comput. J. 1973, 17, 371–376. [Google Scholar] [CrossRef]
- Papoulis, A. A new method of inversion of the Laplace transform. PIB 1957, XIV, 405–414. [Google Scholar] [CrossRef]
- Piessens, R. A bibliography on numerical inversion of the Laplace transform and applications. J. Camp. Appl. Math. 1975, 1, 115–126. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms d[5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of Laplace transforms. IMA J. Appl. Math. 1970, 23, 97–120. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurt, A. Interplay between Non-Markovianity of Noise and Dynamics in Quantum Systems. Entropy 2023, 25, 501. https://doi.org/10.3390/e25030501
Kurt A. Interplay between Non-Markovianity of Noise and Dynamics in Quantum Systems. Entropy. 2023; 25(3):501. https://doi.org/10.3390/e25030501
Chicago/Turabian StyleKurt, Arzu. 2023. "Interplay between Non-Markovianity of Noise and Dynamics in Quantum Systems" Entropy 25, no. 3: 501. https://doi.org/10.3390/e25030501
APA StyleKurt, A. (2023). Interplay between Non-Markovianity of Noise and Dynamics in Quantum Systems. Entropy, 25(3), 501. https://doi.org/10.3390/e25030501






