Spectral Form Factor and Dynamical Localization
Abstract
1. Introduction
2. Definitions and Methods
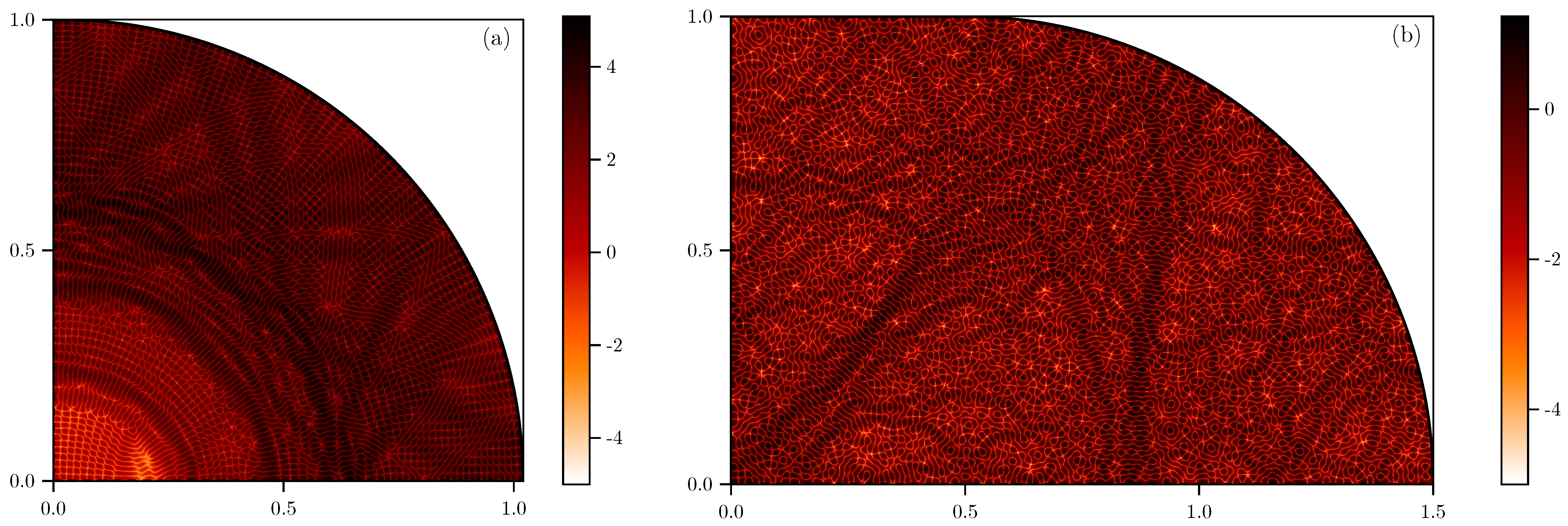
2.1. Quantum Billiards
2.2. Spectral Form Factor
2.3. Dynamical Localization and Level Repulsion
3. Results
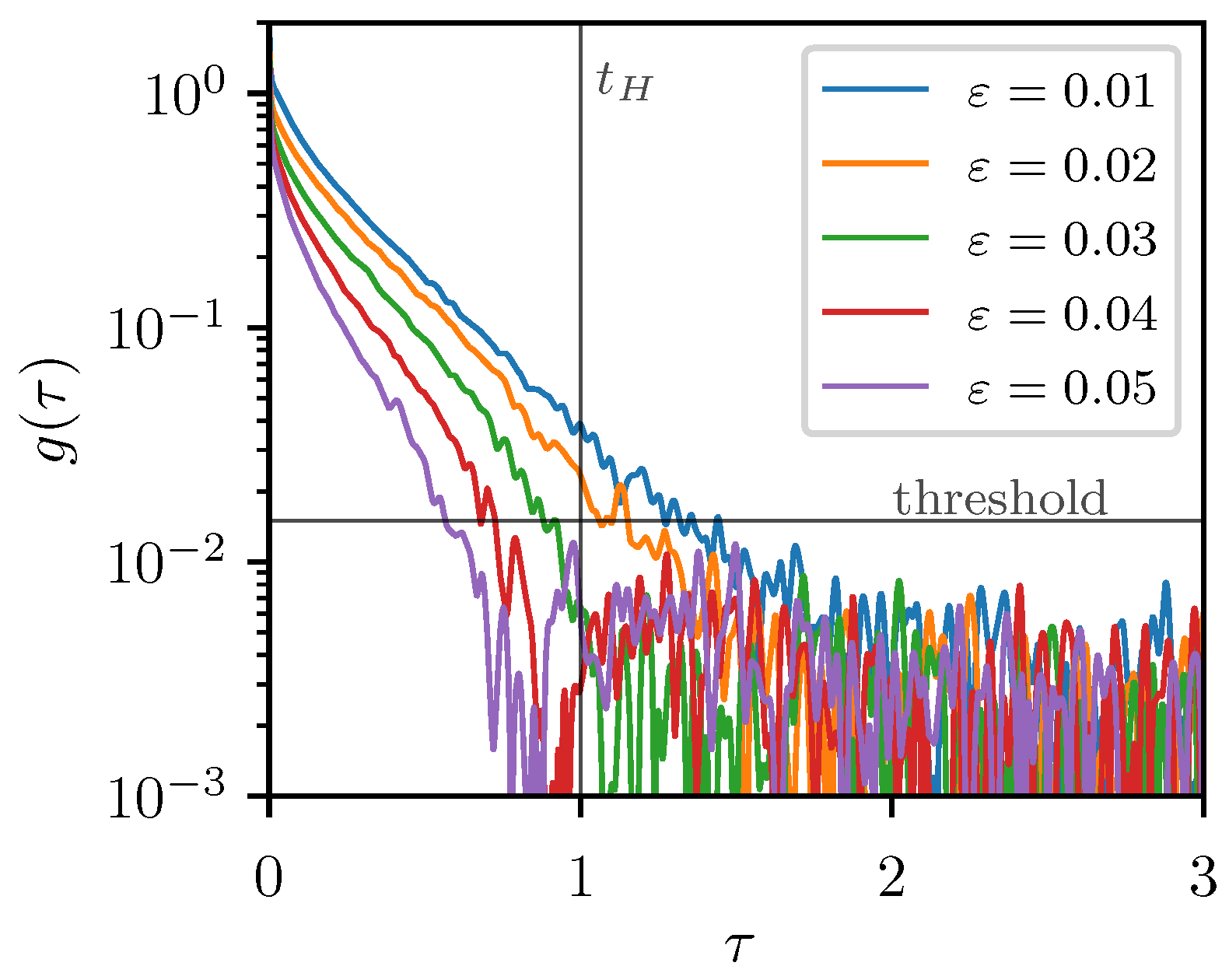
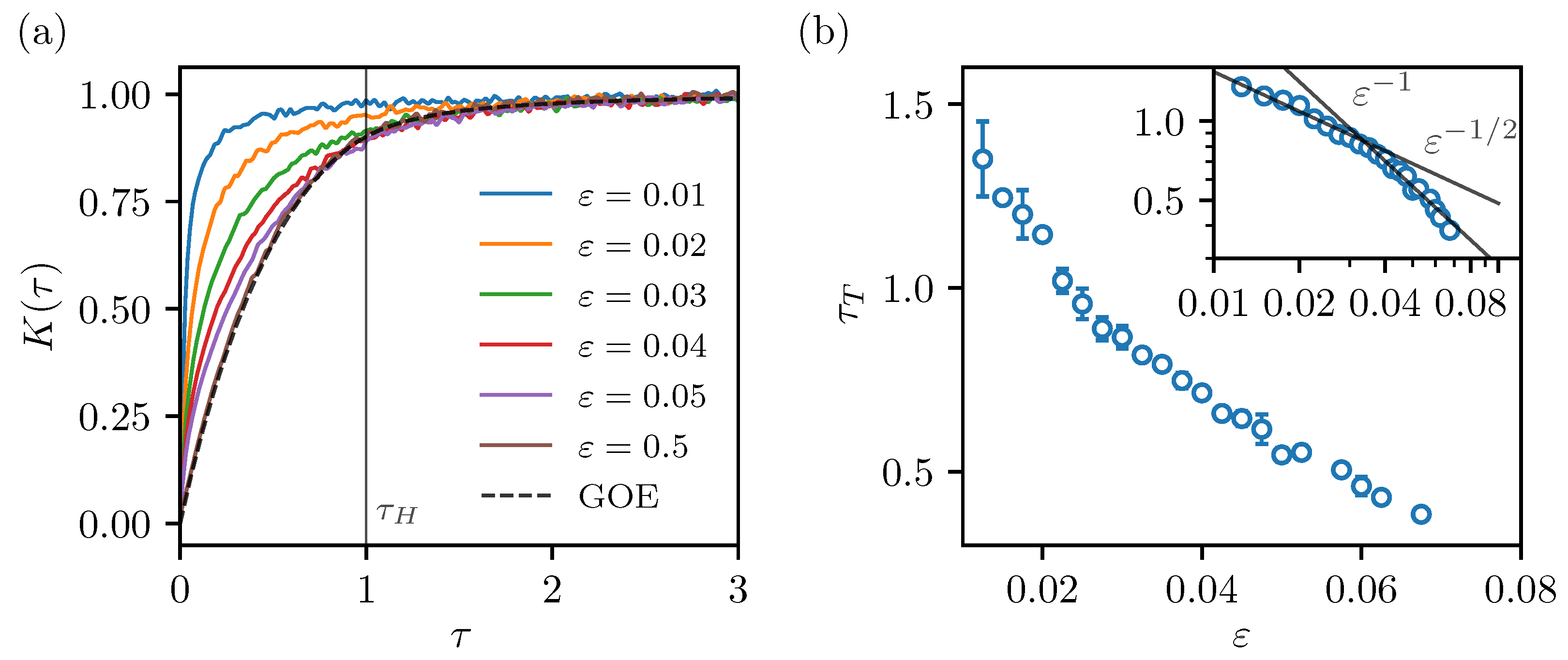
3.1. Transport Times
3.2. Level Repulsion
4. Discussion
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RMT | Random matrix theory |
| SFF | Spectral form factor |
| GOE | Gaussian orthogonal ensemble |
| DL | Dynamical localization |
Appendix A. Extracting the Quantum Transport Times
References
- Stöckmann, H.J. Quantum Chaos—An Introduction; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin, Germany, 2001. [Google Scholar]
- Prange, R. The spectral form factor is not self-averaging. Phys. Rev. Lett. 1997, 78, 2280. [Google Scholar] [CrossRef]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 1984, 52, 1–4. [Google Scholar] [CrossRef]
- Casati, G.; Valz-Gris, F.; Guarnieri, I. On the connection between quantization of nonintegrable systems and statistical theory of spectra. Lett. Nuovo C. 1980, 28, 279–282. [Google Scholar] [CrossRef]
- Berry, M.V. Semiclassical theory of spectral rigidity. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 229–251. [Google Scholar]
- Sieber, M.; Richter, K. Correlations between periodic orbits and their role in spectral statistics. Phys. Scr. 2001, T90, 128. [Google Scholar] [CrossRef]
- Müller, S.; Heusler, S.; Braun, P.; Haake, F.; Altland, A. Semiclassical Foundation of Universality in Quantum Chaos. Phys. Rev. Lett. 2004, 93, 014103. [Google Scholar] [CrossRef]
- Heusler, S.; Müller, S.; Braun, P.; Haake, F. Universal spectral form factor for chaotic dynamics. J. Phys. Math. Gen. 2004, 37, L31. [Google Scholar] [CrossRef]
- Müller, S.; Heusler, S.; Braun, P.; Haake, F.; Altland, A. Periodic-orbit theory of universality in quantum chaos. Phys. Rev. E 2005, 72, 046207. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Prosen, T. Random matrix spectral form factor in kicked interacting fermionic chains. Phys. Rev. E 2020, 102, 060202. [Google Scholar] [CrossRef]
- Roy, D.; Mishra, D.; Prosen, T. Spectral form factor in a minimal bosonic model of many-body quantum chaos. Phys. Rev. E 2022, 106, 024208. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Solution of a minimal model for many-body quantum chaos. Phys. Rev. X 2018, 8, 041019. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J. Spectral statistics in spatially extended chaotic quantum many-body systems. Phys. Rev. Lett. 2018, 121, 060601. [Google Scholar] [CrossRef]
- Moudgalya, S.; Prem, A.; Huse, D.A.; Chan, A. Spectral statistics in constrained many-body quantum chaotic systems. Phys. Rev. Res. 2021, 3, 023176. [Google Scholar] [CrossRef]
- Chan, A.; Shivam, S.; Huse, D.A.; De Luca, A. Many-body quantum chaos and space-time translational invariance. Nat. Commun. 2022, 13, 7484. [Google Scholar] [CrossRef]
- Kos, P.; Ljubotina, M.; Prosen, T. Many-body quantum chaos: Analytic connection to random matrix theory. Phys. Rev. X 2018, 8, 021062. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Exact spectral form factor in a minimal model of many-body quantum chaos. Phys. Rev. Lett. 2018, 121, 264101. [Google Scholar] [CrossRef]
- Kos, P.; Bertini, B.; Prosen, T. Correlations in perturbed dual-unitary circuits: Efficient path-integral formula. Phys. Rev. X 2021, 11, 011022. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Random matrix spectral form factor of dual-unitary quantum circuits. Commun. Math. Phys. 2021, 387, 597–6204. [Google Scholar] [CrossRef]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black holes and random matrices. J. High Energy Phys. 2017, 2017, 1–54. [Google Scholar] [CrossRef]
- Gharibyan, H.; Hanada, M.; Shenker, S.H.; Tezuka, M. Onset of random matrix behavior in scrambling systems. J. High Energy Phys. 2018, 2018, 1–62. [Google Scholar] [CrossRef]
- Khramtsov, M.; Lanina, E. Spectral form factor in the double-scaled SYK model. J. High Energy Phys. 2021, 2021, 1–38. [Google Scholar] [CrossRef]
- Cáceres, E.; Misobuchi, A.; Raz, A. Spectral form factor in sparse SYK models. J. High Energy Phys. 2022, 2022, 1–22. [Google Scholar] [CrossRef]
- Winer, M.; Swingle, B. Hydrodynamic theory of the connected spectral form factor. Phys. Rev. X 2022, 12, 021009. [Google Scholar] [CrossRef]
- Delon, A.; Jost, R.; Lombardi, M. NO2 jet cooled visible excitation spectrum: Vibronic chaos induced by the X2A1-A2B2 interaction. J. Chem. Phys. 1991, 95, 5701–5718. [Google Scholar] [CrossRef]
- Alt, H.; Gräf, H.D.; Guhr, T.; Harney, H.; Hofferbert, R.; Rehfeld, H.; Richter, A.; Schardt, P. Correlation-hole method for the spectra of superconducting microwave billiards. Phys. Rev. E 1997, 55, 6674. [Google Scholar] [CrossRef]
- Šuntajs, J.; Bonča, J.; Prosen, T.; Vidmar, L. Quantum chaos challenges many-body localization. Phys. Rev. E 2020, 102, 062144. [Google Scholar] [CrossRef]
- Prakash, A.; Pixley, J.; Kulkarni, M. Universal spectral form factor for many-body localization. Phys. Rev. Res. 2021, 3, L012019. [Google Scholar] [CrossRef]
- Marklof, J. Spectral form factors of rectangle billiards. Commun. Math. Phys. 1998, 199, 169–202. [Google Scholar] [CrossRef]
- Rahav, S.; Fishman, S. Spectral statistics of rectangular billiards with localized perturbations. Nonlinearity 2002, 15, 1541. [Google Scholar] [CrossRef]
- Wiersig, J. Spectral properties of quantized barrier billiards. Phys. Rev. E 2002, 65, 046217. [Google Scholar] [CrossRef]
- Giraud, O. Periodic orbits and semiclassical form factor in barrier billiards. Commun. Math. Phys. 2005, 260, 183–201. [Google Scholar] [CrossRef]
- Bogomolny, E. Level compressibility of certain random unitary matrices. Entropy 2022, 24, 795. [Google Scholar] [CrossRef]
- Bogomolny, E.; Giraud, O.; Schmit, C. Periodic orbits contribution to the 2-point correlation form factor for pseudo-integrable systems. Commun. Math. Phys. 2001, 222, 327–369. [Google Scholar] [CrossRef]
- Lozej, Č.; Casati, G.; Prosen, T. Quantum chaos in triangular billiards. Phys. Rev. Res. 2022, 4, 013138. [Google Scholar] [CrossRef]
- Borgonovi, F.; Casati, G.; Li, B. Diffusion and localization in chaotic billiards. Phys. Rev. Lett. 1996, 77, 4744. [Google Scholar] [CrossRef]
- Casati, G.; Prosen, T. Quantum localization and cantori in the stadium billiard. Phys. Rev. E 1999, 59, R2516. [Google Scholar] [CrossRef]
- Casati, G.; Prosen, T. The quantum mechanics of chaotic billiards. Phys. D Nonlinear Phenom. 1999, 131, 293–310. [Google Scholar] [CrossRef]
- Grempel, D.; Fishman, S.; Prange, R. Localization in an incommensurate potential: An exactly solvable model. Phys. Rev. Lett. 1982, 49, 833. [Google Scholar] [CrossRef]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Santhanam, M.; Paul, S.; Kannan, J.B. Quantum kicked rotor and its variants: Chaos, localization and beyond. Phys. Rep. 2022, 956, 1–87. [Google Scholar] [CrossRef]
- Batistić, B.; Robnik, M. Dynamical localization of chaotic eigenstates in the mixed-type systems: Spectral statistics in a billiard system after separation of regular and chaotic eigenstates. J. Phys. A Math. Theor. 2013, 46, 315102. [Google Scholar] [CrossRef]
- Batistić, B.; Robnik, M. Quantum localization of chaotic eigenstates and the level spacing distribution. Phys. Rev. E 2013, 88, 052913. [Google Scholar] [CrossRef]
- Batistić, B.; Lozej, Č.; Robnik, M. The Level Repulsion Exponent of Localized Chaotic Eigenstates as a Function of the Classical Transport Time Scales in the Stadium Billiard. Nonlinear Phenom. Complex Syst. 2018, 21, 225–236. [Google Scholar]
- Batistić, B.; Lozej, Č.; Robnik, M. Statistical properties of the localization measure of chaotic eigenstates and the spectral statistics in a mixed-type billiard. Phys. Rev. E 2019, 100, 062208. [Google Scholar] [CrossRef]
- Batistić, B.; Lozej, Č.; Robnik, M. The distribution of localization measures of chaotic eigenstates in the stadium billiard. Nonlinear Phenom. Complex Syst. 2020, 23, 17–32. [Google Scholar] [CrossRef]
- Lozej, Č. Transport and Localization in Classical and Quantum Billiards. Ph.D. Thesis, University of Maribor, Maribor, Slovenia, 2020. [Google Scholar]
- Wang, Q.; Robnik, M. Statistical properties of the localization measure of chaotic eigenstates in Dicke model. Phys. Rev. E 2020, 102, 032212. [Google Scholar] [CrossRef] [PubMed]
- Lozej, Č.; Robnik, M. Aspects of diffusion in the stadium billiard. Phys. Rev. E 2018, 97, 012206. [Google Scholar] [CrossRef] [PubMed]
- Lozej, Č.; Robnik, M. Structure, size, and statistical properties of chaotic components in a mixed-type Hamiltonian system. Phys. Rev. E 2018, 98, 022220. [Google Scholar] [CrossRef]
- Lozej, Č. Stickiness in generic low-dimensional Hamiltonian systems: A recurrence-time statistics approach. Phys. Rev. E 2020, 101, 052204. [Google Scholar] [CrossRef] [PubMed]
- Lozej, Č.; Lukman, D.; Robnik, M. Effects of stickiness in the classical and quantum ergodic lemon billiard. Phys. Rev. E 2021, 103, 012204. [Google Scholar] [CrossRef]
- Vergini, E.; Saraceno, M. Calculation by scaling of highly excited states of billiards. Phys. Rev. E 1995, 52, 2204–2207. [Google Scholar] [CrossRef]
- Barnett, A. Dissipation in Deforming Chaotic Billiards. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 2001. [Google Scholar]
- Lozej, Č.; Batistić, B.; Lukman, D. Quantum Billiards. Available online: https://github.com/clozej/quantum-billiards/tree/crt_public (accessed on 30 January 2023).
- Baltes, H.P.; Hilf, E.R. Spectra of Finite Systems; BI-Wissenschafts: Mannheim, Germany, 1976. [Google Scholar]
- Bunimovich, L.A. On billiards close to dispersing. Mat. Sb. 1974, 136, 49–73. [Google Scholar]
- Bunimovich, L.A. On the ergodic properties of nowhere dispersing billiards. Commun. Math. Phys. 1979, 65, 295–312. [Google Scholar] [CrossRef]
- Lozej, Č.; Lukman, D.; Robnik, M. Phenomenology of quantum eigenstates in mixed-type systems: Lemon billiards with complex phase space structure. Phys. Rev. E 2022, 106, 054203. [Google Scholar] [CrossRef]
- Brody, T. A statistical measure for the repulsion of energy levels. Lett. Nuovo C. (1971–1985) 1973, 7, 482–484. [Google Scholar] [CrossRef]
- Manos, T.; Robnik, M. Dynamical localization in chaotic systems: Spectral statistics and localization measure in the kicked rotator as a paradigm for time-dependent and time-independent systems. Phys. Rev. E 2013, 87, 062905. [Google Scholar] [CrossRef] [PubMed]
- Vivaldi, F.; Casati, G.; Guarneri, I. Origin of long-time tails in strongly chaotic systems. Phys. Rev. Lett. 1983, 51, 727. [Google Scholar] [CrossRef]
- Robnik, M. Classical dynamics of a family of billiards with analytic boundaries. J. Phys. A Math. Gen. 1983, 16, 3971. [Google Scholar] [CrossRef]
- Robnik, M. Quantising a generic family of billiards with analytic boundaries. J. Phys. A Math. Gen. 1984, 17, 1049. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozej, Č. Spectral Form Factor and Dynamical Localization. Entropy 2023, 25, 451. https://doi.org/10.3390/e25030451
Lozej Č. Spectral Form Factor and Dynamical Localization. Entropy. 2023; 25(3):451. https://doi.org/10.3390/e25030451
Chicago/Turabian StyleLozej, Črt. 2023. "Spectral Form Factor and Dynamical Localization" Entropy 25, no. 3: 451. https://doi.org/10.3390/e25030451
APA StyleLozej, Č. (2023). Spectral Form Factor and Dynamical Localization. Entropy, 25(3), 451. https://doi.org/10.3390/e25030451





