Remora Optimization Algorithm with Enhanced Randomness for Large-Scale Measurement Field Deployment Technology
Abstract
1. Introduction
2. Original ROA
3. Proposed PROA
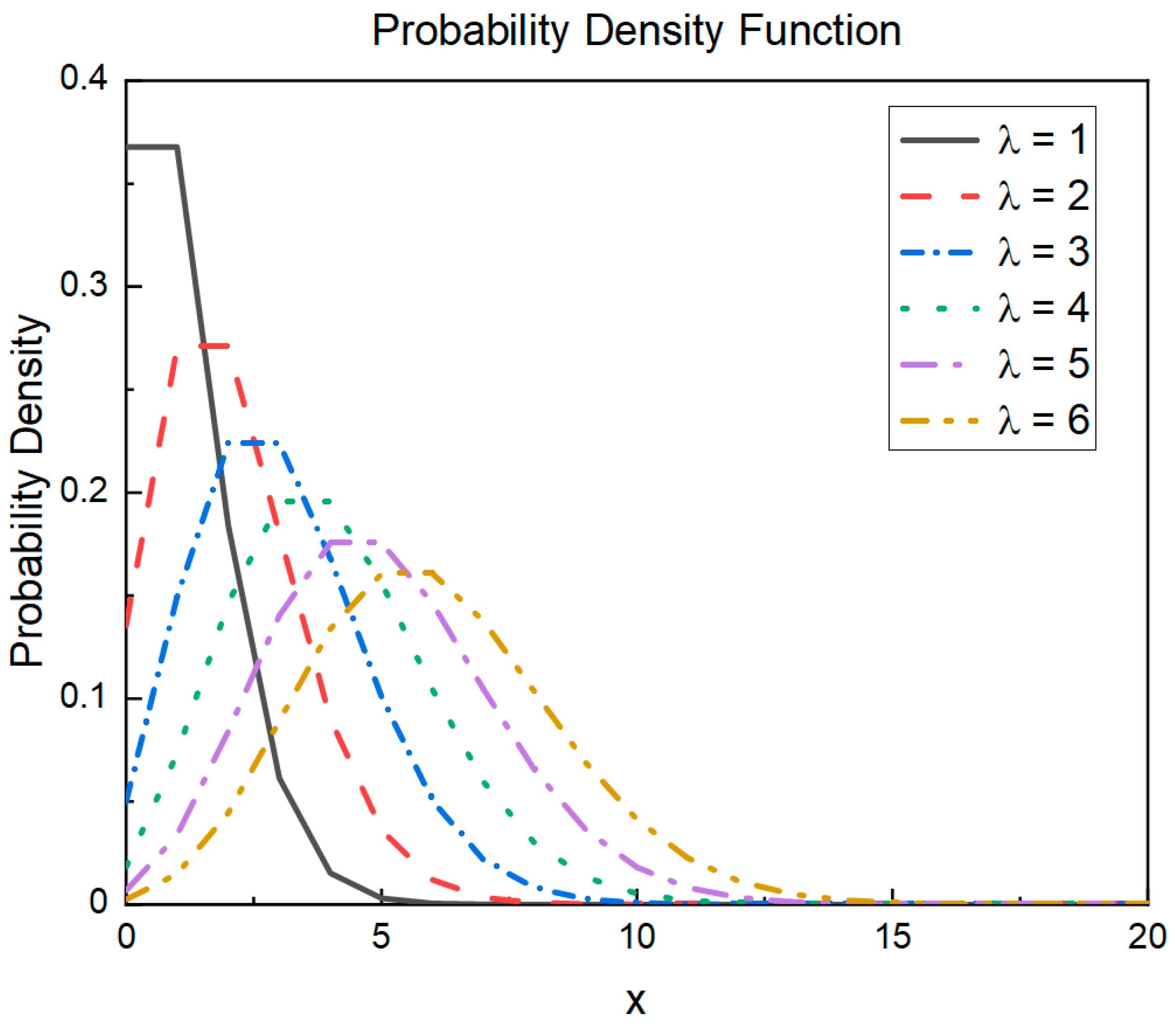
3.1. Poisson-like Randomness Strategy
- The slope was gentle, and there was no sudden change in the function value.
- The peak and surrounding area are close to one side, which is the opposite of the trend of the change in the strength of the search strategy.
- Horizontally mirror the probability density function curve of in Figure 1 such that it conforms to the trend of the search strategy strength changes.
- Parameter curve is obtained by stretching the x-axis according to the maximum number of iterations of the optimization algorithm.
- Because the two parameters have opposite trends, is the parameter curve .
3.2. Enhanced Randomness Strategy
3.3. Steps to the PROA
| Algorithm 1: Pseudocode for the PROA. | |
| Input: population position , the number of iterations , fitness function , and bound . Output: best position, best fitness, and fitness history. | |
| 1: | Initialize the pre-population dataset ; |
| 2: | While carry out |
| 3: | Amend agent if out of bound ; |
| 4: | Calculate of each agent; |
| 5: | Update and ; |
| 6: | For each agent indexed by i carry out |
| 7: | Using Equation (8) to make an experienced attempt with Poisson-like distribution; |
| 8: | Calculate and ; |
| 9: | If then |
| 10: | Perform host feeding by Equation (2); |
| 11: | Else |
| 12: | If then |
| 13: | Using Equation (4) to update the position by WOA policy; |
| 14: | If then |
| 15: | Using Equations (9)–(11) to update the position with enhanced randomness SFO policy; |
| 16: | End if |
| 17: | End if |
| 18: | Add current population to ; |
| 19: | End for |
| 20: | ; |
| 21: | End while |
4. Performance Comparison under the CEC Benchmark Function
4.1. Experimental Configuration
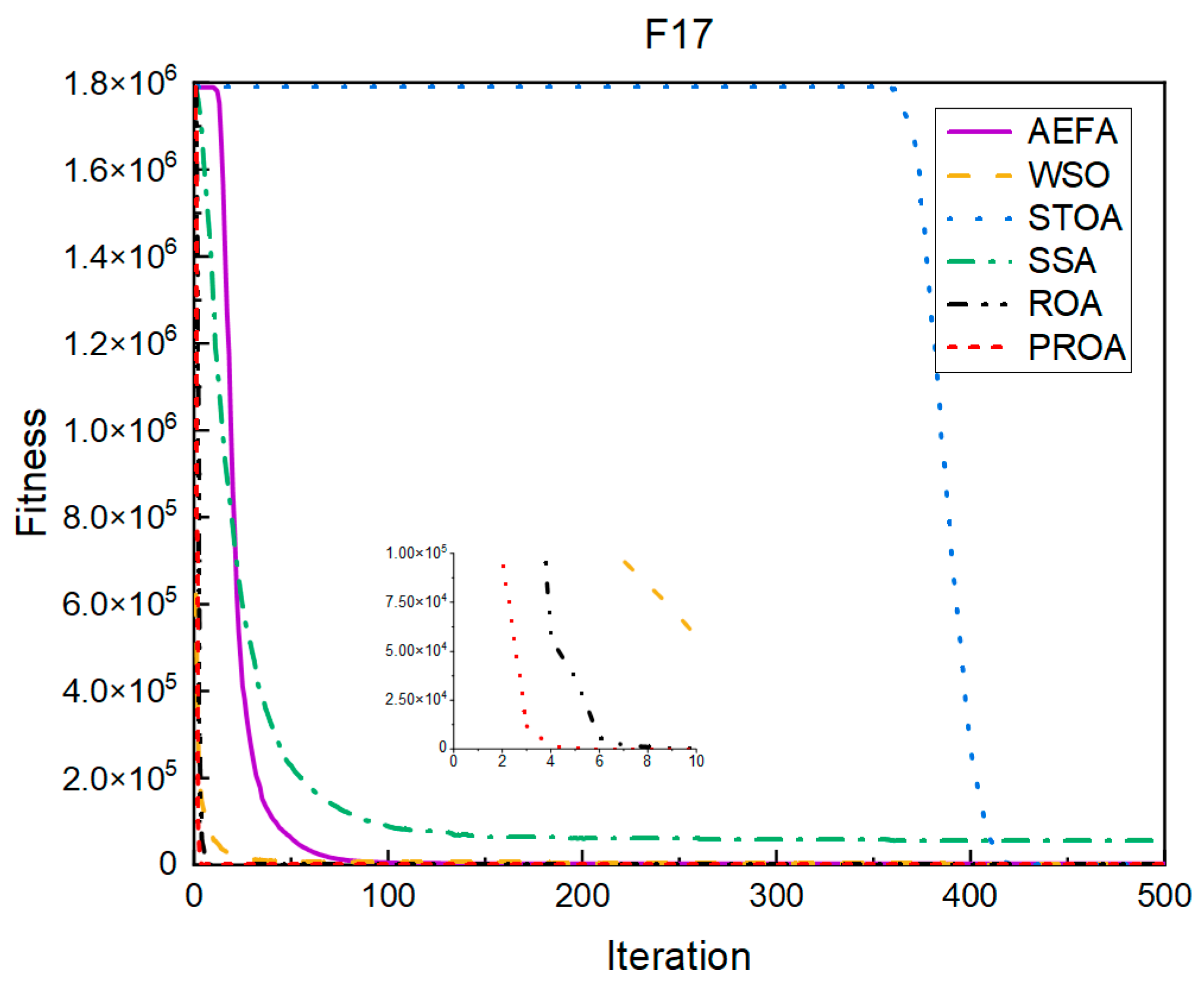
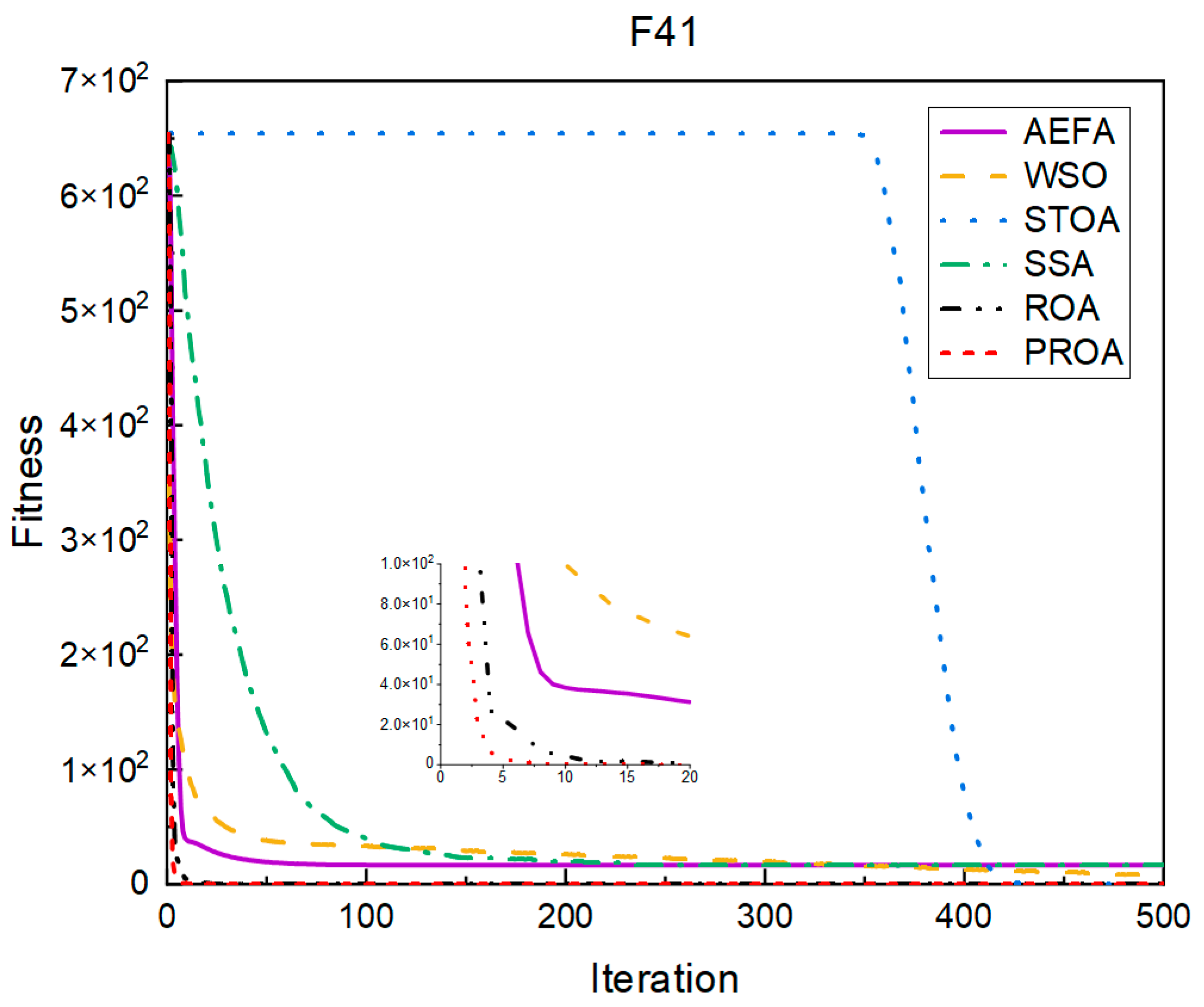
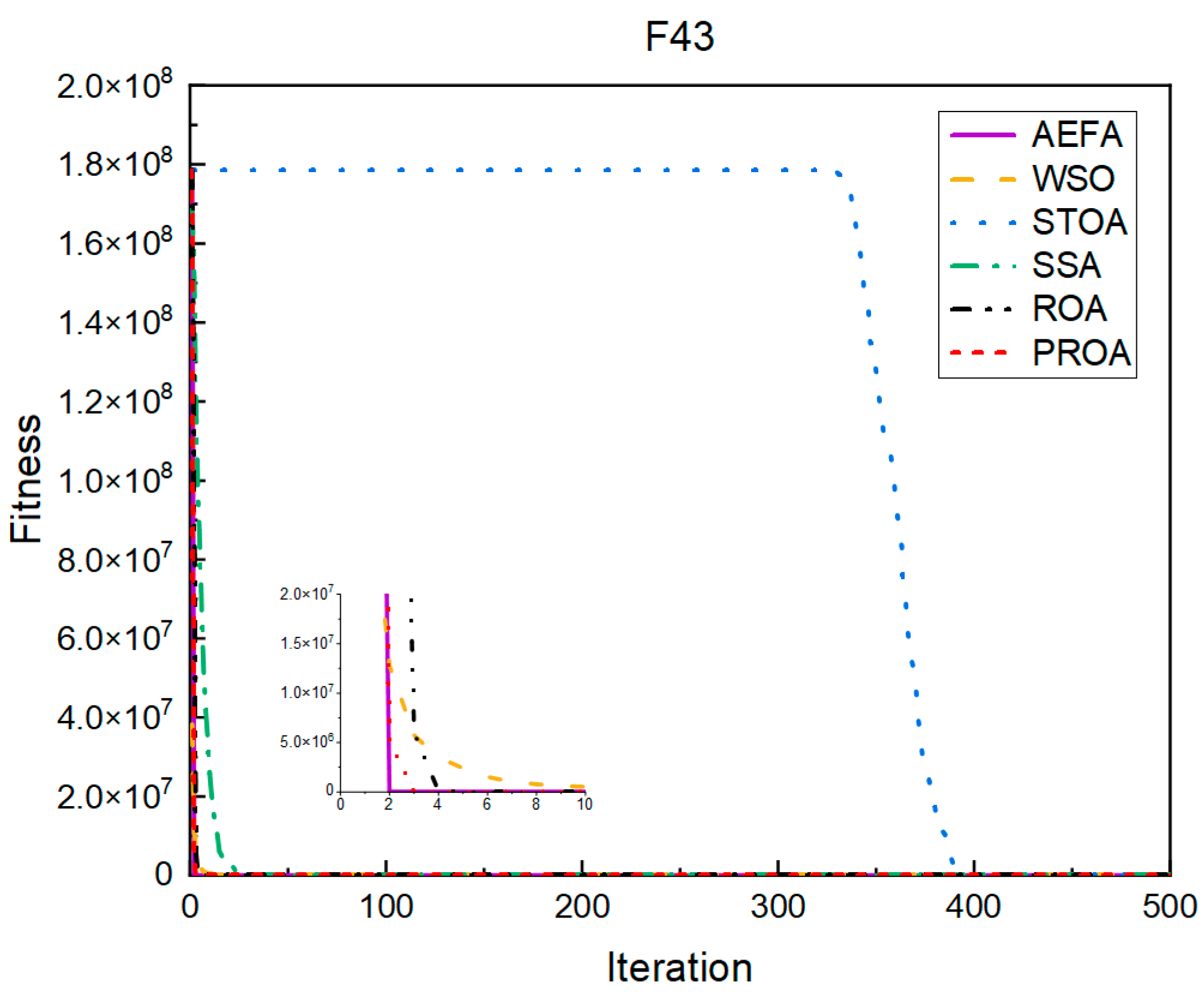
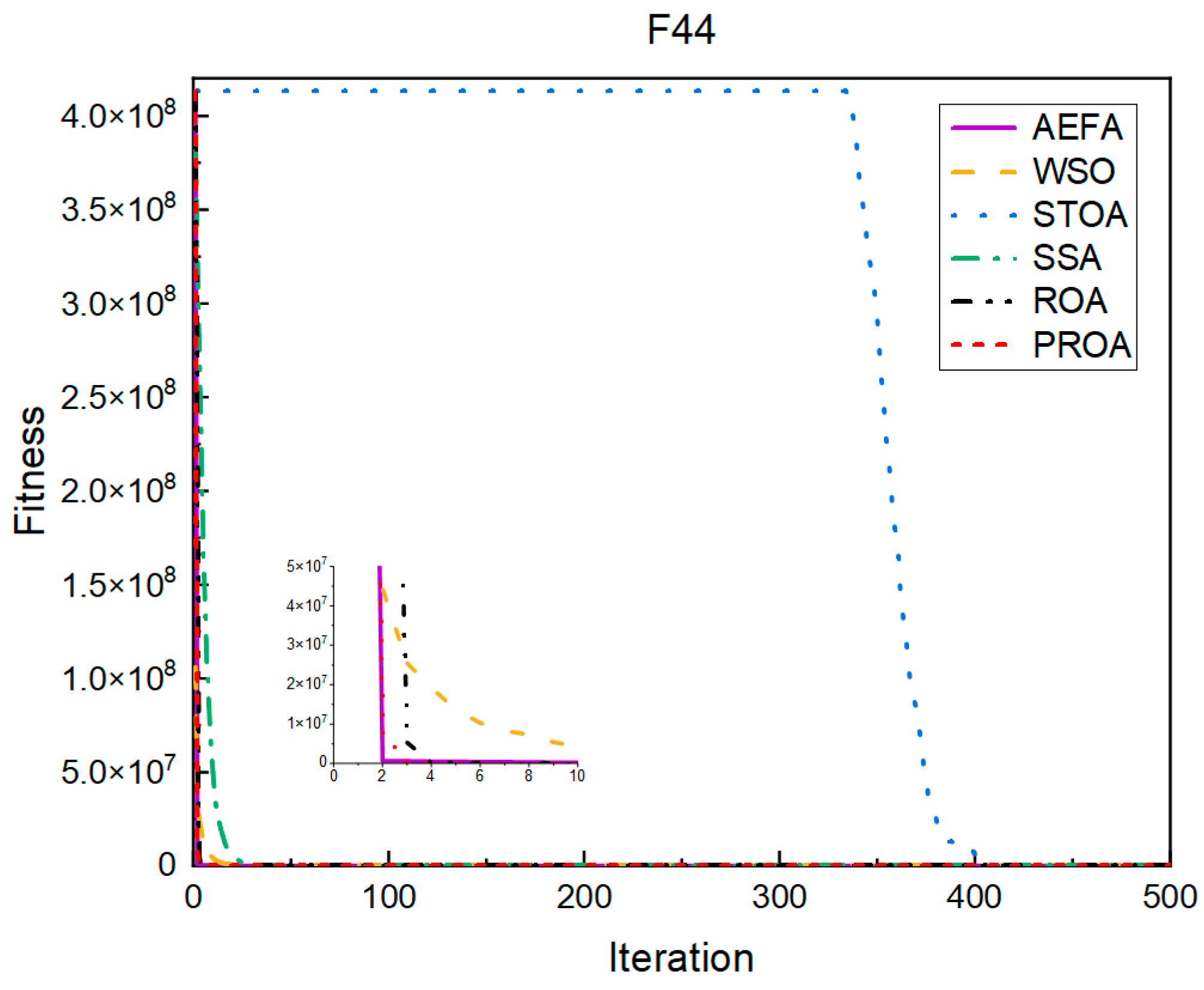
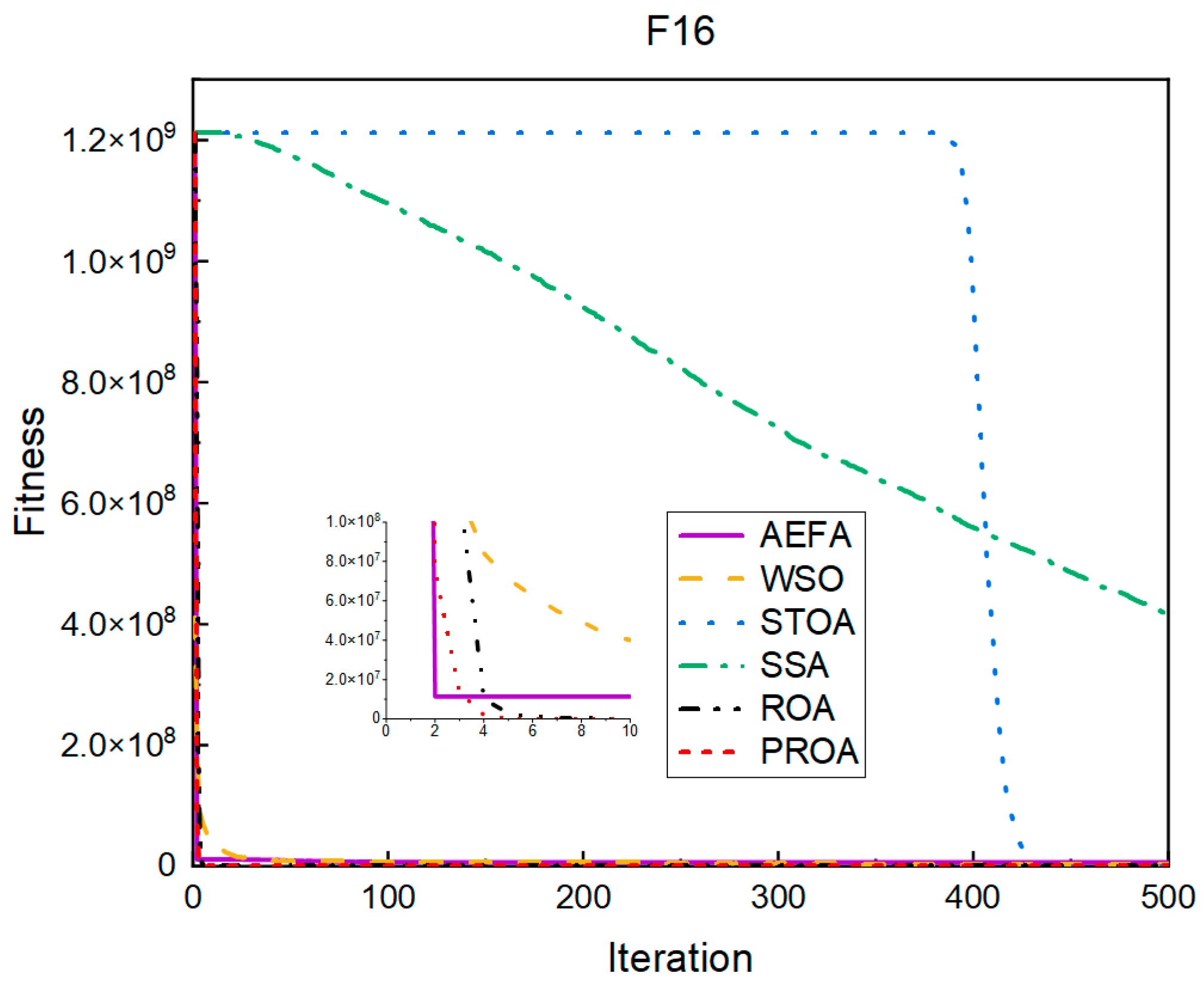
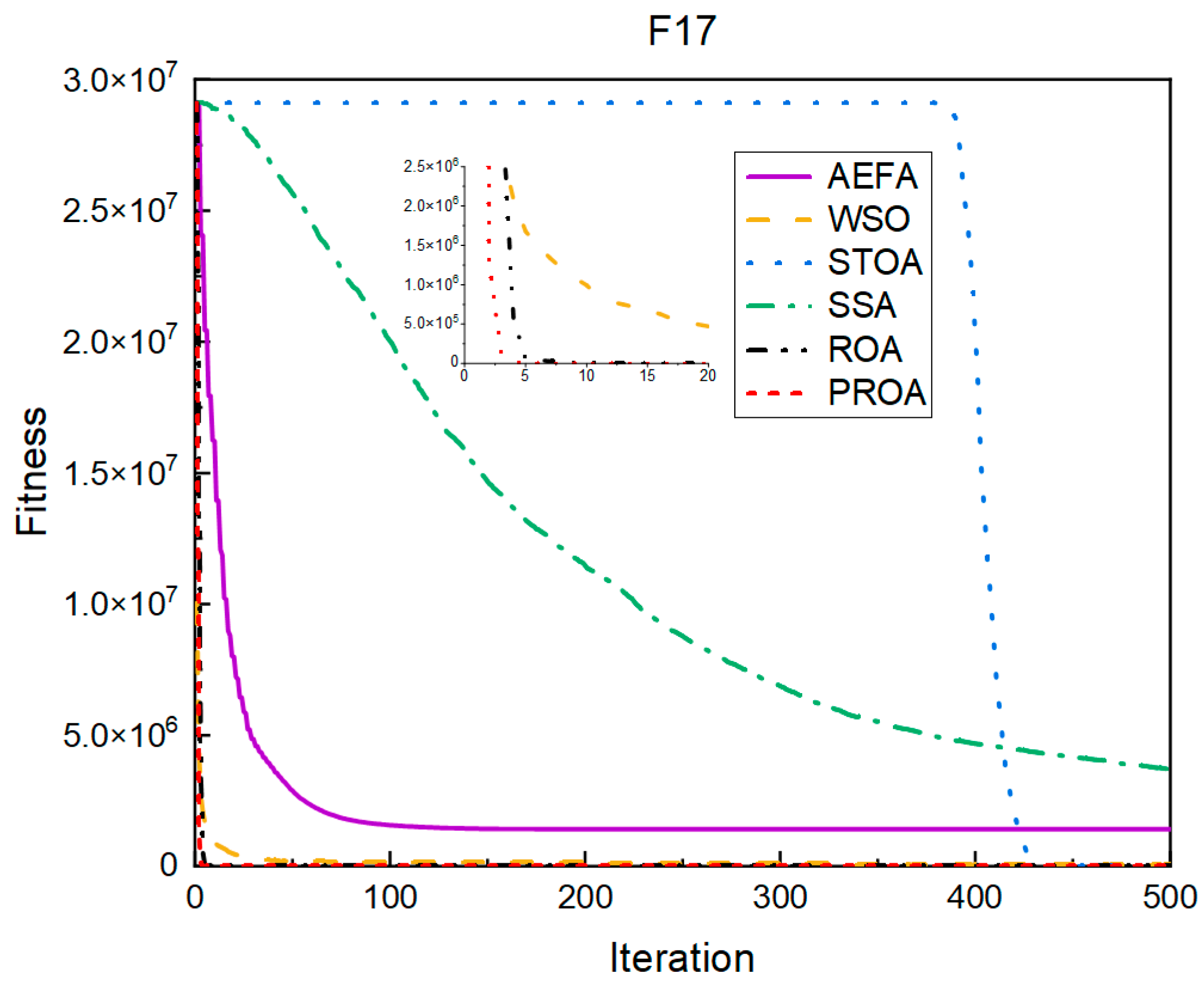
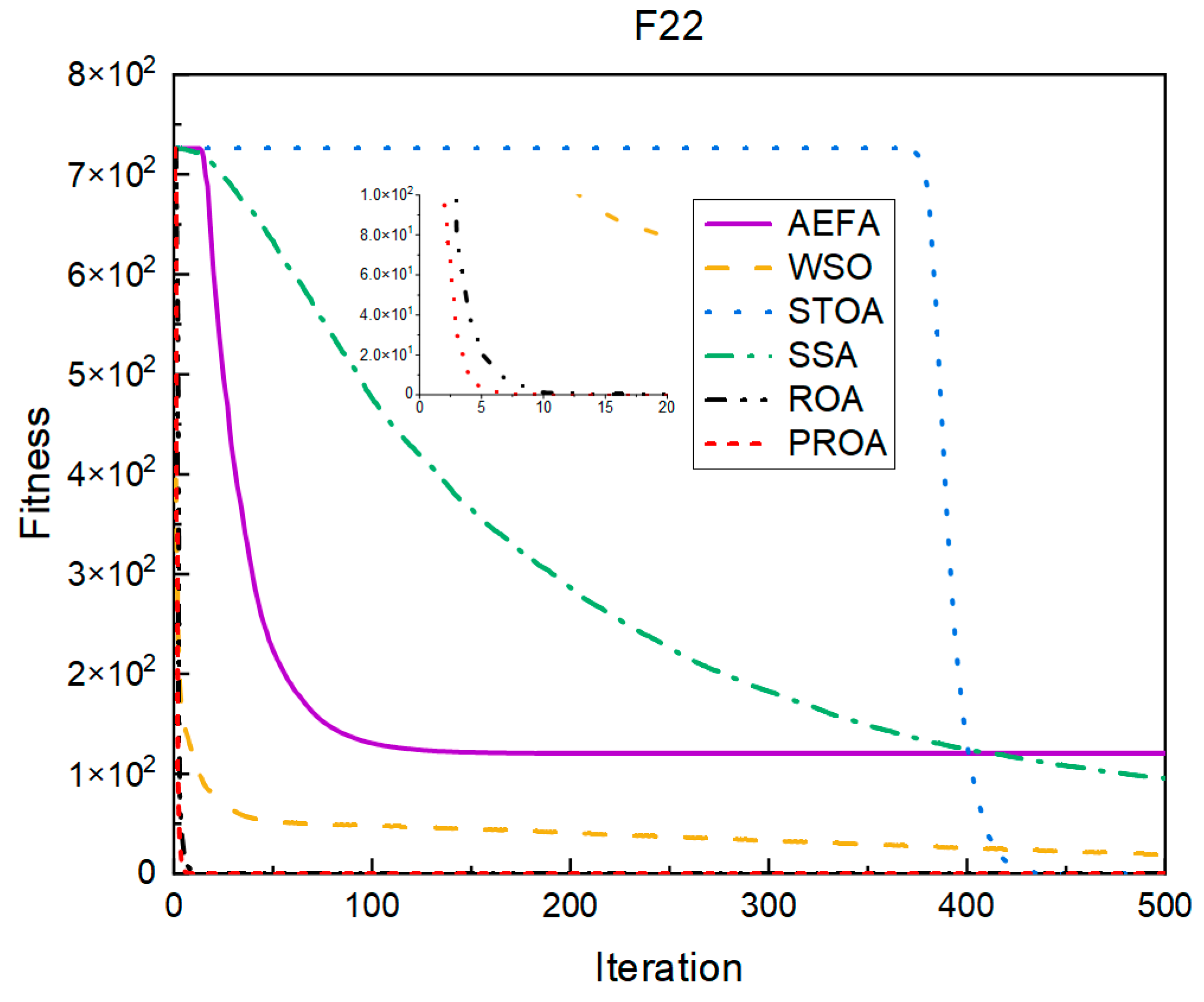
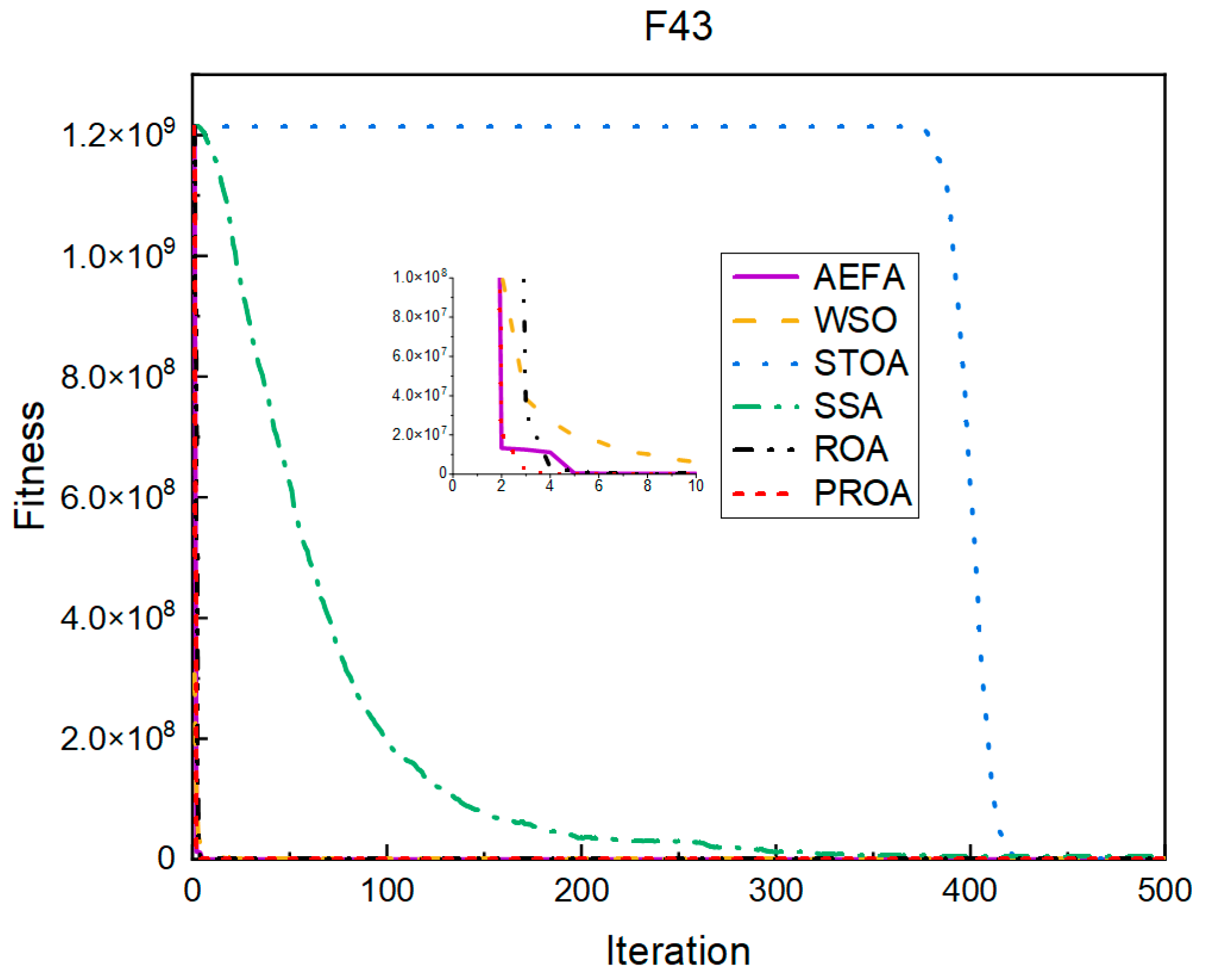
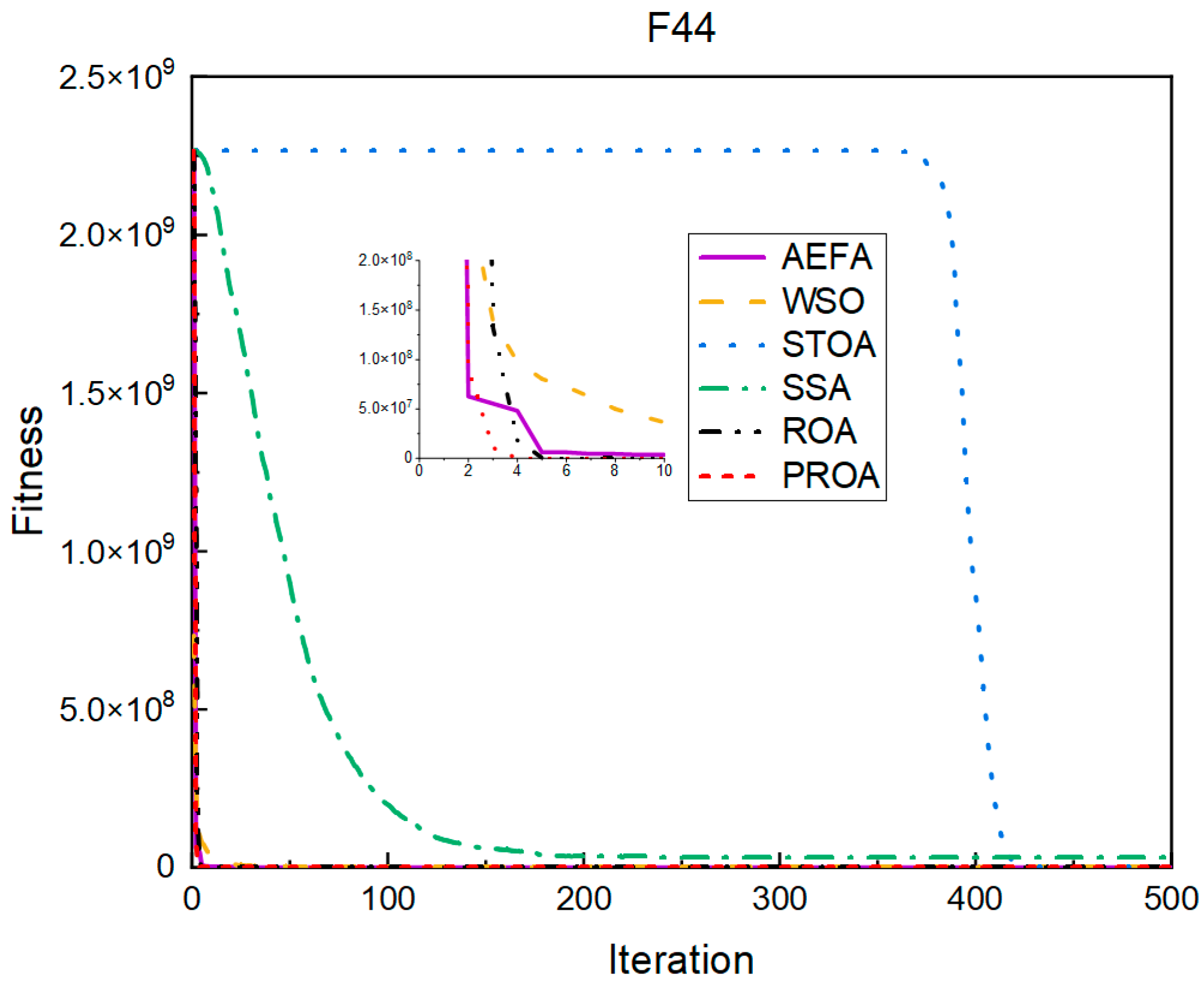
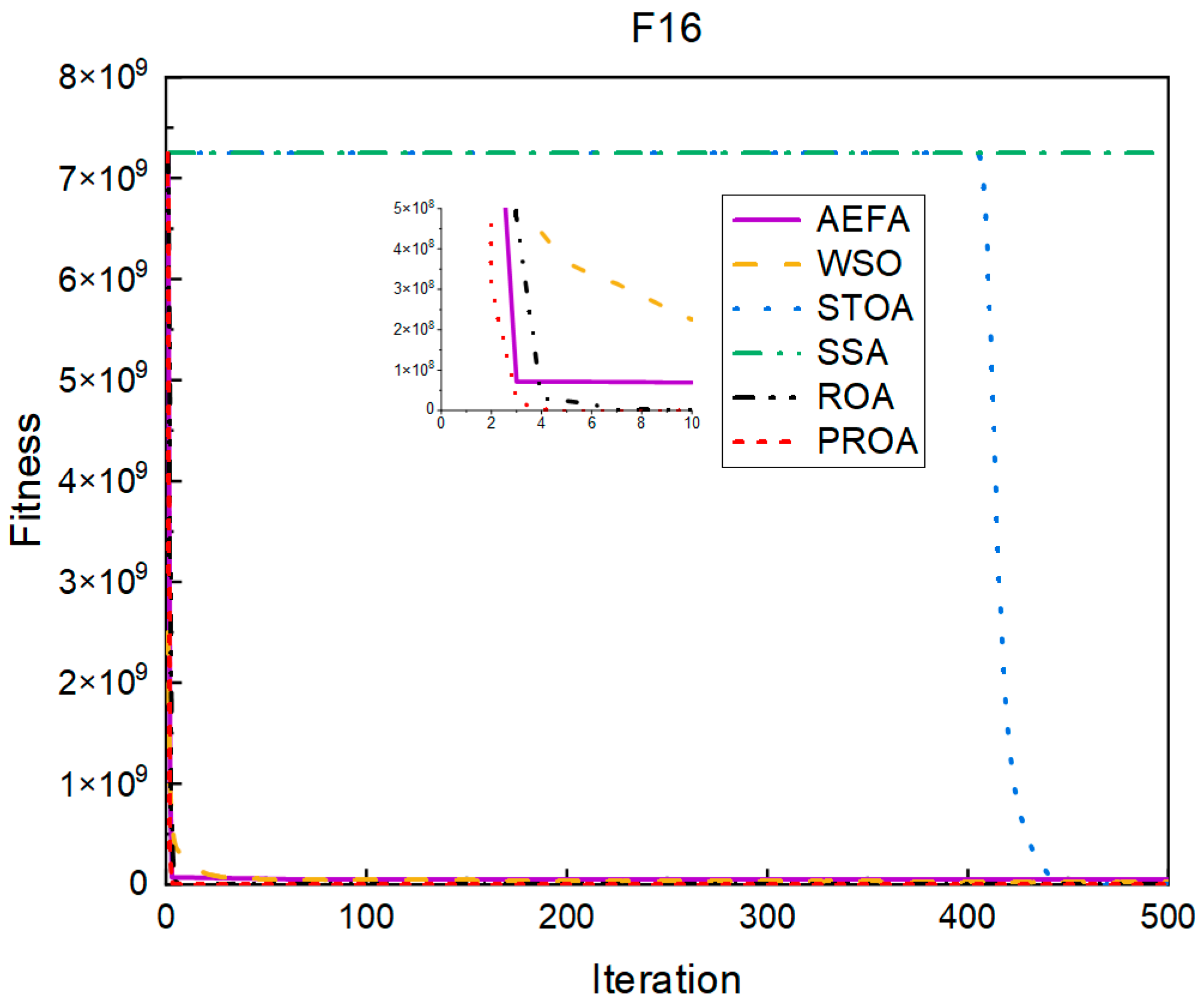
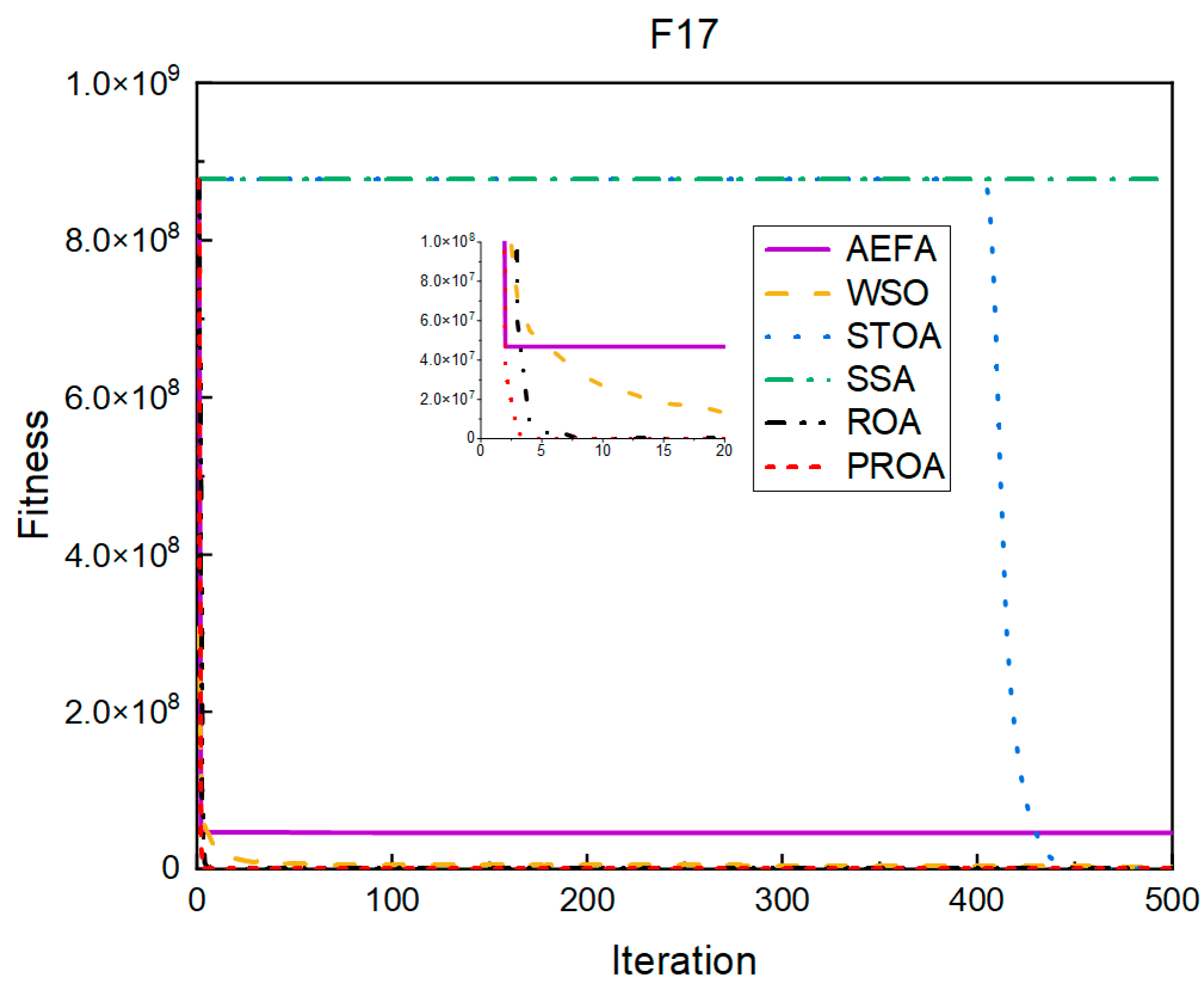
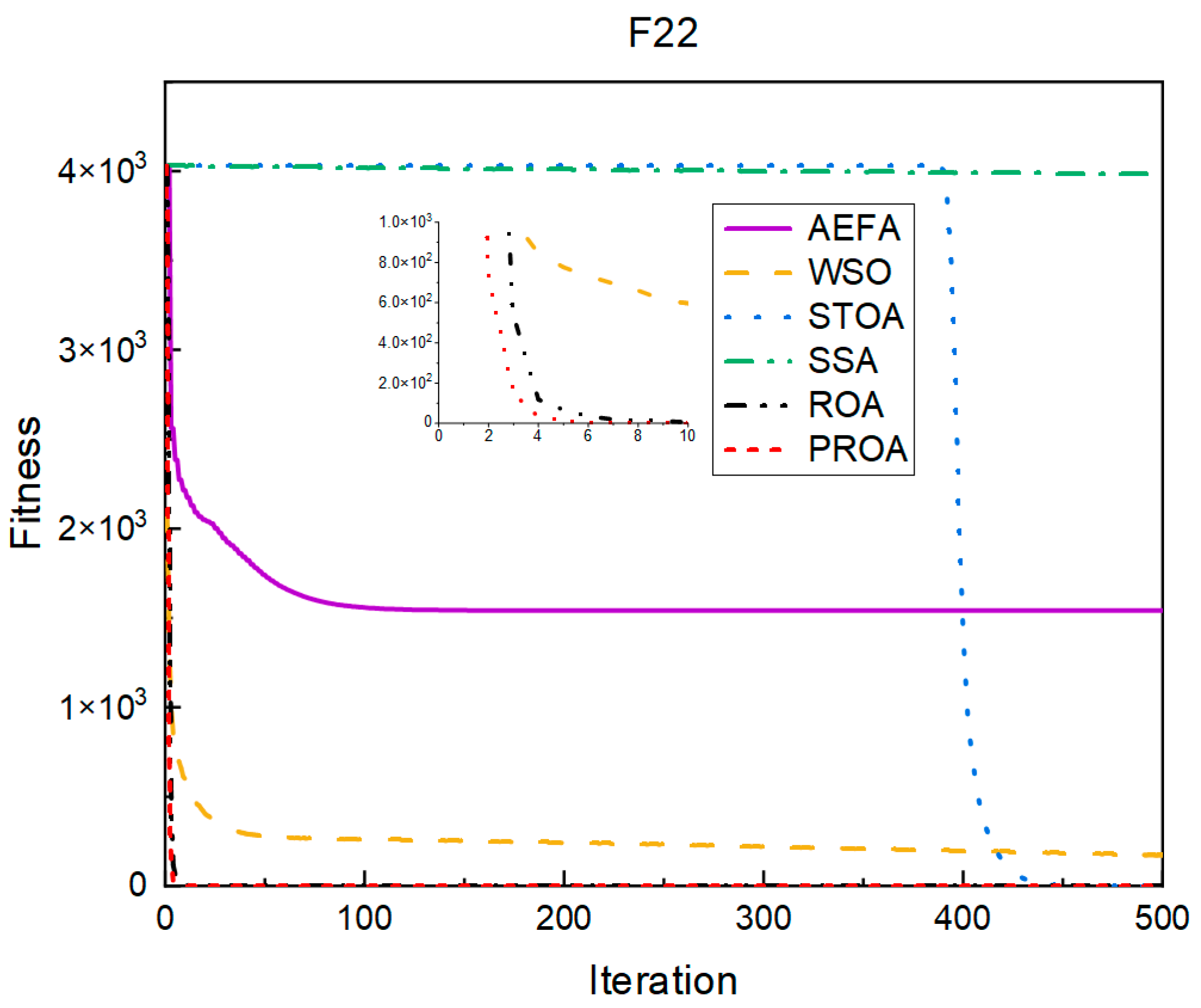
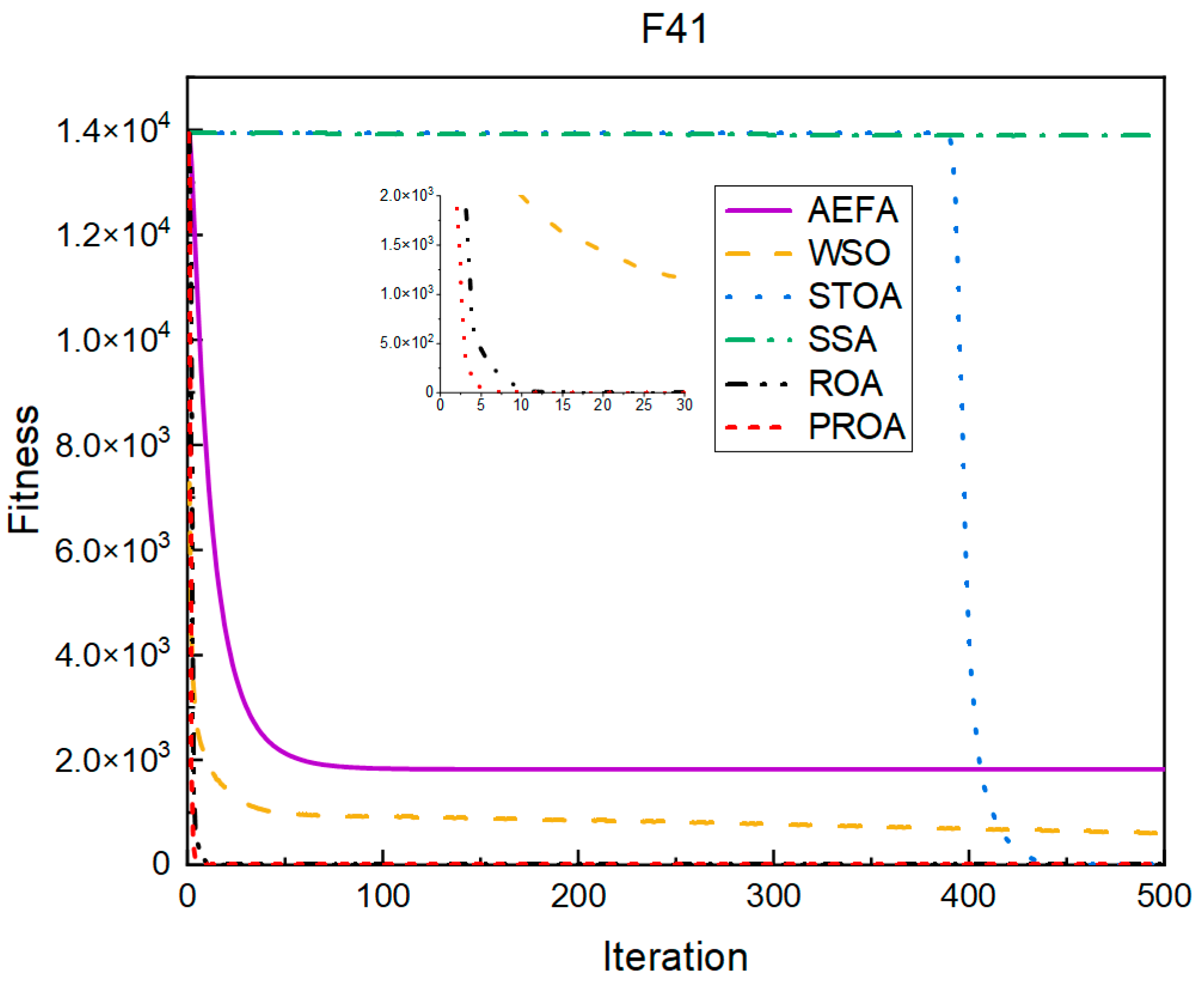
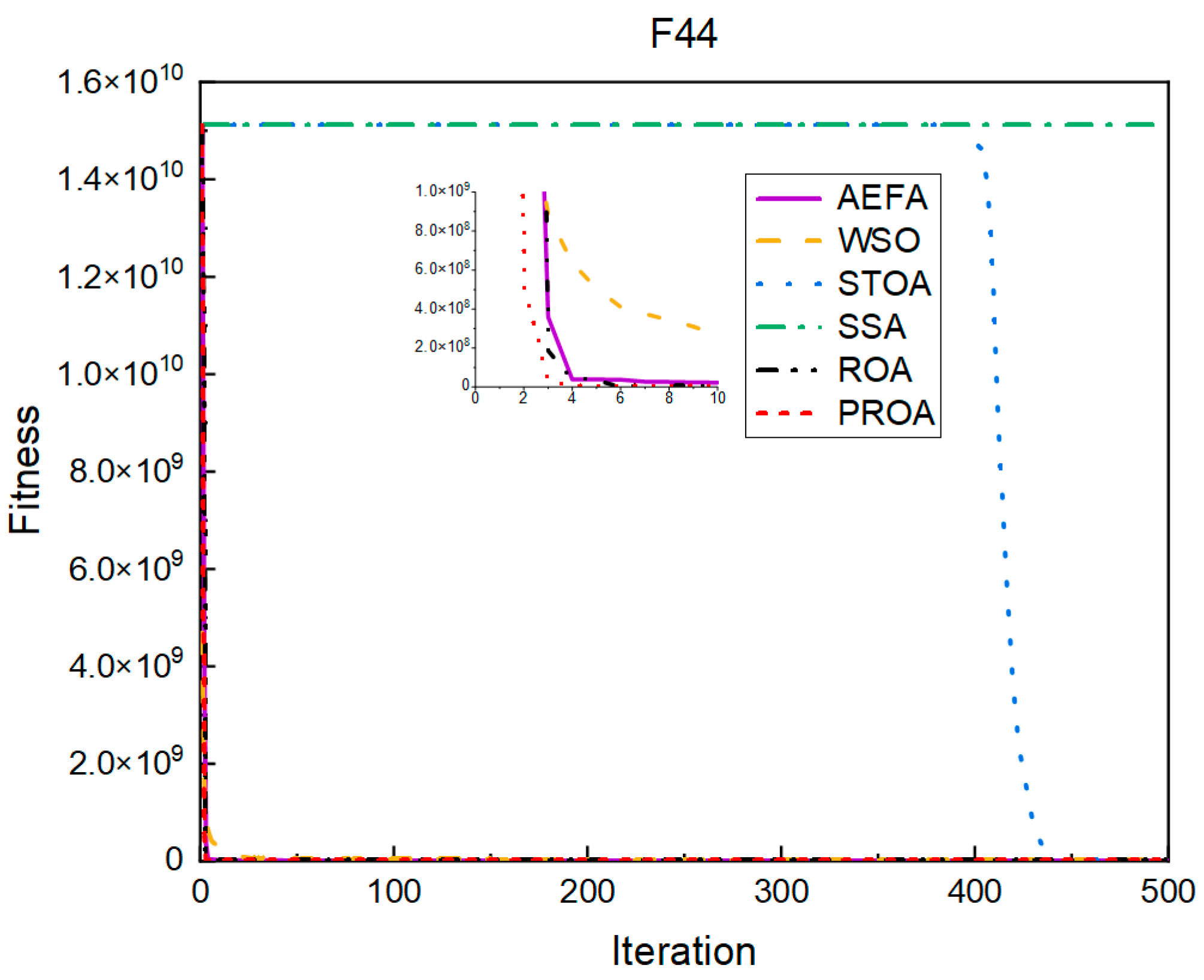
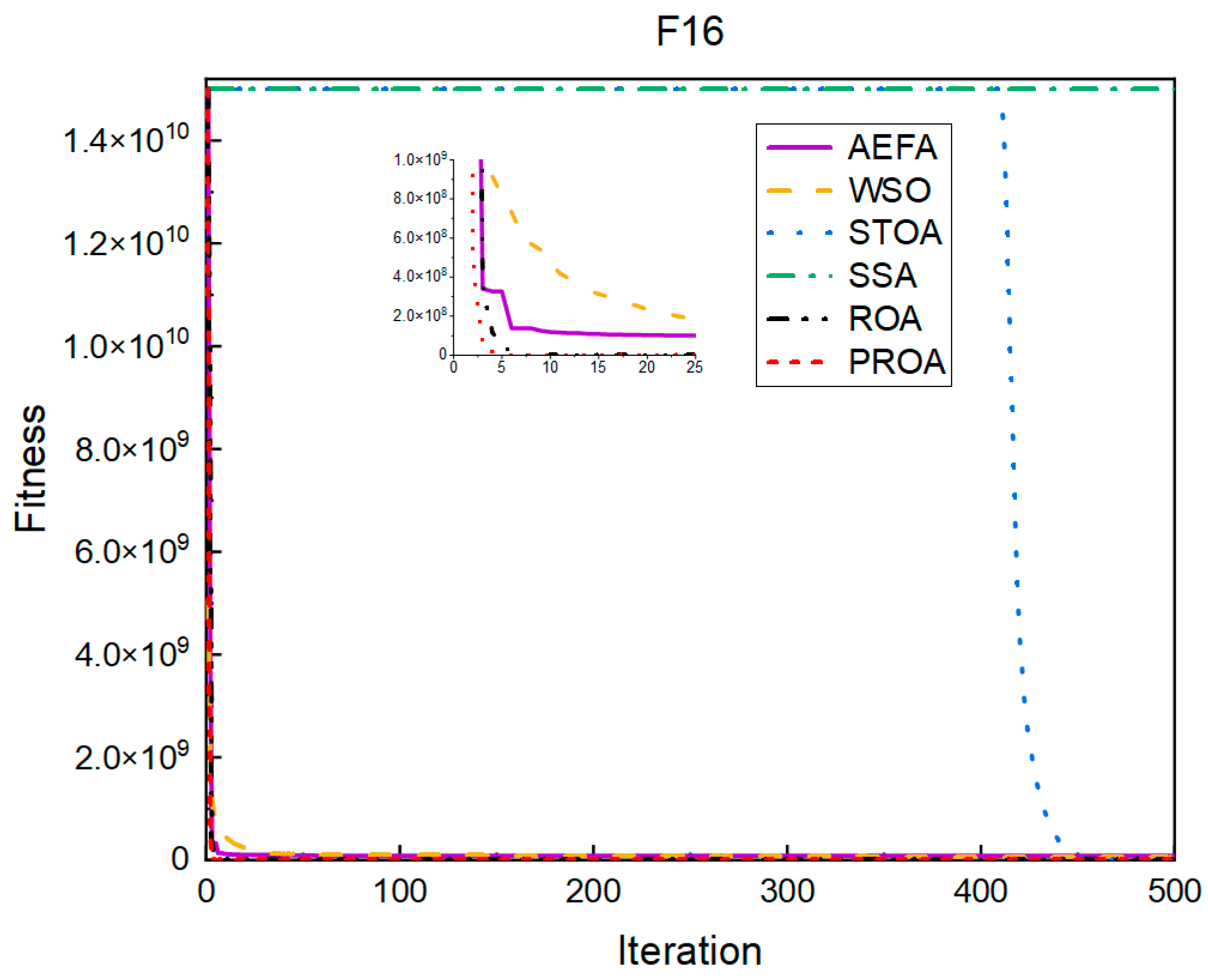
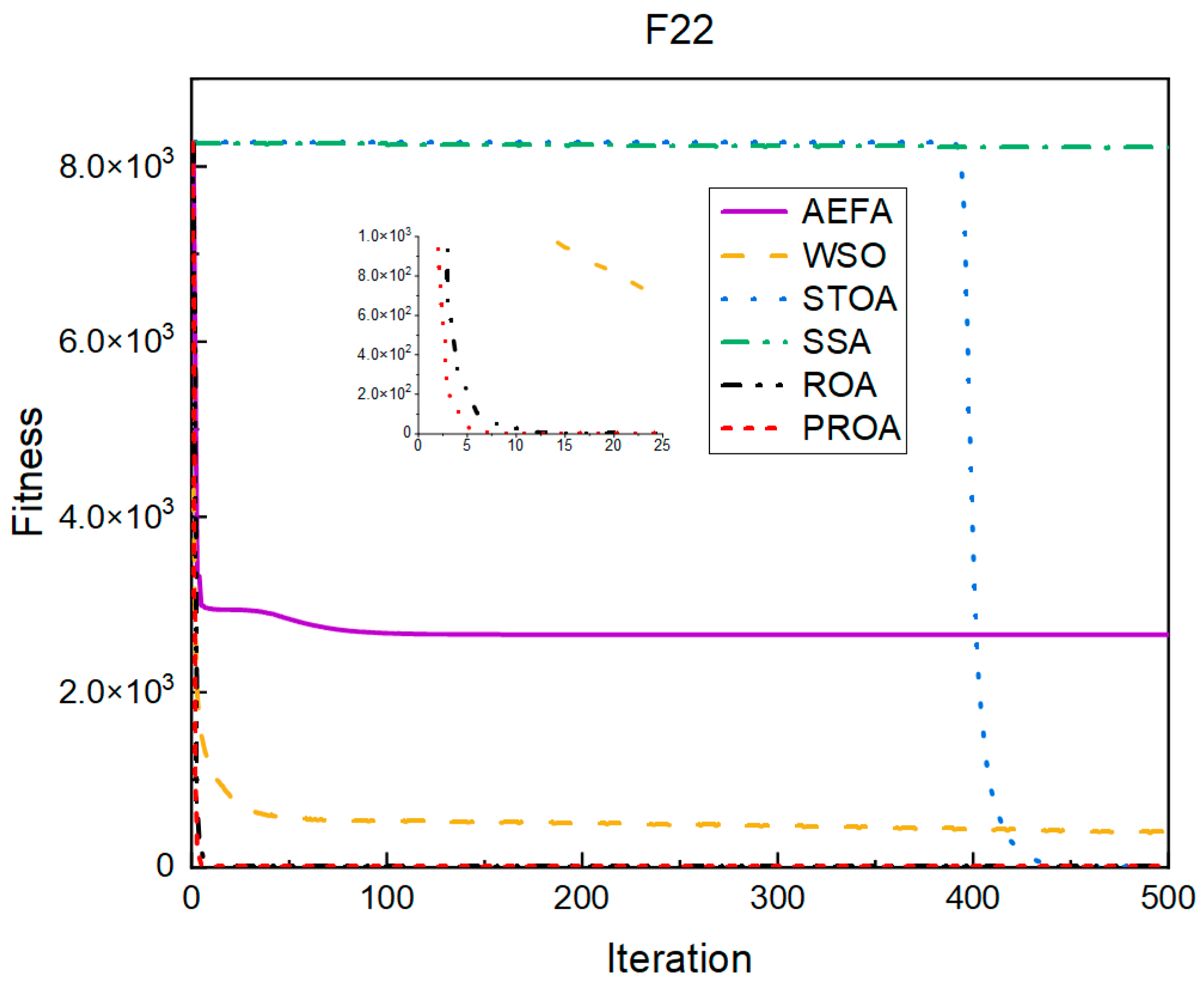
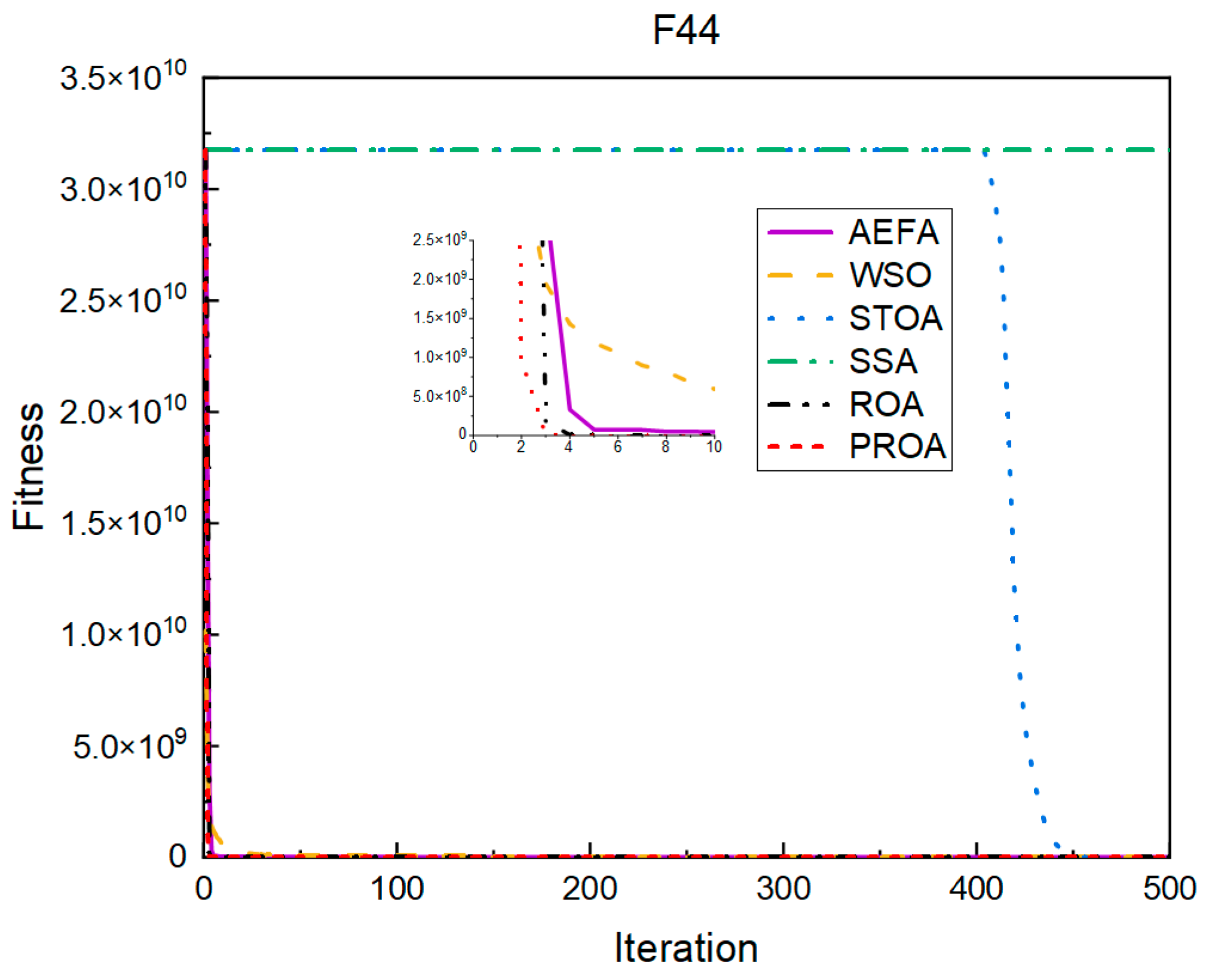
4.2. Comparison of Experimental Results
4.2.1. Comparison of Standard Dimension Results
4.2.2. Comparison of Results under Dimension 100
4.2.3. Comparison of Results under Dimension 500
4.2.4. Comparison of Results under Dimension 1000
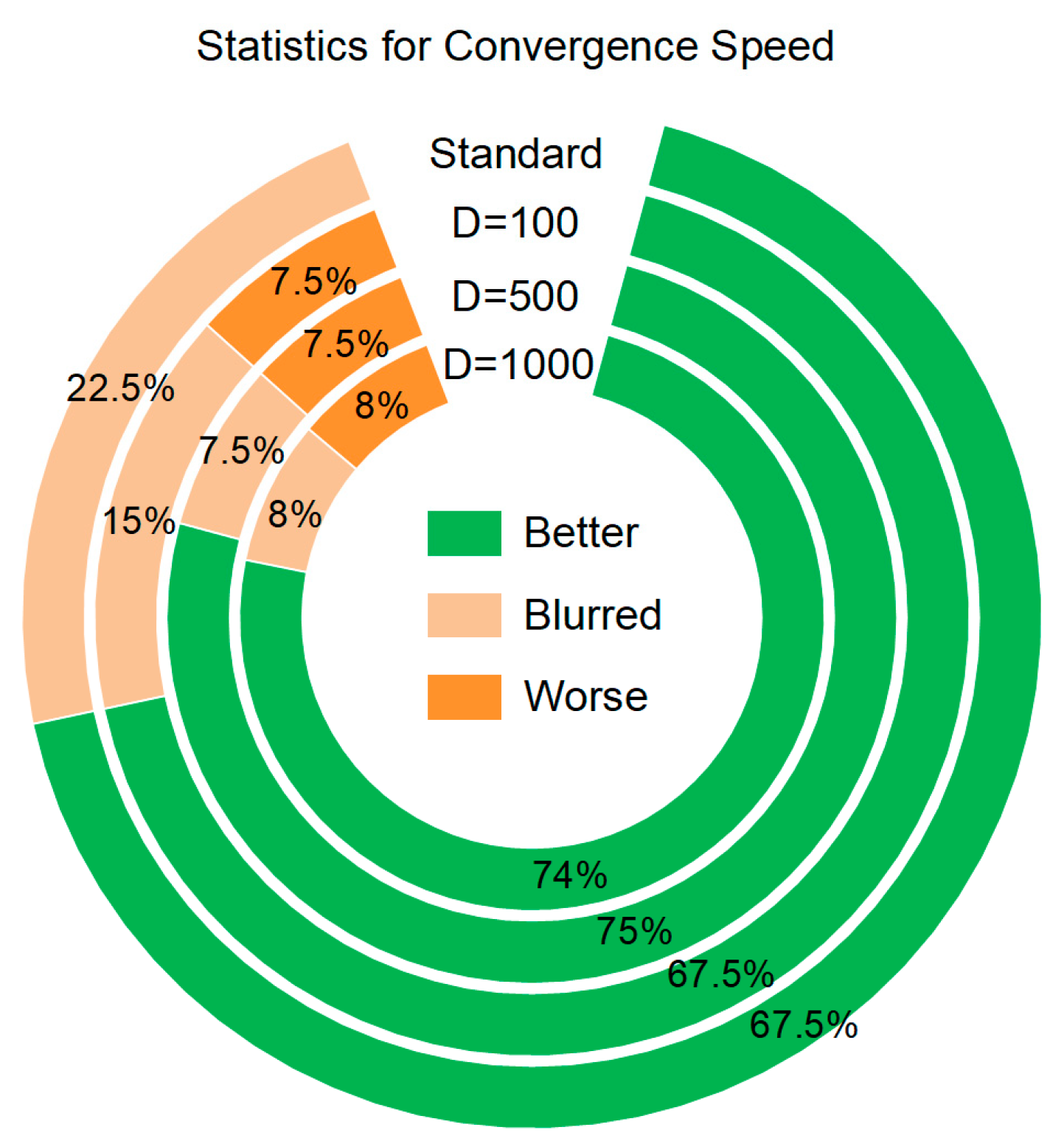
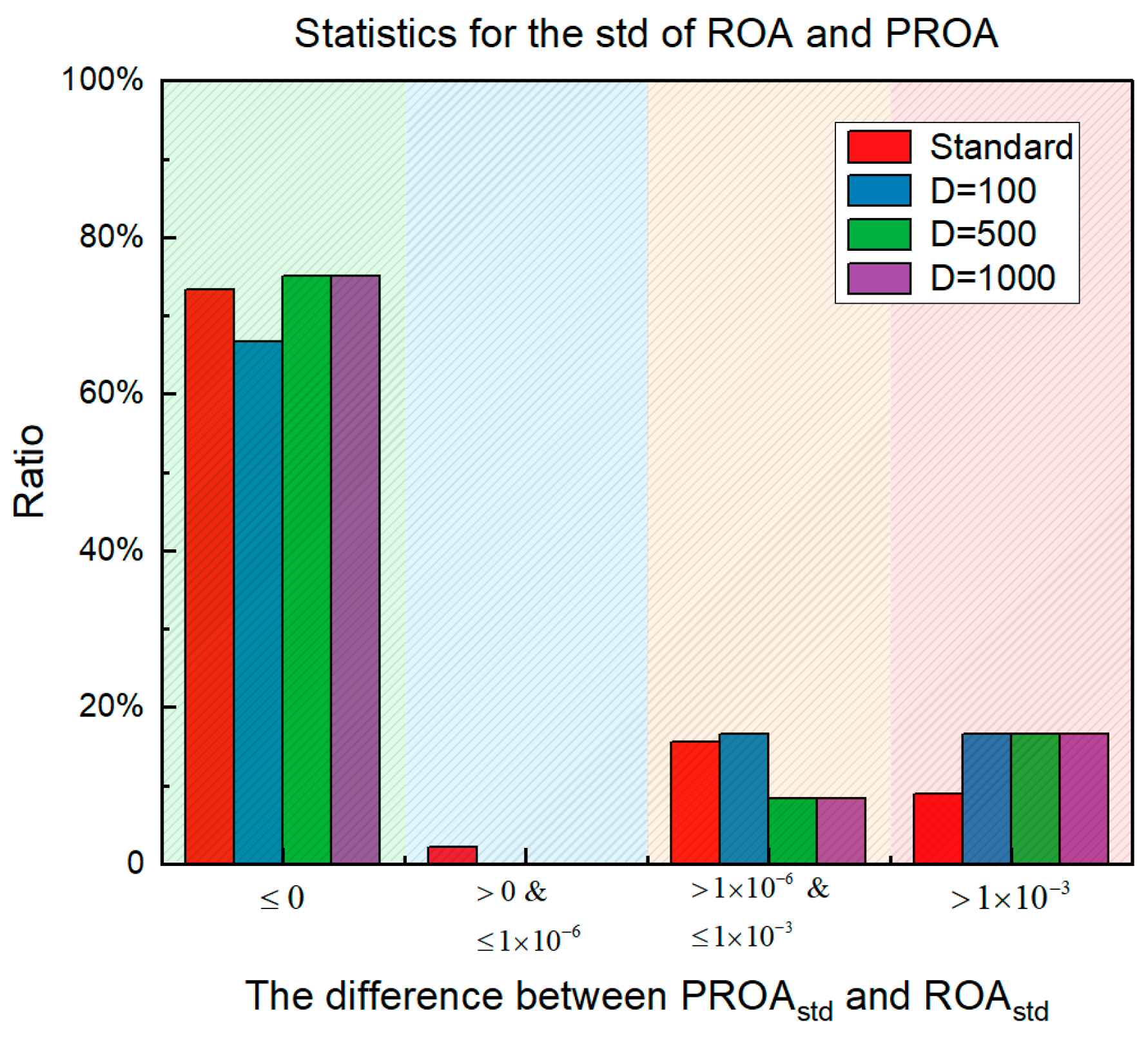
4.3. Results, Statistics, and Performance Analysis
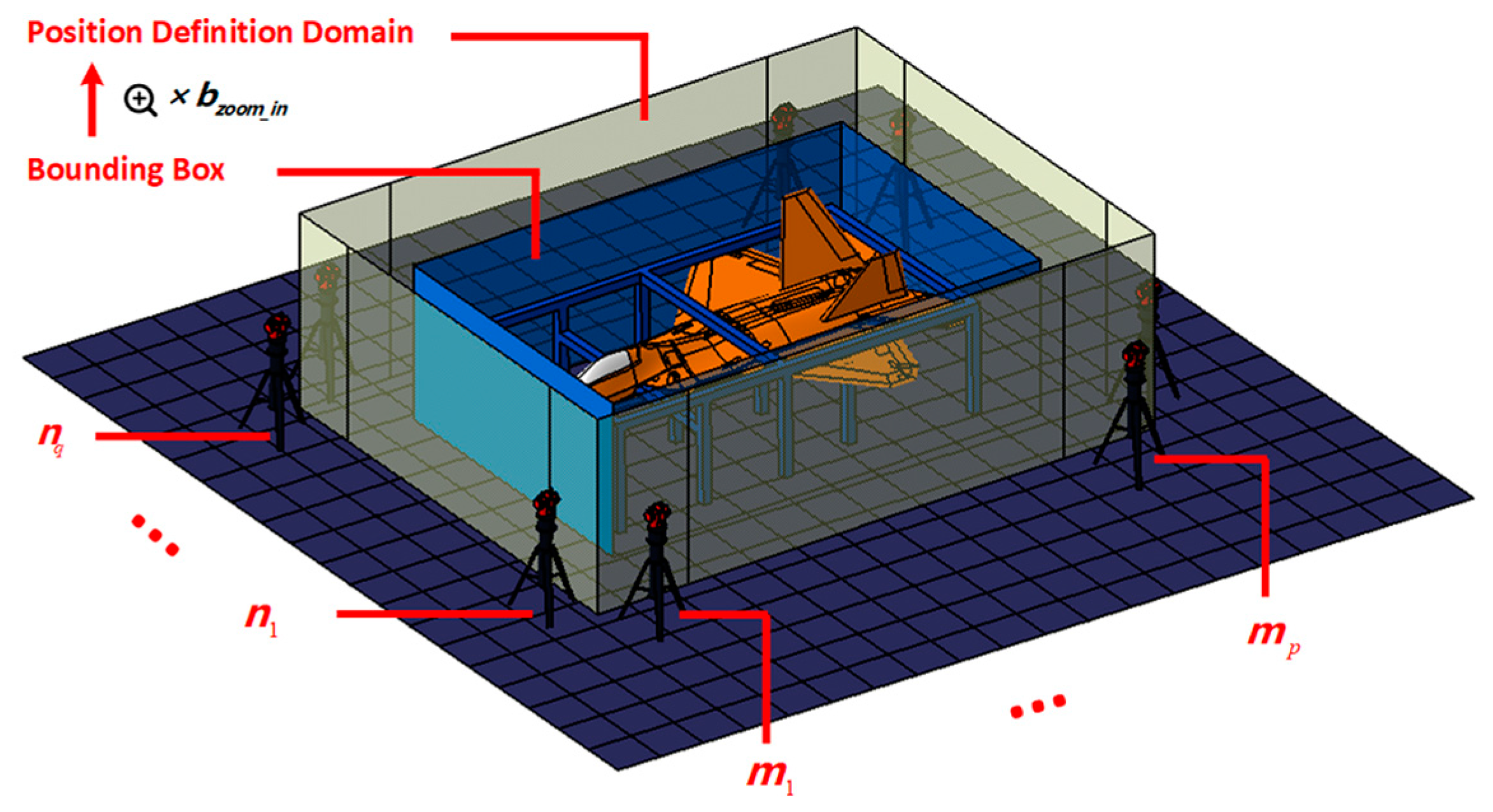
5. PROA Applied to Deployment Planning
5.1. Deployment Planning Model
- A single station can directly measure most features and cover tooling or ground transfer points as much as possible. Simultaneously, priority should be given to selecting transfer points with a large distance and at the edge of the venue.
- The location of the station should avoid areas with frequent changes in temperature and airflow. Excessive fluctuations directly affected the measurement accuracy of the entire measurement field.
- The accuracy of the measuring instrument is closely related to the measurement distance. In the establishment of the range, minimizing the distance between the station and the feature to be measured can reduce the measurement error.
- In the case of tool occlusion, the sum of the fields of view of all the stations should be as large as possible and enclose the entire measurement space.
- Between two adjacent stations, it can be observed that the number of public transfer points on the target to be tested cannot be less than , that is, the constraint .
- The number of public transfer points on the tooling that can be observed between two adjacent stations cannot be less than , that is, constraint .
- The number of public transfer points on the ground between two adjacent stations cannot be less than , that is, the constraint .
- The number of reference points that can be observed from all stations should account for above of the total number of key points, that is, the constraint .
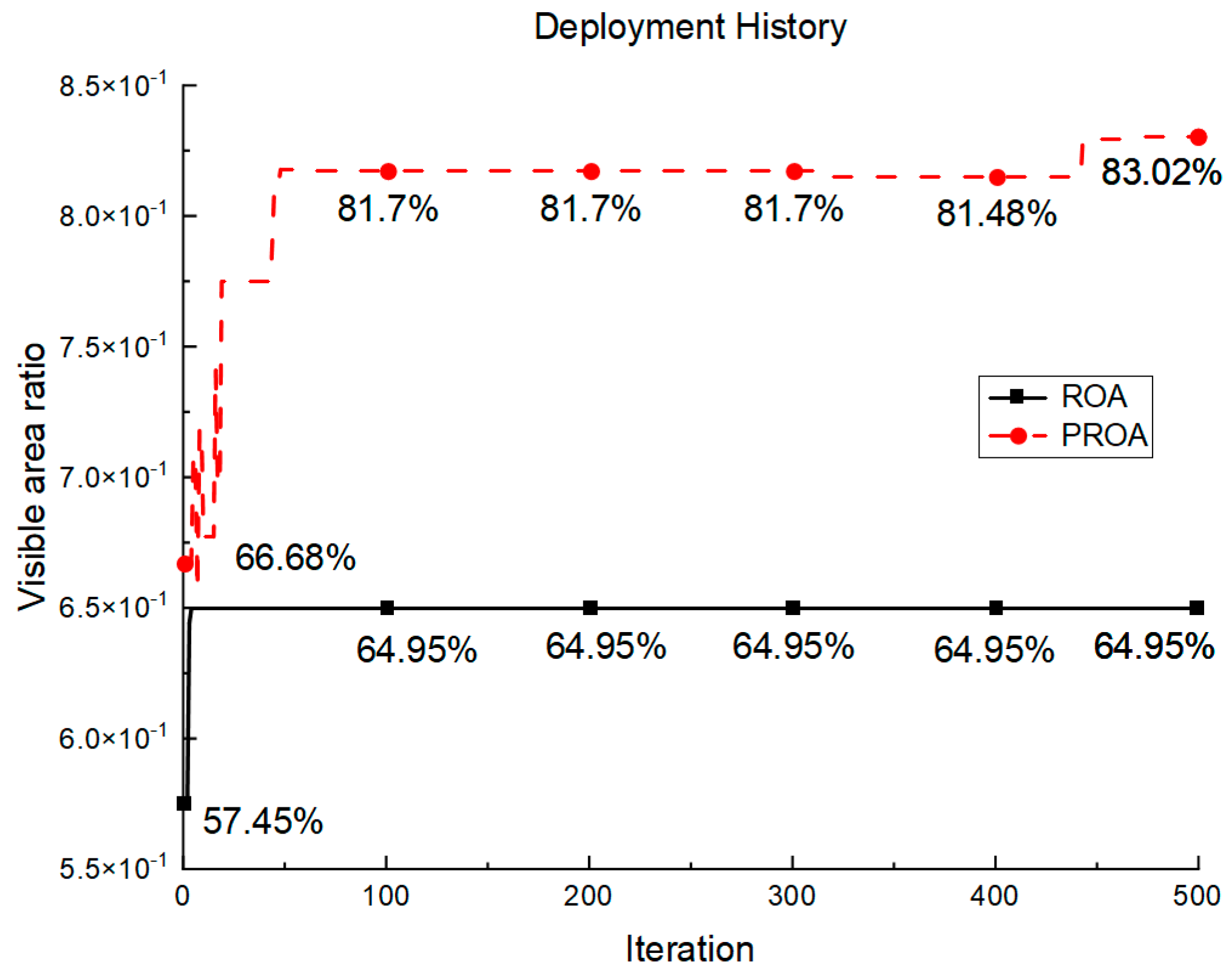
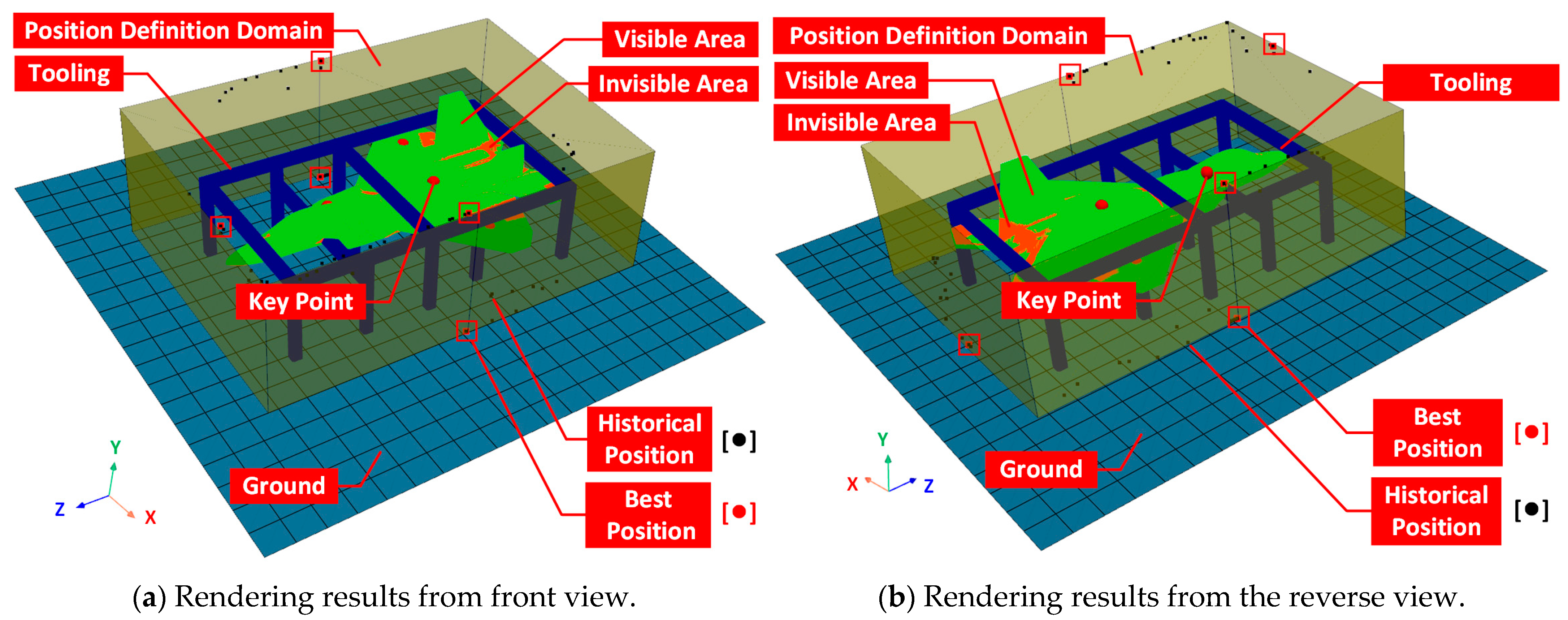
5.2. Simulation Results and 3D Visualization
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Muelaner, J.E.; Wang, Z.; Martin, O.; Jamshidi, J.; Maropoulos, P.G. Estimation of uncertainty in three-dimensional coordinate measurement by comparison with calibrated points. Meas. Sci. Technol. 2010, 21, 025106. [Google Scholar] [CrossRef]
- Suthunyatanakit, K.; Bohez, E.L.; Annanon, K. A new global accessibility algorithm for a polyhedral model with convex polygonal facets. Comput. Des. 2009, 41, 1020–1033. [Google Scholar] [CrossRef]
- Nuñez, A.; Lacasa, L.; Valero, E.; Gómez, J.P.; Luque, B. Detecting series periodicity with horizontal visibility graphs. Int. J. Bifurc. Chaos 2012, 22, 1250160. [Google Scholar] [CrossRef]
- Lin, X. Based on the Full 3D Model, the Measurement Method and Experimental Research of Large Aircraft Parts Assembly Docking. Doctoral Dissertation, Changchun University of Science and Technology, Changchun, China, 2016. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C447WN1SO36whLpCgh0R0Z-iTEMuTidDzndci_h58Y6oubBYhL_o8y-To6aH2TABovVpVwv0SYvb-fpIBBby6sz-&uniplatform=NZKPT (accessed on 3 January 2023).
- Dong, Y.; Cao, L.; Zuo, K. Genetic algorithm based on a new similarity for probabilistic transformation of belief functions. Entropy 2022, 24, 1680. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; He, B.; Fan, Y.; Tan, W.; Qin, T.; Yang, J. Improved black widow spider optimization algorithm integrating multiple strategies. Entropy 2022, 24, 1640. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Zhang, J.; Li, S.; Lv, D.; Li, M. An enhanced differential evolution algorithm with bernstein operator and refracted oppositional-mutual learning strategy. Entropy 2022, 24, 1205. [Google Scholar] [CrossRef] [PubMed]
- Pang, S.; Liu, J.; Zhang, Z.; Fan, X.; Zhang, Y.; Zhang, D.; Hwang, G.H. A photovoltaic power predicting model using the differential evolution algorithm and multi-task learning. Front. Mater. 2022, 9, 938167. [Google Scholar] [CrossRef]
- Opoku, E.; Ahmed, S.; Song, Y.; Nathoo, F. Ant colony system optimization for spatiotemporal modelling of combined EEG and MEG data. Entropy 2021, 23, 329. [Google Scholar] [CrossRef]
- Wu, L.; Qu, J.; Shi, H.; Li, P. Node deployment optimization for wireless sensor networks based on virtual force-directed particle swarm optimization algorithm and evidence theory. Entropy 2022, 24, 1637. [Google Scholar] [CrossRef]
- Dai, T.; Miao, L.; Shao, H.; Shi, Y. Solving gravity anomaly matching problem under large initial errors in gravity aided navigation by using an affine transformation based artificial bee colony algorithm. Front. Neurorobotics 2019, 13, 19. [Google Scholar] [CrossRef]
- Dong, Z.; Zheng, J.; Huang, S.; Pan, H.; Liu, Q. Time-shift multi-scale weighted permutation entropy and GWO-SVM based fault diagnosis approach for rolling bearing. Entropy 2019, 21, 621. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Guo, X.; Wang, Z.; Du, W.; Han, X.; He, G.; Xue, H.; Kou, Y. Research on fault extraction method of variational mode decomposition based on immunized fruit fly optimization algorithm. Entropy 2019, 21, 400. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Wang, S.-H.; Zhang, Y.-D. Detection of abnormal brain in MRI via improved AlexNet and ELM optimized by chaotic bat algorithm. Neural Comput. Appl. 2021, 33, 10799–10811. [Google Scholar] [CrossRef]
- Tong, Y.; Yu, B. Research on hyper-parameter optimization of activity recognition algorithm based on improved cuckoo search. Entropy 2022, 24, 845. [Google Scholar] [CrossRef]
- Deb, S.; Gao, X.-Z.; Tammi, K.; Kalita, K.; Mahanta, P. Recent studies on chicken swarm optimization algorithm: A review (2014–2018). Artif. Intell. Rev. 2020, 53, 1737–1765. [Google Scholar] [CrossRef]
- Kuo, C.L.; Kuruoglu, E.E.; Chan, W.K.V. Neural network structure optimization by simulated annealing. Entropy 2022, 24, 348. [Google Scholar] [CrossRef]
- Shang, R.; Zhang, W.; Li, F.; Jiao, L.; Stolkin, R. Multi-objective artificial immune algorithm for fuzzy clustering based on multiple kernels. Swarm Evol. Comput. 2019, 50, 100485. [Google Scholar] [CrossRef]
- Liao, Y.; Liu, Y.; Chen, C.; Zhang, L. Green building energy cost optimization with deep belief network and firefly algorithm. Front. Energy Res. 2021, 9, 805206. [Google Scholar] [CrossRef]
- Goh, R.; Lee, L.; Seow, H.-V.; Gopal, K. Hybrid harmony search—Artificial intelligence models in credit scoring. Entropy 2020, 22, 989. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Shadravan, S.; Naji, H.; Bardsiri, V. The sailfish optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Almalawi, A.; Khan, A.I.; Alqurashi, F.; Abushark, Y.B.; Alam, M.; Qaiyum, S. Modeling of remora optimization with deep learning enabled heavy metal sorption efficiency prediction onto biochar. Chemosphere 2022, 303, 135065. [Google Scholar] [CrossRef] [PubMed]
- Raamesh, L.; Radhika, S.; Jothi, S. A cost-effective test case selection and prioritization using hybrid battle royale-based remora optimization. Neural Comput. Appl. 2022, 34, 22435–22447. [Google Scholar] [CrossRef]
- Chou, J.-S.; Nguyen, N.-M. FBI inspired meta-optimization. Appl. Soft Comput. 2020, 93, 106339. [Google Scholar] [CrossRef]
- Anita; Yadav, A. AEFA: Artificial electric field algorithm for global optimization. Swarm Evol. Comput. 2019, 48, 93–108. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Dhiman, G.; Kaur, A. STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng. Appl. Artif. Intell. 2019, 82, 148–174. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Tan, C.; Chang, S.; Liu, L. Hierarchical genetic-particle swarm optimization for bistable permanent magnet actuators. Appl. Soft Comput. 2017, 61, 1–7. [Google Scholar] [CrossRef]
- Qiao, W.; Yang, Z. An improved dolphin swarm algorithm based on kernel fuzzy C-means in the application of solving the optimal problems of large-scale function. IEEE Access 2019, 8, 2073–2089. [Google Scholar] [CrossRef]
- Wang, H.; Jin, Y.; Doherty, J. Committee-based active learning for surrogate-assisted particle swarm optimization of expensive problems. IEEE Trans. Cybern. 2017, 47, 2664–2677. [Google Scholar] [CrossRef] [PubMed]
- Kan, G.; Zhang, M.; Liang, K.; Wang, H.; Jiang, Y.; Li, J.; Ding, L.; He, X.; Hong, Y.; Zuo, D.; et al. Improving water quantity simulation & forecasting to solve the energy-water-food nexus issue by using heterogeneous computing accelerated global optimization method. Appl. Energy 2018, 210, 420–433. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl.-Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Samma, H.; Sama, A.S.B. Rules embedded harris hawks optimizer for large-scale optimization problems. Neural Comput. Appl. 2022, 34, 13599–13624. [Google Scholar] [CrossRef] [PubMed]
- Prasad, S.; Kumar, D.V. Trade-offs in PMU and IED deployment for active distribution state estimation using multi-objective evolutionary algorithm. IEEE Trans. Instrum. Meas. 2018, 67, 1298–1307. [Google Scholar] [CrossRef]
- Agrawal, B.N.; Platzer, M.F. Standard Handbook for Aerospace Engineers; McGraw-Hill Education: New York, NY, USA, 2018; ISBN 978-1-259-58517-3. [Google Scholar]
- Katz, S.; Tal, A.; Basri, R. Direct visibility of point sets. In ACM SIGGRAPH 2007 Papers; Association for Computing Machinery: New York, NY, USA, 2007; p. 24-es. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Zhao, J.; Yang, X.; Xi, M. Position deployment optimization of maneuvering conventional missile based on improved whale optimization algorithm. Int. J. Aerosp. Eng. 2022, 2022, 4373879. [Google Scholar] [CrossRef]









| No. | Function | D 1 | Range | Formulation |
|---|---|---|---|---|
| F16 | Rosenbrock | 30 | [−30, 30] | |
| F17 | Dixon–Price | 30 | [−10, 10] | |
| F22 | Rastrigin | 30 | [−5.12, 5.12] | |
| F41 | Griewank | 30 | [−600, 600] | |
| F43 | Penalized | 30 | [−50, 50] | |
| F44 | Penalized2 | 30 | [−50, 50] |
| Function | Metric | AEFA | WSO | STOA | SSA | ROA | PROA |
|---|---|---|---|---|---|---|---|
| F16 | Mean | 5.45 × 104 | 1.21 × 105 | 2.85 × 101 | 3.23 × 106 | 1.08 × 100 | 2.05 × 10−2 |
| Std | 1.25 × 105 | 1.08 × 105 | 4.08 × 10−1 | 1.58 × 107 | 4.18 × 100 | 5.20 × 10−2 | |
| F17 | Mean | 2.87 × 103 | 8.46 × 102 | 6.73 × 10−1 | 5.63 × 104 | 3.99 × 10−1 | 2.49 × 10−1 |
| Std | 1.19 × 104 | 8.98 × 102 | 4.06 × 10−2 | 1.02 × 105 | 2.85 × 10−1 | 4.18 × 10−3 | |
| F22 | Mean | 1.15 × 100 | 2.17 × 100 | 0.00 × 100 | 7.86 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 2.87 × 100 | 1.20 × 100 | 0.00 × 100 | 1.21 × 101 | 0.00 × 100 | 0.00 × 100 | |
| F41 | Mean | 1.66 × 101 | 7.85 × 100 | 4.88 × 10−2 | 1.64 × 101 | 0.00 × 100 | 0.00 × 100 |
| Std | 5.84 × 100 | 4.13 × 100 | 6.15 × 10−2 | 4.35 × 101 | 0.00 × 100 | 0.00 × 100 | |
| F43 | Mean | 2.67 × 101 | 3.67 × 100 | 1.52 × 10−1 | 1.32 × 102 | 1.69 × 10−4 | 9.50 × 10−6 |
| Std | 9.25 × 100 | 4.90 × 100 | 5.98 × 10−2 | 1.22 × 102 | 3.80 × 10−4 | 1.81 × 10−5 | |
| F44 | Mean | 6.25 × 102 | 1.07 × 103 | 2.04 × 100 | 3.04 × 103 | 6.76 × 10−3 | 4.68 × 10−5 |
| Std | 2.03 × 102 | 2.72 × 103 | 2.44 × 10−1 | 7.28 × 102 | 1.35 × 10−2 | 1.55 × 10−4 |
| Function | Metric | AEFA | WSO | STOA | SSA | ROA | PROA |
|---|---|---|---|---|---|---|---|
| F16 | Mean | 6.68 × 106 | 1.58 × 106 | 1.10 × 102 | 4.17 × 108 | 1.38 × 101 | 8.67 × 10−2 |
| Std | 2.57 × 106 | 7.11 × 105 | 1.46 × 101 | 3.75 × 108 | 3.19 × 101 | 1.80 × 10−1 | |
| F17 | Mean | 1.41 × 106 | 3.70 × 104 | 1.42 × 100 | 3.71 × 106 | 6.14 × 10−1 | 2.54 × 10−1 |
| Std | 4.84 × 105 | 2.14 × 104 | 5.09 × 10−1 | 2.06 × 106 | 3.58 × 10−1 | 6.42 × 10−3 | |
| F22 | Mean | 1.20 × 102 | 1.88 × 101 | 4.34 × 10−5 | 9.55 × 101 | 0.00 × 100 | 0.00 × 100 |
| Std | 3.22 × 101 | 4.32 × 100 | 7.00 × 10−5 | 3.88 × 101 | 0.00 × 100 | 0.00 × 100 | |
| F41 | Mean | 1.26 × 102 | 6.46 × 101 | 4.80 × 10−2 | 3.84 × 102 | 0.00 × 100 | 0.00 × 100 |
| Std | 1.69 × 101 | 1.34 × 101 | 6.57 × 10−2 | 1.41 × 102 | 0.00 × 100 | 0.00 × 100 | |
| F43 | Mean | 2.42 × 102 | 9.56 × 102 | 3.96 × 10−1 | 5.12 × 106 | 2.70 × 10−4 | 5.84 × 10−6 |
| Std | 6.28 × 102 | 5.54 × 103 | 5.02 × 10−1 | 3.62 × 107 | 1.43 × 10−3 | 1.24 × 10−5 | |
| F44 | Mean | 7.87 × 104 | 1.64 × 105 | 1.10 × 101 | 3.28 × 107 | 1.17 × 10−1 | 7.19 × 10−5 |
| Std | 1.19 × 105 | 2.59 × 105 | 7.92 × 10−1 | 1.12 × 108 | 5.78 × 10−1 | 8.77 × 10−5 |
| Function | Metric | AEFA | WSO | STOA | SSA | ROA | PROA |
|---|---|---|---|---|---|---|---|
| F16 | Mean | 4.94 × 107 | 2.03 × 107 | 2.04 × 104 | 7.24 × 109 | 1.32 × 102 | 2.61 × 10−1 |
| Std | 7.66 × 106 | 4.27 × 106 | 1.87 × 104 | 2.29 × 108 | 1.96 × 102 | 3.29 × 10−1 | |
| F17 | Mean | 4.59 × 107 | 2.42 × 106 | 2.74 × 103 | 8.77 × 108 | 8.16 × 10−1 | 3.37 × 10−1 |
| Std | 4.95 × 106 | 6.15 × 105 | 2.05 × 103 | 3.49 × 107 | 3.20 × 10−1 | 1.81 × 10−1 | |
| F22 | Mean | 1.54 × 103 | 1.71 × 102 | 2.72 × 10−2 | 3.98 × 103 | 0.00 × 100 | 0.00 × 100 |
| Std | 1.08 × 102 | 1.71 × 101 | 2.53 × 10−2 | 1.02 × 102 | 0.00 × 100 | 0.00 × 100 | |
| F41 | Mean | 1.82 × 103 | 6.01 × 102 | 2.94 × 10−1 | 1.39 × 104 | 0.00 × 100 | 0.00 × 100 |
| Std | 6.10 × 101 | 5.11 × 101 | 2.04 × 10−1 | 2.70 × 102 | 0.00 × 100 | 0.00 × 100 | |
| F43 | Mean | 2.75 × 105 | 2.13 × 105 | 5.12 × 100 | 8.25 × 109 | 1.18 × 10−4 | 5.00 × 10−6 |
| Std | 2.63 × 105 | 2.15 × 105 | 4.48 × 100 | 6.39 × 108 | 3.04 × 10−4 | 1.06 × 10−5 | |
| F44 | Mean | 8.40 × 106 | 4.99 × 106 | 3.83 × 102 | 1.51 × 1010 | 2.98 × 10−1 | 5.35 × 10−4 |
| Std | 3.12 × 106 | 3.17 × 106 | 2.87 × 102 | 9.20 × 108 | 7.00 × 10−1 | 1.05 × 10−3 |
| Function | Metric | AEFA | WSO | STOA | SSA | ROA | PROA |
|---|---|---|---|---|---|---|---|
| F16 | Mean | 8.39 × 107 | 5.33 × 107 | 3.09 × 105 | 1.50 × 1010 | 1.82 × 102 | 6.81 × 10−1 |
| Std | 8.79 × 106 | 1.06 × 107 | 4.38 × 105 | 2.93 × 108 | 3.35 × 102 | 1.09 × 100 | |
| F17 | Mean | 4.24 × 107 | 1.30 × 107 | 8.78 × 104 | 3.63 × 109 | 9.07 × 10−1 | 4.89 × 10−1 |
| Std | 3.96 × 106 | 2.49 × 106 | 8.20 × 104 | 1.01 × 108 | 2.27 × 10−1 | 2.91 × 10−1 | |
| F22 | Mean | 2.66 × 103 | 3.92 × 102 | 1.47 × 10−1 | 8.21 × 103 | 0.00 × 100 | 0.00 × 100 |
| Std | 1.20 × 102 | 3.76 × 101 | 1.08 × 10−1 | 1.48 × 102 | 0.00 × 100 | 0.00 × 100 | |
| F41 | Mean | 8.15 × 103 | 1.32 × 103 | 8.81 × 10−1 | 2.83 × 104 | 0.00 × 100 | 0.00 × 100 |
| Std | 1.42 × 102 | 1.48 × 102 | 4.75 × 10−1 | 4.13 × 102 | 0.00 × 100 | 0.00 × 100 | |
| F43 | Mean | 1.14 × 106 | 1.13 × 106 | 3.13 × 102 | 1.75 × 1010 | 1.01 × 10−4 | 2.16 × 10−6 |
| Std | 6.52 × 105 | 1.30 × 106 | 2.10 × 103 | 6.93 × 108 | 1.83 × 10−4 | 3.84 × 10−6 | |
| F44 | Mean | 2.42 × 107 | 1.65 × 107 | 2.72 × 103 | 3.18 × 1010 | 2.18 × 10−1 | 9.81 × 10−4 |
| Std | 4.93 × 106 | 5.46 × 106 | 2.52 × 103 | 1.32 × 109 | 4.93 × 10−1 | 1.83 × 10−3 |
| No. | Parameter | Symbol | Value |
|---|---|---|---|
| 1 | Key point (xyz) | / | 220, 24, −640 −230, 24, −640 19, 62, −590 −19, 60, −290 |
| 2 | Number of laser trackers | 6 | |
| 3 | Bounding box magnification factor | 0.2 | |
| 4 | Number of populations | 20 | |
| 5 | Maximum number of iterations | 500 | |
| 6 | The number of public transfer points on the target to be tested can be seen between two adjacent stations | 2 | |
| 7 | The number of public transfer points on the tooling can be seen between two adjacent stations | 1 | |
| 8 | The number of public transfer points seen on the ground between two adjacent stations | 2 | |
| 9 | The proportion of the number of key points that can be seen in all stations | 0.75 | |
| 10 | Penalty factor | 106 |
| Algorithm | Min | Max | Mean | Std |
|---|---|---|---|---|
| ROA | 64.95% | 80.18% | 75.82% | 0.0350 |
| PROA | 73.51% | 83.02% | 79.63% | 0.0225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Liu, Y.; Li, L.; Lin, X.; Guo, L. Remora Optimization Algorithm with Enhanced Randomness for Large-Scale Measurement Field Deployment Technology. Entropy 2023, 25, 450. https://doi.org/10.3390/e25030450
Yan D, Liu Y, Li L, Lin X, Guo L. Remora Optimization Algorithm with Enhanced Randomness for Large-Scale Measurement Field Deployment Technology. Entropy. 2023; 25(3):450. https://doi.org/10.3390/e25030450
Chicago/Turabian StyleYan, Dongming, Yue Liu, Lijuan Li, Xuezhu Lin, and Lili Guo. 2023. "Remora Optimization Algorithm with Enhanced Randomness for Large-Scale Measurement Field Deployment Technology" Entropy 25, no. 3: 450. https://doi.org/10.3390/e25030450
APA StyleYan, D., Liu, Y., Li, L., Lin, X., & Guo, L. (2023). Remora Optimization Algorithm with Enhanced Randomness for Large-Scale Measurement Field Deployment Technology. Entropy, 25(3), 450. https://doi.org/10.3390/e25030450









