Quantum Advantage of Thermal Machines with Bose and Fermi Gases
Abstract
1. Introduction
2. Formulation
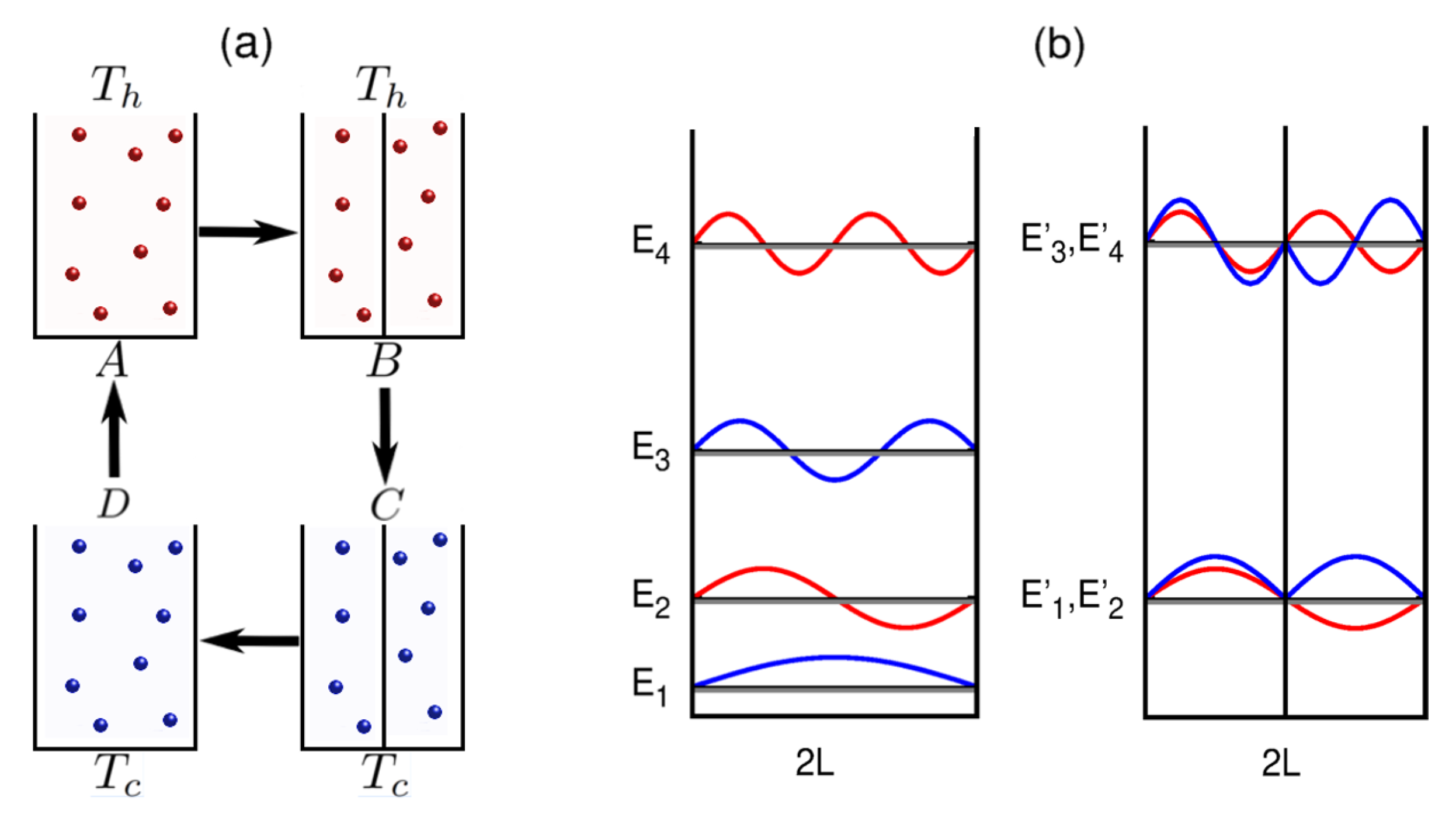
2.1. Quantum Stirling Cycle
2.2. The Working Medium
2.3. Statistics of Quantum Particles
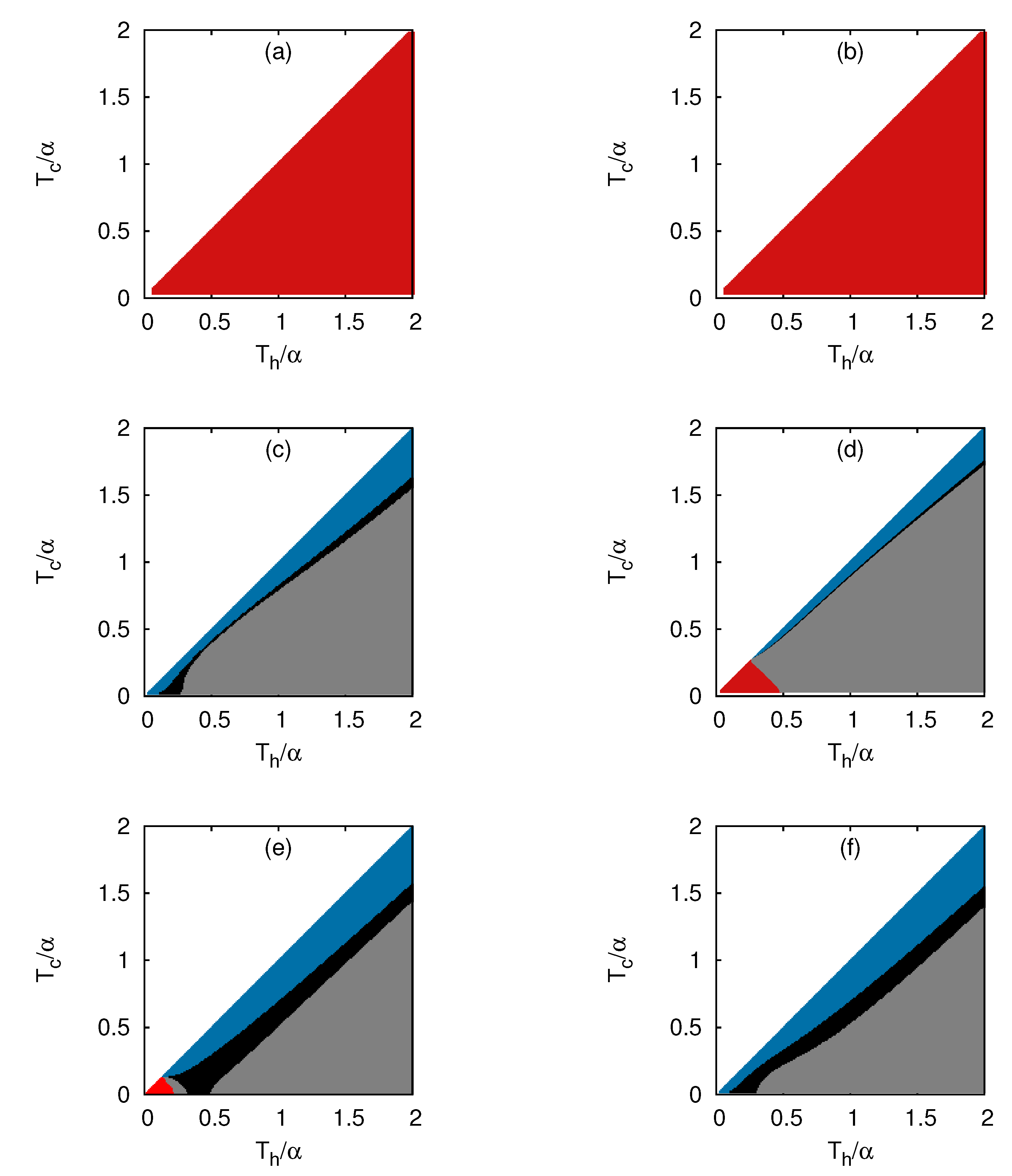
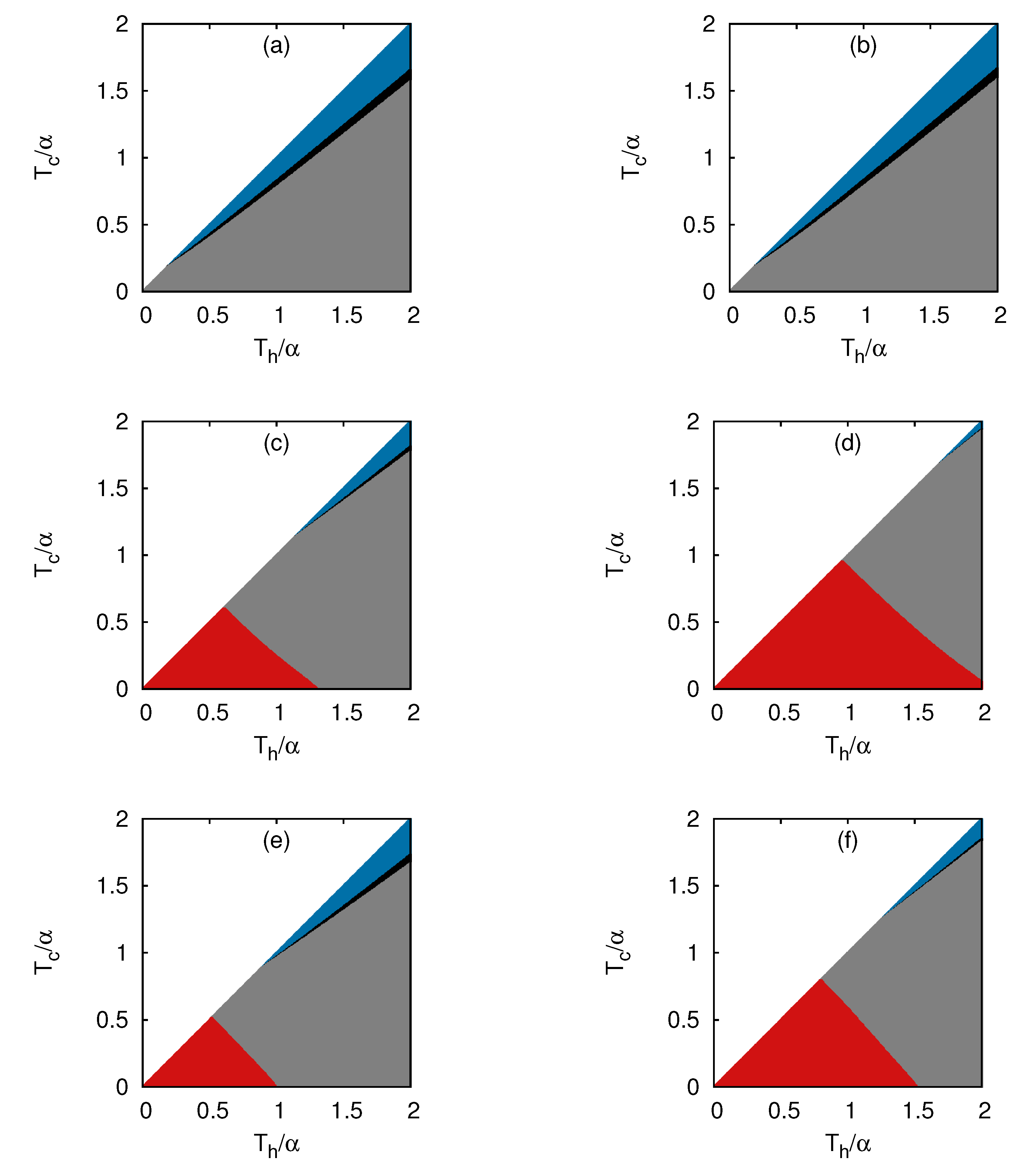
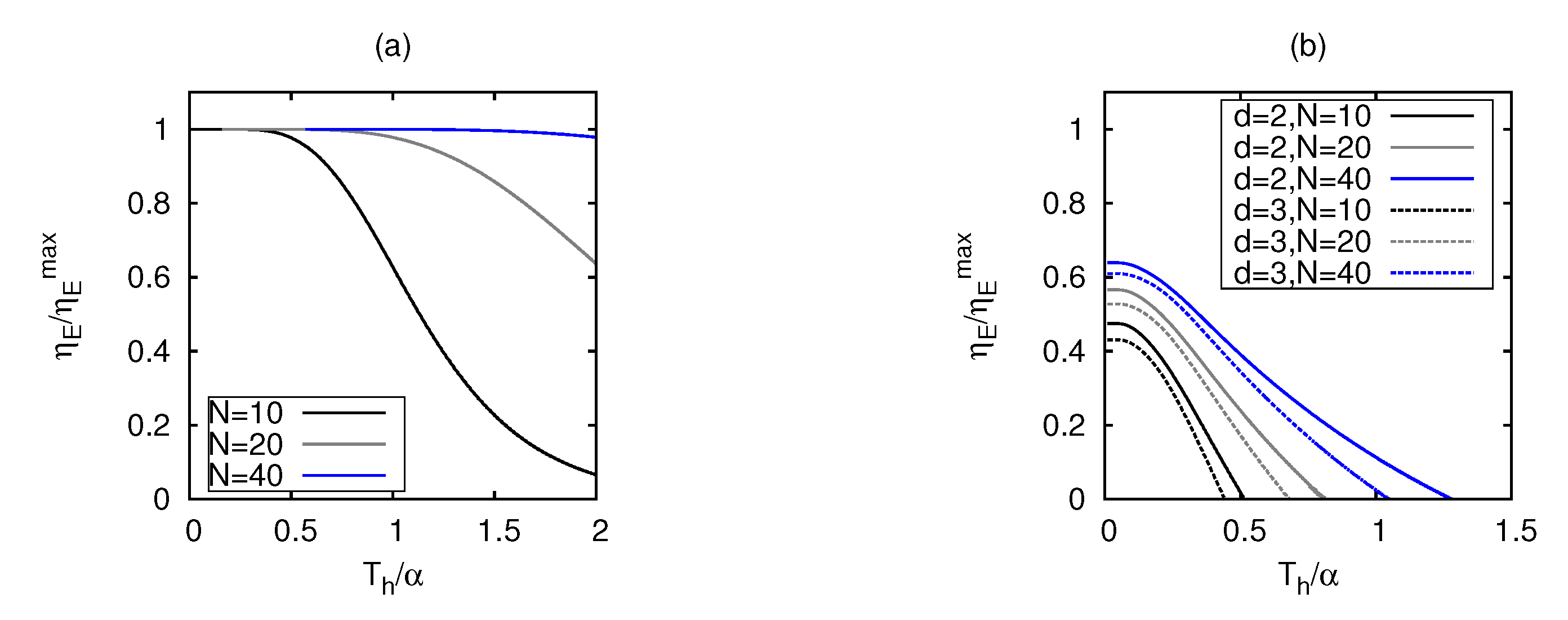
3. Results
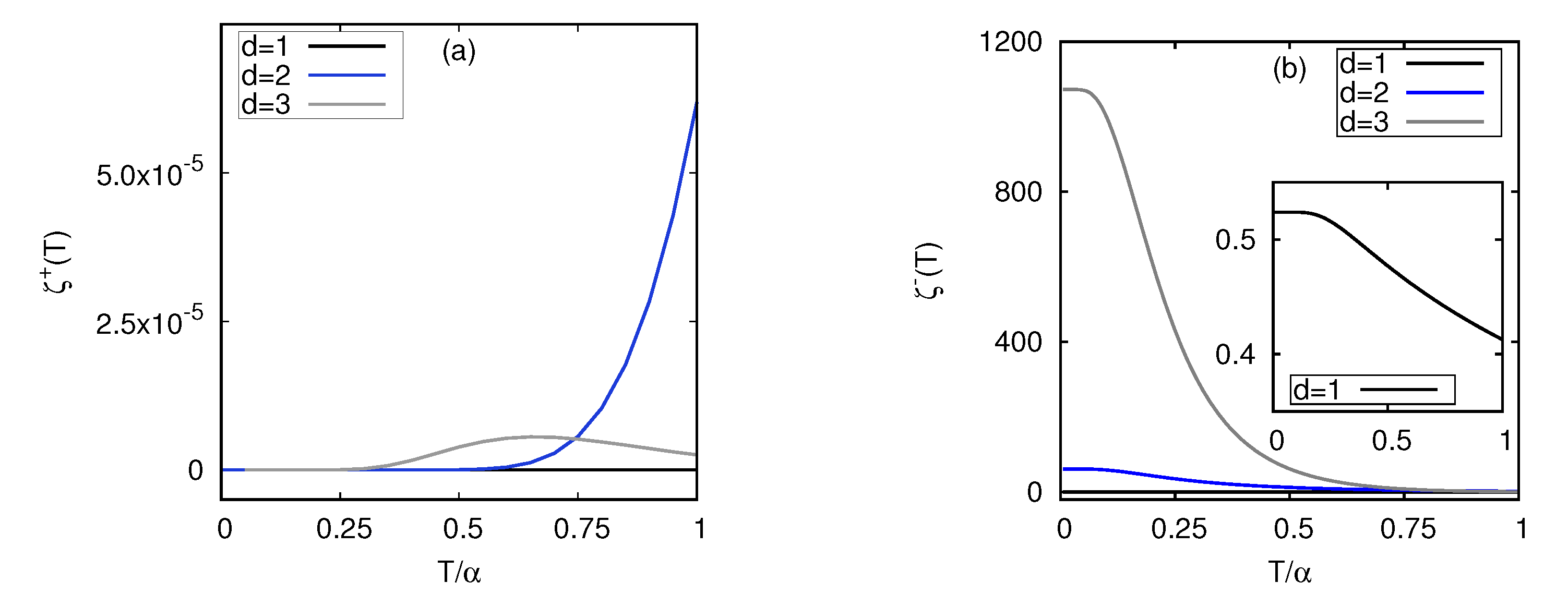
3.1. Analytical Approach for Extremely Low Temperature & Limit of the Cycle
3.1.1. Fermions
3.1.2. Bosons
3.2. Dependence on Average Particle Number N
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Binder, F.; Correa, L.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Fundamental Theories of Physics; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Deffner, S.; Campbell, S. Quantum Thermodynamics: An Introduction to the Thermodynamics of Quantum Information; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar]
- Bhattacharjee, S.; Dutta, A. Quantum thermal machines and batteries. Eur. Phys. J. B 2021, 94, 239. [Google Scholar] [CrossRef]
- Şişman, A.; Saygin, H. Re-Optimisation of Otto Power Cycles Working with Ideal Quantum Gases. Phys. Scr. 2001, 64, 108. [Google Scholar] [CrossRef]
- Jaramillo, J.; Beau, M.; del Campo, A. Quantum supremacy of many-particle thermal machines. New J. Phys. 2016, 18, 075019. [Google Scholar] [CrossRef]
- Beau, M.; Jaramillo, J.; Del Campo, A. Scaling-Up Quantum Heat Engines Efficiently via Shortcuts to Adiabaticity. Entropy 2016, 18, 168. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Watanabe, G.; Yu, Y.C.; Guan, X.W.; del Campo, A. An interaction-driven many-particle quantum heat engine and its universal behavior. NPJ Quantum Inf. 2019, 5, 88. [Google Scholar] [CrossRef]
- Watanabe, G.; Venkatesh, B.P.; Talkner, P.; Hwang, M.J.; del Campo, A. Quantum Statistical Enhancement of the Collective Performance of Multiple Bosonic Engines. Phys. Rev. Lett. 2020, 124, 210603. [Google Scholar] [CrossRef]
- Mukherjee, V.; Divakaran, U. Many-body quantum thermal machines. J. Phys. Condens. Matter 2021, 33, 454001. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Bylinskii, A.; Gangloff, D.; Islam, R.; Aspuru-Guzik, A.; Vuletic, V. Single-Atom Heat Machines Enabled by Energy Quantization. Phys. Rev. Lett. 2018, 120, 170601. [Google Scholar] [CrossRef]
- Thomas, G.; Das, D.; Ghosh, S. Quantum heat engine based on level degeneracy. Phys. Rev. E 2019, 100, 012123. [Google Scholar] [CrossRef]
- Gluza, M.; Sabino, J.; Ng, N.H.; Vitagliano, G.; Pezzutto, M.; Omar, Y.; Mazets, I.; Huber, M.; Schmiedmayer, J.; Eisert, J. Quantum Field Thermal Machines. PRX Quantum 2021, 2, 030310. [Google Scholar] [CrossRef]
- Myers, N.M.; Deffner, S. Bosons outperform fermions: The thermodynamic advantage of symmetry. Phys. Rev. E 2020, 101, 012110. [Google Scholar] [CrossRef]
- Bouton, Q.; Nettersheim, J.; Burgardt, S.; Adam, D.; Lutz, E.; Widera, A. A quantum heat engine driven by atomic collisions. Nat. Commun. 2021, 12, 2063. [Google Scholar] [CrossRef]
- Salamon, P.; Nitzan, A.; Andresen, B.; Berry, R.S. Minimum entropy production and the optimization of heat engines. Phys. Rev. A 1980, 21, 2115–2129. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z. The effect of field dependent heat capacity on regeneration in magnetic Ericsson cycles. J. Appl. Phys. 1991, 69, 6245–6247. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. On the classical limit of quantum thermodynamics in finite time. J. Chem. Phys. 1992, 97, 4398–4412. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. A quantum-mechanical heat engine operating in finite time. A model consisting of spin-1/2 systems as the working fluid. J. Chem. Phys. 1992, 96, 3054–3067. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D Appl. Phys. 1994, 27, 1144–1149. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z. The effect of thermal resistances and regenerative losses on the performance characteristics of a magnetic Ericsson refrigeration cycle. J. Appl. Phys. 1998, 84, 1791–1795. [Google Scholar] [CrossRef]
- Chen, J.; Schouten, J.A. The comprehensive influence of several major irreversibilities on the performance of an Ericsson heat engine. Appl. Therm. Eng. 1999, 19, 555–564. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S. Comment on Quantum-mechanical Carnot engine. J. Phys. A Math. Gen. 2001, 34, 1529–1533. [Google Scholar] [CrossRef]
- Arnaud, J.; Chusseau, L.; Philippe, F. Carnot cycle for an oscillator. Eur. J. Phys. 2002, 23, 489. [Google Scholar] [CrossRef]
- Abah, O.; Roßnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-Ion Heat Engine at Maximum Power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Mukherjee, V. Quantum-enhanced finite-time Otto cycle. Phys. Rev. Res. 2020, 2, 033083. [Google Scholar] [CrossRef]
- Mukherjee, V.; Kofman, A.G.; Kurizki, G. Anti-Zeno quantum advantage in fast-driven heat machines. Commun. Phys. 2020, 3, 8. [Google Scholar] [CrossRef]
- Misra, A.; Opatrný, T.; Kurizki, G. Work extraction from single-mode thermal noise by measurements: How important is information? Phys. Rev. E 2022, 106, 054131. [Google Scholar] [CrossRef]
- Misra, A.; Singh, U.; Bera, M.N.; Rajagopal, A.K. Quantum Rényi relative entropies affirm universality of thermodynamics. Phys. Rev. E 2015, 92, 042161. [Google Scholar] [CrossRef]
- Gupt, N.; Bhattacharyya, S.; Ghosh, A. Statistical generalization of regenerative bosonic and fermionic Stirling cycles. Phys. Rev. E 2021, 104, 054130. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774–4790. [Google Scholar] [CrossRef]
- Chen, J.; Lin, B.; Hua, B. The performance of a quantum heat engine working with spin systems. J. Phys. D Appl. Phys. 2002, 35, 2051–2057. [Google Scholar] [CrossRef]
- Lin, B.; Chen, J.; Hua, B. The optimal performance of a quantum refrigeration cycle working with harmonic oscillators. J. Phys. D Appl. Phys. 2003, 36, 406–413. [Google Scholar] [CrossRef]
- Henrich, M.J.; Rempp, F.; Mahler, G. Quantum thermodynamic Otto machines: A spin-system approach. Eur. Phys. J. Spec. Top. 2007, 151, 157–165. [Google Scholar] [CrossRef]
- Thomas, G.; Johal, R.S. Friction due to inhomogeneous driving of coupled spins in a quantum heat engine. Eur. Phys. J. B 2014, 87, 166. [Google Scholar] [CrossRef]
- Levy, A.; Gelbwaser-Klimovsky, D. Quantum Features and Signatures of Quantum Thermal Machines. In Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 87–126. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Huang, X.L.; Xu, H.; Niu, X.Y.; Fu, Y.D. A special entangled quantum heat engine based on the two-qubit Heisenberg XX model. Phys. Scr. 2013, 88, 065008. [Google Scholar] [CrossRef]
- Huang, X.L.; Liu, Y.; Wang, Z.; Niu, X.Y. Special coupled quantum Otto cycles. Eur. Phys. J. Plus 2014, 129, 4. [Google Scholar] [CrossRef]
- Abah, O.; Lutz, E. Optimal performance of a quantum Otto refrigerator. EPL (Europhys. Lett.) 2016, 113, 60002. [Google Scholar] [CrossRef]
- Stefanatos, D. Optimal efficiency of a noisy quantum heat engine. Phys. Rev. E 2014, 90, 012119. [Google Scholar] [CrossRef]
- Stefanatos, D. Exponential bound in the quest for absolute zero. Phys. Rev. E 2017, 96, 042103. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Klaers, J.; Faelt, S.; Imamoglu, A.; Togan, E. Squeezed Thermal Reservoirs as a Resource for a Nanomechanical Engine beyond the Carnot Limit. Phys. Rev. X 2017, 7, 031044. [Google Scholar] [CrossRef]
- Niedenzu, W.; Mukherjee, V.; Ghosh, A.; Kofman, A.G.; Kurizki, G. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018, 9, 165. [Google Scholar] [CrossRef]
- Ghosh, A.; Mukherjee, V.; Niedenzu, W.; Kurizki, G. Are quantum thermodynamic machines better than their classical counterparts? Eur. Phys. J. Spec. Top. 2019, 227, 2043–2051. [Google Scholar] [CrossRef]
- Chatterjee, S.; Koner, A.; Chatterjee, S.; Kumar, C. Temperature-dependent maximization of work and efficiency in a degeneracy-assisted quantum Stirling heat engine. Phys. Rev. E 2021, 103, 062109. [Google Scholar] [CrossRef]
- Chattopadhyay, P.; Mitra, A.; Paul, G.; Zarikas, V. Bound on Efficiency of Heat Engine from Uncertainty Relation Viewpoint. Entropy 2021, 23, 439. [Google Scholar] [CrossRef]
- Pathria, R.; Beale, P.D. 7–Ideal Bose Systems. In Statistical Mechanics, 3rd ed.; Pathria, R., Beale, P.D., Eds.; Academic Press: Boston, MA, USA, 2011; pp. 179–229. [Google Scholar] [CrossRef]
- Pathria, R.; Beale, P.D. 8–Ideal Fermi Systems. In Statistical Mechanics, 3rd ed.; Pathria, R., Beale, P.D., Eds.; Academic Press: Boston, MA, USA, 2011; pp. 231–273. [Google Scholar] [CrossRef]
- Chowdhury, D.; Stauffer, D. Principles of Equilibrium Statistical Mechanics; WILEY-VCH: Hoboken, NJ, USA, 2000. [Google Scholar]
- Griffiths, D. Introduction to Quantum Mechanics; Pearson Prentice Hall: London, UK, 2005. [Google Scholar]
- Belloni, M.; Robinett, R. The infinite well and Dirac delta function potentials as pedagogical, mathematical and physical models in quantum mechanics. Phys. Rep. 2014, 540, 25–122. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Fried, E.; Anand, L. The Mechanics and Thermodynamics of Continua; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Paolucci, S. Continuum Mechanics and Thermodynamics of Matter; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Batalhão, T.B.; Souza, A.M.; Mazzola, L.; Auccaise, R.; Sarthour, R.S.; Oliveira, I.S.; Goold, J.; De Chiara, G.; Paternostro, M.; Serra, R.M. Experimental Reconstruction of Work Distribution and Study of Fluctuation Relations in a Closed Quantum System. Phys. Rev. Lett. 2014, 113, 140601. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef]
- Deng, S.; Chenu, A.; Diao, P.; Li, F.; Yu, S.; Coulamy, I.; del Campo, A.; Wu, H. Superadiabatic quantum friction suppression in finite-time thermodynamics. Sci. Adv. 2018, 4, eaar5909. [Google Scholar] [CrossRef]
- Josefsson, M.; Svilans, A.; Burke, A.M.; Hoffmann, E.A.; Fahlvik, S.; Thelander, C.; Leijnse, M.; Linke, H. A quantum-dot heat engine operating close to the thermodynamic efficiency limits. Nat. Nanotechnol. 2018, 13, 920–924. [Google Scholar] [CrossRef]
- von Lindenfels, D.; Gräb, O.; Schmiegelow, C.T.; Kaushal, V.; Schulz, J.; Mitchison, M.T.; Goold, J.; Schmidt-Kaler, F.; Poschinger, U.G. Spin Heat Engine Coupled to a Harmonic-Oscillator Flywheel. Phys. Rev. Lett. 2019, 123, 080602. [Google Scholar] [CrossRef]
- Sattler, K.D. Handbook of Nanophysics: Nanotubes and Nanowires; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Liu, Y.S.; Yang, X.F.; Hong, X.K.; Si, M.S.; Chi, F.; Guo, Y. A high-efficiency double quantum dot heat engine. Appl. Phys. Lett. 2013, 103, 093901. [Google Scholar] [CrossRef]
- Du, J.; Shen, W.; Zhang, X.; Su, S.; Chen, J. Quantum-dot heat engines with irreversible heat transfer. Phys. Rev. Res. 2020, 2, 013259. [Google Scholar] [CrossRef]
- Stern, M.; Umansky, V.; Bar-Joseph, I. Exciton Liquid in Coupled Quantum Wells. Science 2014, 343, 55–57. [Google Scholar] [CrossRef]
- Gangloff, D.; Bylinskii, A.; Counts, I.; Jhe, W.; Vuletić, V. Velocity tuning of friction with two trapped atoms. Nat. Phys. 2015, 11, 915–919. [Google Scholar] [CrossRef]
- Bylinskii, A.; Gangloff, D.; Vuletic, V. Tuning friction atom-by-atom in an ion-crystal simulator. Science 2015, 348, 1115–1118. [Google Scholar] [CrossRef]
- Karpa, L.; Bylinskii, A.; Gangloff, D.; Cetina, M.; Vuletić, V. Suppression of Ion Transport due to Long-Lived Subwavelength Localization by an Optical Lattice. Phys. Rev. Lett. 2013, 111, 163002. [Google Scholar] [CrossRef]
- Carnot, S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer atte puissance. Ann. Sci. L’école Norm. Supér. 1872, 1, 393–457. [Google Scholar] [CrossRef]
- Chen, J.; Dong, H.; Sun, C.P. Bose-Fermi duality in a quantum Otto heat engine with trapped repulsive bosons. Phys. Rev. E 2018, 98, 062119. [Google Scholar] [CrossRef]
- Mackel, N.E.; Yang, J.; del Campo, A. Quantum Alchemy and Universal Orthogonality Catastrophe in One-Dimensional Anyons. arXiv 2022, arXiv:2210.10776v1. [Google Scholar]
- Schroeder, D.V. An Introduction to Thermal Physics; Addison Wesley: San Francisco, CA, USA, 2000. [Google Scholar]
- Arovas, D. Arovas Lecture Notes on Thermodynamics and Statistical Mechanics; University of California: San Diego, CA, USA, 2013. [Google Scholar]
- Acharyya, M. Noninteracting fermions in infinite dimensions. Eur. J. Phys. 2010, 31, L89–L91. [Google Scholar] [CrossRef]
- Blumenson, L.E. A Derivation of n-Dimensional Spherical Coordinates. Am. Math. Mon. 1960, 67, 63–66. [Google Scholar] [CrossRef]
- Cowan, B. On the Chemical Potential of Ideal Fermi and Bose Gases. J. Low Temp. Phys. 2019, 197, 412–444. [Google Scholar] [CrossRef]
- Myers, N.M.; Peña, F.J.; Negrete, O.; Vargas, P.; Chiara, G.D.; Deffner, S. Boosting engine performance with Bose–Einstein condensation. New J. Phys. 2022, 24, 025001. [Google Scholar] [CrossRef]
- Niedenzu, W.; Mazets, I.; Kurizki, G.; Jendrzejewski, F. Quantized refrigerator for an atomic cloud. Quantum 2019, 3, 155. [Google Scholar] [CrossRef]
| Modes of Operation | W | ||
|---|---|---|---|
| Engine | >0 | <0 | <0 |
| Refrigerator | <0 | >0 | >0 |
| Accelerator | >0 | <0 | >0 |
| Heater | <0 | <0 | >0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sur, S.; Ghosh, A. Quantum Advantage of Thermal Machines with Bose and Fermi Gases. Entropy 2023, 25, 372. https://doi.org/10.3390/e25020372
Sur S, Ghosh A. Quantum Advantage of Thermal Machines with Bose and Fermi Gases. Entropy. 2023; 25(2):372. https://doi.org/10.3390/e25020372
Chicago/Turabian StyleSur, Saikat, and Arnab Ghosh. 2023. "Quantum Advantage of Thermal Machines with Bose and Fermi Gases" Entropy 25, no. 2: 372. https://doi.org/10.3390/e25020372
APA StyleSur, S., & Ghosh, A. (2023). Quantum Advantage of Thermal Machines with Bose and Fermi Gases. Entropy, 25(2), 372. https://doi.org/10.3390/e25020372






