A Well-Posed Fractional Order Cholera Model with Saturated Incidence Rate
Abstract
1. Introduction
- This paper addresses a new mathematical model of cholera disease which involves the Caputo fractional derivative.
- The fundamental characteristics of the new model are discussed in detail.
- A numerical scheme is developed to carry out numerical simulations.
- The effect of awareness is studied.
- Comparative results in this research show an obvious linkage between the mathematical and biological mechanisms.
2. Preliminary Definitions and Theorems
3. Model Formulation
4. Well-Posednessof the Model
4.1. Positivity and Boundedness
4.2. Existence and Uniqueness
4.3. Existence of Equilibrium Solutions
- Disease-free equilibrium is given as;
- Endemic equilibrium is given as;whereand can be obtained by solving,where
4.4. Basic Reproduction Ratio
4.5. Stability Analysis of the Equilibria
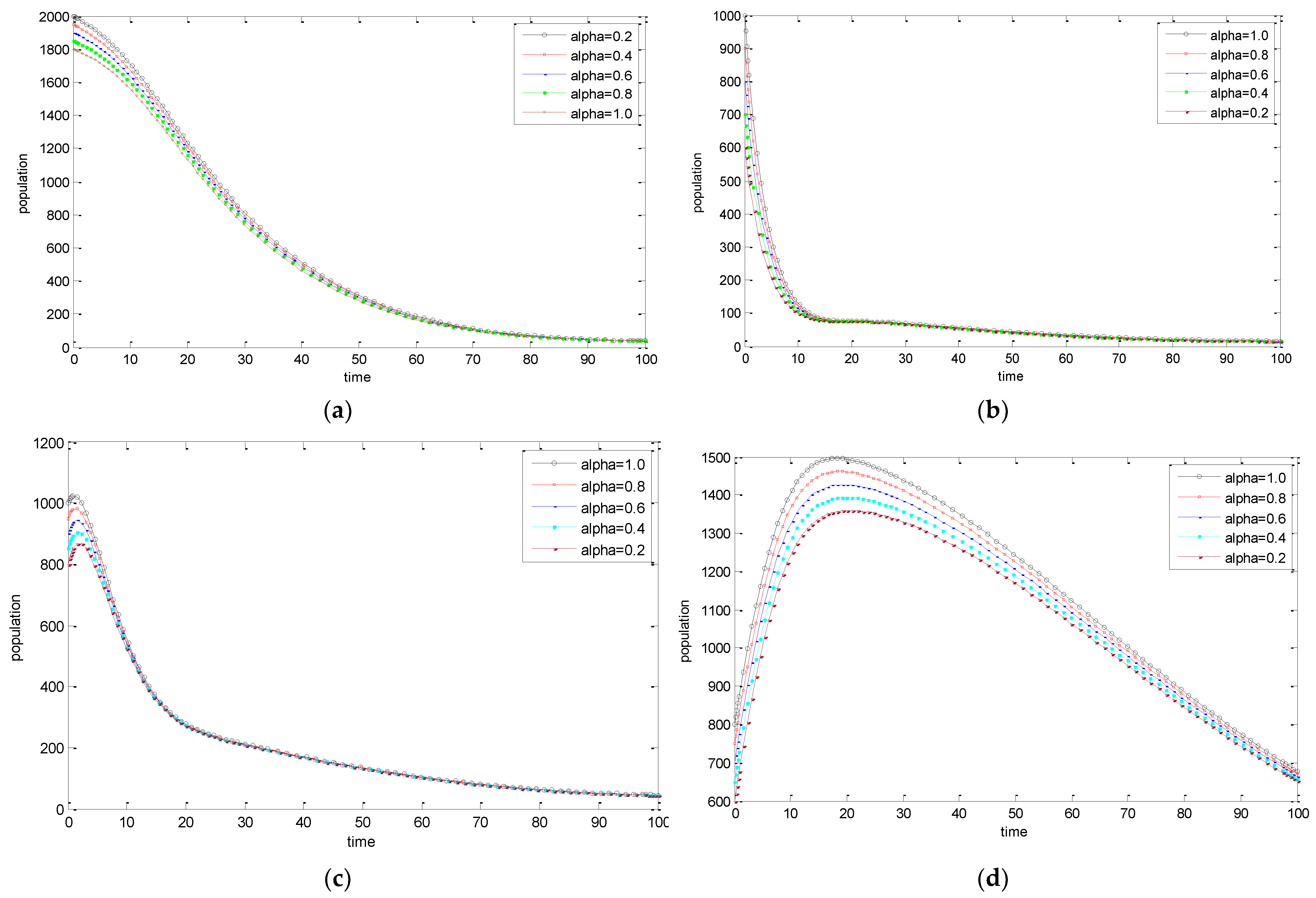
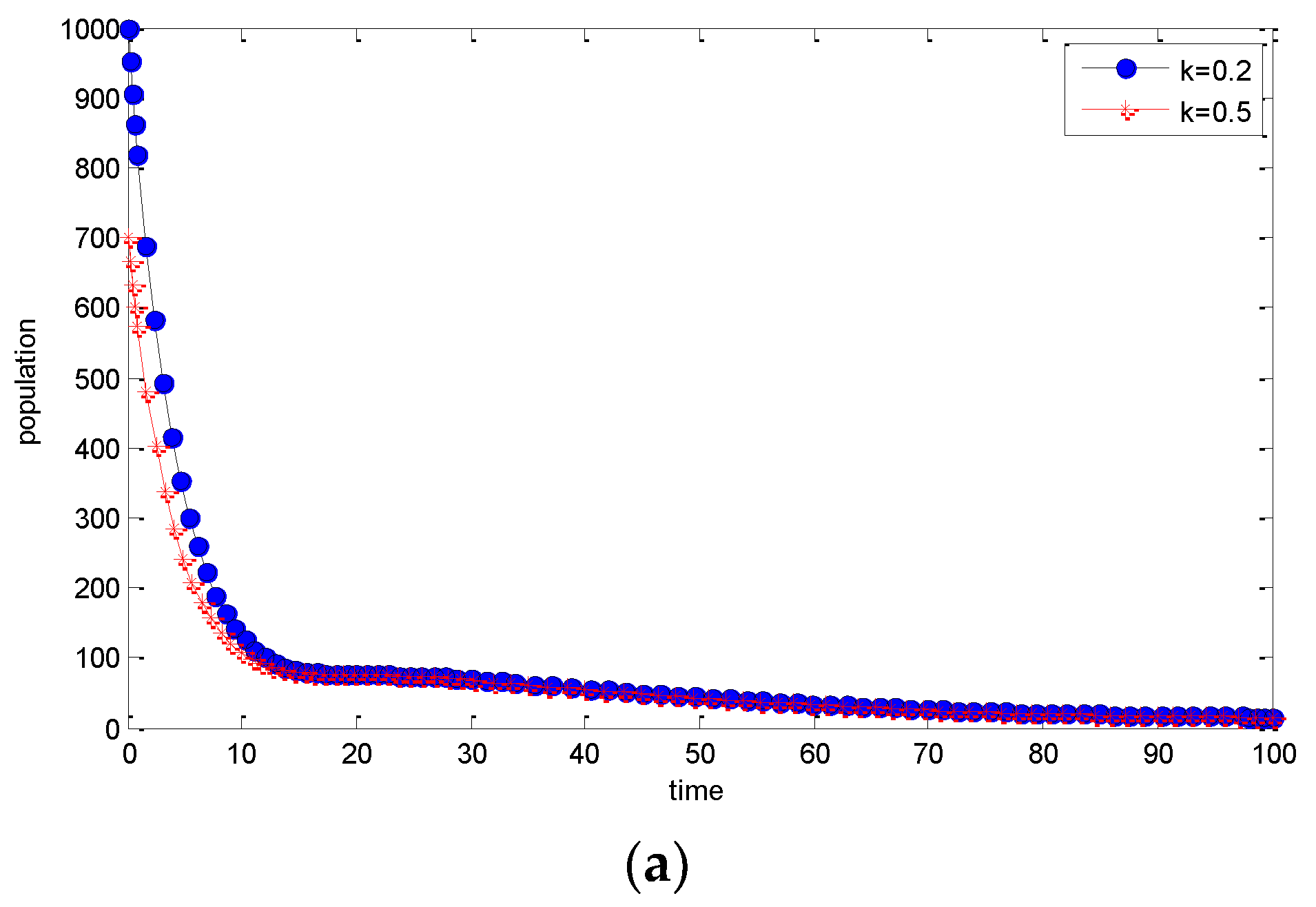
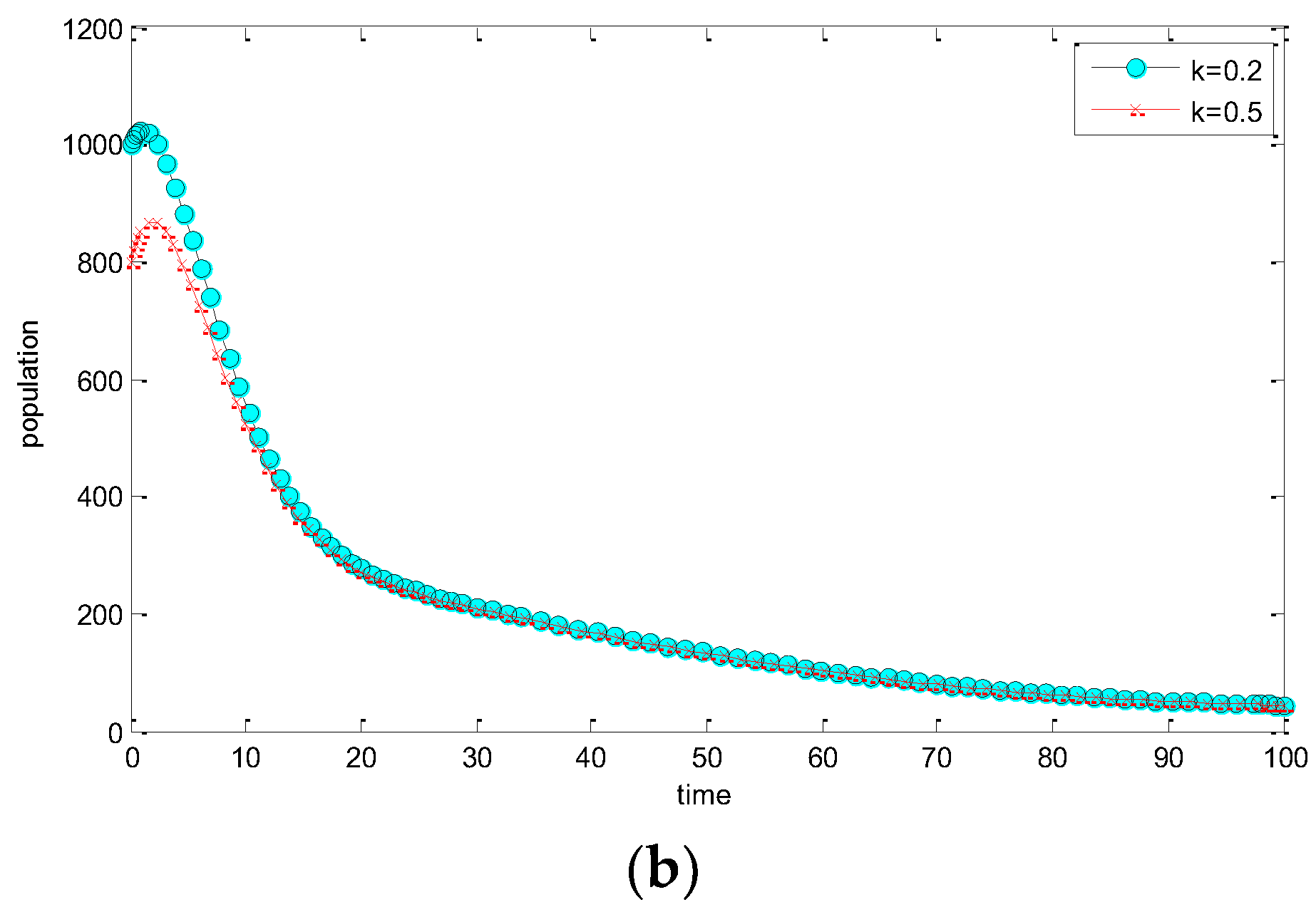
5. Numerical Simulations
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ganesan, D.; Gupta, S.S.; Legros, D. Cholera surveillance and estimation of burden of cholera. Vaccine 2020, 38, A13–A17. [Google Scholar] [CrossRef] [PubMed]
- Idoga, P.E.; Toycan, M.; Zayyad, M.A. Analysis of factors contributing to the spread of cholera in developing countries. Eurasian J. Med. 2019, 51, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Llanes, R.; Somarriba, L.; Hern’andez, G.; Bardaj, Y.; Aguila, A.; Mazumder, R.N. Low detection of vibrio cholera carriage in healthcare workers returning to 12 Latin American countries from Haiti. Epidemiol. Infect. 2015, 143, 1016–1019. [Google Scholar] [CrossRef] [PubMed]
- Momba, M.; El-Liethy, M.A. Vibrio Cholerae and Cholera Biotypes; Global Water Pathogen Project: Pretoria, South Africa, 2018. [Google Scholar]
- Javidi, M.; Ahmad, B. A study of a fractional-order cholera model. Appl. Math. Inf. Sci. 2014, 8, 2195–2206. [Google Scholar] [CrossRef]
- Lamond, E.; Kinyanjui, J. Cholera Outbreak Guidelines: Preparedness, Prevention and Control; Oxfam GB: Oxford, UK, 2012. [Google Scholar]
- Eskandari, Z.; Avazzadeh, Z.; Khoshsiar, G.; Li, B. Dynamics and bifurcations of a discrete—Time Lotka–Volterra model using nonstandard finite difference discretization method. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Liu, X.; Arfan, M.; Ur Rahman, M.; Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Eng. 2022, 3, 1–5. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Marinov, T.; Marinova, R. Adaptive SIR model with vaccination: Simultaneous identification of rates and functions illustrated with COVID-19. Sci. Rep. 2022, 12, 1–13. [Google Scholar]
- Alam, A.; LaRocque, R.C.; Harris, J.B.; Vanderspurt, C.; Ryan, E.T.; Qadri, F.; Calderwood, S.B. Hyperinfectivity of human-passaged Vibrio cholerae can be modelled by growth in the infant mouse. Infect. Immun. 2005, 73, 6674–6679. [Google Scholar] [CrossRef]
- Codeço, C. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMC Infect. Dis. 2001, 1, 1–14. [Google Scholar] [CrossRef]
- Hartley, D.M., Jr.; Morris, J.; Smith, D. Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 2006, 3, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Mukandavire, Z.; Liao, S.; Wang, J.; Gaff, H.; Smith, D.; Morris, J. Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc. Natl. Acad. Sci. USA 2011, 108, 8767–8772. [Google Scholar] [CrossRef] [PubMed]
- Nelson, E.; Harris, J.; Morris, J.; Calderwood, S.; Camilli, A. Cholera transmission: The host, pathogen and bacteriophage dynamics. Nat. Rev. Microbiol. 2009, 7, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Z.; Tien, J.H.; Van den Driessche, P. Cholera models with hyper infectivity and temporary immunity. Bull. Math. Biol. 2012, 74, 2423–2445. [Google Scholar] [CrossRef]
- Shuai, Z.; van den Driessche, P. Modeling and control of cholera on networks with a common water source. J. Biol. Dyn. 2015, 9, 90–103. [Google Scholar] [CrossRef]
- Escalante-Martínez, J.E.; Gómez-Aguilar, J.F.; Calderón-Ramón, C.; Aguilar-Meléndez, A.; Padilla-Longoria, P. Synchronized bioluminescence behavior of a set of fireflies involving fractional operators of Liouville Caputo type. Int. J. Biomath. 2018, 11, 1–24. [Google Scholar] [CrossRef]
- Escalante-Martínez, J.E.; Gómez-Aguilar, J.F.; Calderón-Ramón, C.; Aguilar-Meléndez, A.; Padilla-Longoria, P. A mathematical model of circadian rhythms synchronization using fractional differential equations system of coupled van der Pol oscillators. Int. J. Biomath. 2018, 11, 1850041. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar] [CrossRef]
- Aguilar, J.F.G. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 2018, 133, 1–20. [Google Scholar]
- Capasso, V.; Serio, G. A generalization of the Kermack-Mckendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Liu, W.M.; Levin, S.A.; Iwasa, Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 1986, 23, 187–204. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Ruan, S. Global analysis of an epidemic model with non monotone incidence rate. Math. Biosci. 2007, 208, 419–429. [Google Scholar] [CrossRef] [PubMed]
- Leo, J. Complexity of Epidemics Models: A Case-Study of Cholera in Tanzania. In Digital Transformation for Sustainability; Marx Gómez, J., Lorini, M.R., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Tchatat, D.; Kolaye, G.; Bowong, S.; Temgoua, A. Theoretical assessment of the impact of awareness programs on cholera transmission dynamic. Int. J. Nonlinear Sci. Numer. Simul. 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Abdeljawad, T.; Din, A. Modeling the dynamics of stochastic norovirus epidemic model with time-delay. Fractals 2022, 30, 1–13. [Google Scholar] [CrossRef]
- Lemos-Paião, A.; Silva, C.; Torres, D. A cholera mathematical model with vaccination and the biggest outbreak of world’s history. AIMS Math. 2018, 3, 448–463. [Google Scholar] [CrossRef]
- Capasso, V.; Paveri-Fontana, S. A mathematical model for the 1973 cholera epidemic in the European Mediterranean region. Rev. D’epidémiologie Et De St. 1979, 27, 121–132. [Google Scholar]
- Nishiura, H.; Tsuzuki, S.; Yuan, B.; Yamaguchi, T.; Asai, Y. Transmission dynamics of cholera in Yemen, 2017: A real time forecasting Theoret. Biol. Med. Model. 2017, 14, 14. [Google Scholar] [CrossRef]
- Neilan, R.; Schaefer, E.; Gaff, H.; Fister, K.; Lenhart, S. Modeling optimal intervention strategies for cholera. Bull. Math. Biol. 2010, 72, 2004–2018. [Google Scholar]
- Luchko, Y.; Yamamoto, M. General time-fractional diffusion equation: Some uniqueness and existence results for the initial-boundary-value problems. Fract. Calculus Appl. Anal. 2016, 19, 676–695. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Vahid, K.Z.; Pirouz, H.M.; Asad, J.H. A new and general fractional Lagrangian approach: A capacitor microphone case study. Res. Phys. 2021, 31, 104950. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Application of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Ullah, M.; Baleanu, D. A new fractional SICA model and numerical method for the transmission of HIV/AIDS. Math. Methods Appl. Sci. 2021, 44, 8648–8659. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Khan, M.; Parvez, M.; Islam, S.; Khan, I.; Shafie, S.; Gul, T. Mathematical Analysis of Typhoid Model with Saturated Incidence Rate. Adv. Stud. Biol. 2015, 7, 65–78. [Google Scholar] [CrossRef]
| Parameter | Meaning |
|---|---|
| Λ | Birthrate |
| β | Disease contact rate |
| Natural death rate | |
| Disease-induced death rate in the Exposed class | |
| γ | Rate at which the Exposed become Susceptible |
| 𝜉 | Rate at which the Infectious become Susceptible |
| 𝜂 | Rate at which the Exposed become Infectious |
| d | Disease-induced death rate in the Infectious class |
| Rate of recovery | |
| k | Awareness parameter |
| Fraction of individuals joining the Exposed class |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baba, I.A.; Humphries, U.W.; Rihan, F.A. A Well-Posed Fractional Order Cholera Model with Saturated Incidence Rate. Entropy 2023, 25, 360. https://doi.org/10.3390/e25020360
Baba IA, Humphries UW, Rihan FA. A Well-Posed Fractional Order Cholera Model with Saturated Incidence Rate. Entropy. 2023; 25(2):360. https://doi.org/10.3390/e25020360
Chicago/Turabian StyleBaba, Isa Abdullahi, Usa Wannasingha Humphries, and Fathalla A. Rihan. 2023. "A Well-Posed Fractional Order Cholera Model with Saturated Incidence Rate" Entropy 25, no. 2: 360. https://doi.org/10.3390/e25020360
APA StyleBaba, I. A., Humphries, U. W., & Rihan, F. A. (2023). A Well-Posed Fractional Order Cholera Model with Saturated Incidence Rate. Entropy, 25(2), 360. https://doi.org/10.3390/e25020360









