Design and Analysis of Joint Group Shuffled Scheduling Decoding Algorithm for Double LDPC Codes System
Abstract
1. Introduction
1.1. Related Work and Motivation of Shuffled Scheduling Decoding
1.2. Related Work on D-LDPC Codes Systems
1.3. Main Contribution
- (1)
- From a global viewpoint, the D-LDPC codes structure is considered as a whole, and a joint shuffled scheduling decoding strategy is introduced to the D-LDPC codes system.
- (2)
- A grouping method for the joint shuffled scheduling decoding strategy, which relies on the types or the length of the VNs, is introduced.
- (3)
- A novel EXIT algorithm to calculate the channel and source decoding thresholds for the general D-LDPC coding structure with the JGSSD algorithm is proposed.
- (4)
- A comparison between the SSSD algorithm and the JGSSD algorithm is conducted, including decoding performance, decoding complexity and decoding latency.
1.4. Paper Organization
2. Preliminaries of D-LDPC Codes Systems
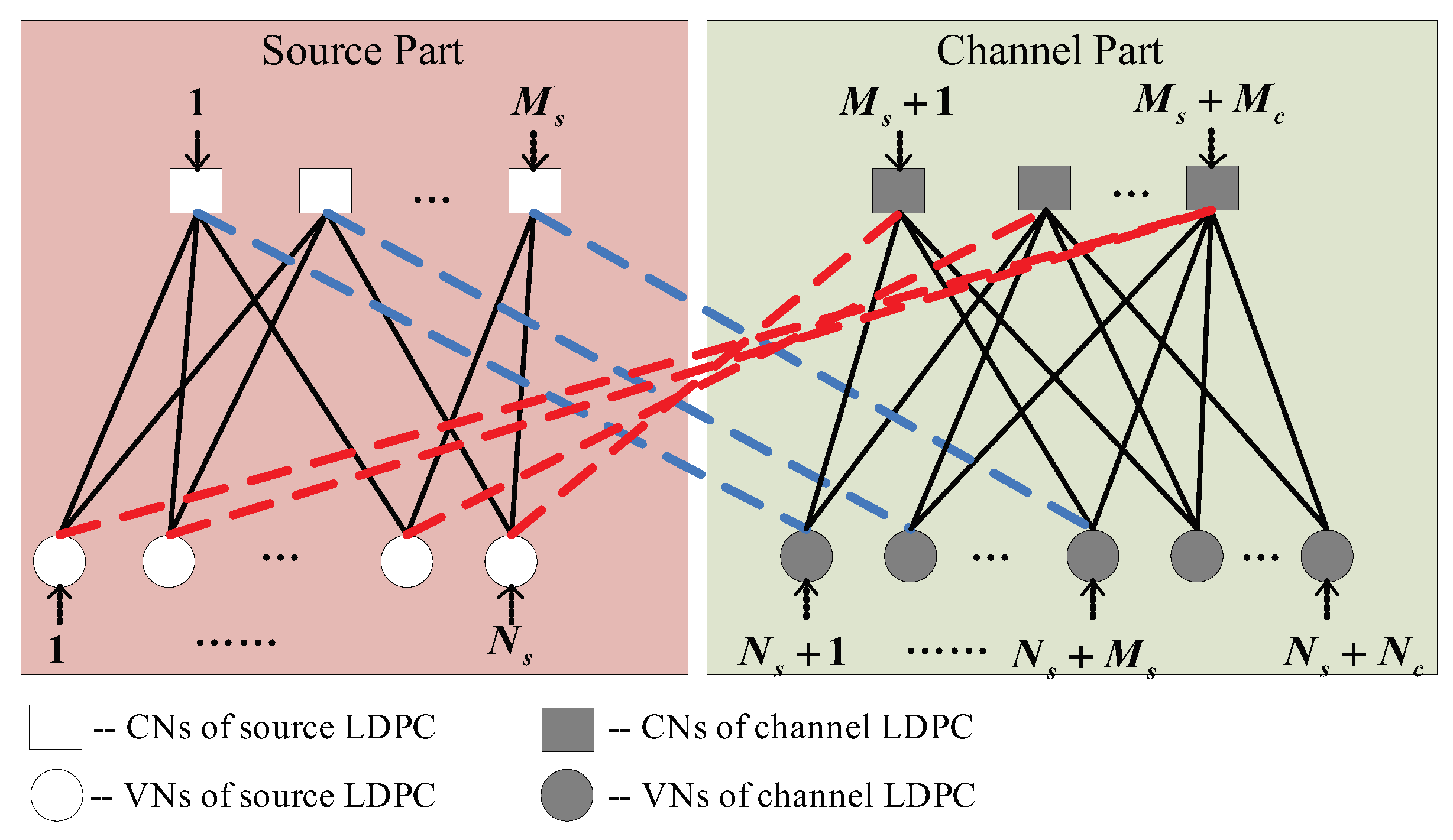
2.1. The D-LDPC Coding Structure
2.2. Transmission System Model
- (1)
- Update all the C2V messages for each of the CNs in the channel part;
- (2)
- Update all the V2C messages for each of the VNs in the source part;
- (3)
- Update all the C2V messages for each of the CNs in the source part;
- (4)
- Update all the V2C messages for each of the VNs in the channel part;
- (5)
- The source part and channel part exchange decoding information through and (i.e., the dashed blue and red lines in Figure 1);
- (6)
- Estimate the codeword based on the posterior LLRs at the VNs;
- (7)
- Repeat Steps (1) to (6), unless (i) the estimated codeword and satisfy and (ii) the maximum iteration number K is reached.
3. Joint Group Shuffled Scheduling Decoding Algorithm
- represents the LLR of the n-th bit of original source .
- represents the LLR of the n-th bit of codeword .
- represents the LLR from the m-th CN to the n-th VN at k-th iteration.
- represents the LLR from the n-th VN to the m-th CN at k-th iteration.
- represents the LLRs of the n-th bit at k-th iteration.
4. Analysis of the D-LDPC Codes System with JGSSD Algorithm
4.1. Joint Shuffled Extrinsic Information Algorithm
- : the extrinsic MI from j-th VN to i-th CN at k-th iteration;
- : the extrinsic MI from i-th CN to j-th VN at k-th iteration;
- : the a priori MI from j-th VN to i-th CN at k-th iteration;
- : the a priori MI from i-th CN to j-th VN at k-th iteration;
- : the MI between a posteriori LLR evaluated by j-th VN and the corresponding source bit at k-th iteration.
4.2. Decoding Threshold Calculation
5. Simulation and Comparison
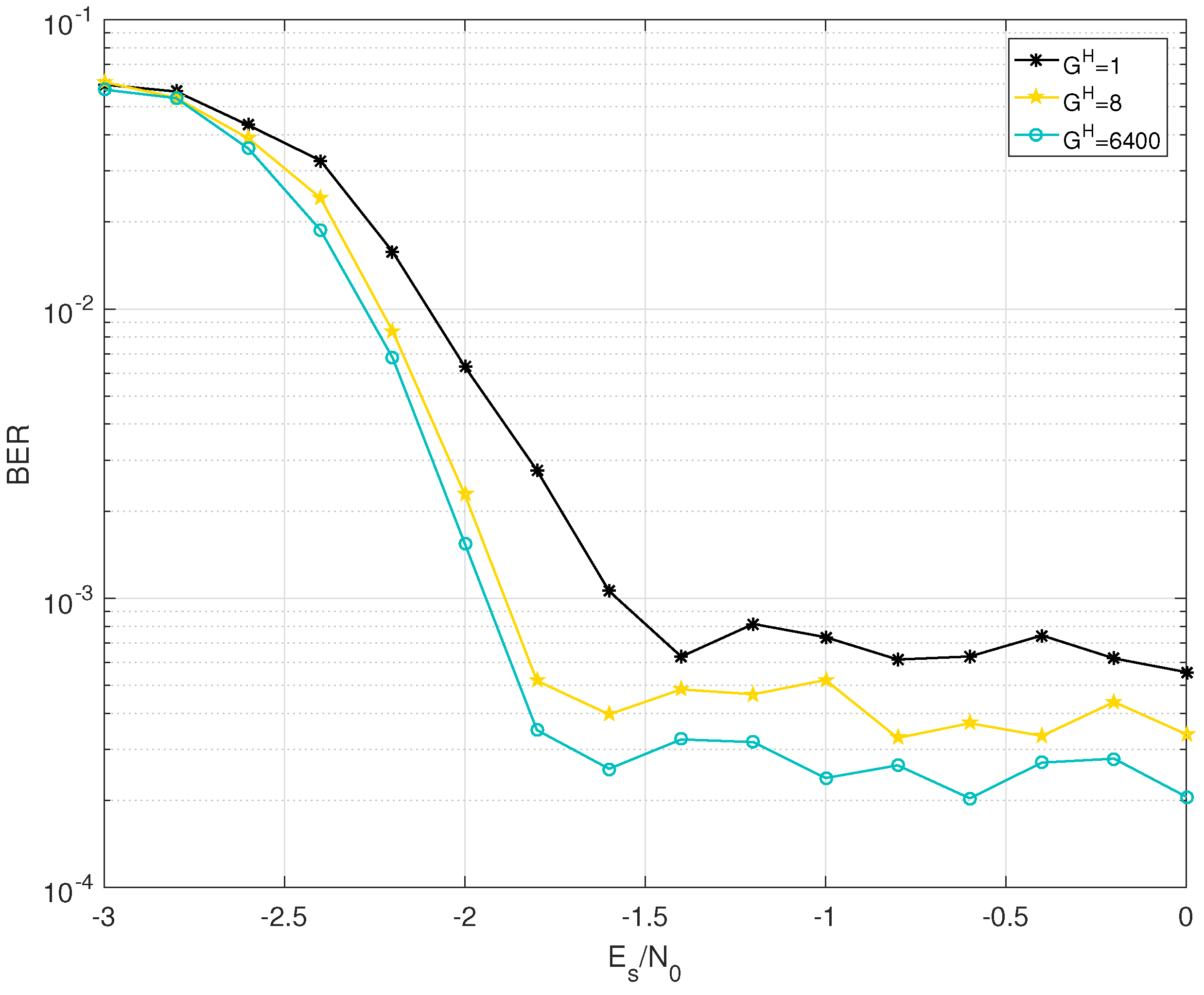
5.1. BER Performance
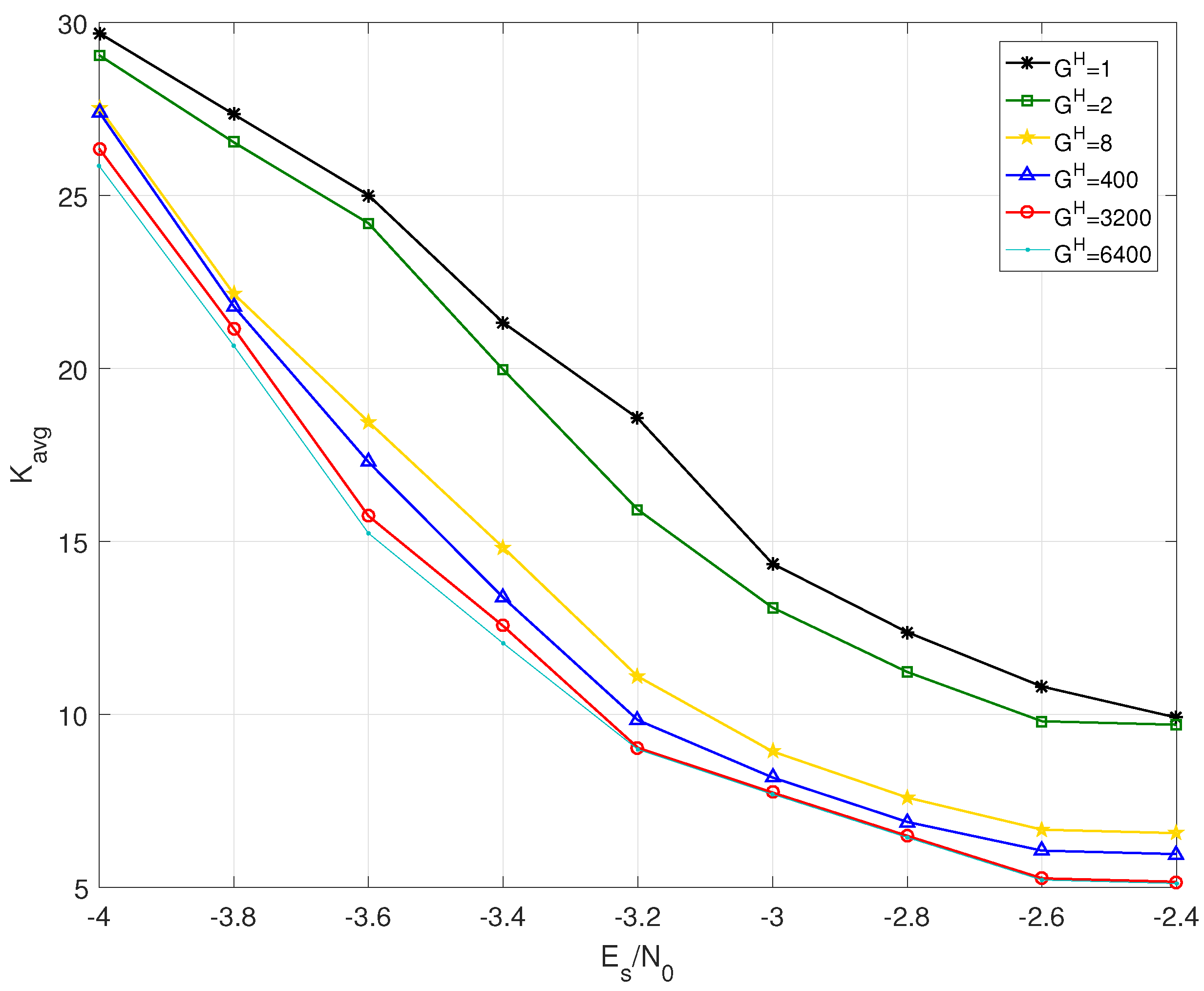
5.2. Decoding Complexity and Latency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AWGN | additive white Gaussian noise |
| APP | a posteriori probability |
| BER | bit error rate |
| BP | belief propagation |
| CNs | check nodes |
| C2V | check-to-variable |
| D-LDPC | double low-density parity-check |
| EXIT | extrinsic information transfer |
| IBP | iterative belief propagation |
| IoT | Internet of things |
| JBP | joint belief propagation |
| JEXIT | joint extrinsic information transfer |
| JPEXIT | joint protograph EXIT |
| JGSSD | joint group shuffled scheduling decoding |
| JSCC | joint source-channel coding |
| JSEXIT | joint shuffled EXIT |
| LLR | log-likelihood-ratio |
| MI | mutual information |
| PEG | progressive edge growth |
| SPEXIT | source protograph EXIT |
| SSSD | separated shuffled scheduling decoding |
| SWD | sliding window decoding |
| V2C | variable-to-check |
| VNs | variable nodes |
References
- Chen, Q.; Wang, L.; Chen, P.; Chen, G. Optimization of component elements in integrated communication systems: A survey. IEEE Commun. Surv. Tutor. 2019, 3, 2977–2999. [Google Scholar] [CrossRef]
- Fresia, M.; Perez-cruz, F.; Poor, H.V.; Verdu, S. Joint source and channel coding. IEEE Signal Process. Mag. 2010, 6, 104–113. [Google Scholar] [CrossRef]
- Bi, C.; Liang, J. Joint source-channel coding of jpeg 2000 image transmission over two-way multi-relay networks. IEEE Trans. Image Process. 2017, 7, 3594–3608. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Lin, C.; Zhang, X.; Guo, Z. A novel JSCC scheme for UEP-based scalable video transmission over MIMO systems. IEEE Trans. Circuits Syst. Video Technol. 2015, 6, 1002–1015. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Sun, Y.; Guo, S.; Wu, J. Green industrial Internet of Things architecture: An energy-efficient perspective. IEEE Commun. Mag. 2016, 12, 48–54. [Google Scholar] [CrossRef]
- Zhang, J.; Fossorier, M.P.C. Shuffled iterative decoding. IEEE Trans. Commun. 2005, 2, 209–213. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, L.; Hong, S.; Lau, F.; Sham, C. Joint shuffled scheduling decoding algorithm for DP-LDPC codes-based JSCC systems. IEEE Wirel. Commun. Lett. 2019, 6, 1696–1699. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, L.; Hong, S.; Chen, G. Generalized joint shuffled scheduling decoding algorithm for the JSCC system based on protograph-LDPC codes. IEEE Access 2021, 9, 128372–128380. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Chen, P. A joint source and channel coding scheme based on simple protograph structured codes. In Proceedings of the Symposium of on Communications and Information Technologies (ISCIT), Sydney, Australia, 2–5 October 2012; pp. 65–69. [Google Scholar]
- Lin, H.; Lin, S.; Abdel-Ghaffar, K. Integrated code design for a joint source and channel LDPC coding scheme. In Proceedings of the IEEE Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 12–17 February 2017; pp. 1–9. [Google Scholar]
- He, J.; Li, Y.; Wu, G.; Qian, S.; Xue, Q.; Matsumoto, T. Performance improvement of joint source-channel coding with unequal power allocation. IEEE Wirel. Commun. Lett. 2017, 5, 582–585. [Google Scholar] [CrossRef]
- Neto, H.; Henkel, W. Multi-edge optimization of low-density parity-check codes of joint source-channel coding. In Proceedings of the IEEE Systems, Communication and Coding (SCC), Munich, Germany, 21–24 January 2013. [Google Scholar]
- Chen, C.; Wang, L.; Xiong, Z. Matching criterion between source statistics and source coding rate. IEEE Commun. Lett. 2015, 9, 1504–1507. [Google Scholar] [CrossRef]
- Chen, Q.; Hong, S.; Chen, Y. Design of linking matrix in JSCC scheme based on double protograph LDPC codes. IEEE Access 2019, 7, 92176–92183. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L.; Liu, S. The design of protograph LDPC codes as source code in a JSCC system. IEEE Commun. Lett. 2018, 4, 672–675. [Google Scholar] [CrossRef]
- Chen, Q.; Lau, F.C.M.; Wu, H.; Chen, C. Analysis and improvement of error-floor performance for JSCC Scheme based on double protograph LDPC codes. IEEE Trans. Veh. Technol. 2020, 12, 14316–14329. [Google Scholar] [CrossRef]
- Wu, H.; Wang, L.; Hong, S.; He, J. Performance of joint source channel coding based on protograph LDPC codes over Rayleigh fading channels. IEEE Commun. Lett. 2014, 4, 652–655. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Hong, S.; Xiong, Z. Performance improvement of JSCC scheme through redesigning channel codes. IEEE Commun. Lett. 2016, 6, 1088–1091. [Google Scholar] [CrossRef]
- Hong, S.; Ke, J.; Wang, L. Global design of double protograph LDPC codes for joint source-channel coding. IEEE Commun. Lett. 2023, 2, 424–427. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Hong, S.; Chen, Y. Integrated design of JSCC scheme based on double protograph LDPC codes system. IEEE Commun. Lett. 2019, 2, 218–221. [Google Scholar] [CrossRef]
- Nguyen, T.; Nosratinia, A.; Divsalar, D. The design of rate-compatible protograph LDPC codes. IEEE Trans. Commun. 2012, 10, 2841–2850. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L.; Lau, F. Joint optimization of protograph LDPC code pair for joint source and channel coding. IEEE Trans. Commum. 2018, 8, 3255–3267. [Google Scholar] [CrossRef]
- Liu, S.; Chen, C.; Wang, L.; Hong, S. Edge connection optimization for JSCC system based on DP-LDPC codes. IEEE Wirel. Commun. Lett. 2019, 4, 996–999. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Chen, J.; Hong, S. Joint component design for the JSCC system based on DP-LDPC codes. IEEE Trans. Commum. 2020, 9, 5808–5818. [Google Scholar] [CrossRef]
- Neto, H.V.B.; Henkel, W. Information shortening for joint source-channel coding schemes based on low-density parity-check codes. In Proceedings of the 8th International Symposium on Turbo Codes and Iterative Information Processing (ISTC), Bremen, Germany, 18–22 August 2014; pp. 1–5. [Google Scholar]
- Chen, Q.; Wang, L. Design and analysis of joint source channel coding schemes over non-standard coding channels. IEEE Trans. Veh. Technol. 2020, 8, 5369–5380. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, L.; Chen, G. Joint coding/decoding optimization for DC-BICM system: Collaborative design. IEEE Commun. Lett. 2021, 8, 2487–2491. [Google Scholar] [CrossRef]
- Song, D.; Ren, J.; Wang, L.; Chen, G. Designing a common DP-LDPC codes pair for variable on-body channels. IEEE Trans. Wirel. Commun. 2022, 11, 9596–9609. [Google Scholar] [CrossRef]
- Golmohammadi, A.; Mitchell, D.G.M. Concatenated spatially coupled LDPC codes with sliding window decoding for joint source—Channel coding. IEEE Trans. Commun. 2022, 2, 851–864. [Google Scholar] [CrossRef]
- Lian, Q.; Chen, Q.; Zhou, L.; He, Y.; Xie, X. Adaptive decoding algorithm with variable sliding window for double SC-LDPC coding system. IEEE Commun. Lett. 2023, 2, 404–408. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, L.; Hong, S. Joint early stopping criterions for protograph LDPC codes-based JSCC system in images transmission. Entropy 2021, 23, 1392. [Google Scholar] [CrossRef]
- Deng, L.; Shi, Z.; Li, O.; Ji, J. Joint coding and adaptive image transmission scheme based on DP-LDPC codes for IoT scenarios. IEEE Access 2019, 7, 18437–18449. [Google Scholar] [CrossRef]
- Hu, X.-Y.; Eleftheriou, E.; Arnold, D.M. Regular and irregular progressive edge—Growth Tanner graphs. IEEE Trans. Inf. Theory 2005, 1, 386–398. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, L.; Hong, S.; Chen, G. Design of code pair for protograph—LDPC codes—Based JSCC system with joint shuffled scheduling decoding algorithm. IEEE Commun. Lett. 2021, 12, 3770–3774. [Google Scholar] [CrossRef]



| IBP (e.g., [2]) | SSSD [7,8] | JGSSD | |
|---|---|---|---|
| Decoding order | Parallel | Serial | Parallel and Sequential |
| EXIT algorithm | ∖ | only for algorithm SSSD with the case | both for the SSSD and JGSSD with the case and |
| Complexity | High | Low | Adaptive |
| Latency | Low | High | Adaptive |
| Adaptive judgement | No | No | Yes |
| 0.04 | 0.07 | ||
|---|---|---|---|
| 0.072 | dB | dB | |
| 0.073 | dB | dB | |
| 0.077 | dB | dB | |
| 0.078 | dB | dB | |
| 0.079 | dB | dB | |
| 0.07 | 0.11 | ||
|---|---|---|---|
| 0.118 | dB | dB | |
| 0.119 | dB | dB | |
| 0.125 | dB | dB | |
| 0.128 | dB | dB | |
| 0.129 | dB | dB | |
| Grouping Strategy | Gain at BER = | Error Floor Level | ||
|---|---|---|---|---|
| 0 | 0 | |||
| 0.05 dB | 0.01 dB | - | - | |
| 0.08 dB | 0.12 dB | |||
| 0.18 dB | 0.18 dB | - | - | |
| 0.19 dB | 0.22 dB | - | - | |
| 0.19 dB | 0.22 dB | |||
| Grouping Strategy | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Ren, Y.; Zhou, L.; Chen, C.; Liu, S. Design and Analysis of Joint Group Shuffled Scheduling Decoding Algorithm for Double LDPC Codes System. Entropy 2023, 25, 357. https://doi.org/10.3390/e25020357
Chen Q, Ren Y, Zhou L, Chen C, Liu S. Design and Analysis of Joint Group Shuffled Scheduling Decoding Algorithm for Double LDPC Codes System. Entropy. 2023; 25(2):357. https://doi.org/10.3390/e25020357
Chicago/Turabian StyleChen, Qiwang, Yanzhao Ren, Lin Zhou, Chen Chen, and Sanya Liu. 2023. "Design and Analysis of Joint Group Shuffled Scheduling Decoding Algorithm for Double LDPC Codes System" Entropy 25, no. 2: 357. https://doi.org/10.3390/e25020357
APA StyleChen, Q., Ren, Y., Zhou, L., Chen, C., & Liu, S. (2023). Design and Analysis of Joint Group Shuffled Scheduling Decoding Algorithm for Double LDPC Codes System. Entropy, 25(2), 357. https://doi.org/10.3390/e25020357










