Adaptive Bit-Labeling Design for Probabilistic Shaping Based on Residual Source Redundancy
Abstract
1. Introduction
- By studying the effects of bit-labeling in JSCCM systems, it is found that good bit-labelings for different source codes or different source probabilities could be different.
- Based on the achievable system rate analysis, a new shaping scheme for the JSCCM system is proposed by optimizing the bit-labeling.
- In contrast to the fixed Gray labeling [16], the adaptive design of bit-labelings for the JSCCM system is proposed according to the source codes and the source probabilities. Since it is much simpler to switch between labelings than to optimize the source-channel code pairs for different source probabilities, it is attractive for systems with changing source statistics.
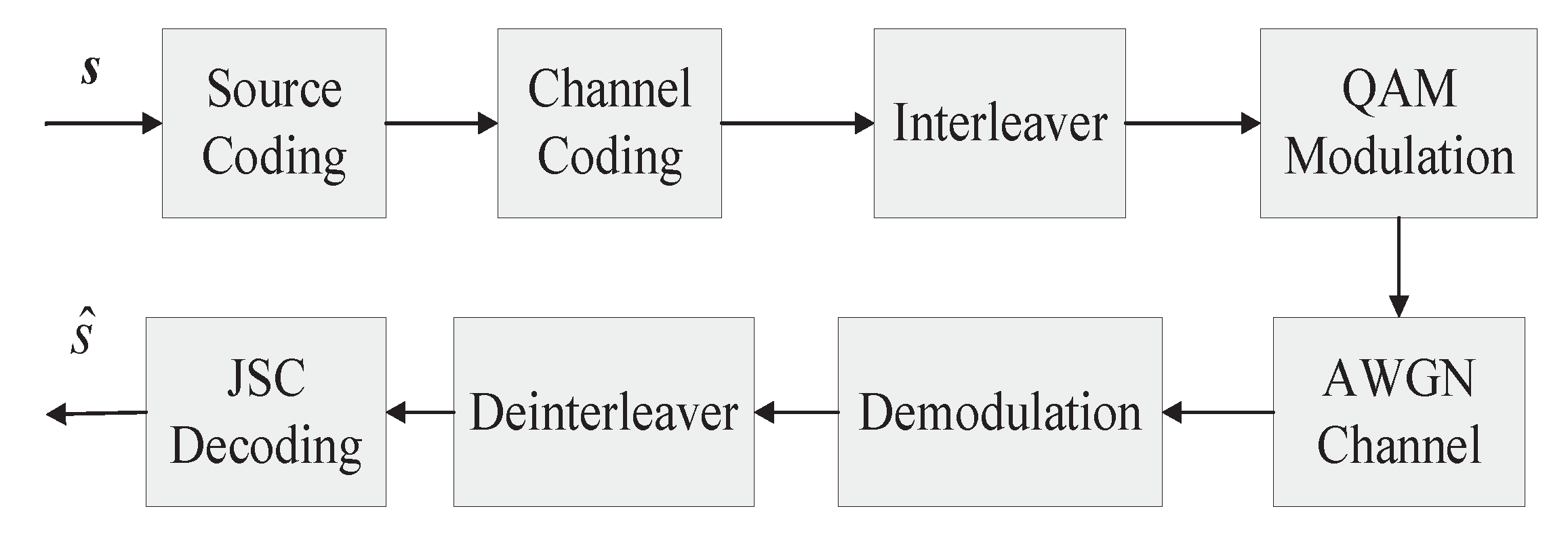
2. System Model
3. Analysis and Design of Bit-Labeling
3.1. Effects of Bit-Labelings
3.2. An Adaptive Design Scheme of Bit-Labeling
| Algorithm 1 Adaptive Bit-Labeling Design |
Require:
|
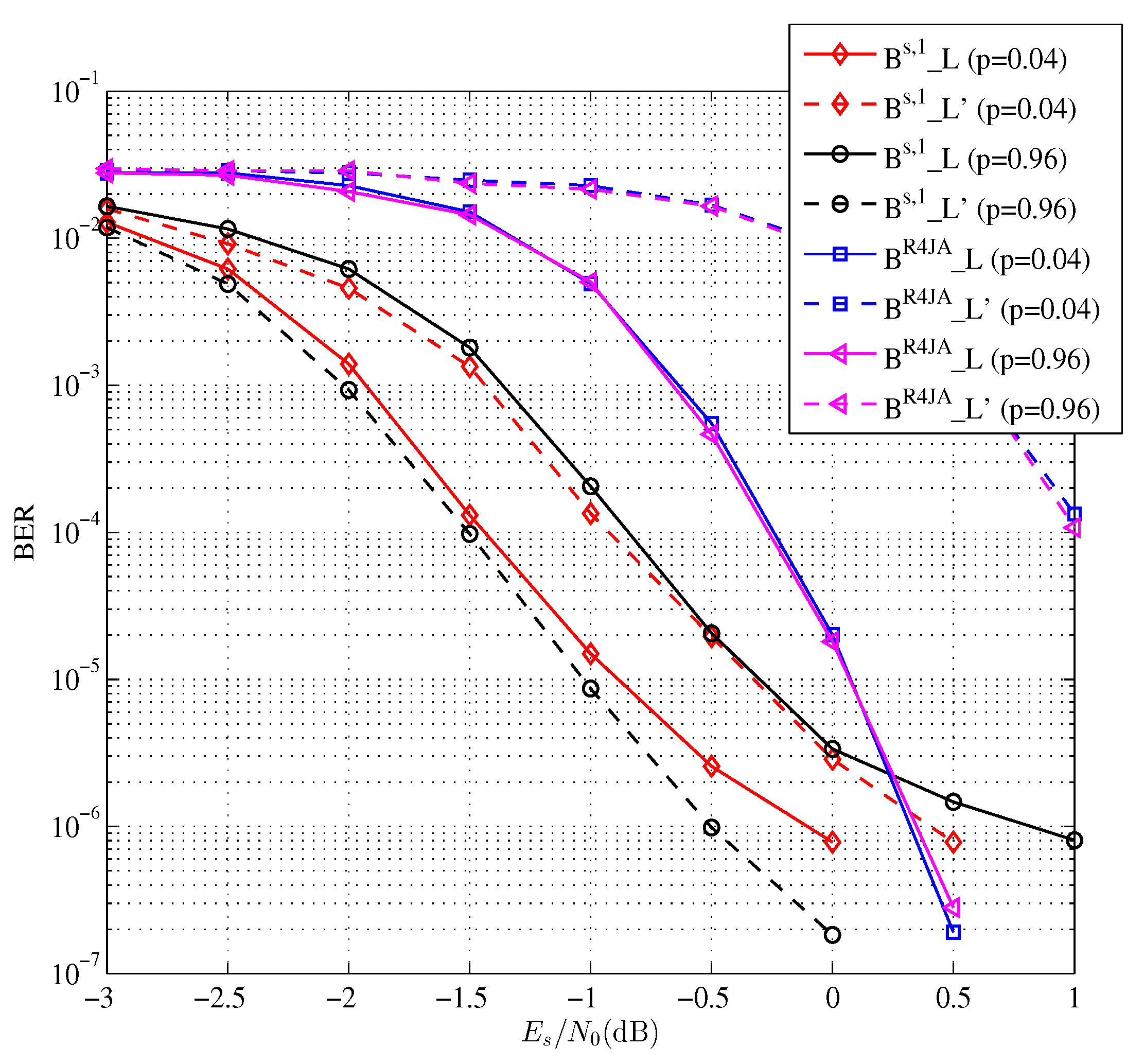
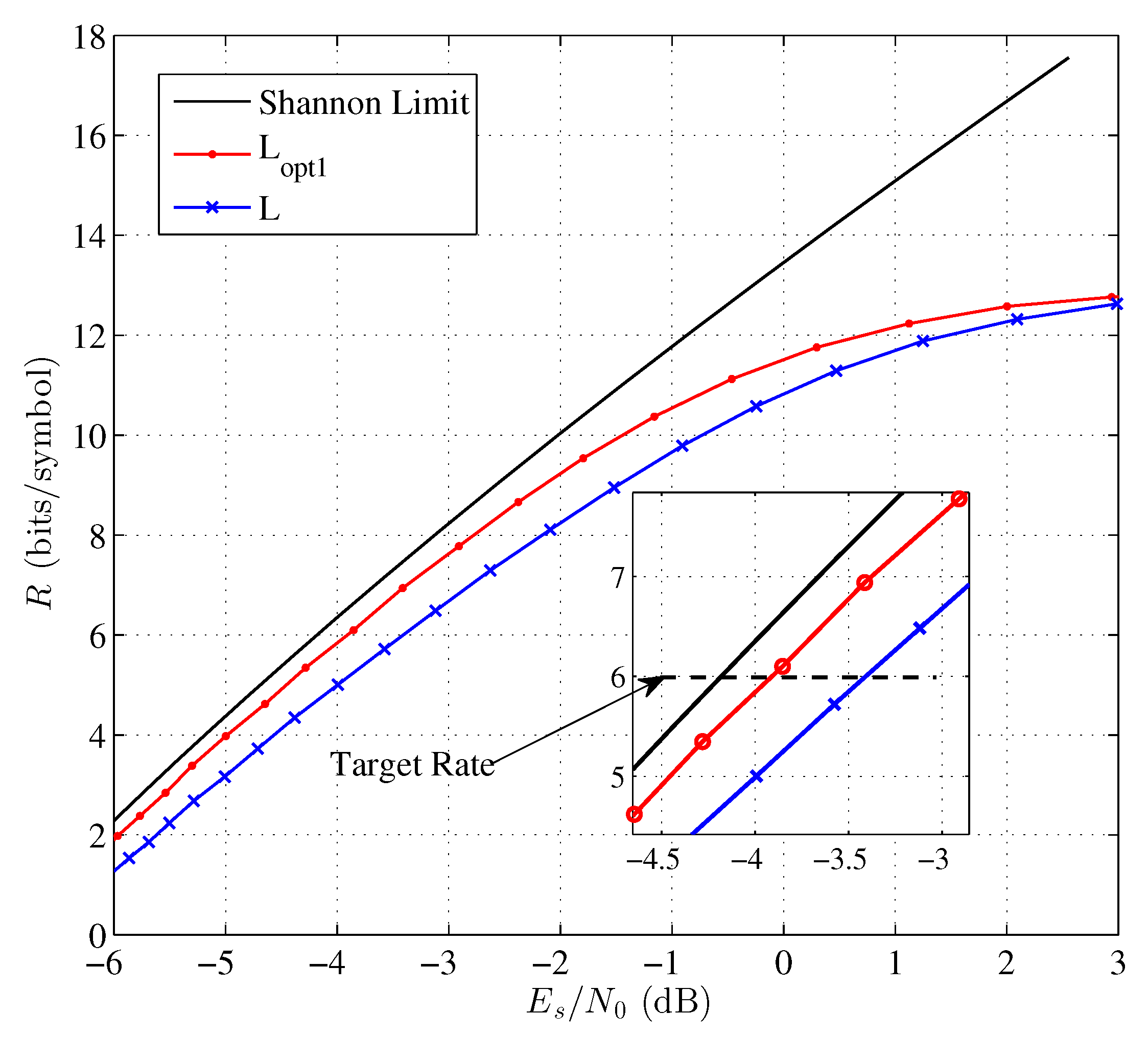
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | Additive white Gaussian noise |
| BER | Bit error rate |
| BICM | Bit interleaved coded modulation |
| DM | Distribution matcher |
| JSCC | Joint source-channel coding |
| JSCCM | Joint source-channel coded modulation |
| PAS | Probabilistic amplitude shaping |
| PEG | Progressive edge growth |
| QAM | Quadrature amplitude modulation |
References
- Caire, G.; Taricco, G.; Biglieri, E. Bit-interleaved coded modulation. IEEE Trans. Inf. Theory 1998, 3, 927–946. [Google Scholar] [CrossRef]
- Forney, G.D.; Gallager, R.G.; Lang, G.; Longstaff, F.; Qureshi, S. Efficient modulation for band-limited channels. IEEE J. Sel. Areas Commun. 1984, 5, 632–647. [Google Scholar] [CrossRef]
- Böcherer, G.; Steiner, F.; Schulte, P. Bandwidth efficient and rate-matched low-density parity-check coded modulation. IEEE Trans. Commun. 2015, 12, 4651–4665. [Google Scholar] [CrossRef]
- Steiner, F.; Böcherer, G.; Liva, G. Bit-metric decoding of non-binary LDPC codes with probabilistic amplitude shaping. IEEE Commun. Lett. 2018, 11, 2210–2213. [Google Scholar] [CrossRef]
- Steiner, F.; Böcherer, G.; Liva, G. Protograph-based LDPC code design for shaped bit-metric decoding. IEEE J. Sel. Areas Commun. 2016, 2, 397–407. [Google Scholar] [CrossRef]
- Corlay, V.; Gresset, N. A simple sign-bit probabilistic shaping scheme. IEEE Commun. Lett. 2022, 4, 763–767. [Google Scholar] [CrossRef]
- Kang, W. A probabilistic shaping scheme for bit-interleaved coded modulation with iterative decoding. IEEE Commun. Lett. 2022, 11, 2517–2521. [Google Scholar] [CrossRef]
- Schulte, P.; Böcherer, G. Constant composition distribution matching. IEEE Trans. Inf. Theory. 2016, 62, 1–5. [Google Scholar] [CrossRef]
- Perkert, R.; Kaindl, M.; Hindelang, T. Iterative source and channel decoding for GSM. In Proceedings of the IEEE ICASSP, Salt Lake City, UT, USA, 7–11 May 2001; pp. 2649–2652. [Google Scholar]
- Othman, N.S.; El-Hajjar, M.; Alamri, O.; Hanzo, L. Soft-bit assisted iterative AMR-WB source-decoding and turbo-detection of channel-coded differential space-time spreading using sphere packing modulation. In Proceedings of the IEEE VTC-Spring, Dublin, Ireland, 22–25 April 2007; pp. 2010–2014. [Google Scholar]
- Kliewer, J.; Gortz, N. Iterative source-channel decoding for robust image transmission. In Proceedings of the IEEE ICASSP, Orlando, FL, USA, 13–17 May 2002; pp. 2173–2176. [Google Scholar]
- Zhu, G.; Alajaji, F. Joint Source-Channel Turbo Coding for Binary Markov Sources. IEEE Trans. Signal Process. 2006, 5, 1065–1075. [Google Scholar]
- Nasruminallah; El-Hajjar, M.; Othman, N.S.; Quang, A.P.; Hanzo, L. Over-complete mapping aided, soft-bit assisted iterative unequal error protection H.264 joint source and channel decoding. In Proceedings of the IEEE VTC-Fall, Calgary, AB, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Chen, Q.; He, Y.; Chen, C.; Zhou, L. Optimization of protograph LDPC codes via surrogate channel for unequal power allocation. IEEE Trans. Commun. 2023. early access. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Wang, L.; He, Y.-C.; Chen, Y. Probabilistic shaping for protograph LDPC-coded modulation by residual source redundancy. IEEE Trans. Commun. 2021, 7, 4267–4281. [Google Scholar] [CrossRef]
- Agrell, E.; Lassing, J.; Ström, E.G.; Ottosson, T. On the optimality of the binary reflected Gray code. IEEE Trans. Inf. Theory 2004, 12, 3170–3182. [Google Scholar] [CrossRef]
- Nguyen, V. Design of Capacity-Approaching Protograph-Based LDPC Coding Systems. Ph.D. Dissertation, University of Texas at Dallas, Dallas, TX, USA, December 2012. [Google Scholar]
- He, J.; Li, Y.; Wu, G.; Qian, S.; Xue, Q.; Matsumoto, T. Performance improvement of joint source-channel coding with unequal power allocation. IEEE Wirel. Commun. Lett. 2017, 5, 582–585. [Google Scholar] [CrossRef]
- Divsalar, D.; Dolinar, S.; Jones, C.R.; Andrews, K. Capacity approaching protograph codes. IEEE J. Sel. Areas. Commun. 2009, 6, 876–888. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L.; Lau, F.C.M. Joint optimization of protpgraph LDPC code pair for joint source and channel coding. IEEE Trans. Commun. 2018, 8, 3255–3267. [Google Scholar] [CrossRef]
- Uchikawa, H. Design of non-precoded protograph-based LDPC codes. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2779–2783. [Google Scholar]
- Chen, Q.; Wang, L. Design and Analysis of Joint Source Channel Coding Schemes Over Non-Standard Coding Channels. IEEE Trans. Veh. Technol. 2020, 5, 5369–5380. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, L.; Cai, G.; Chen, G. Iterative receiver for M-ary DCSK systems. IEEE Trans. Commun. 2015, 11, 3929–3936. [Google Scholar] [CrossRef]
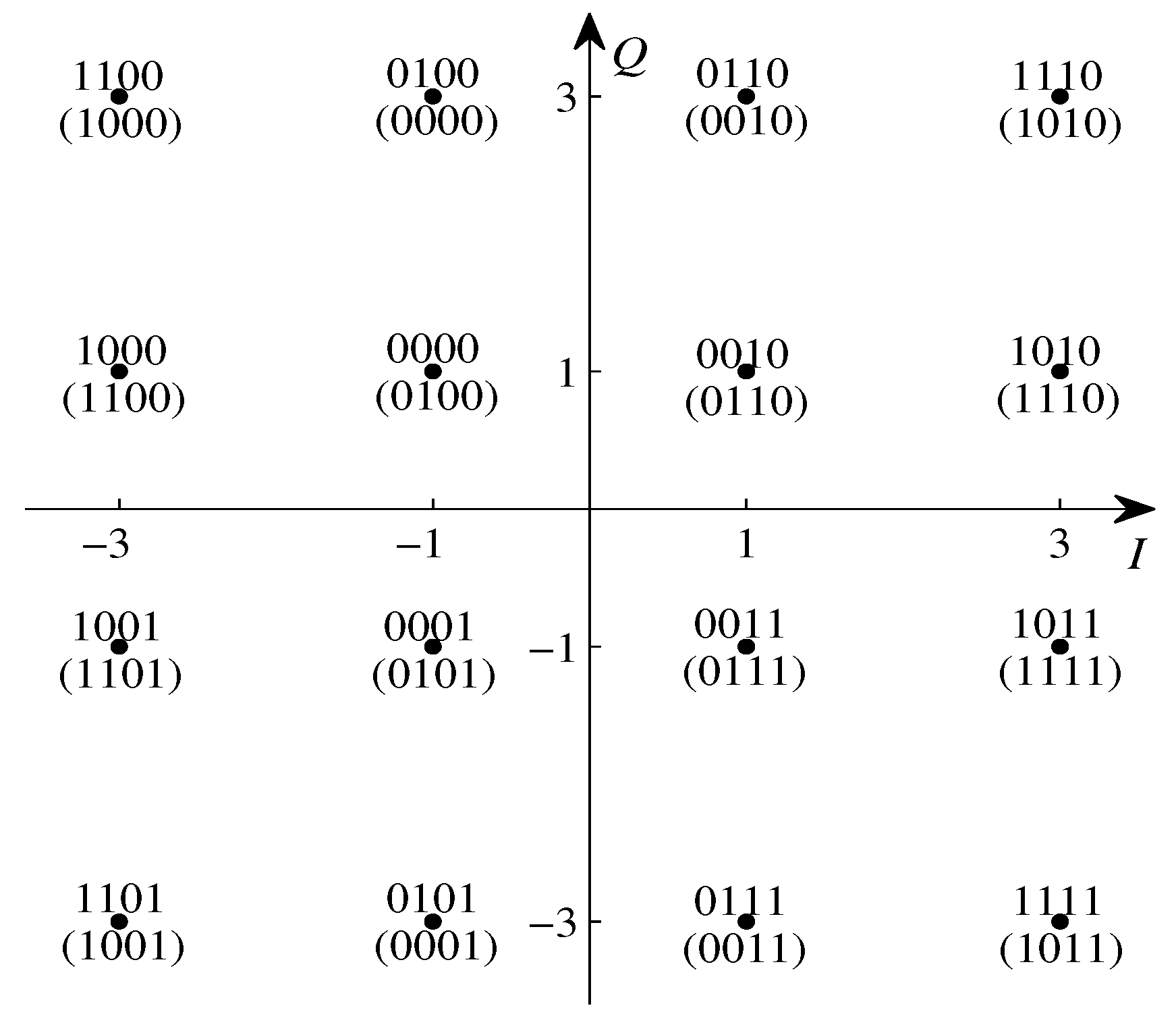
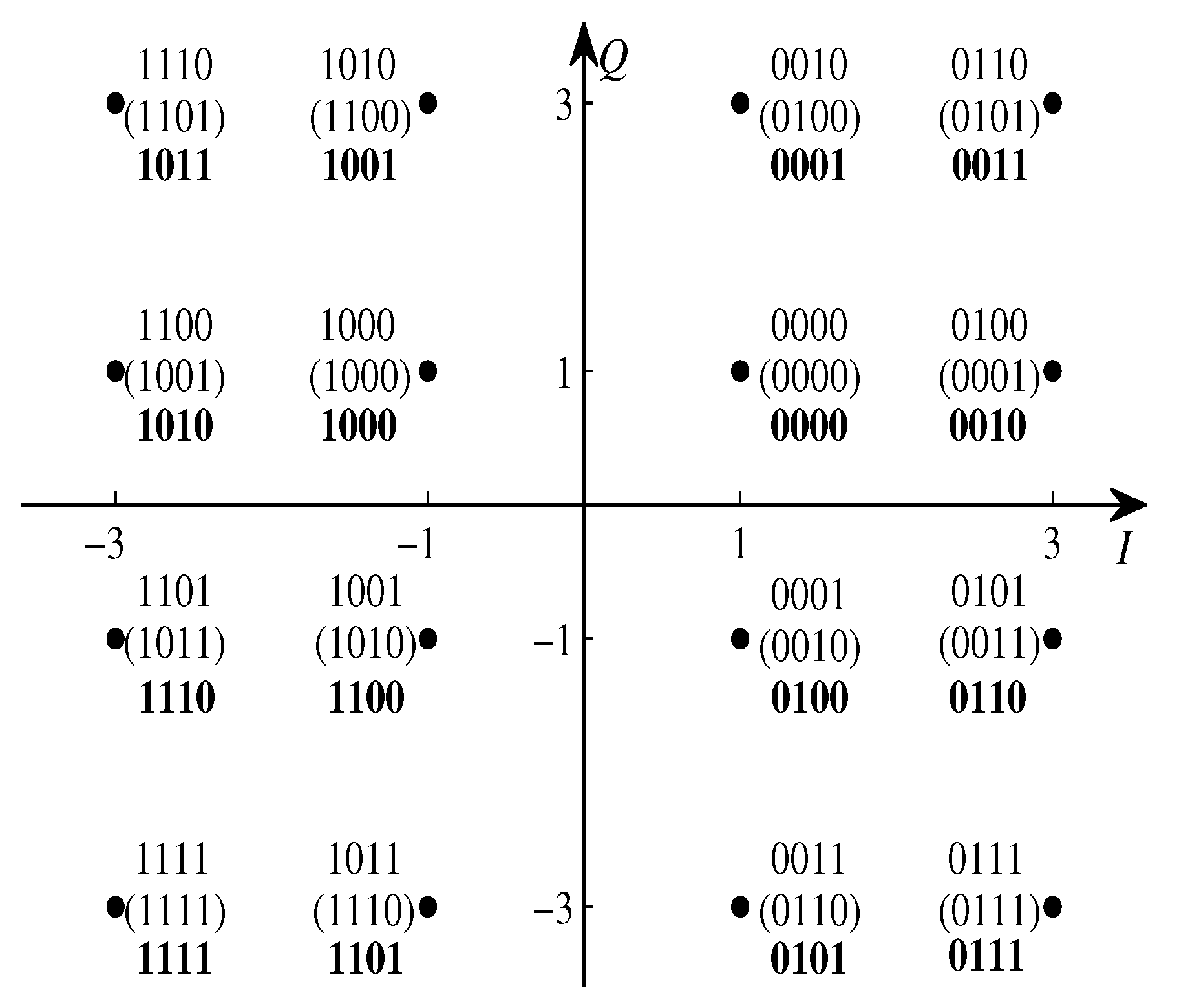
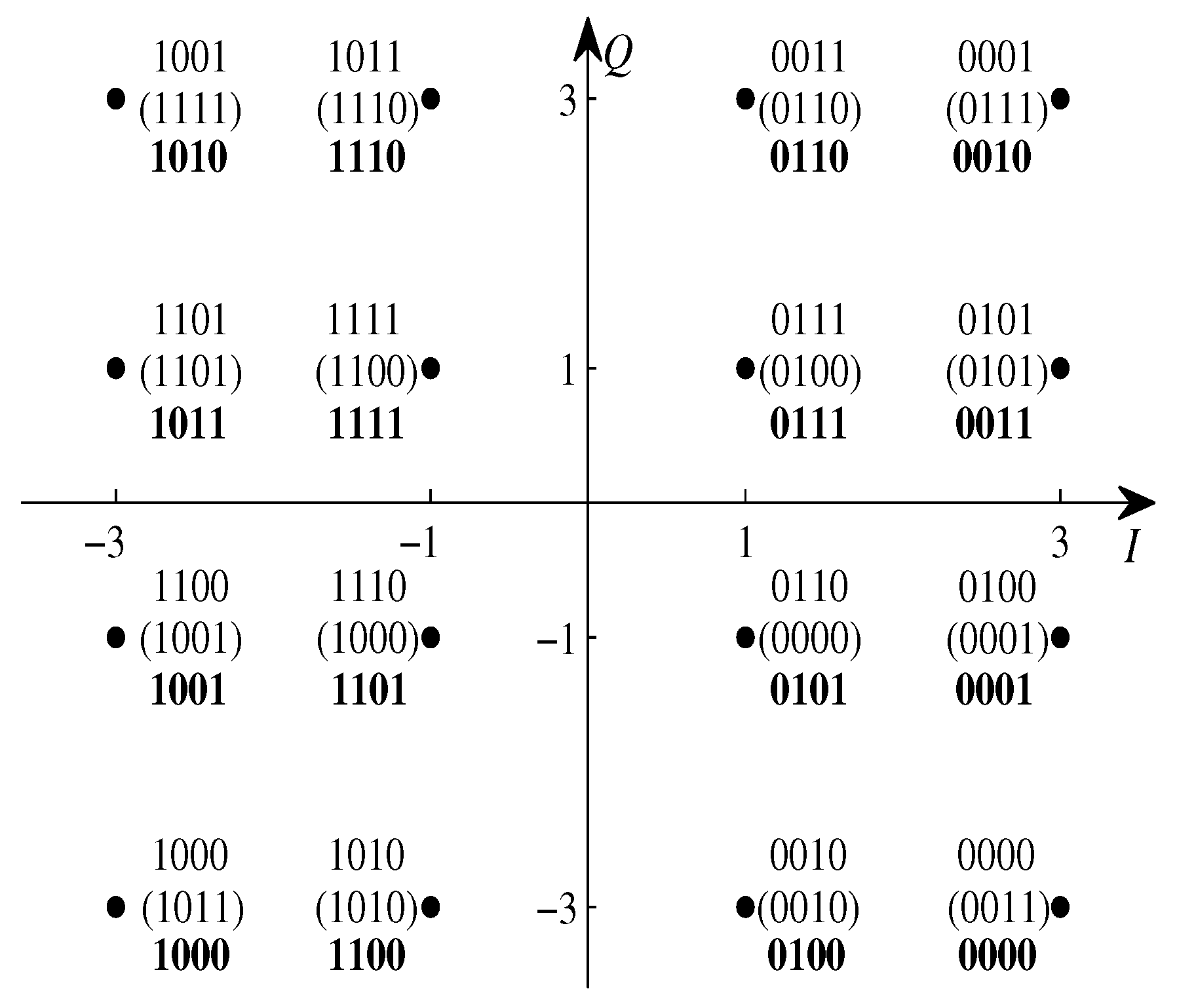
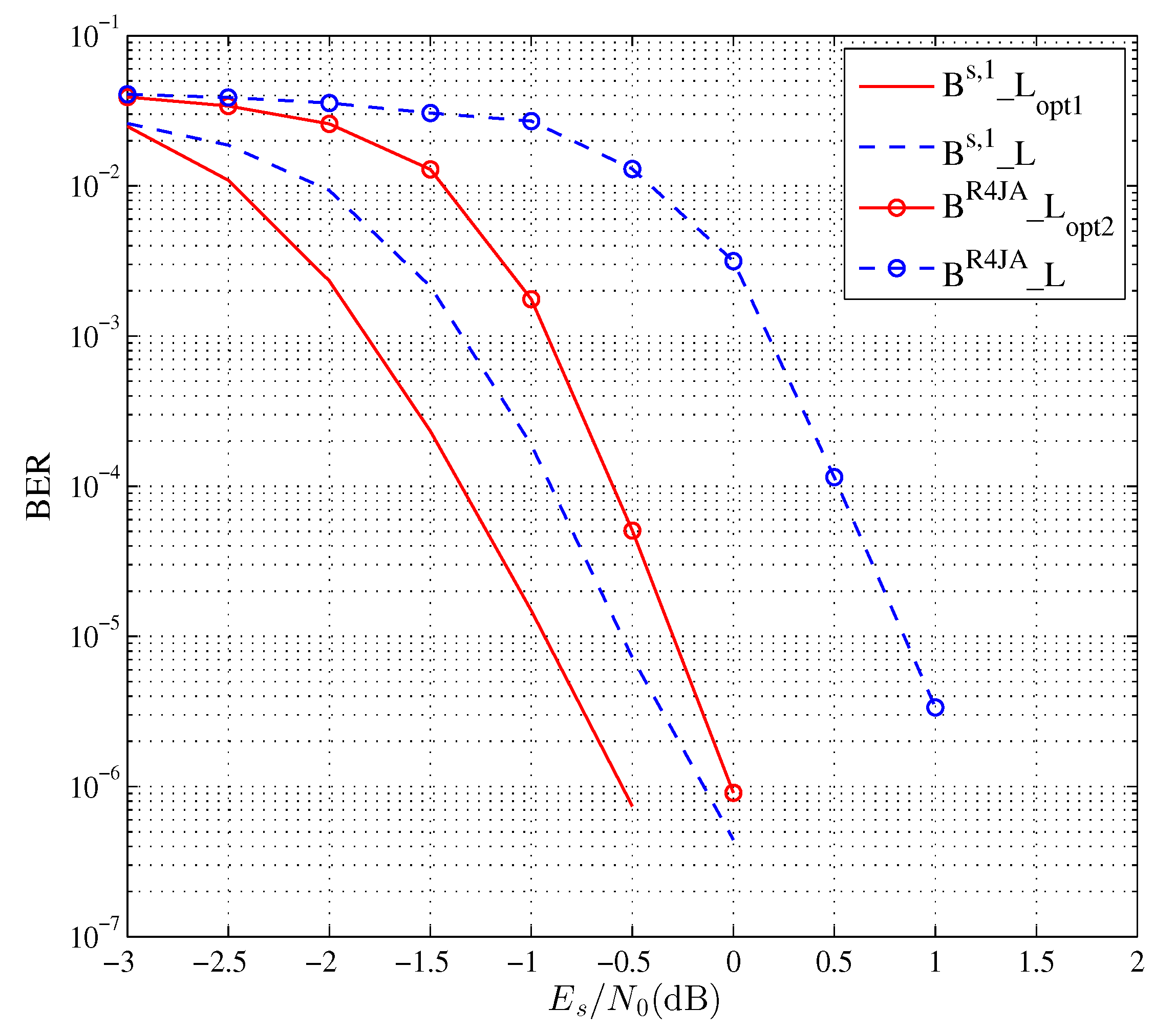
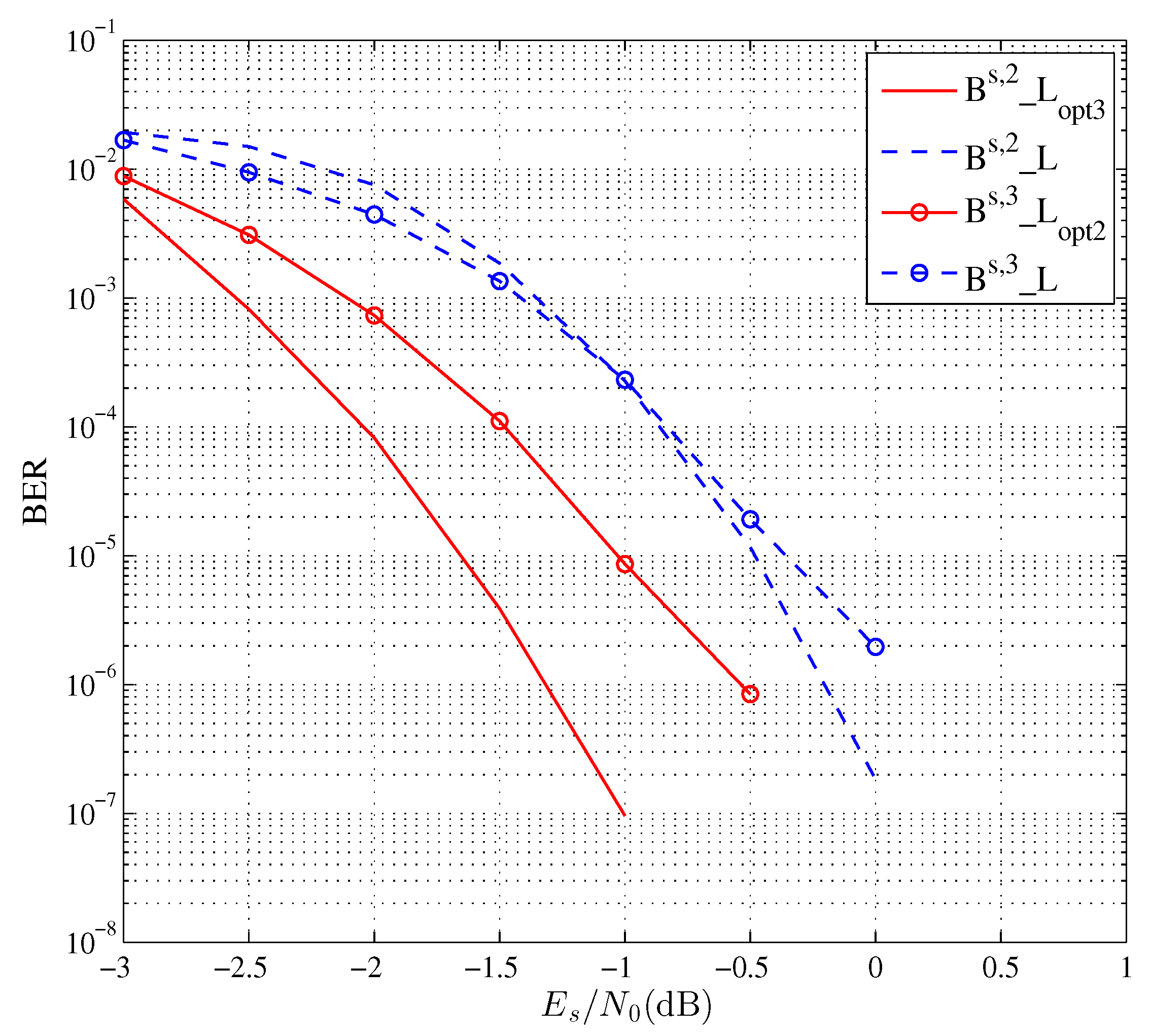
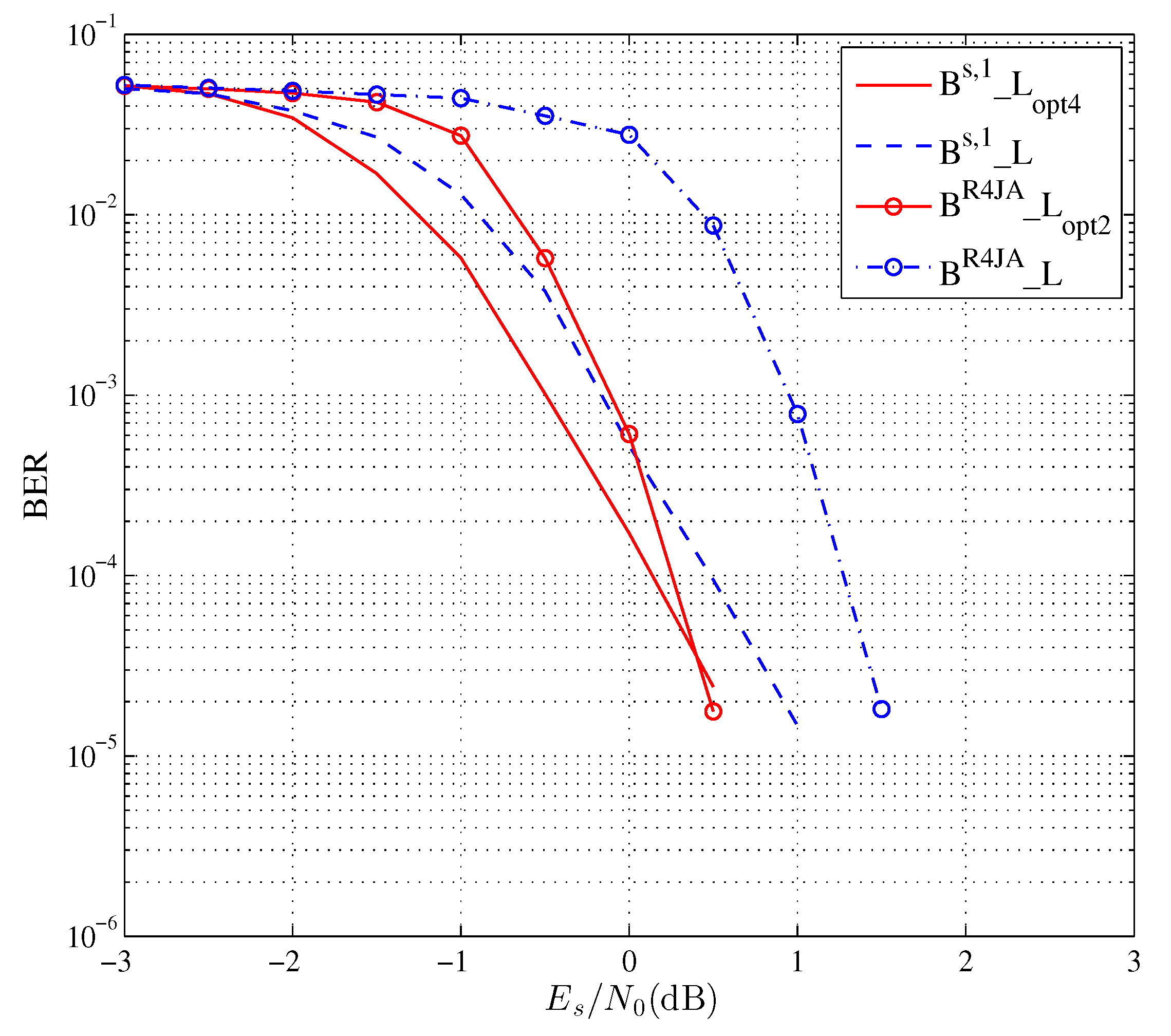
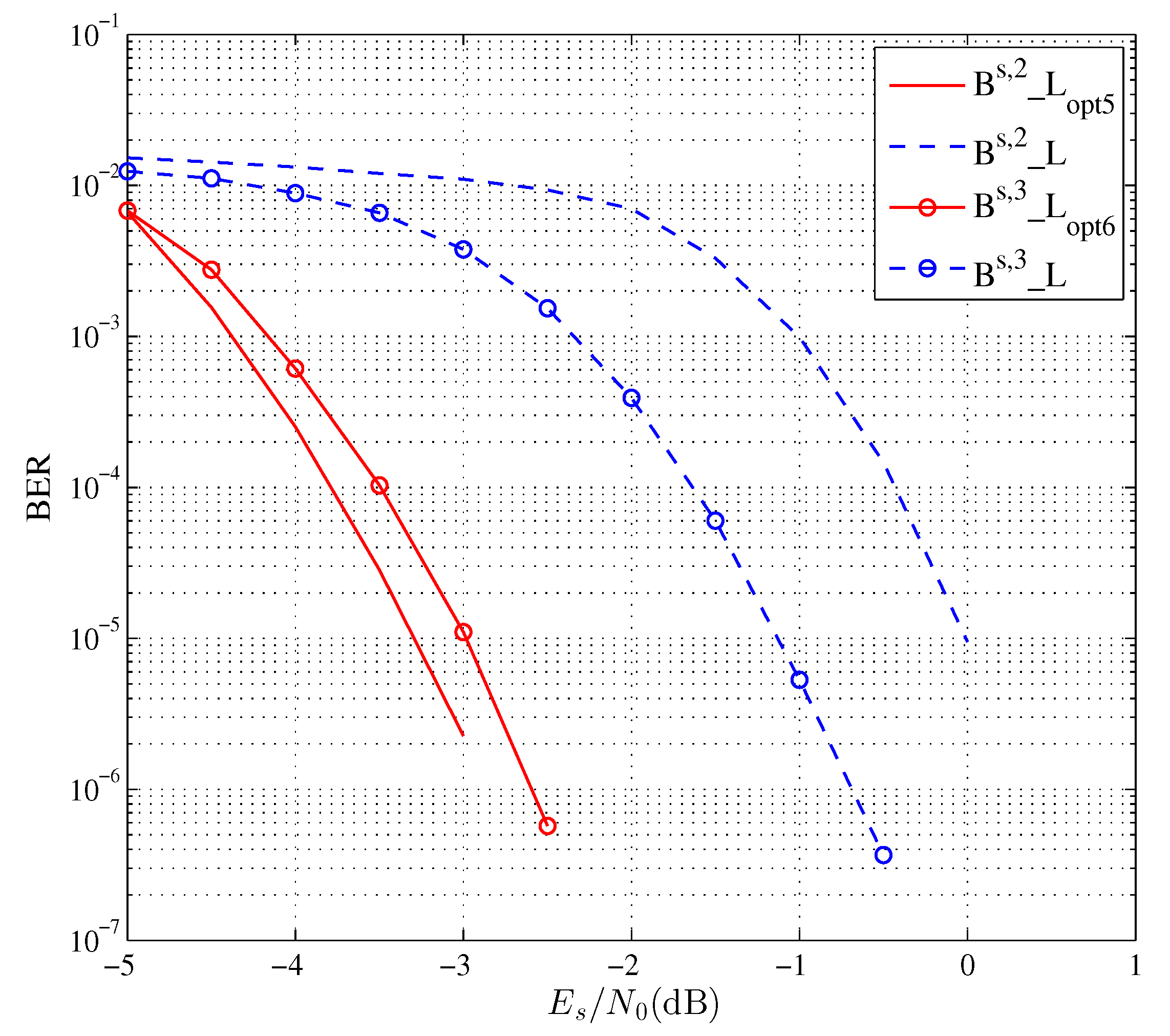
| Source Probability | Source Code | Target Rate (Bits/Symbol) | Optimized Labeling |
|---|---|---|---|
| 6 | |||
| 6 | |||
| 8 | |||
| 8 | |||
| 6 | |||
| 6 | |||
| 8 | |||
| 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Chen, Q.; Liu, S.; Zhou, L. Adaptive Bit-Labeling Design for Probabilistic Shaping Based on Residual Source Redundancy. Entropy 2023, 25, 586. https://doi.org/10.3390/e25040586
Chen C, Chen Q, Liu S, Zhou L. Adaptive Bit-Labeling Design for Probabilistic Shaping Based on Residual Source Redundancy. Entropy. 2023; 25(4):586. https://doi.org/10.3390/e25040586
Chicago/Turabian StyleChen, Chen, Qiwang Chen, Sanya Liu, and Lin Zhou. 2023. "Adaptive Bit-Labeling Design for Probabilistic Shaping Based on Residual Source Redundancy" Entropy 25, no. 4: 586. https://doi.org/10.3390/e25040586
APA StyleChen, C., Chen, Q., Liu, S., & Zhou, L. (2023). Adaptive Bit-Labeling Design for Probabilistic Shaping Based on Residual Source Redundancy. Entropy, 25(4), 586. https://doi.org/10.3390/e25040586











