Working with Convex Responses: Antifragility from Finance to Oncology
Abstract
1. Introduction: Where the Idea of Antifragility Came From
- The expectation must be conditioned on absence of “blowup”, that is, the left tail of the distribution must be constrained (see Geman et al., 2015) [4], which involves all higher moments of .
- The payoff functions are almost never monotone.
- Taking into account higher moments of the distributions is analogous to going beyond second-order effects: third, fourth, etc.
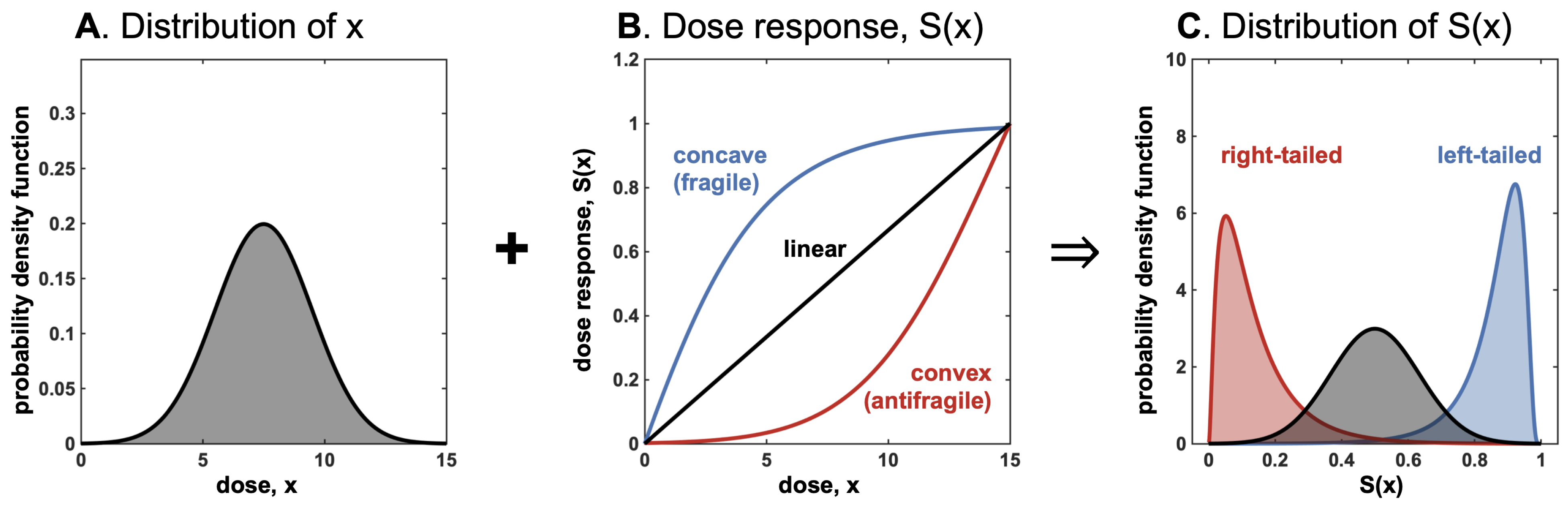
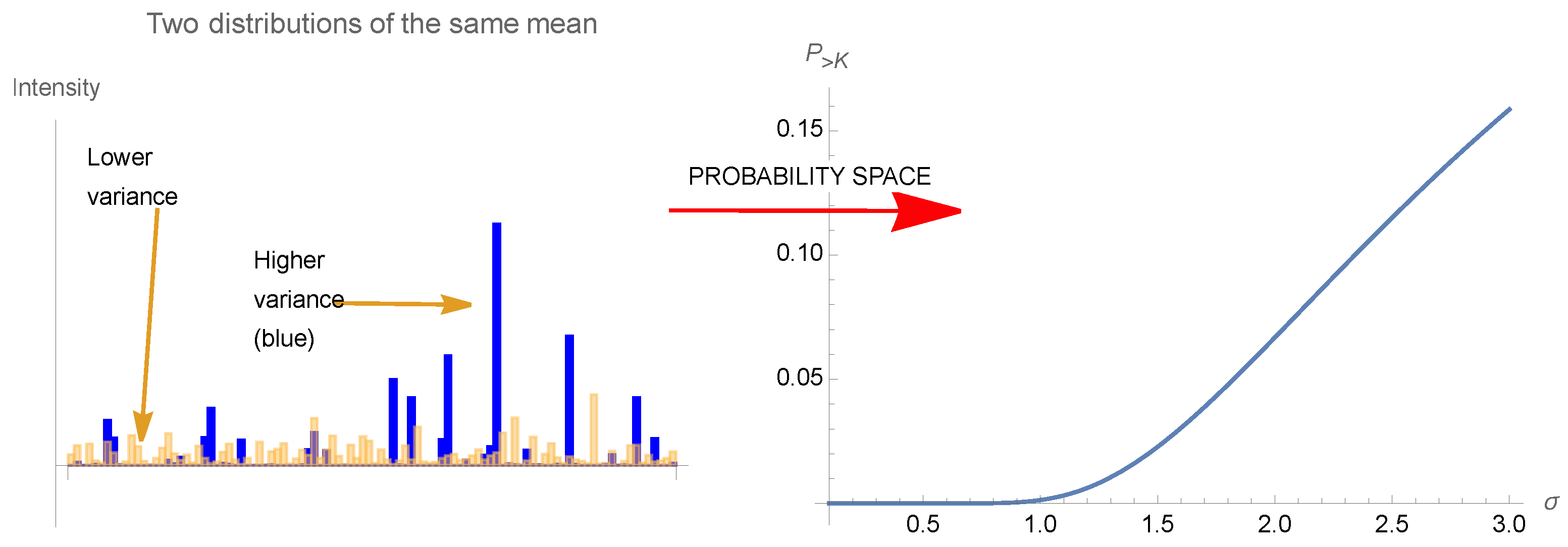
Simply, a coffee cup on a table suffers more from large deviations than from the cumulative effect of some shocks—conditional on being unbroken, it has to suffer more from “tail” events than regular ones around the center of the distribution, the ‘at-the-money’ category. This is the case of elements of nature that have survived: conditional on being in existence, then the class of events around the mean should matter considerably less than tail events, particularly when the probabilities decline faster than the inverse of the harm, which is the case of all used monomodal probability distributions. Further, what has exposure to tail events suffers from uncertainty; typically, when systems—a building, a bridge, a nuclear plant, an airplane, or a bank balance sheet—are made robust to a certain level of variability and stress but may fail or collapse if this level is exceeded, then they are particularly fragile to uncertainty about the distribution of the stressor, hence to model error, as this uncertainty increases the probability of dipping below the robustness level, bringing a higher probability of collapse. In the opposite case, the natural selection of an evolutionary process is particularly antifragile, indeed a more volatile environment increases the relative survival rate of robust species and eliminates those whose superiority over other species is highly dependent on environmental parameters.
2. Medicine and Convexity
- A convex response to energy balance over a fixed time window necessarily implies gains from intermittent fasting in some situations and under some strict conditions (that is, higher variance in the distribution of nutrients) over some range within the limits of that time window;
- The presence of metabolic problems in populations that have a steady supply of food intake, as well as evidence of human fitness to an environment that provides moderate variations in the availability of food, both necessarily imply a concave response to food within a range and time frame.
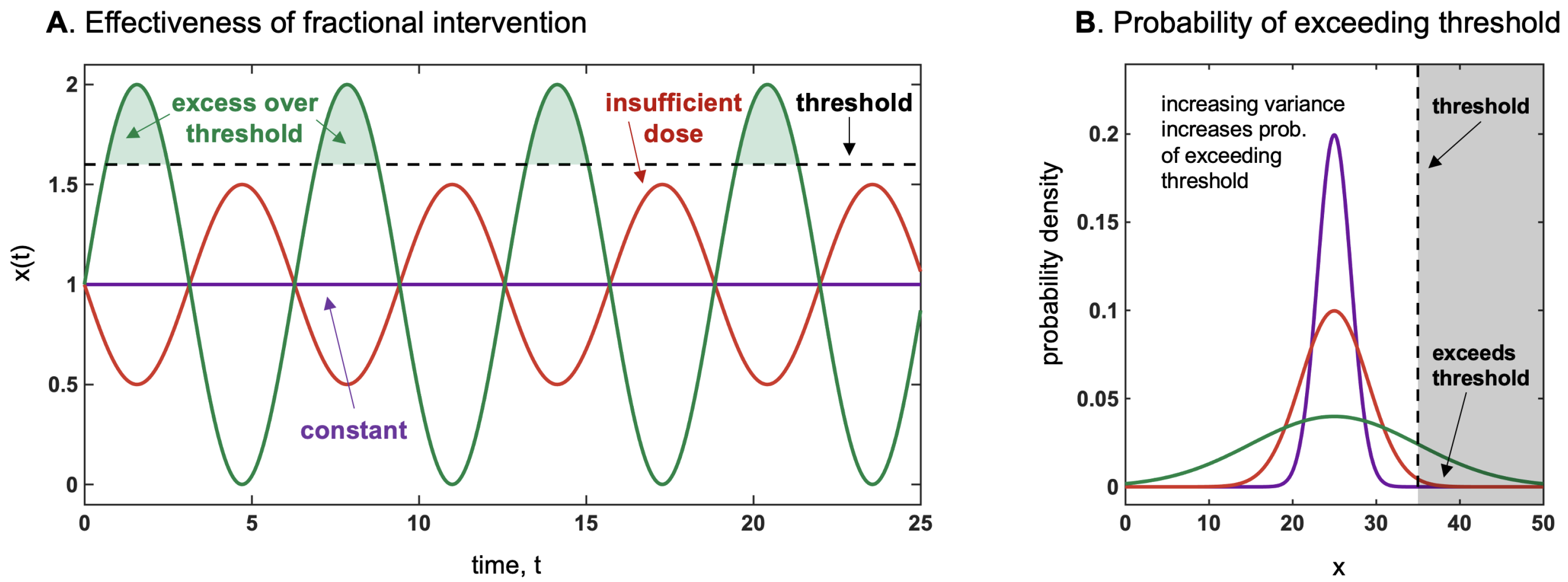
Antifragility in Treatment Scheduling
3. Antifragility in Oncology
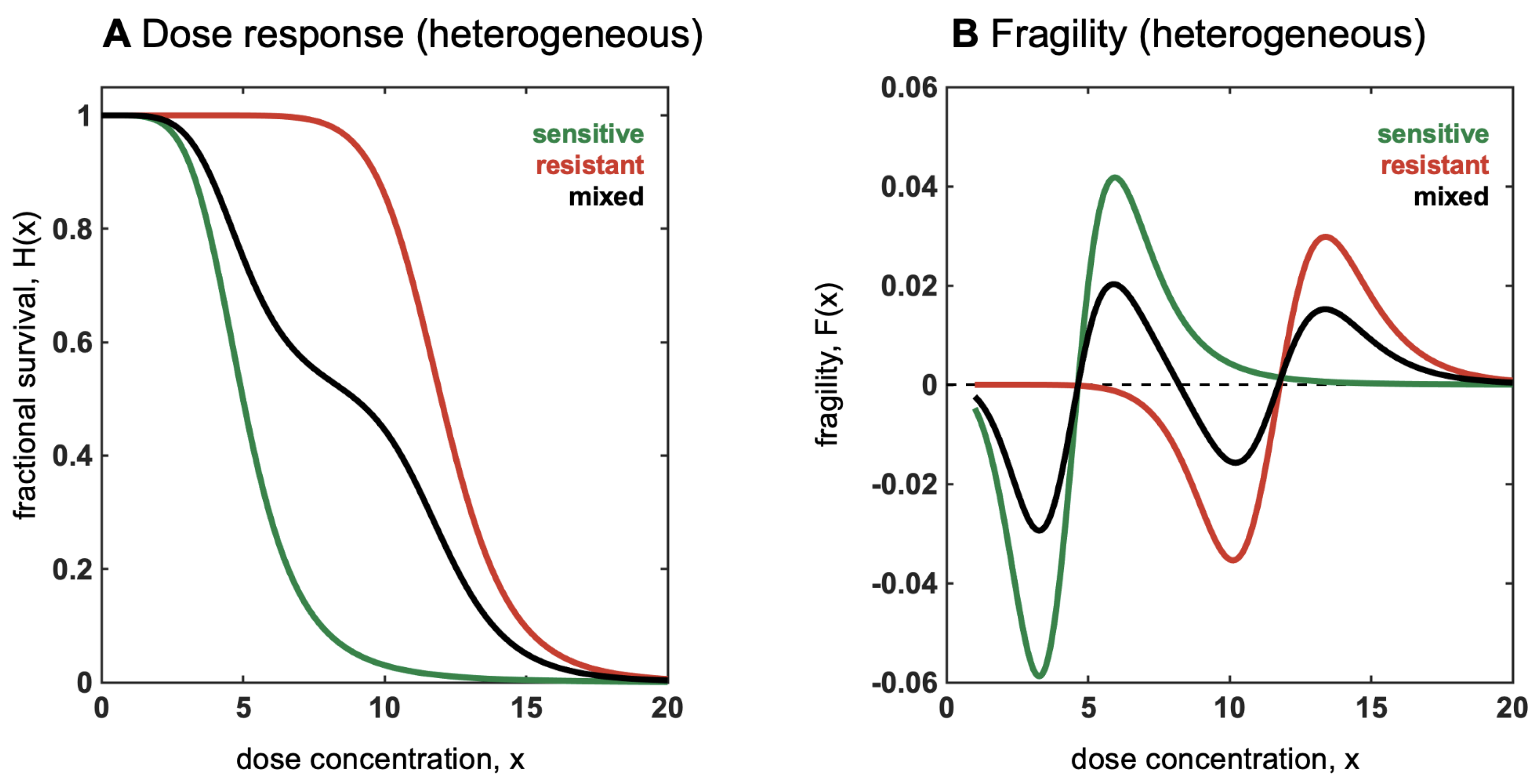
3.1. Defining (Local) Fragility in Oncology
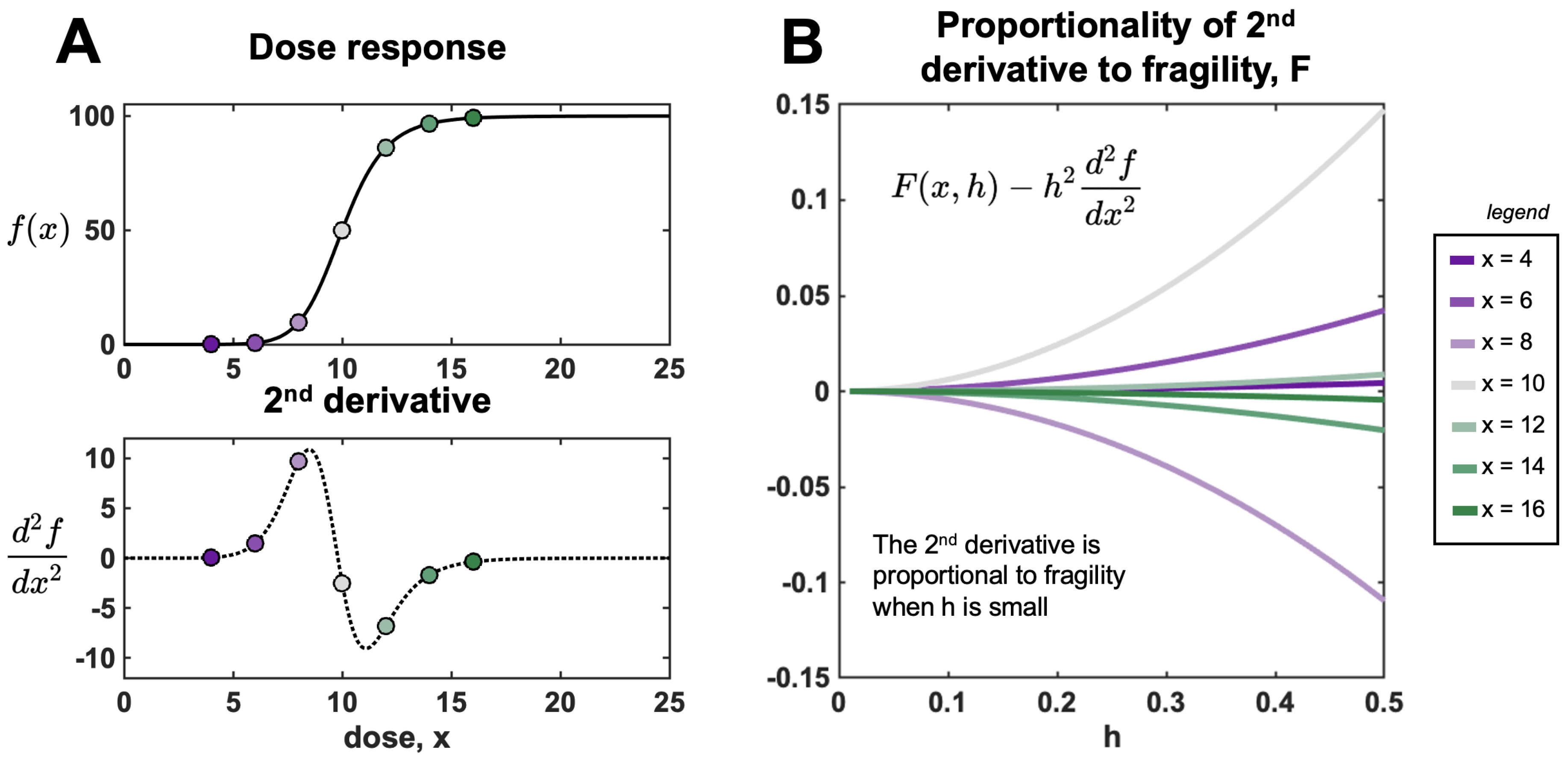
3.2. Fragility and Taylor Series Approximations
3.3. Fragility and Finite Differences
3.4. Applications of Hill Function
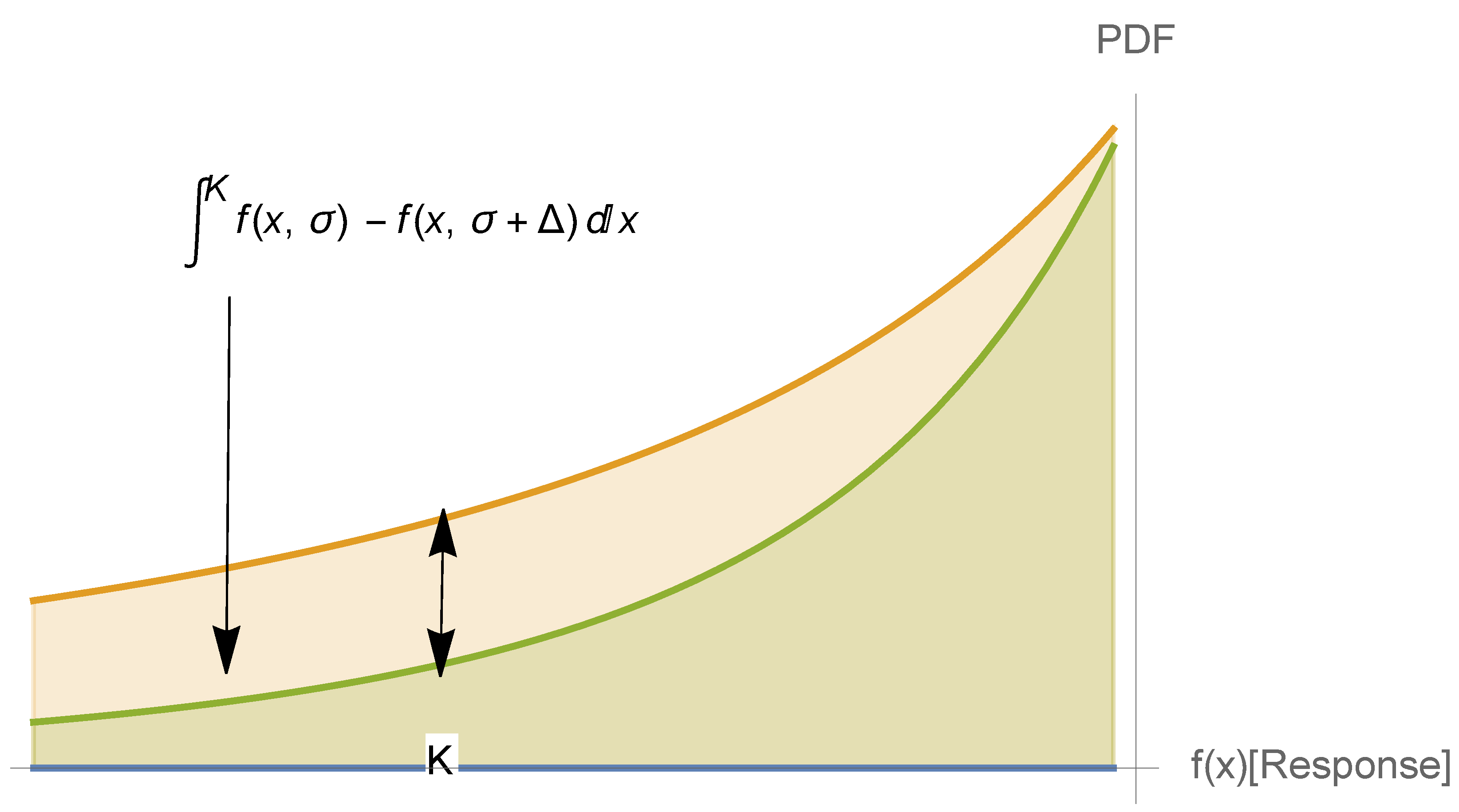
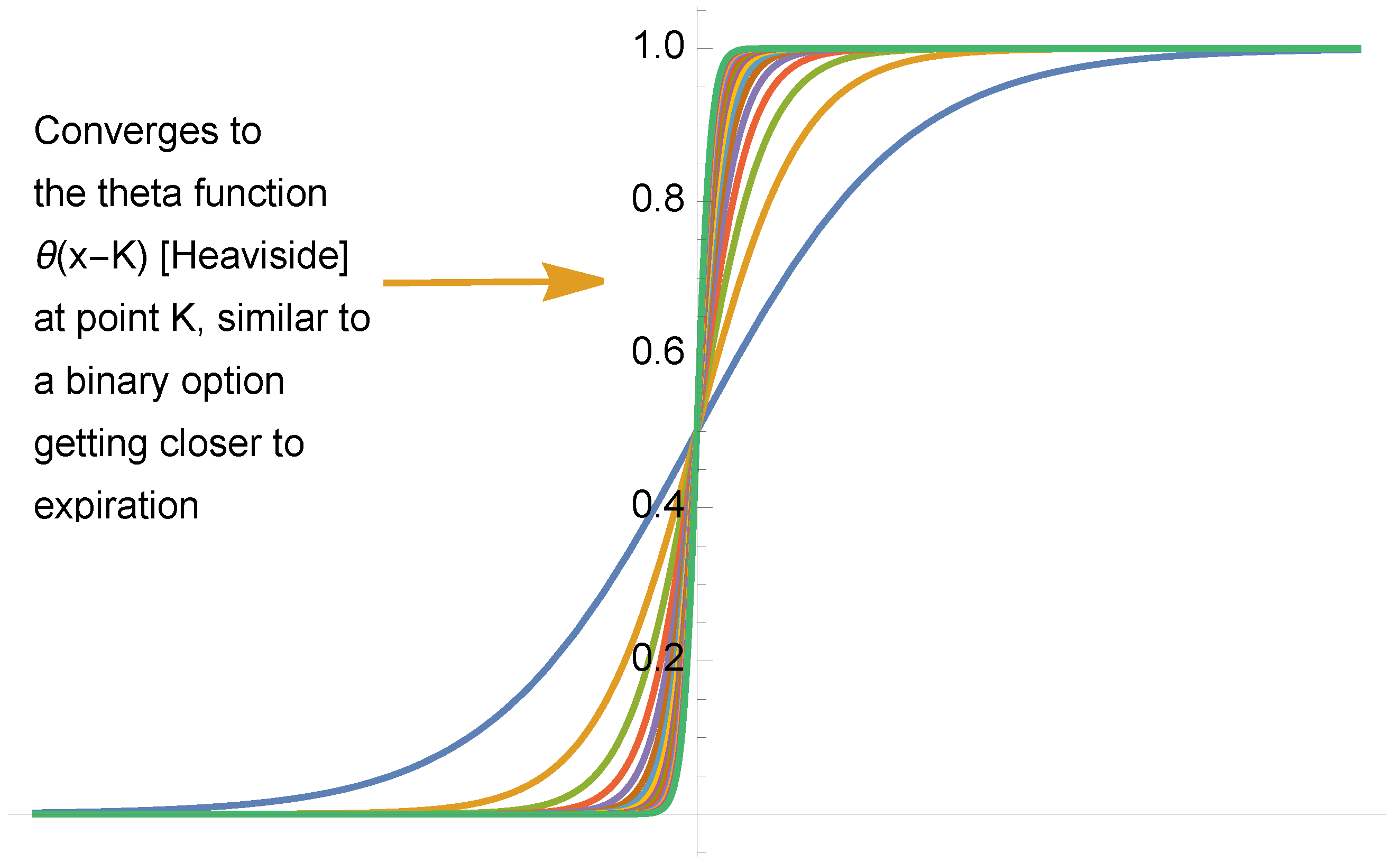
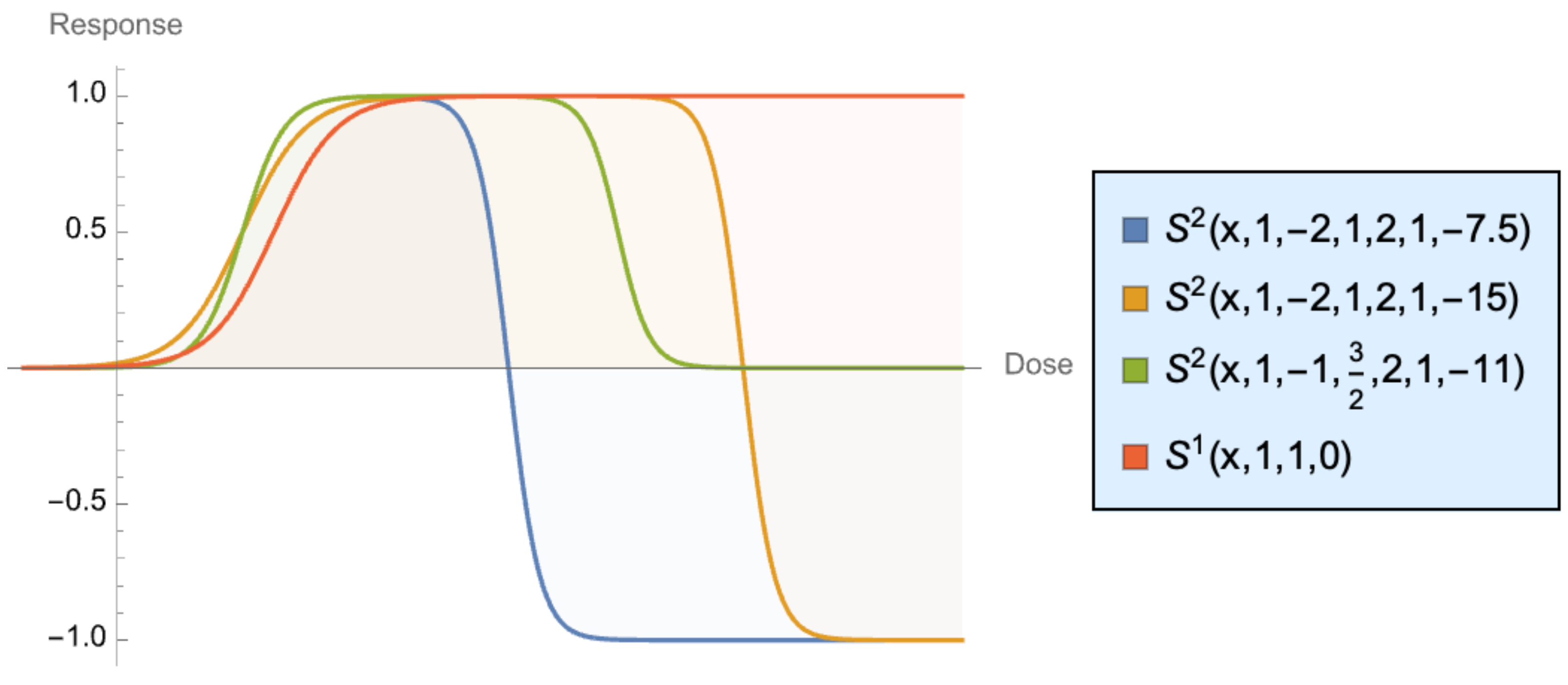
3.5. The First-Order Sigmoid Curve
- Pure sigmoids with smoothness characteristics expressed in trigonometric or exponential form, :
- Gompertz functions (a vague classification that includes above curves but can also mean special functions).
- Special functions with support in such as the error function
- Special functions with support in , such aswhere is the beta regularized function.
- Special functions with support inwhere is the gamma regularized function.
- Piecewise sigmoids, such as the CDF of the Student distribution
3.6. Some Necessary Relations Leading to a Sigmoid Curve
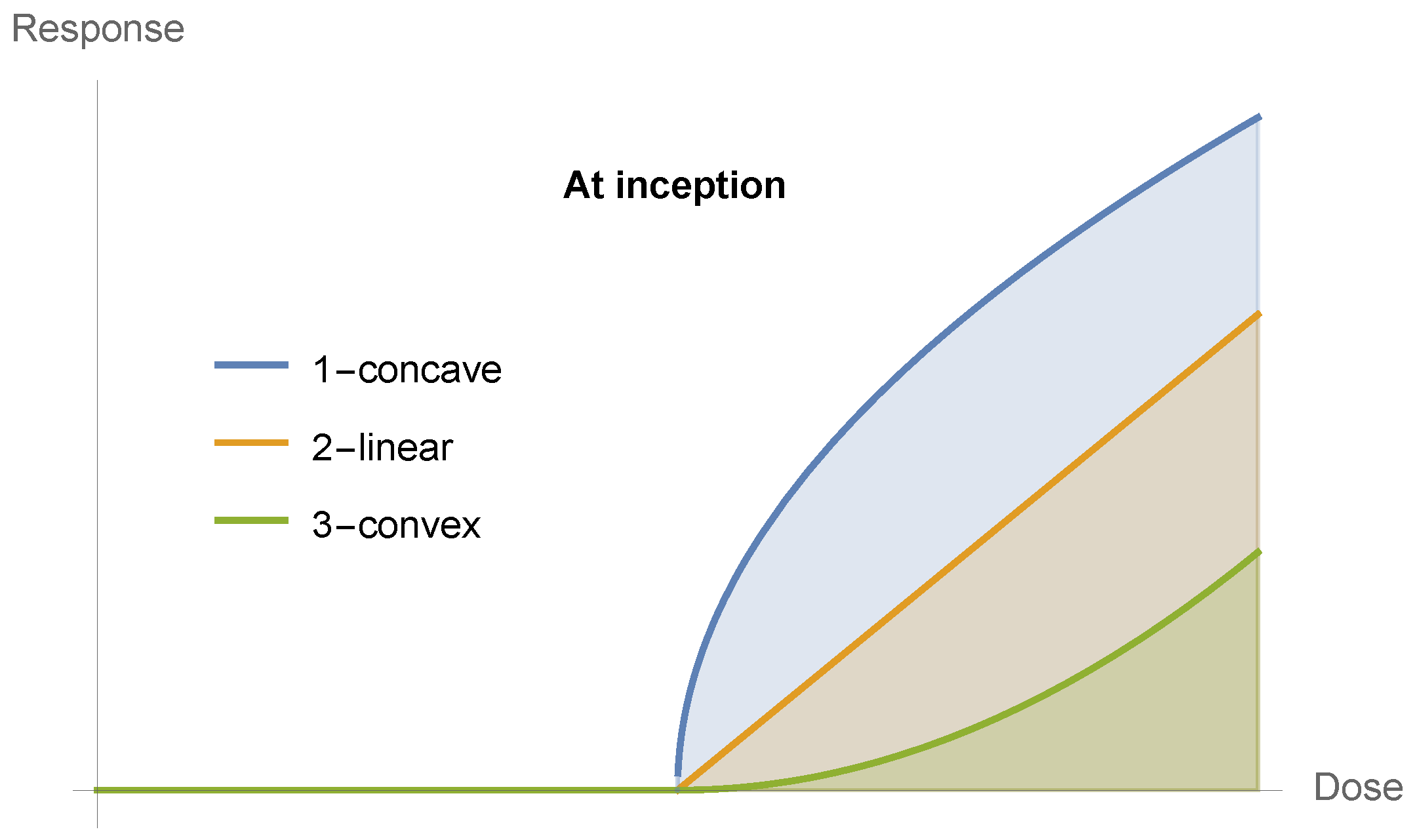
4. The Generalized Dose–Response Curve
- (−∞) = , and
- () = , and (equivalently for the first and last of the following conditions)
- ≥ 0 for x∈ (−∞, ), < 0 for x∈ (, ), and ≥ 0 for x∈ (, ∞), with .
Antifragility and Heterogeneity
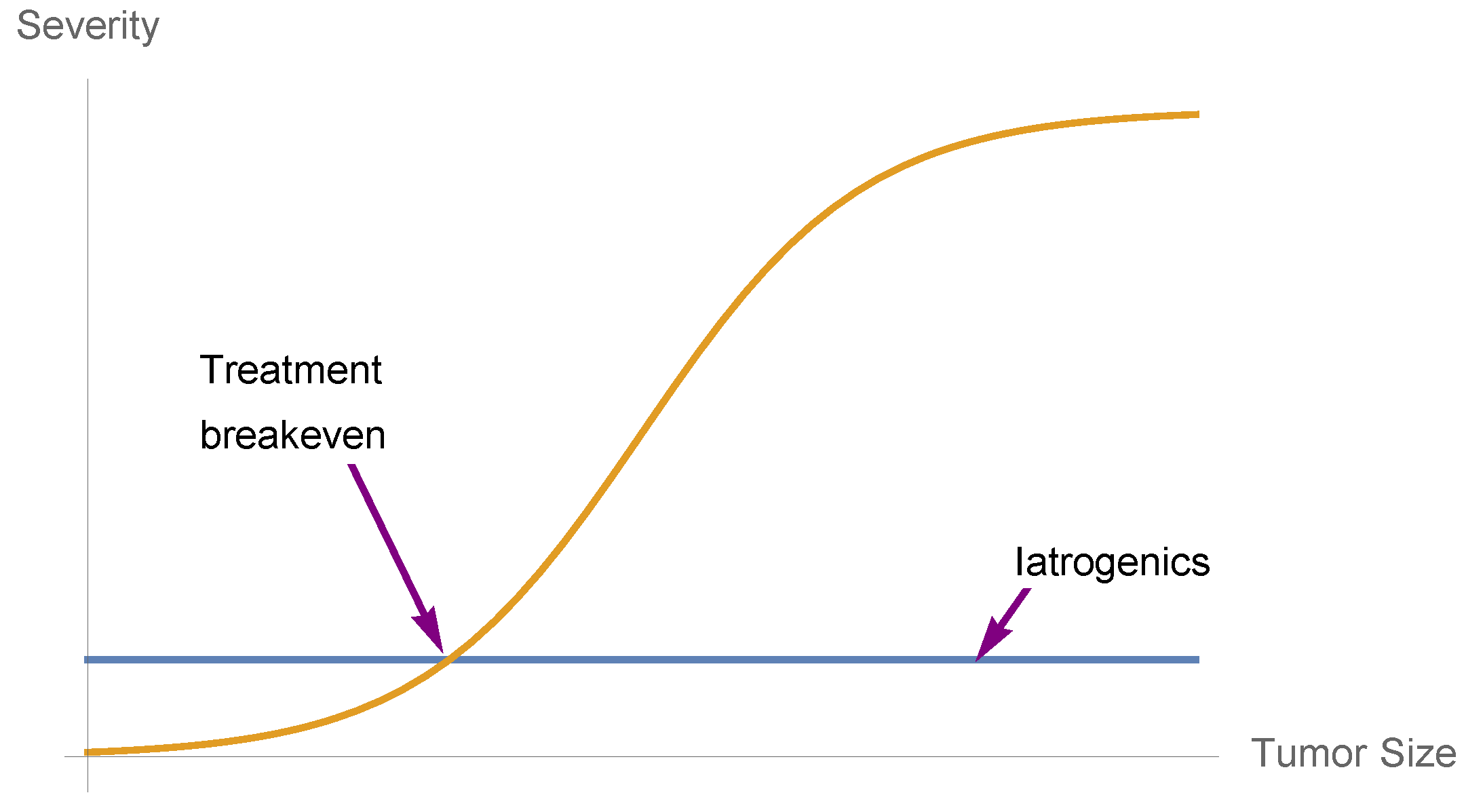
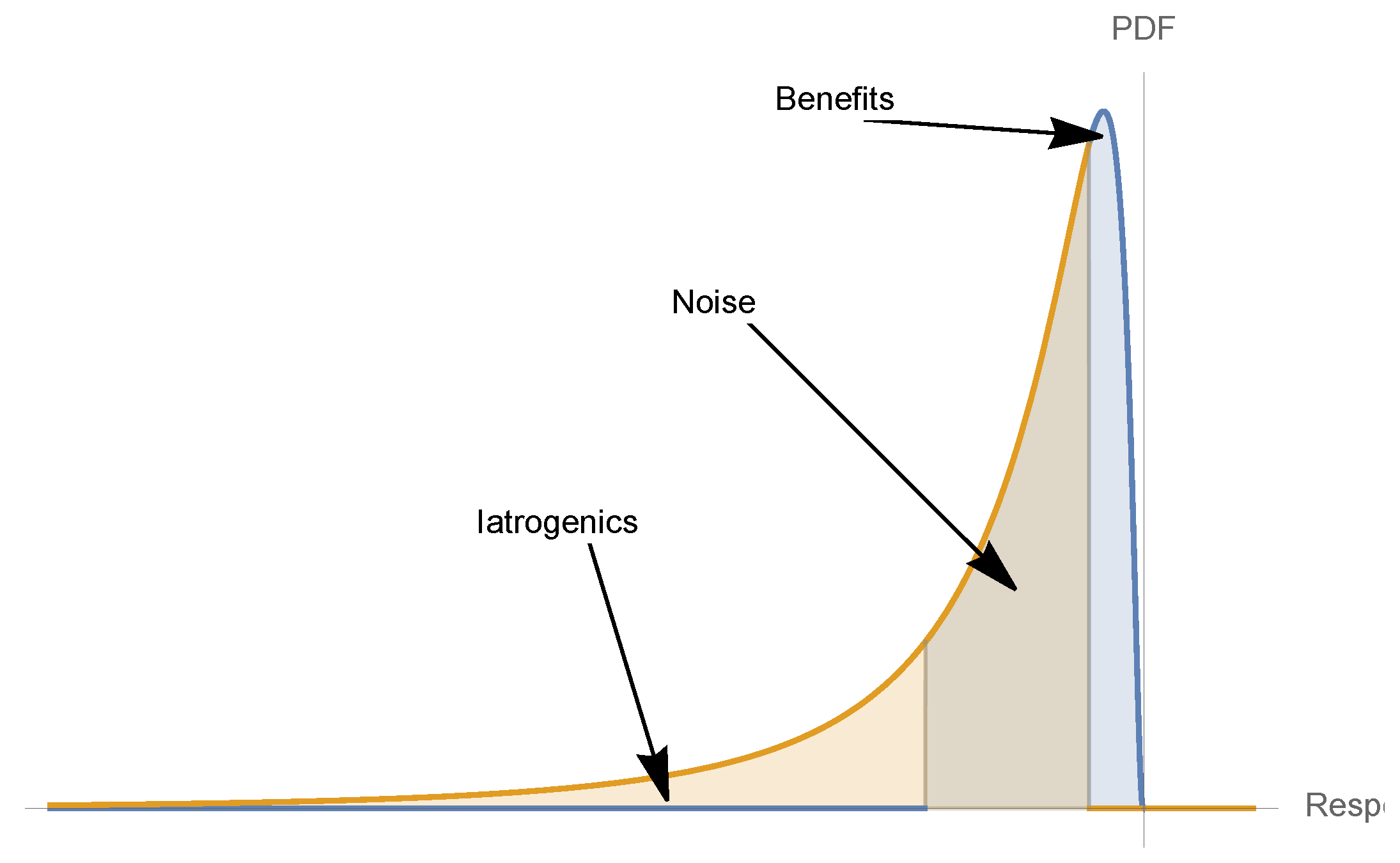
5. Nonlinearities and Medical Iatrogenics
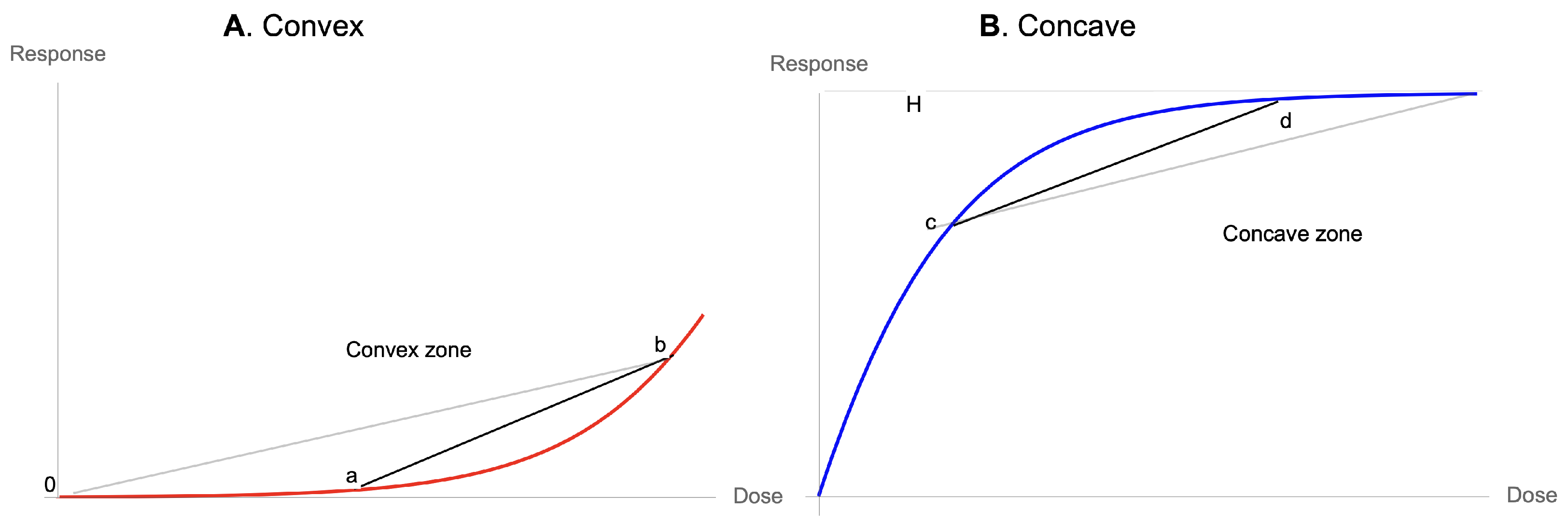
- Convexity for a dose-response function increases fragility (from the expansion of the left tail in response to the increase in the scale of the distribution).
- Detection of a nonlinearity allows the prediction of fragility and helps formulate probabilistic decisions without much knowledge of the probability distribution beyond minimum standard attributes.
- The presence of concavity in the tails of the distribution implies a silent risk.
5.1. Effect Reversal
The standard model currently in use applies a linear scale, extrapolating cancer risk from high doses to low doses of ionizing radiation. However, our discovery of DSB clustering over such large distances casts considerable doubts on the general assumption that risk to ionizing radiation is proportional to dose, and instead provides a mechanism that could more accurately address risk dose dependency of ionizing radiation.
5.2. Nonlinearity of NNT and the Consequences
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Antifragility Indirectly Detected in the Various Literature
| Field | Papers |
|---|---|
| Mithridatization and hormesis | Kaiser (2003) [16], Rattan (2008) [46], Calabrese and Baldwin (2002, 2003a, 2003b) [17,47,48], Aruguman et al. (2006) [49]. |
| Caloric restriction and hormesis | Martin, Mattson et al. (2006) [12] |
| Cancer treatment and fasting | Longo et al. (2010) [50], Safdie et al. (2009) [51], Raffaghelo et al. (2010), [52], Lee et al. (2012) [53] |
| Aging and intermittence | Fontana et al. [54] |
| For brain effects | Anson, Guo, et al. (2003) [55], Halagappa, Guo, et al. (2007) [56], Stranahan and Mattson (2012) [57]. The long-held belief that the brain needed glucose, not ketones, and that the brain does not go through autophagy, has been progressively replaced. |
| Yeast and longevity under restriction | Fabrizio et al. (2001) [58]; SIRT1, Longo et al. (2006) [59], Michan et al. (2010) [60] |
| Diabetes, remission or reversal | Taylor (2008) [61], Lim et al. (2011) [62], Boucher et al. (2004) [63]; diabetes management by diet alone, early insights in Wilson et al. (1980) [64]. Couzin (2008) [65] gives insight that blood sugar stabilization does not have the effect anticipated (there need to be stressors). The ACCORD study (Action to Control Cardiovascular Risk in Diabetes) found no benefits from lowering blood glucose levels. Synthesis, Skyler et al. (2009) [66], old methods, Westman and Vernon (2008) [67]. Bariatric (or other) surgery as alternative to intermittent fasting: Pories (1995) [68], Guidone et al. (2006) [69], Rubino et al. 2006 [70] |
| Ramadan and effect of fasting | Trabelsi et al. (2012) [71], Akanji et al. (2012). Note that the Ramadan time window is short (12 to 17 h) and possibly fraught with overeating so conclusions need to take into account energy balance and that the considered effect is at the low-frequency part of the timescale. |
| Caloric restriction | Harrison (1984), Wiendruch (1996), Pischon (2008) |
| Autophagy for cancer | Kondo et al. (2005) [72] |
| Autophagy (general) | Danchin et al. (2011) [73], He et al. (2012) [74] |
| Fractional dosage | Wu et al. (2016) [75] |
| Jensen’s inequality in exercise | Many such as Schnohr and Marott (2011) [76], intermittent extremes vs. moderate physical activity. |
| Cluster of ailments | Yaffe and Blackwell (2004) [77], Alzheimer and hyperinsulenemia, Razay and Wilcock (1994) [78]; Luchsinger, Tang, et al. (2002) [79], Luchsinger Tang et al. (2004) [80] Janson, Laedtke, et al. (2004) [81]. |
| Benefits ofsome type ofstress (and convexity of the effect) | For the different results from the two types of stressors, short and chronic, Dhabar (2009) “A hassle a day may keep the pathogens away: the fight-or-flight stress response and the augmentation of immune function” [82]. For the benefits of stress on boosting immunity and cancer resistance (squamous cell carcinoma), Dhabhar et al. (2010) [83], Dhabhar et al. (2012) [84], Ansbacher et al. (2013) [85] |
| Iatrogenics of hygiene and systematic elimination of germs | Rook (2011) [86], Rook (2012) [87] (auto-immune diseases from absence of stressors), Mégraud and Lamouliatte (1992) [88] for Helyobacter Pilori and incidence of cancer. |
Appendix B. Simple Convexity and Its Effects
Appendix C. Relaxing the Assumption of Fixed Treatment Schedules
References
- Taleb, N.N. Antifragile: Things That Gain from Disorder; Random House and Penguin: New York, NY, USA, 2012. [Google Scholar]
- Taleb, N.N.; Douady, R. Mathematical definition, mapping, and detection of (anti) fragility. Quant. Financ. 2013, 13, 1677–1689. [Google Scholar] [CrossRef]
- Taleb, N.N. Dynamic Hedging: Managing Vanilla and Exotic Options; John Wiley and Sons (Wiley Series in Financial Engineering): Hoboken, NJ, USA, 1997. [Google Scholar]
- Geman, D.; Geman, H.; Taleb, N. Tail Risk Constraints and Maximum Entropy. Entropy 2015, 17, 3724. [Google Scholar] [CrossRef]
- Taleb, N.N. The Statistical Consequences of Fat Tails; STEM Academic Press: New York, NY, USA, 2020. [Google Scholar]
- Brewster, J.F.; Graham, M.R.; Mutch, W.A.C. Convexity, jensen’s inequality and benefits of noisy mechanical ventilation. J. R. Soc. Interface 2005, 2, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Amato, M.B.P.; Barbas, C.S.V.; Medeiros, D.M.; Magaldi, R.B.; Schettino, G.P.; Lorenzi-Filho, G.; Kairalla, R.A.; Deheinzelin, D.; Munoz, C.; Oliveira, R.; et al. Effect of a Protective-Ventilation Strategy on Mortality Acute Respiratory Distress Syndrome. N. Engl. J. Med. 1998, 338, 347–354. [Google Scholar] [CrossRef]
- Funk, D.J.; Graham, M.R.; Girling, L.G.; Thliveris, J.A.; McManus, B.M.; Walker, E.K.; Rector, E.S.; Hillier, C.; Scott, J.E.; Mutch, W.A.C. A comparison of biologically variable ventilation to recruitment manoeuvres in a porcine model of acute lung injury. Respir. Res. 2004, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Arold, S.P.; Suki, B.; Alencar, A.M.; Lutchen, K.R.; Ingenito, E.P. Variable ventilation induces endogenous surfactant release in normal guinea pigs. Am. J. Physiol.-Lung Cell. Mol. 2003, 285, L370–L375. [Google Scholar] [CrossRef]
- Graham, M.R.; Haberman, C.J.; Brewster, J.F.; Girling, L.G.; McManus, B.M.; Mutch, W.A.C. Mathematical modelling to centre low tidal volumes following acute lung injury: A study with biologically variable ventilation. Respir. Res. 2005, 6, 64. [Google Scholar] [CrossRef]
- Den Hartigh, R.; Hill, Y. Conceptualizing and measuring psychological resilience: What can we learn from physics? New Ideas Psychol. 2022, 66, 100934. [Google Scholar] [CrossRef]
- Martin, B.; Mattson, M.P.; Maudsley, S. Caloric restriction and intermittent fasting: Two potential diets for successful brain aging. Ageing Res. Rev. 2006, 5, 332–353. [Google Scholar] [CrossRef]
- Fontana, L.; Weiss, E.; Villareal, D.; Klein, S.; Holloszy, J. Long-term effects of calorie or protein restriction on serum IGF-1 and IGFBP-3 concentration in humans. Aging Cell. 2008, 7, 681–687. [Google Scholar] [CrossRef]
- Lee, C.; Longo, V. Fasting vs dietary restriction in cellular protection and cancer treatment: From model organisms to patients. Oncogene 2011, 30, 3305–3316. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, D.; Schultz, J.; Matin, A. Starvation-induced cross protection against heat or H2O2 challenge in Escherichia coli. J. Ofbacteriol. 1988, 170, 3910–3914. [Google Scholar] [CrossRef]
- Kaiser, J. Sipping from a poisoned chalice. Science 2003, 302, 376. [Google Scholar] [CrossRef]
- Calabrese, E.; Baldwin, L. Hormesis: The dose-response revolution. Annu. Rev. Pharmacol. Toxicol. 2003, 43, 175–197. [Google Scholar] [CrossRef]
- Staňková, K.; Brown, J.; Dalton, W.; Gatenby, R. Optimizing cancer treatment using game theory: A review. JAMA Oncol. 2019, 5, 96–103. [Google Scholar] [CrossRef] [PubMed]
- West, J.; Desai, B.; Strobl, M.; Pierik, L.; Ver Velde, R.; Armagost, C.; Miles, R.; Robertson-Tessi, M.; Marusyk, A.; Anderson, A. Antifragile therapy. BioRxiv 2021. [Google Scholar] [CrossRef]
- Piccart, M.; Biganzoli, L.; Leo, A.D. The impact of chemotherapy dose density and dose intensity on breast cancer outcome: What have we learned? Eur. J. Cancer 2000, 36, 4–10. [Google Scholar] [CrossRef]
- Citron, M. Dose-dense chemotherapy: Principles, clinical results and future perspectives. Breast Care 2008, 3, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Skipper, H.; Schabel, F.; Wilcox, W. Experimental evaluation of potential anticancer agents XIII, on the criteria and kinetics associated with“ curability” of experimental leukemia. Cancer Chemother. Rep. 1964, 35, 3–111. [Google Scholar]
- Kerbel, R.; Kamen, B. The anti-angiogenic basis of metronomic chemotherapy. Nat. Rev. Cancer 2004, 4, 423–436. [Google Scholar] [CrossRef]
- Amin, D.; Sergina, N.; Ahuja, D.; McMahon, M.; Blair, J.; Wang, D.; Hann, B.; Koch, K.; Shokat, K.; Moasser, M. Resiliency and vulnerability in the HER2-HER3 tumorigenic driver. Sci. Transl. Med. 2010, 2, 16ra7. [Google Scholar] [CrossRef]
- Griffiths, J.; Chen, J.; Cosgrove, P.; O’Dea, A.; Sharma, P.; Ma, C.; Trivedi, M.; Kalinsky, K.; Wisinski, K.; O’Regan, R.; et al. Serial single-cell genomics reveals convergent subclonal evolution of resistance as patients with early-stage breast cancer progress on endocrine plus CDK4/6 therapy. Nat. Cancer 2021, 2, 658–671. [Google Scholar] [CrossRef] [PubMed]
- Chmielecki, J.; Foo, J.; Oxnard, G.; Hutchinson, K.; Ohashi, K.; Somwar, R.; Wang, L.; Amato, K.; Arcila, M.; Sos, M.; et al. Optimization of dosing for EGFR-mutant non–small cell lung cancer with evolutionary cancer modeling. Sci. Transl. Med. 2011, 3, 90ra59. [Google Scholar] [CrossRef] [PubMed]
- Schöttle, J.; Chatterjee, S.; Volz, C.; Siobal, M.; Florin, A.; Rokitta, D.; Hinze, Y.; Dietlein, F.; Plenker, D.; König, K.; et al. Intermittent high-dose treatment with erlotinib enhances therapeutic efficacy in EGFR-mutant lung cancer. Oncotarget 2015, 6, 38458. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, R.; Chen, X.; Lee, S.; Pan, J.; Xiong, D.; Hu, J.; Miller, M.; Szabo, E.; Lubet, R.; et al. Effect of weekly or daily dosing regimen of Gefitinib in mouse models of lung cancer. Oncotarget 2017, 8, 72447. [Google Scholar] [CrossRef]
- Grommes, C.; Oxnard, G.; Kris, M.; Miller, V.; Pao, W.; Holodny, A.; Clarke, J.; Lassman, A. Pulsatile high-dose weekly erlotinib for CNS metastases from EGFR mutant non-small cell lung cancer. Neuro-oncology 2011, 13, 1364–1369. [Google Scholar] [CrossRef]
- Hafner, M. Growth Rate Inhib. Metrics Correct Confounders Meas. Sensit. Cancer Drugs. Nat. Methods 2016, 13, 521–527. [Google Scholar] [CrossRef] [PubMed]
- Meyer, C.; Wooten, D.; Paudel, B.; Bauer, J.; Hardeman, K.; Westover, D.; Lovly, C.; Harris, L.; Tyson, D.; Quaranta, V. Quantifying drug combination synergy along potency and efficacy axes. Cell Syst. 2019, 8, 97–108. [Google Scholar] [CrossRef]
- Cunningham, J. A call for integrated metastatic management. Nat. Ecol. Evol. 2019, 3, 996–998. [Google Scholar] [CrossRef]
- Taleb, N.N. (Anti)Fragility and Convex Responses in Medicine. In Proceedings of the International Conference On Complex Systems, Proceedings, Cambridge, MA, USA, 22–27 July 2018; pp. 299–325. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Taleb, N.N.; Canetti, E.; Kinda, T.; Loukoianova, E.; Schmieder, C. A new heuristic measure of fragility and tail risks: Application to stress testing. International Monetary Fund. 2018. Available online: https://www.imf.org/external/pubs/ft/wp/2012/wp12216.pdf (accessed on 8 February 2023).
- Neumaier, T.; Swenson, J.; Pham, C.; Polyzos, A.; Lo, A.T.; Yang, P.; Dyball, J.; Asaithamby, A.; Chen, D.J.; Bissell, M.J.; et al. Evidence for formation of dna repair centers and dose-response nonlinearity in human cells. Proc. Natl. Acad. Sci. USA 2012, 109, 443–448. [Google Scholar] [CrossRef]
- Tubiana, M.; Aurengo, A.; Averbeck, D.; Masse, R. Recent reports on the effect of low doses of ionizing radiation and its dose–effect relationship. Radiat. Environ. Biophys. 2006, 44, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, A.; Stafford, K.C., III. Hormones and endocrine-disrupting chemicals: Low-dose effects and nonmonotonic dose responses. J. Med. Entomol 2010, 47, 862–867. [Google Scholar] [CrossRef] [PubMed]
- Kalager, M.; Adami, H.-O.; Bretthauer, M.; Tamimi, R.M. Overdiagnosis of invasive breast cancer due to mammography screening: Results from the norwegian screening program. Ann. Intern. Med. 2012, 156, 491–499. [Google Scholar] [CrossRef]
- Morrell, S.; Barratt, A.; Irwig, L.; Howard, K.; Biesheuvel, C.; Armstrong, B. Estimates of overdiagnosis of invasive breast cancer associated with screening mammography. Cancer Causes Control 2010, 21, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.; Silva, A.; Gillies, R.; Frieden, B. Adaptive therapy. Cancer Res. 2009, 69, 4894–4903. [Google Scholar] [CrossRef]
- West, J.; You, L.; Zhang, J.; Gatenby, R.; Brown, J.; Newton, P.; Anderson, A. Towards Multidrug Adaptive Therapy. Cancer Res. 2020, 80, 1578–1589. [Google Scholar] [CrossRef]
- Cunningham, J.; Brown, J.; Gatenby, R.; Staňková, K. Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer. J. Theor. Biol. 2018, 459, 67–78. [Google Scholar] [CrossRef]
- Zhang, J.; Cunningham, J.; Brown, J.; Gatenby, R. Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nat. Commun. 2017, 8, 1816. [Google Scholar] [CrossRef]
- Tracey, A. FDA’s Brian Booth: “We need to reconsider our approach to dose selection”. Cancer Lett. 2022, 48, 12–16. [Google Scholar]
- Rattan, S.I. Hormesis in aging. Ageing Res. Rev. 2008, 7, 63–78. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, E.J.; Baldwin, L.A. Defining hormesis. Hum. Exp. Toxicol. 2002, 21, 91–97. [Google Scholar] [CrossRef]
- Calabrese, E.J.; Baldwin, L.A. The hormetic dose-response model is more common than the threshold model in toxicology. Toxicol. Sci. 2003, 71, 246–250. [Google Scholar] [CrossRef]
- Arumugam, T.V.; Gleichmann, M.; Tang, S.-C.; Mattson, M.P. Hormesis/preconditioning mechanisms, the nervous system and aging. Ageing Res. Rev. 2006, 5, 165–178. [Google Scholar] [CrossRef]
- Longo, V.D.; Fontana, L. Calorie restriction and cancer prevention: Metabolic and molecular mechanisms. Trends Pharmacol. 2010, 31, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Safdie, F.M.; Dorff, T.; Quinn, D.; Fontana, L.; Wei, M.; Lee, C.; Cohen, P.; Longo, V.D. Fasting and cancer treatment in humans: A case series report. Aging (Albany NY) 2009, 1, 988–1007. [Google Scholar] [CrossRef]
- Raffaghello, L.; Safdie, F.; Bianchi, G.; Dorff, T.; Fontana, L.; Longo, V.D. Fasting and differential chemotherapy protection in patients. Cell Cycle 2010, 9, 4474–4476. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Raffaghello, L.; Brandhorst, S.; Safdie, F.M.; Bianchi, G.; Martin-Montalvo, A.; Pistoia, V.; Wei, M.; Hwang, S.; Merlino, A.; et al. Fasting Cycles Retard Growth Tumors Sensitize A Range Cancer Celltypes Chemotherapy. Sci. Transl. Med. 2012, 4, 124ra27. [Google Scholar] [CrossRef]
- Fontana, L.; Kennedy, B.K.; Longo, V.D.; Seals, D.; Melov, S. Medical research: Treat ageing. Nature 2014, 511, 405–407. [Google Scholar] [CrossRef]
- Anson, R.M.; Guo, Z.; de Cabo, R.; Iyun, T.; Rios, M.; Hagepanos, A.; Ingram, D.K.; Lane, M.A.; Mattson, M.P. Intermittent fasting dissociates beneficial effects of dietary restriction on glucose metabolism and neuronal resistance to injury from calorie intake. Proc. Natl. Acad. Sci. USA 2003, 100, 6216–6220. [Google Scholar] [CrossRef]
- Halagappa, V.K.M.; Guo, Z.; Pearson, M.; Matsuoka, Y.; Cutler, R.G.; LaFerla, F.M.; Mattson, M.P. Intermittent fasting and caloric restriction ameliorate age-related behavioral deficits in the triple-transgenic mouse model of alzheimer’s disease. Neurobiol. Dis. 2007, 26, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Stranahan, A.M.; Mattson, M.P. Recruiting adaptive cellular stress responses for successful brain ageing. Nat. Rev. Neurosci. 2012, 13, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Fabrizio, P.; Pozza, F.; Pletcher, S.D.; Gendron, C.M.; Longo, V.D. Regulation of longevity and stress resistance by sch9 in yeast. Science 2001, 292, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Longo, V.D.; Kennedy, B.K. Sirtuins in aging and age-related disease. Cell 2006, 126, 257–268. [Google Scholar] [CrossRef]
- Michán, S.; Li, Y.; Chou, M.M.-H.; Parrella, E.; Ge, H.; Long, J.M.; Allard, J.S.; Lewis, K.; Miller, M.; Xu, W.; et al. Sirt1 is essential for normal cognitive function and synaptic plasticity. J. Neurosci. 2010, 30, 9695–9707. [Google Scholar] [CrossRef]
- Taylor, R. Pathogenesis of type 2 diabetes: Tracing the reverse route from cure to cause. Diabetologia 2008, 51, 1781–1789. [Google Scholar] [CrossRef] [PubMed]
- Lim, E.L.; Hollingsworth, K.; Aribisala, B.S.; Chen, M.; Mathers, J.; Taylor, R. Reversal of type 2 diabetes: Normalisation of beta cell function in association with decreased pancreas and liver triacylglycerol. Diabetologia 2011, 54, 2506–2514. [Google Scholar] [CrossRef]
- Boucher, A.; Lu, D.; Burgess, S.C.; Telemaque-Potts, S.; Jensen, M.V.; Mulder, H.; Wang, M.-Y.; Unger, R.H.; Sherry, A.D.; Newgard, C.B. Biochemical mechanism of lipid-induced impairment of glucose-stimulated insulin secretion and reversal with a malate analogue. J. Biol. 2004, 279, 27263–27271. [Google Scholar] [CrossRef]
- Wilson, E.A.; Hadden, D.; Merrett, J.; Montgomery, D.; Weaver, J. Dietary management of maturity-onset diabetes. Br. Med. J. 1980, 280, 1367–1369. [Google Scholar] [CrossRef]
- Couzin, J. Deaths in diabetes trial challenge a long-held theory. Science 2008, 319, 884–885. [Google Scholar] [CrossRef]
- Skyler, J.S.; Bergenstal, R.; Bonow, R.O.; Buse, J.; Deedwania, P.; Gale, E.A.; Howard, B.V.; Kirkman, M.S.; Kosiborod, M.; Reaven, P.; et al. Intensive glycemic control and the prevention of cardiovascular events: Implications of the accord, advance, and va diabetes trials: A position statement of the american diabetes association and a scientific statement of the american college of cardiology foundation and the american heart association. J. Am. Coll. Cardiol. 2009, 53, 298–304. [Google Scholar] [PubMed]
- Westman, E.C.; Vernon, M.C. Has carbohydrate-restriction been forgotten as a treatment for diabetes mellitus? A perspective on the accord study design. Nutr. Metab. 2008, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Pories, W.J.; Swanson, M.S.; MacDonald, K.G.; Long, S.B.; Morris, P.G.; Brown, B.M.; Barakat, H.A. Who would have thought it? An operation proves to be the most effective therapy for adult-onset diabetes mellituss. Ann. Surg. 1995, 222, 339. [Google Scholar] [CrossRef]
- Guidone, C.; Manco, M.; Valera-Mora, E.; Iaconelli, A.; Gniuli, D.; Mari, A.; Nanni, G.; Castagneto, M.; Calvani, M.; Mingrone, G. Mechanisms of recovery from type 2 diabetes after malabsorptive bariatric surgery. Diabetes 2006, 55, 2025–2031. [Google Scholar] [CrossRef]
- Rubino, F.; Forgione, A.; Cummings, D.E.; Vix, M.; Gnuli, D.; Mingrone, G.; Castagneto, M.; Marescaux, J. The mechanism of diabetes control after gastrointestinal bypass surgery reveals a role of the proximal small intestine in the pathophysiology of type 2 diabetes. Ann. Surg. 2006, 244, 741–749. [Google Scholar] [CrossRef]
- Trabelsi, K.; Stannard, S.R.; Maughan, R.J.; Jamoussi, K.; Zeghal, K.M.; Hakim, A. Effect of resistance training during ramadan on body composition, and markers of renal function, metabolism, inflammation and immunity in tunisian recreational bodybuilders. Intern. J. Sport Nutr. Exer. Metabo. 2012, 22, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Kondo, Y.; Kanzawa, T.; Sawaya, R.; Kondo, S. The role of autophagy in cancer development and response to therapy. Nat. Rev. Cancer 2005, 5, 726–734. [Google Scholar] [CrossRef]
- Danchin, A.; Binder, P.M.; Noria, S. Antifragility and tinkering in biology (and in business) flexibility provides an efficient epigenetic way to manage risk. Genes 2011, 2, 998–1016. [Google Scholar] [CrossRef]
- He, C.; Bassik, M.C.; Moresi, V.; Sun, K.; Wei, Y.; Zou, Z.; An, Z.; Loh, J.; Fisher, J.; Sun, Q.; et al. Exercise-induced bcl2-regulated autophagy is required for muscle glucose homeostasis. Nature 2012, 481, 511–515. [Google Scholar] [CrossRef]
- Wu, J.T.; Peak, C.M.; Leung, G.M.; Lipsitch, M. Fractional dosing of yellow fever vaccine to extend supply: A modeling study. Lancet 2016, 388, 2904–2911. [Google Scholar] [CrossRef]
- Schnohr, P.; Marott, J.L.; Jensen, J.S.; Jensen, G.B. Intensity versus duration of cycling, impact on all-cause and coronary heart disease mortality: The copenhagen city heart study. Eur. J. Cardiovascular Prev. Rehabil. 2011, 19, 73–80. [Google Scholar] [CrossRef]
- Yaffe, K.; Blackwell, T.; Kanaya, A.; Davidowitz, N.; Barrett-Connor, E.; Krueger, K. Diabetes, impaired fasting glucose, and development of cognitive impairment in older women. Neurology 2004, 63, 658–663. [Google Scholar] [CrossRef] [PubMed]
- Razay, G.; Wilcock, G.K. Hyperinsulinaemia and alzheimer’s disease. Age Ageing 1994, 23, 396–399. [Google Scholar] [CrossRef]
- Luchsinger, J.A.; Tang, M.-X.; Shea, S.; Mayeux, R. Caloric intake and the risk of alzheimer disease. Arch. Neurol. 2002, 59, 1258–1263. [Google Scholar] [CrossRef] [PubMed]
- Luchsinger, J.A.; Tang, M.-X.; Shea, S.; Mayeux, R. Hyperinsulinemia and risk of alzheimer disease. Neurology 2004, 63, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Janson, J.; Laedtke, T.; Parisi, J.E.; O’Brien, P.; Petersen, R.C.; Butler, P.C. Increased risk of type 2 diabetes in alzheimer disease. Diabetes 2004, 53, 474–481. [Google Scholar] [CrossRef]
- Dhabhar, F.S. A hassle a day may keep the pathogens away: The fight-or-flight stress response and the augmentation of immune function. Integr. Comp. Biol. 2009, 49, 215–236. [Google Scholar] [CrossRef] [PubMed]
- Dhabhar, F.S.; Saul, A.N.; Daugherty, C.; Holmes, T.H.; Bouley, D.M.; Oberyszyn, T.M. Short-term stress enhances cellular immunity and increases early resistance to squamous cell carcinoma. Brain, Behav. Andimmunity 2010, 24, 127–137. [Google Scholar] [CrossRef]
- Dhabhar, F.S.; Saul, A.N.; Holmes, T.H.; Daugherty, C.; Neri, E.; Tillie, J.M.; Kusewitt, D.; Oberyszyn, T.M. High-anxious individuals show increased chronic stress burden, decreased protective immunity, and increased cancer progression in a mouse model of squamous cell carcinoma. PLoS ONE 2012, 7, e33069. [Google Scholar] [CrossRef]
- Aschbacher, K.; O’Donovan, A.; Wolkowitz, O.M.; Dhabhar, F.S.; Su, Y.; Epel, E. Good stress, bad stress and oxidative stress: Insights from anticipatory cortisol reactivity. Psychoneuroendocrinology 2013, 38, 1698–1708. [Google Scholar] [CrossRef]
- Rook, G.A. Hygiene and other early childhood influences on the subsequent function of the immune system. Dig. Dis. 2011, 29, 144–153. [Google Scholar] [CrossRef]
- Rook, G.A. Hygiene hypothesis and autoimmune diseases. Clin. Rev. Allergy Immunol. 2012, 42, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Mégraud, F.; Lamouliatte, H. Helicobacter pylori and duodenal ulcer. Dig. Dis. Sci. 1992, 37, 769–772. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
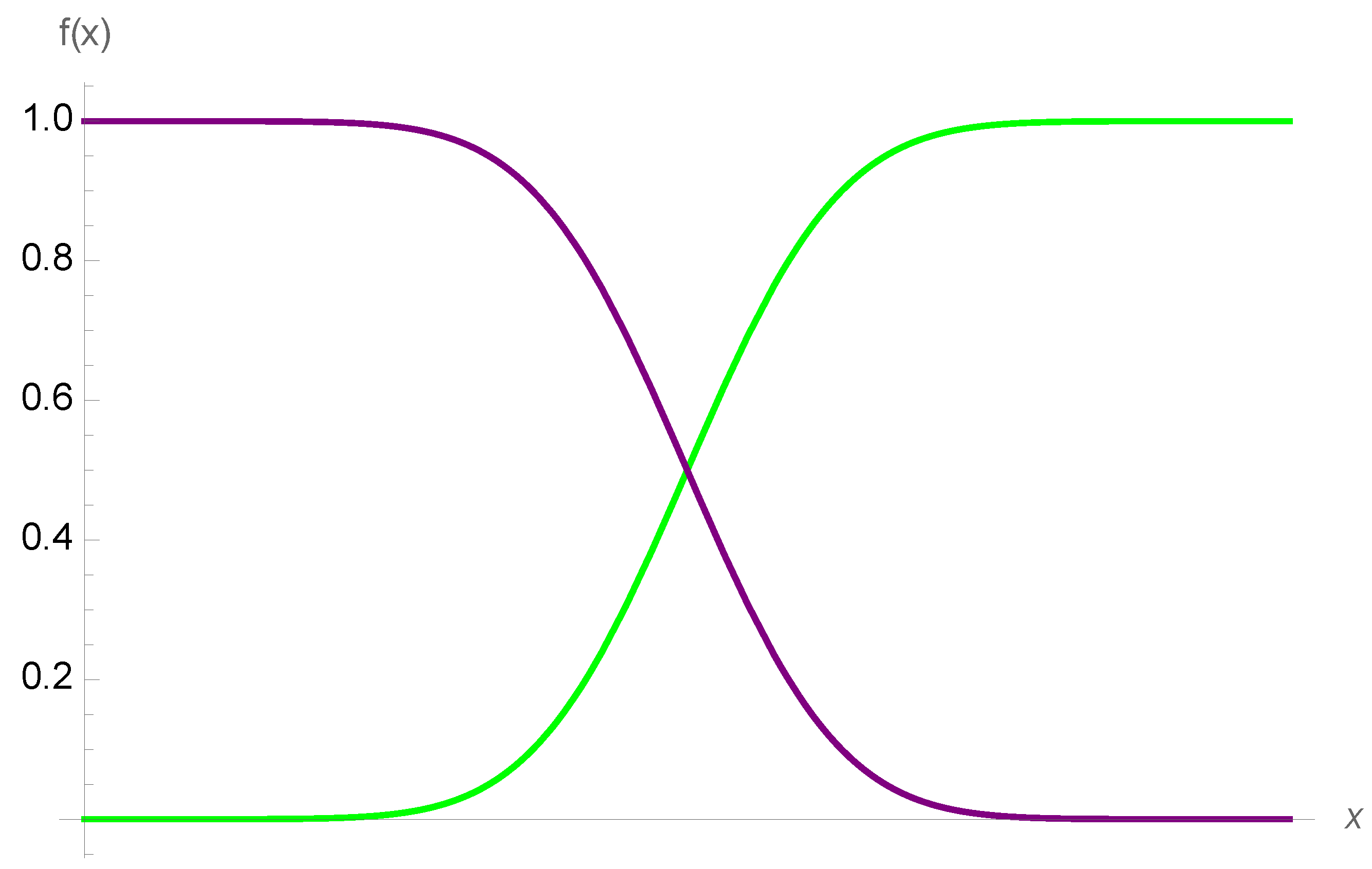

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taleb, N.N.; West, J. Working with Convex Responses: Antifragility from Finance to Oncology. Entropy 2023, 25, 343. https://doi.org/10.3390/e25020343
Taleb NN, West J. Working with Convex Responses: Antifragility from Finance to Oncology. Entropy. 2023; 25(2):343. https://doi.org/10.3390/e25020343
Chicago/Turabian StyleTaleb, Nassim Nicholas, and Jeffrey West. 2023. "Working with Convex Responses: Antifragility from Finance to Oncology" Entropy 25, no. 2: 343. https://doi.org/10.3390/e25020343
APA StyleTaleb, N. N., & West, J. (2023). Working with Convex Responses: Antifragility from Finance to Oncology. Entropy, 25(2), 343. https://doi.org/10.3390/e25020343








