Kernel Partial Least Squares Feature Selection Based on Maximum Weight Minimum Redundancy
Abstract
1. Introduction
2. KPLS Method and Feature Selection
2.1. PLS Method
2.2. KPLS Method
2.3. Improved MWMR Method
3. Proposed KPLS Feature Selection on the Basis of the Improved MWMR Method
- (1)
- Calculation of the latent matrix using the KPLS algorithm;
- (2)
- Calculation of the feature weighting score (W_score(fi|c)) based on the feature, fi, and the class label, c, of the dataset;
- (3)
- Calculation of the feature redundancy score (R_score(fi|fj)) based on the features fi and fj of the dataset;
- (4)
- Calculation of the objective function, , according to the feature weighting score and feature redundancy score;
- (5)
- Selection of an optimal feature subset on the basis of the objective function, .
| Algorithm 1. KPLS based on maximum weight minimum redundancy (KPLS-MWMR). |
| Input: Feature dataset, , class label, , feature number, k, weight factor, . Output: A selected feature subset, F*. (1) Initialize the feature dataset, F; (2) Let the feature set ; (3) Calculate the latent matrix: F = KPLS(X,Y) using the KPLS algorithm [29]; (4) Calculate the feature weighting score: W_score (F|Y) using the Relief F algorithm [20]; (5) Arrange the feature weighting score in descending order: [WS, rank] = descend(W_score(F|Y)); (6) Form a feature subset S = X(:, rank); (7) Select the optimal feature subset F* = S(:, 1); (8) For each j < k; (9) f1 = S(:, j); (10) w = WS(:, j); (11) Compute the feature redundancy score, r = R_score(f1|(S − F*)) using the PCC algorithm [15]; (12) Calculate the evaluation criteria, according to Equation (5); (13) Arrange the values of R in descending order: [weight, rank] = descend(R); (14) Update F*: F* = [ F*, S (:, rank(1))]; (15) Delete the selected optimal feature in S: S(:,rank(1)) = [ ]; (16) Update j: j = j + 1; (17) Repeat; (18) End; (19) Return the optimal subset F* of k features. |
4. Experimental Results
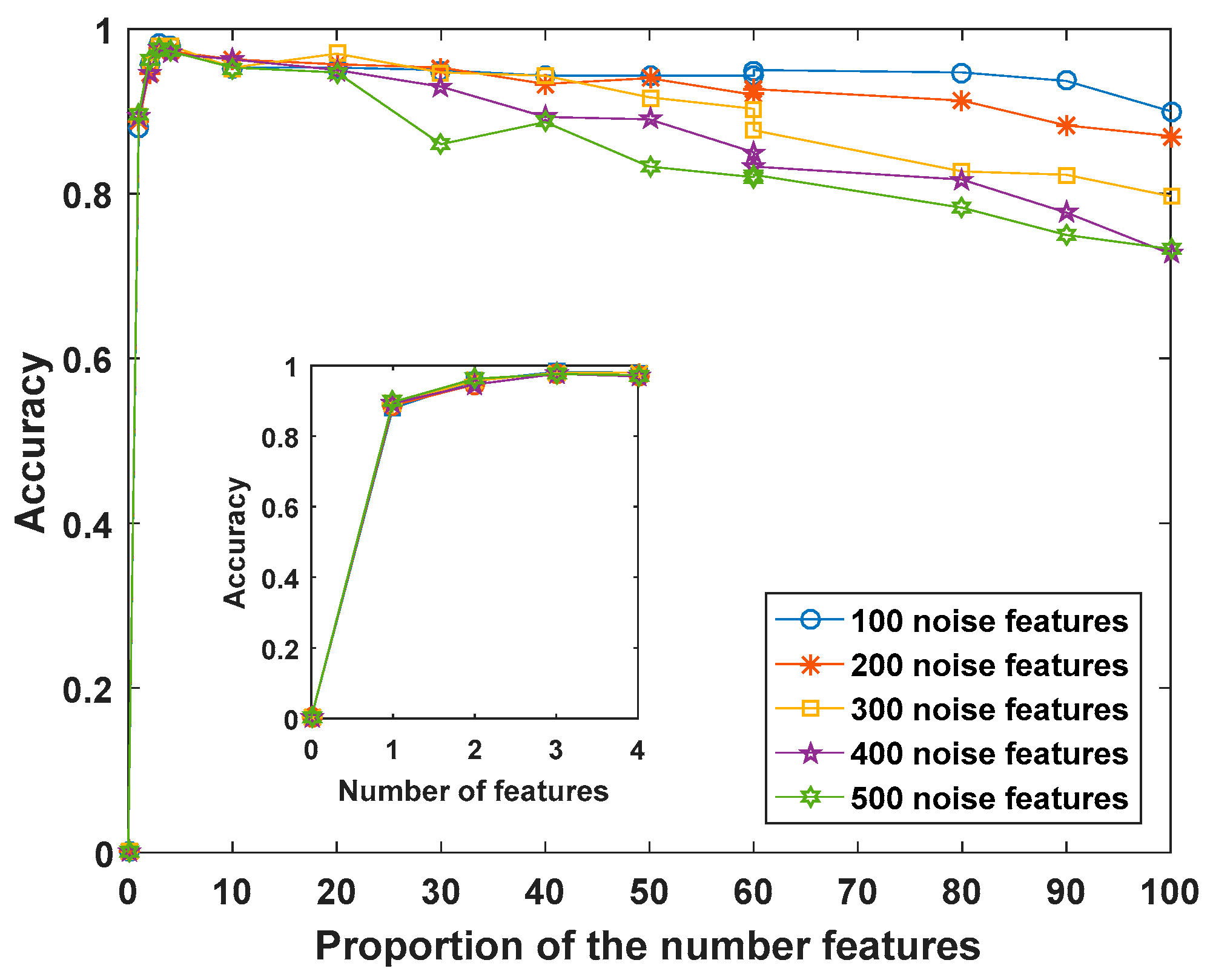
4.1. Experiments Were Performed Using Synthetic Data
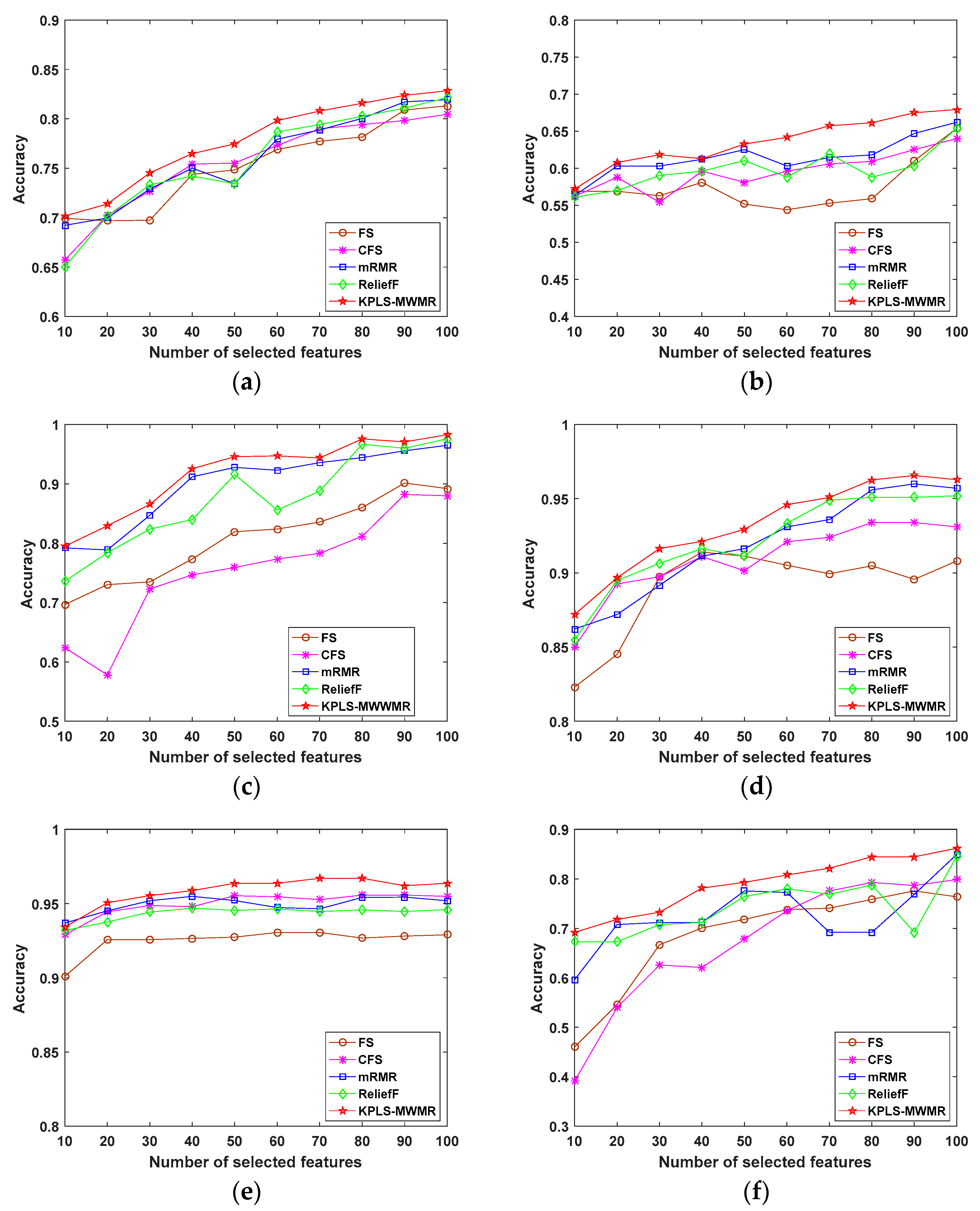
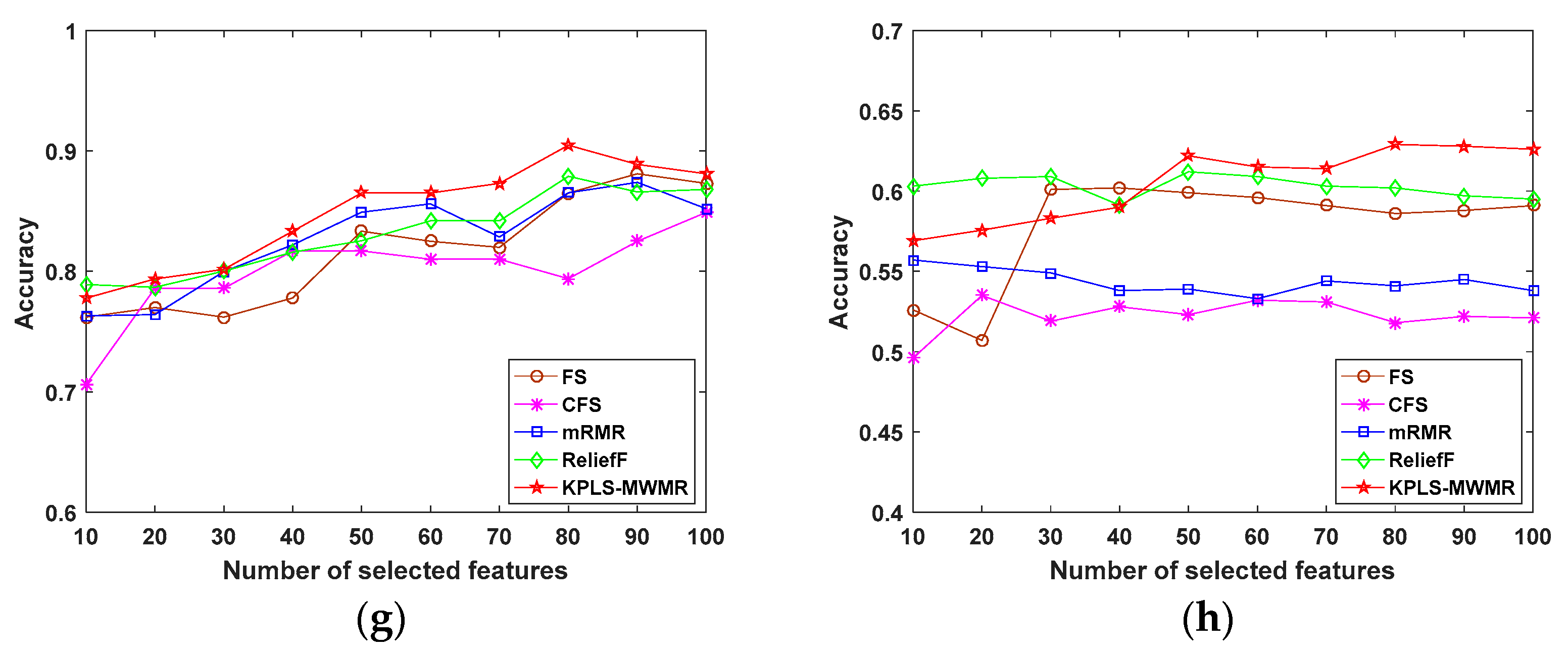
4.2. Experiments Performed Using Public Data
- (1)
- Classification accuracy
- (2)
- Kappa coefficient
- (3)
- F1-score
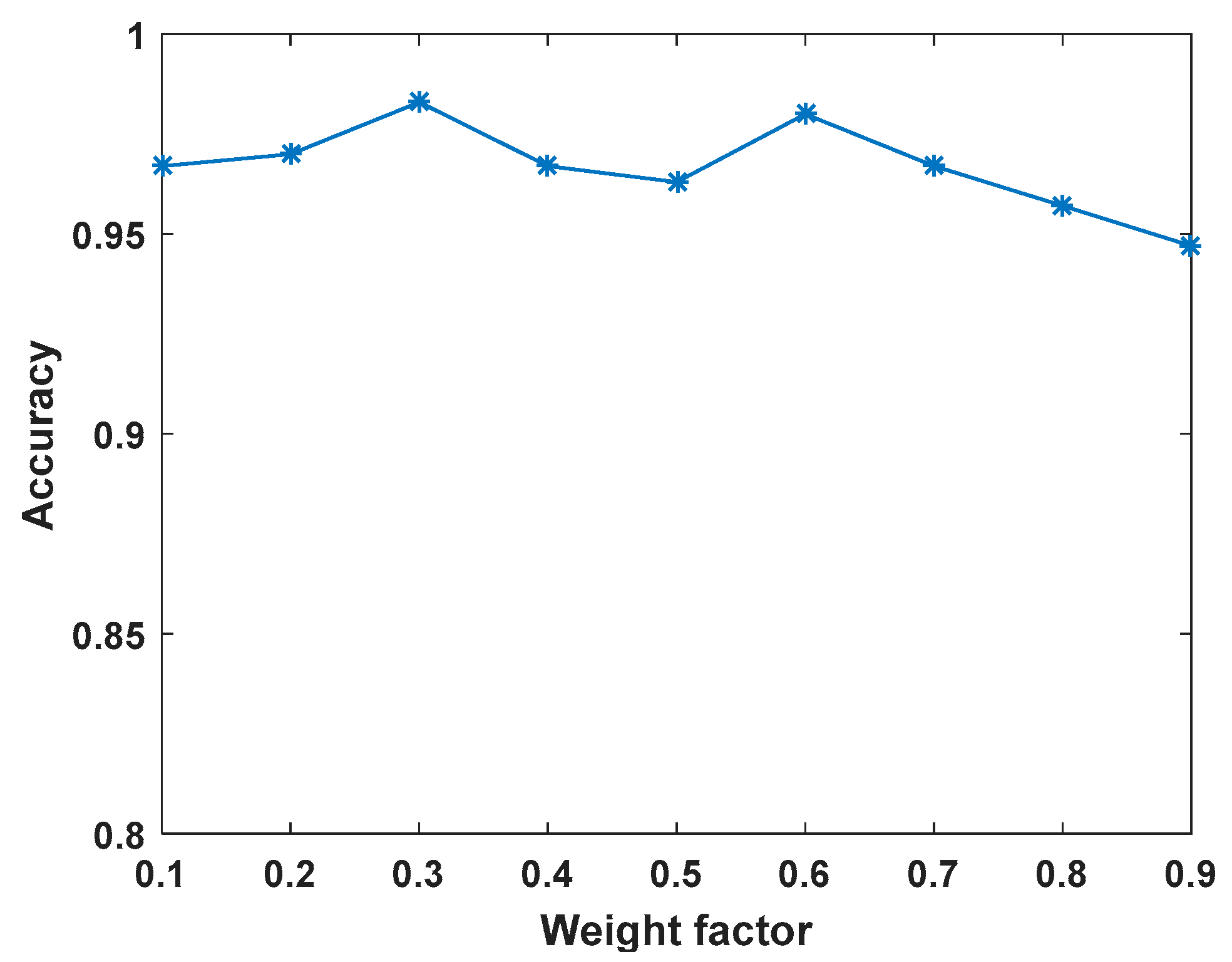
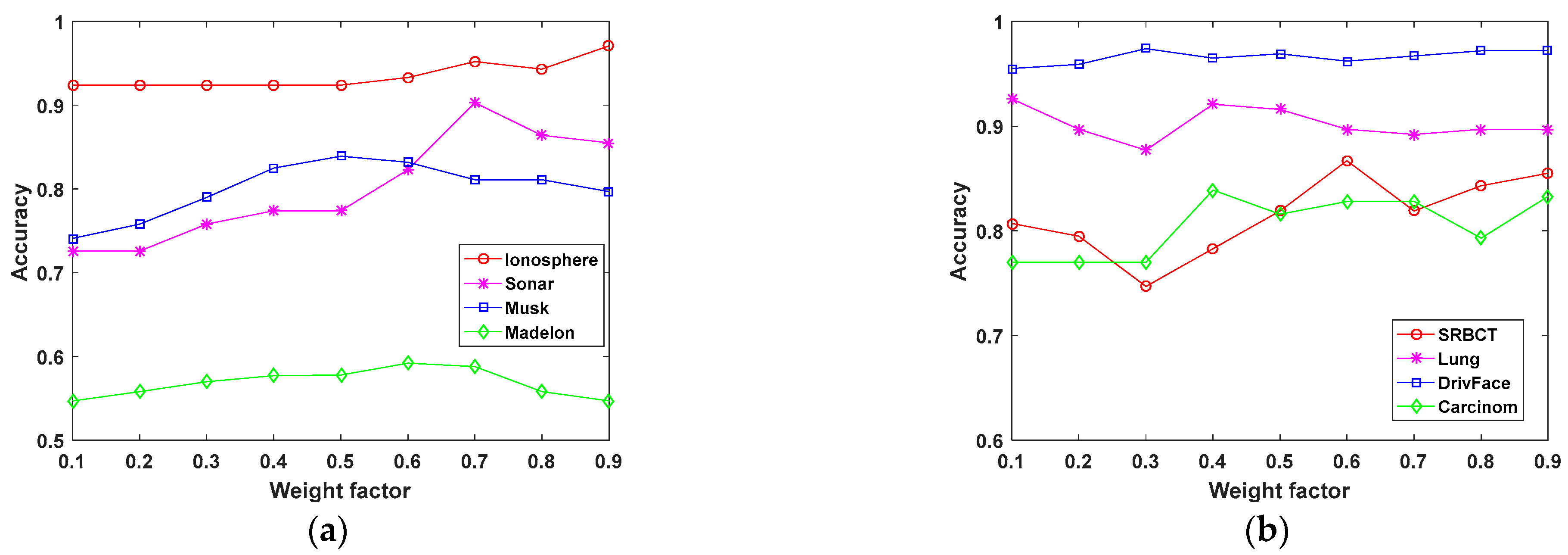
4.3. Weight Factor Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, J.; Luo, J.W.; Wang, S.L.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Solorio-Fernández, S.; Carrasco-Ochoa, J.A.; Martínez-Trinidad, J.F. A review of unsupervised feature selection methods. Artif. Intell. Rev. 2020, 53, 907–948. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Muneeswaran, K. Feature selection using hybrid poor and rich optimization algorithm for text classification. Pattern Recog. Lett. 2021, 147, 63–70. [Google Scholar]
- Raghuwanshi, G.; Tyagi, V. A novel technique for content based image retrieval based on region-weight assignment. Multimed Tools Appl. 2019, 78, 1889–1911. [Google Scholar] [CrossRef]
- Liu, K.; Jiao, Y.; Du, C.; Zhang, X.; Chen, X.; Xu, F.; Jiang, C. Driver Stress Detection Using Ultra-Short-Term HRV Analysis under Real World Driving Conditions. Entropy 2023, 25, 194. [Google Scholar] [CrossRef]
- Ocloo, I.X.; Chen, H. Feature Selection in High-Dimensional Modes via EBIC with Energy Distance Correlation. Entropy 2023, 25, 14. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Dy, J.G.; Brodley, C.E. Feature selection for unsupervised learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Lal, T.N.; Chapelle, O.; Weston, J.; Elisseeff, A.; Zadeh, L. Embedded methods. In Feature Extraction Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 137–165. [Google Scholar]
- Hu, L.; Gao, W.; Zhao, K.; Zhang, P.; Wang, F. Feature selection considering two types of feature relevancy and feature interdependency. Expert Syst. Appl. 2018, 93, 423–434. [Google Scholar] [CrossRef]
- Stańczyk, U. Pruning Decision Rules by Reduct-Based Weighting and Ranking of Features. Entropy 2022, 24, 1602. [Google Scholar] [CrossRef] [PubMed]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Yilmaz, T.; Yazici, A.; Kitsuregawa, M. RELIEF-MM: Effective modality weighting for multimedia information retrieval. Mul. Syst. 2014, 20, 389–413. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Unsupervised feature selection based on maximum information and minimum redundancy for hyperspectral images. Pattern Recog. 2016, 51, 295–309. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Zhu, R. Feature selection based on mutual information with correlation coefficient. Appl. Intell. 2021, 52, 5457–5474. [Google Scholar] [CrossRef]
- Ramasamy, M.; Meena Kowshalya, A. Information gain based feature selection for improved textual sentiment analysis. Wirel. Pers. Commun. 2022, 125, 1203–1219. [Google Scholar] [CrossRef]
- Huang, M.; Sun, L.; Xu, J.; Zhang, S. Multilabel feature selection using relief and minimum redundancy maximum relevance based on neighborhood rough sets. IEEE Access 2020, 8, 62011–62031. [Google Scholar] [CrossRef]
- Eiras-Franco, C.; Guijarro-Berdias, B.; Alonso-Betanzos, A.; Bahamonde, A. Scalable feature selection using ReliefF aided by locality-sensitive hashin. Int. J. Intell. Syst. 2021, 36, 6161–6179. [Google Scholar] [CrossRef]
- Paramban, M.; Paramasivan, T. Feature selection using efficient fusion of fisher score and greedy searching for alzheimer’s classification. J. King Saud Univ. Com. Inform. Sci. 2021, 34, 4993–5006. [Google Scholar]
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. In Proceedings of the Advances in Neural Information Processing Systems 18 Neural Information Processing Systems (NIPS 2005), Vancouver, BC, Canada, 5–8 December 2005. [Google Scholar]
- Zhang, D.; Chen, S.; Zhou, Z.-H. Constraint score: A new filter method for feature selection with pairwise constraints. Pattern Recog. 2008, 41, 1440–1451. [Google Scholar] [CrossRef]
- Palma-Mendoza, R.J.; De-Marcos, L.; Rodriguez, D.; Alonso-Betanzos, A. Distributed correlation-based feature selection in spark. Inform. Sci. 2018, 496, 287–299. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th International Conference Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wu, L.; Kong, J.; Li, Y.; Zhang, B. Maximum weight and minimum redundancy: A novel framework for feature subset selection. Pattern Recog. 2013, 46, 1616–1627. [Google Scholar] [CrossRef]
- Tran, T.N.; Afanador, N.L.; Buydens, L.M.; Blanchet, L. Interpretation of variable importance in partial least squares with significance multivariate correlation (SMC). Chemom. Intell. Lab. Syst. 2014, 138, 153–160. [Google Scholar] [CrossRef]
- Rosipal, R.; Trejo, L.J. Kernel partial least squares regression in reproducing kernel hilbert space. J. Mach. Learn. Res. 2001, 2, 97–123. [Google Scholar]
- Qiao, J.; Yin, H. Optimizing kernel function with applications to kernel principal analysis and locality preserving projection for feature extraction. J. Inform. Hiding Mul. Sig. Process. 2013, 4, 280–290. [Google Scholar]
- Zhang, D.L.; Qiao, J.; Li, J.B.; Chu, S.C.; Roddick, J.F. Optimizing matrix mapping with data dependent kernel for image classification. J. Inform. Hiding Mul. Sig. Process. 2014, 5, 72–79. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Talukdar, U.; Hazarika, S.M.; Gan, J.Q. A kernel partial least square based feature selection method. Pattern Recog. 2018, 83, 91–106. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Lin, C.; Tang, J.L.; Li, B.X. Embedded supervised feature selection for multi-class data. In Proceedings of the 2017 SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017; pp. 516–524. [Google Scholar]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/mL/index.php (accessed on 27 October 2022).
- Li, J.; Liu, H. Kent Ridge Biomedical Data Set Repository; Nanyang Technological University: Singapore, 2004. [Google Scholar]
- Rigby, A.S. Statistical methods in epidemiology. v. towards an understanding of the kappa coefficient. Disabil. Rehabil. 2000, 22, 339–344. [Google Scholar] [CrossRef]
- Liu, C.; Wang, W.; Wang, M.; Lv, F.; Konan, M. An efficient instance selection algorithm to reconstruct training set for support vector machine. Knowl. Based Syst. 2017, 116, 58–73. [Google Scholar] [CrossRef]

| Algorithms | Top Three Features | Accuracy |
|---|---|---|
| FS | f1, f2, f3 | 0.973 |
| CFS | f52, f58, f3 | 0.907 |
| mRMR | f3, f2, f1 | 0.973 |
| ReliefF | f3, f2, f1 | 0.977 |
| KPLS-MWMR | f1, f3, f2 | 0.983 |
| Datasets | Instances | Features | Class | Training |
|---|---|---|---|---|
| Ionosphere | 351 | 34 | 2 | 246 |
| Sonar | 208 | 60 | 2 | 146 |
| Musk | 4776 | 166 | 2 | 3343 |
| Arrhythmia | 452 | 274 | 13 | 316 |
| SRBCT | 83 | 2308 | 4 | 58 |
| Lung | 203 | 3312 | 5 | 142 |
| DrivFace | 606 | 6400 | 3 | 424 |
| Carcinom | 174 | 9182 | 11 | 122 |
| LSVT | 126 | 310 | 2 | 88 |
| Madelon | 2000 | 500 | 2 | 1400 |
| Datasets | Feature Selection Method | ||||
|---|---|---|---|---|---|
| FS | CFS | mRMR | ReliefF | KPLS-MWMR | |
| Musk | 0.4807 | 0.5019 | 0.4519 | 0.4397 | 0.5143 |
| Arrhythmia | 0.1726 | 0.2277 | 0.3244 | 0.2772 | 0.3410 |
| SRBCT | 0.7510 | 0.6698 | 0.8994 | 0.8829 | 0.9383 |
| Lung | 0.8087 | 0.7864 | 0.8271 | 0.8876 | 0.8367 |
| DrivFace | 0.4295 | 0.7050 | 0.6832 | 0.6460 | 0.7062 |
| Carcinom | 0.6770 | 0.6295 | 0.7438 | 0.7303 | 0.7649 |
| LSVT | 0.5935 | 0.5490 | 0.6369 | 0.5714 | 0.6871 |
| Madelon | 0.1980 | 0.0450 | 0.0780 | 0.2240 | 0.2277 |
| Datasets | Feature Selection Method | ||||
|---|---|---|---|---|---|
| FS | CFS | mRMR | ReliefF | KPLS-MWMR | |
| Musk | 0.7403 | 0.7504 | 0.7259 | 0.7193 | 0.7564 |
| Arrhythmia | 0.4576 | 0.4851 | 0.4134 | 0.4951 | 0.4954 |
| SRBCT | 0.8027 | 0.7828 | 0.9300 | 0.9191 | 0.9642 |
| Lung | 0.7654 | 0.7947 | 0.8186 | 0.8930 | 0.8230 |
| DrivFace | 0.5864 | 0.8057 | 0.7891 | 0.7689 | 0.8094 |
| Carcinom | 0.6519 | 0.6034 | 0.7206 | 0.7099 | 0.7315 |
| LSVT | 0.7941 | 0.7705 | 0.8168 | 0.7824 | 0.8433 |
| Madelon | 0.5990 | 0.5230 | 0.5390 | 0.6120 | 0.6220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhou, S. Kernel Partial Least Squares Feature Selection Based on Maximum Weight Minimum Redundancy. Entropy 2023, 25, 325. https://doi.org/10.3390/e25020325
Liu X, Zhou S. Kernel Partial Least Squares Feature Selection Based on Maximum Weight Minimum Redundancy. Entropy. 2023; 25(2):325. https://doi.org/10.3390/e25020325
Chicago/Turabian StyleLiu, Xiling, and Shuisheng Zhou. 2023. "Kernel Partial Least Squares Feature Selection Based on Maximum Weight Minimum Redundancy" Entropy 25, no. 2: 325. https://doi.org/10.3390/e25020325
APA StyleLiu, X., & Zhou, S. (2023). Kernel Partial Least Squares Feature Selection Based on Maximum Weight Minimum Redundancy. Entropy, 25(2), 325. https://doi.org/10.3390/e25020325







