Kullback–Leibler Divergence of an Open-Queuing Network of a Cell-Signal-Transduction Cascade
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Culture
2.2. Antibody Array Assay
3. Results
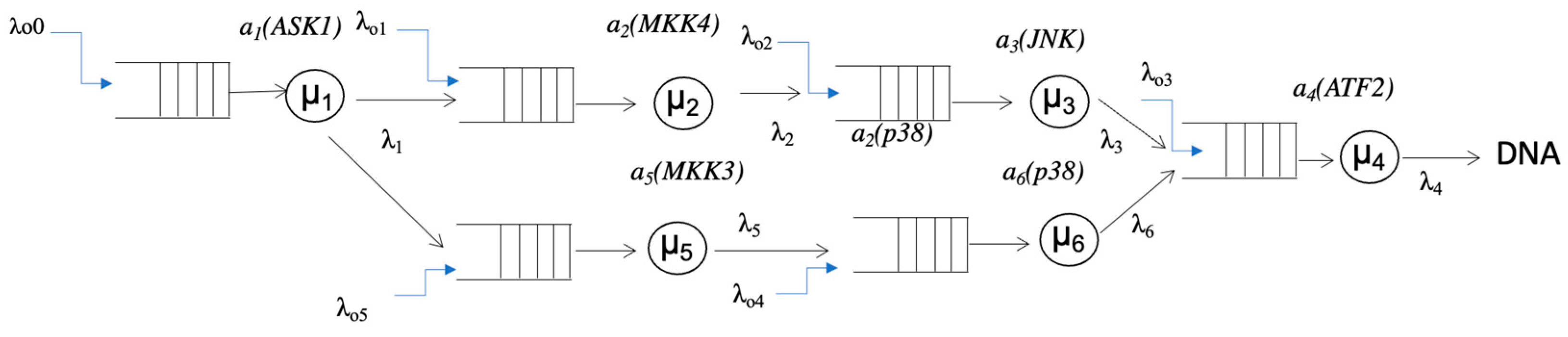
3.1. Queueing Model of Signal Transduction
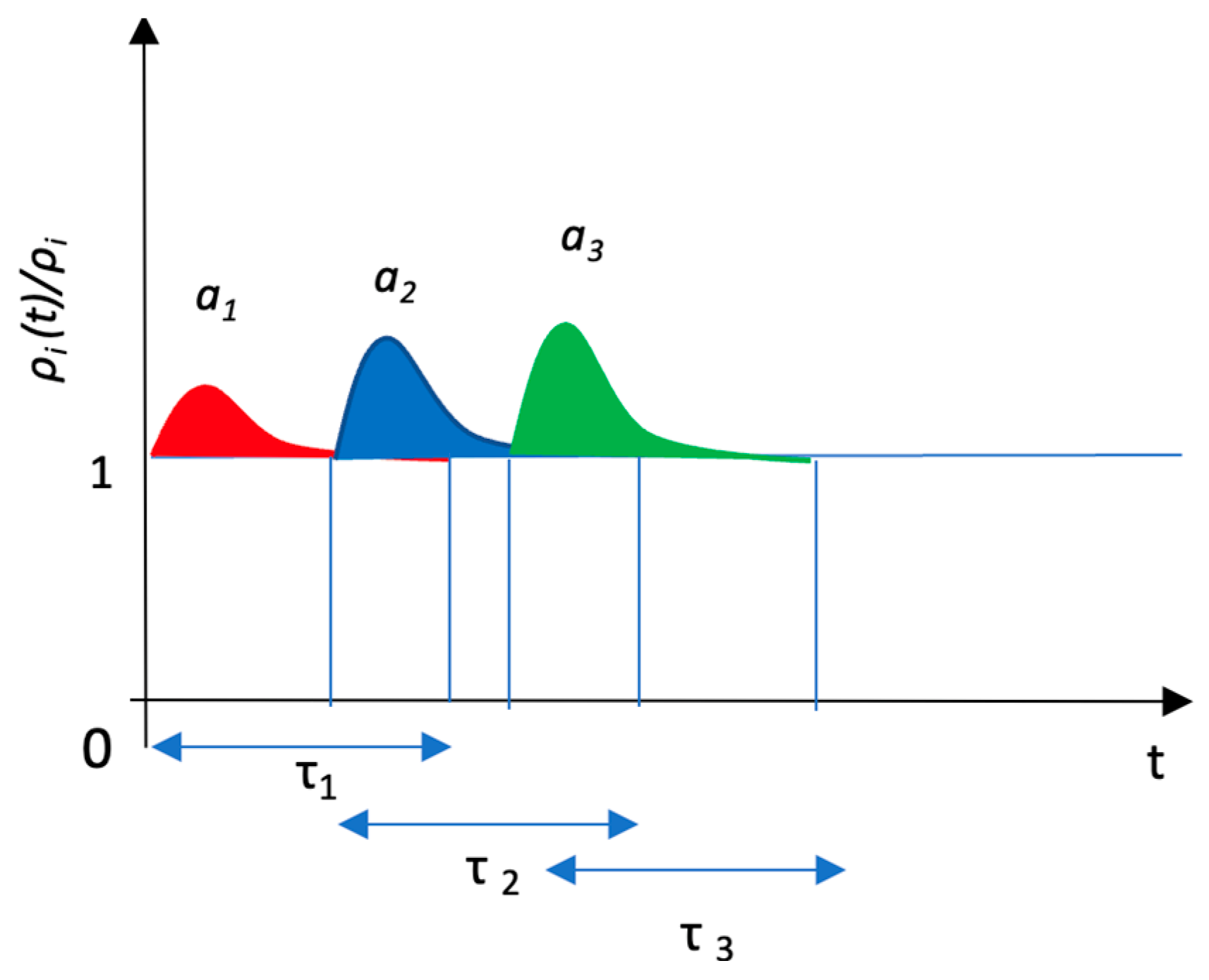
3.2. Kullback–Leibler Divergence of JQN
3.3. Chemical Potential in JQN
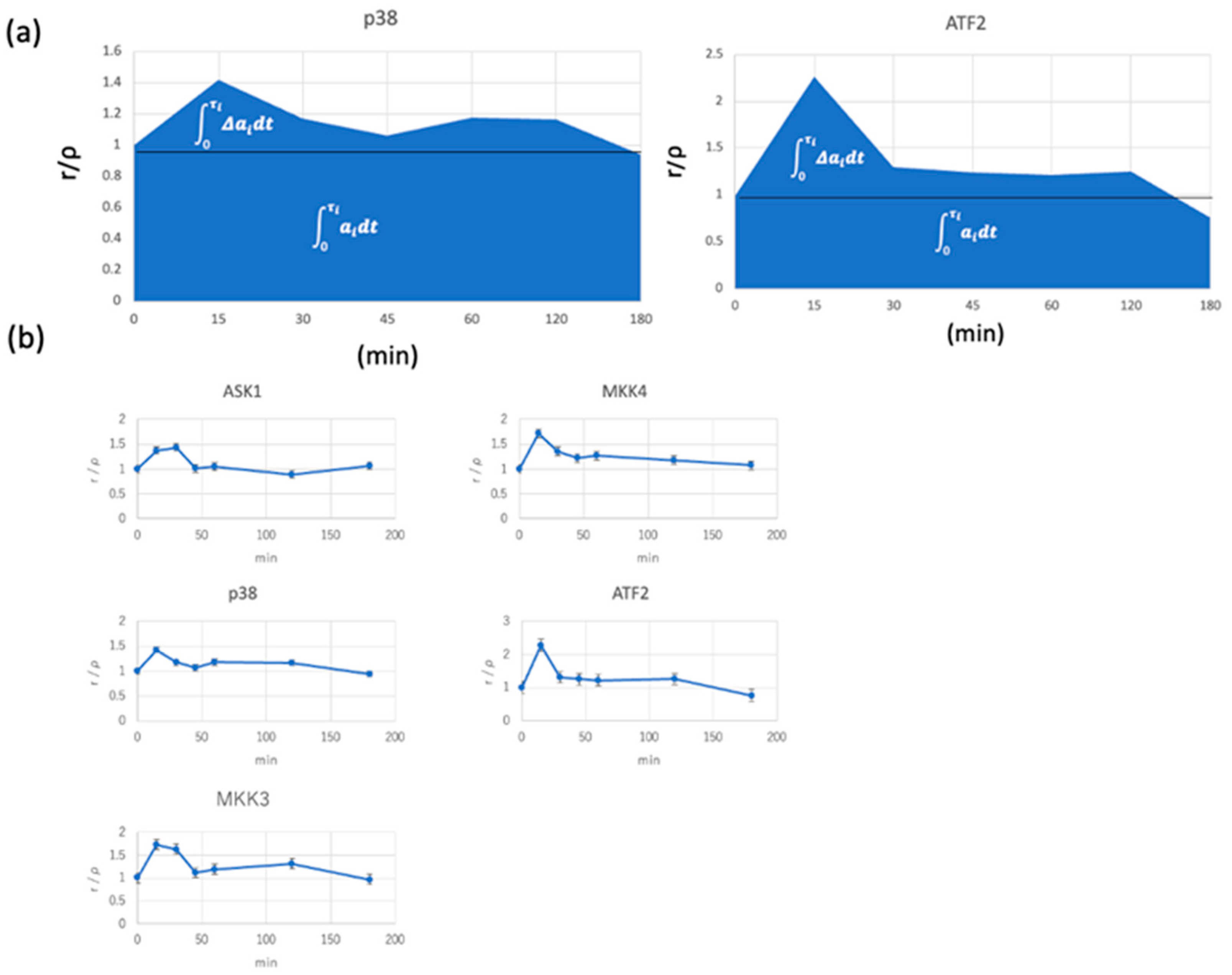
3.4. Application of KLD Theory to Signal-Transduction Analysis
4. Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation for Equation (18) in the Text
References
- Liu, A.C.H.; Cathelin, S.; Yang, Y.; Dai, D.L.; Manikoth Ayyathan, D.; Hosseini, M.; Minden, M.D.; Tierens, A.; Chan, S.M. Targeting STAT5 signaling overcomes resistance to IDH inhibitors in acute myeloid leukemia through suppression of stemness. Cancer Res. 2022, 82, 4325–4339. [Google Scholar] [CrossRef]
- Vilaplana, J.; Solsona, F.; Abella; Filgueira, R.; Rius, J. The cloud paradigm applied to e-Health. BMC Med. Inform. Decis. Mak. 2013, 13, 35. [Google Scholar] [CrossRef]
- Barankai, N.; Fekete, A.; Vattay, G. Effect of network structure on phase transitions in queuing networks. Phys. Rev. E 2012, 86, 066111. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.J.; Wu, C. Mathematically modelling the effects of pacing, finger strategies and urgency on numerical typing performance with queuing network model human processor. Ergonomics 2012, 55, 1180–1204. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y. Queuing network modeling of the psychological refractory period (PRP). Psychol. Rev. 2008, 115, 913–954. [Google Scholar] [CrossRef]
- Koizumi, N.; Kuno, E.; Smith, T.E. Modeling patient flows using a queuing network with blocking. Health Care Manag. Sci. 2005, 8, 49–60. [Google Scholar] [CrossRef]
- Kendall, D.G. Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain. Ann. Math. Statist. 1953, 24, 338–354. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Kulkarni, R.V. Stochastic gene expression conditioned on large deviations. Phys. Biol. 2017, 14, 03LT01. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.W.; Kim, S.M.; Chae, Y.M.; Song, Y.U. Application of Queueing Theory to the Analysis of Changes in Outpatients’ Waiting Times in Hospitals Introducing EMR. Healthc. Inform. Res. 2017, 23, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Franco, C.; Herazo-Padilla, N.; Castañeda, J.A. A queueing Network approach for capacity planning and patient Scheduling: A case study for the COVID-19 vaccination process in Colombia. Vaccine 2022, 40, 7073–7086. [Google Scholar] [CrossRef]
- Qureshi, S.M.; Bookey-Bassett, S.; Purdy, N.; Greig, M.A.; Kelly, H.; Neumann, W.P. Modelling the impacts of COVID-19 on nurse workload and quality of care using process simulation. PLoS ONE 2022, 17, e0275890. [Google Scholar] [CrossRef]
- Lee, K.H.; Kimmel, M. Analysis of two mechanisms of telomere maintenance based on the theory of g-Networks and stochastic automata networks. BMC Genom. 2020, 21, 587. [Google Scholar] [CrossRef] [PubMed]
- Stein, V.; Alexandrov, K. Protease-based synthetic sensing and signal amplification. Proc. Natl. Acad. Sci. USA 2014, 111, 15934–15939. [Google Scholar] [CrossRef] [PubMed]
- Steiner, P.J.; Williams, R.J.; Hasty, J.; Tsimring, L.S. Criticality and Adaptivity in Enzymatic Networks. Biophys. J. 2016, 111, 1078–1087. [Google Scholar] [CrossRef] [PubMed]
- Hochendoner, P.; Ogle, C.; Mather, W.H. A queueing approach to multi-site enzyme kinetics. Interface Focus 2014, 4, 20130077. [Google Scholar] [CrossRef] [PubMed]
- Clement, E.J.; Schulze, T.T.; Soliman, G.A.; Wysocki, B.J.; Davis, P.H.; Wysocki, T.A. Stochastic Simulation of Cellular Metabolism. IEEE Access 2020, 8, 79734–79744. [Google Scholar] [CrossRef] [PubMed]
- Kloska, S.M.; Pałczyński, K.; Marciniak, T.; Talaśka, T.; Miller, M.; Wysocki, B.J.; Davis, P.H.; Soliman, G.A.; Wysocki, T.A. Queueing theory model of mTOR complexes’ impact on Akt-mediated adipocytes response to insulin. PLoS ONE 2022, 17, e0279573. [Google Scholar] [CrossRef]
- Ayub, Q.; Ngadi, A.; Rashid, S.; Habib, H.A. Priority Queue Based Reactive Buffer Management Policy for Delay Tolerant Network under City Based Environments. PLoS ONE 2018, 13, e0191580. [Google Scholar] [CrossRef]
- Cho, W.K.; Min, B.; Goh, K.I.; Kim, I.M. Generalized priority-queue network dynamics: Impact of team and hierarchy. Phys. Rev. E 2010, 81, 066109. [Google Scholar] [CrossRef]
- Jackson, J.R. Jobshop-Like Queueing Systems. Manag. Sci. 1963, 10, 131–142. [Google Scholar] [CrossRef]
- Tsuruyama, T. Nonlinear thermodynamics of biological signal transduction for predicting conservation of entropy production rate. J. Theor. Biol. 2021, 523, 110716. [Google Scholar] [CrossRef]
- Tsuruyama, T. Non-equilibrium thermodynamics of biological signal transduction predicts conservation of entropy production rate. J. Theor. Biol. 2019, 472, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Kiso-Farnè, K.; Tsuruyama, T. Epidermal growth factor receptor cascade prioritizes the maximization of signal transduction. Sci. Rep. 2022, 12, 16950. [Google Scholar] [CrossRef]
- Bristamas, D.; Nakazato, D. The distributional Little’s law and its applications. Oper. Res. 1992, 43, 298–310. [Google Scholar]
- Aarabi, P. Localization-based sensor validation using the Kullback-Leibler divergence. IEEE Trans. Syst. Man Cybern. B Cybern. 2004, 34, 1007–1016. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.P.; Ghosh, M. A Kullback-Leibler Divergence for Bayesian Model Diagnostics. Open J. Stat. 2011, 1, 172–184. [Google Scholar] [CrossRef]
- Cannon, L.; Garcia, C.A.V.; Piovoso, M.J.; Zurakowski, R. Prospective HIV Clinical Trial Comparison by Expected Kullback-Leibler Divergence. Proc. Am. Control Conf. 2016, 2016, 1295–1300. [Google Scholar] [CrossRef] [PubMed]
- Seghouane, A.K.; Amari, S. The AIC criterion and symmetrizing the Kullback-Leibler divergence. IEEE Trans. Neural Netw. 2007, 18, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Roldan, E.; Parrondo, J.M. Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems. Phys. Rev. E 2012, 85, 031129. [Google Scholar] [CrossRef]
- Tsuruyama, T. Analysis of Cell Signal Transduction Based on Kullback–Leibler Divergence: Channel Capacity and Conservation of Its Production Rate during Cascade. Entropy 2018, 20, 438. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Qiao, L.; Nachbar, R.B.; Kevrekidis, I.G.; Shvartsman, S.Y. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLoS Comput. Biol. 2007, 3, 1819–1826. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ubl, J.J.; Stricker, R.; Reiser, G. Thrombin (PAR-1)-induced proliferation in astrocytes via MAPK involves multiple signaling pathways. Am. J. Physiol. Cell Physiol. 2002, 283, C1351–C1364. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S.; Liu, S.; Liu, Y.J.; Liu, J.W.; Liu, T.J.; Wang, X.Q.; Yan, Q. Overexpression of fucosyltransferase IV promotes A431 cell proliferation through activating MAPK and PI3K/Akt signaling pathways. J. Cell Physiol. 2010, 225, 612–619. [Google Scholar] [CrossRef]
- Yoon, J.; Deisboeck, T.S. Investigating differential dynamics of the MAPK signaling cascade using a multi-parametric global sensitivity analysis. PLoS ONE 2009, 4, e4560. [Google Scholar] [CrossRef]
- Yu, Y.; Fan, S.M.; Ye, Y.C.; Tashiro, S.; Onodera, S.; Ikejima, T. The tyrphostin AG1478 augments oridonin-induced A431 cell apoptosis by blockage of JNK MAPK and enhancement of oxidative stress. Free Radic. Res. 2012, 46, 1393–1405. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Kang, S.; Liu, C.; Hao, Y. Resveratrol enhances the effects of ALA-PDT on skin squamous cells A431 through p38/ MAPK signaling pathway. Cancer Biomark. 2018, 21, 797–803. [Google Scholar] [CrossRef]
- Xin, X.; Zhou, L.; Reyes, C.M.; Liu, F.; Dong, L.Q. APPL1 mediates adiponectin-stimulated p38 MAPK activation by scaffolding the TAK1-MKK3-p38 MAPK pathway. Am. J. Physiol. Metab. 2011, 300, E103–E110. [Google Scholar] [CrossRef]
- Llopis, A.; Salvador, N.; Ercilla, A.; Guaita-Esteruelas, S.; Barrantes Idel, B.; Gupta, J.; Gaestel, M.; Davis, R.J.; Nebreda, A.R.; Agell, N. The stress-activated protein kinases p38α/β and JNK1/2 cooperate with Chk1 to inhibit mitotic entry upon DNA replication arrest. Cell Cycle 2012, 11, 3627–3637. [Google Scholar] [CrossRef]
- Nebreda, A.R.; Porras, A. p38 MAP kinases: Beyond the stress response. Trends Biochem. Sci. 2000, 25, 257–260. [Google Scholar] [CrossRef]
- Kyriakis, J.M.; Avruch, J. Mammalian MAPK signal transduction pathways activated by stress and inflammation: A 10-year update. Physiol. Rev. 2012, 92, 689–737. [Google Scholar] [CrossRef] [PubMed]
- Tsuruyama, T. The Conservation of Average Entropy Production Rate in a Model of Signal Transduction: Information Thermodynamics Based on the Fluctuation Theorem. Entropy 2018, 20, 303. [Google Scholar] [CrossRef] [PubMed]
| Mean (μ) | Standard Deviation | |
|---|---|---|
| ASK1 (Phospho-Ser83) | 3.27 | 0.76 |
| MKK4 (Phospho-Thr261) | 3.43 | 0.70 |
| p38 (Phospho-Thr180) | 3.07 | 0.73 |
| MKK3(Phospho-Ser189) | 3.19 | 0.20 |
| ATF2(Phospho-Thr69 or 51) | 3.03 | 0.50 |
| Negative control | 0.00 | 0.00 |
| Δμ | Cohen’s Factor d | |
| ASK1 (Phospho-Ser83)-MKK4 (Phospho-Th261) | 0.16 | 0.22 |
| MKK4 (Phospho-Th261)-p38 (Phospho-Thr183) | 0.36 | 0.50 |
| MKK3(Phospho-Ser189)-p38 | 0.12 | 0.22 |
| p38 (Phospho-Thr183)-ATF2(Phospho-Thr69 or 51) | 0.04 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuruyama, T. Kullback–Leibler Divergence of an Open-Queuing Network of a Cell-Signal-Transduction Cascade. Entropy 2023, 25, 326. https://doi.org/10.3390/e25020326
Tsuruyama T. Kullback–Leibler Divergence of an Open-Queuing Network of a Cell-Signal-Transduction Cascade. Entropy. 2023; 25(2):326. https://doi.org/10.3390/e25020326
Chicago/Turabian StyleTsuruyama, Tatsuaki. 2023. "Kullback–Leibler Divergence of an Open-Queuing Network of a Cell-Signal-Transduction Cascade" Entropy 25, no. 2: 326. https://doi.org/10.3390/e25020326
APA StyleTsuruyama, T. (2023). Kullback–Leibler Divergence of an Open-Queuing Network of a Cell-Signal-Transduction Cascade. Entropy, 25(2), 326. https://doi.org/10.3390/e25020326





