Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning
Abstract
1. Introduction
2. Fuzzy-Type Support Vector Machines and Fuzzy Membership Functions
2.1. Fuzzy-Type Support Vector Machines (FSVMs)
2.2. Common Fuzzy MFs and Their Limitations for Class Imbalance Learning
2.3. Intuitionistic Fuzzy MF and Its Limitation for Class Imbalance Learning
- (1)
- Membership Function:
- (2)
- Nonmembership Function:
- To provide a more reliable measure to estimate the importance of each instance.
- To propose a more preferable fuzzy MF to ensure the fairness of the classification method.
3. Relative Density-Based Intuitionistic Fuzzy Support Vector Machines (RIFSVM)
3.1. Relative Density Estimate Based on a k-Nearest-Neighbor Distances
- (1)
- The within-class relative density refers to the relative density of an instance in its own class. For example, the within-class relative density of positive instance is , the is the distance between and the -th nearest neighbor in the positive instances, where . The larger the value of , the lower the relative density of the instance, then the lower the probability that the instance belongs to this class.
- (2)
- The between-class relative density refers to the relative density of an instance in another class. The between-class relative density of positive instance , for instance, is , the is the distance between and the -th nearest neighbor in the negative instances, where . The larger the value of , the lower the relative density of the instance, then the farther is from the negative instances, that is the lower the probability that the instance belongs to the negative class.
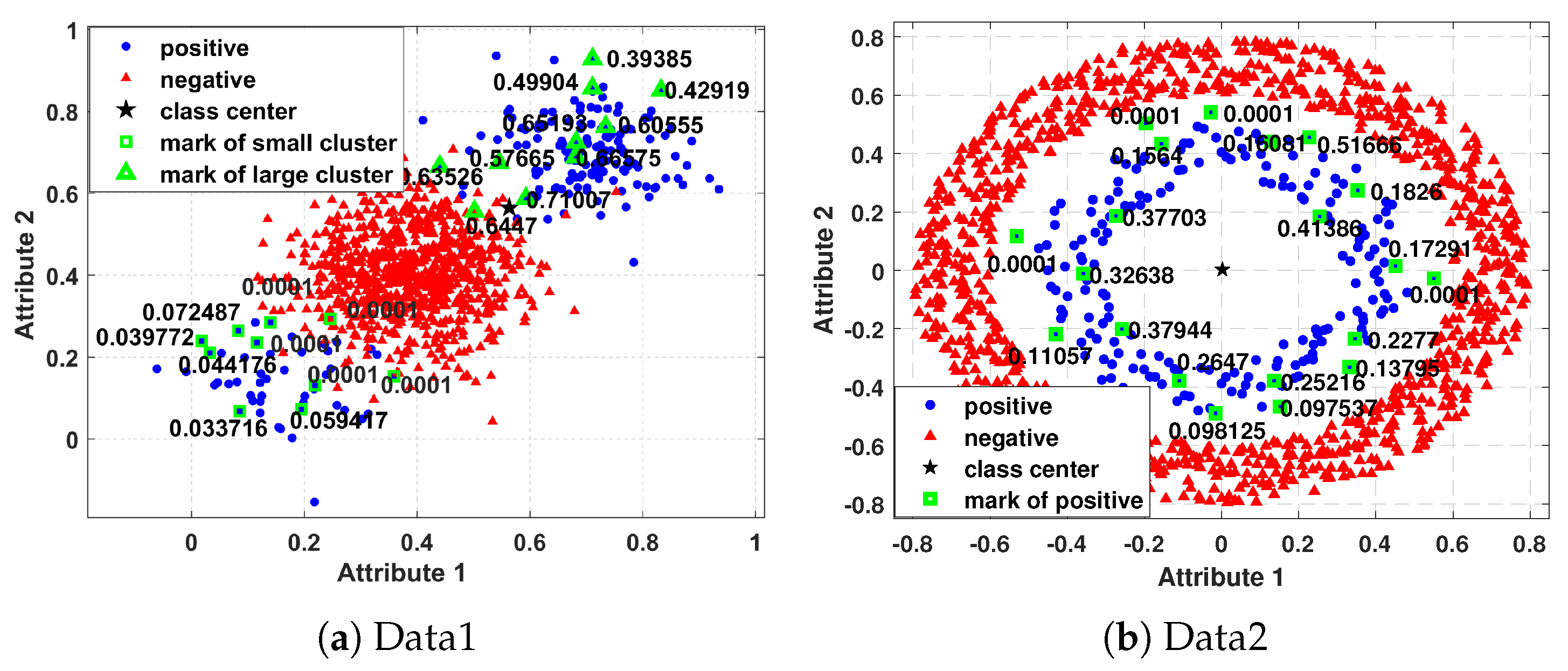
3.2. Relative Density-Based Intuitionistic MFs for Class Imbalance Learning
- to lessen the impact of class imbalance;
- to reduce the negative impact of noise and outliers.
- (1)
- Determination of fuzzy value of majority class
- (2)
- Determination of fuzzy value of minority class
3.3. Relative Density-Based Intuitionistic Fuzzy Support Vector Machines
| Algorithm 1 RIFSVM algorithm |
|
4. Experiments and Analysis
4.1. Evaluation Metrics for Imbalanced Classification
4.2. Experiments on the Synthetic Imbalanced Datasets
4.3. Experiments on Benchmark Datasets
4.3.1. Experimental Procedure and Results
- (1)
- IFSVM [20]: It uses the membership and non-membership calculated by the sample distribution information to determine the fuzzy value of the instance. The parameter , and , where .
- (2)
- ACFSVM [26]: It assigns the fuzzy value to the majority class instances based on the affinity and class probability and assigns 1 as the fuzzy value of minority class instances to highlight the importance of minority instances. The kernel nearest neighbor parameter k is chosen from the set and the parameter is selected from the set .
- (3)
- GFSVM [25]: It is the supplement and extension of FSVM-CIL, a new distance and a new fuzzy value function, namely Gaussian fuzzy function, is proposed. The parameters and in the Gaussian function are selected from sets and , respectively.
- (4)
- EFTWSVM [27]: It uses the information entropy of instances to calculate fuzzy values to minority instances, it fully utilizes the prior information of instances; it assigns 1 as the fuzzy value of minority class instances. Then the fuzzy values obtained are used in the improved TWSVM. The parameters of EFTWSVM is taken as 0.05, the value of K for K-NN is 10.
- (5)
- RFLSTSVM [28]: It assigns a more robust fuzzy value to majority class instances and assigns 1 as the fuzzy value of minority class instances, then trains the LSTSVM model on this training set. The parameter of RFLSTSVM is selected from the set .
- (6)
- FSVM-WD and FSVM-BD [29]: They are all proposed based on relative density, and the sum of fuzzy values of positive and negative class instances is set as 1 to ensure the robustness of the model. The distinction is that while FSVM-WD is based on information about within-class relative densities, FSVM-BD is based on the between-class relative densities. These two methods use the same strategy to calculate the fuzzy values of instances. The parameters of them are set as , .
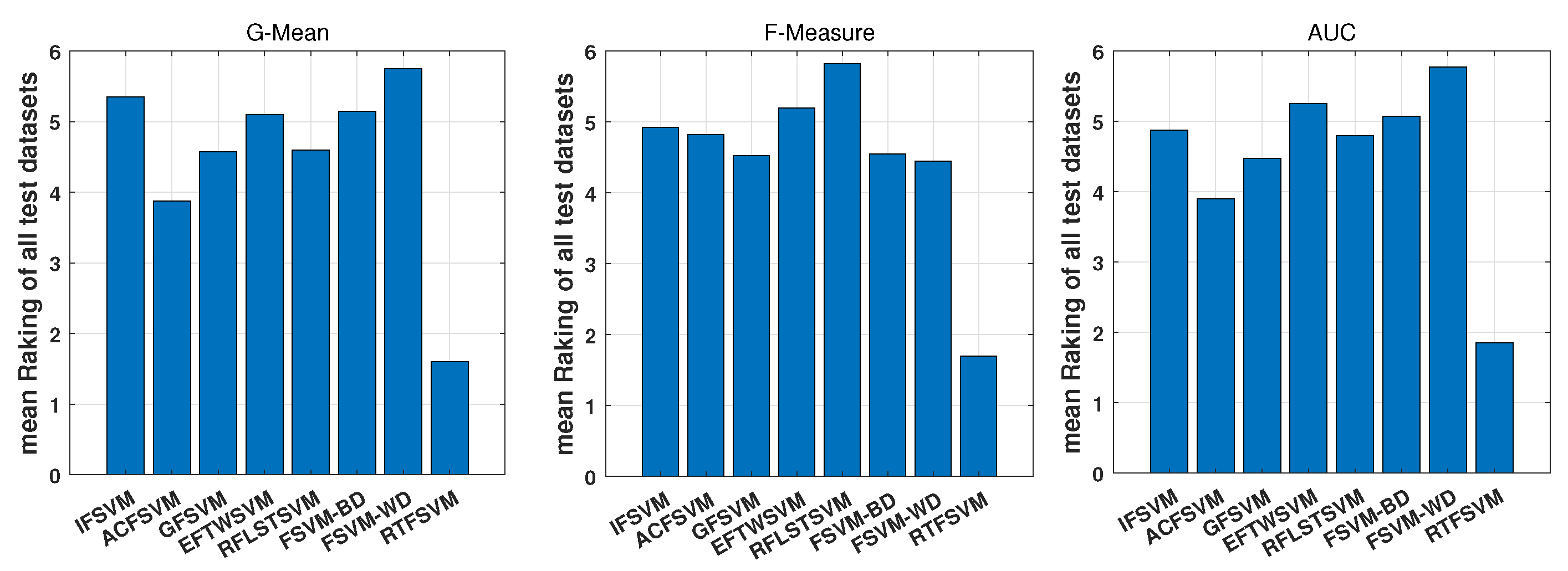
4.3.2. Statistical Comparisons by Friedman Test
4.3.3. Influences of Parameter k on the Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raghuwanshi, B.S.; Shukla, S. Class-specific extreme learning machine for handling binary class imbalance problem. Neural Netw. 2018, 105, 206–217. [Google Scholar] [CrossRef] [PubMed]
- Tao, X.; Li, Q.; Guo, W.; Ren, C.; Li, C.; Liu, R.; Zou, J. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification. Inf. Sci. 2019, 487, 31–56. [Google Scholar] [CrossRef]
- Romani, M.; Vigliante, M.; Faedda, N.; Rossetti, S.; Pezzuti, L.; Guidetti, V.; Cardona, F. Face memory and face recognition in children and adolescents with attention deficit hyperactivity disorder: A systematic review. Neurosci. Biobehav. Rev. 2018, 89, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Laxmi, S.; Gupta, S.K. Multi-category intuitionistic fuzzy twin support vector machines with an application to plant leaf recognition. Eng. Appl. Artif. Intell. Int. J. Intell.-Real-Time Autom. 2022, 110, 110. [Google Scholar] [CrossRef]
- Yadav, A.; Singh, A.; Dutta, M.K.; Travieso, C.M. Machine learning-based classification of cardiac diseases from PCG recorded heart sounds. Neural Comput. Appl. 2019, 32, 17843–17856. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Z. Feature extraction by PCA and diagnosis of breast tumors using SVM with DE-based parameter tuning. Int. J. Mach. Learn. Cybern. 2019, 10, 591–601. [Google Scholar] [CrossRef]
- Yi, M.; Zhou, C.; Yang, L.; Yang, J.; Tang, T.; Jia, Y.; Yuan, X. Bearing Fault Diagnosis Method Based on RCMFDE-SPLR and Ocean Predator Algorithm Optimizing Support Vector Machine. Entropy 2022, 24, 1696. [Google Scholar] [CrossRef] [PubMed]
- Jurgovsky, J.; Granitzer, M.; Ziegler, K.; Calabretto, S.; Portier, P.E.; He-Guelton, L.; Caelen, O. Sequence Classification for Credit-Card Fraud Detection. Expert Syst. Appl. 2018, 100, 234–245. [Google Scholar] [CrossRef]
- Carneiro, N.; Figueira, G.; Costa, M. A data mining based system for credit-card fraud detection in e-tail. Decis. Support Syst. 2017, 95, 91–101. [Google Scholar] [CrossRef]
- Sebastiani, F. Machine learning in automated text categorization. ACM Comput. Surv. 2002, 34, 1–47. [Google Scholar] [CrossRef]
- Tan, S. Neighbor-weighted k-nearest neighbor for unbalanced text corpus. Expert Syst. Appl. 2005, 28, 667–671. [Google Scholar] [CrossRef]
- Rodríguez Alvarez, Y.; García Lorenzo, M.M.; Caballero Mota, Y.; Filiberto Cabrera, Y.; García Hilarión, I.M.; Machado Montes de Oca, D.; Bello Pérez, R. Fuzzy prototype selection-based classifiers for imbalanced data. Case study. Pattern Recognit. Lett. 2022, 163, 183–190. [Google Scholar] [CrossRef]
- Cherkassky, V. The nature of statistical learning theory. IEEE Trans. Neural Netw. 1997, 8, 1564. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Zhou, S.; Zhang, J.; Han, B.; Chen, Y.; Ye, F. Risk-Averse support vector classifier machine via moments penalization. Int. J. Mach. Learn. Cybern. 2022, 13, 3341–3358. [Google Scholar] [CrossRef]
- Boser, B.E. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Amsterdam, The Netherlands, 7–10 July 2008; Volume 5, pp. 144–152. [Google Scholar]
- Zhang, X. Using class-center vectors to build support vector machines. In Neural Networks for Signal Processing IX, Proceedings of the 1999 IEEE Signal Processing Society Workshop (Cat. No. 98TH8468), Madison, WI, USA, 25 August 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 3–11. [Google Scholar]
- Lin, C.F.; Wang, S.D. Fuzzy support vector machines. IEEE Trans. Neural Netw. 2002, 13, 464–471. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Ming-Hu, H.A.; Huang, S.; Wang, C.; Wang, X.L. Intuitionistic Fuzzy Support Vector Machine. J. Hebei Univ. Sci. Ed. 2011, 31, 226–229. [Google Scholar]
- Ha, M.; Wang, C.; Chen, J. The support vector machine based on intuitionistic fuzzy number and kernel function. Soft Comput. 2013, 17, 635–641. [Google Scholar] [CrossRef]
- Rezvani, S.; Wang, X.; Pourpanah, F. Intuitionistic Fuzzy Twin Support Vector Machines. IEEE Trans. Fuzzy Syst. 2019, 27, 2140–2151. [Google Scholar] [CrossRef]
- Rezvani, S.; Wang, X. Class imbalance learning using fuzzy ART and intuitionistic fuzzy twin support vector machines. Inf. Sci. 2021, 578, 659–682. [Google Scholar] [CrossRef]
- Batuwita, R.; Palade, V. FSVM-CIL: Fuzzy support vector machines for class imbalance learning. IEEE Trans. Fuzzy Syst. 2010, 18, 558–571. [Google Scholar] [CrossRef]
- Liu, J. Fuzzy support vector machine for imbalanced data with borderline noise. Fuzzy Sets Syst. 2021, 413, 64–73. [Google Scholar] [CrossRef]
- Borah, P.; Gupta, D. Affinity and transformed class probability-based fuzzy least squares support vector machines. Fuzzy Sets Syst. 2022, 443, 203–235. [Google Scholar] [CrossRef]
- Deepak, G.; Bharat, R.; Parashjyoti, B. A fuzzy twin support vector machine based on information entropy for class imbalance learning. Neural Comput. Appl. 2018, 31, 7153–7164. [Google Scholar]
- Richhariya, B.; Tanveer, M. A robust fuzzy least squares twin support vector machine for class imbalance learning. Appl. Soft Comput. 2018, 71, 418–432. [Google Scholar] [CrossRef]
- Yu, H.; Changyin, S.; Yang, X.; Zheng, S.; Zou, H. Fuzzy Support Vector Machine With Relative Density Information for Classifying Imbalanced Data. IEEE Trans. Fuzzy Syst. 2019, 27, 2353–2367. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdu, S. Divergence Estimation for Multidimensional Densities Via k-Nearest-Neighbor Distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Fukunaga, K.; Hostetler, L. Optimization of k nearest neighbor density estimates. IEEE Trans. Inf. Theory 2003, 19, 320–326. [Google Scholar] [CrossRef]
- Lin, C.F.; Wang, S.D. Fuzzy Support Vector Machines with Automatic Membership Setting. In Support Vector Machines: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2005; Volume 177, pp. 251–253. [Google Scholar]
- Fan, Q.; Wang, Z.; Li, D.; Gao, D.; Zha, H. Entropy-based Fuzzy Support Vector Machine for Imbalanced Datasets. Knowl.-Based Syst. 2016, 115, 87–99. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, D.; Hualong, Y. Fuzzy weighted extreme learning machine for imbalanced software detect prediction. J. Jiangsu Univ. Sci. Technol. 2019, 33, 7. [Google Scholar]
- Biau, G.; Devroye, L. The k-nearest neighbor density estimate. In Lectures on the Nearest Neighbor Method; Springer International Publishing: Cham, Switzerland, 2015; pp. 25–32. [Google Scholar]
- Ron, K. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Demiar, J.; Schuurmans, D. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]

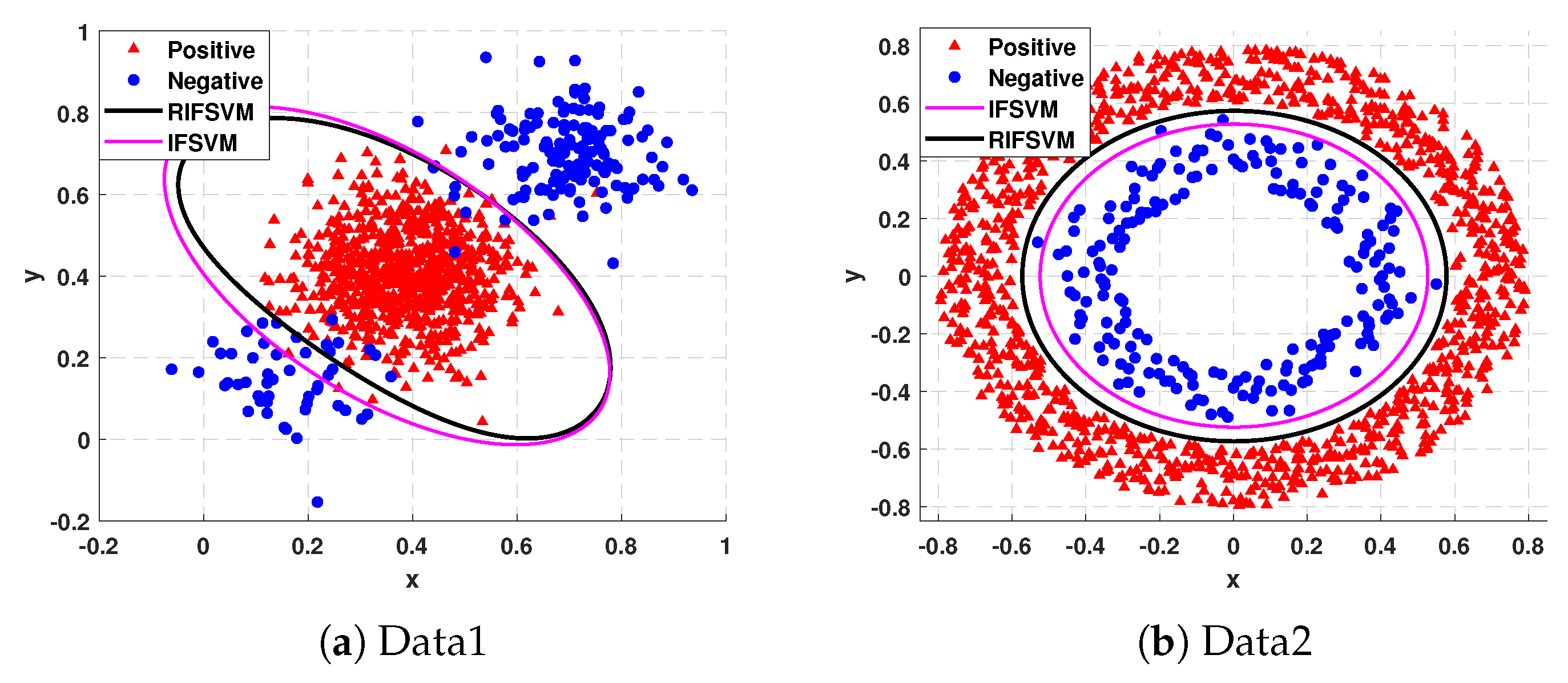



| Results (%) | Se | Sp | G-M | F-M | AUC | |
|---|---|---|---|---|---|---|
| Data 1 | IFSVM | 86.50 | 99.00 | 92.75 | 90.81 | 92.75 |
| RIFSVM | 92.50 | |||||
| Data 2 | IFSVM | 98.00 | 98.99 | 98.99 | 99.00 | |
| RIFSVM |
| Dataset | Feature | Instance | Positive | Negative | Minority Class | Majoritt Class | IR |
|---|---|---|---|---|---|---|---|
| Liver | 6 | 345 | 145 | 200 | class 1 | class 2 | 1:1.38 |
| Seed | 7 | 210 | 70 | 140 | class 1 | others | 1:2.00 |
| Wine | 13 | 178 | 48 | 130 | class 1 | others | 1:2.71 |
| Haberman | 3 | 306 | 81 | 225 | class 2 | class 1 | 1:2.78 |
| Glass | 4 | 150 | 50 | 100 | class 0,1,2,3 | class 4,5,6 | 1:3.19 |
| Vehicle | 18 | 846 | 199 | 647 | ‘van’ | others | 1:3.25 |
| Abalone | 8 | 326 | 67 | 259 | class 16 | class 6 | 1:3.86 |
| Ecoli | 7 | 336 | 52 | 284 | ‘pp’ | others | 1:5.46 |
| Balance | 4 | 625 | 49 | 576 | ‘B’ | others | 1:11.76 |
| Libra | 90 | 360 | 24 | 336 | class 15 | others | 1:14.00 |
| Yeast | 8 | 1484 | 429 | 1055 | class 2 | others | 1:2.46 |
| Yeast1 | 8 | 1484 | 163 | 1321 | class 4 | others | 1:8.10 |
| Yeast2 | 8 | 514 | 51 | 463 | class 5 | class 1 | 1:9.07 |
| Yeast3 | 8 | 464 | 35 | 429 | class 7 | class 2 | 1:12.25 |
| Yeast4 | 8 | 1484 | 44 | 1440 | class 6 | others | 1:32.72 |
| Yeast5 | 8 | 1484 | 35 | 1449 | class 7 | others | 1:41.40 |
| Block | 10 | 5473 | 560 | 4913 | others | class 1 | 1:8.77 |
| Block1 | 10 | 5473 | 329 | 5144 | class 2 | others | 1:9.07 |
| Block2 | 10 | 5144 | 231 | 4913 | class 3,4,5 | class 1 | 1:21.27 |
| Block3 | 10 | 5028 | 115 | 4913 | class 5 | class 1 | 1:42.72 |
| Dataset | Results | IF SVM | ACF SVM | GF SVM | ETW SVM | RFLST SVM | FSVM -BD | FSVM -WD | RIF SVM |
|---|---|---|---|---|---|---|---|---|---|
| Liver | Gm | 67.82 | 60.10 | 64.48 | 66.52 | 65.85 | 67.47 | 64.33 | |
| F | 62.08 | 58.00 | 61.55 | 60.41 | 61.54 | 58.18 | 64.00 | ||
| AUC | 69.90 | 66.21 | 65.96 | 68.47 | 68.88 | 68.84 | 65.09 | 71.34 | |
| Seed | Gm | 89.21 | 93.62 | 92.44 | 93.65 | 93.33 | 87.04 | 91.05 | |
| F | 85.71 | 91.20 | 89.40 | 89.42 | 89.53 | 84.62 | 88.89 | ||
| AUC | 89.29 | 93.89 | 92.50 | 93.39 | 93.75 | 87.50 | 91.01 | ||
| Wine | Gm | 88.19 | 96.17 | 93.24 | 91.35 | 88.19 | 94.28 | 87.71 | |
| F | 87.50 | 93.55 | 91.58 | 88.50 | 87.50 | 94.12 | 75.00 | ||
| AUC | 88.89 | 96.24 | 93.80 | 91.79 | 88.89 | 94.44 | 88.46 | ||
| haberman | Gm | 57.01 | 62.43 | 61.57 | 63.65 | 67.96 | 65.83 | 62.36 | |
| F | 42.86 | 47.24 | 46.43 | 48.45 | 52.72 | 53.33 | 50.00 | ||
| AUC | 62.08 | 62.88 | 63.23 | 64.10 | 68.10 | 68.33 | 66.32 | ||
| Glass | Gm | 79.96 | 77.17 | 79.95 | 69.30 | 69.82 | 80.14 | ||
| F | 60.95 | 40.61 | 62.67 | 32.22 | 33.67 | 72.30 | |||
| AUC | 81.28 | 77.82 | 81.28 | 70.64 | 71.82 | 80.13 | |||
| Vehicle | Gm | 96.64 | 94.98 | 98.14 | 96.63 | 96.64 | 97.94 | ||
| F | 94.87 | 90.82 | 96.85 | 95.45 | 94.91 | 96.20 | |||
| AUC | 96.66 | 94.99 | 98.14 | 96.68 | 96.66 | 97.94 | |||
| Abalone | Gm | 94.25 | 94.83 | 95.59 | 90.64 | 92.24 | 92.15 | 93.93 | |
| F | 84.49 | 84.84 | 85.55 | 78.62 | 79.27 | 82.62 | 81.25 | ||
| AUC | 94.34 | 94.92 | 95.69 | 90.66 | 92.38 | 92.23 | 94.12 | ||
| Ecoli | Gm | 90.24 | 92.21 | 93.46 | 93.42 | 94.14 | 92.58 | 85.53 | |
| F | 75.00 | 77.03 | 83.67 | 82.83 | 81.15 | 73.68 | 82.22 | ||
| AUC | 90.36 | 92.45 | 93.50 | 93.70 | 94.16 | 92.86 | 86.46 | ||
| Balance | Gm | 87.42 | 77.78 | 68.34 | 70.39 | 74.47 | |||
| F | 77.78 | 28.46 | 33.58 | 26.81 | 28.29 | ||||
| AUC | 88.00 | 80.26 | 74.22 | 74.64 | 75.61 | ||||
| Libra | Gm | 91.96 | 95.03 | 86.21 | 90.69 | 92.93 | 91.81 | 86.60 | |
| F | 91.43 | 62.44 | 79.28 | 82.22 | 87.30 | 89.21 | 85.71 | ||
| AUC | 92.50 | 95.13 | 87.05 | 91.98 | 93.38 | 92.35 | 87.50 | ||
| Yeast | Gm | 60.95 | 68.42 | 54.89 | 69.74 | 60.45 | 60.89 | 65.51 | |
| F | 49.31 | 52.82 | 42.57 | 57.29 | 46.81 | 49.65 | 53.75 | ||
| AUC | 65.30 | 67.28 | 62.04 | 70.00 | 62.87 | 65.61 | 67.71 | ||
| Yeast1 | Gm | 71.44 | 84.83 | 83.16 | 80.68 | 83.04 | 77.81 | 78.83 | |
| F | 59.52 | 67.53 | 70.77 | 70.86 | 56.82 | 67.83 | 57.49 | ||
| AUC | 73.82 | 85.03 | 84.04 | 82.11 | 83.19 | 79.99 | 80.82 | ||
| Yeast2 | Gm | 84.95 | 89.43 | 88.80 | 88.96 | 88.75 | 89.57 | 90.38 | |
| F | 72.73 | 80.72 | 82.81 | 84.21 | 70.50 | 75.00 | 70.77 | 85.71 | |
| AUC | 85.61 | 89.81 | 89.28 | 89.46 | 88.95 | 89.73 | 90.43 | ||
| Yeast3 | Gm | 91.93 | 84.02 | 84.02 | 80.65 | 81.02 | 89.44 | 89.56 | |
| F | 78.56 | 76.92 | 76.92 | 75.24 | 63.81 | 81.82 | |||
| AUC | 92.04 | 85.13 | 85.13 | 82.51 | 82.28 | 90.00 | 90.00 | ||
| Yeast4 | Gm | 83.01 | 81.54 | 81.76 | 83.06 | 82.09 | 78.78 | 78.78 | |
| F | 66.67 | 63.55 | 69.17 | 58.96 | 59.69 | 66.67 | 66.67 | ||
| AUC | 83.95 | 83.09 | 83.37 | 83.24 | 83.17 | 80.89 | 80.89 | ||
| Yeast5 | Gm | 49.73 | 68.07 | 65.04 | 64.92 | 60.27 | 61.14 | 53.27 | |
| F | 33.33 | 34.21 | 44.00 | 40.80 | 39.23 | 41.88 | 36.36 | ||
| AUC | 61.96 | 70.31 | 70.77 | 70.60 | 67.91 | 68.53 | 63.94 | ||
| Block | Gm | 90.86 | 94.06 | 93.08 | 93.76 | 94.23 | 89.03 | 87.32 | |
| F | 83.07 | 82.87 | 83.26 | 79.96 | 81.02 | 80.18 | 80.37 | ||
| AUC | 91.12 | 94.11 | 93.18 | 93.87 | 94.05 | 89.40 | 87.92 | ||
| Block1 | Gm | 93.28 | 93.78 | 93.47 | 92.66 | 89.73 | 92.41 | 93.09 | |
| F | 87.60 | 79.15 | 77.69 | 81.23 | 77.79 | 79.17 | 86.15 | ||
| AUC | 93.46 | 93.88 | 93.59 | 92.87 | 90.12 | 92.64 | 93.28 | ||
| Block2 | Gm | 80.43 | 93.44 | 89.57 | 93.33 | 87.82 | 85.80 | 93.06 | |
| F | 65.22 | 65.29 | 64.58 | 65.98 | 63.20 | 63.34 | 65.37 | ||
| AUC | 82.20 | 89.97 | 93.40 | 93.72 | 89.59 | 86.75 | 93.09 | ||
| Block3 | Gm | 85.67 | 87.69 | 83.62 | 82.98 | 81.78 | 74.72 | 71.97 | |
| F | 78.16 | 50.19 | 49.22 | 53.99 | 53.39 | 50.04 | 50.06 | ||
| AUC | 86.60 | 88.30 | 84.59 | 84.13 | 83.21 | 84.40 | 75.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Zhou, S.; Zhang, D.; Chen, L. Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning. Entropy 2023, 25, 34. https://doi.org/10.3390/e25010034
Fu C, Zhou S, Zhang D, Chen L. Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning. Entropy. 2023; 25(1):34. https://doi.org/10.3390/e25010034
Chicago/Turabian StyleFu, Cui, Shuisheng Zhou, Dan Zhang, and Li Chen. 2023. "Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning" Entropy 25, no. 1: 34. https://doi.org/10.3390/e25010034
APA StyleFu, C., Zhou, S., Zhang, D., & Chen, L. (2023). Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning. Entropy, 25(1), 34. https://doi.org/10.3390/e25010034







