Behavioral Propagation Based on Passionate Psychology on Single Networks with Limited Contact
Abstract
:1. Introduction
2. Materials and Methods
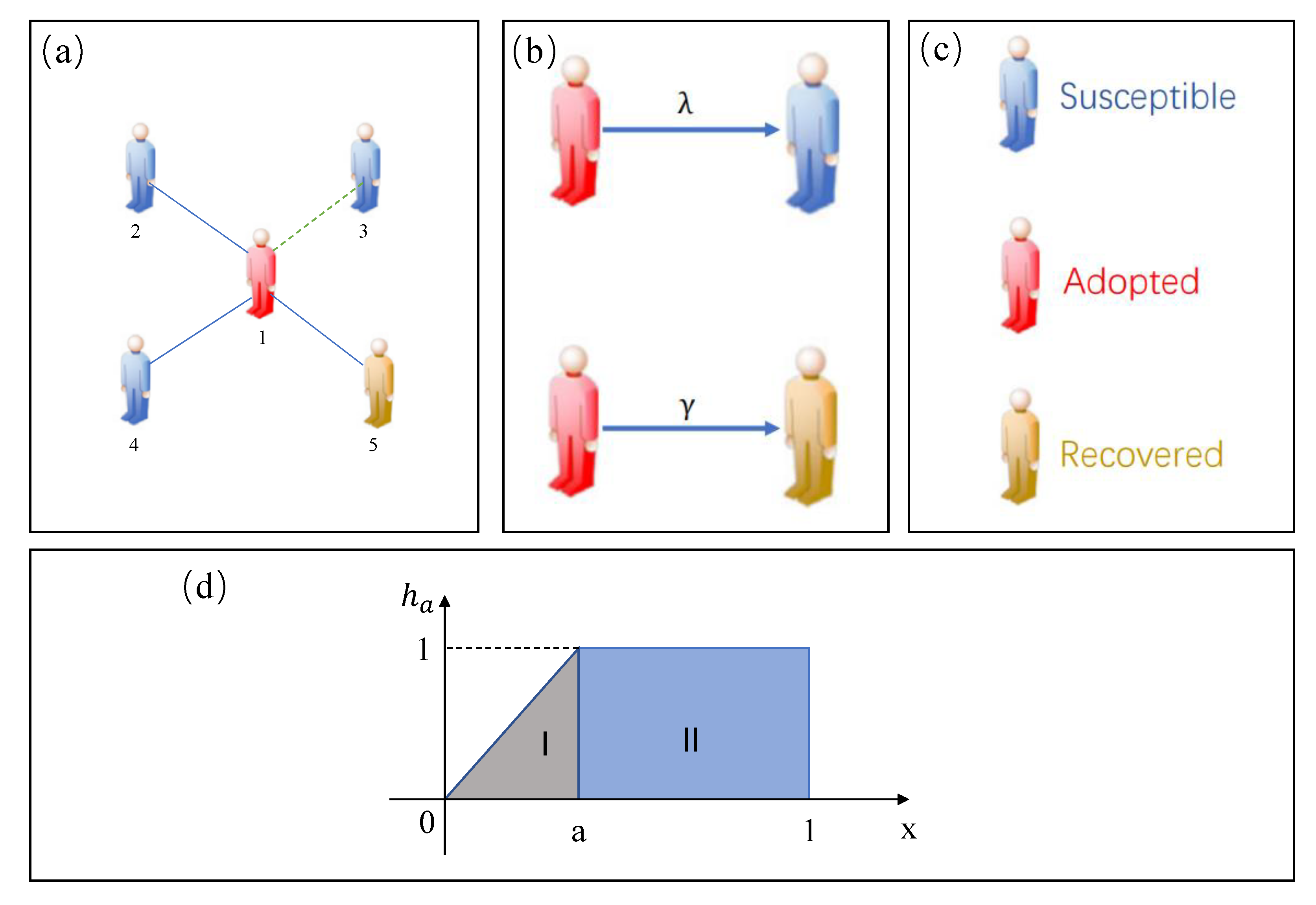
2.1. Model Descriptions
2.2. Theory Analysis
2.3. Parameter Settings
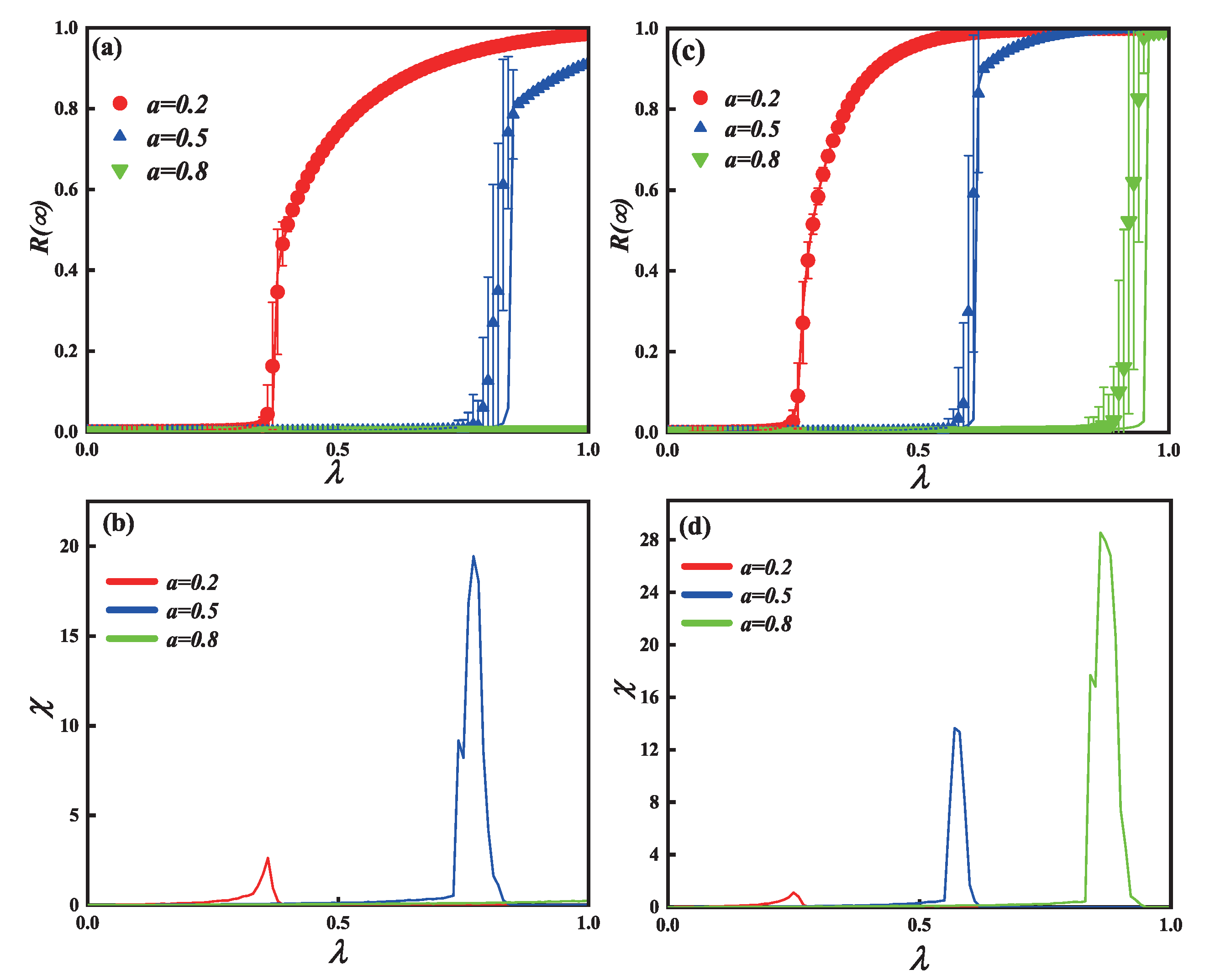
3. Simulation and Discussion
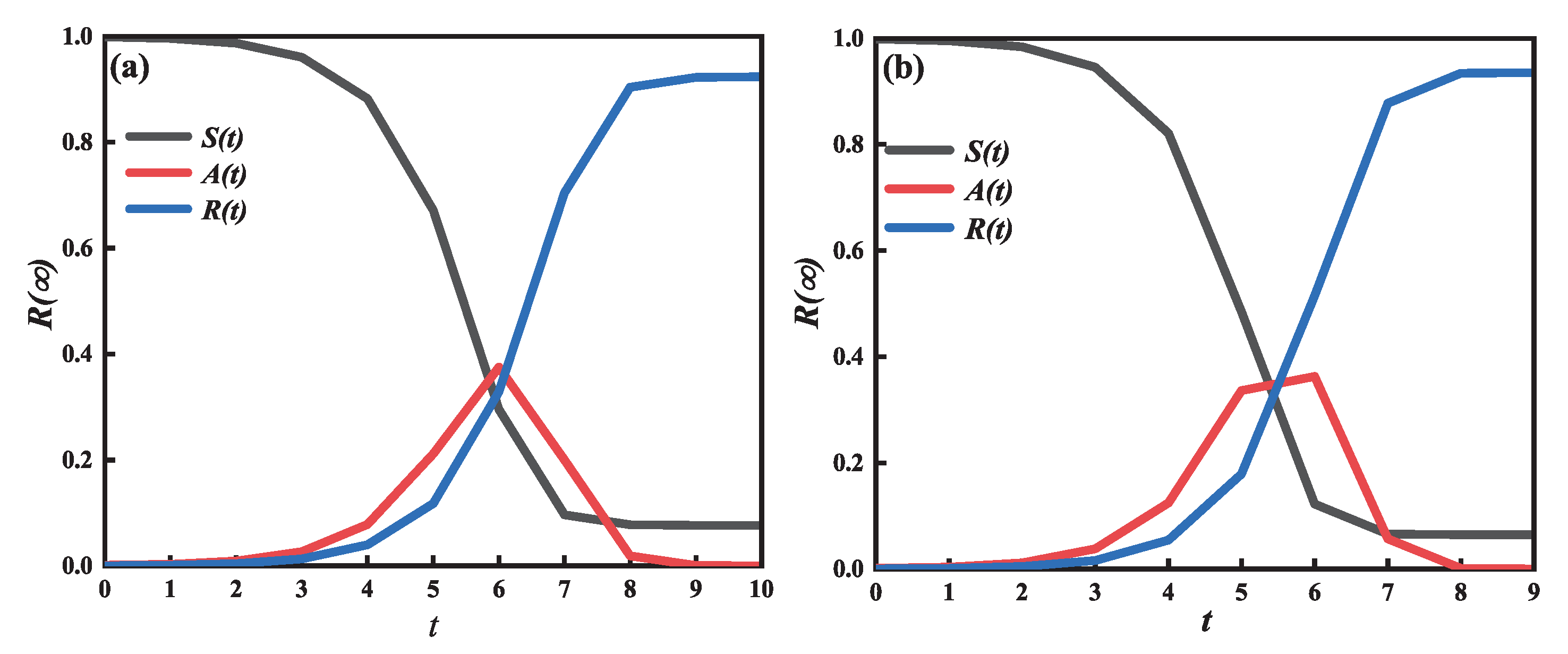
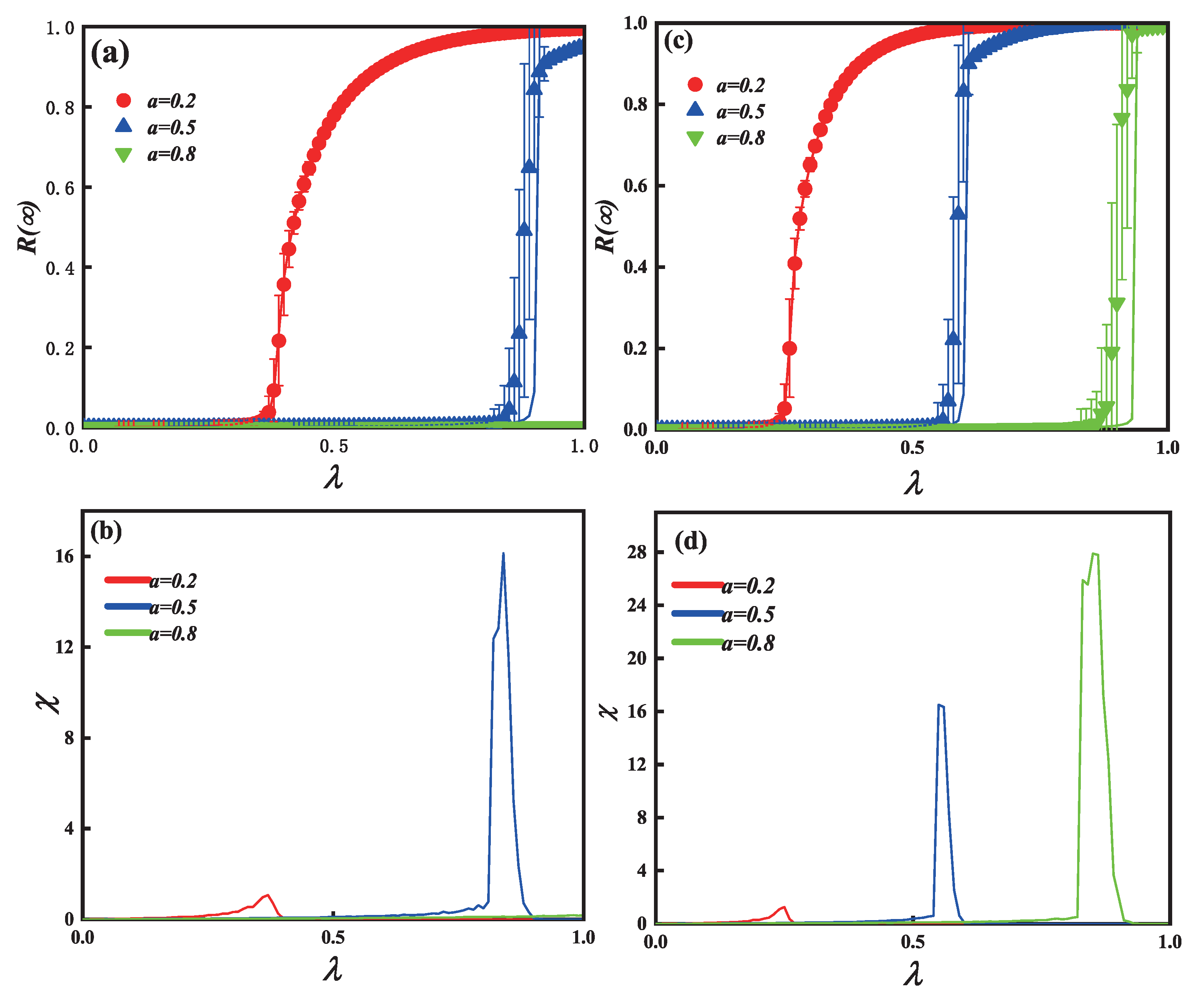
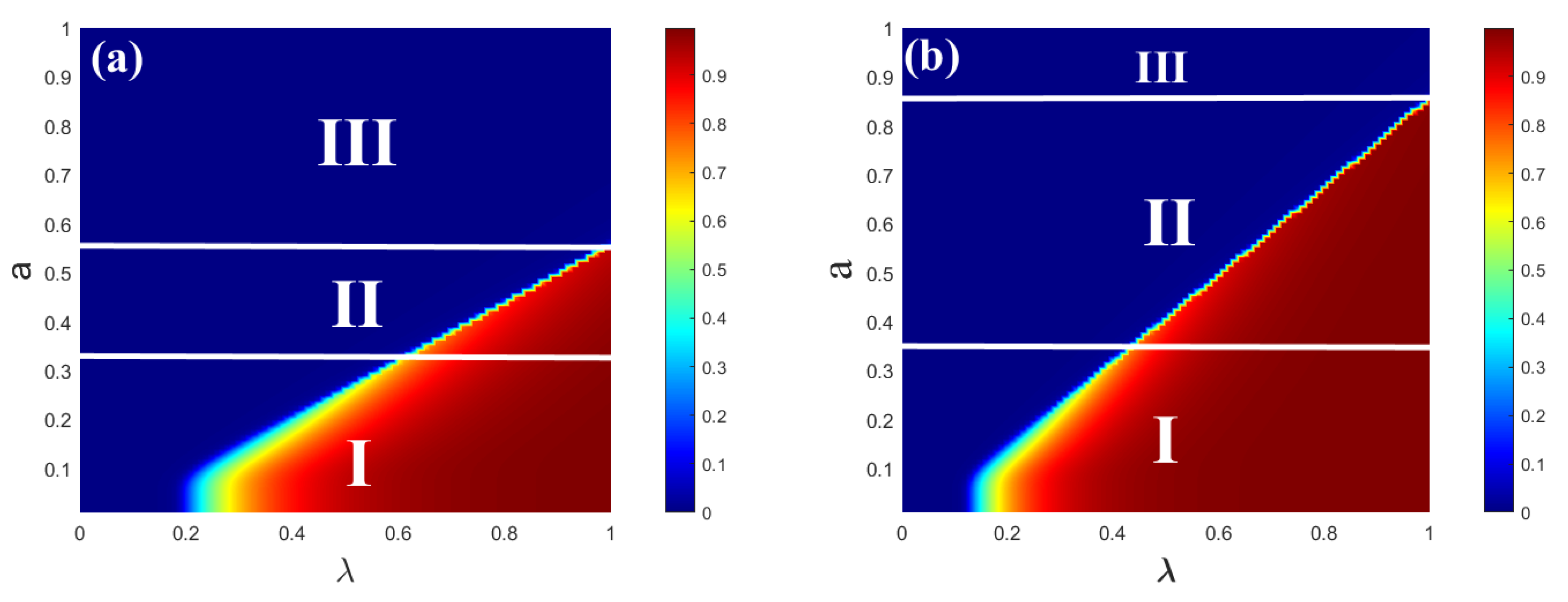
3.1. Information Propagation on Single-Layer Limited ER Network
3.2. Information Propagation on Single-Layer Limited SF Network
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mu, Y.; Chan, T.L.; Yuan, H.Y.; Lo, W.C. Transmission Dynamics of Tuberculosis with Age-specific Disease Progression. Bull. Math. Biol. 2022, 73, 73. [Google Scholar] [CrossRef]
- Qu, J.Y.; Tang, M.; Liu, Y.; Guan, S.G. The relative importance of structure and dynamics on node influence in reversible spreading processes. Front. Phys. 2021, 16, 51503. [Google Scholar] [CrossRef]
- Makridis, C.A. The social transmission of economic sentiment on consumption. Eur. Econ. Rev. 2022, 148, 104232. [Google Scholar] [CrossRef]
- Jadhav, M.M.; Dongre, G.; Purandare, R. Resource allocation in 5G network using Orthogonal Frequency Division Multiplexing-Hybrid Automatic Repeat Request. Commun. Syst. 2022, 35, 18. [Google Scholar] [CrossRef]
- Anwar, N.; Ahmad, I.; Kiani, A.K.; Naz, S.; Shoaib, M.; Raja, M.A.Z. Intelligent predictive stochastic computing for nonlinear differential delay computer virus model. Waves Random Complex Media 2022, 10, 2155327. [Google Scholar] [CrossRef]
- Au, A. Guanxi in an age of digitalization: Toward assortation and value homophily in new tie-formation. J. Chin. Sociol. 2022, 9, 7. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Yu, P.; Xu, Z. The impact of different strategy update mechanisms on information dissemination under hyper network vision. Commun. Nonlinear Sci. Numer. Simul. 2022, 113, 106585. [Google Scholar] [CrossRef]
- Roche, S.; Spring, A.; Moore, A. Childhood neighborhoods and health: Census-based neighborhood measures versus residential lived experiences. Health Place 2022, 78, 102902. [Google Scholar] [CrossRef]
- Li, C.L.; Cheng, C.Y.; Li, C.H. Global dynamics of two-strain epidemic model with single-strain vaccination in complex networks. Phys. Rev. E 2022, 69, 103738. [Google Scholar] [CrossRef]
- Nie, Y.; Zhong, X.; Lin, T.; Wang, W. Homophily in competing behavior spreading among the heterogeneous population with higher-order interactions. Appl. Math. Comput. 2022, 432, 127380. [Google Scholar] [CrossRef]
- Wu, J.; Xu, K.; Zheng, M. Distinct spreading patterns induced by coexisting channels in information spreading dynamics. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 083134. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Holtz, D.; Jaffe, S.; Suri, S.; Sinha, S.; Weston, J.; Joyce, C.; Shah, N. The effects of remote work on collaboration among information workers. Nat. Hum. Behav. 2022, 6, 164. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Wang, Y.; Zhang, N.; Yang, H.; Wang, W. Influence of heterogeneity of infection thresholds on epidemic spreading with neighbor resource supporting. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 083124. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Wei, R.; Tian, Y.; Tian, H.; Zhu, X. Information propagation influenced by individual fashion-passion trend on multi-layer weighted network. Chaos Solitons Fractals 2022, 160, 112200. [Google Scholar] [CrossRef]
- Yu, J.; Liu, Z.; Han, X. Cooperation Evolution in Multiplex Networks With the Heterogeneous Diffusion Model. IEEE Access 2021, 9, 86074–86082. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Li, J. Improving Dam Seepage Prediction Using Back- Propagation Neural Network and Genetic Algorithm. Math. Probl. Eng. 2021, 2020, 1404295. [Google Scholar]
- He, L.; Wang, S.; Gu, Y.; Pang, Q.; Wu, Y.; Ding, J.; Yan, J. Seepage behavior assessment of earth-rock dams based on Bayesian network. Int. J. Distrib. Sens. Netw. 2021, 17, 15501477211058672. [Google Scholar] [CrossRef]
- Ruan, Z.; Zhang, L.; Shu, X. Social contagion with negative feedbacks. Phys. A Stat. Mech. Its Appl. 2022, 608, 128304. [Google Scholar] [CrossRef]
- Li, W.; Nie, Y.; Li, W.; Su, S.; Wang, W. Two competing simplicial irreversible epidemics on simplicial complex. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 093135. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.R.; Lu, L.; Hu, M.B.; Xu, S.; Zhang, Y.C. Percolation on complex networks: Theory and application. Phys. Rep.-Rev. Sect. Phys. Lett. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Diaz-Diaz, F.; San Miguel, M.; Meloni, S. Echo chambers and information transmission biases in homophilic and heterophilic networks. Sci. Rep. 2022, 12, 9350. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, F.; Stivala, A.; Lomi, A. Multiple clocks in network evolution. Waves Random Complex Media 2022, 15, 19–41. [Google Scholar] [CrossRef]
- Ghosh, D.; Frasca, M.; Rizzo, A.; Majhi, S.; Rakshit, S.; Alfaro-Bittner, K.; Boccaletti, S. The synchronized dynamics of time-varying networks. Phys. Rep. 2022, 949, 1–63. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.F.; Zhu, P.C.; Ma, C. Interplay of simplicial awareness contagion and epidemic spreading on time-varying multiplex networks. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 083110. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Shu, P.; Zhu, Y.X.; Tang, M.; Zhang, Y.C. Dynamics of social contagions with limited contact capacity. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 103102. [Google Scholar] [CrossRef]
- Thomas, C.; Andrew, P.H.; Paul, R.A.; Robert, J.V.; Martyn, S. The psychology of passion: A meta-analytical review of a decade of research on intrapersonal outcomes. Motiv. Emot. 2015, 39, 631–655. [Google Scholar]
- Feng, B.; Chen, M. The Impact of Entrepreneurial Passion on Psychology and Behavior of Entrepreneurs. Front. Psychol. 2020, 11, 1733. [Google Scholar] [CrossRef]
- Dodds, P.S.; Harris, K.D.; Danforth, C.M. Limited Imitation Contagion on Random Networks: Chaos, Universality, and Unpredictability. Phys. Rev. Lett. 2013, 110, 158701. [Google Scholar] [CrossRef]
- Fan, J.; Zhao, D.; Xia, C.; Tanimoto, J. Coupled spreading between information and epidemics on multiplex networks with simplicial complexes. Phys. Rev. E 2015, 92, 012820. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, X.; Qiwen, Y.; Hui, T.; Qimei, C. Propagation characteristic of adoption thresholds heterogeneity in double-layer networks with edge weight distribution. Phys. A Stat. Mech. Its Appl. 2022, 591, 126768. [Google Scholar]
- Leng, H.; Zhao, Y.; Wang, D. Message passing approach for social contagions based on the trust probability with multiple influence factors. Phys. A-Stat. Mech. Its Appl. 2021, 587, 126510. [Google Scholar] [CrossRef]
- Peng, X.L.; Zhang, Y.D. Contagion dynamics on adaptive multiplex networks with awareness-dependent rewiring. Chin. Phys. B 2021, 30, 058901. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Tian, Y.; Zhu, X. Behavioral Propagation Based on Passionate Psychology on Single Networks with Limited Contact. Entropy 2023, 25, 303. https://doi.org/10.3390/e25020303
Liu S, Tian Y, Zhu X. Behavioral Propagation Based on Passionate Psychology on Single Networks with Limited Contact. Entropy. 2023; 25(2):303. https://doi.org/10.3390/e25020303
Chicago/Turabian StyleLiu, Siyuan, Yang Tian, and Xuzhen Zhu. 2023. "Behavioral Propagation Based on Passionate Psychology on Single Networks with Limited Contact" Entropy 25, no. 2: 303. https://doi.org/10.3390/e25020303
APA StyleLiu, S., Tian, Y., & Zhu, X. (2023). Behavioral Propagation Based on Passionate Psychology on Single Networks with Limited Contact. Entropy, 25(2), 303. https://doi.org/10.3390/e25020303





