1. Introduction
Data privacy protection is a critically important area of research, especially as data collection from individuals increases and proliferates rapidly. Data often contains sensitive information that could pose privacy risks if released without proper processing. To ensure the privacy of individuals, many countries have enacted privacy protection laws, such as the General Data Protection Regulation (GDPR) in the European Union, the Personal Data Protection Act (PDPA) in Singapore, and the Personal Information Protection Law (PIPL) in China. These laws aim to regulate data handling practices and safeguard individuals’ personal information. As data collection and usage continue to grow exponentially, effective privacy protection techniques remain vital to uphold individuals’ rights while enabling data-driven innovation.
Preserving data privacy presents several challenges, the most significant being the prevention of information leakage during data release. Data can contain different types of information; therefore, it is crucial to identify confidential data and assess the potential consequences of a data breach. Identifying and classifying sensitive data are key steps in developing an effective data privacy protection strategy. Once the sensitive data has been identified, organizations can determine the appropriate data privacy protection measures to implement. To protect individuals’ privacy, it may be necessary to anonymize the data while considering the type of data, the intended use, and the potential privacy risks.
Data anonymization is a practical and widely adopted approach to protecting individual privacy when releasing data. Anonymization techniques aim to reduce the risk of unauthorized disclosure by converting personal information into anonymous data. This balanced approach to safeguarding privacy mitigates the original details in the dataset to some extent [
1]. Anonymizing data involves modifying quasi-identifier values to reduce specificity, enhancing privacy protection while preserving data utility [
2].
Data containing confidential information about individuals is prone to privacy breaches, so it is essential to protect sensitive information from privacy threats [
3]. One way to protect personal privacy is to erase direct identifier attributes, such as names and addresses, before releasing the original data to the public. This process, known as de-identification, is insufficient to protect privacy, as a study by Sweeney [
4] showed that 87% of Americans can still be uniquely identified based on just three quasi-identifiers: gender, age, and postal code. To prevent privacy threats, researchers have proposed several privacy models, including
k-anonymity (KA) [
5],
l-diversity (LD) [
6], and
t-closeness (TC) [
7]. In the following, we briefly overview these models and their anonymization operations.
Anonymization techniques have become increasingly important for ensuring privacy in data publishing. Among these techniques, KA is widely used by researchers [
5]. KA aims to protect privacy by modifying quasi-identifiers to ensure that each record is indistinguishable from at least
k-1 other records. It is important that individual records remain faithful to the original data while meeting privacy requirements after anonymization [
8]. Generalization, suppression, and perturbation are the main anonymization operations used to achieve k-anonymization algorithms:
Generalization replaces some quasi-identifier values with parent values in the equivalent class, while specialization is the opposite operation. Generalization preserves data privacy but reduces data accuracy [
3]. Excessive generalization results in significant information loss (IL) and reduced data quality [
9].
Suppression replaces specific quasi-identifier values with asterisks (*), while the disclosure is the opposite. Suppression causes more IL than generalization. For example, suppose we have a dataset of people’s ages. We could generalize this dataset by replacing all ages with a range of ages, such as 20–30, 30–40, and so on. This would reduce the accuracy of the dataset, but it would still preserve some information about the people’s ages. On the other hand, if we suppress data points from the dataset, we would be losing information altogether.
Perturbation involves modifying a feature’s value by replacing it with another value to minimize the difference between the original and modified datasets. One of the most popular perturbation techniques is microaggregation, which clusters records in the dataset with a restriction on cluster size. Microaggregation replaces the values of each record in the anonymized dataset with the values of the cluster center to which the record belongs. This approach is more effective than generalization and suppression [
10] and simplifies further data analysis.
Table 1 shows a sample of de-identified original data, and
Table 2 shows its 3-anonymized version. The Weight, Gender, and Age attributes are set as quasi-identifier attributes, and disease is the sensitive attribute. All records in a cluster share the same values for the quasi-identifier attributes, making them indistinguishable from each other. However, the 3-anonymity model in
Table 2 does not prevent attribute disclosure. For example, if an adversary knows that a person’s record is in cluster C1 in
Table 3, they can infer that the person has pneumonia.
While KA is effective in preventing identity disclosure, it remains vulnerable to attribute disclosure attacks. Specifically, if the range of sensitive attribute values within a k-anonymous cluster is limited, there is a risk of inferring the value of individuals’ sensitive attributes. Several extended KA models have been proposed to address this issue [
11], including LD [
6], which ensures a minimum degree of diversity (
l) of sensitive values in each cluster.
Table 3 shows 3-anonymity and 2-diversity to the original data presented in
Table 1. All records within each cluster in
Table 3 have the same value for the quasi-identifier but contain distinct values for the sensitive attribute. This means that even if an adversary knows the cluster containing a target individual’s record, they cannot narrow down or disclose the person’s specific sensitive value (disease).
However, LD also has drawbacks [
12]. For example, if an attacker knows that a person’s record is in cluster C2 in
Table 3, they can infer that the person has the Flu with a probability of 66%. To address these limitations, Li et al. [
7] introduced the concept of TC.
To meet TC requirements, the distribution of sensitive information must be similar for each group of indistinguishable records and the entire original dataset.
Table 4 shows an anonymized version of the original data from
Table 1 that satisfies 3-anonymity and 0.33-closeness. This anonymized table is safe for public release because it protects the privacy of the individuals in the dataset. In addition to protecting against the attacks mentioned above, TC also offers safeguards against potential skewness attacks and similarity attacks, as detailed in [
7].
TC provides stronger privacy guarantees compared to other techniques like LD. It protects against attribute disclosure by restricting the distance between sensitive attribute distributions in any cluster and the original distribution. The parameter t effectively controls the balance between privacy protection and data utility. Decreasing t enhances privacy by requiring sensitive attribute distributions to more closely mirror the original distribution. However, it can reduce utility if overly strict clustering is needed to satisfy the tighter threshold. Conversely, increasing t may compromise privacy protection as it allows more divergence from the original distribution. However, it can improve utility by permitting more flexible clustering.
The Earth Mover’s Distance (EMD) [
13] is used to calculate the TC metric using variational distance [
7,
14] as follows:
where
and
are the probabilities of distributions
P and
Q, respectively. It is assumed that
=
=
m and both
P and
Q are normalized distributions, that is
=
= 1.
As
Figure 1 shows, there is an inverse relationship between data privacy and data utility, meaning that improving one inevitably reduces the other [
15]. Therefore, a fundamental goal of anonymization is to balance these two factors when creating an anonymized dataset suitable for publication. This balance requires determining an acceptable trade-off between privacy and utility.
Table 5 summarizes the key abbreviations used throughout this paper for ease of reference.
The Contribution
In recent years, researchers have explored clustering-based anonymization methods to protect people’s privacy from potential intruders [
16,
17,
18,
19,
20]. These methods involve identifying important attributes to anonymize and using clustering techniques to group records according to their characteristics and similarities. The desired level of privacy protection can be achieved by modifying the attribute values of records within each cluster [
21].
Byun et al. formulated the KA problem as a clustering problem and proposed the
k-member algorithm to achieve optimal KA [
20]. To enhance this algorithm, Honda et al. [
22] developed a fuzzy variant of the
k-member algorithm. Rahimi et al. [
23] successfully implemented all three KA, LD, and TC restrictions on the original microdata using the X-means clustering algorithm. Langari et al. [
24] also satisfied all three aforementioned constraints by formulating the anonymization problem as an optimization problem and subsequently employing an evolutionary algorithm and modifications to sensitive attribute values. Abbasi et al. [
16] introduced a clustering process using the K-means++ method to achieve optimal KA.
Most real-world datasets contain non-numerical data (categorical data), which presents challenges for anonymization using generalization and suppression since categorical features lack natural distance metrics. For example, quantifying the distance between two different occupations, such as ‘dentist’ and ‘farmer’, is difficult. Therefore, most existing anonymization methods often focus on numerical data. This paper designs a novel approach for anonymizing categorical data using a greedy and information-theoretic clustering-based algorithm to protect microdata privacy against identity and attribute disclosure attacks.
The algorithm aims to minimize mutual information loss of records within each cluster while ensuring strict privacy protection. To this end, the clustering-based anonymization algorithm operates on a binary data table converted from the original data table. The output is an anonymized binary data table where some attribute values have been modified to achieve strict privacy protection.
The proposed method is specifically designed to anonymize non-numerical microdata so it can be publicly released for research and knowledge discovery while protecting privacy. We evaluated the proposed algorithm against four different approaches, including state-of-the-art methods, on three different datasets. The results demonstrated its superiority in achieving strict privacy protection while preserving data utility. It ensures that each cluster satisfies both KA and TC, protecting the anonymized data against identity and attribute disclosure attacks.
To summarize, the key contributions of this study are:
Proposing a 3-phase anonymization algorithm that aims to achieve strict privacy protection while maximizing the data utility.
To form clusters, we used the loss of mutual information and proposed an agglomerative clustering based on information bottleneck.
Considering the diversity of sensitive values in addition to the similarity of quasi-identifier values during clustering to reduce the cost of implementing privacy constraints.
The paper is structured as follows:
Section 2 introduces the key fundamental concepts necessary to understand privacy-preserving data anonymization, while
Section 3 reviews existing methods.
Section 4 then provides a detailed explanation of the proposed anonymization algorithm. In
Section 5, an empirical performance evaluation and comparison of GCAA is conducted against four state-of-the-art benchmark methods. Both the privacy protections and utility preservation of the different algorithms are analyzed and discussed. Finally,
Section 6 offers conclusions and outlines potential future work.
3. Related Work
Most state-of-the-art anonymization techniques use a clustering-based KA algorithm to achieve privacy preservation. These techniques partition input data into distinct clusters, containing a minimum of k records, before applying anonymization operations to create an anonymized output. The following section investigates several representative approaches to privacy-preserving.
LeFevre et al. [
31] introduced the
Incognito algorithm, a bottom-up approach that utilizes global generalization to generate an optimal
k-anonymous dataset. However, this method has a high level of IL due to the full-domain generalization technique, which can negatively impact the usefulness of the anonymized data. To address this issue, Ref. [
32] proposed a top-down greedy algorithm called
Mondrian, which uses local recoding to generate an optimal
k-anonymous dataset.
Byun et al. [
20] proposed a clustering-based approach to solve the KA problem using a
k-member greedy algorithm to find the optimal solution. The method partitions the dataset into clusters with at least
k members and generalizes the quasi-identifier values in each cluster to achieve KA. However, it is sensitive to outlier records because it selects the furthest record from the previous cluster to create a new one, which leads to a high amount of IL. Honda et al. [
22] introduced a fuzzy version of this approach that considers the degree of fuzzy membership when assigning records to clusters. However, this approach may overfit the data to satisfy KA, a significant drawback.
Abbasi et al. [
16] proposed a clustering-based approach for privacy preservation in healthcare datasets. They first used the normal distribution function to identify and remove less frequent data, which is more vulnerable to privacy breaches. Then, they used the K-means++ algorithm to generate clusters during the clustering process. Finally, they applied the KA algorithm to each cluster separately to achieve the desired level of privacy preservation.
Truta et al. [
29] proposed a
p-sensitive
k-anonymous technique to protect against homogeneity and background knowledge attacks. The algorithm ensures that each equivalent class has at least
p distinct values
. However, this technique leads to a high degree of IL when the distribution of sensitive attribute values is not uniform. To enhance this approach, Sun et al. [
28] proposed two improved versions of the
p-sensitive
k-anonymity technique:
-sensitive
k-anonymity and
-sensitive
k-anonymity. Their approach first categorizes the sensitive attributes and then focuses more on the categories of sensitive values rather than their specific values. However, this method may still result in a high amount of IL in particular scenarios.
Solanas et al. [
33] proposed a heuristic microaggregation-based algorithm to apply
p-sensitive
k-anonymity to the original dataset. Their algorithm first creates clusters with at least
k members that satisfy the
p-sensitive
k-anonymity property. To achieve this, it randomly selects a record and then adds the closest records with different sensitive values to form the cluster. Finally, the algorithm anonymizes the original dataset by replacing the values of each record with the values of the cluster centroid to which the record belongs. This method reduces the loss of information and provides higher data utility than other
p-sensitive
k-anonymity techniques.
Existing approaches that incorporate diversity in sensitive values have limitations, especially in protecting individuals’ privacy from attribute disclosure attacks. Researchers have suggested a privacy-preserving model known as TC to address this drawback.
Rahime et al. [
23] proposed a 3-layer clustering algorithm that applied KA, LD, and TC constraints for anonymizing the original dataset. This approach protected individuals’ privacy against identity and attribute disclosure attacks, but its main weakness was the high amount of IL.
Langari et al. [
24] proposed a hybrid approach for anonymizing graph and tabular data. Their method first partitions the data into clusters with at least
k members using the fuzzy clustering technique and then uses the Firefly evolutionary algorithm to optimize the anonymization and clustering parameters simultaneously. LD and TC were implemented using the modification of sensitive values. However, its scalability is questionable due to the use of an evolutionary algorithm.
Our Contributions against the Existing Methodology
Table 6 summarizes several state-of-the-art algorithms. These algorithms use different anonymization techniques and operations. According to the table, most algorithms were designed to satisfy only the KA constraint and do not adequately protect anonymized data against attribute disclosure attacks. Algorithms that provide more protection by satisfying LD or TC constraints suffer from a high amount of IL or low data utility. This is because almost all of these algorithms only consider the similarity of quasi-identifiers when creating clusters. Therefore, to satisfy the privacy limitation, they are forced to merge more clusters, which in the worst case, could result in a single cluster with zero data utility.
Most anonymization techniques use generalization operations, which tend to incur high levels of IL (except for the algorithms in [
24,
33]). However, anonymization inherently reduces data usefulness to some degree by obscuring details. Therefore, it is crucial to consider the trade-off between privacy and IL to maintain the utility of anonymized data for knowledge extraction.
Compared to the proposed method, most investigated approaches perform poorly in maintaining the trade-off between privacy protection and data usefulness. Additionally, unlike the proposed method, some of these techniques remove data points from the table as outliers, while others change the values of the sensitive attributes to meet the LD and TC requirements. This leads to a significant decrease in the usefulness of the data.
To overcome the limitations of prior work, a new greedy, information-theoretic clustering algorithm is proposed for microdata anonymization. It differs from existing techniques in several important ways:
The proposed algorithm clusters data points by considering both the similarity of quasi-identifier values and the diversity of sensitive values within each cluster. This approach ensures that clusters have high intra-cluster similarity for quasi-identifiers and high intra-cluster diversity for sensitive attribute, which reduces both the modification of values and the merging of clusters as a result of increasing the usefulness of the data.
The proposed algorithm protects released data from identity and attribute disclosure attacks by satisfying the KA and TC privacy constraints. These constraints ensure that individuals are indistinguishable from the anonymized data and that the distribution of sensitive attribute values is preserved.
As shown in
Figure 1, there is a trade-off between data privacy and data utility. Existing methods prioritize data privacy at the expense of data utility, but our algorithm achieves strict privacy by adhering to KA and TC while minimizing IL. This approach strikes a balance between data privacy and utility, ensuring that the anonymized data remains useful for its intended purposes.
4. Proposed Approach
Creating a dataset that satisfies the TC constraint through generalization involves solving an optimization problem to determine the minimum generalization required to meet the TC requirement. A common strategy for this is an iterative process of progressively generalizing one or more attributes until the resulting dataset meets the TC constraint.
Traditional methods for achieving TC first cluster records into groups containing at least k members to ensure KA. KA can be achieved through generalization techniques that replace quasi-identifier values with broader categories or microaggregation techniques that substitute original values with statistical approximations. Next, the methods merge clusters of records to construct a t-close dataset. The clusters are progressively merged to minimize the distance between sensitive attribute distributions across merged clusters. The distance metric guides the selection of cluster mergers, identifying combinations that most reduce divergence between clusters’ sensitive field distributions. This process continues by merging clusters until all satisfy the threshold for TC.
Generating t-close datasets using the traditional methods is costly, primarily due to the reduction in data utility. A key factor is the lack of consideration for sensitive attribute value diversity during initial clustering. Real-world datasets often contain records with similar quasi-identifiers but different sensitive attribute values. To enhance data utility, our proposed approach generates clusters having more similar quasi-identifiers and more diverse sensitive values. Additionally, merging clusters to achieve t-closeness can severely compromise data utility, sometimes rendering it entirely useless (all clusters merged into one). A more effective strategy could be to swap records between clusters instead of merging clusters, which could potentially mitigate this problem.
Pre-processing, clustering, and adjustment are the three phases of the proposed approach to generating anonymized datasets. In the pre-processing phase, the original data table
T is converted into a binary table,
, with values of 1 or 0.
is then normalized to the range [0, 1] and divided into two subtables: quasi-identifier,
, and sensitive attribute,
. In the clustering phase, a bottom-up clustering algorithm is used to generate clusters with similar quasi-identifier values but distinct sensitive values within each cluster. Finally, to create the anonymized table
, which satisfies the KA and TC requirements for strict privacy, we apply an adjustment process. The quasi-identifier values in each cluster are replaced with the centroid quasi-identifier value to anonymize the data.
Figure 4 shows the overall workflow of the proposed approach.
4.1. Pre-Processing
The original input data table T contains n records from the set , each of them having m values of attributes from the set which is represented by the matrix M.
First of all, attribute values are converted to binary values. Let feature from the set have a value domain = {, ,..., } (for each ). Therefore, each record takes exactly one value from the set for its jth feature. Let F = ∪∪...∪ be the set of all possible values of the attributes in the original table. Also, let be equal to the size of F.
In this case, the original matrix converted to a matrix
with the size
, where each record
in this matrix is a vector with binary values of features size
d. If the record
r contains the attribute value
f, the value of
equals 1, otherwise is equal to 0. For example, according to
Table 7, the first feature is the
Gender, and its values domain is {
Male,
Female}. In the binary table, if the person is male, only the attribute
Male value is 1 and
Female value is 0, and vice versa.
Next, we identify quasi-identifiers and sensitive attributes in the data table and partition the feature set into two sets, and . We then construct two sub-tables, and , from the original data table, ensuring that each record retains its unique across both sub-tables. In the next step, we normalize the values in both sub-tables to lie within the interval [0, 1], so that the sum of the values for each record in each sub-table equals 1.
Let
R and
F (
and
) be discrete random variables whose values are taken from sets
and
, respectively. In this case, each record in the two sub-tables has the conditional probability distribution
(for all
∈
) and
(for all
∈
), respectively. The normalized sub-tables of the original
Table 7 are shown in
Table 8 and
Table 9.
4.2. Clustering
The two sub-tables generated in the previous phase,
and
, serve as input to the clustering phase. The proposed bottom-up clustering algorithm simultaneously considers both
and
to group the records. The goal is to form clusters where quasi-identifier values are highly similar within each cluster, but sensitive values remain diverse. Algorithm 1 outlines the bottom-up clustering process.
| Algorithm 1 The Pseudocode for the Clustering Process |
- 1:
Input: Microdata table T with dimensions, parameters K, T, , and - 2:
Output: Clusters () - 3:
Let n: the number of records, m: be the number of features, and d: the size of the feature values domain, S: the distribution of sensitive values in the dataset. - 4:
Convert data table T to binary table with dimensions - 5:
Select quasi-identifiers and sensitive attributes, then establish two sub-tables and with unique - 6:
Initially, let each record be a distinct cluster, - 7:
Calculate based on Equation ( 6) for - 8:
while do - 9:
Calculate based on Equation ( 13) for all - 10:
Select a pair of clusters , that have minimum - 11:
if then - 12:
if then - 13:
Merge and , and update both sub-tables based on Equations ( 8) and ( 9) and go to Line 7 - 14:
else - 15:
Select the next pair of clusters and go to Line 12 - 16:
end if - 17:
else - 18:
Select the next pair of clusters and go to Line 11 - 19:
end if - 20:
end while - 21:
Return obtained clusters
|
A
k-clustering
partitions the records of data table
T into
k clusters
{
}, where each cluster
has three properties as follows: (1)
, (2)
for all
, (3)
. We define the probability of each record
r in data table
T as
, where
n is the number of records in
T. Then, for each cluster
we have:
For example, from
Table 8 and
Table 9, one can conclude that
for
. In addition,
and
are the feature vectors for the quasi-identifier and sensitive attribute of record
, respectively. They are equal to
and
.
Initially, each record is assumed to be an independent cluster. We denote this partition as
, where
is a partition with
n clusters {
,
,...,
} such that:
At each iteration, the proposed algorithm seeks to generate a new cluster with similar quasi-identifier values and distinct sensitive values from the existing clusters. To this end, we employ the Agglomerative Information Bottleneck algorithm [
34]. The algorithm starts with a
partition. In this case,
=
, and in each step, it merges two clusters, reducing the number of clusters by one. According to the definition of mutual information, this causes an increase in the uncertainty of predicting the features with respect to clusters, or, equivalently, a reduction of the information that clusters contain about the values of the features, i.e.,
. We use
to represent this information reduction. Therefore, at each step, the algorithm attempts to merge the pair of clusters with the minimum
.
After merging two clusters
and
, new cluster
has:
for all
f∈
F. Tishaby et al. [
35] showed that:
for all
.
in Equation (
10) is the Jensen-Shannon divergence defined below:
where
is KL divergence, and
is avarge distribution of
and
and calculated by Equation (
9). Finally, the
,
which
is calculated with the following formula:
where
=
.
At each step, the proposed algorithm calculates
of each pair of clusters
(
) for both sub-tables
and
as
and
, respectively. Then
is calculated according to the following formula:
At each step, the algorithm aims to merge the pair of clusters with the minimum value. However, if two clusters have identical quasi-identifiers (i.e., ), the algorithm selects the pair of clusters with the highest diversity in sensitive values for merging. By following this strategy, we can step-by-step create clusters of records with similar quasi-identifiers but different sensitive values. This process reduces IL and improves the quality of anonymous data.
To create balanced clusters and minimize changes during TC enforcement, our algorithm imposes two additional restrictions on merging. To speed up the process and create more evenly sized clusters, we remove any cluster that has between
k and
(i.e.,
) data points from the clustering process. To make it easier to enforce TC during the adjustment phase, two clusters are merged only if they meet the following criteria:
where
S is the distribution of sensitive values in the entire dataset, and
is the distribution of sensitive values in cluster
i.
The algorithm runs until it reaches a stopping point, defined as follows: if the change in mutual information after each merging step exceeds the threshold , the merging process stops, and the final clusters are formed.
4.3. Adjustment
The adjustment phase is a crucial step in the proposed algorithm to satisfy the KA and TC constraints. It takes as input the set of clusters generated in the clustering phase, denoted as
,
,...,
, and outputs a new set of clusters, denoted as
,
,...,
(
), that all satisfy the KA and TC constraints while preserving the data quality. The resulting anonymized table
can be easily constructed using the modified clusters. Algorithms 2 and 3 present the pseudocode for the adjustment phase.
| Algorithm 2 The Pseudocode for the Adjustment Phase |
- 1:
Input: Clusters , parameter K and T - 2:
Output: Clusters C CC (), Anonymized table - 3:
Let , , , and be empty sets - 4:
Let SortedList: Sort all clusters based on their EMD in descending order - 5:
for i = 1, 2,..., c do - 6:
if satisfy KA and TC then - 7:
ADD To - 8:
else - 9:
ADD To - 10:
end if - 11:
end for - 12:
for j = 1, 2,..., do - 13:
if ≥ K then - 14:
ADD To - 15:
else - 16:
ADD To - 17:
end if - 18:
end for - 19:
for all clusters c in do - 20:
while c is not empty do - 21:
Randomly select a record r From c - 22:
c = c∖ - 23:
p = Findthebestcluster(SortedList, r) - 24:
p = p∪ - 25:
end while - 26:
end for - 27:
for all clusters c in do - 28:
while c is not empty do - 29:
Randomly select a record r from c - 30:
c = c∖ - 31:
p = Findthebestcluster(SortedList, r) - 32:
p = p∪ - 33:
end while - 34:
end for
|
| Algorithm 3 Function: Findthebestcluster(C,r) |
- 1:
Input: A set of clusters C that sorted based on their EMD in descending order, and a record r - 2:
Output: A cluster c∈C such that the (c∪, S) is decreased - 3:
Let n = , best = null - 4:
for i = 1, 2,..., n do - 5:
if (∪r, S) <(, S) then - 6:
best = with the lowest value - 7:
break - 8:
end if - 9:
end for - 10:
Return best
|
The input set of clusters is partitioned into two subsets: , which contains the clusters that satisfy both KA and TC, and , which contains the clusters that do not meet one or both of these constraints. is further partitioned into two subsets: , which contains clusters with more than k records, and , which contains clusters with less than or equal to k records.
The algorithm then proceeds to modify the clusters in by transferring their records to clusters in using the Findthebestcluster function to minimize the EMD between the merged clusters. If the EMD of the modified cluster is less than or equal to the predefined threshold T, the cluster is moved from to .
The process continues until is empty. If is not empty, the algorithm selects the cluster with the highest EMD value and transfers its records to the best cluster based on the Findthebestcluster function until all clusters in satisfy the TC constraint and are moved to .
5. Performance Evaluation and Discussion
To evaluate the proposed algorithm, we use two metrics to measure the quality of anonymized datasets.
Normalized Avarege QI-group (CAVG): The metric was proposed by [
32]. It measures the quality of the KA constraint. The closer the value to 1, the better the result. The normalized average group is defined as follows:
where C is the number of clusters and
k is the privacy parameter.
Average Distortion Ratio (ADR): This metric measures the amount of distortion (IL) introduced by the anonymization process. If a feature value is not changed, there is no distortion. If a feature value is changed, the distortion increases by 1. The metric is defined as follows:
where
if
jth features of record
i is modified and 0 otherwise,
N is the number of records, and
d is the domain of the feature values.
To assess the effectiveness of the algorithm in protecting against identity and attribute disclosure attacks, we use two penalty criteria: P and P. These criteria are defined as follows:
These criteria enable an evaluation of the algorithm’s ability to satisfy the desired privacy constraints while minimizing the risk of information disclosure.
The proposed anonymization algorithm was developed in Python version 3 and implemented on a personal computer with a 2.6 GHz (Core i7) processor and 16 GB of memory. The effectiveness of the proposed Greedy Clustering-based Anonymization Algorithm (GCAA) was compared to four other clustering-based anonymization techniques: K-anonymity L-diversity T-closeness 3Layer (KLT3L) [
23], K-member Fuzzy Clustering Firefly Algorithm (KFCFA) [
24], P-Sensitive K-Anonymity (PSKA) [
28], and Fuzzy K-Member Clustering (FKMC) [
22]. The comparison was performed in terms of their ability to protect against identity and attribute disclosure attacks.
To ensure a fair comparison with existing methods, we designed our experiment to match the setup of [
24] as closely as possible. We used three microdata sets (
https://snap.stanford.edu/data/, accessed on 10 February 2023) that were also used in the [
24]. Each dataset contained a table of records, with each record having a set of features. The details of the microdata sets are summarized in
Table 10.
The level of protection against intruder attacks increases with higher values of
k and
t but at the cost of increased I. To assess the performance of our algorithm under different conditions, we considered three different privacy scenarios, each with different parameter values. A summary of the scenarios is presented in
Table 11.
Considering the privacy requirements and the potential severity of intruder attacks, we chose different values for the anonymization parameters
k and
t for each privacy scenario. As shown in
Table 11, we considered three scenarios, ranging from simple to strict, with corresponding values of
l set to 3, 4, and 6, respectively. We also set the parameters
and
to ⌊
⌋ and 0.5, respectively. To terminate the clustering process, we monitored the difference between two consecutive
values for merging. Clustering was stopped when this value exceeded 0.5, at which point the current clusters were considered to be the final clusters.
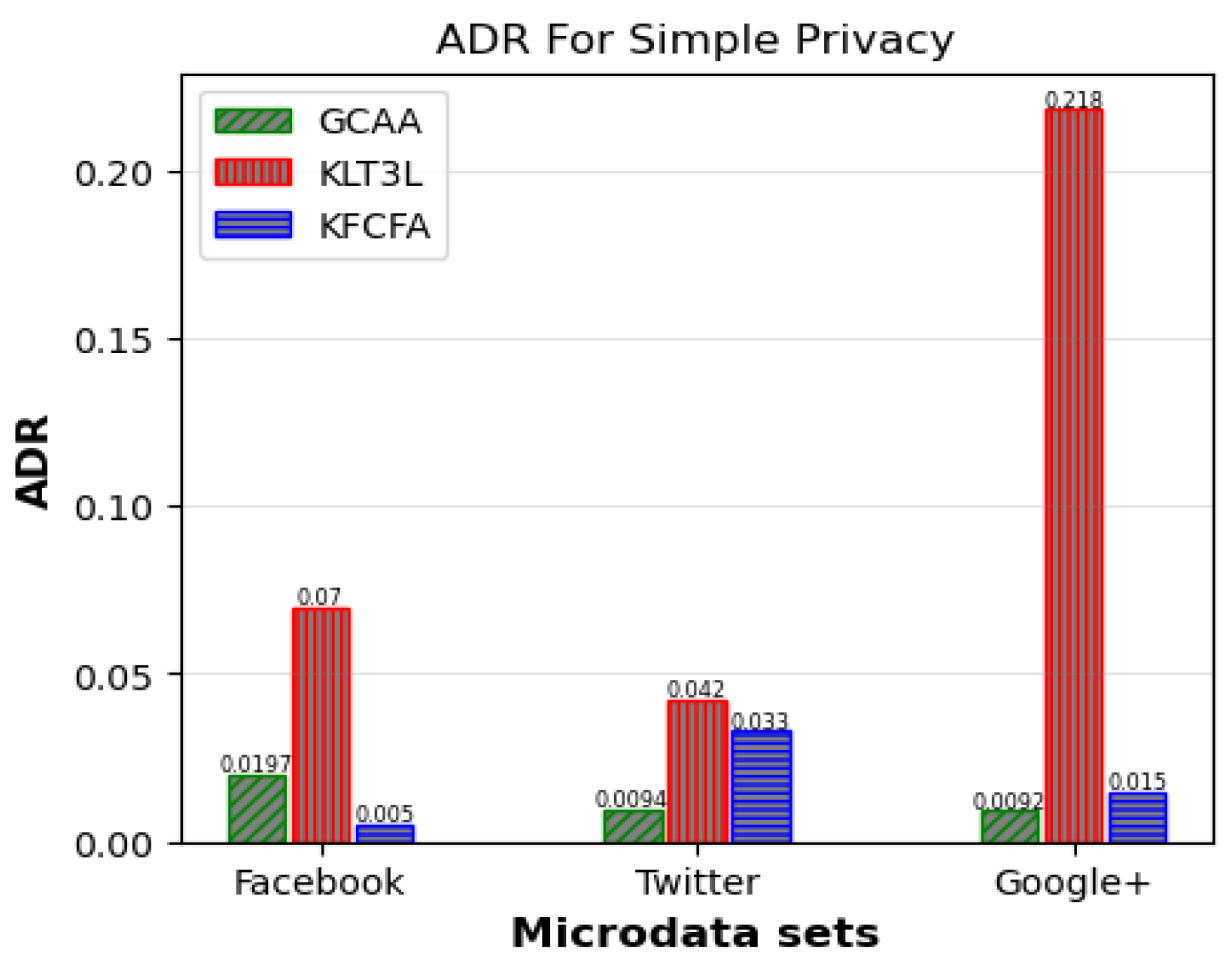
5.1. Experimental Result for Simple Privacy Scenario
Table 12 displays the results obtained for a simple privacy scenario on the Facebook micro dataset using the proposed algorithm. In this scenario, the algorithm generated 70 clusters from the data. Cluster sizes ranged from a minimum of four records to a maximum of eight records. All clusters satisfied the LD requirement, containing at least
l distinct sensitive attribute values. Sensitive attribute diversity within clusters varied between 3 and 7 different values.
Importantly, all clusters generated by the algorithm satisfied both KA and TC privacy criteria. This is because the clustering process prioritized forming groups with a high diversity of sensitive values. Additionally, none of the 70 clusters produced were susceptible to attribute disclosure attacks. By ensuring sensitive attribute diversity within each cluster, the proposed method successfully anonymized the data while preventing homogeneity and skewness of sensitive values that could otherwise compromise privacy according to the attribute disclosure attack model.
It is worth noting that, unlike other techniques, our proposed approach did not remove any records from the original data table as outliers. These results demonstrate the effectiveness of the algorithm in achieving both KA and TC privacy goals while preserving data utility, as shown by retaining all records. A key advantage of our approach compared to other anonymization methods is the ability to satisfy strong privacy standards without eliminating any records. By clustering records rather than discarding outliers, more of the original information can be retained for analysis purposes. Maintaining all records has important implications for data utility, as no information is lost due to outlier removal. This highlights the strengths of the proposed method.
Table 12 shows that while the FKMC method performed best in terms of CAVG and ADR, it suffered from a significantly high P
error. Although PSKA and FKMC had no P
errors, they remained susceptible to attribute disclosure due to their non-zero P
penalty errors. Only the KLT3L and KFCFA methods generated clusters that fully satisfied the TC constraint, making them truly comparable to the proposed GCAA approach in terms of privacy protection.
The proposed GCAA method generates more balanced clusters than KLT3L and KFCFA, which improves CAVG by 78% and 33%, respectively, compared to KLT3L and KFCFA. Moreover, GCAA significantly reduces ADR compared to KLT3L, although it does not outperform KFCFA. KFCFA changes sensitive values to achieve TC, which significantly reduces data utility, whereas GCAA does not require such changes.
Table 12 also reports the average CPU running time of each model. The proposed GCAA algorithm showed computational performance that was nearly three times faster than the KFCFA approach. This significant difference can be attributed to KFCFA’s use of an evolutionary algorithm during its optimization process, which induces greater computational overhead compared to GCAA.
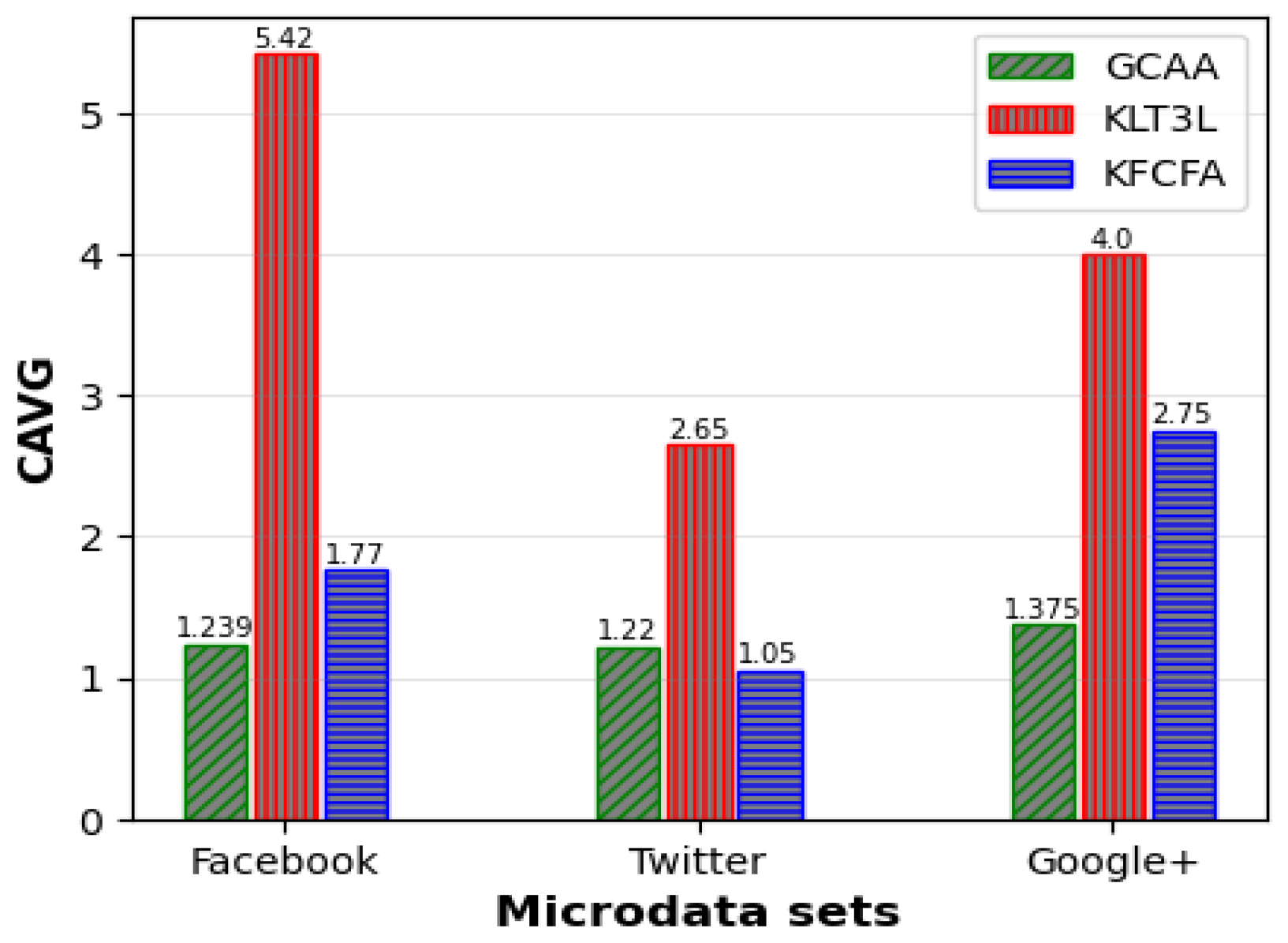
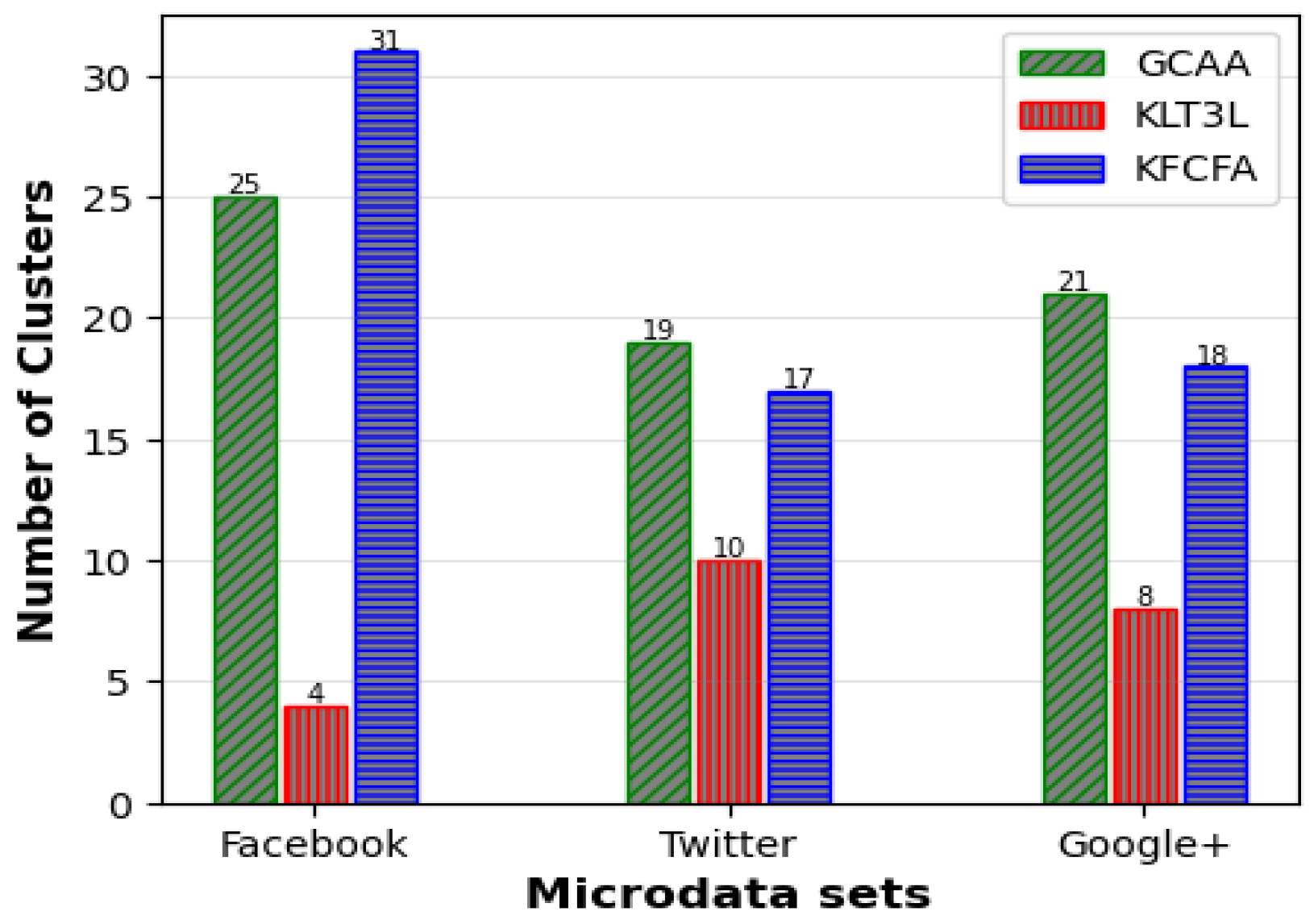
Figure 5,
Figure 6 and
Figure 7 show a comparative analysis of C, CAVG, and ADR for three microdata sets. The results show that the proposed GCAA algorithm performs better than KLT3L on all three datasets and outperforms KFCFA in most cases.
Figure 5 reveals that GCAA produces more balanced clusters than KLT3L for all three datasets, resulting in higher C values. Moreover,
Figure 6 shows that GCAA consistently outperforms KLT3L in terms of CAVG across all datasets. Finally,
Figure 7 demonstrates that GCAA significantly reduces ADR compared to KLT3L on all three datasets.
In addition, GCAA achieves competitive results with KFCFA, outperforming it in terms of C and CAVG on two datasets, as shown in
Figure 5 and
Figure 6. While KFCFA performs slightly better than GCAA in terms of ADR on one dataset,
Figure 7 shows that GCAA still achieves excellent results with a lower ADR than KFCFA on the other two datasets.
5.2. Experimental Result for Medium Privacy Scenario
To limit the anonymization process, the experimenters increased
k to 6 and decreased
t to 0.5. The results were compared across different models, as shown in
Table 13.
Similar to the previous scenario, FKMC outperformed other methods in terms of C and CAVG. At the same time, GCAA, KLT3L, and KFCFA were superior to PSKA and FKMC due to more robust privacy protection. These methods satisfied the TC constraint in all clusters, resulting in zero P
error. KLT3L merged many clusters to satisfy the TC constraint, resulting in a reduction in the number of final clusters to 12. This resulted in a larger CAVG of 4.82, which is almost four times larger than GCAA, and an ADR that was twice as large. KFCFA outperformed the proposed GCAA in this experiment, as shown in
Figure 8 and
Figure 9.
These figures compare the C and CAVG criteria for GCAA, KLT3L, and KFCFA in the medium privacy scenario on three microdata sets. The proposed GCAA had a lower CAVG error in all datasets than KLT3L. KFCFA performed better than GCAA on the Facebook and Twitter datasets, but GCAA had fewer errors than KFCFA on the Google+ dataset.
Figure 10 shows a similar comparison for ADR criteria, with the proposed GCAA performing better than KLT3L in most cases.
5.3. Experimental Result for Strict Privacy Scenario
To evaluate the algorithms under an even more restrictive privacy setting, the experimenters increased the KA parameter
k to 8 and decreased the TC parameter
t to 0.3.
Table 14 shows the results of different approaches on the Facebook microdata set. KLT3L and KFCFA generated 4 and 25 clusters, respectively, with CAVGs of 10.48 and 1.735. The proposed GCAA algorithm improved the ADR error by 70.5% and 0.7% compared to KLT3L and KFCFA, respectively.
Figure 11,
Figure 12 and
Figure 13 compare the C, CAVG, and ADR results obtained from the proposed GCAA, KLT3L, and KFCFA under the strict privacy scenario on three microdata sets. The proposed approach showed superior performance by generating more balanced clusters on the Twitter and Google+ datasets, resulting in less error than the other two methods for CAVG and ADR criteria. Although KFCFA produced more clusters on the Facebook dataset than the proposed GCAA, the ADR error was not lower because KFCFA significantly changed the feature values to achieve TC.
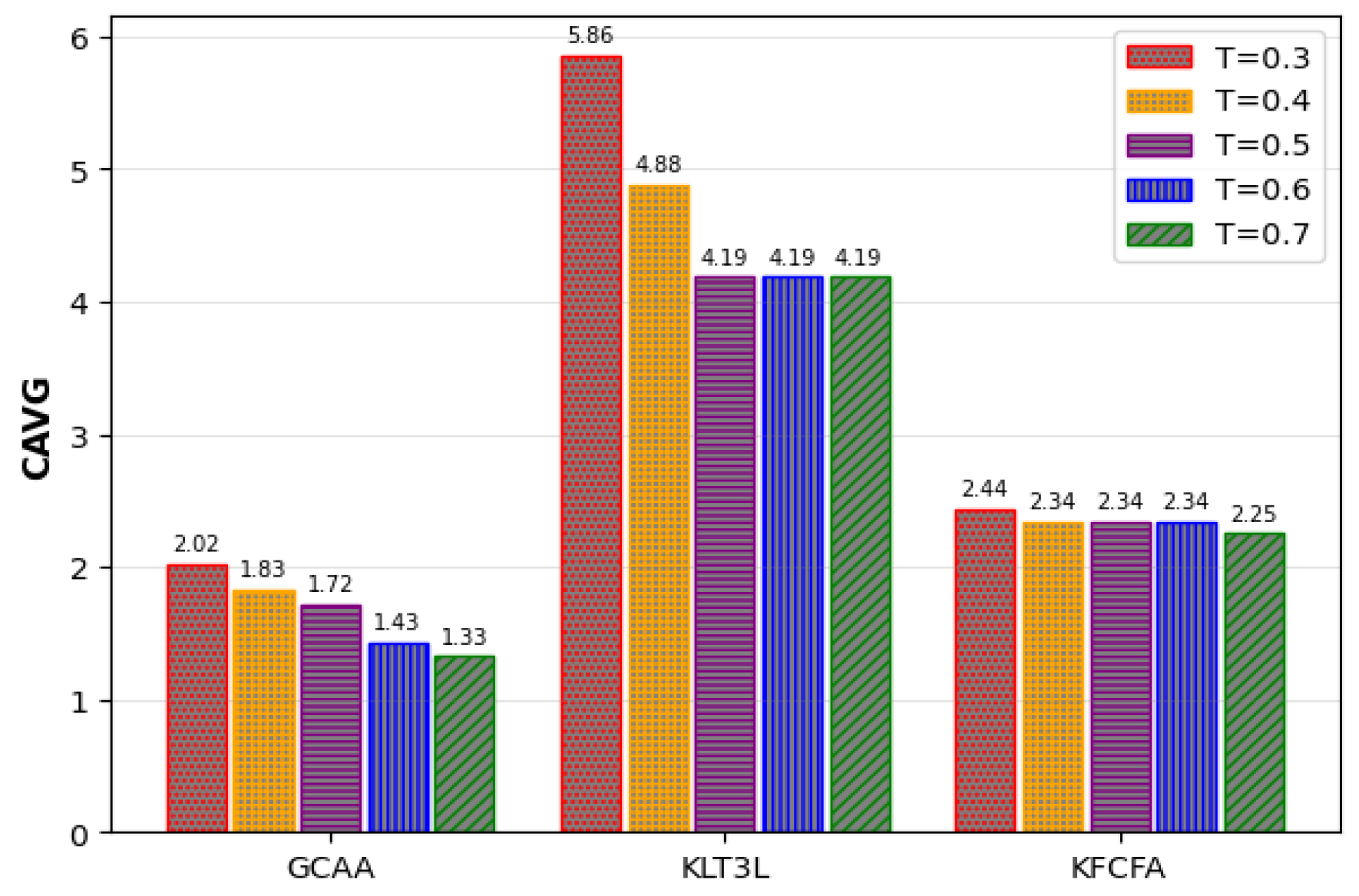
5.4. Experimental Result for Different Values of Parameter T
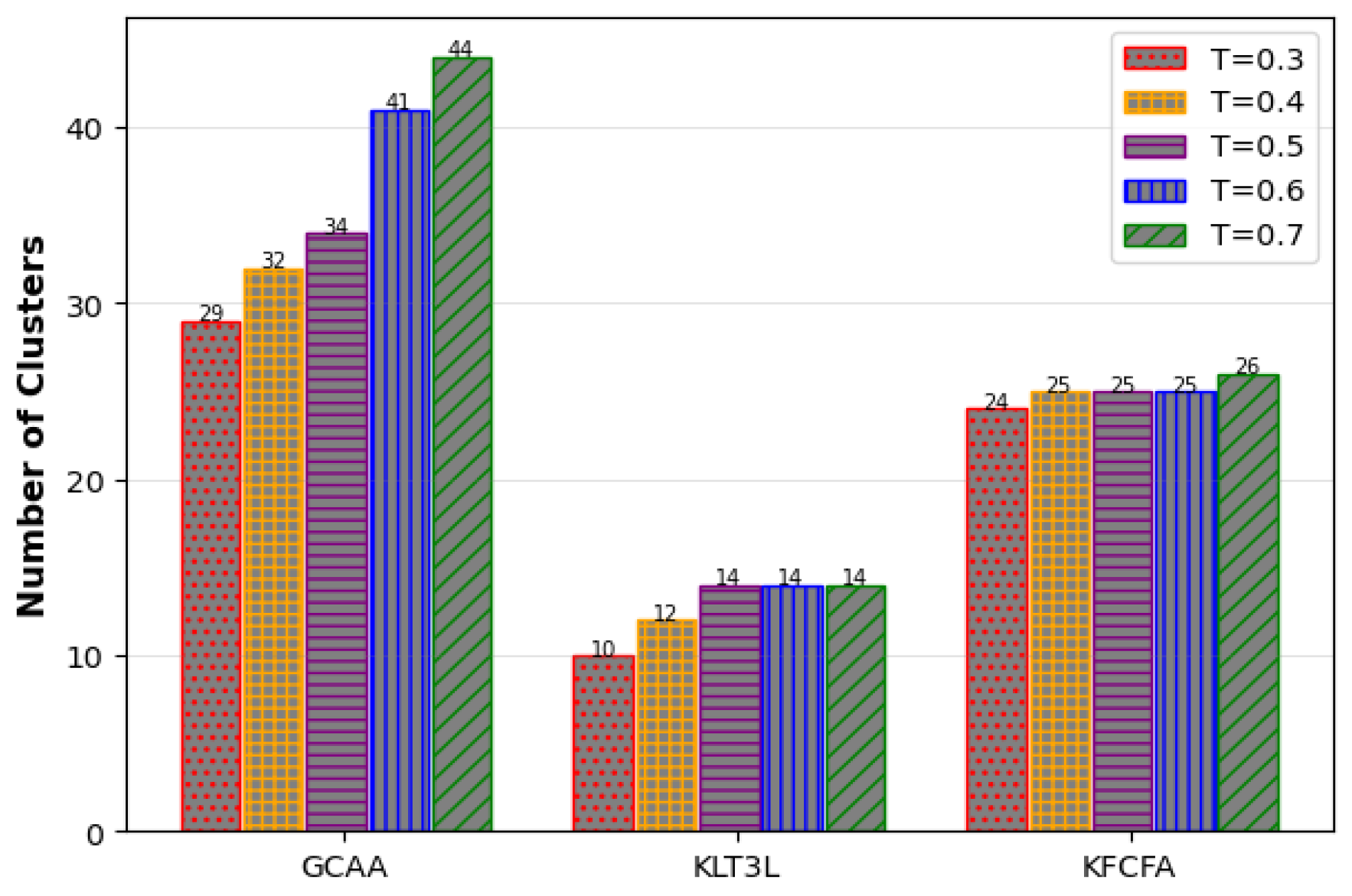
To investigate the impact of the parameter t, a set of experiments was carried out where the parameter t was systematically varied from 0.3 to 0.7, while holding k and l fixed at 6 and 4, respectively. In this analysis, the Google+ microdata set was used to observe the effect of changing t on the C, CAVG, and ADR criteria. Since decreasing t complicates the problem of achieving the TC constraint, it is expected to increase various error rates. As a result, with a decrease in t, CAVG increases, indicating the appearance of larger clusters.
Figure 14 and
Figure 15 show that the proposed GCAA performs better than KLT3L and KFCFA in terms of C and CAVG metrics, especially in scenarios where privacy is very important. However, as seen in
Figure 16, ADR increases for all methods as
t decreases. Despite its shortcomings, the proposed GCAA still outperforms KLT3L and KFCFA in strict privacy settings.
5.5. Discussion
In terms of privacy, the proposed GCAA strategy along with KLT3L and KFCFA fully addresses the risks of identity and attribute disclosure attacks by satisfying both the KA and TC requirements. The PSKA and FKMC methods only partially mitigate these risks, as they do not perfectly satisfy TC. However, the resistance of GCAA and some other algorithms to similarity attacks could be improved. Specifically, they currently lack a criterion for determining the semantic similarity of attribute values during clustering. For example, in a medical context, the algorithms have no way to judge that diseases like colon cancer and liver cancer should be considered highly similar rather than diverse, for the purpose of TC. Not accounting for such attribute-relatedness weakens protections against similarity attacks.
In terms of data utility, FKMC and PSKA methods had the lowest amount of IL, as measured by ADR, and therefore the best data utility. The proposed method and KFCFA performed similarly well, but the KLT method lost a significant amount of IL. This suggests that the proposed method is effective at preserving the usefulness of anonymized data for future knowledge extraction.
In terms of computational efficiency, the clustering phase has a time complexity of , where d is the size of the attribute’s domain and n is the number of records. However, if , it can be concluded that the time complexity is . The proposed adjustment phase for splitting and merging clusters has a time complexity of .
In terms of average execution time, the proposed method outperforms KFCFA but underperforms other methods. KFCFA is slow, unscalable, and computationally expensive due to its evolutionary nature. The proposed method is also slower than other methods due to its time complexity. Because it provides a high level of privacy protection and data utility, the proposed method is suitable for anonymizing publishable data in inactive mode, where the data owner publishes the entire anonymized dataset after making some modifications to the original data [
36]. In this case, the data owner prioritizes the level of privacy and utility of anonymized data.
These findings are consistent with the results of other experiments, highlighting the effectiveness of the proposed GCAA approach in achieving high privacy protection while minimizing the distortion of the original data. A brief review of the above, key findings emerge:
As privacy protection increases, the data becomes more distorted, which reduces its usefulness. This is consistent with
Figure 1.
The proposed GCAA method, as well as the KLT3L and KFCFA methods, can protect data from identity and attribute disclosure attacks by meeting both KA and TC.
The KLT3L algorithm has higher error measures (CAVG and ADR) than the proposed methods because it needs to merge more clusters and make more errors to meet the TC constraint.
The proposed GCAA outperforms the KFCFA method in some cases, while the KFCFA method produces better results in other cases. However, changing the values of sensitive features to meet the TC constraint can reduce the usefulness of the data.
The results demonstrate the effectiveness of the proposed GCAA algorithm. The main reasons are: (1) It considers the diversity of sensitive feature values and the similarity of quasi-identifier values simultaneously during clustering (2) It generates evenly sized clusters that are consistent with the KA and TC constraints. (3) It uses an adjustment algorithm to produce an anonymized dataset with maximum data utility.
6. Conclusions and Future Works
The proposed Greedy Clustering-based Anonymization Algorithm (GCAA) provides a novel contribution to the field of data privacy. It uses information theory concepts and performs bottom-up hierarchical clustering to form clusters with similar quasi-identifier values and diverse sensitive attribute values. The algorithm iteratively merges pairs of clusters with the minimum loss of mutual information and reduces the EMD criterion. Clusters with a cardinality between k and removed from the clustering process to ensure that balanced clusters satisfying the KA and TC constraints are formed.
In the adjustment phase, the GCAA algorithm enforces the KA and TC constraints by splitting and merging clusters that do not meet these requirements while reducing the EMD. We evaluated GCAA’s performance based on the CAVG and ADR criteria and compared it with four other methods: KLT3L, KFCFA, PSKA, and FFKMC. Our experimental results demonstrate that GCAA efficiently forms balanced clusters while providing robust privacy protection and preserving data quality. GCAA is a faster method than KFCFA that provides similar levels of privacy protection and IL. However, the proposed algorithm may require a longer execution time than some other methods due to its time complexity.
The proposed algorithm exhibits several limitations. Firstly, it is tailored for non-numeric data, rendering it unsuitable for numerical data anonymization. Secondly, the algorithm is confined to single-sensitive attribute scenarios. Finally, the algorithm is restricted to tabular data and is ill-suited for graphical or structural data analysis. GCAA has practical applications in anonymizing scalable microdata where privacy preservation is crucial while retaining useful information for data mining purposes.
The primary objectives of our future research to enhance the proposed method include:
Defining a criterion to evaluate the similarity between attribute values based on the proposed structure, thereby reinforcing the algorithm against similarity attacks.
Extending the proposed method to handle datasets with multiple sensitive attributes.
Expanding the algorithm to anonymize numerical data in addition to non-numerical data.
Other suitable clustering methods for categorical data could also be considered, such as partitioning around medoids using the Gower coefficient [
37]. This method is well-suited for datasets containing binary values, similar to the data used in our experiments. Evaluating the performance of partition around medoids and comparing it to the proposed approach may provide additional insights.
Reducing the time complexity of the algorithm.