Spatiotemporal Variations of the Frequency–Magnitude Distribution in the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence
Abstract
1. Introduction
2. Methodological Approach Based on NESP
Non-Extensive Fragment–Asperity Model for Seismic Energies
3. Seismological Data
4. Results
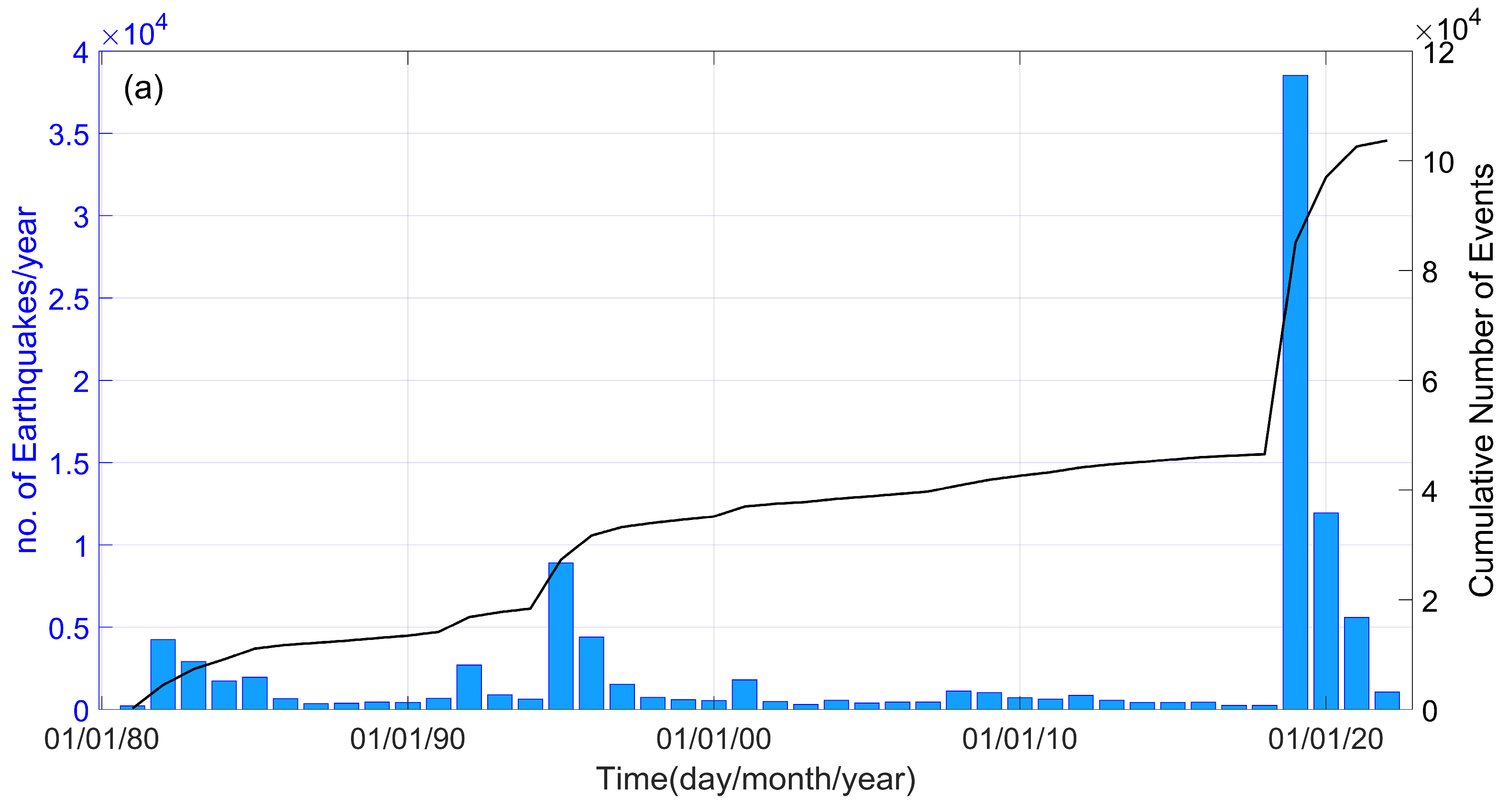
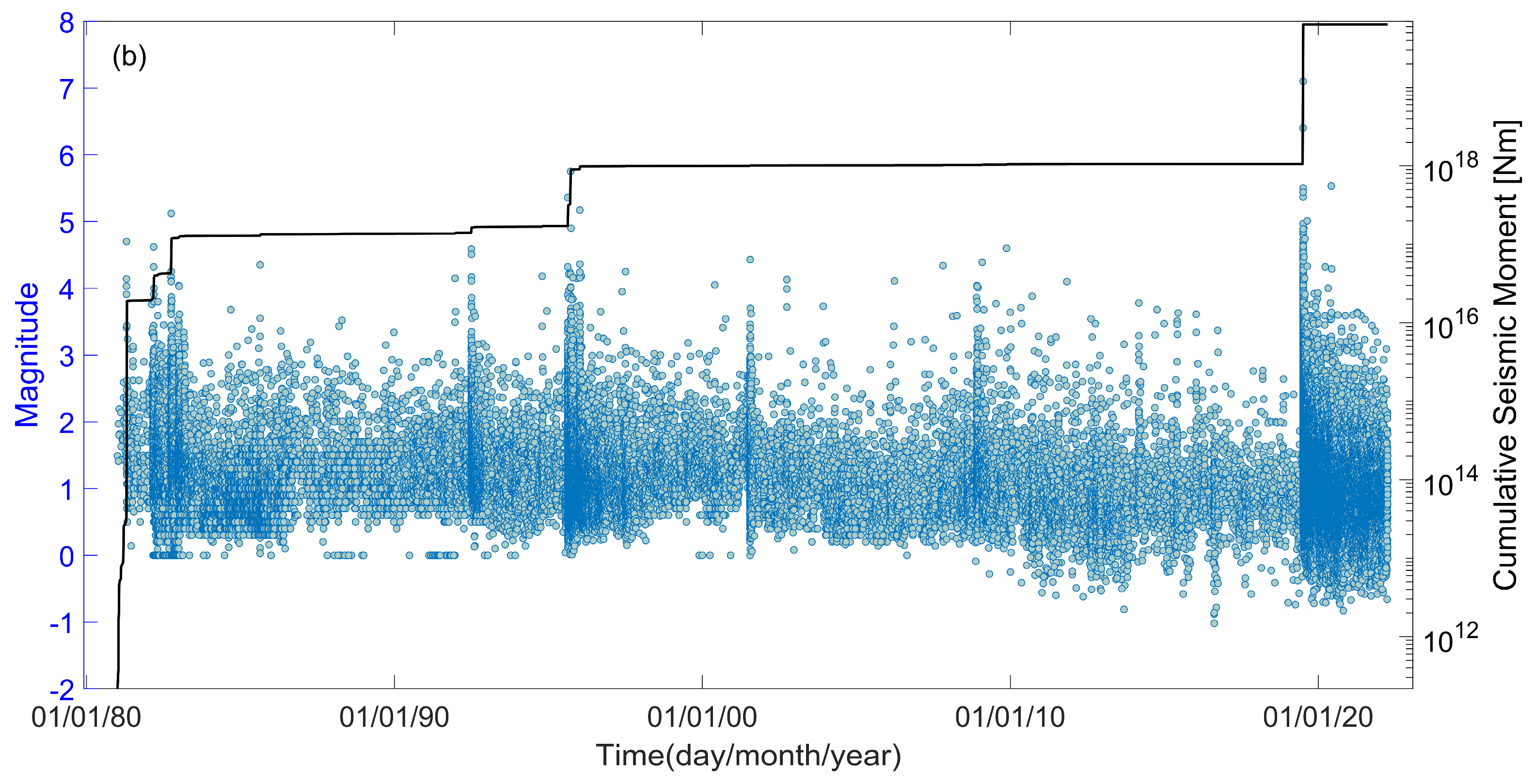
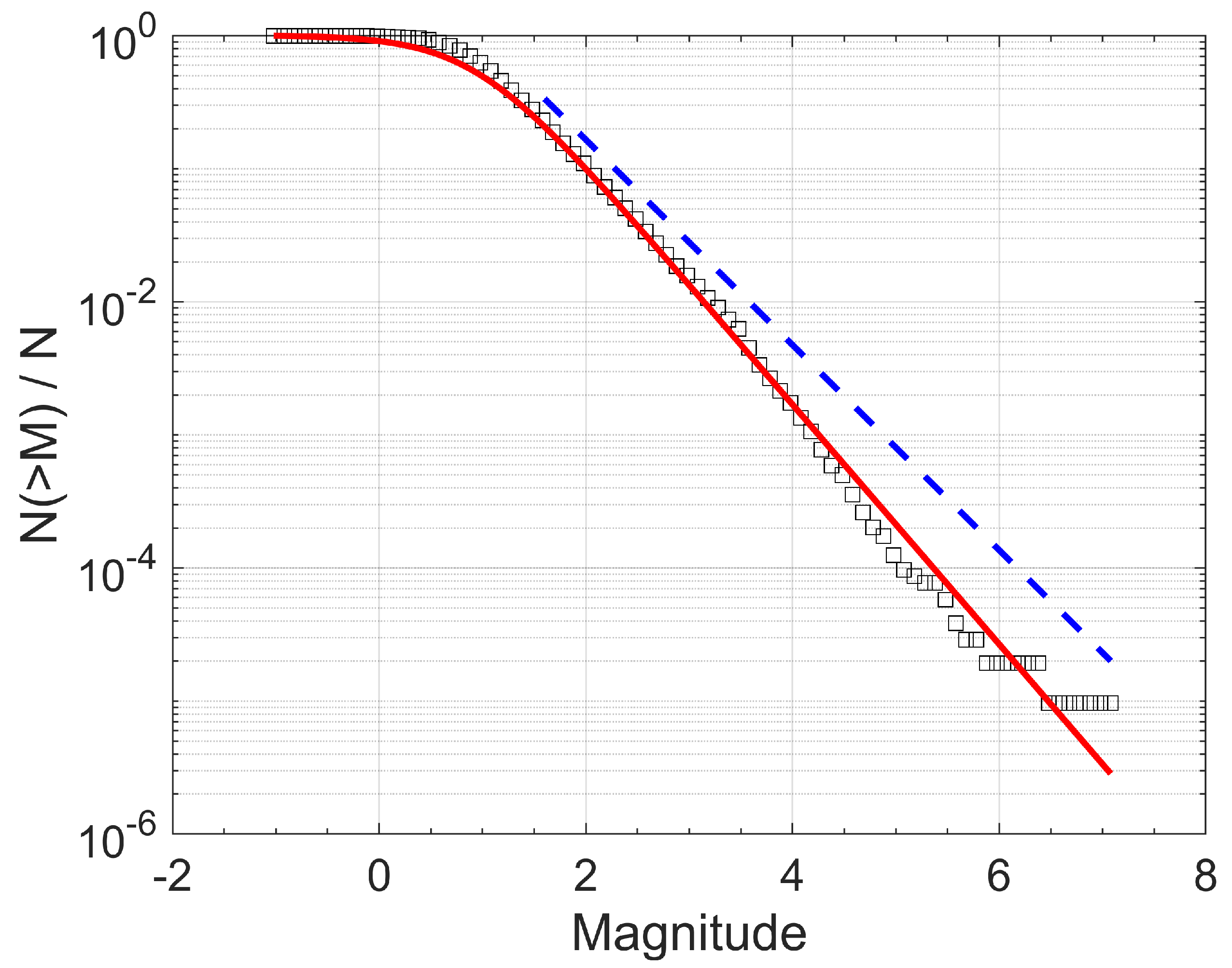
4.1. Frequency–Magnitude Distribution during 1981–2022
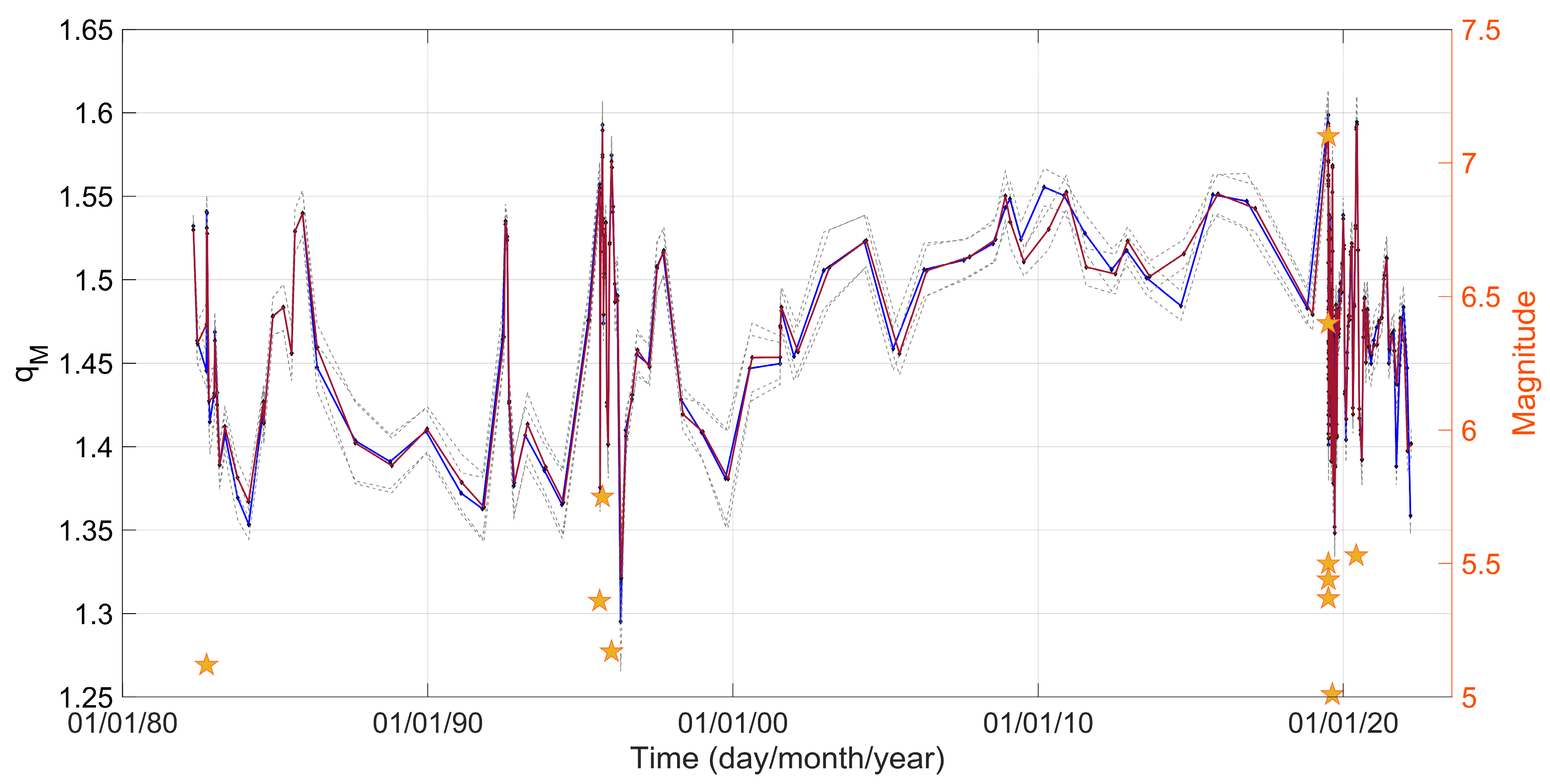
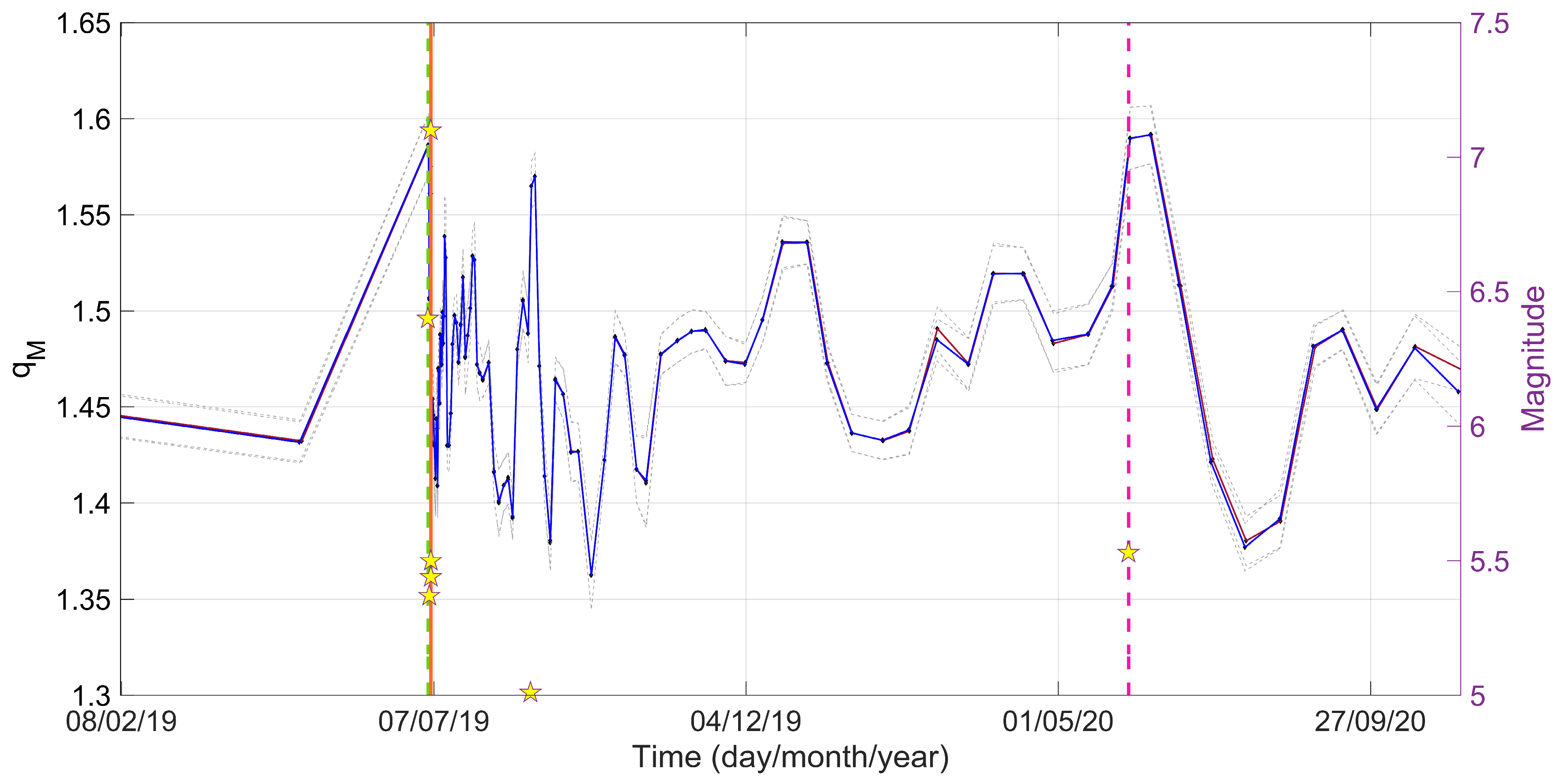
4.2. Variations of qM Values with Time
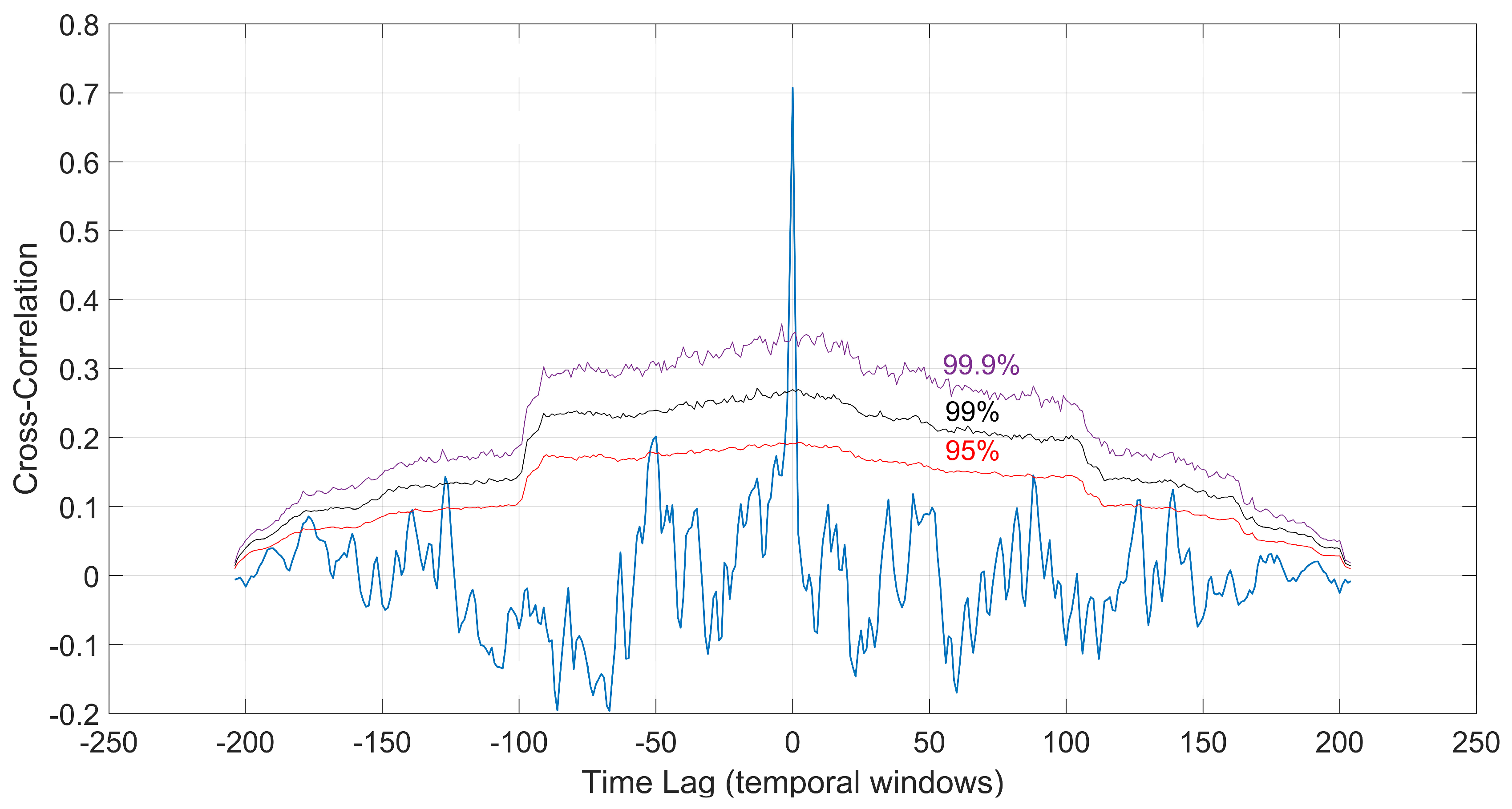
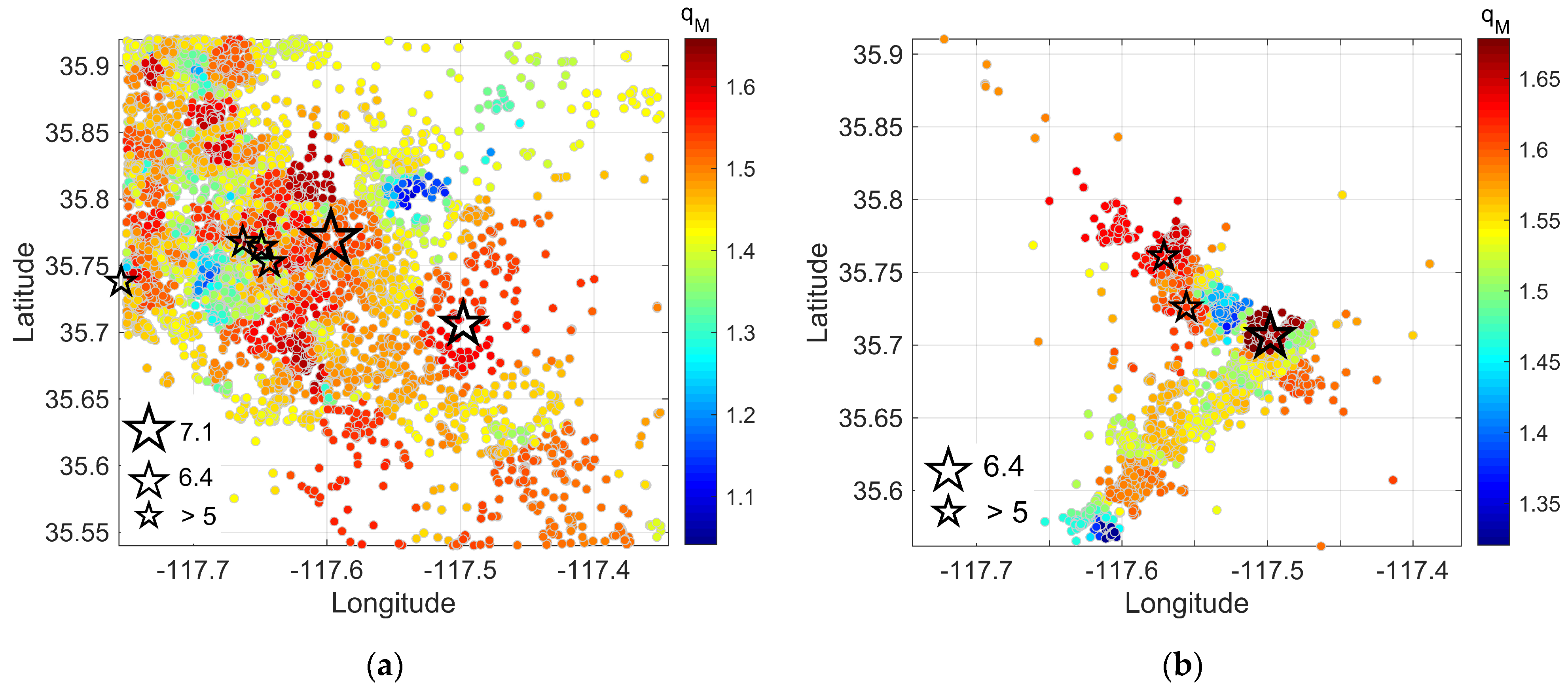
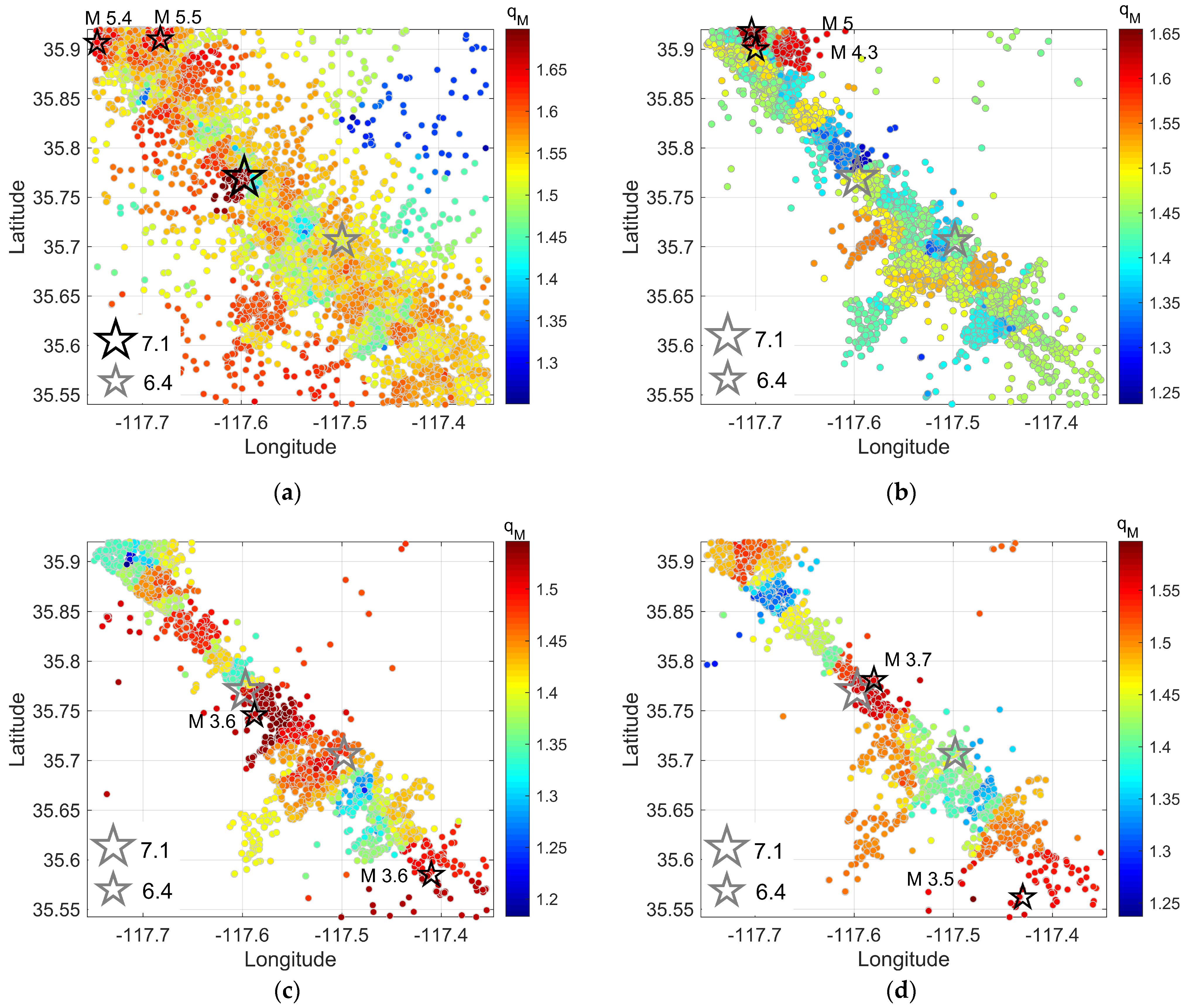
4.3. Spatiotemporal Distributions of qM Values
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ross, Z.E.; Idini, B.; Jia, Z.; Stephenson, O.L.; Zhong, M.; Wang, X.; Zhan, Z.; Simons, M.; Fielding, E.J.; Yun, S.-H.; et al. Hierarchical Interlocked Orthogonal Faulting in the 2019 Ridgecrest Earthquake Sequence. Science 2019, 366, 346–351. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Qiu, Q.; Wang, Y.; Zhang, P.; Li, T.; Zheng, W. Orthogonal Fault Rupture and Rapid Postseismic Deformation Following 2019 Ridgecrest, California, Earthquake Sequence Revealed from Geodetic Observations. Geophys. Res. Lett. 2020, 47, e2019GL086888. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Soldani, M.; Piscini, A.; Sabbagh, D.; Cianchini, G.; Perrone, L.; Orlando, M. Swarm Satellite Magnetic Field Data Analysis Prior to 2019 Mw = 7.1 Ridgecrest (California, USA) Earthquake. Geosciences 2020, 10, 502. [Google Scholar] [CrossRef]
- DuRoss, C.B.; Gold, R.D.; Dawson, T.E.; Scharer, K.M.; Kendrick, K.J.; Akciz, S.O.; Angster, S.J.; Bachhuber, J.; Bacon, S.; Bennett, S.E.K.; et al. Surface Displacement Distributions for the July 2019 Ridgecrest, California, Earthquake Ruptures. Bull. Seismol. Soc. Am. 2020, 110, 1400–1418. [Google Scholar] [CrossRef]
- Wang, K.; Dreger, D.S.; Tinti, E.; Bürgmann, R.; Taira, T. Rupture Process of the 2019 Ridgecrest, California Mw 6.4 Foreshock and Mw 7.1 Earthquake Constrained by Seismic and Geodetic Data. Bull. Seismol. Soc. Am. 2020, 110, 1603–1626. [Google Scholar] [CrossRef]
- Fialko, Y. Estimation of Absolute Stress in the Hypocentral Region of the 2019 Ridgecrest, California, Earthquakes. JGR Solid Earth 2021, 126, e2021JB022000. [Google Scholar] [CrossRef]
- Jin, Z.; Fialko, Y. Finite Slip Models of the 2019 Ridgecrest Earthquake Sequence Constrained by Space Geodetic Data and Aftershock Locations. Bull. Seismol. Soc. Am. 2020, 110, 1660–1679. [Google Scholar] [CrossRef]
- Wang, K.; Bürgmann, R. Co- and Early Postseismic Deformation Due to the 2019 Ridgecrest Earthquake Sequence Constrained by Sentinel-1 and COSMO-SkyMed SAR Data. Seismol. Res. Lett. 2020, 91, 1998–2009. [Google Scholar] [CrossRef]
- Hauksson, E.; Hutton, K.; Kanamori, H.; Jones, L.; Mori, J.; Hough, S.; Roquemore, G. Preliminary Report on the 1995 Ridgecrest Earthquake Sequence in Eastern California. Seismol. Res. Lett. 1995, 66, 54–60. [Google Scholar] [CrossRef][Green Version]
- Sotolongo-Costa, O.; Posadas, A. Fragment-Asperity Interaction Model for Earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Tsallis, C. Nonadditive Entropy and Nonextensive Statistical Mechanics—An Overview after 20 Years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and Natural Time: The Case of Seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef]
- Telesca, L. Maximum Likelihood Estimation of the Nonextensive Parameters of the Earthquake Cumulative Magnitude Distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.I. Nonextensive Statistical Mechanics and Thermodynamics: Historical Background and Present Status. In Nonextensive Statistical Mechanics and Its Applications; Abe, S., Okamoto, Y., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2001; Volume 560, pp. 3–98. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Tirnakli, U.; Borges, E.P. The Standard Map: From Boltzmann-Gibbs Statistics to Tsallis Statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; França, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive Models for Earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef] [PubMed]
- Lay, T.; Wallace, T. Modern Global Seismology; Academic Press, Inc.: Cambridge, MA, USA, 1995; 521p. [Google Scholar]
- Telesca, L. Tsallis-Based Nonextensive Analysis of the Southern California Seismicity. Entropy 2011, 13, 1267–1280. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-Extensivity and Long-Range Correlations in the Earthquake Activity at the West Corinth Rift (Greece). Nonlin. Process. Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. A Nonextensive Statistical Physics Analysis of the 1995 Kobe, Japan Earthquake. Pure Appl. Geophys. 2015, 172, 1923–1931. [Google Scholar] [CrossRef]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized Statistical Mechanics Approaches to Earthquakes and Tectonics. Proc. R. Soc. A 2016, 472, 20160497. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Telesca, L. A Non-Extensive Approach in Investigating the Seismicity of L’Aquila Area (Central Italy), Struck by the 6 April 2009 Earthquake ( ML = 5.8). Terra Nova 2010, 22, 87–93. [Google Scholar] [CrossRef]
- Antonopoulos, C.G.; Michas, G.; Vallianatos, F.; Bountis, T. Evidence of q -Exponential Statistics in Greek Seismicity. Phys. A Stat. Mech. Its Appl. 2014, 409, 71–77. [Google Scholar] [CrossRef]
- Chochlaki, K.; Michas, G.; Vallianatos, F. Complexity of the Yellowstone Park Volcanic Field Seismicity in Terms of Tsallis Entropy. Entropy 2018, 20, 721. [Google Scholar] [CrossRef]
- Aki, K. Maximum Likelihood Estimate of b in the Formula log10N=a-bm and Its Confidence Limits. Bull. Earthq. Res. 1965, 43, 237–239. [Google Scholar]
- Michas, G. Generalized Statistical Mechanics Description of Fault and Earthquake populations in Corinth Rift (Greece). Ph.D. Thesis, University College London, London, UK, 2016. [Google Scholar]
- Hauksson, E.; Yang, W.; Shearer, P.M. Waveform Relocated Earthquake Catalog for Southern California (1981 to June 2011). Bull. Seismol. Soc. Am. 2012, 102, 2239–2244. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A Moment Magnitude Scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1994, 34, 185–188. [Google Scholar] [CrossRef]
- Utsu, T. Estimation of parameter values in the formula for the magnitude-frequency relation of earthquake occurrence. Zisin 1978, 31, 367–382. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Schultz, R.; Telesca, L. The Cross-Correlation and Reshuffling Tests in Discerning Induced Seismicity. Pure Appl. Geophys. 2018, 175, 3395–3401. [Google Scholar] [CrossRef]
- Michas, G.; Pavlou, K.; Vallianatos, F.; Drakatos, G. Correlation Between Seismicity and Water Level Fluctuations in the Polyphyto Dam, North Greece. Pure Appl. Geophys. 2020, 177, 3851–3870. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Moroz, I.M.; Roberts, S.J. Testing the Assumptions of Linear Prediction Analysis in Normal Vowels. J. Acoust. Soc. Am. 2006, 119, 549–558. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L. Analysis of Italian Seismicity by Using a Nonextensive Approach. Tectonophysics 2010, 494, 155–162. [Google Scholar] [CrossRef]
- Valverde-Esparza, S.M.; Ramírez-Rojas, A.; Flores-Márquez, E.L.; Telesca, L. Non-Extensivity Analysis of Seismicity within Four Subduction Regions in Mexico. Acta Geophys. 2012, 60, 833–845. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-Extensive and Natural Time Analysis of Seismicity before the Mw6.4, October 12, 2013 Earthquake in the South West Segment of the Hellenic Arc. Phys. A Stat. Mech. Its Appl. 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Michas, G.; Papadakis, G.; Vallianatos, F. A Non-Extensive Approach in Investigating Greek Seismicity. Geosociety 2013, 47, 1177. [Google Scholar] [CrossRef][Green Version]
- Stein, R.S. The Role of Stress Transfer in Earthquake Occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Ebel, J.E.; Bonjer, K.-P.; Oncescu, M.C. Paleoseismicity: Seismicity Evidence for Past Large Earthquakes. Seismol. Res. Lett. 2000, 71, 283–294. [Google Scholar] [CrossRef]
- Enescu, B.; Ito, K. Values of b and p: Their variations and relation to physical processes for earthquakes in Japan. Ann. Disas. Prev. Res. Inst. Kyoto Univ. 2003, 46, 709–719. [Google Scholar]
- Gulia, L.; Wiemer, S. Real-Time Discrimination of Earthquake Foreshocks and Aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, A.M. Anomalies and Transient Variations of b -Value in Italy during the Major Earthquake Sequences: What Truth Is There to This? Geophys. J. Int. 2022, 232, 1545–1555. [Google Scholar] [CrossRef]
- Wiemer, S.; Katsumata, K. Spatial Variability of Seismicity Parameters in Aftershock Zones. J. Geophys. Res. 1999, 104, 13135–13151. [Google Scholar] [CrossRef]
- Ramírez-Rojas, A.; Flores-Márquez, E.L. Nonlinear Statistical Features of the Seismicity in the Subduction Zone of Tehuantepec Isthmus, Southern México. Entropy 2022, 24, 480. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S.; Vannucci, G. Pseudoprospective Evaluation of the Foreshock Traffic-Light System in Ridgecrest and Implications for Aftershock Hazard Assessment. Seismol. Res. Lett. 2020, 91, 2828–2842. [Google Scholar] [CrossRef]
- Kanamori, H. The Nature of Seismicity Patterns Before Large Earthquakes. In Maurice Ewing Series; Simpson, D.W., Richards, P.G., Eds.; American Geophysical Union: Washington, DC, USA, 2013; pp. 1–19. [Google Scholar] [CrossRef]
- Huang, K.; Tang, L.; Feng, W. Spatiotemporal Distributions of b Values Following the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence. Pure Appl. Geophys. 2023, 180, 2529–2542. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sardeli, E.; Michas, G.; Pavlou, K.; Vallianatos, F. Spatiotemporal Variations of the Frequency–Magnitude Distribution in the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence. Entropy 2023, 25, 1612. https://doi.org/10.3390/e25121612
Sardeli E, Michas G, Pavlou K, Vallianatos F. Spatiotemporal Variations of the Frequency–Magnitude Distribution in the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence. Entropy. 2023; 25(12):1612. https://doi.org/10.3390/e25121612
Chicago/Turabian StyleSardeli, Eirini, Georgios Michas, Kyriaki Pavlou, and Filippos Vallianatos. 2023. "Spatiotemporal Variations of the Frequency–Magnitude Distribution in the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence" Entropy 25, no. 12: 1612. https://doi.org/10.3390/e25121612
APA StyleSardeli, E., Michas, G., Pavlou, K., & Vallianatos, F. (2023). Spatiotemporal Variations of the Frequency–Magnitude Distribution in the 2019 Mw 7.1 Ridgecrest, California, Earthquake Sequence. Entropy, 25(12), 1612. https://doi.org/10.3390/e25121612







