Pointer States and Quantum Darwinism with Two-Body Interactions
Abstract
:1. Introduction
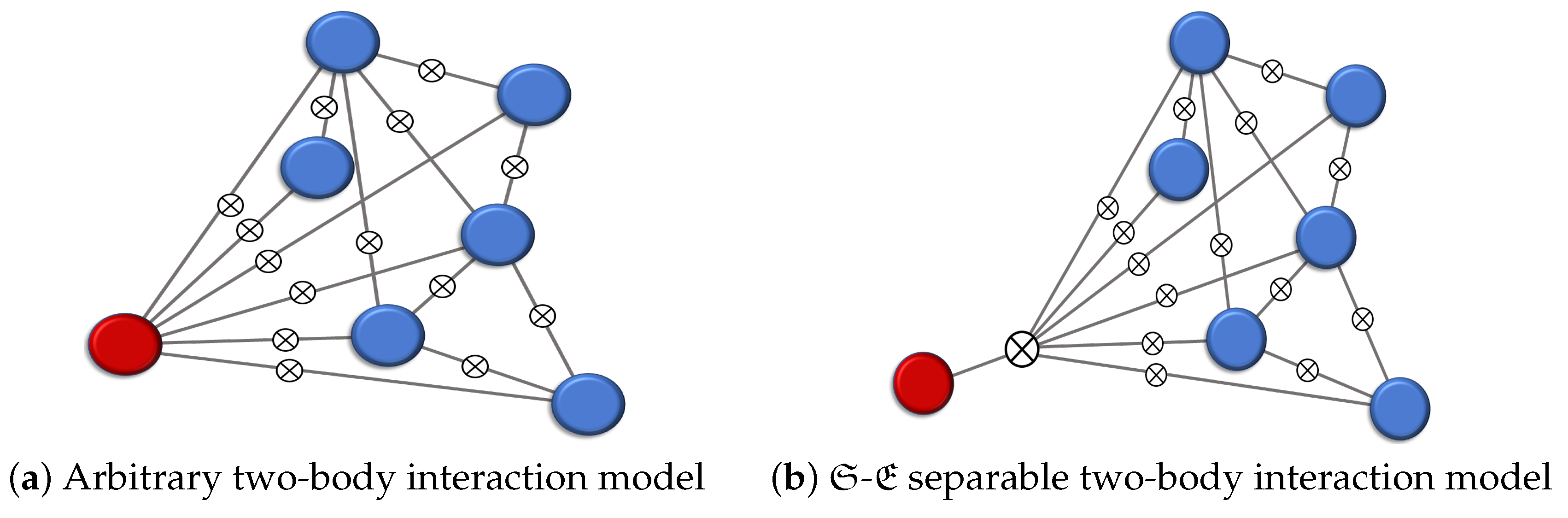
2. Structure of the Hamiltonian
2.1. Existence of a Pointer Basis
2.2. Further Conditions for Quantum Darwinism
3. Coefficients of the Hamiltonian
3.1. Solving the Dynamics
3.2. Rate and Irreversibility of Information Transfer
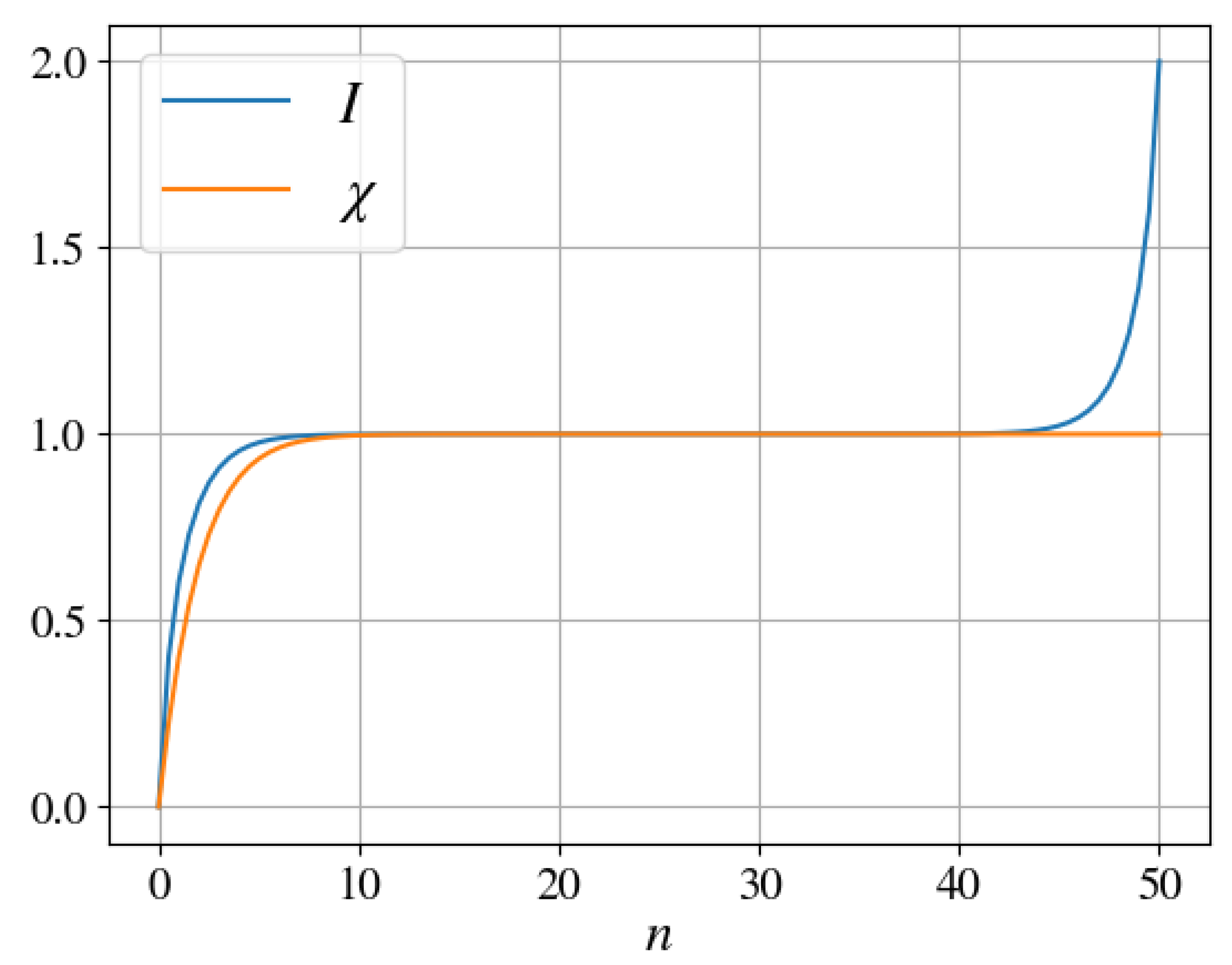
3.3. Quantum Darwinism—The Classical Plateau
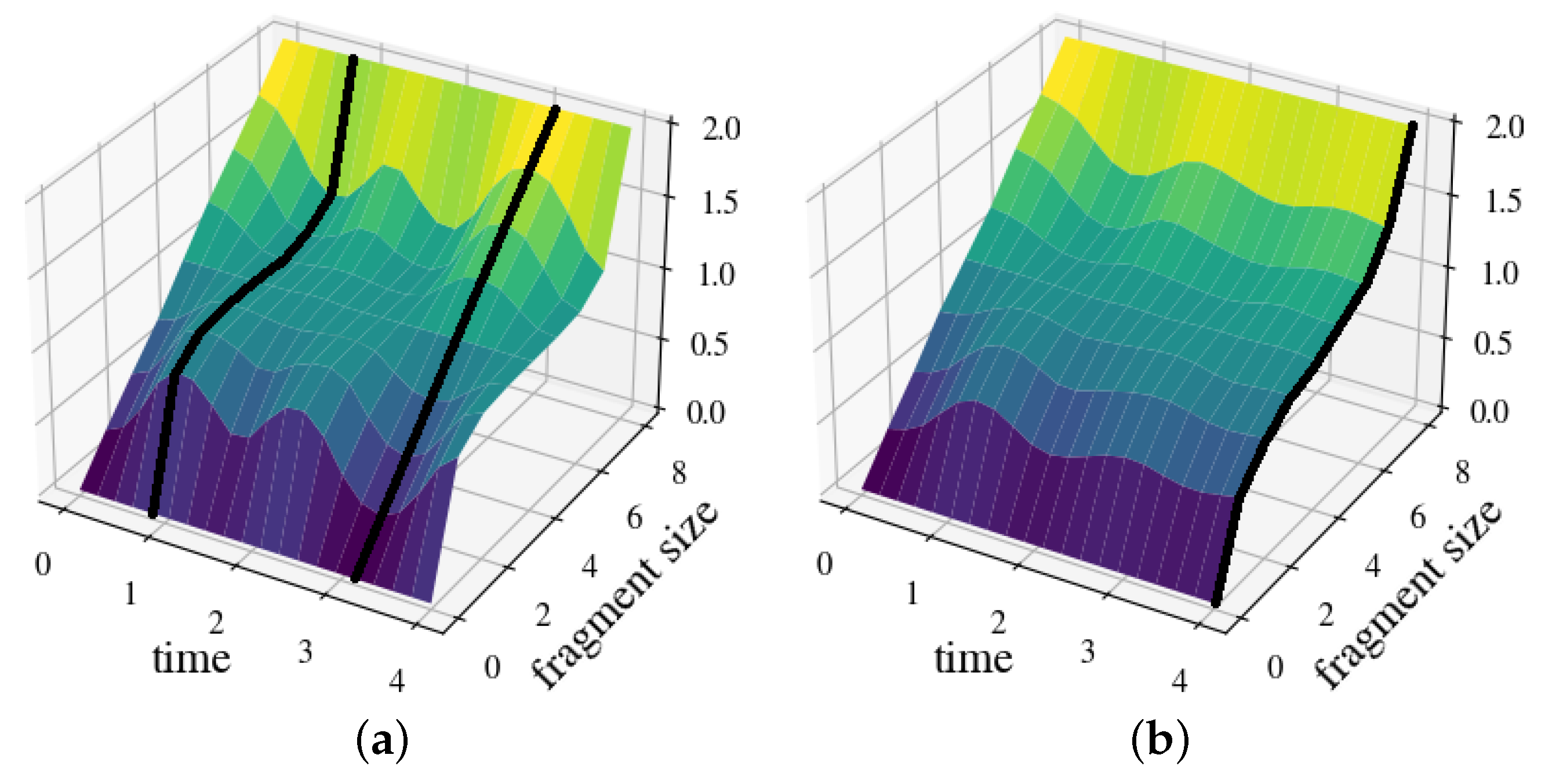
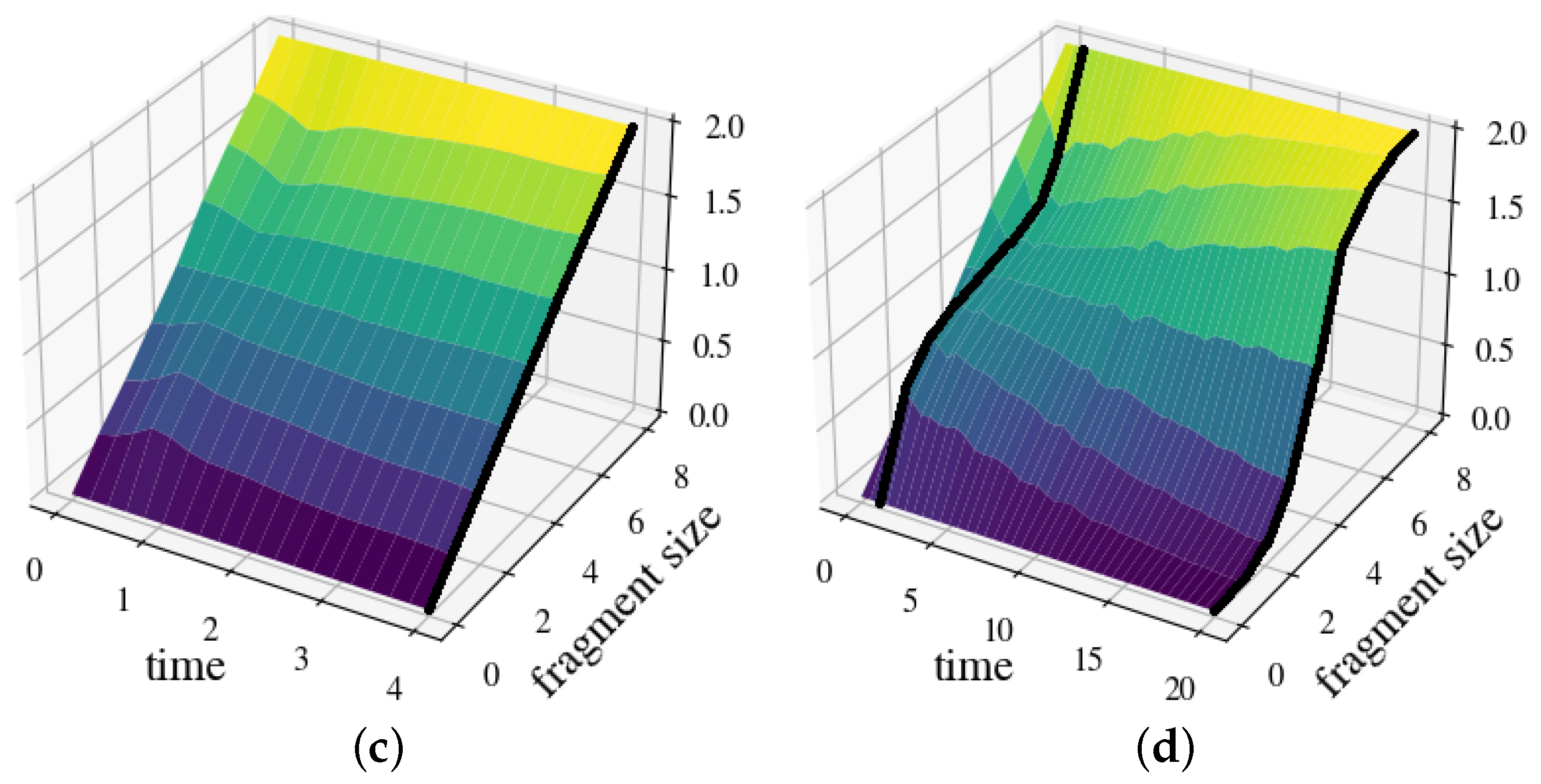
4. Representative Examples
4.1. Continuous Parallel Decoherence Interaction
4.2. Discrete Parallel Decoherence Interaction
4.3. Continuous Orthogonal Decoherence Interaction
4.4. Continuous Parallel Decoherence Interaction with Scrambling
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Hamiltonians with a Pointer Basis
Appendix B. Average Decoherence Factors
Appendix C. Mutual Information and Asymptotics
References
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Zurek, W.H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516–1525. [Google Scholar] [CrossRef]
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862–1880. [Google Scholar] [CrossRef]
- Brasil, C.A.; de Castro, L.A. Understanding the pointer states. Eur. J. Phys. 2015, 36, 065024. [Google Scholar] [CrossRef]
- Zurek, W. Einselection and decoherence from an information theory perspective. Ann. Phys. 2000, 512, 855–864. [Google Scholar] [CrossRef]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 2005, 72, 042113. [Google Scholar] [CrossRef]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Objective Properties from Subjective Quantum States: Environment as a Witness. Phys. Rev. Lett. 2004, 93, 220401. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181. [Google Scholar] [CrossRef]
- Girolami, D.; Touil, A.; Yan, B.; Deffner, S.; Zurek, W.H. Redundantly Amplified Information Suppresses Quantum Correlations in Many-Body Systems. Phys. Rev. Lett. 2022, 129, 010401. [Google Scholar] [CrossRef]
- Touil, A.; Anza, F.; Deffner, S.; Crutchfield, J.P. Branching States as the Emergent Structure of a Quantum Universe. arXiv 2022, arXiv:2208.05497. [Google Scholar]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 2006, 73, 062310. [Google Scholar] [CrossRef]
- Deffner, S.; Laflamme, R.; Paz, J.P.; Zwolak, M. (Eds.) Quantum Darwinism and Friends; MDPI Books: Basel, Switzerland, 2023. [Google Scholar] [CrossRef]
- Riedel, C.J.; Zurek, W.H. Quantum Darwinism in an Everyday Environment: Huge Redundancy in Scattered Photons. Phys. Rev. Lett. 2010, 105, 020404. [Google Scholar] [CrossRef] [PubMed]
- Riedel, C.J.; Zurek, W.H. Redundant information from thermal illumination: Quantum Darwinism in scattered photons. New J. Phys. 2011, 13, 073038. [Google Scholar] [CrossRef]
- Hayden, P.; Preskill, J. Black holes as mirrors: Quantum information in random subsystems. J. High Energy Phys. 2007, 2007, 120. [Google Scholar] [CrossRef]
- Swingle, B. Unscrambling the physics of out-of-time-order correlators. Nat. Phys. 2018, 14, 988–990. [Google Scholar] [CrossRef]
- Touil, A.; Deffner, S. Quantum scrambling and the growth of mutual information. Quantum Sci. Technol. 2020, 5, 035005. [Google Scholar] [CrossRef]
- Bao, N.; Kikuchi, Y. Hayden-Preskill decoding from noisy Hawking radiation. J. High Energy Phys. 2021, 2021, 17. [Google Scholar] [CrossRef]
- Chen, B.; Czech, B.; Wang, Z.Z. Quantum information in holographic duality. Rep. Prog. Phys. 2022, 85, 046001. [Google Scholar] [CrossRef]
- Fisher, M.P.; Khemani, V.; Nahum, A.; Vijay, S. Random Quantum Circuits. Ann. Rev. Cond. Mat. Phys. 2023, 14, 335–379. [Google Scholar] [CrossRef]
- Swingle, B.; Bentsen, G.; Schleier-Smith, M.; Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 2016, 94, 040302. [Google Scholar] [CrossRef]
- Yoshida, B.; Yao, N.Y. Disentangling Scrambling and Decoherence via Quantum Teleportation. Phys. Rev. X 2019, 9, 011006. [Google Scholar] [CrossRef]
- Xu, Z.; García-Pintos, L.P.; Chenu, A.; del Campo, A. Extreme Decoherence and Quantum Chaos. Phys. Rev. Lett. 2019, 122, 014103. [Google Scholar] [CrossRef] [PubMed]
- Touil, A.; Deffner, S. Information Scrambling versus Decoherence—Two Competing Sinks for Entropy. PRX Quantum 2021, 2, 010306. [Google Scholar] [CrossRef]
- Zanardi, P.; Anand, N. Information scrambling and chaos in open quantum systems. Phys. Rev. A 2021, 103, 062214. [Google Scholar] [CrossRef]
- Xu, Z.; Chenu, A.; Prosen, T.c.v.; del Campo, A. Thermofield dynamics: Quantum chaos versus decoherence. Phys. Rev. B 2021, 103, 064309. [Google Scholar] [CrossRef]
- Domínguez, F.D.; Rodríguez, M.C.; Kaiser, R.; Suter, D.; Álvarez, G.A. Decoherence scaling transition in the dynamics of quantum information scrambling. Phys. Rev. A 2021, 104, 012402. [Google Scholar] [CrossRef]
- Cornelius, J.; Xu, Z.; Saxena, A.; Chenu, A.; del Campo, A. Spectral Filtering Induced by Non-Hermitian Evolution with Balanced Gain and Loss: Enhancing Quantum Chaos. Phys. Rev. Lett. 2022, 128, 190402. [Google Scholar] [CrossRef]
- Han, L.P.; Zou, J.; Li, H.; Shao, B. Quantum Information Scrambling in Non-Markovian Open Quantum System. Entropy 2022, 24, 1532. [Google Scholar] [CrossRef]
- Andreadakis, F.; Anand, N.; Zanardi, P. Scrambling of algebras in open quantum systems. Phys. Rev. A 2023, 107, 042217. [Google Scholar] [CrossRef]
- Riedel, C.J.; Zurek, W.H.; Zwolak, M. The rise and fall of redundancy in decoherence and quantum Darwinism. New J. Phys. 2012, 14, 083010. [Google Scholar] [CrossRef]
- Giorgi, G.L.; Galve, F.; Zambrini, R. Quantum Darwinism and non-Markovian dissipative dynamics from quantum phases of the spin-1/2 XX model. Phys. Rev. A 2015, 92, 022105. [Google Scholar] [CrossRef]
- Ryan, E.; Paternostro, M.; Campbell, S. Quantum Darwinism in a structured spin environment. Phys. Lett. A 2021, 416, 127675. [Google Scholar] [CrossRef]
- Zwolak, M.; Quan, H.T.; Zurek, W.H. Quantum Darwinism in a Mixed Environment. Phys. Rev. Lett. 2009, 103, 110402. [Google Scholar] [CrossRef]
- Campbell, S.; Çakmak, B.; Müstecaplıoğlu, O.E.; Paternostro, M.; Vacchini, B. Collisional unfolding of quantum Darwinism. Phys. Rev. A 2019, 99, 042103. [Google Scholar] [CrossRef]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism in Quantum Brownian Motion. Phys. Rev. Lett. 2008, 101, 240405. [Google Scholar] [CrossRef] [PubMed]
- Blume-Kohout, R.; Zurek, W.H. A Simple Example of “Quantum Darwinism”: Redundant Information Storage in Many-Spin Environments. Found. Phys. 2005, 35, 1857–1876. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Holevo, A.S. Bounds for the quantity of information transmitted by a quantum communication channel. Peredachi Inform. 1973, 9, 3. [Google Scholar]
- Nielsen, M.A.; Chuang, I.; Grover, L.K. Quantum Computation and Quantum Information. Am. J. Phys. 2002, 70, 558–559. [Google Scholar] [CrossRef]
- Touil, A.; Yan, B.; Girolami, D.; Deffner, S.; Zurek, W.H. Eavesdropping on the Decohering Environment: Quantum Darwinism, Amplification, and the Origin of Objective Classical Reality. Phys. Rev. Lett. 2022, 128, 010401. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1948; Volume 55.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duruisseau, P.; Touil, A.; Deffner, S. Pointer States and Quantum Darwinism with Two-Body Interactions. Entropy 2023, 25, 1573. https://doi.org/10.3390/e25121573
Duruisseau P, Touil A, Deffner S. Pointer States and Quantum Darwinism with Two-Body Interactions. Entropy. 2023; 25(12):1573. https://doi.org/10.3390/e25121573
Chicago/Turabian StyleDuruisseau, Paul, Akram Touil, and Sebastian Deffner. 2023. "Pointer States and Quantum Darwinism with Two-Body Interactions" Entropy 25, no. 12: 1573. https://doi.org/10.3390/e25121573
APA StyleDuruisseau, P., Touil, A., & Deffner, S. (2023). Pointer States and Quantum Darwinism with Two-Body Interactions. Entropy, 25(12), 1573. https://doi.org/10.3390/e25121573







