Robustness and Complexity of Directed and Weighted Metabolic Hypergraphs
Abstract
1. Introduction
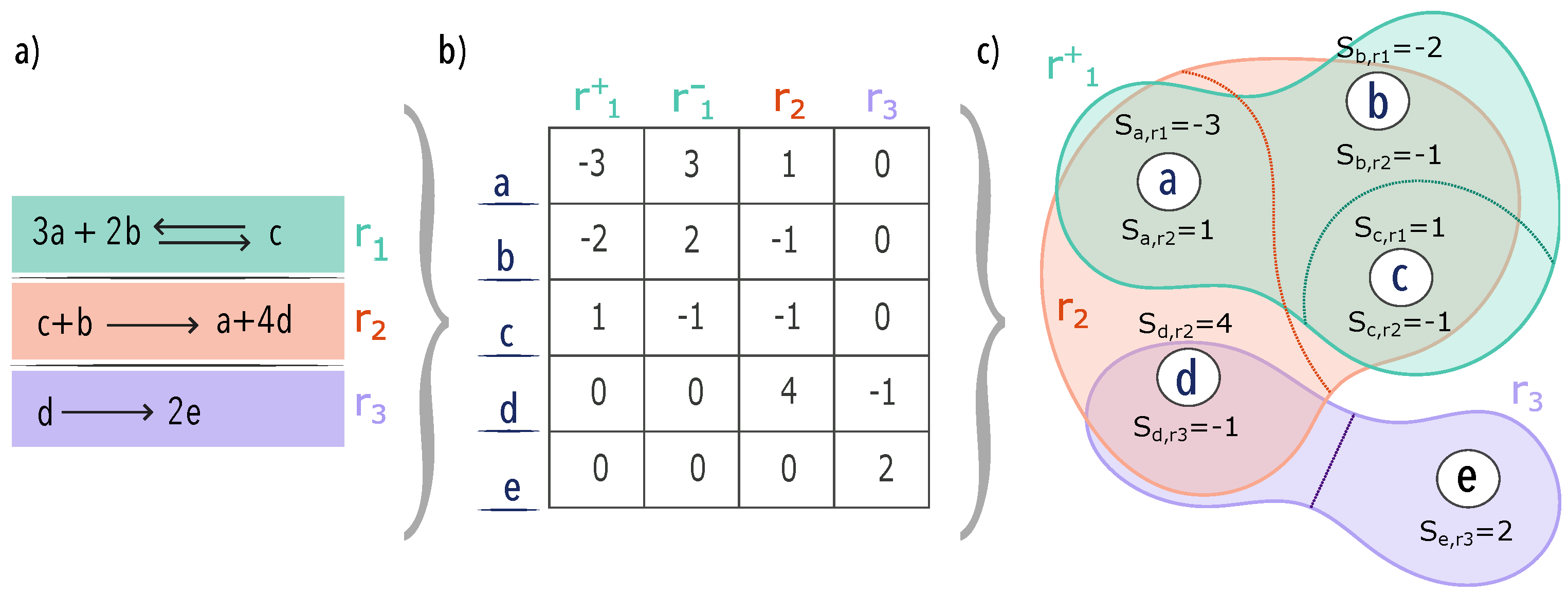
2. Metabolic Networks as Hypergraphs
2.1. Hypergraphs Definition
2.2. Metabolic Hypergraphs
2.3. Literature Background
2.4. Dataset
3. Measurements
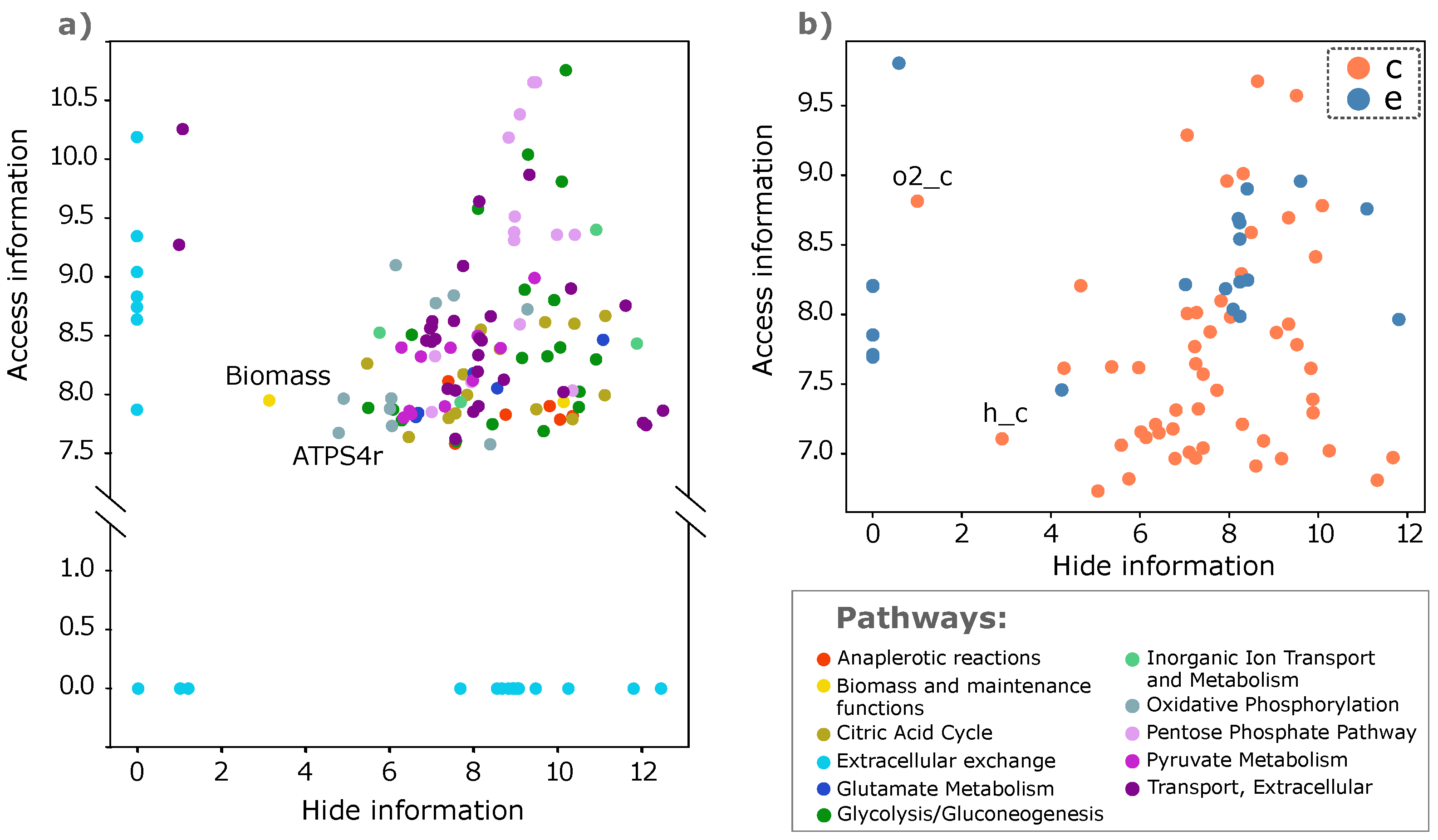
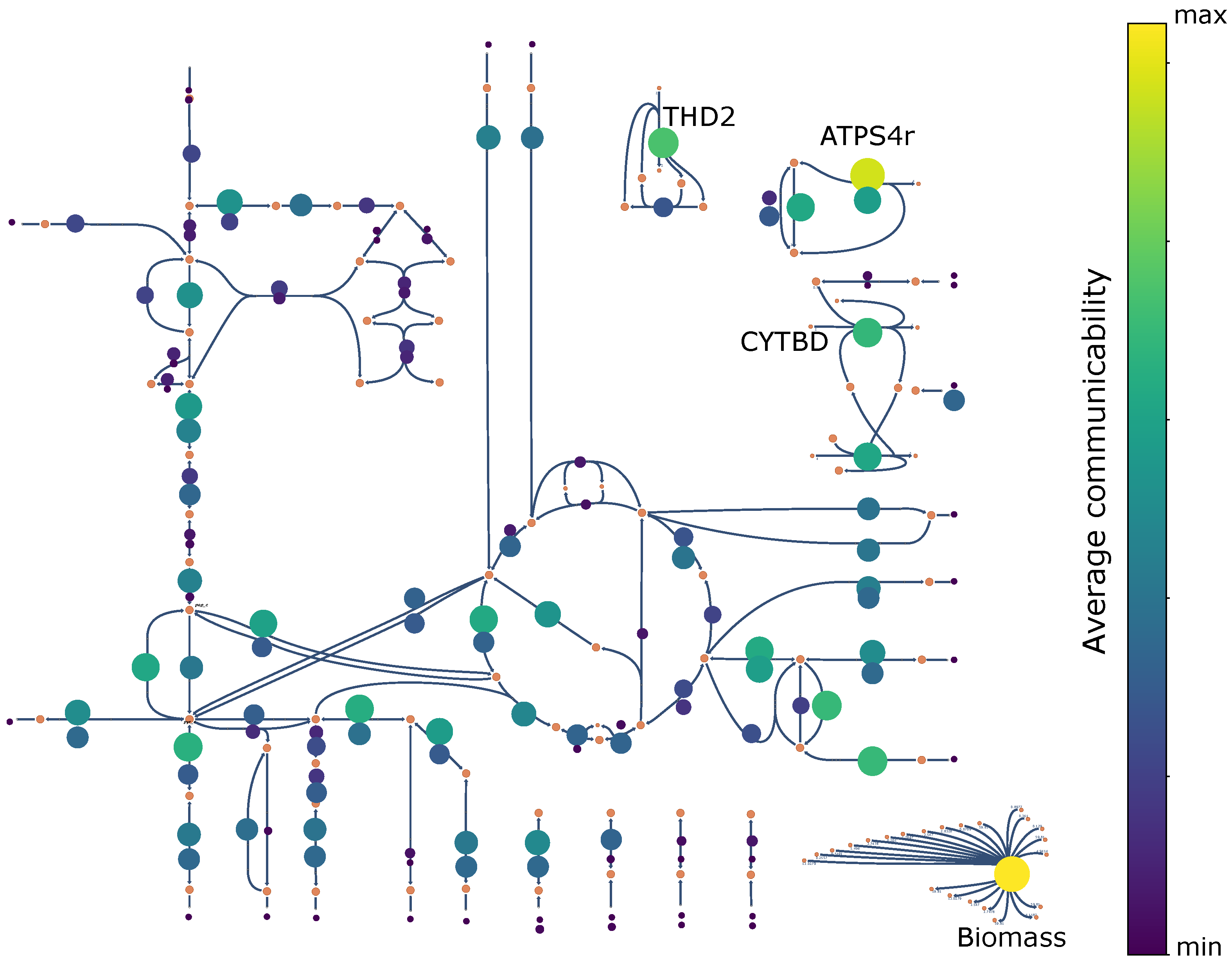
3.1. Hypergraph Communicability
3.2. Hypergraph Search Information
4. Results and Discussion
4.1. Exploring the E. coli Core Model: A Practical Example
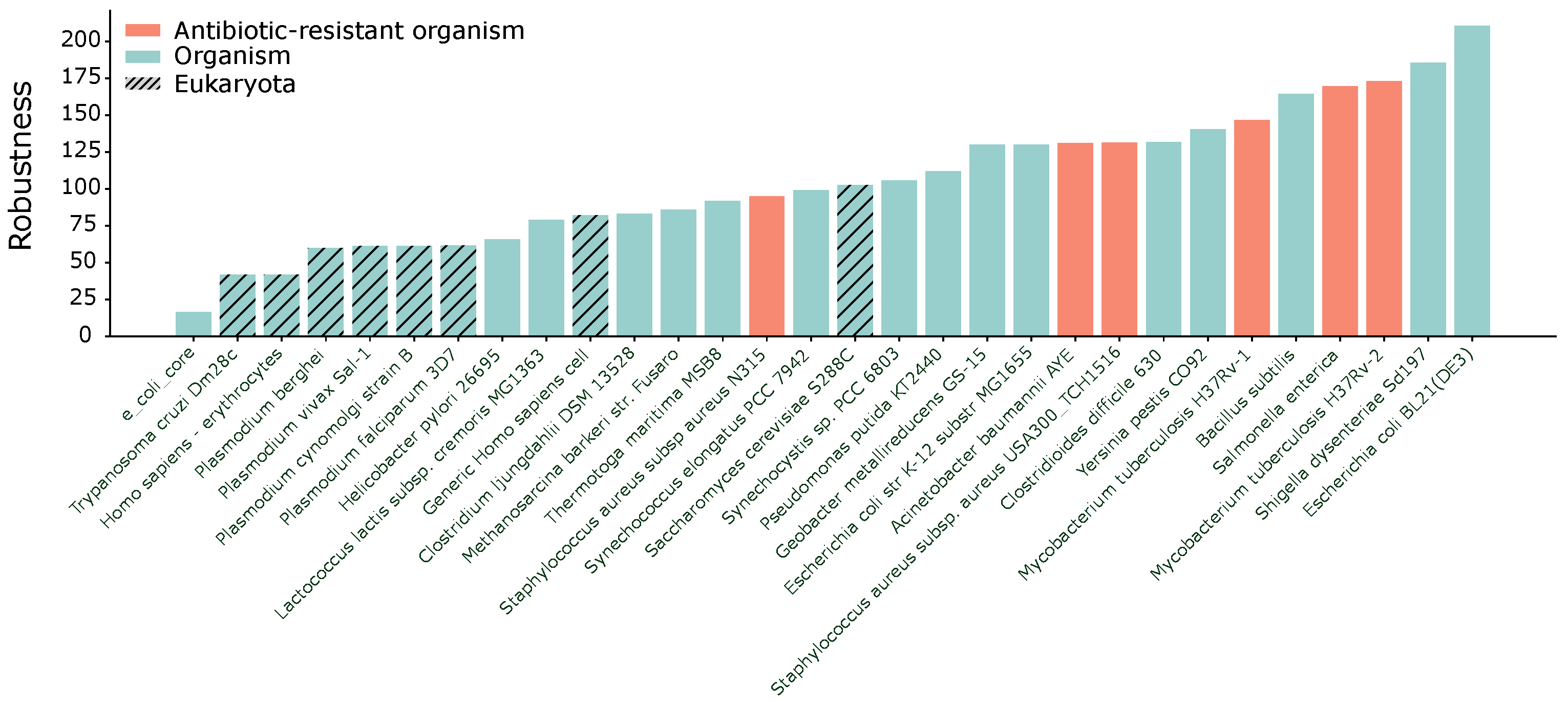
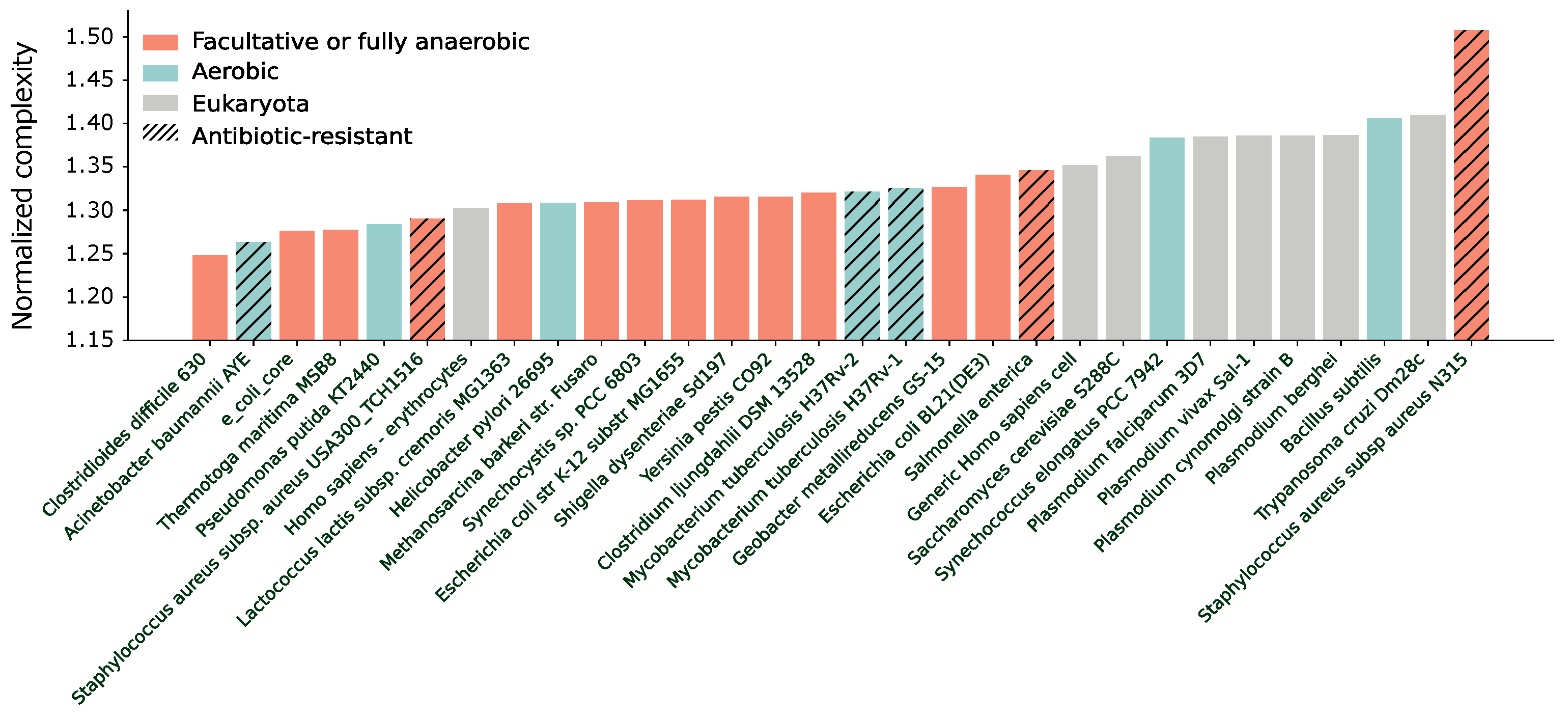
4.2. Robustness and Complexity across Organisms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. BiGG Models
| Organism | BiGG Model | Metabolites | Reactions | Hyperedges |
|---|---|---|---|---|
| Saccharomyces cerevisiae S288C | iND750 | 1059 | 1266 | 1702 |
| Pseudomonas putida KT2440 | iJN746 | 907 | 1054 | 1415 |
| Plasmodium cynomolgi strain B | iAM_Pc455 | 907 | 1074 | 1563 |
| e_coli_core | e_coli_core | 72 | 95 | 141 |
| Staphylococcus aureus subsp. aureus USA300_TCH1516 | iYS854 | 1335 | 1453 | 1872 |
| Mycobacterium tuberculosis H37Rv-1 | iNJ661 | 825 | 1022 | 1293 |
| Mycobacterium tuberculosis H37Rv-2 | iEK1008 | 998 | 1224 | 1500 |
| Clostridium ljungdahlii DSM 13528 | iHN637 | 698 | 773 | 988 |
| Yersinia pestis CO92 | iPC815 | 1552 | 1960 | 2507 |
| Shigella dysenteriae Sd197 | iSDY_1059 | 1888 | 2529 | 3172 |
| Escherichia coli str. K-12 substr. MG1655 | iJR904 | 761 | 1075 | 1329 |
| Lactococcus lactis subsp. cremoris MG1363 | iNF517 | 650 | 730 | 979 |
| Helicobacter pylori 26695 | iIT341 | 485 | 554 | 737 |
| Homo sapiens | iAB_RBC_283 | 342 | 469 | 645 |
| Homo sapiens2 | iAT_PLT_636 | 738 | 1008 | 1455 |
| Plasmodium falciparum 3D7 | iAM_Pf480 | 909 | 1083 | 1576 |
| Escherichia coli BL21(DE3) | iEC1356_Bl21DE3 | 1918 | 2730 | 3376 |
| Synechococcus elongatus PCC 7942 | iJB785 | 768 | 843 | 1064 |
| Plasmodium berghei | iAM_Pb448 | 903 | 1067 | 1554 |
| Trypanosoma cruzi Dm28c | iIS312 | 606 | 519 | 806 |
| Staphylococcus aureus subsp aureus N315 | iSB619 | 655 | 729 | 945 |
| Thermotoga maritima MSB8 | iLJ478 | 570 | 652 | 852 |
| Methanosarcina barkeri str. Fusaro | iAF692 | 628 | 690 | 900 |
| Clostridioides difficile 630 | iCN900 | 885 | 1222 | 1455 |
| Plasmodium vivax Sal-1 | iAM_Pv461 | 909 | 1078 | 1570 |
| Bacillus subtilis | iYO844 | 990 | 1250 | 1589 |
| Synechocystis sp. PCC 6803 | iJN678 | 795 | 862 | 1086 |
| Geobacter metallireducens GS-15 | iAF987 | 1109 | 1281 | 1642 |
| Acinetobacter baumannii AYE | iCN718 | 888 | 1013 | 1436 |
| Salmonella enterica | STM_v1_0 | 1802 | 2528 | 3133 |
References
- Campbell, N.A.; Urry, L.A.; Cain, M.L.; Wasserman, S.A.; Minorsky, P.V.; Reece, J.B. Biology: A Global Approach, Eleventh Edition, Global Edition; Pearson: New York, NY, USA, 2018; ISBN 9781292170435. [Google Scholar]
- Dräger, A.; Planatscher, H. Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.-H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; pp. 1249–1251. ISBN 9781441998620/9781441998637. [Google Scholar]
- Ma, H.; Zeng, A.-P. Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics 2003, 19, 270–277. [Google Scholar] [CrossRef] [PubMed]
- Stitt, M.; Sulpice, R.; Keurentjes, J. Metabolic networks: How to identify key components in the regulation of metabolism and growth. Plant Physiol. 2010, 152, 428–444. [Google Scholar] [CrossRef] [PubMed]
- Renz, A.; Mostolizadeh, R.; Dräger, A. Systems Medicine; Wolkenhauer, O., Ed.; Academic Press: Oxford, UK, 2021; pp. 362–371. ISBN 978-0-12-816078-7. [Google Scholar]
- Guimerà, R.; Nunes Amaral, L.A. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef]
- Niu, X.; Doyle, C.; Korniss, G.; Szymanski, B.K. The impact of variable commitment in the naming game on consensus formation. Sci. Rep. 2017, 7, 41750. [Google Scholar] [CrossRef]
- Centola, D.; Becker, J.; Brackbill, D.; Baronchelli, A. Experimental evidence for tip** points in social convention. Science 2018, 360, 1116–1119. [Google Scholar] [CrossRef] [PubMed]
- Baronchelli, A. The emergence of consensus: A primer. R. Soc. Open Sci. 2018, 5, 172189. [Google Scholar] [CrossRef] [PubMed]
- Benson, A.R.; Abebe, R.; Schaub, M.T.; Jadbabaie, A.; Kleinberg, J. Simplicial closure and higher-order link prediction. Proc. Natl. Acad. Sci. USA 2018, 115, E11221–E11230. [Google Scholar] [CrossRef]
- Iacopini, I.; Petri, G.; Barrat, A.; Latora, V. Simplicial models of social contagion. Nat. Commun. 2019, 10, 2485. [Google Scholar] [CrossRef]
- de Arruda, G.F.; Petri, G.; Moreno, Y. Social contagion models on hypergraphs. Phys. Rev. Res. 2020, 2, 023032. [Google Scholar] [CrossRef]
- Landry, N.W.; Restrepo, J.G. The effect of heterogeneity on hypergraph contagion models. Chaos: An Interdisciplinary. J. Nonlinear Sci. 2020, 30, 103117. [Google Scholar]
- Barrat, A.; Ferraz de Arruda, G.; Iacopini, I.; Moreno, Y. Social contagion on higher-order structures. In Higher-Order Systems; Springer: Cham, Switzerland, 2022; pp. 329–346. [Google Scholar]
- Ferraz de Arruda, G.; Tizzani, M.; Moreno, Y. Phase transitions and stability of dynamical processes on hypergraphs. Commun. Phys. 2021, 4, 24. [Google Scholar] [CrossRef]
- Alvarez-Rodriguez, U.; Battiston, F.; de Arruda, G.F.; Moreno, Y.; Perc, M.; Latora, V. Evolutionary dynamics of higher-order interactions in social networks. Nat. Hum. Behav. 2021, 5, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Neuhäuser, L.; Mellor, A.; Lambiotte, R. Multibody interactions and nonlinear consensus dynamics on networked systems. Phys. Rev. E 2020, 101, 032310. [Google Scholar] [CrossRef] [PubMed]
- Bodó, Á; Katona, G.Y.; Simon, P.L. SIS epidemic propagation on hypergraphs. Bull. Math. Biol. 2016, 78, 713–735. [Google Scholar] [CrossRef] [PubMed]
- Ferraz De Arruda, G.; Petri, G.; Rodriguez, P.M.; Moreno, Y. Multistability, intermittency, and hybrid transitions in social contagion models on hypergraphs. Nat. Commun. 2023, 14, 1375. [Google Scholar] [CrossRef]
- Higham, D.J.; de Kergorlay, H.L. Mean field analysis of hypergraph contagion models. SIAM J. Appl. Math. 2022, 82, 1987–2007. [Google Scholar] [CrossRef]
- Higham, D.J.; De Kergorlay, H.L. Epidemics on hypergraphs: Spectral thresholds for extinction. Proc. R. Soc. A 2021, 477, 20210232. [Google Scholar] [CrossRef]
- Stewart, I.; Golubitsky, M.; Pivato, M. Symmetry groupoids and patterns of synchrony in coupled cell networks. SIAM J. Appl. Dyn. Syst. 2003, 2, 609–646. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.; Török, A. Patterns of synchrony in coupled cell networks with multiple arrows. SIAM J. Appl. Dyn. Syst. 2005, 4, 78–100. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I. Nonlinear dynamics of networks: The groupoid formalism. Bull. Am. Math. Soc. 2006, 43, 305–364. [Google Scholar] [CrossRef]
- Yu, S.; Yang, H.; Nakahara, H.; Santos, G.S.; Nikolić, D.; Plenz, D. Higher-order interactions characterized in cortical activity. J. Neurosci. 2011, 31, 17514–17526. [Google Scholar] [CrossRef] [PubMed]
- Bairey, E.; Kelsic, E.D.; Kishony, R. High-order species interactions shape ecosystem diversity. Nat. Commun. 2016, 7, 12285. [Google Scholar] [CrossRef] [PubMed]
- Battiston, F.; Amico, E.; Barrat, A.; Bianconi, G.; de Arruda, G.F.; Franceschiello, B.; Iacopini, I.; Kéfi, S.; Latora, V.; Moreno, Y.; et al. The physics of higher-order interactions in complex systems. Nat. Phys. 2021, 17, 1093. [Google Scholar] [CrossRef]
- Cervantes-Loreto, A.; Ayers, C.A.; Dobbs, E.K.; Brosi, B.J.; Stouffer, D.B. The context dependency of pollinator interference: How environmental conditions and co-foraging species impact floral visitation. Ecol. Lett. 2021, 24, 1443–1454. [Google Scholar] [CrossRef] [PubMed]
- Franzese, N.; Groce, A.; Murali, T.M.; Ritz, A. Hypergraph-based connectivity measures for signaling pathway topologies. PLoS Comput. Biol. 2019, 15, e1007384. [Google Scholar] [CrossRef]
- Klamt, S.; Haus, U.U.; Theis, F. Hypergraphs and cellular networks. PLoS Comput. Biol. 2009, 5, e1000385. [Google Scholar] [CrossRef]
- Larhlimi, A.; Blachon, S.; Selbig, J.; Nikoloski, Z. Robustness of metabolic networks: A review of existing definitions. Biosystems 2011, 106, 1–8. [Google Scholar] [CrossRef]
- Yeung, M.; Thiele, I.; Palsson, B.Ø. Estimation of the number of extreme pathways for metabolic networks. BMC Bioinform. 2007, 8, 363. [Google Scholar] [CrossRef]
- Ghaderi, S.; Haraldsdóttir, H.S.; Ahookhosh, M.; Arreckx, S.; Fleming, R.M. Structural conserved moiety splitting of a stoichiometric matrix. J. Theor. Biol. 2020, 499, 110276. [Google Scholar] [CrossRef]
- Pearcy, N.; Chuzhanova, N.; Crofts, J.J. Complexity and robustness in hypernetwork models of metabolism. J. Theor. Biol. 2016, 406, 99–104. [Google Scholar] [CrossRef]
- Mulas, R.; Zhang, D. Spectral theory of Laplace operators on oriented hypergraphs. Discret. Math. 2021, 344, 112372. [Google Scholar] [CrossRef]
- Jost, J.; Mulas, R. Hypergraph Laplace operators for chemical reaction networks. Adv. Math. 2019, 351, 870–896. [Google Scholar] [CrossRef]
- Chitra, U.; Raphael, B. Random Walks on Hypergraphs with Edge-Dependent Vertex Weights. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 1172–1181. [Google Scholar]
- Beguerisse-Díaz, M.; Bosque, G.; Oyarzún, D.; Picó, J.; Barahona, M. Flux-dependent graphs for metabolic networks. NPJ Syst. Biol. Appl. 2018, 4, 32. [Google Scholar] [CrossRef] [PubMed]
- Link, H.; Christodoulou, D.; Sauer, U. Advancing metabolic models with kinetic information. Curr. Opin. Biotechnol. 2014, 29, 8–14. [Google Scholar] [CrossRef]
- Adadi, R.; Volkmer, B.; Milo, R.; Heinemann, M.; Shlomi, T. Prediction of microbial growth rate versus biomass yield by a metabolic network with kinetic parameters. PLoS Comput. Biol. 2012, 8, e1002575. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Srinivasan, S.; Cluett, W.R.; Mahadevan, R. Constructing kinetic models of metabolism at genome-scales: A review. Biotechnol. J. 2015, 10, 1345–1359. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Oberhardt, M.A.; Palsson, B.Ø.; Papin, J.A. Applications of genome-scale metabolic reconstructions. Mol. Syst. Biol. 2009, 5, 320. [Google Scholar] [CrossRef]
- Fang, X.; Lloyd, C.J.; Palsson, B.O. Reconstructing organisms in silico: Genome-scale models and their emerging applications. Nat. Rev. Microbiol. 2020, 18, 731–743. [Google Scholar] [CrossRef]
- Traversa, P.; de Arruda, G.F.; Moreno, Y. From unbiased to maximal entropy random walks on hypergraphs. arXiv 2023, arXiv:2306.09499. [Google Scholar]
- Banerjee, A. On the spectrum of hypergraph. Linear Algebra Its Appl. 2021, 614, 82–110. [Google Scholar] [CrossRef]
- King, Z.A.; Lu, J.; Dräger, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016, 44, D515–D522. [Google Scholar] [CrossRef]
- Bigg Models. Available online: http://bigg.ucsd.edu/models (accessed on 20 June 2022).
- Estrada, E.; Hatano, N.; Benzi, M. The physics of communicability in complex networks. Phys. Rep. 2012, 514, 89–119. [Google Scholar] [CrossRef]
- Estrada, E.; Hatano, N. Communicability in complex networks. Phys. Rev. E 2008, 77, 036111. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. The many facets of the Estrada indices of graphs and networks. SeMA J. 2022, 79, 57–125. [Google Scholar] [CrossRef]
- Jun, W.; Barahona, M.; Yue-Jin, T.; Hong-Zhong, D. Natural connectivity of complex networks. Chin. Phys. Lett. 2010, 27, 078902. [Google Scholar] [CrossRef]
- Rosvall, M.; Trusina, A.; Minnhagen, P.; Sneppen, K. Networks and cities: An information perspective. Phys. Rev. Lett. 2005, 94, 028701. [Google Scholar] [CrossRef]
- Sneppen, K.; Trusina, A.; Rosvall, M. Hide-and-seek on complex networks. Europhys. Lett. 2005, 69, 853. [Google Scholar] [CrossRef][Green Version]
- Orth, J.D.; Fleming, R.M.; Palsson, B.Ø. Reconstruction and use of microbial metabolic networks: The core Escherichia coli metabolic model as an educational guide. Ecosal Plus 2010, 4, 10–128. [Google Scholar] [CrossRef]
- E. Coli Core Fba Escher Map. Available online: https://sbrg.github.io/escher-fba/ (accessed on 21 September 2023).
- Becker, S.A.; Palsson, B.Ø. Genome-scale reconstruction of the metabolic network in Staphylococcus aureus N315: An initial draft to the two-dimensional annotation. BMC Microbiol. 2005, 5, 8. [Google Scholar] [CrossRef] [PubMed]
- Seif, Y.; Monk, J.M.; Mih, N.; Tsunemoto, H.; Poudel, S.; Zuniga, C.; Broddrick, J.; Zengler, K.; Palsson, B.O. A computational knowledge-base elucidates the response of Staphylococcus aureus to different media types. PLoS Comput. Biol. 2019, 15, e1006644. [Google Scholar] [CrossRef] [PubMed]
- Jamshidi, N.; Palsson, B.Ø. Investigating the metabolic capabilities of Mycobacterium tuberculosis H37Rv using the in silico strain iNJ 661 and proposing alternative drug targets. BMC Syst. Biol. 2007, 1, 26. [Google Scholar] [CrossRef] [PubMed]
- Kavvas, E.S.; Seif, Y.; Yurkovich, J.T.; Norsigian, C.; Poudel, S.; Greenwald, W.W.; Ghatak, S.; Palsson, B.O.; Monk, J.M. Updated and standardized genome-scale reconstruction of Mycobacterium tuberculosis H37Rv, iEK1011, simulates flux states indicative of physiological conditions. BMC Syst. Biol. 2018, 12, 25. [Google Scholar] [CrossRef]
- Norsigian, C.J.; Kavvas, E.; Seif, Y.; Palsson, B.O.; Monk, J.M. iCN718, an updated and improved genome-scale metabolic network reconstruction of Acinetobacter baumannii AYE. Front. Genet. 2018, 9, 121. [Google Scholar] [CrossRef]
- Thiele, I.; Hyduke, D.R.; Steeb, B.; Fankam, G.; Allen, D.K.; Bazzani, S.; Charusanti, P.; Chen, F.C.; Fleming, R.M.; Hsiung, C.A.; et al. A community effort towards a knowledge-base and mathematical model of the human pathogen Salmonella Typhimurium LT2. BMC Syst. Biol. 2011, 5, 8. [Google Scholar] [CrossRef]
- Bordbar, A.; Jamshidi, N.; Palsso, B.Ø. iAB-RBC-283: A proteomically derived knowledge-base of erythrocyte metabolism that can be used to simulate its physiological and patho-physiological states. BMC Syst. Biol. 2011, 5, 110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traversa, P.; Ferraz de Arruda, G.; Vazquez, A.; Moreno, Y. Robustness and Complexity of Directed and Weighted Metabolic Hypergraphs. Entropy 2023, 25, 1537. https://doi.org/10.3390/e25111537
Traversa P, Ferraz de Arruda G, Vazquez A, Moreno Y. Robustness and Complexity of Directed and Weighted Metabolic Hypergraphs. Entropy. 2023; 25(11):1537. https://doi.org/10.3390/e25111537
Chicago/Turabian StyleTraversa, Pietro, Guilherme Ferraz de Arruda, Alexei Vazquez, and Yamir Moreno. 2023. "Robustness and Complexity of Directed and Weighted Metabolic Hypergraphs" Entropy 25, no. 11: 1537. https://doi.org/10.3390/e25111537
APA StyleTraversa, P., Ferraz de Arruda, G., Vazquez, A., & Moreno, Y. (2023). Robustness and Complexity of Directed and Weighted Metabolic Hypergraphs. Entropy, 25(11), 1537. https://doi.org/10.3390/e25111537






