Fundamental Relation for the Ideal Gas in the Gravitational Field and Heat Flow
Abstract
:1. Introduction
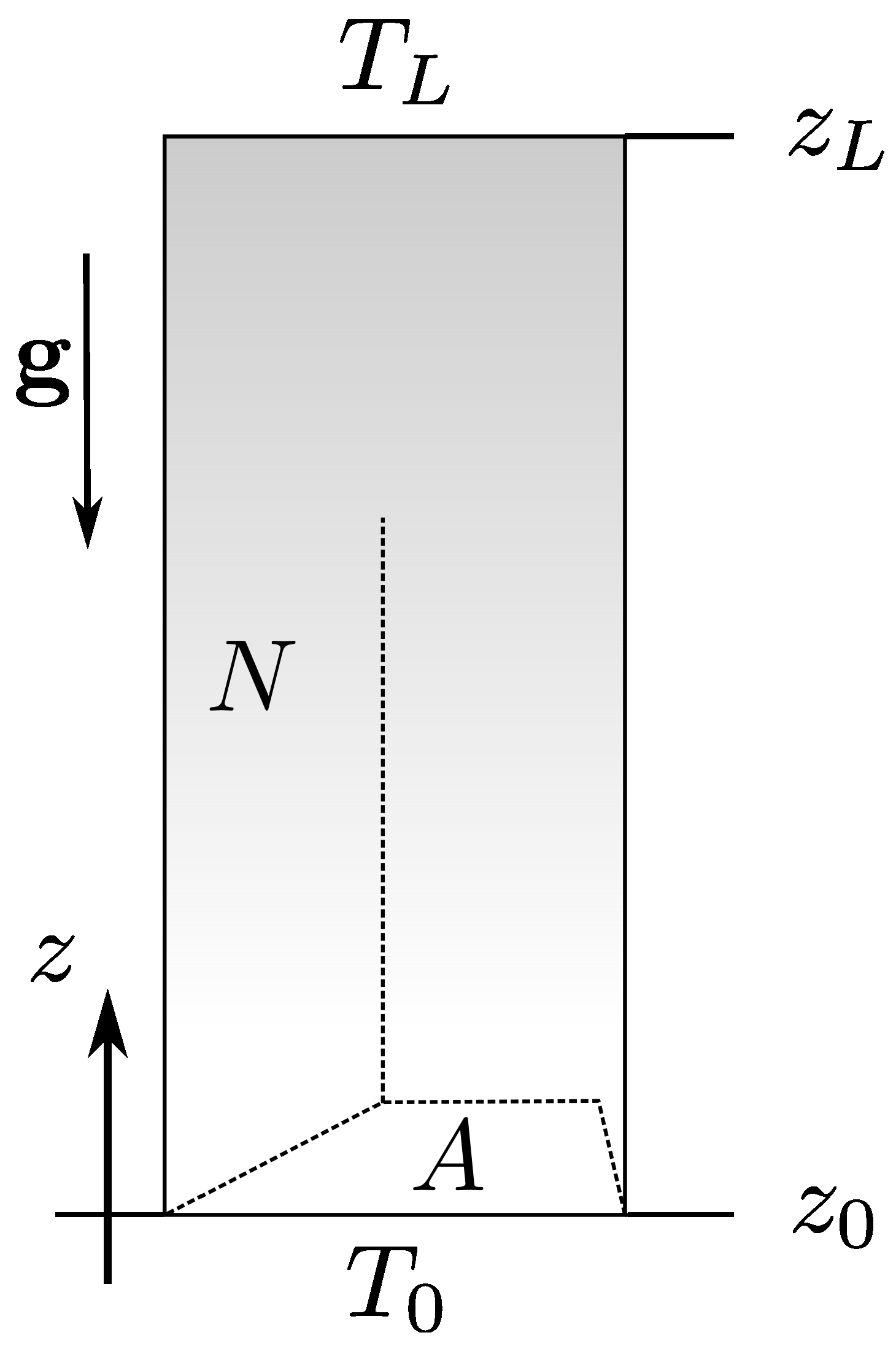
2. The Irreversible Hydrodynamics Approach
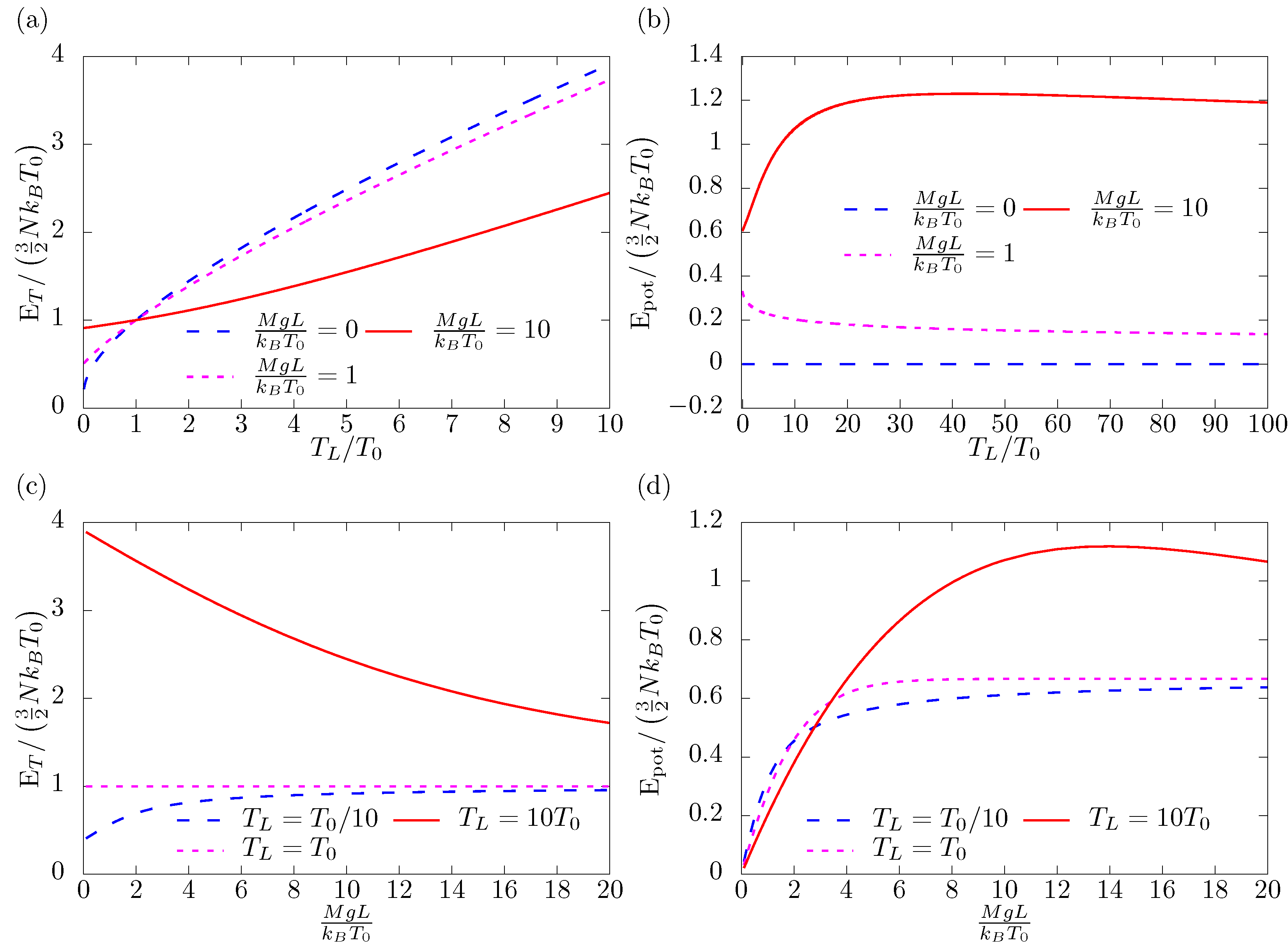
3. Energies
4. Equations of State
5. Fundamental Relation
6. Work
7. Heat
8. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Displacement of the Column’s Base
References
- Kubo, R. Thermodynamics: An Advanced Course with Problems and Solutions; North-Holland: Amsterdam, The Netherlands; New York, NY, USA, 1976; Volume 1. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Hołyst, R.; Makuch, K.; Maciołek, A.; Żuk, P.J. Thermodynamics of stationary states of the ideal gas in a heat flow. J. Chem. Phys. 2022, 157, 194108. [Google Scholar] [CrossRef] [PubMed]
- Hołyst, R.; Makuch, K.; Giżyński, K.; Maciołek, A.; Żuk, P.J. Fundamental Relation for Gas of Interacting Particles in a Heat Flow. Entropy 2023, 25, 1295. [Google Scholar] [CrossRef] [PubMed]
- Maciołek, A.; Hołyst, R.; Makuch Karol, G.K.; Żuk, P.J. Parameters of state in the global thermodynamics of binary ideal gas mixtures in a stationary heat flow. Entropy, 2023; sumbitted. [Google Scholar]
- Jones, I.P. A Comparison Problem for Numerical Methods in Fluid Dynamics: The Double Glazing Problem. In Numerical Methods in Fluids in Thermal Problems; Lewis, R.W., Morgan, K., Eds.; Pineridge Press: Swansea, UK, 1979; pp. 338–348. [Google Scholar]
- Wan, D.C.; Patnaik, B.S.V.; Wei, G.W. A new benchmark quality solution for the buoyancy-driven cavity by discrete singular convolution. Numer. Heat Transf. Part B Fundam. 2001, 40, 199–228. [Google Scholar]
- Bénard, H. Les tourbillons cellulaires dans une nappe liquide. Rev. Gen. Sci. Pure Appl. 1900, 11, 1261–1271. [Google Scholar]
- Rayleigh, L. LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Getling, A.V. Rayleigh-Bénard Convection: Structures and Dynamics; World Scientific: Singapore, 1998; Volume 11. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Mizerski, K.A. Foundations of Convection with Density Stratification; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Kays, W.; Crawford, M. Convective Heat and Mass Transfer; McGraw-Hill Series in Management; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK; Clarendon Press: New York, NY, USA, 1986. [Google Scholar]
- Berberan-Santos, M.N.; Bodunov, E.N.; Pogliani, L. On the barometric formula. Am. J. Phys. 1997, 65, 404–412. [Google Scholar] [CrossRef]
- Lente, G.; Osz, K. Barometric formulas: Various derivations and comparisons to environmentally relevant observations. ChemTexts 2020, 6, 13. [Google Scholar] [CrossRef]
- Kim, H.C.; Kang, G. Equation of state in the presence of gravity. J. Korean Phys. Soc. 2016, 69, 1597–1602. [Google Scholar] [CrossRef]
- Roman, F.L.; Gonzalez, A.; White, J.A.; Velasco, S. Microcanonical ensemble study of a gas column under gravity. Z. Phys. B Condens. Matter 1997, 104, 353–361. [Google Scholar] [CrossRef]
- Grøn, Ø. Entropy and gravity. Entropy 2012, 14, 2456–2477. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hołyst, R.; Żuk, P.J.; Makuch, K.; Maciołek, A.; Giżyński, K. Fundamental Relation for the Ideal Gas in the Gravitational Field and Heat Flow. Entropy 2023, 25, 1483. https://doi.org/10.3390/e25111483
Hołyst R, Żuk PJ, Makuch K, Maciołek A, Giżyński K. Fundamental Relation for the Ideal Gas in the Gravitational Field and Heat Flow. Entropy. 2023; 25(11):1483. https://doi.org/10.3390/e25111483
Chicago/Turabian StyleHołyst, Robert, Paweł J. Żuk, Karol Makuch, Anna Maciołek, and Konrad Giżyński. 2023. "Fundamental Relation for the Ideal Gas in the Gravitational Field and Heat Flow" Entropy 25, no. 11: 1483. https://doi.org/10.3390/e25111483
APA StyleHołyst, R., Żuk, P. J., Makuch, K., Maciołek, A., & Giżyński, K. (2023). Fundamental Relation for the Ideal Gas in the Gravitational Field and Heat Flow. Entropy, 25(11), 1483. https://doi.org/10.3390/e25111483




