Effects of Structural Relaxation of Glass-Forming Melts on the Overall Crystallization Kinetics in Cooling and Heating
Abstract
:1. Introduction
2. Basic Equations
2.1. Johnson–Mehl–Avrami–Kolmogorov (JMAK) Equation
2.2. Description of the Rates of Nucleation and Growth and the Kinetics of Relaxation
2.3. Possible Extensions
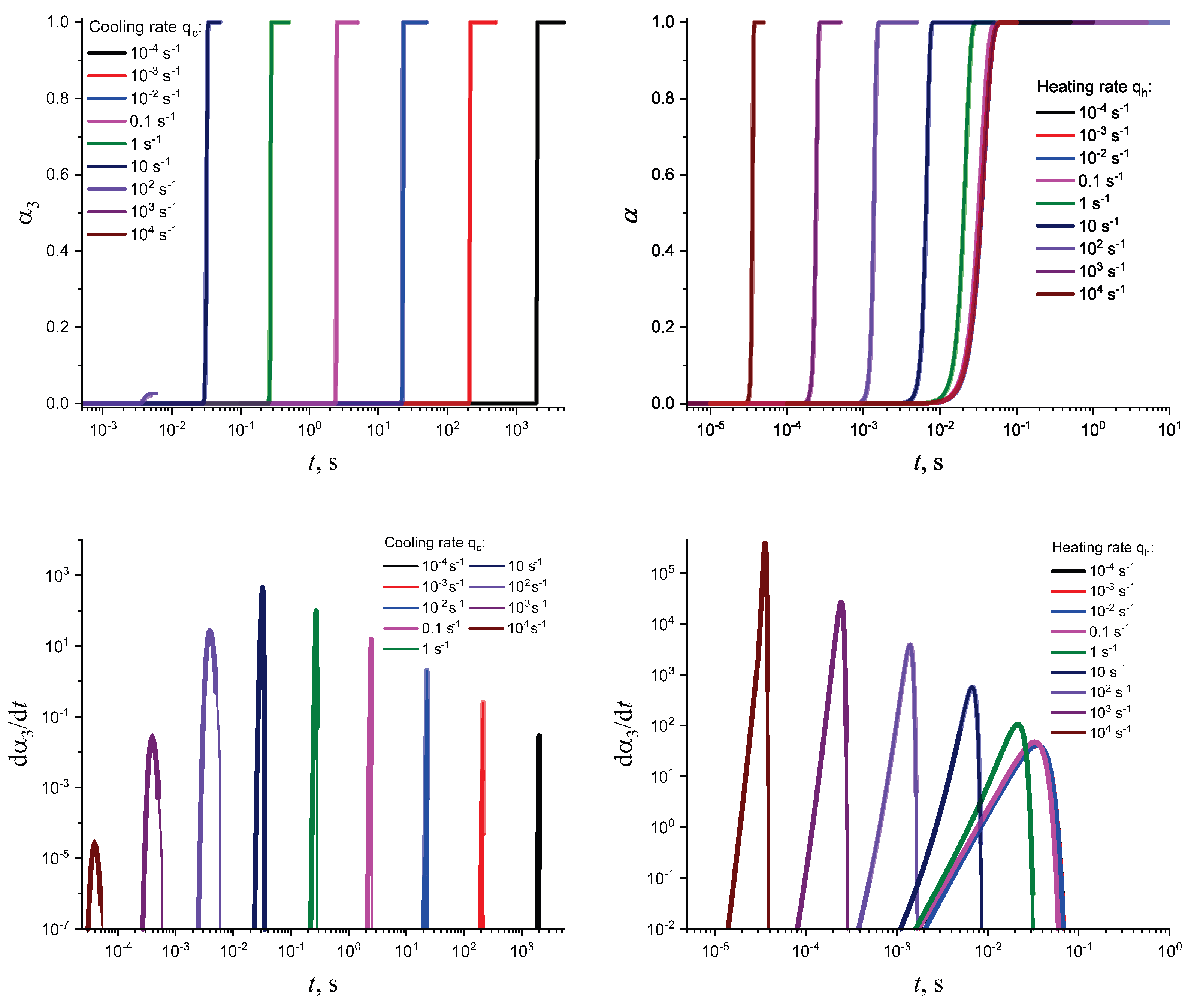
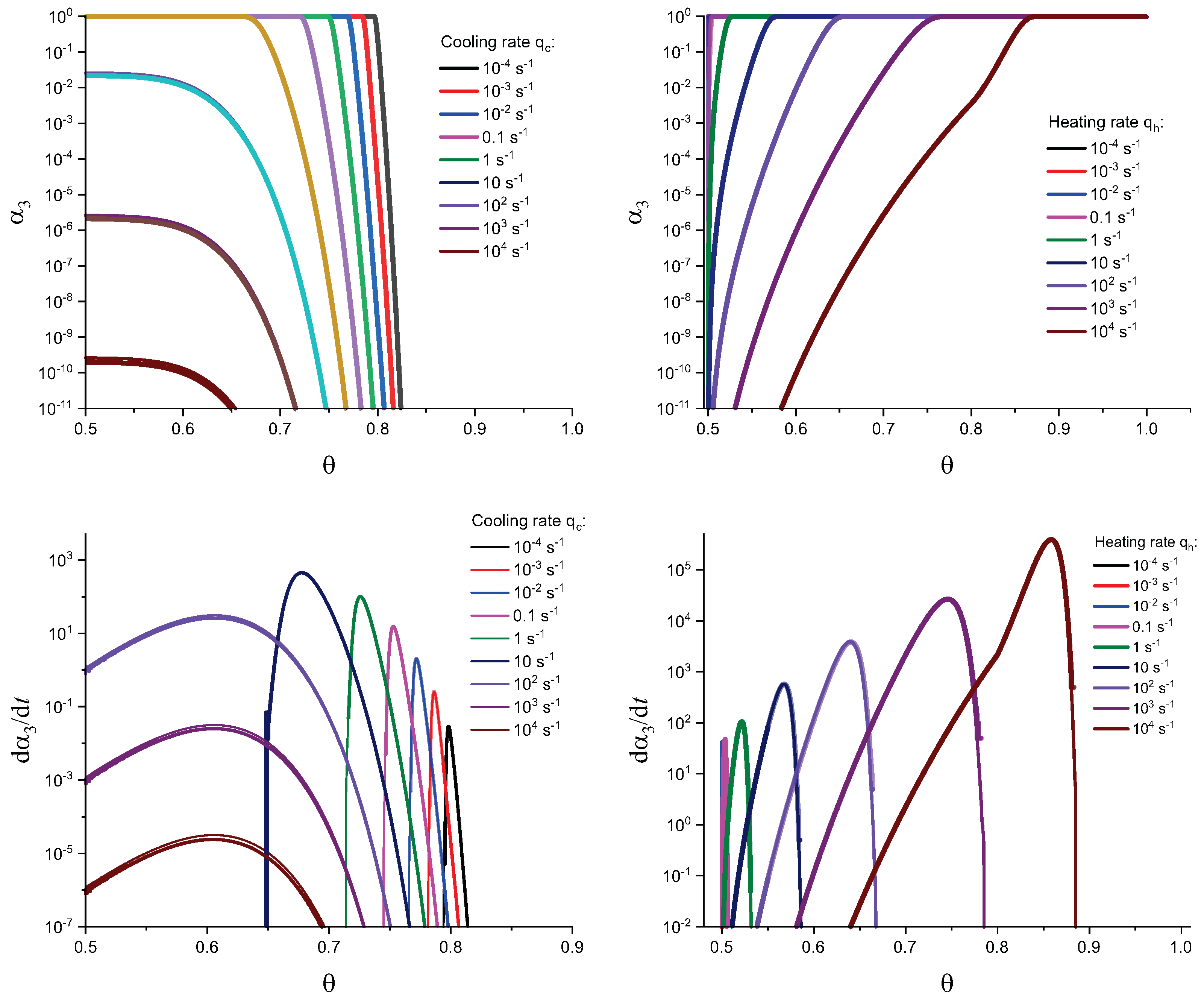
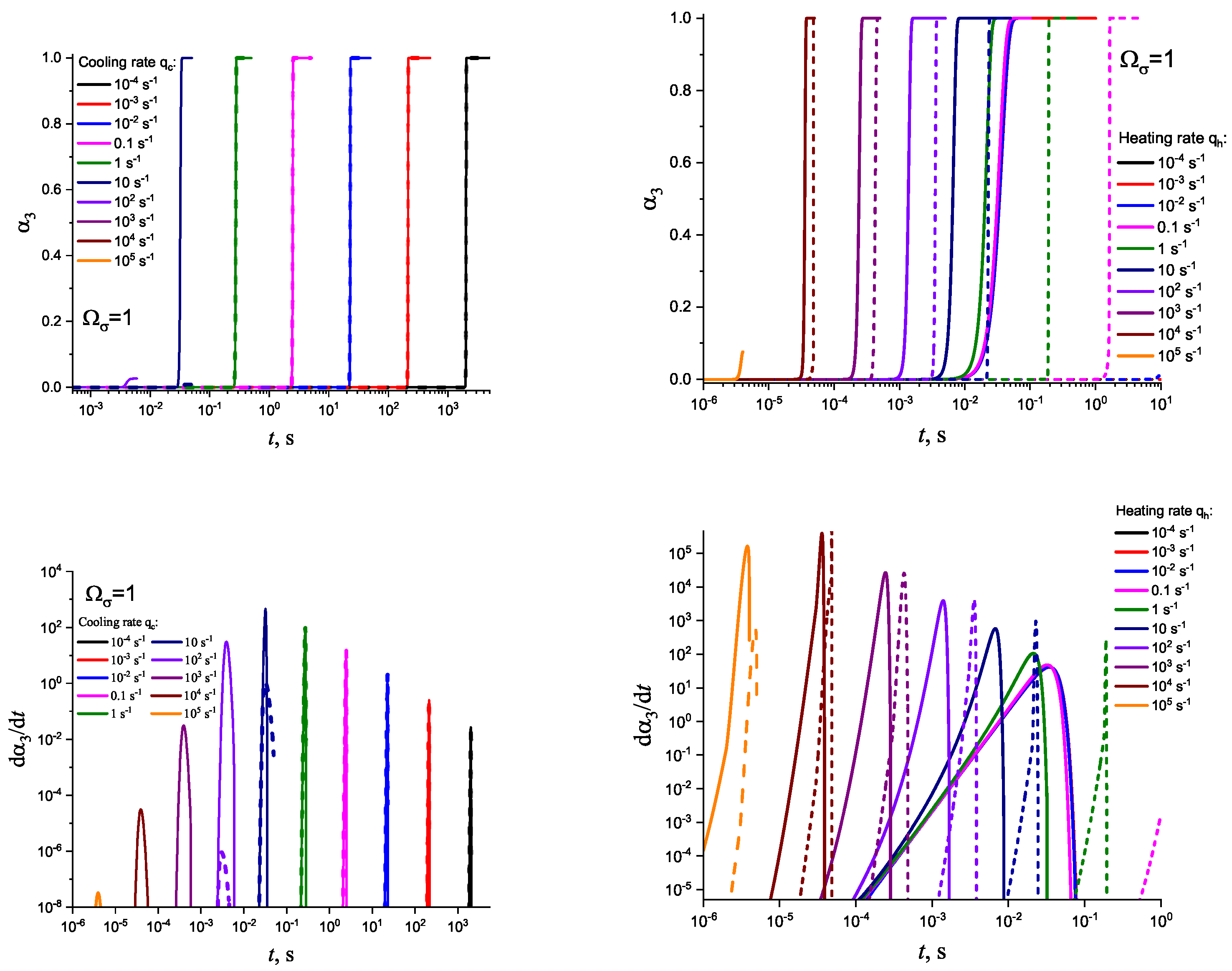
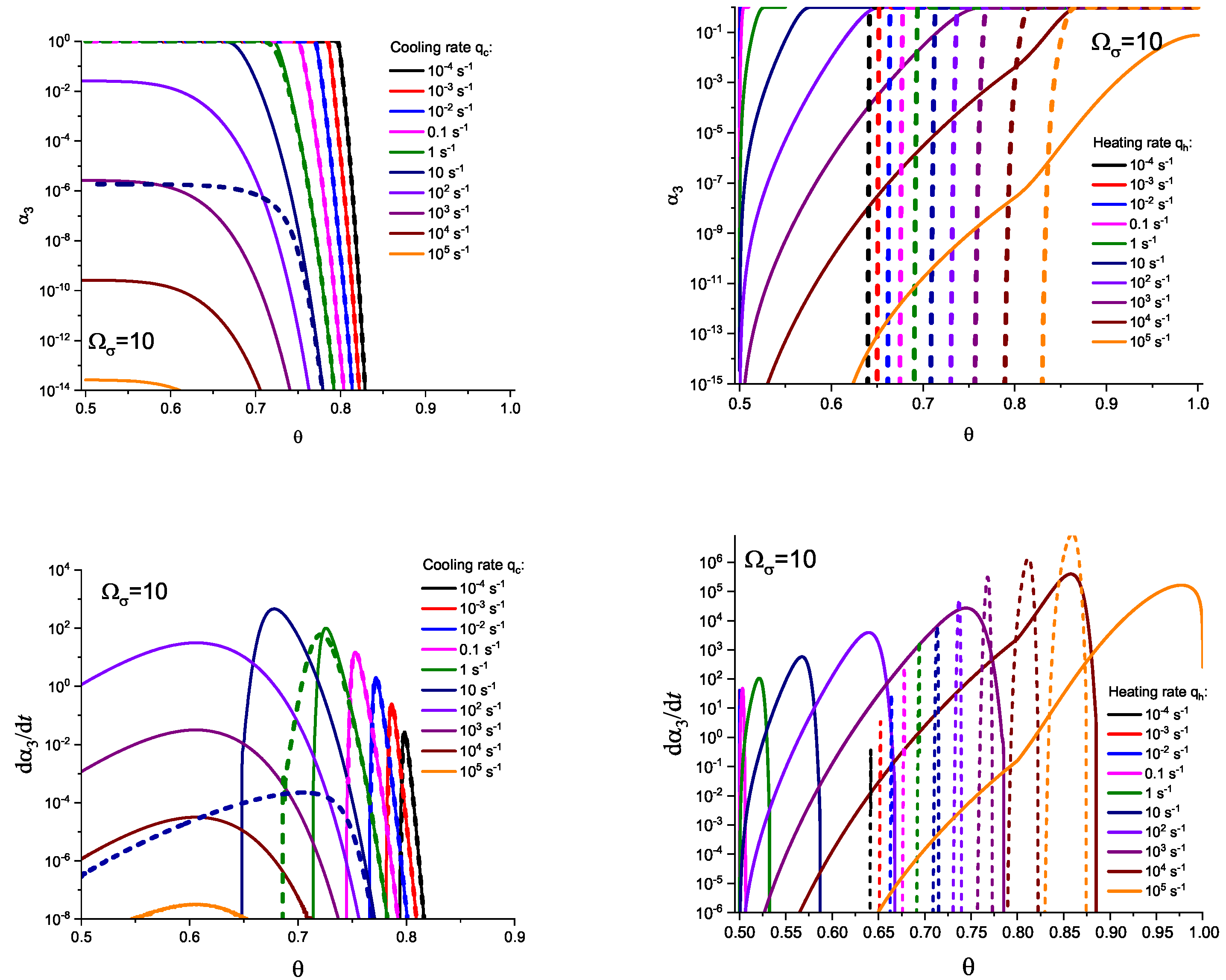
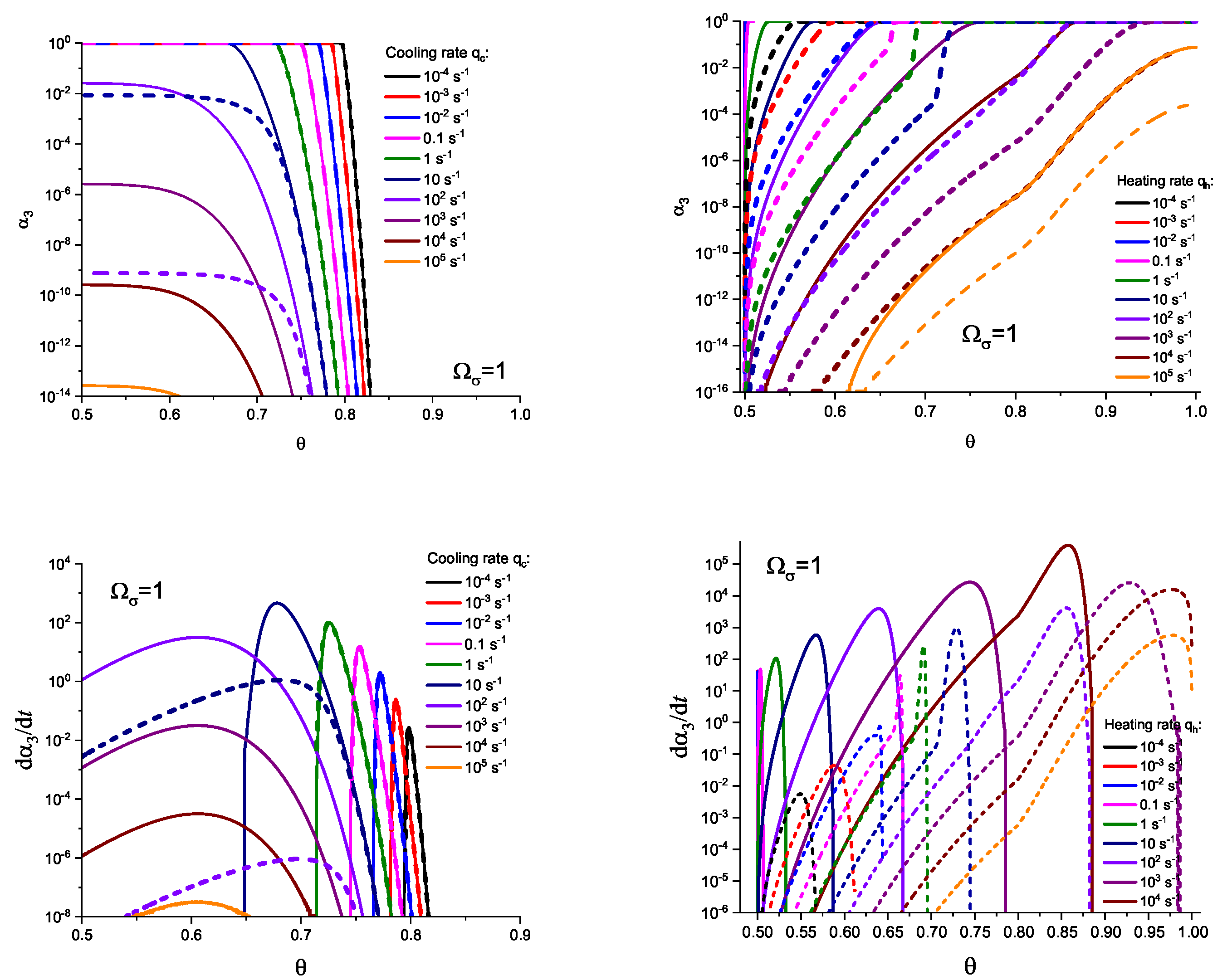
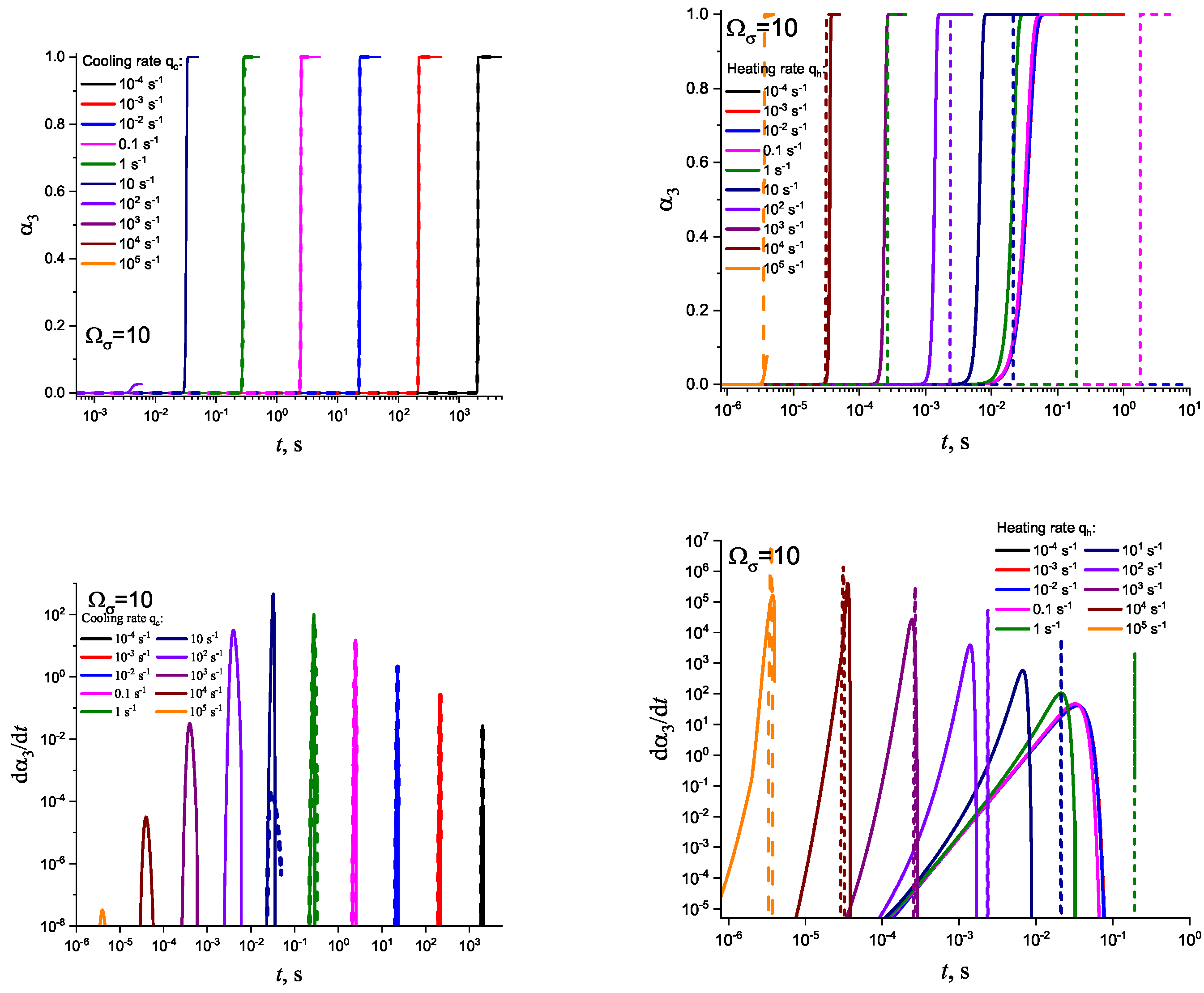
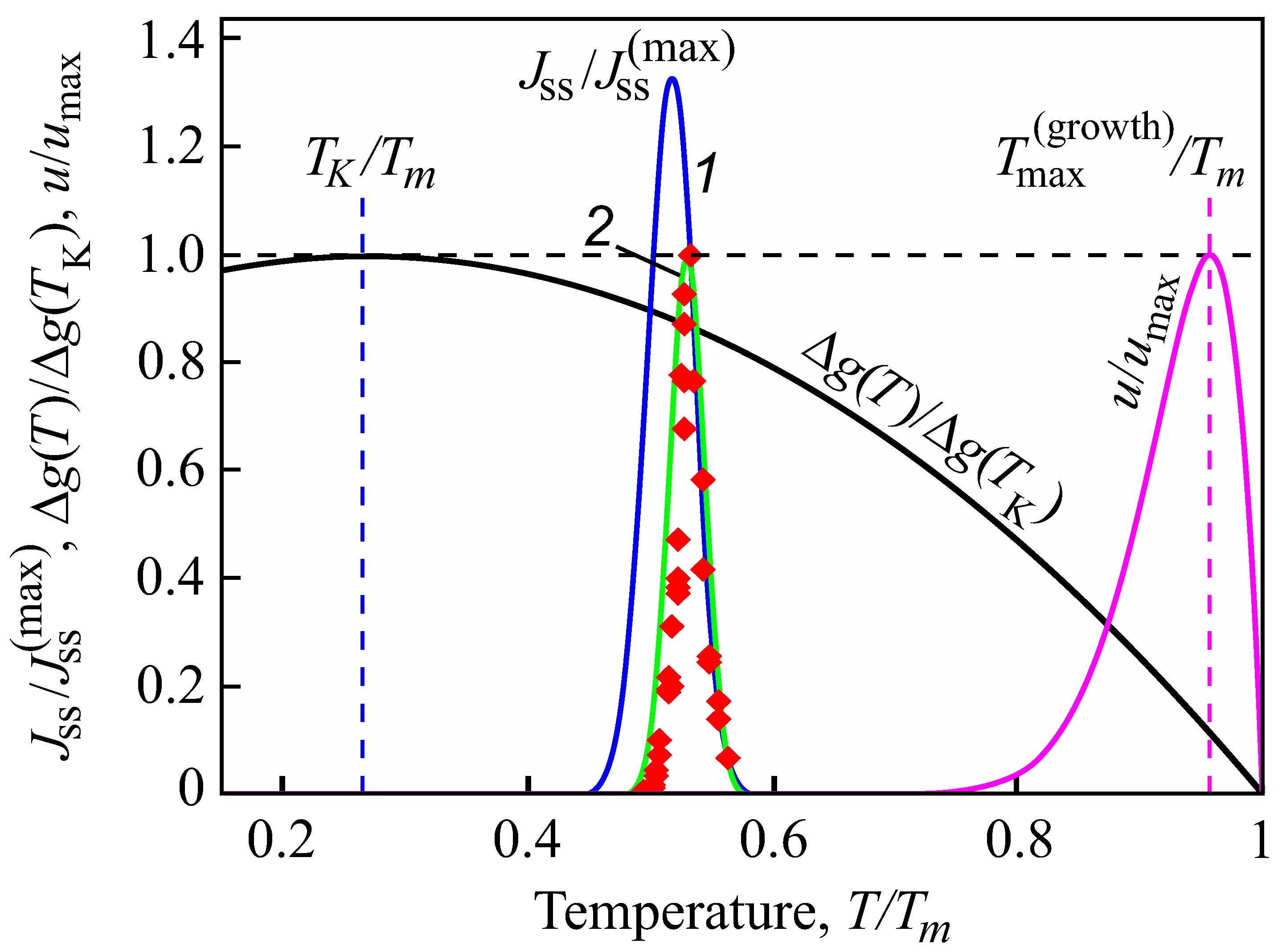
3. Results of Numerical Computations
4. Theoretical Analysis
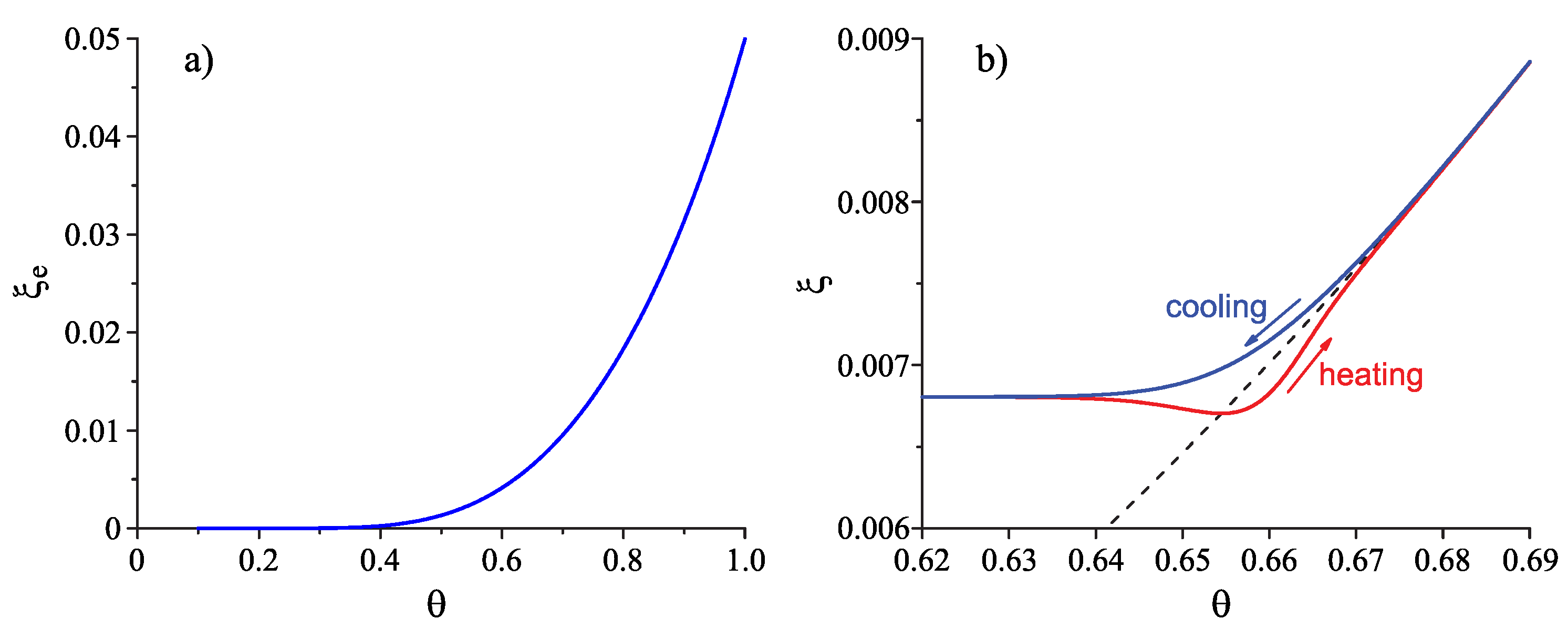
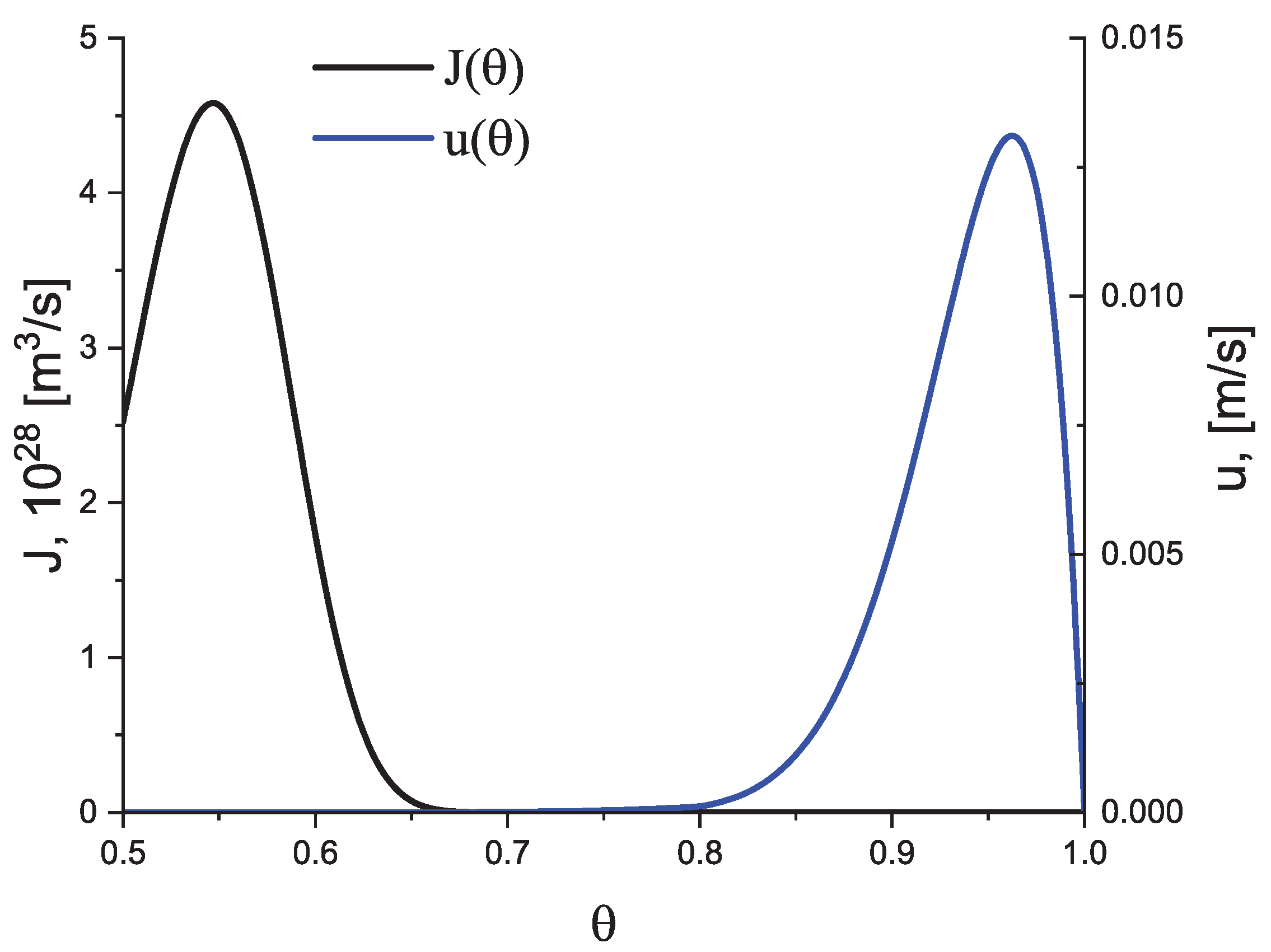
4.1. Some General Considerations
4.2. Cold Crystallization Peak Temperature in Heating as a Function of the Heating Rate: Homogeneous Nucleation
4.3. Crystallization Peak Temperature in Cooling as a Function of the Cooling Rate: Heterogeneous Nucleation
5. Summary of Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Characteristic Times of Relaxation and Crystallization: Some General Considerations
“Let us denote by the temperature at which the two kinds of barriers become equal. may be above or below the glass–transformation point, , as defined in terms of the ’conventional’ duration of an experiment. If is above , it will be impossible for the liquid to be studied as a liquid at temperatures between and , other than by experiments of much shorter duration than the ’conventional’ one, since it will crystallize spontaneously during any experiments requiring more time than the average time between simple molecular jumps. According to the concepts presented in the previous part of this paper, adequate measurements under these circumstances would result in glass-like properties for the liquid. On the other hand, if is below , it is still possible to distinguish between a glassy state and a true metastable liquid between and . But below no such distinction is possible; the glass is then the only experimentally attainable form of the liquid …Accordingly, provided the free energy barriers vary with the temperature in the way that we have postulated, it is not permissible to extrapolate the curves in figures 3 to 6 indefinitely below and to infer thereby the existence of a ’thermodynamic’ glass–like transition”.
“Suppose that when the temperature is lowered a point is eventually reached at which the free energy barrier to crystal nucleation becomes reduced to the same height as the barriers to the simpler motions…At such temperatures the liquid would be expected to crystallize just as rapidly as it changed its typically liquid structure to conform to a temperature or pressure change in its surroundings…There are good theoretical reasons for believing in the existence of such a ‘pseudo-critical temperature’” ([54], pp. 220 and 247).
“In the past there has been a considerable amount of speculation concerning the existence of a critical point between crystalline and liquid states analogous to the critical point between liquids and gases. No experimental evidence for or against such a critical point has ever been found [75], though there is reason to believe that none is possible (Bernal [76]; but see Frenkel … [77]). It is apparent, however, that the behavior with which we are here concerned has a certain similarity to the behavior at a critical point in that here, as at a true critical point, the free energy barrier between the crystal and the liquid disappears. On the other hand, there is a fundamental difference in that the two states do not really merge and their free energies are decidedly different …, so that one cannot go reversibly from the one state to the other without a normal phase change” ([54], p. 248).
“The decrease of to zero is a failing of this particular model, since there is no point at which the liquid becomes unstable relative to the solid.”
“Nonetheless, it does indicate that a properly constructed density-functional model could describe the transition from a nucleation and growth mechanism to a spinodal transformation, which the CNT cannot do”.
Appendix B. Application of the Lattice-Hole Model in the Computations and Some Possible Generalization of this Model
References
- Yinnon, H.; Uhlmann, D.R. Applications of thermoanalytical techniques to the study of crystallization kinetics in glass-forming liquids, Part 1: Theory. J. Non-Cryst. Solids 1983, 54, 253–275. [Google Scholar] [CrossRef]
- Schick, C.; Mathot, V. (Eds.) Fast Scanning Calorimetry; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Vyazovkin, S.; Sbirrazzuoli, N. Review: Nonisothermal Crystallization Kinetics by DSC: Practical Overview. Processes 2023, 11, 1438. [Google Scholar] [CrossRef]
- Skripov, V.P.; Koverda, V.P. Spontaneous Crystallization of Undercooled Liquids; Nauka: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Henderson, D.W. Thermal analysis of non-isothermal crystallization kinetics in glass-forming liquids. J. Non-Cryst. Solids 1979, 30, 301–315. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schmelzer, J., Jr. Kinetics of Nucleation at Increasing Supersaturation. J. Colloid Interface Sci. 1999, 215, 345–355. [Google Scholar] [CrossRef]
- Kashchiev, D.; Borissova, A.; Hammond, R.B.; Roberts, K.J. Effect of cooling rate on the critical undercooling for crystallization. J. Cryst. Growth 2010, 312, 698–704. [Google Scholar] [CrossRef]
- Yang, B.; Abyzov, A.S.; Zhuravlev, E.; Gao, Y.; Schmelzer, J.W.P.; Schick, C. Size and rate dependence of crystal nucleation in single tin drops by fast scanning calorimetry. J. Chem. Phys. 2013, 138, 054501. [Google Scholar] [CrossRef]
- Yang, B.; Perepezko, J.H.; Schmelzer, J.W.P.; Gao, Y.; Schick, C. Dependence of crystal nucleation on prior liquid overheating by differential fast scanning calorimeter. J. Chem. Phys. 2014, 140, 104513. [Google Scholar] [CrossRef]
- Tanaka, K.K.; Kimura, Y. Theoretical Analysis of Crystallization by Homogeneous Nucleation of Water Droplets. Phys. Chem. Chem. Phys. 2019, 21, 2410–2418. [Google Scholar] [CrossRef]
- Deubener, J.; Schmelzer, J.W.P. Statistical Approach to Crystal Nucleation in Glass-forming Liquids. Entropy 2021, 23, 246. [Google Scholar] [CrossRef]
- Todorova, S.; Gutzow, I.; Schmelzer, J.W.P. Kinetics of nucleation at increasing or decreasing supersaturation. In Nucleation Theory and Applications; Schmelzer, J.W.P., Röpke, G., Priezzhev, V.B., Eds.; Workshop Proceedings 2000–2002; Joint Institute for Nuclear Research Publishing Department: Dubna, Russia, 2002; pp. 215–233. [Google Scholar]
- Sestak, J.; Berggren, G. Study of the kinetics of the mechanism of solid–state reactions at increasing temperatures. Thermochim. Acta 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Dimitra, K.; Konstantinos, C. Nonisothermal Crystallization Kinetics: Studying the Validity of Different Johnson–Mehl–Avrami–Erofeev–Kolmogorov (JMAEK) Based Equations. Thermochim. Acta 2021, 704, 179030. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Blaine, R.L.; Kissinger, H.E. Homer Kissinger and the Kissinger equation. Thermochim. Acta 2012, 540, 1–6. [Google Scholar] [CrossRef]
- Vyazovkin, S. Is the Kissinger Equation Applicable to the Processes that Occur on Cooling? Macromol. Rapid Commun. 2002, 23, 771–775. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V.; Fokin, V.M.; Abyzov, A.S.; Zanotto, E.D. Effects of Glass Transition and Structural Relaxation on Crystal Nucleation: Theoretical Description and Model Analysis. Entropy 2020, 22, 1098. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schick, C. Dependence of Crystallization Processes of Glass-forming Melts on Prehistory: A Theoretical Approach to a Quantitative Treatment. Phys. Chem. Glas. Eur. J. Glass Sci. Technol. 2012, B53, 99–106. [Google Scholar]
- Fokin, V.M.; Abyzov, A.S.; Yuritsyn, N.S.; Schmelzer, J.W.P.; Zanotto, E.D. Effect of structural relaxation on crystal nucleation in glasses. Acta Mater. 2021, 203, 116472. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy’” by Zanotto and Mauro. Entropy 2018, 20, 704. [Google Scholar] [CrossRef]
- Golovchak, R.; Kozdras, A.; Balitska, V.; Shpotyuk, O.J. Step-wise kinetics of natural physical ageing in arsenic selenide glasses. J. Phys. Condens. Matter 2012, 24, 505106. [Google Scholar] [CrossRef]
- Song, L.; Xu, W.; Huo, J.; Wang, J.Q.; Wang, X.; Li, R. Two–step relaxations in metallic glasses during isothermal annealing. Intermetallics 2018, 93, 101–105. [Google Scholar] [CrossRef]
- Morvan, A.; Delpouve, N.; Vella, A.; Saiter–Fourcin, A. Physical aging of selenium glass: Assessing the double mechanism of equilibration and the crystallization process. J. Non-Cryst. Solids 2021, 570, 121013. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Müller, R.; Möller, J.; Gutzow, I.S. Elastic Stresses, Stress Relaxation, and Crystallization: Theory. Phys. Chem. Glas. 2002, 43 C, 291–300. [Google Scholar]
- Schmelzer, J.W.P.; Müller, R.; Möller, J.; Gutzow, I.S. Theory of Nucleation in Viscoelastic Media: Application to Phase Formation in Glassforming Melts. J. Non-Cryst. Solids 2003, 315, 144–160. [Google Scholar]
- Schmelzer, J.W.P.; Potapov, O.V.; Fokin, V.M.; Müller, R.; Reinsch, S. The Effect of Elastic Stress Evolution and Relaxation on Crystal Nucleation in Lithium Disilicate Glasses. J. Non-Cryst. Solids 2004, 333, 150–160. [Google Scholar]
- Abyzov, A.S.; Fokin, V.M.; Rodrigues, A.M.; Zanotto, E.D.; Schmelzer, J.W.P. The effect of elastic stresses on the thermodynamic barrier for crystal nucleation. J. Non-Cryst. Solids 2016, 432, 325–333. [Google Scholar]
- Schmelzer, J.W.P.; Schick, C. General concepts of crystallization: Some recent results and possible future developments. In Crystallization as Studied by Broadband Dielectric Spectroscopy; Kremer, F., Ed.; Springer: Cham, Switzerland, 2020; pp. 1–22. [Google Scholar]
- Rodrigues, L.R.; Abyzov, A.S.; Fokin, V.M.; Zanotto, E.D. Effect of structural relaxation on crystal nucleation in a sodalime–silica glass. J. Am. Ceram. Soc. 2021, 104, 3212–3223. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Abyzov, A.S.; Fokin, V.M.; Schmelzer, J.W.P.; Zanotto, E.D. Relaxation effect on crystal nucleation in a glass unveiled by experimental, numerical, and analytical approaches. Acta Mater. 2022, 223, 117458. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Fokin, V.M.; Yuritsyn, N.S.; Nascimento, M.L.F.; Schmelzer, J.W.P.; Zanotto, E.D. Crystal nucleation in a L2S-glass during aging well below Tg. J. Chem. Phys. 2023, 158, 064501. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Abyzov, A.S.; Fokin, V.M.; Ramirez Acosta, M.H.; Nascimento, M.L.F.; Zanotto, E.D. Effect of structure relaxation on crystal nucleation and isothermal overall crystallization in glasses. Present special issue (in preparation)
- Schmelzer, J.W.P.; Tropin, T.V. Theory of Crystal Nucleation of Glass-forming Liquids: Some New Developments. Int. J. Appl. Glass Sci. 2022, 13, 171–198. [Google Scholar] [CrossRef]
- Tammann, G. Der Glaszustand (English: The Vitreous State); Leopold Voss Verlag: Leipzig, Germany, 1933. [Google Scholar]
- Gutzow, I.; Grigorova, T.; Avramov, I.; Schmelzer, J.W.P. Generic Phenomenology of Vitrification and Relaxation and the Kohlrausch and Maxwell Equations. Phys. Chem. Glas. 2002, 43 C, 477–486. [Google Scholar]
- Ngai, K.L. Universal properties of relaxation and diffusion in complex materials: Originating from fundamental physics with rich applications. Prog. Mater. Sci. 2023, 139, 101130. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Baidakov, V.G. Time of formation of the first supercritical nucleus, time-lag, and the steady-state nucleation rate. Int. J. Appl. Glass Sci. 2017, 8, 48–60. [Google Scholar]
- Kashchiev, D. Nucleation at existing cluster size distributions. Surf. Sci. 1969, 18, 389–397. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C. Kauzmann paradox and the crystallization of glass-forming melts. J. Non-Cryst. Solids 2018, 501, 21–35. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Kashchiev, D. The kinetics of overall crystallization of undercooled melts in terms of the non-steady state theory of nucleation. In Advances in Nucleation and Crystallization in Glasses; Hench, L.L., Freiman, S.W., Eds.; American Ceramic Society: Columbus, OH, USA, 1971; pp. 116–122. [Google Scholar]
- Slezov, V.V. Kinetics of First–Order Phase Transitions; WILEY–VCH: Berlin/Weinheim, Germany, 2009. [Google Scholar]
- Möller, J.; Schmelzer, J.W.P.; Avramov, I. Kinetics of Segregation and Crystallization with Stress Development and Stress Relaxation. Phys. Status Solidi 1996, b 196, 49–62. [Google Scholar]
- Schmelzer, J.W.P.; Zanotto, E.D.; Avramov, I.; Fokin, V.M. Stress Development and Stress Relaxation During Crystal Growth in Glass-Forming Melts. J. Non–Cryst. Solids 2006, 352, 434–443. [Google Scholar]
- Schmelzer, J.W.P.; Boltachev, G.S.; Baidakov, V.G. Classical and Generalized Gibbs’ Approaches and the Work of Critical Cluster Formation in Nucleation Theory. J. Chem. Phys. 2006, 124, 194503. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Schmelzer, J.W.P.; Fokin, V.M.; Zanotto, E.D. Crystallization of supercooled liquids: Self–consistency correction of the steady-state nucleation rate. Entropy 2020, 22, 558. [Google Scholar] [CrossRef]
- Ostwald, W. Studien über die Bildung und Umwandlung fester Körper. 1. Abhandlung: Übersättigung und Überkaltung (Engl: Studies on the formation and transformation of solid bodies. 1. Analysis: Supersaturation and undercooling). Z. Für Phys. Chem. 1897, 22, 289–330. [Google Scholar] [CrossRef]
- Xu, S.; Hou, Z.; Chuai, X.; Wang, Y. Overview of Secondary Nucleation: From Fundamentals to Application. Ind. Eng. Chem. Res. 2020, 59, 18335–18356. [Google Scholar] [CrossRef]
- Yang, B.; Gao, Y.; Zou, C.; Zhai, Q.; Abyzov, A.S.; Zhuravlev, E.; Schmelzer, J.W.P.; Schick, C. Cooling rate dependence of undercooling of pure Sn single drop by fast scanning calorimetry. Appl. Phys. A 2011, 104, 189–196. [Google Scholar] [CrossRef]
- Chen, B.; Torkelson, J.M. Development of rigid amorphous fraction in cold–crystallized syndiotactic polystyrene films confined near the nanoscale: Novel analysis via ellipsometry. J. Polym. Sci. 2022, 60, 1631. [Google Scholar] [CrossRef]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Mauro, J.C. The glassy state of matter: Its definition and ultimate fate. J. Non-Crystalline Solids 2017, 471, 490–495. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Glass transition, crystallization of glass-forming melts, and entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef]
- Tipeev, A.O.; Schmelzer, J.W.P.; Zanotto, E.D. Comment on: “Spinodal limits of supercooled liquid Al deduced from configuration heredity of crystal clusters”. Comput. Mater. Sci. 2022, 207, 111316. [Google Scholar]
- Uhlmann, D.R. A kinetic treatment of glass formation. J. Non–Cryst. Solids 1972, 7, 337–348. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Androsch, R.; Schick, C. Experimental test of Tammann’s nuclei development approach in crystallization of macromolecules. Cryst. Growth Design 2015, 15, 786–798. [Google Scholar] [CrossRef]
- Andrianov, R.A.; Androsch, R.; Zhang, R.; Mukhametzyanov, T.A.; Abyzov, A.S.; Schmelzer, J.W.; Schick, C. Growth and dissolution of crystal nuclei in poly(L-lactic acid) (PLLA) in Tammann’s development method. Polymer 2020, 196, 122453. [Google Scholar] [CrossRef]
- Andrianov, R.A.; Schmelzer, J.W.P.; Androsch, R.; Mukhametzyanov, T.A.; Schick, C. Radial growth rate of near–critical crystal nuclei in poly(L–lactic acid) (PLLA) in Tammann’s two–stage development method. J. Chem. Phys. 2023, 158, 054504. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Jariyavidyanont, K.; Du, M.; Zhuravlev, E.; Schick, C.; Androsch, R. Nucleation and crystallization kinetics of polyamide 12 investigated by fast scanning calorimetry. J. Polym. Sci. 2022, 60, 842–855. [Google Scholar] [CrossRef]
- Mukhametzyanov, T.; Schmelzer, J.W.P.; Yarko, E.; Abdullin, A.; Ziganshin, M.; Sedov, I.; Schick, C. Crystal Nucleation and Growth in Cross–Linked Poly(ε–caprolactone) (PCL). Polymers 2021, 13, 3617. [Google Scholar] [CrossRef] [PubMed]
- Mukhametzyanov, T.; Andrianov, R.A.; Bolmatenkov, D.N.; Yagofarov, M.I.; Solomonov, B.N.; Schick, C. Nucleation and crystallization of deeply supercooled benzocaine, a rapidly crystallizing organic compound: A Fast scanning calorimetry investigation. Thermochim. Acta 2023, 730, 179613. [Google Scholar] [CrossRef]
- Tammann, G. Über die Abhängigkeit der Zahl der Kerne, welche sich in verschiedenen unterkühlten Flüssigkeiten bilden, von der Temperatur (Engl: On the dependence of the number of nuclei, forming in different undercooled liquids, on temperature). Z. Phys. Chem. 1898, 25, 441–479. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C.; Zanotto, E.D. Crystallization in glass-forming liquids: Maxima of nucleation, growth, and overall crystallization rates. J. Non-Cryst. Solids 2015, 429, 24–32. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Pressure-induced crystallization of liquids: Maxima of nucleation, growth, and overall crystallization rates. Int. J. Appl. Glass Sci. 2018, 9, 198–207. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Crystallization of glass: What we know, what we need to know. Int. J. Appl. Glass Sci. 2016, 7, 253–261. [Google Scholar] [CrossRef]
- Andreev, N.S.; Mazurin, O.V.; Porai-Koshits, E.A.; Roscova, G.P.; Filipovich, V.N. Liquid Phase Separation in Glasses; Nauka: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Mazurin, O.V.; Porai–Koshits, E.A.; Andreev, N.S. Phase Separation in Glass; North–Holland Publishers: Amsterdam, The Netherlands; New York, NY, USA, 1984. [Google Scholar]
- Davis, M.J. Effect of the Growth Treatment on Two-Stage Nucleation Experiments. J. Amer. Ceram. Soc. 2001, 84, 492–496. [Google Scholar] [CrossRef]
- Davis, M.J.; Ihinger, P.D. Effects of thermal history on crystal nucleation in silicate melt: Numerical simulations. J. Geophys. Res. 2002, 107, 2284. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Schmelzer, J.W.P.; Todorova, S. Frozen–In Fluctuations, Immiscibility and Crystallization in Oxide Melts and the Structural and Thermodynamic Nature of Glasses. Phys. Chem. Glasses Eur. J. Glass Sci. Technol. 2008, 49, 136–148. [Google Scholar]
- Schmelzer, J.W.P.; Gutzow, I.S. Glasses and the Glass Transition; WILEY–VCH: Berlin, Germany; Weinheim, Germany, 2011. [Google Scholar]
- Simon, F. On the range of stability of the fluid state. Trans. Faraday Soc. 1937, 33, 65–73. [Google Scholar] [CrossRef]
- Bernal, J.D. An attempt at a molecular theory of liquid structure. Trans. Faraday Soc. 1937, 33, 27–40. [Google Scholar] [CrossRef]
- Frenkel, Y.I. The Kinetic Theory of Liquids; Oxford University Press: Oxford, UK, 1946. [Google Scholar]
- Skripov, V.P.; Baidakov, V.G. Absence of a spinodal in undercooled liquids. Teplofizika Vysokikh Temperatur 1972, 10, 1226–1230, English version is available in High Temp. 1972, 10, 1102–1106. [Google Scholar]
- Skripov, V.P.; Faizullin, M.Z. Crystal–Liquid–Gas Phase Transitions and Thermodynamic Similarity; Wiley–VCH: Berlin, Germany; Weinheim, Germany, 2006. [Google Scholar]
- Landau, L.D. On the theory of phase transitions. Zhurn. Eksper. Teor. Fiz. 1937, 7, 19–32. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Academy of Sciences Publishing House: Berlin, Germany, 1987. [Google Scholar]
- Gibbs, J.W. The Collected Works, Volume 1, Thermodynamics; Longmans & Green: New York, NY, USA; London, UK; Toronto, ON, Canada, 1928. [Google Scholar]
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Pergamon–Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Turnbull, D. Under What Conditions can a Glass be Formed? Contemp. Phys. 1969, 10, 473–488. [Google Scholar] [CrossRef]
- Angell, C.A.; MacFarlane, D.R.; Oguni, M. The Kauzmann Paradox, Metastable Liquids, and Glasses: A Summary. Ann. N. Y. Acad. Sci. 1986, 484, 241–247. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmelzer, J.W.P.; Tropin, T.V.; Schick, C. Effects of Structural Relaxation of Glass-Forming Melts on the Overall Crystallization Kinetics in Cooling and Heating. Entropy 2023, 25, 1485. https://doi.org/10.3390/e25111485
Schmelzer JWP, Tropin TV, Schick C. Effects of Structural Relaxation of Glass-Forming Melts on the Overall Crystallization Kinetics in Cooling and Heating. Entropy. 2023; 25(11):1485. https://doi.org/10.3390/e25111485
Chicago/Turabian StyleSchmelzer, Jürn W. P., Timur V. Tropin, and Christoph Schick. 2023. "Effects of Structural Relaxation of Glass-Forming Melts on the Overall Crystallization Kinetics in Cooling and Heating" Entropy 25, no. 11: 1485. https://doi.org/10.3390/e25111485
APA StyleSchmelzer, J. W. P., Tropin, T. V., & Schick, C. (2023). Effects of Structural Relaxation of Glass-Forming Melts on the Overall Crystallization Kinetics in Cooling and Heating. Entropy, 25(11), 1485. https://doi.org/10.3390/e25111485







