Diffusion Probabilistic Modeling for Video Generation
Abstract
:1. Introduction
- 1.
- We show how to use diffusion probabilistic models to generate videos autoregressively. This enables a new path towards probabilistic video forecasting while achieving perceptual qualities better than or comparable with likelihood-free methods such as GANs.
- 2.
- 3.
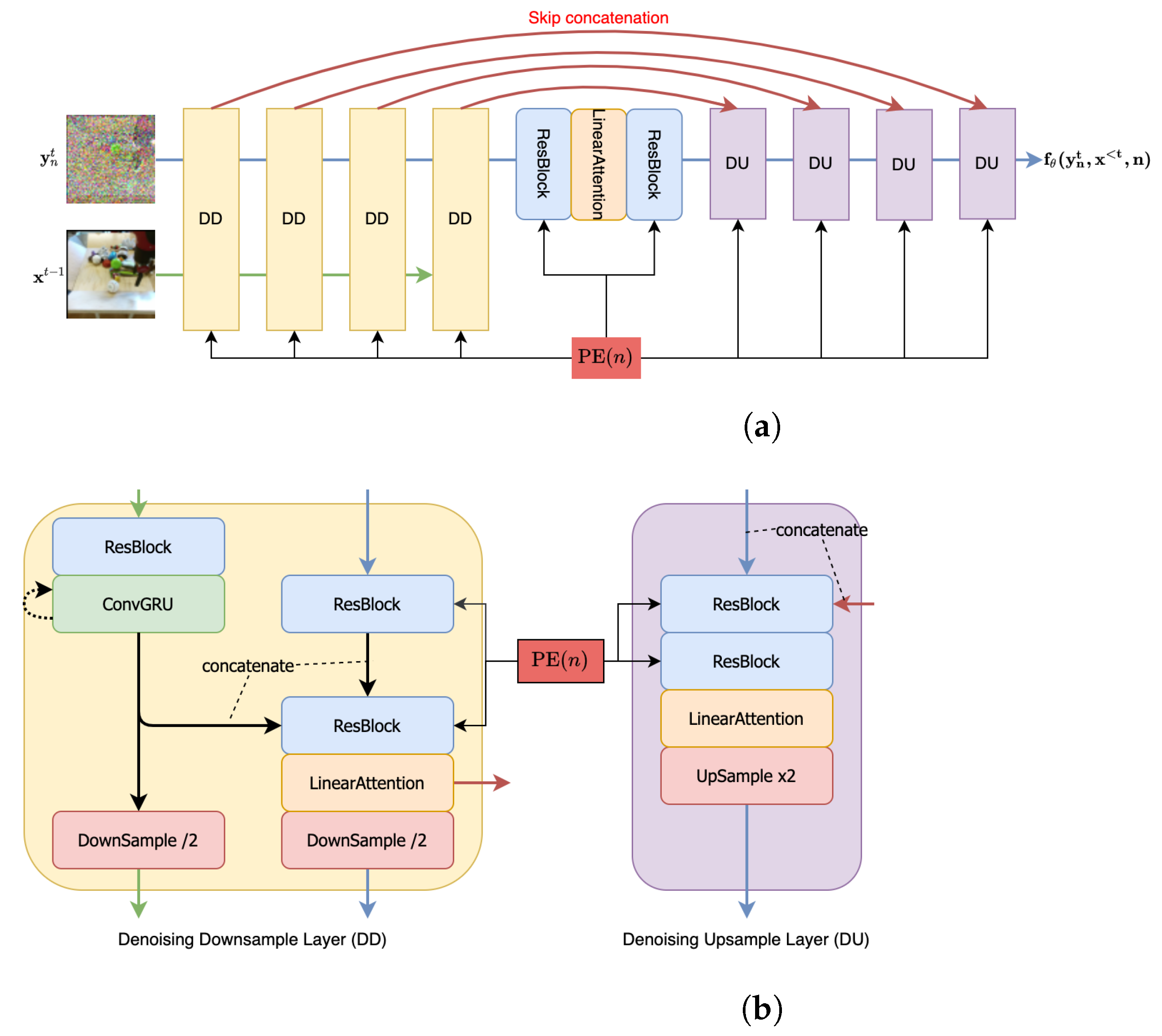
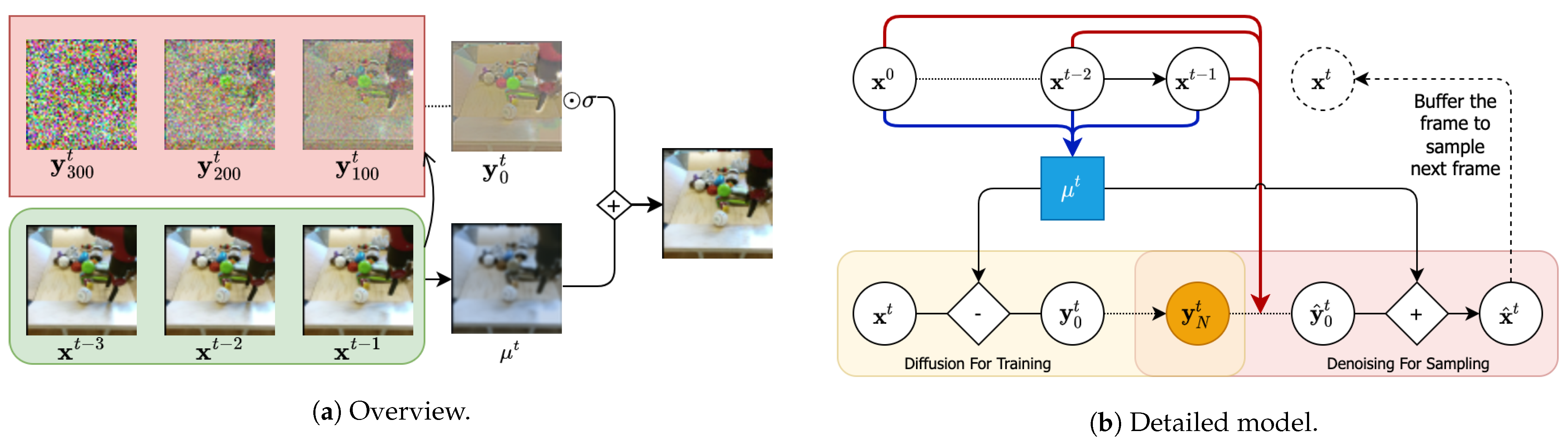
- Our ablation studies demonstrate that modeling residuals from the predicted next frame yields better results than directly modeling the next frames. This observation is consistent with recent findings in neural video compression. Figure 1a summarizes the main idea of our approach (Figure 1b has more details).
2. Related Work
2.1. Video Generation Models
2.2. Diffusion Probabilistic Models
2.3. Neural Video Compression Models
3. A Diffusion Probabilistic Model for Video
3.1. Background on Diffusion Probabilistic Models
3.2. Residual Video Diffusion Model
| Algorithm 1: Training |
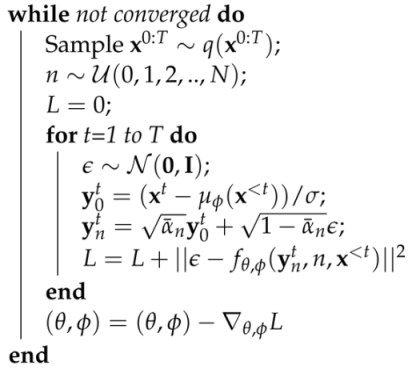 |
| Algorithm 2: Generation |
 |
4. Experiments
4.1. Datasets
4.2. Training and Testing Details
4.3. Baseline Models
4.4. Evaluation Metrics
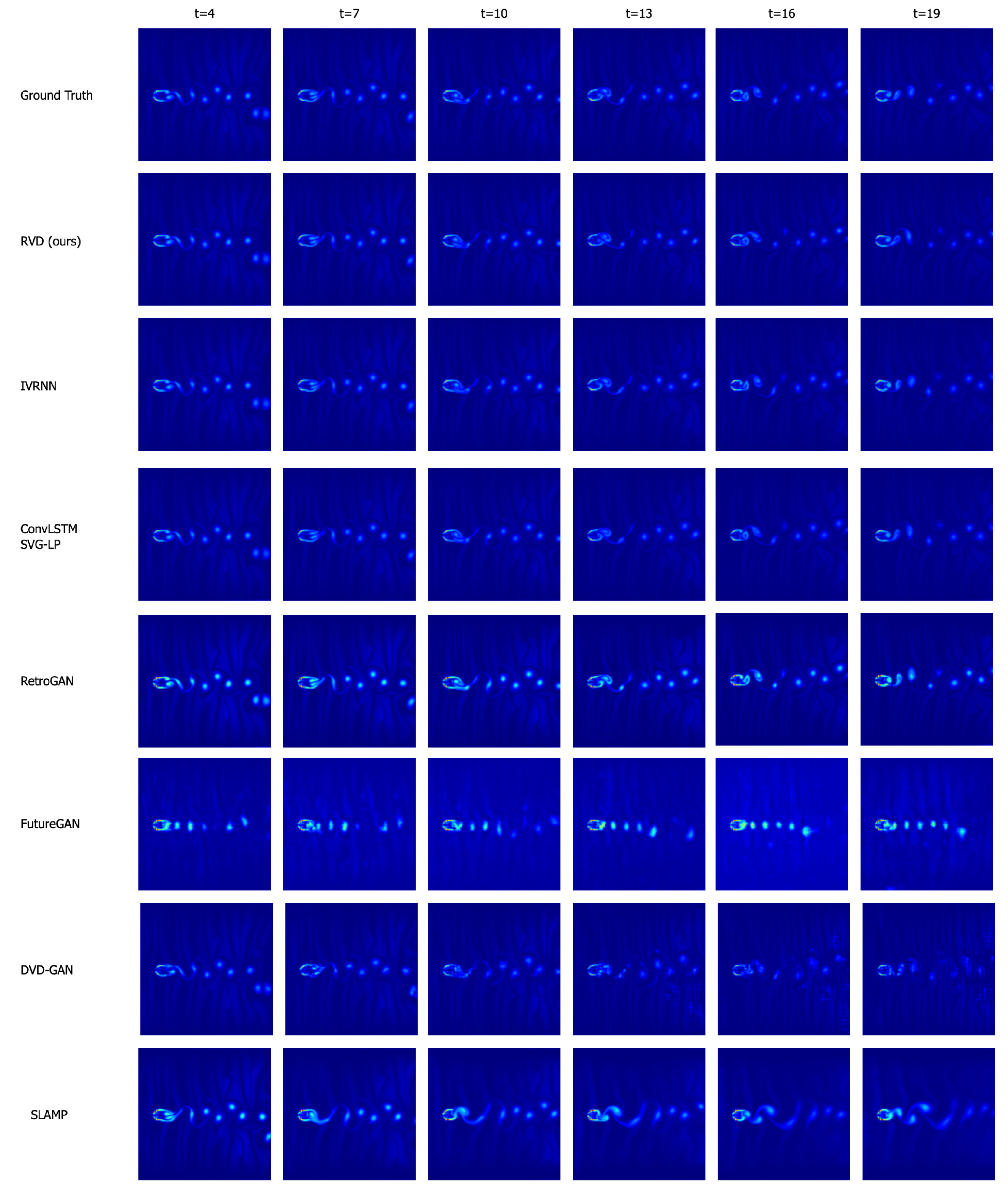
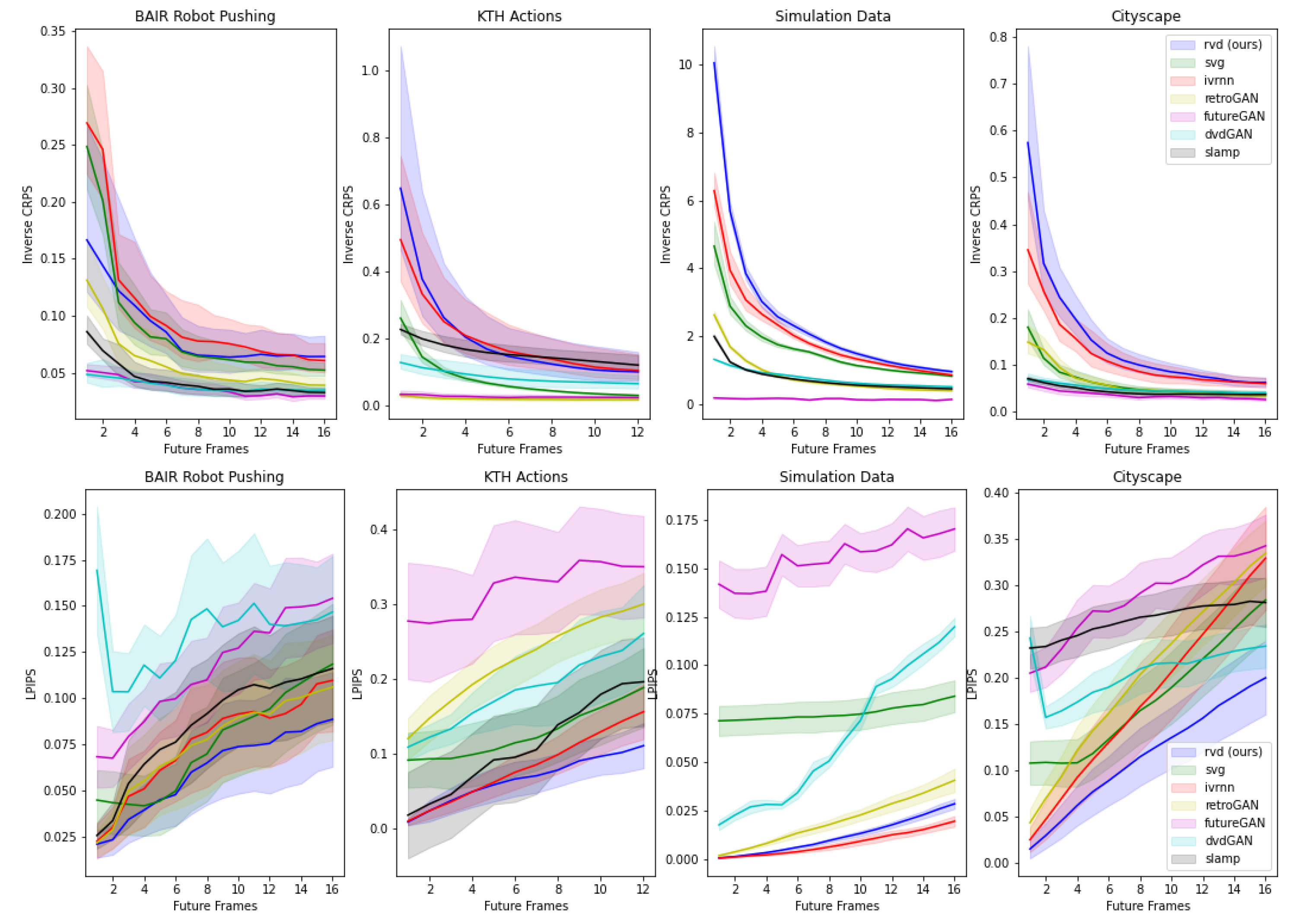
4.5. Qualitative and Quantitative Analysis
4.6. Ablation Studies
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. About CRPS
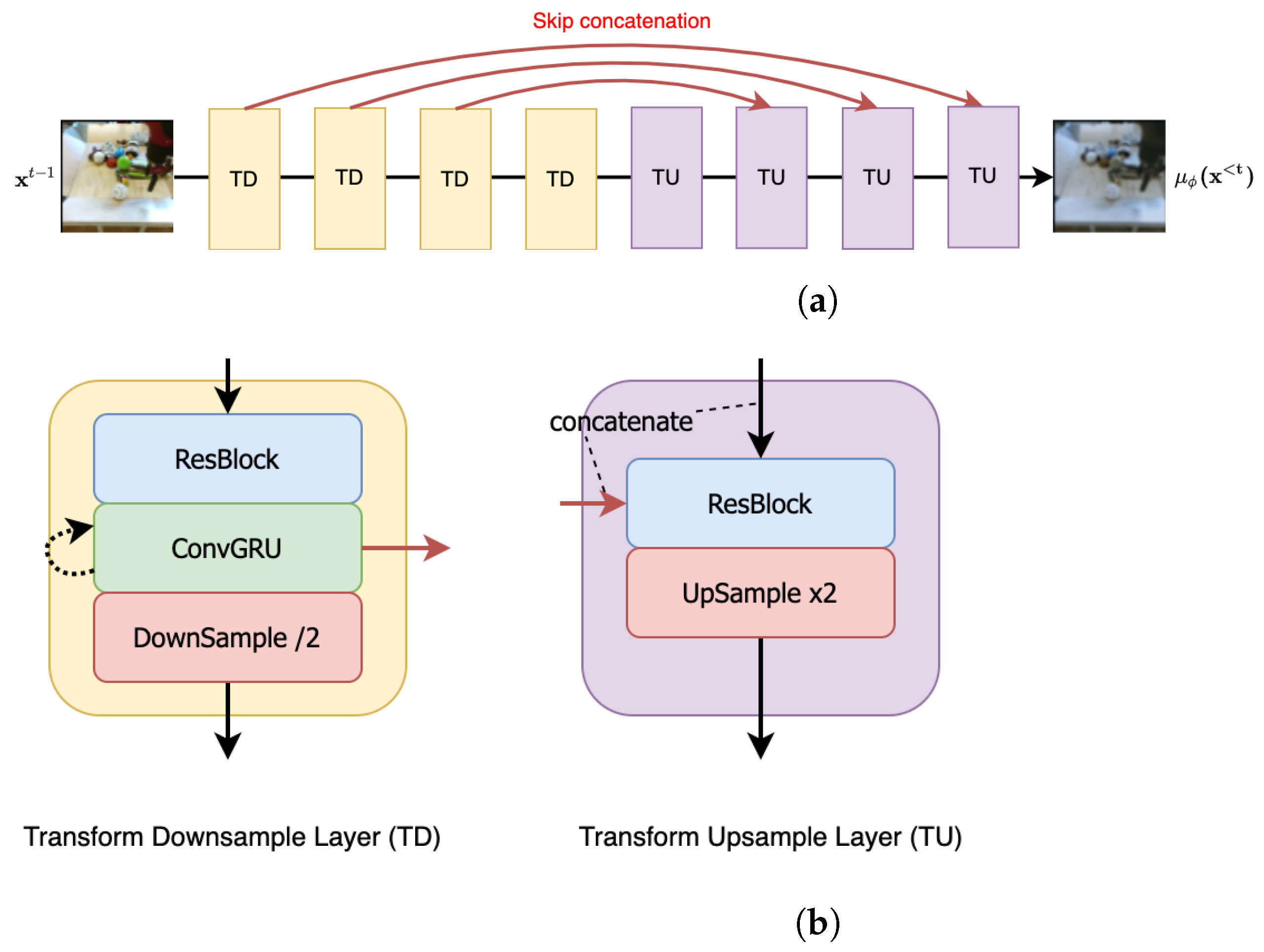
Appendix B. Architecture
- Channel Dim refers to the channel dimension of all the components in the first downsampling layer of the U-Net [92] style structure used in our approach.
- Denoising/Transform Multipliers are the channel dimension multipliers for subsequent downsampling layers (including the first layer) in the denoising/transform modules. The upsampling layer multipliers follow the reverse sequence.
- Each ResBlock [93] leverages a standard implementation of the ResNet block with kernel, LeakyReLU activation and Group Normalization.
- All ConvGRU [94] use a kernel to deal with the temporal information.
- Each LinearAttention module involves 4 attention heads, each involving 16 dimensions.
- To condition our architecture on the denoising step n, we use positional encodings to encode n and add this encoding to the ResBlocks (as in Figure A1).
| Video Resolutions | Channel Dim | Denoising Multipliers | Transform Multipliers |
|---|---|---|---|
| 64 × 64 | 48 | 1, 2, 4, 8 () | 1, 2, 2, 4 () |
| 128 × 128 | 64 | 1, 1, 2, 2, 4, 4 () | 1, 2, 3, 4 () |
Appendix C. Deriving the Optimization Objective
Appendix D. Additional Generated Samples


References
- Oprea, S.; Martinez-Gonzalez, P.; Garcia-Garcia, A.; Castro-Vargas, J.A.; Orts-Escolano, S.; Garcia-Rodriguez, J.; Argyros, A. A review on deep learning techniques for video prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2806–2826. [Google Scholar] [CrossRef]
- Vondrick, C.; Pirsiavash, H.; Torralba, A. Anticipating visual representations from unlabeled video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 98–106. [Google Scholar]
- Ha, D.; Schmidhuber, J. World models. arXiv 2018, arXiv:1803.10122. [Google Scholar]
- Liu, Z.; Yeh, R.A.; Tang, X.; Liu, Y.; Agarwala, A. Video frame synthesis using deep voxel flow. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4463–4471. [Google Scholar]
- Bhattacharyya, A.; Fritz, M.; Schiele, B. Long-term on-board prediction of people in traffic scenes under uncertainty. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4194–4202. [Google Scholar]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Lombardo, S.; Schroers, C.; Mandt, S. Deep generative video compression. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 9287–9298. [Google Scholar]
- Lu, G.; Ouyang, W.; Xu, D.; Zhang, X.; Cai, C.; Gao, Z. Dvc: An end-to-end deep video compression framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11006–11015. [Google Scholar]
- Agustsson, E.; Minnen, D.; Johnston, N.; Balle, J.; Hwang, S.J.; Toderici, G. Scale-space flow for end-to-end optimized video compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtually, 14–19 June 2020; pp. 8503–8512. [Google Scholar]
- Yang, R.; Mentzer, F.; Van Gool, L.; Timofte, R. Learning for video compression with recurrent auto-encoder and recurrent probability model. IEEE J. Sel. Top. Signal Process. 2020, 15, 388–401. [Google Scholar] [CrossRef]
- Yang, R.; Yang, Y.; Marino, J.; Mandt, S. Hierarchical Autoregressive Modeling for Neural Video Compression. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Yang, Y.; Mandt, S.; Theis, L. An Introduction to Neural Data Compression. arXiv 2022, arXiv:2202.06533. [Google Scholar]
- Babaeizadeh, M.; Finn, C.; Erhan, D.; Campbell, R.H.; Levine, S. Stochastic Variational Video Prediction. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Denton, E.; Fergus, R. Stochastic video generation with a learned prior. In Proceedings of the International Conference on Machine Learning, Alvsjo, Sweden, 10–15 July 2018; pp. 1174–1183. [Google Scholar]
- Castrejon, L.; Ballas, N.; Courville, A. Improved conditional vrnns for video prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 Octorber–2 November 2019; pp. 7608–7617. [Google Scholar]
- Aigner, S.; Körner, M. Futuregan: Anticipating the future frames of video sequences using spatio-temporal 3d convolutions in progressively growing gans. arXiv 2018, arXiv:1810.01325. [Google Scholar] [CrossRef]
- Kwon, Y.H.; Park, M.G. Predicting future frames using retrospective cycle gan. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1811–1820. [Google Scholar]
- Lee, A.X.; Zhang, R.; Ebert, F.; Abbeel, P.; Finn, C.; Levine, S. Stochastic adversarial video prediction. arXiv 2018, arXiv:1804.01523. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-Based Generative Modeling through Stochastic Differential Equations. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Song, Y.; Durkan, C.; Murray, I.; Ermon, S. Maximum likelihood training of score-based diffusion models. Adv. Neural Inf. Process. Syst. 2021, 34, 1415–1428. [Google Scholar]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Marino, J. Predictive coding, variational autoencoders, and biological connections. Neural Comput. 2021, 34, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Yang, Y.; Marino, J.; Mandt, S. Insights from Generative Modeling for Neural Video Compression. arXiv 2021, arXiv:2107.13136. [Google Scholar] [CrossRef] [PubMed]
- Marino, J.; Chen, L.; He, J.; Mandt, S. Improving sequential latent variable models with autoregressive flows. In Proceedings of the 2nd Symposium on Advances in Approximate Bayesian Inference, Virtually, 22 June 2021. [Google Scholar]
- Akan, A.K.; Erdem, E.; Erdem, A.; Guney, F. Slamp: Stochastic Latent Appearance and Motion Prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Virtually, 11–17 October 2021; pp. 14728–14737. [Google Scholar]
- Clark, A.; Donahue, J.; Simonyan, K. Adversarial video generation on complex datasets. arXiv 2019, arXiv:1907.06571. [Google Scholar]
- Dorkenwald, M.; Milbich, T.; Blattmann, A.; Rombach, R.; Derpanis, K.G.; Ommer, B. Stochastic image-to-video synthesis using cinns. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtually, 19–25 June 2021; pp. 3742–3753. [Google Scholar]
- Nam, S.; Ma, C.; Chai, M.; Brendel, W.; Xu, N.; Kim, S.J. End-to-end time-lapse video synthesis from a single outdoor image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1409–1418. [Google Scholar]
- Wu, C.; Huang, L.; Zhang, Q.; Li, B.; Ji, L.; Yang, F.; Sapiro, G.; Duan, N. Godiva: Generating open-domain videos from natural descriptions. arXiv 2021, arXiv:2104.14806. [Google Scholar]
- Singer, U.; Polyak, A.; Hayes, T.; Yin, X.; An, J.; Zhang, S.; Hu, Q.; Yang, H.; Ashual, O.; Gafni, O.; et al. Make-a-video: Text-to-video generation without text-video data. arXiv 2022, arXiv:2209.14792. [Google Scholar]
- Gafni, O.; Polyak, A.; Ashual, O.; Sheynin, S.; Parikh, D.; Taigman, Y. Make-a-scene: Scene-based text-to-image generation with human priors. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; pp. 89–106. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Zhang, H.; Koh, J.Y.; Baldridge, J.; Lee, H.; Yang, Y. Cross-modal contrastive learning for text-to-image generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtually, 19–25 June 2021; pp. 833–842. [Google Scholar]
- Zhou, Y.; Zhang, R.; Chen, C.; Li, C.; Tensmeyer, C.; Yu, T.; Gu, J.; Xu, J.; Sun, T. LAFITE: Towards Language-Free Training for Text-to-Image Generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Liu, G.; Tao, A.; Kautz, J.; Catanzaro, B. Video-to-Video Synthesis. arXiv 2018, arXiv:1808.06601. [Google Scholar]
- Saito, M.; Saito, S.; Koyama, M.; Kobayashi, S. Train sparsely, generate densely: Memory-efficient unsupervised training of high-resolution temporal gan. Int. J. Comput. Vis. 2020, 128, 2586–2606. [Google Scholar] [CrossRef]
- Yu, S.; Tack, J.; Mo, S.; Kim, H.; Kim, J.; Ha, J.W.; Shin, J. Generating Videos with Dynamics-aware Implicit Generative Adversarial Networks. In Proceedings of the International Conference on Learning Representations, Virtually, 25–29 April 2022. [Google Scholar]
- Byeon, W.; Wang, Q.; Srivastava, R.K.; Koumoutsakos, P. Contextvp: Fully context-aware video prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 753–769. [Google Scholar]
- Finn, C.; Goodfellow, I.; Levine, S. Unsupervised learning for physical interaction through video prediction. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Lotter, W.; Kreiman, G.; Cox, D. Deep Predictive Coding Networks for Video Prediction and Unsupervised Learning. In Proceedings of the International Conference on Learning Representations, Palais des Congres Neptune, France, 24–26 April 2017. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhutdinov, R. Unsupervised Learning of Video Representations using LSTMs. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Walker, J.; Gupta, A.; Hebert, M. Dense optical flow prediction from a static image. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 2443–2451. [Google Scholar]
- Villegas, R.; Yang, J.; Hong, S.; Lin, X.; Lee, H. Decomposing Motion and Content for Natural Video Sequence Prediction. In Proceedings of the International Conference on Learning Representations, Palais des Congres Neptune, France, 24–26 April 2017. [Google Scholar]
- Liang, X.; Lee, L.; Dai, W.; Xing, E.P. Dual motion GAN for future-flow embedded video prediction. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1744–1752. [Google Scholar]
- Li, Y.; Mandt, S. Disentangled sequential autoencoder. In Proceedings of the International Conference on Machine Learning, Alvsjo, Sweden, 10–15 July 2018; pp. 5670–5679. [Google Scholar]
- Kumar, M.; Babaeizadeh, M.; Erhan, D.; Finn, C.; Levine, S.; Dinh, L.; Kingma, D. Videoflow: A flow-based generative model for video. arXiv 2019, arXiv:1903.01434. [Google Scholar]
- Unterthiner, T.; van Steenkiste, S.; Kurach, K.; Marinier, R.; Michalski, M.; Gelly, S. Towards accurate generative models of video: A new metric & challenges. arXiv 2018, arXiv:1812.01717. [Google Scholar]
- Villegas, R.; Pathak, A.; Kannan, H.; Erhan, D.; Le, Q.V.; Lee, H. High fidelity video prediction with large stochastic recurrent neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Babaeizadeh, M.; Saffar, M.T.; Nair, S.; Levine, S.; Finn, C.; Erhan, D. Fitvid: Overfitting in pixel-level video prediction. arXiv 2021, arXiv:2106.13195. [Google Scholar]
- Villegas, R.; Erhan, D.; Lee, H. Hierarchical long-term video prediction without supervision. In Proceedings of the International Conference on Machine Learning, Alvsjo, Sweden, 10–15 July 2018; pp. 6038–6046. [Google Scholar]
- Yan, W.; Zhang, Y.; Abbeel, P.; Srinivas, A. Videogpt: Video generation using vq-vae and transformers. arXiv 2021, arXiv:2104.10157. [Google Scholar]
- Rakhimov, R.; Volkhonskiy, D.; Artemov, A.; Zorin, D.; Burnaev, E. Latent video transformer. arXiv 2020, arXiv:2006.10704. [Google Scholar]
- Lee, W.; Jung, W.; Zhang, H.; Chen, T.; Koh, J.Y.; Huang, T.; Yoon, H.; Lee, H.; Hong, S. Revisiting Hierarchical Approach for Persistent Long-Term Video Prediction. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Bayer, J.; Osendorfer, C. Learning stochastic recurrent networks. arXiv 2014, arXiv:1411.7610. [Google Scholar]
- Chung, J.; Kastner, K.; Dinh, L.; Goel, K.; Courville, A.C.; Bengio, Y. A recurrent latent variable model for sequential data. arXiv 2015, arXiv:1506.02216. [Google Scholar]
- Wu, B.; Nair, S.; Martin-Martin, R.; Fei-Fei, L.; Finn, C. Greedy hierarchical variational autoencoders for large-scale video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtually, 19–25 June 2021; pp. 2318–2328. [Google Scholar]
- Zhao, L.; Peng, X.; Tian, Y.; Kapadia, M.; Metaxas, D. Learning to forecast and refine residual motion for image-to-video generation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 387–403. [Google Scholar]
- Franceschi, J.Y.; Delasalles, E.; Chen, M.; Lamprier, S.; Gallinari, P. Stochastic Latent Residual Video Prediction. In Proceedings of the 37th International Conference on Machine Learning, Virtually, 13–18 July 2020; pp. 3233–3246. [Google Scholar]
- Blau, Y.; Michaeli, T. The perception-distortion tradeoff. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6228–6237. [Google Scholar]
- Vondrick, C.; Pirsiavash, H.; Torralba, A. Generating videos with scene dynamics. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Tulyakov, S.; Liu, M.Y.; Yang, X.; Kautz, J. Mocogan: Decomposing motion and content for video generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1526–1535. [Google Scholar]
- Gui, J.; Sun, Z.; Wen, Y.; Tao, D.; Ye, J. A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications. IEEE Trans. Knowl. Data Eng. 2021, 35, 3313–3332. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. arXiv 2021, arXiv:2104.07636. [Google Scholar] [CrossRef]
- Pandey, K.; Mukherjee, A.; Rai, P.; Kumar, A. DiffuseVAE: Efficient, Controllable and High-Fidelity Generation from Low-Dimensional Latents. arXiv 2022, arXiv:2201.00308. [Google Scholar]
- Chen, N.; Zhang, Y.; Zen, H.; Weiss, R.J.; Norouzi, M.; Chan, W. WaveGrad: Estimating Gradients for Waveform Generation. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Kong, Z.; Ping, W.; Huang, J.; Zhao, K.; Catanzaro, B. DiffWave: A Versatile Diffusion Model for Audio Synthesis. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Luo, S.; Hu, W. Diffusion probabilistic models for 3d point cloud generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtually, 19–25 June 2021; pp. 2837–2845. [Google Scholar]
- Rasul, K.; Seward, C.; Schuster, I.; Vollgraf, R. Autoregressive denoising diffusion models for multivariate probabilistic time series forecasting. In Proceedings of the International Conference on Machine Learning, Virtually, 18–24 July 2021; pp. 8857–8868. [Google Scholar]
- Ho, J.; Salimans, T.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video Diffusion Models. arXiv 2022, arXiv:2204.03458. [Google Scholar]
- Voleti, V.; Jolicoeur-Martineau, A.; Pal, C. MCVD-Masked Conditional Video Diffusion for Prediction, Generation, and Interpolation. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Brock, A.; Donahue, J.; Simonyan, K. Large Scale GAN Training for High Fidelity Natural Image Synthesis. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Papamakarios, G.; Pavlakou, T.; Murray, I. Masked autoregressive flow for density estimation. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Schapire, R.E. A brief introduction to boosting. In Proceedings of the Ijcai, Stockholm, Sweden, 31 July–6 August 1999; Volume 99, pp. 1401–1406. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the International Conference on Machine Learning, Virtually, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
- Kolen, J.F.; Kremer, S.C. A Field Guide to Dynamical Recurrent Networks; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ebert, F.; Finn, C.; Lee, A.X.; Levine, S. Self-Supervised Visual Planning with Temporal Skip Connections. In Proceedings of the CoRL, Mountain View, CA, USA, 13–15 November 2017; pp. 344–356. [Google Scholar]
- Schuldt, C.; Laptev, I.; Caputo, B. Recognizing human actions: A local SVM approach. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 3, pp. 32–36. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Chirila, D.B. Towards Lattice Boltzmann Models for Climate Sciences: The GeLB Programming Language with Applications. Ph.D. Thesis, Universität Bremen, Bremen, Gremany, 2018. [Google Scholar]
- Unterthiner, T.; van Steenkiste, S.; Kurach, K.; Marinier, R.; Michalski, M.; Gelly, S. FVD: A new metric for video generation. In Proceedings of the ICLR 2019 Workshop for Deep Generative Models for Highly Structured Data, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Matheson, J.E.; Winkler, R.L. Scoring rules for continuous probability distributions. Manag. Sci. 1976, 22, 1087–1096. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Gneiting, T.; Ranjan, R. Comparing density forecasts using threshold-and quantile-weighted scoring rules. J. Bus. Econ. Stat. 2011, 29, 411–422. [Google Scholar] [CrossRef]
- Smaira, L.; Carreira, J.; Noland, E.; Clancy, E.; Wu, A.; Zisserman, A. A short note on the kinetics-700-2020 human action dataset. arXiv 2020, arXiv:2010.10864. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising Diffusion Implicit Models. In Proceedings of the International Conference on Learning Representations, Virtually, 3–7 May 2021. [Google Scholar]
- Salimans, T.; Ho, J. Progressive distillation for fast sampling of diffusion models. arXiv 2022, arXiv:2202.00512. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Ballas, N.; Yao, L.; Pal, C.; Courville, A.C. Delving Deeper into Convolutional Networks for Learning Video Representations. In Proceedings of the ICLR (Poster), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]


| FVD↓ | LPIPS↓ | CRPS↓ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KTH | BAIR | Sim | City | KTH | BAIR | Sim | City | KTH | BAIR | Sim | City | |
| RVD (ours) | 1351 | 1272 | 20 | 997 | 0.06 | 0.06 | 0.01 | 0.11 | 6.51 | 12.86 | 0.58 | 9.84 |
| IVRNN | 1375 | 1337 | 24 | 1234 | 0.08 | 0.07 | 0.008 | 0.18 | 6.17 | 11.74 | 0.65 | 11.00 |
| SLAMP | 1451 | 1749 | 2998 | 1853 | 0.05 | 0.08 | 0.30 | 0.23 | 6.18 | 24.8 | 2.53 | 23.6 |
| SVG-LP | 1783 | 1631 | 21 | 1465 | 0.12 | 0.08 | 0.01 | 0.20 | 18.24 | 13.96 | 0.75 | 19.34 |
| RetroGAN | 2503 | 2038 | 28 | 1769 | 0.28 | 0.07 | 0.02 | 0.20 | 27.49 | 19.42 | 1.60 | 20.13 |
| DVD-GAN | 2592 | 3097 | 147 | 2012 | 0.18 | 0.10 | 0.06 | 0.21 | 12.05 | 27.2 | 1.42 | 21.61 |
| FutureGAN | 4111 | 3297 | 319 | 5692 | 0.33 | 0.12 | 0.16 | 0.29 | 37.13 | 27.97 | 6.64 | 29.31 |
| FVD↓ | LPIPS↓ | CRPS↓ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KTH | BAIR | Sim | City | KTH | BAIR | Sim | City | KTH | BAIR | Sim | City | |
| VD (2 + 6) | 1523 | 1374 | 37 | 1321 | 0.066 | 0.066 | 0.014 | 0.127 | 6.10 | 12.75 | 0.68 | 13.42 |
| SimpleRVD (2 + 6) | 1532 | 1338 | 45 | 1824 | 0.065 | 0.063 | 0.024 | 0.163 | 5.80 | 12.98 | 0.65 | 10.78 |
| RVD (2 + 6) | 1351 | 1272 | 20 | 997 | 0.066 | 0.060 | 0.011 | 0.113 | 6.51 | 12.86 | 0.58 | 9.84 |
| RVD (2 + 3) | 1663 | 1381 | 33 | 1074 | 0.072 | 0.072 | 0.018 | 0.112 | 6.67 | 13.93 | 0.63 | 10.59 |
| IVRNN (4 + 8) | 1375 | 1337 | 24 | 1234 | 0.082 | 0.075 | 0.008 | 0.178 | 6.17 | 11.74 | 0.65 | 11.00 |
| IVRNN (4 + 4) | 2754 | 1508 | 150 | 3145 | 0.097 | 0.074 | 0.040 | 0.278 | 7.25 | 13.64 | 1.36 | 18.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Srivastava, P.; Mandt, S. Diffusion Probabilistic Modeling for Video Generation. Entropy 2023, 25, 1469. https://doi.org/10.3390/e25101469
Yang R, Srivastava P, Mandt S. Diffusion Probabilistic Modeling for Video Generation. Entropy. 2023; 25(10):1469. https://doi.org/10.3390/e25101469
Chicago/Turabian StyleYang, Ruihan, Prakhar Srivastava, and Stephan Mandt. 2023. "Diffusion Probabilistic Modeling for Video Generation" Entropy 25, no. 10: 1469. https://doi.org/10.3390/e25101469
APA StyleYang, R., Srivastava, P., & Mandt, S. (2023). Diffusion Probabilistic Modeling for Video Generation. Entropy, 25(10), 1469. https://doi.org/10.3390/e25101469






