Learning Energy-Based Models in High-Dimensional Spaces with Multiscale Denoising-Score Matching
Abstract
:1. Introduction and Motivation
Score Matching, Denoising-Score Matching and Deep-Energy Estimators
2. A Geometric View of Denoising-Score Matching
3. Learning Energy-Based Model with Multiscale Denoising-Score Matching
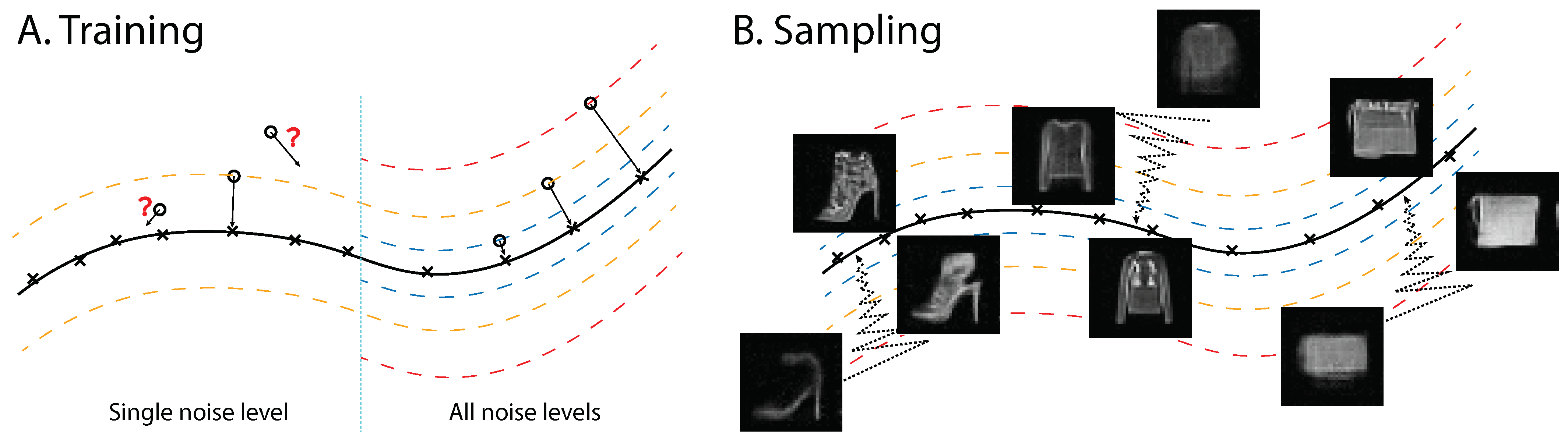
3.1. Multiscale Denoising-Score Matching
3.2. Sampling by Annealed Langevin Dynamics
4. Image Modeling Results
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EBM | Energy-based model |
| GAN | Generative Adversarial Networks |
| SM | Score matching |
| MDSM | Three-letter acronym |
| MNIST | Modified National Institute of Standards and Technology database |
| CelebA | CelebFaces Attributes Dataset |
| CIFAR-10 | Tiny image classification dataset https://www.cs.toronto.edu/~kriz/cifar.html, accessed on March 2019 |
| ResNet | Residual Networks |
| HMC | Hamiltonian Monte Carlo |
| AIS | Annealed Importance Sampling |
| OOD | Out of distribution |
| NCSN | Noise Conditional Score Networks |
Appendix A. MDSM Objective
Appendix B. Problem with Single-Noise Denoising-Score Matching

Appendix C. Overfitting Test
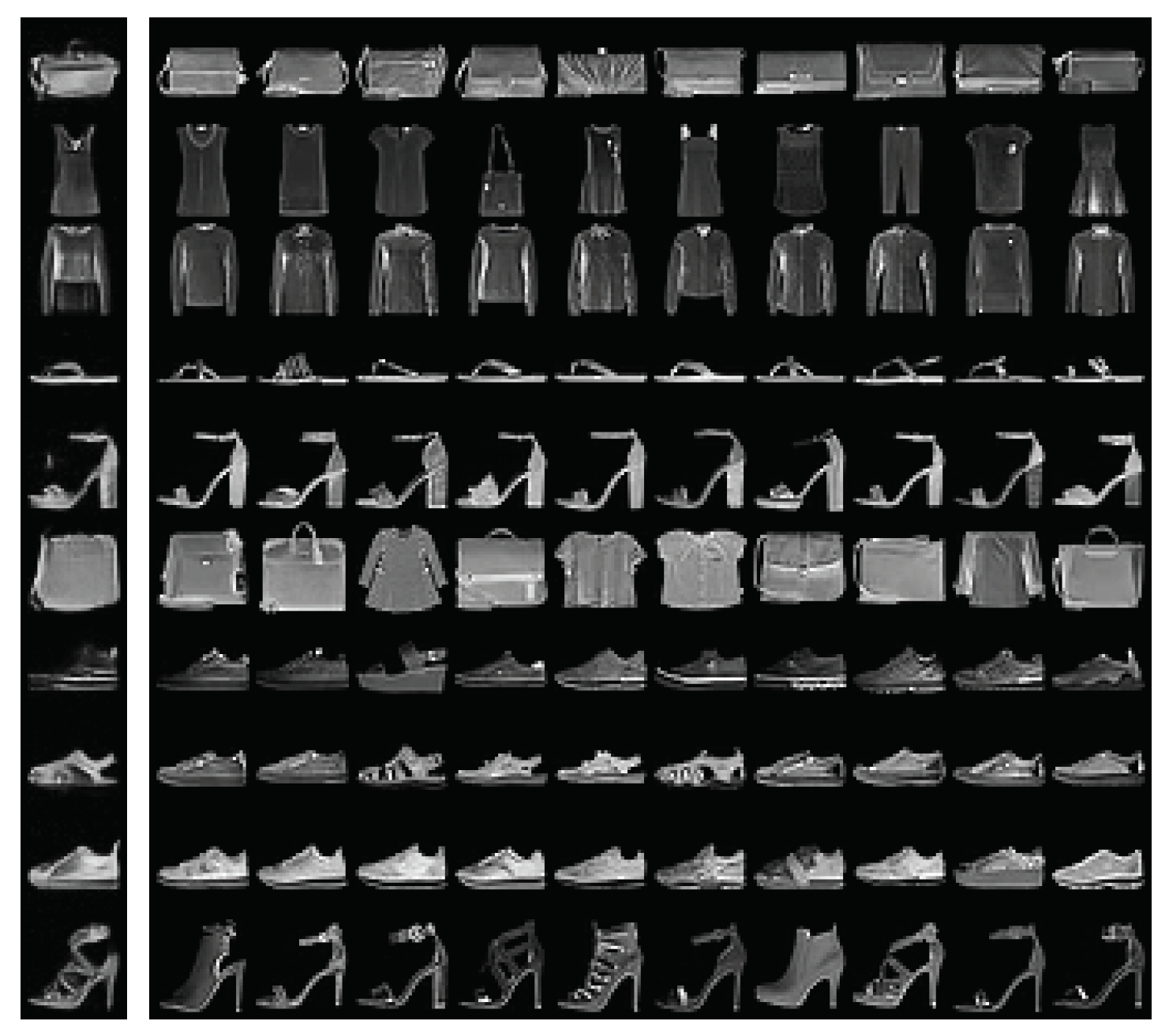
Appendix D. Details on Training and Sampling
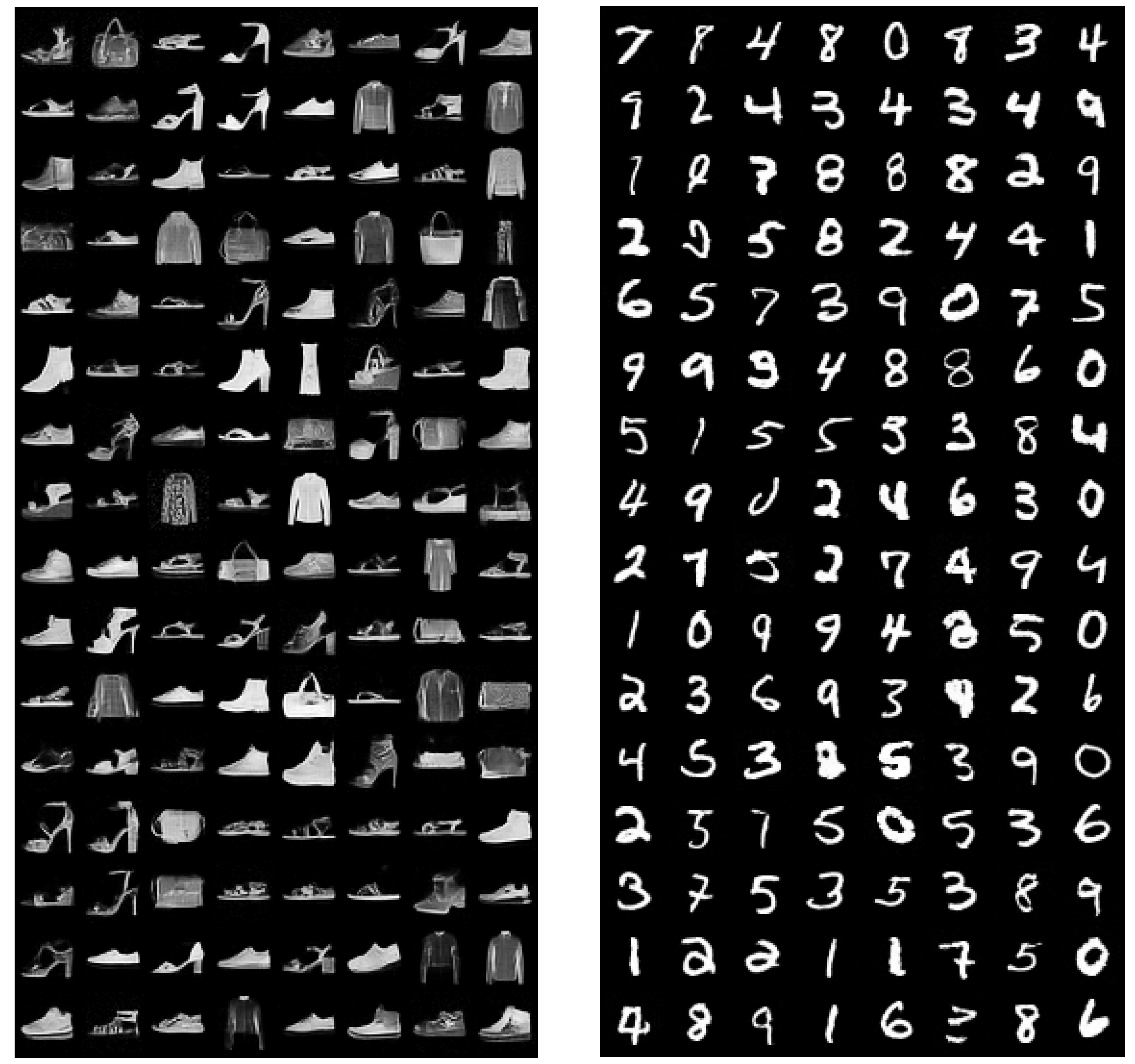
Appendix E. Extended Samples and Inpainting Results



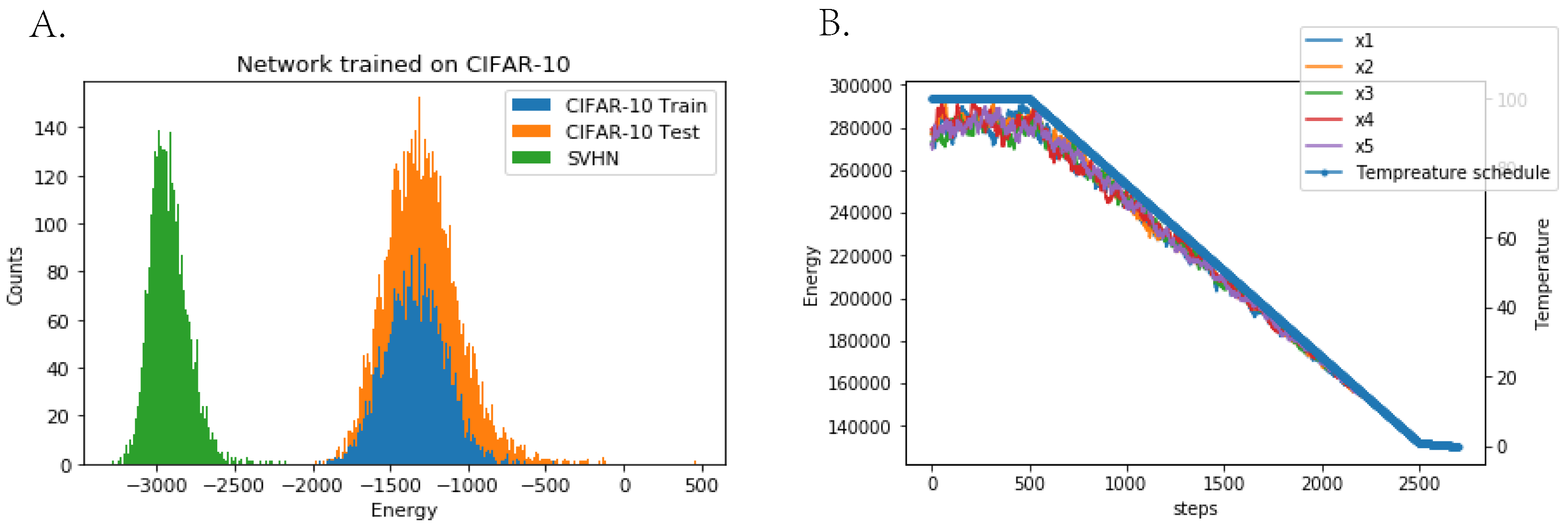
Appendix F. Sampling Process and Energy Value Comparison
References
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. (JMLR) 2010, 11, 12. [Google Scholar]
- Zhai, S.; Cheng, Y.; Lu, W.; Zhang, Z. Deep Structured Energy Based Models for Anomaly Detection. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 16 June 2016. [Google Scholar] [CrossRef]
- Choi, H.; Jang, E.; Alemi, A.A. Waic, but why? Generative ensembles for robust anomaly detection. arXiv 2018, arXiv:1810.01392. [Google Scholar]
- Nijkamp, E.; Hill, M.; Han, T.; Zhu, S.C.; Wu, Y.N. On the Anatomy of MCMC-based Maximum Likelihood Learning of Energy-Based Models. In Proceedings of the Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Du, Y.; Mordatch, I. Implicit generation and generalization in energy-based models. arXiv 2019, arXiv:1903.08689. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- LeCun, Y.; Chopra, S.; Hadsell, R.; Ranzato, M.; Huang, F. A tutorial on energy-based learning. In Predicting Structured Data; Bakir, G., Hofman, T., Schölkopf, B., Smola, A., Eds.; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Ngiam, J.; Chen, Z.; Koh, P.W.; Ng, A.Y. Learning deep energy models. In Proceedings of the International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear Independent Components Estimation. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative flow with invertible 1 × 1 convolutions. In Advances in Neural Information Processing Systems 31 (NeurIPS 2018); Curran Associates, Inc.: Red Hook, NY, USA, 2018. [Google Scholar]
- van den Oord, A.; Kalchbrenner, N.; Kavukcuoglu, K. Pixel Recurrent Neural Networks. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Ostrovski, G.; Dabney, W.; Munos, R. Autoregressive Quantile Networks for Generative Modeling. In Proceedings of the International Conference on Machine Learning (ICML), Vienna, Austria, 10–15 July 2018. [Google Scholar]
- Hinton, G.E. Products of experts. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Bratislava, Slovakia, 14–17 September 1999. [Google Scholar]
- Haarnoja, T.; Tang, H.; Abbeel, P.; Levine, S. Reinforcement learning with deep energy-based policies. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 7–9 August 2017. [Google Scholar]
- Kumar, R.; Goyal, A.; Courville, A.; Bengio, Y. Maximum Entropy Generators for Energy-Based Models. arXiv 2019, arXiv:1901.08508. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In Proceedings of the International Conference on Machine Learning (ICML), Helsinki, Finland, 5–9 July 2008. [Google Scholar]
- Hyvärinen, A. Estimation of non-normalized statistical models by score matching. J. Mach. Learn. Res. (JMLR) 2005, 6, 4. [Google Scholar]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1107. [Google Scholar] [CrossRef]
- Johnson, O.T. Information Theory and the Central Limit Theorem; World Scientific: Singapore, 2004. [Google Scholar]
- DasGupta, A. Asymptotic Theory of Statistics and Probability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Vincent, P. A connection between score matching and denoising autoencoders. Neural Comput. 2011, 23, 1661–1674. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; LeCun, Y. Regularized estimation of image statistics by Score Matching. In Advances in Neural Information Processing Systems 23 (NIPS 2010); Curran Associates, Inc.: Red Hook, NY, USA, 2010. [Google Scholar]
- Drucker, H.; Le Cun, Y. Double backpropagation increasing generalization performance. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Seattle, WA, USA, 8–12 July 1991. [Google Scholar]
- Saremi, S.; Mehrjou, A.; Schölkopf, B.; Hyvärinen, A. Deep energy estimator networks. arXiv 2018, arXiv:1805.08306. [Google Scholar]
- Saremi, S.; Hyvärinen, A. Neural Empirical Bayes. arXiv 2019, arXiv:1903.02334. [Google Scholar]
- Song, Y.; Ermon, S. Generative Modeling by Estimating Gradients of the Data Distribution. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019); Curran Associates, Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, N. Probabilistic non-linear principal component analysis with Gaussian process latent variable models. J. Mach. Learn. Res. (JMLR) 2005, 6, 11. [Google Scholar]
- Vershynin, R. High-Dimensional Probability: An Introduction with Applications in Data Science; Cambridge University Press: Cambridge, UK, 2018; Volume 47. [Google Scholar]
- Tao, T. Topics in Random Matrix Theory; American Mathematical Society: Providence, RI, USA, 2012; Volume 132. [Google Scholar]
- Karklin, Y.; Simoncelli, E.P. Efficient coding of natural images with a population of noisy linear-nonlinear neurons. Adv. Neural Inf. Process. Syst. (NIPS) 2011, 24. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Neal, R.M. Annealed importance sampling. Stat. Comput. 2001, 11, 125–139. [Google Scholar] [CrossRef]
- Jordan, R.; Kinderlehrer, D.; Otto, F. The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal. 1998, 29, 1–17. [Google Scholar] [CrossRef]
- Bellec, G.; Kappel, D.; Maass, W.; Legenstein, R.A. Deep Rewiring: Training very sparse deep networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2015. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on computer vision (ECCV), Amsterdam, The Netherlands, 12–14 October 2016. [Google Scholar]
- Fan, F.; Cong, W.; Wang, G. A new type of neurons for machine learning. Int. J. Numer. Methods Biomed. Eng. (JNMBE) 2018, 34, e2920. [Google Scholar] [CrossRef] [PubMed]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI) 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Barratt, S.; Sharma, R. A note on the inception score. In Proceedings of the International Conference on Machine Learning (ICML), Workshop on Theoretical Foundations and Applications of Deep Generative Models, Stockholm, Sweden, 10 July–15 July 2018. [Google Scholar]
- Neal, R.M. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Salakhutdinov, R.; Murray, I. On the quantitative analysis of deep belief networks. In Proceedings of the International Conference on Machine learning (ICML), Helsinki, Finland, 5–9 July 2008. [Google Scholar]
- Burda, Y.; Grosse, R.B.; Salakhutdinov, R. Accurate and conservative estimates of MRF log-likelihood using reverse annealing. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), San Diego, CA, USA, 9–12 May 2015. [Google Scholar]
- Behrmann, J.; Grathwohl, W.; Chen, R.T.Q.; Duvenaud, D.; Jacobsen, J. Invertible Residual Networks. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Chen, T.Q.; Behrmann, J.; Duvenaud, D.; Jacobsen, J. Residual Flows for Invertible Generative Modeling. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Nalisnick, E.T.; Matsukawa, A.; Teh, Y.W.; Görür, D.; Lakshminarayanan, B. Do Deep Generative Models Know What They Don’t Know? In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Song, Y.; Garg, S.; Shi, J.; Ermon, S. Sliced Score Matching: A Scalable Approach to Density and Score Estimation. In Proceedings of the Conference on Uncertainty in Artificial Intelligence (UAI), Tel Aviv, Israel, 22–26 July 2019. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education Limited: London, UK, 2016. [Google Scholar]


| Model | IS ↑ | FID ↓ | Likelihood | NLL (bits/dim) ↓ |
|---|---|---|---|---|
| iResNet [51] | - | 65.01 | Yes | 3.45 |
| PixelCNN [12] | 4.60 | 65.93 | Yes | 3.14 |
| PixelIQN [13] | 5.29 | 49.46 | Yes | - |
| Residual Flow [52] | - | 46.37 | Yes | 3.28 |
| GLOW [11] | - | 46.90 | Yes | 3.35 |
| EBM (ensemble) [5] | 6.78 | 38.2 | Yes | - 1 |
| MDSM (Ours) | 8.31 | 31.7 | Yes | 7.04 2 |
| SNGAN [53] | 8.22 | 21.7 | No | - |
| NCSN [28] | 8.91 | 25.32 | No | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Y.; Sommer, F.T. Learning Energy-Based Models in High-Dimensional Spaces with Multiscale Denoising-Score Matching. Entropy 2023, 25, 1367. https://doi.org/10.3390/e25101367
Li Z, Chen Y, Sommer FT. Learning Energy-Based Models in High-Dimensional Spaces with Multiscale Denoising-Score Matching. Entropy. 2023; 25(10):1367. https://doi.org/10.3390/e25101367
Chicago/Turabian StyleLi, Zengyi, Yubei Chen, and Friedrich T. Sommer. 2023. "Learning Energy-Based Models in High-Dimensional Spaces with Multiscale Denoising-Score Matching" Entropy 25, no. 10: 1367. https://doi.org/10.3390/e25101367
APA StyleLi, Z., Chen, Y., & Sommer, F. T. (2023). Learning Energy-Based Models in High-Dimensional Spaces with Multiscale Denoising-Score Matching. Entropy, 25(10), 1367. https://doi.org/10.3390/e25101367






