Reconsideration of Temperature Determined by the Excited-State Population Distribution of Hydrogen Atoms Based on Tsallis Entropy and Its Statistics in Hydrogen Plasma in Non-Equilibrium State
Abstract
:1. Introduction
2. Background
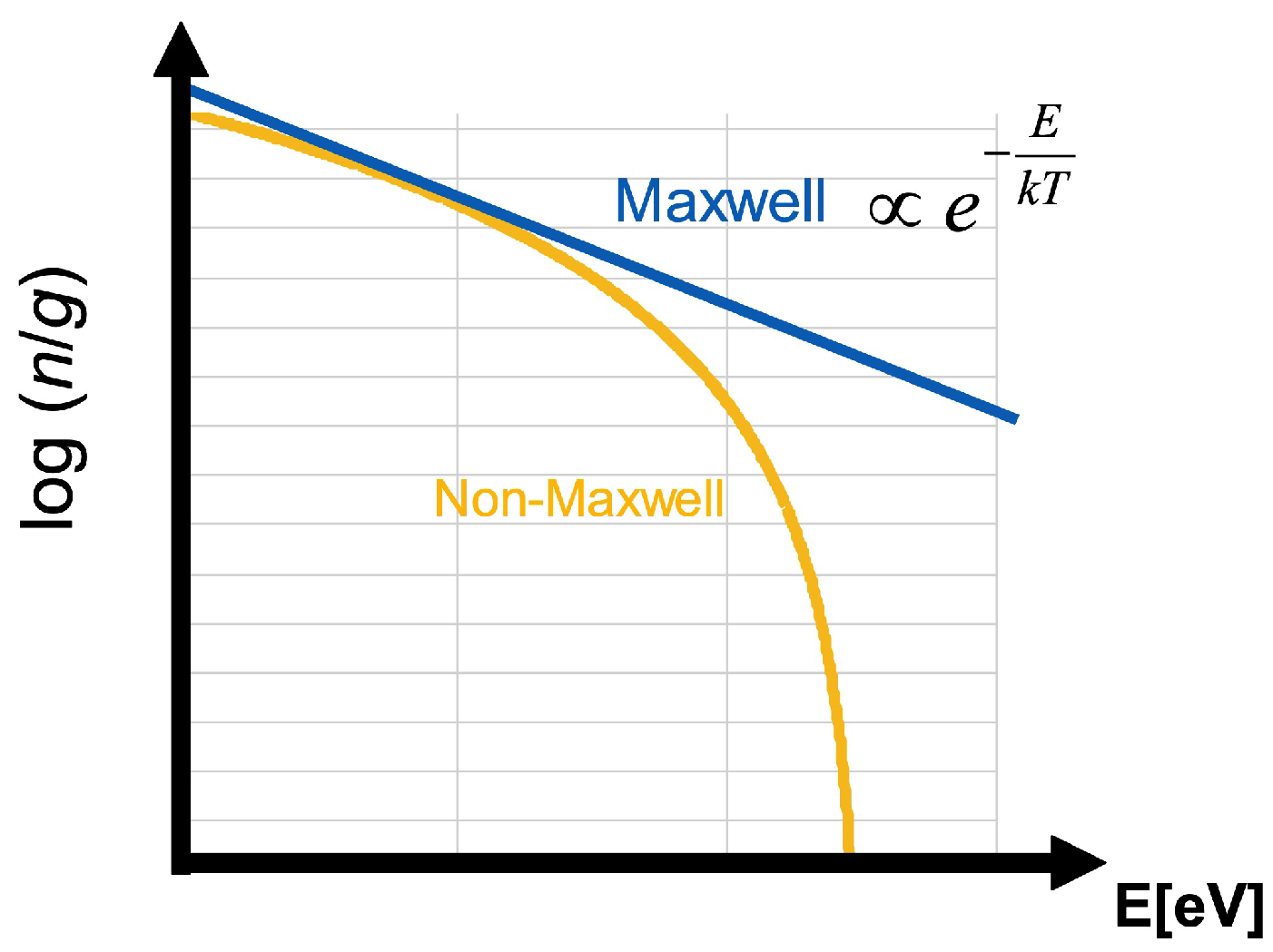
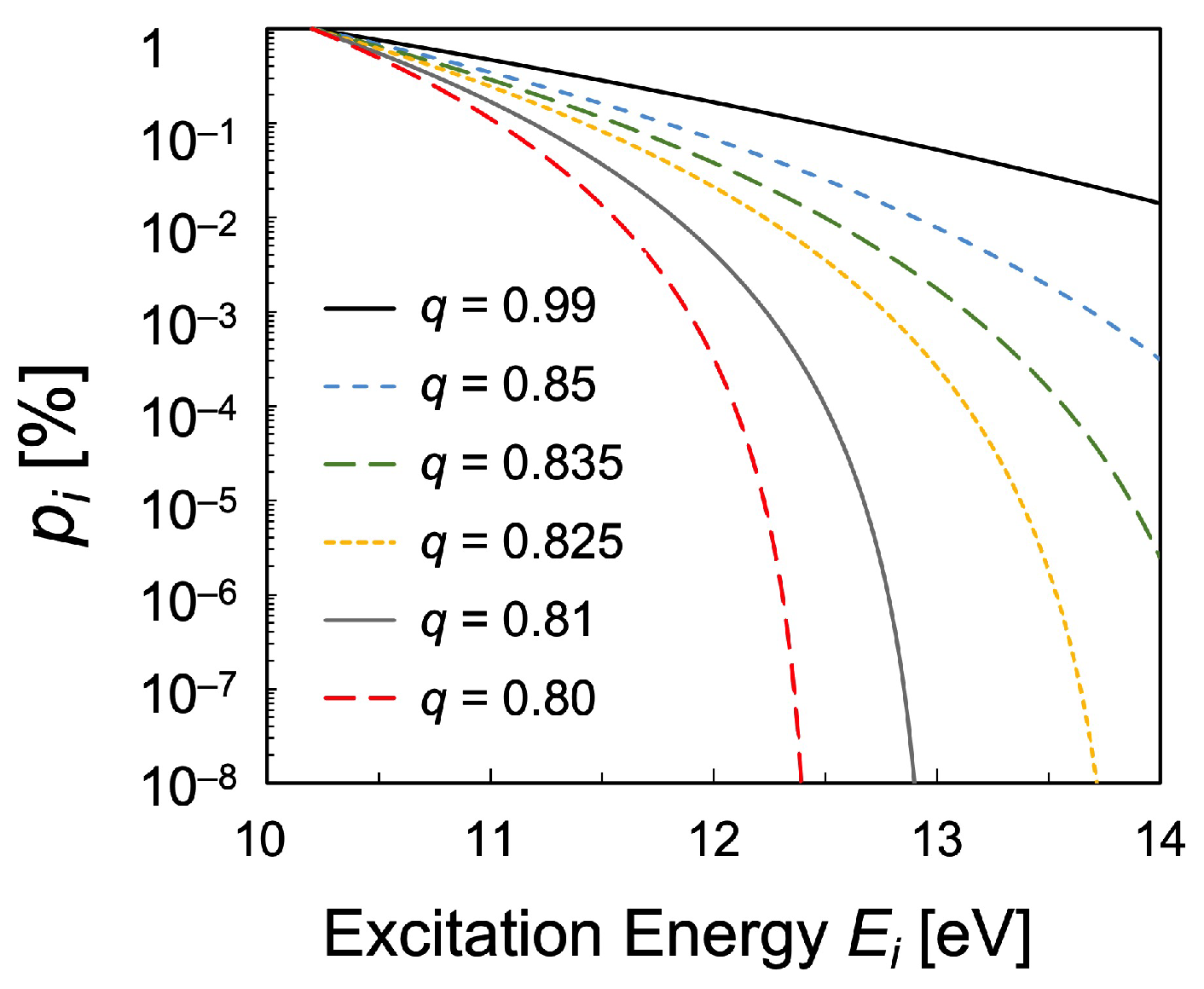
2.1. Tsallis Statistics
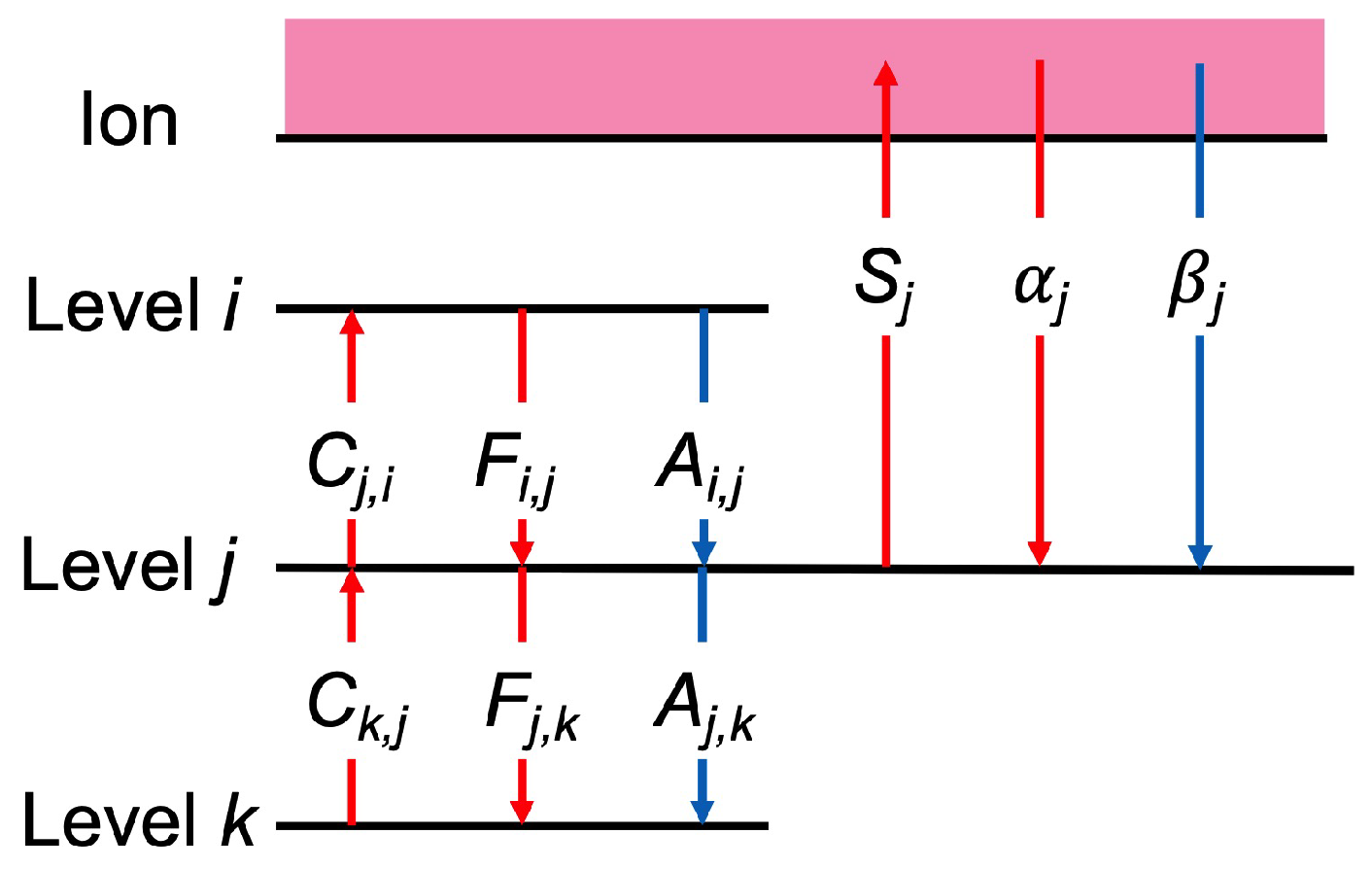
2.2. Collisional Radiative Model (CR-Model)
3. Results and Discussion
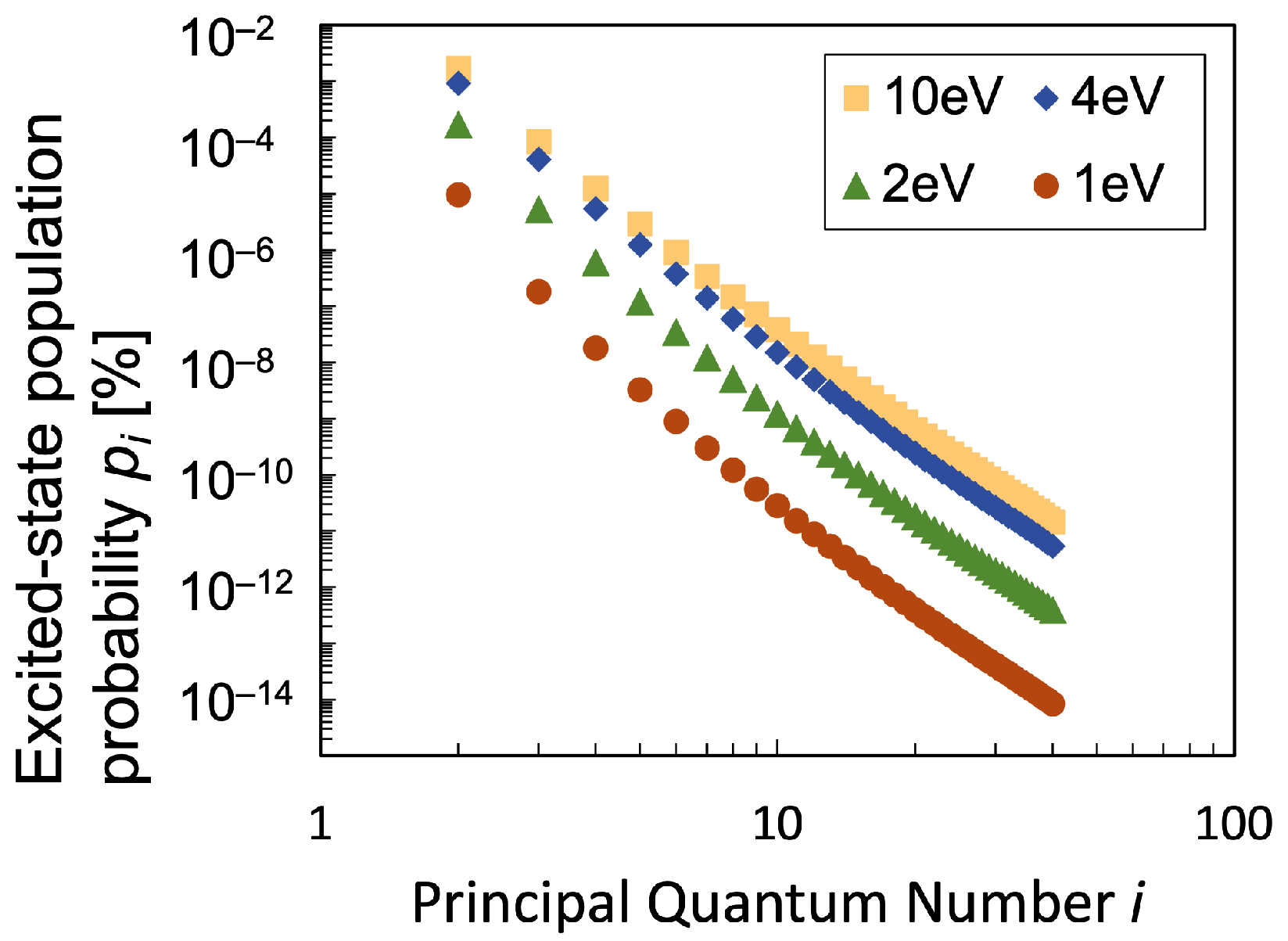
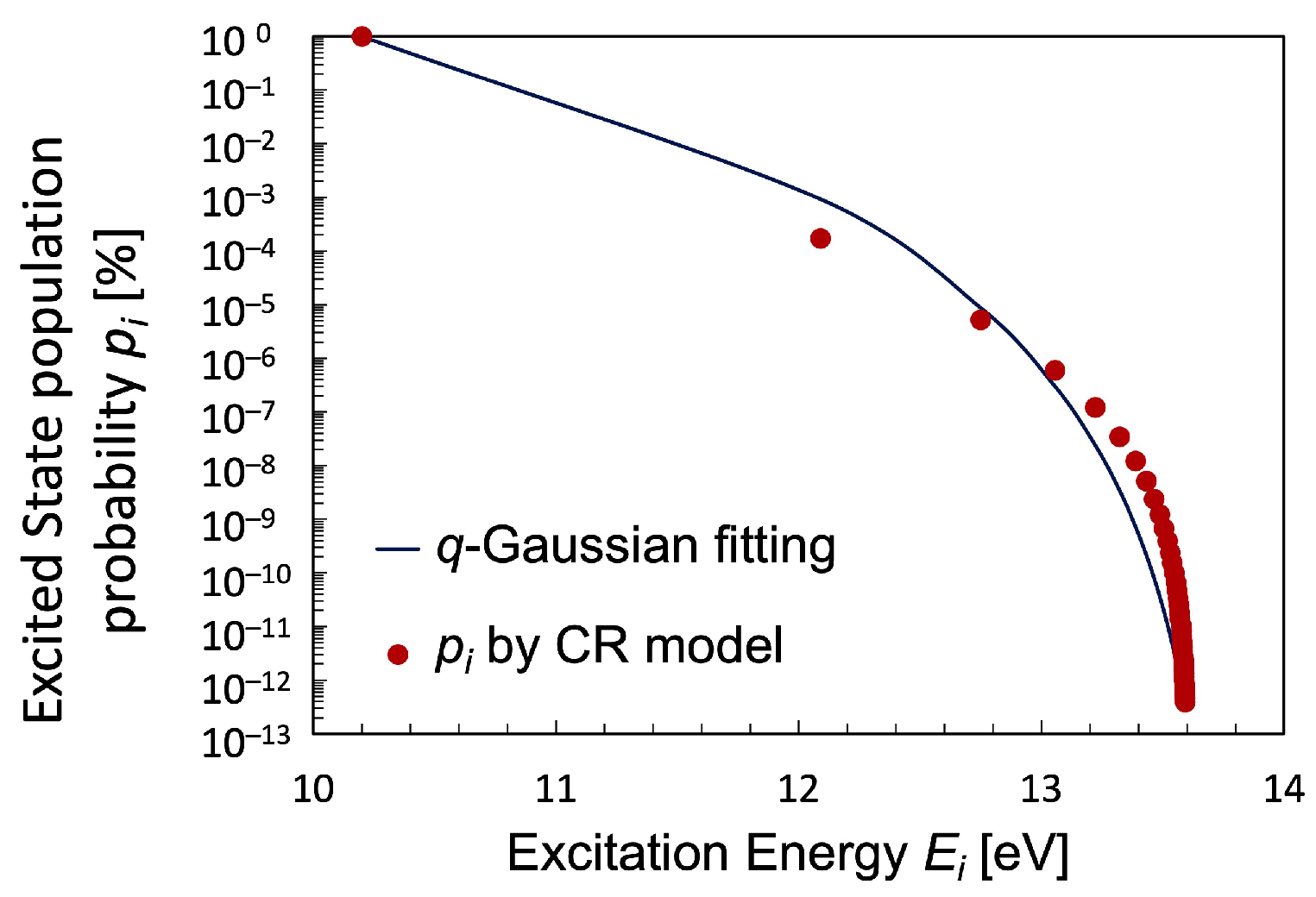
3.1. The Excited State Population Densities
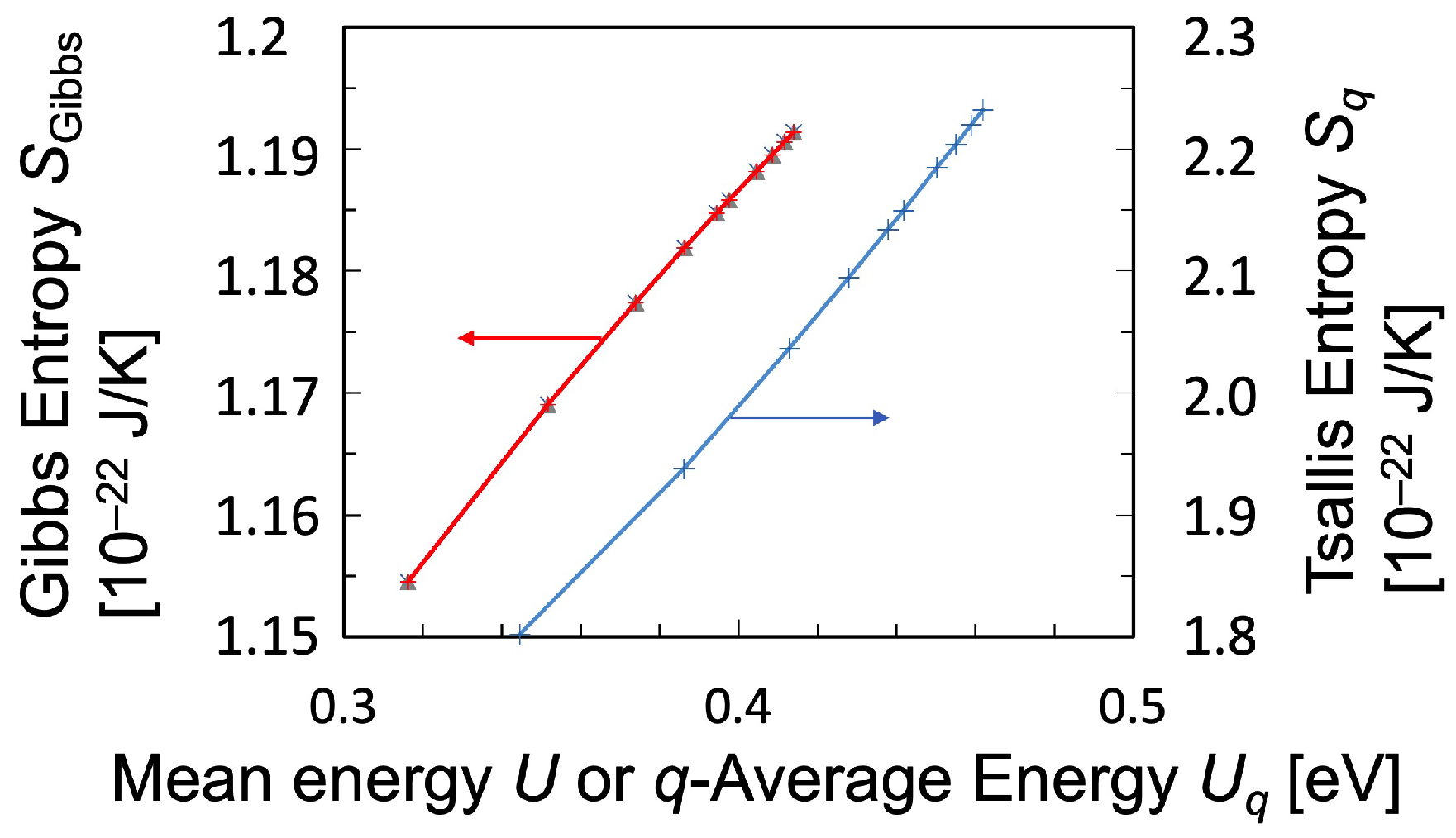
3.2. Entropy
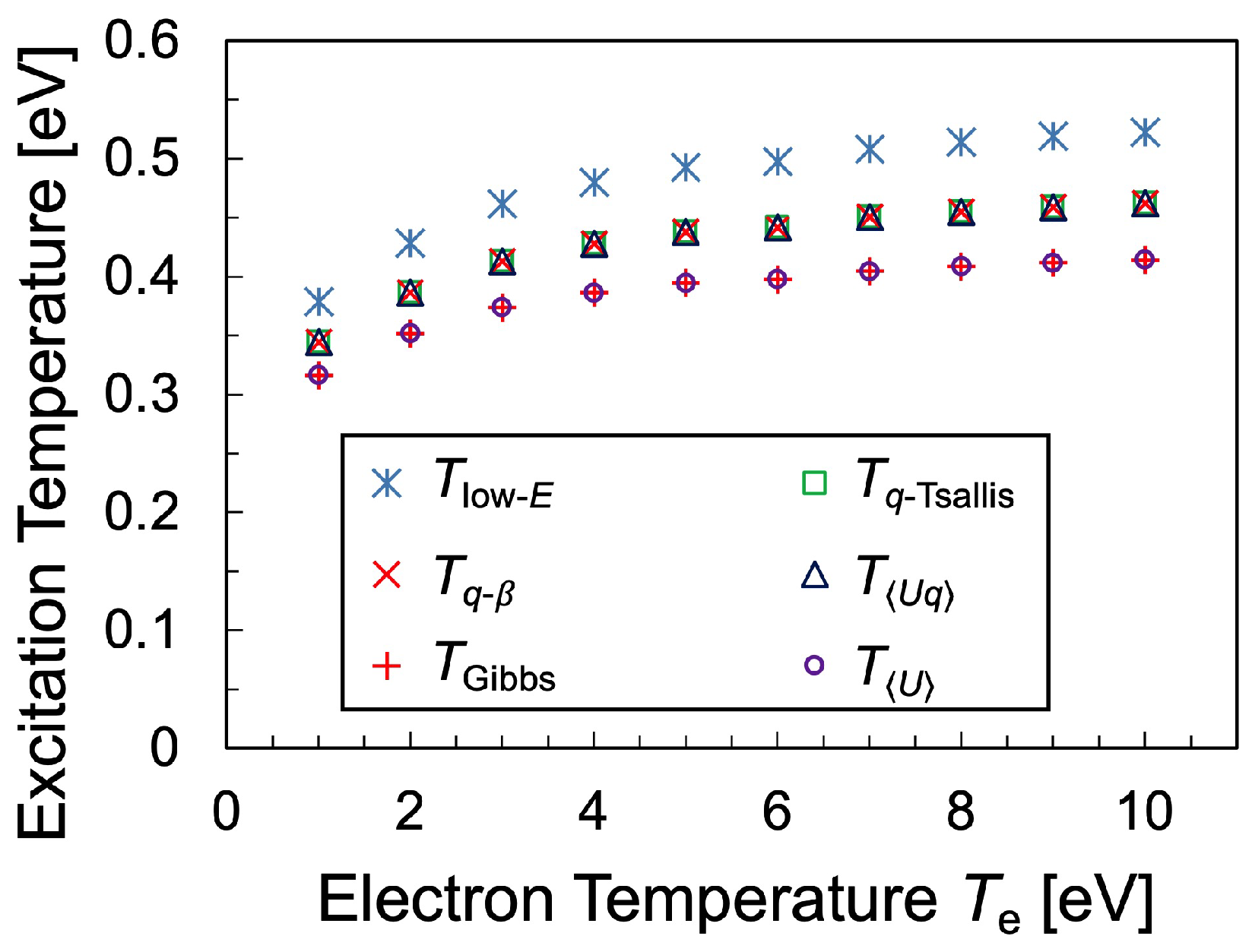
3.3. Temperature Determined on Statistical Physics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voráč, J.; Lukáš, K.; Synek, P. Deducing rotational quantum-state distributions from overlapping molecular spectra. Rev. Sci. Instrum. 2019, 90, 123102. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C.; Kroemer, H. Thermal Physics, 2nd ed.; Freeman & Co.: New York, NY, USA, 1980. [Google Scholar]
- Akatsuka, H.; Suzuki, M. Stationary population inversion of hydrogen in an arc-heated magnetically trapped expanding hydrogen-helium plasma jet. Phys. Rev. E 1994, 49, 1534–1544. [Google Scholar] [CrossRef] [PubMed]
- Akatsuka, H. Optical Emission Spectroscopic (OES) analysis for diagnostics of electron density and temperature in nonequilibrium argon plasma based on collisional-radiative model. Adv. Phys.-X 2019, 4, 257–281. [Google Scholar]
- McNamara, S.A.M.; Asunta, O.; Bland, J.; Buxton, P.F.; Colgan, C.; Dnestrovskii, A.; Gemmell, M.; Gryaznevich, M.; Hoffman, D.; Janky, F. Achievement of ion temperatures in excess of 100 million degrees Kelvin in the compact high-field spherical tokamak ST40. Nucl. Fusion 2023, 63, 054002. [Google Scholar] [CrossRef]
- Song, T.; Moreau, P.; Aichelin, J.; Bratkovskaya, E. Exploring non-equilibrium quark-gluon plasma effects on charm transport coefficients. Phys. Rev. C 2020, 101, 044901. [Google Scholar] [CrossRef]
- Álvarez, R.; Cotrino, J.; Palmero, A. On the kinetic and thermodynamic electron temperatures in non-thermal plasmas. Europhys. Lett. 2014, 105, 15001. [Google Scholar] [CrossRef]
- Akatsuka, H.; Tanaka, Y. Discussion on Electron Temperature of Gas-Discharge Plasma with Non-Maxwellian Electron Energy Distribution Function Based on Entropy and Statistical Physics. Entropy 2023, 25, 276. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Nouno, T.; Suyari, H. Sedimentation model and Tsallis statistics. RIMS Kokyuroku 2003, 1340, 35–44. [Google Scholar]
- Wilk, G.; Włodarczyk, Z. Interpretation of the nonextensivity parameter q in some applications of Tsallis statistics and Lévy distributions. Phys. Rev. Lett. 2000, 84, 2770. [Google Scholar] [CrossRef]
- Ourabah, K.; Gougam, L.A.; Tribeche, M. Nonthermal and suprathermal distributions as a consequence of superstatistics. Phys. Rev. E 2015, 91, 012133. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C.; Anjos, J.C.; Borges, E.P. Fluxes of cosmic rays: A delicately balanced stationary state. Phys. Lett. A 2003, 310, 372–376. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Iliopoulos, A.C.; Tsoutsouras, V.G.; Sarafopoulos, D.V.; Sfiris, D.S.; Karakatsanis, L.P.; Pavlos, E.G. First and second order non-equilibrium phase transition and evidence for non-extensive Tsallis statistics in Earth’s magnetosphere. Physica A 2011, 390, 2819–2839. [Google Scholar] [CrossRef]
- Boghosian, B.M. Thermodynamic description of the relaxation of two-dimensional turbulence using Tsallis statistics. Phys. Rev. E 1996, 53, 4754–4763. [Google Scholar] [CrossRef]
- Beck, C.; Lewis, G.S.; Swinney, H.L. Measuring nonextensitivity parameters in a turbulent Couette-Taylor flow. Phys. Rev. E 2001, 63, 035303. [Google Scholar] [CrossRef]
- Bediaga, I.; Curado, E.M.F.; Miranda, J. A nonextensive thermodynamical equilibrium approach in e+e−→ hadrons. Physica A 2000, 286, 156–163. [Google Scholar] [CrossRef]
- Tsallis, C. Black hole entropy: A closer look. Entropy 2019, 22, 17. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Faraoni, V. From nonextensive statistics and black hole entropy to the holographic dark universe. Phys. Rev. D 2022, 105, 044042. [Google Scholar] [CrossRef]
- Guha, A.; Das, P.K. An extensive study of Bose-Einstein condensation in liquid helium using Tsallis statistics. Phys. A Stat. Mech. Its Appl. 2018, 497, 272–284. [Google Scholar] [CrossRef]
- Enciso, L.; Gun, M.; Ruiz, M.S.; Razzitte, A.C. Entropy in multifractal non equilibrium structures of dielectric breakdown. J. Stat. Mech. 2019, 2019, 094011. [Google Scholar] [CrossRef]
- Reis, J.L., Jr.; Amorim, J.; Dal Pino, A., Jr. Rotational temperature measurements in molecular plasmas using nonadditive Tsallis statistics. Physica A 2014, 404, 192–199. [Google Scholar] [CrossRef]
- Pressé, S.; Lee, J.; Dill, K.A. Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 2013, 85, 1115–1141. [Google Scholar] [CrossRef]
- Suyari, H. The unique non self-referential q-canonical distribution and the physical temperature derived from the maximum entropy principle in Tsallis statistics. Prog. Theor. Phys. Suppl. 2006, 162, 79–86. [Google Scholar] [CrossRef]
- Prato, D.; Tsallis, C. Nonextensive foundation of Lévy distributions. Phys. Rev. E 1999, 60, 2398–2401. [Google Scholar] [CrossRef] [PubMed]
- Abe, S.; Martínez, S.; Pennini, F.; Plastino, A. Nonextensive thermodynamic relations. Phys. Lett. A 2001, 281, 126–130. [Google Scholar] [CrossRef]
- Fujimoto, T. Kinetics of ionization-recombination of a plasma and population density of excited ions. I. Equilibrium plasma. J. Phys. Soc. Jpn. 1979, 47, 265–272. [Google Scholar] [CrossRef]
- Fujimoto, T. Kinetics of ionization-recombination of a plasma and population density of excited ions. II. Ionizing plasma. J. Phys. Soc. Jpn. 1979, 47, 273–281. [Google Scholar] [CrossRef]
- Fujimoto, T. Kinetics of ionization-recombination of a plasma and population density of excited ions. III. Recombining plasma-high-temperature case. J. Phys. Soc. Jpn. 1980, 49, 1561–1568. [Google Scholar] [CrossRef]
- Fujimoto, T. Kinetics of ionization-recombination of a plasma and population density of excited ions. IV. Recombining plasma-low-temperature case. J. Phys. Soc. Jpn. 1980, 49, 1569–1576. [Google Scholar] [CrossRef]
- Fujimoto, T. Kinetics of ionization-recombination of a plasma and population density of excited ions. V. Ionization-recombination and equilibrium plasma. J. Phys. Soc. Jpn. 1985, 54, 2905–2914. [Google Scholar] [CrossRef]
- Sawada, K.; Fujimoto, T. Temporal relaxation of excited-level populations of atoms and ions in a plasma: Validity range of the quasi-steady-state solution of coupled rate equations. Phys. Rev. E 1994, 49, 5565–5573. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, T. A collisional radiative model for helium and its application to a discharge plasma. J. Quant. Spectrosc. Radiat. Transfer. 1979, 21, 439–455. [Google Scholar] [CrossRef]
- Shimizu, Y.; Kittaka, Y.; Nezu, A.; Matsuura, H.; Akatsuka, H. Excited state distributions of hydrogen atoms in the microwave discharge hydrogen plasma and the effect of electron energy probabilistic function. bIEEE Trans. Plasma Sci. 2015, 43, 1758–1768. [Google Scholar] [CrossRef]
- Cooper, J. Plasma spectroscopy. Rep. Prog. Phys. 1966, 29, 35–130. [Google Scholar] [CrossRef]
- Suyari, H. Mathematical structures derived from the q-multinomial coefficient in Tsallis statistics. Physica A 2006, 368, 63–82. [Google Scholar] [CrossRef]

| 1: Initialize | |
| 2: Iterate | until convergence |
| [eV] | q | |||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kikuchi, K.; Akatsuka, H. Reconsideration of Temperature Determined by the Excited-State Population Distribution of Hydrogen Atoms Based on Tsallis Entropy and Its Statistics in Hydrogen Plasma in Non-Equilibrium State. Entropy 2023, 25, 1400. https://doi.org/10.3390/e25101400
Kikuchi K, Akatsuka H. Reconsideration of Temperature Determined by the Excited-State Population Distribution of Hydrogen Atoms Based on Tsallis Entropy and Its Statistics in Hydrogen Plasma in Non-Equilibrium State. Entropy. 2023; 25(10):1400. https://doi.org/10.3390/e25101400
Chicago/Turabian StyleKikuchi, Koji, and Hiroshi Akatsuka. 2023. "Reconsideration of Temperature Determined by the Excited-State Population Distribution of Hydrogen Atoms Based on Tsallis Entropy and Its Statistics in Hydrogen Plasma in Non-Equilibrium State" Entropy 25, no. 10: 1400. https://doi.org/10.3390/e25101400
APA StyleKikuchi, K., & Akatsuka, H. (2023). Reconsideration of Temperature Determined by the Excited-State Population Distribution of Hydrogen Atoms Based on Tsallis Entropy and Its Statistics in Hydrogen Plasma in Non-Equilibrium State. Entropy, 25(10), 1400. https://doi.org/10.3390/e25101400






