Hypernetwork Link Prediction Method Based on Fusion of Topology and Attribute Features
Abstract
:1. Introduction
- We propose a general link prediction framework for the attribute hypernetwork, which integrates the structure and attribute characteristics of entities. Through a dual channel encoder, the interaction between network structure and node attributes is captured, and adopting hypergraph neural networks learns high-order interactions of nodes and attributes so that node information can be effectively transmitted through shared attributes.
- We introduce the node level-attention mechanism in structure encoding to model the importance of node neighbors to capture the neighborhood information of nodes; We introduce the hyperedge-level attention mechanism in the joint embedding module to consider the influence of different nodes in each hyperedge to screen the key nodes from a large amount of information. In this way, high-quality node embedding and hyperedge embedding can be obtained.
- Numerous experiments on six datasets have verified the efficiency of the TA-HLP model in link prediction. Compared with the latest hyperlink prediction model [2,10,14,18,19,20,21,22,23,24,25], the TA-HLP model has significantly improved under the AUC and recall indicators. At the same time, ablation experiments have also proved the effectiveness of the joint encode and the attention mechanisms.
2. Related Work
3. Notations and Problem Statement
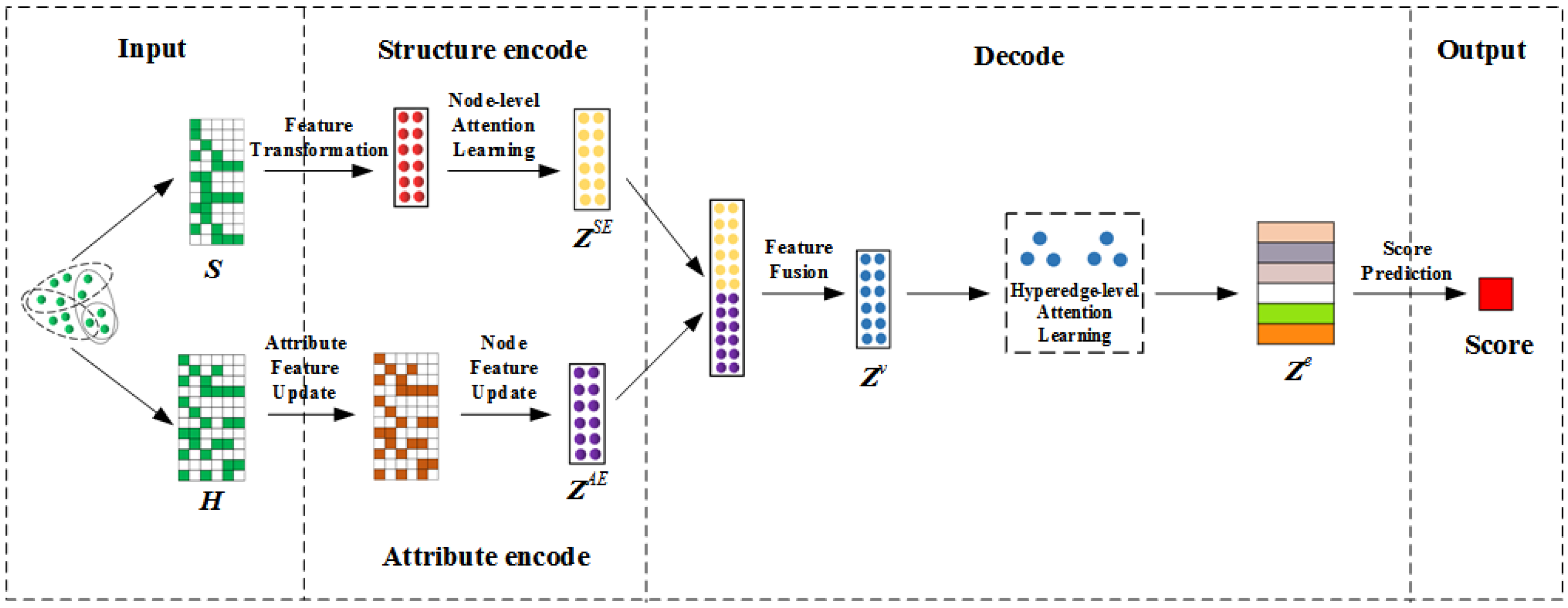
4. Proposed Method
- Based on the topological relationship, the structure encoder adopts a node-level attention mechanism to learn neighbors with different weights, so as to obtain the structural feature embedding of nodes.
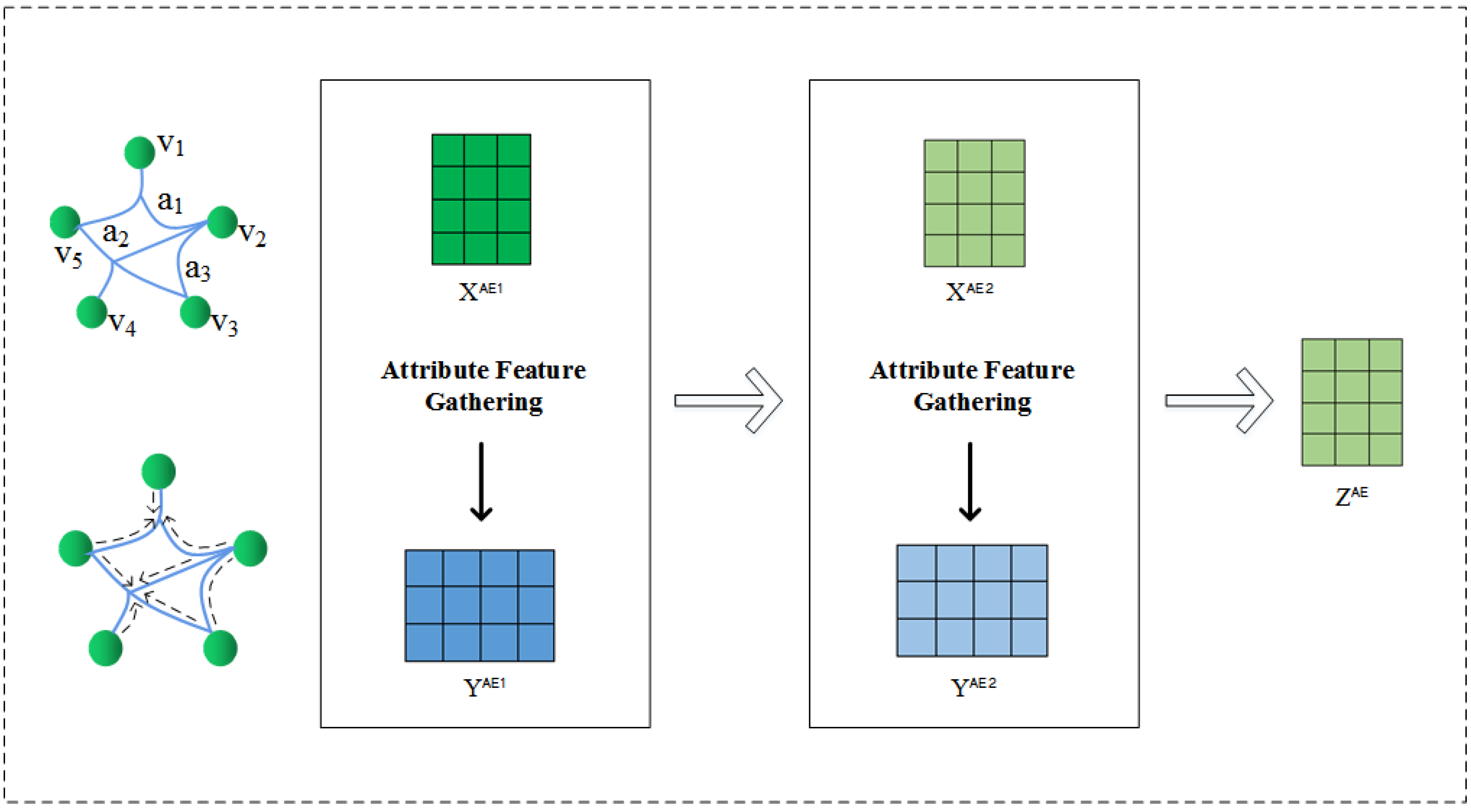
- Based on attribute information, the attribute encoder uses hypergraph neural network to capture the potential association between entities and attributes to obtain the attribute feature embedding of nodes.
- The decoder combines the structure and attribute features in two independent semantic spaces, and then adopts the hyperedge-level attention mechanism to learn the importance of different nodes in each hyperedge. After the weight information is aggregated, the hyperedge is embedded.
- Input hyperedge embedding and learn a hyperlink scoring function to judge the hyperedges that have more remarkable similarity with the original network’s mode and behavior at the two levels of network structure and content attributes, i.e., the possible missing hyperedges of the original network.
4.1. Encode
4.1.1. Structure Encoder
4.1.2. Attribute Encoder
4.2. Decode
4.2.1. Feature Fusion
4.2.2. Hyperedge Embedding
4.2.3. Hyperlink Prediction
4.3. Loss Function
| Algorithm 1 TA-HLP. |
| Input:: Structure incidence matrix, : Attribute incidence matrix, X: Attribute characteristic matrix, T: Max epochs |
| Output:: Embedded representation of nodes, : Embedded representation of hyperedges |
|
5. Experiment
5.1. Datasets
5.2. Baseline Methods
5.3. Evaluation Indicators
5.4. Experimental Design and Analysis
- From the overall observation, compared with all baseline methods, TA-HLP has achieved the most significant effect on all indicators under different datasets. The AUC score increased by 5–10 percentage points, and the recall increased by 5–7 percentage points. The superiority of the model in link prediction performance is verified. TA-HLP can enhance the expression learning ability of the original network and achieve more comprehensive and accurate prediction.
- DeepWalk, LINE, and node2vec are all traditional complex network embedding methods. To predict hyperlinks, we calculate the average value of pairwise similarity to represent the similarity of the entire hyperedge, neither maintaining the irresolvability of the hyperedge nor ignoring the content attributes of the node. Although CMM and DHNE use hypergraphs to model the relationship between nodes that transcend pairwise connections, they ignore the attribute information of nodes. Therefore, the performance of these two methods on data sets is poor, which proves that both higher-order structure and attribute modalities are necessary for link prediction. Their complementary relationship can enhance the depth of network embedding and better characterize network information. C3MM believes that the newly generated hyperlinks in the network are more likely to have evolved from the recently closed cliques, mainly from the perspective of temporal evolution. Similarly, there is no systematic learning for the attribute information of data, so our data is only slightly improved compared with the CMM method.
- NHP, HGNN, HyperGCN, Hyper-SAGNN, and Hyper-Atten all combine the deep neural network, and also consider the network structure and attribute characteristics. The experimental results also prove their effectiveness. However, in the modeling process, they simply use the attribute characteristics of the convolutional layer aggregation node. They do not fully use the potential higher-order interaction between entities and attributes, resulting in poor prediction performance. To fully mine the association between nodes and attributes, this model adopts a hypergraph structure to model the correlation between nodes and attributes. Each attribute is defined as a hyperedge and nodes with the same attribute form the adjacency relationship. At the same time, the deep association between nodes and attributes is captured based on the “node attribute node” transformation. We also introduce a two-layer attention mechanism for reinforcement learning of important nodes, so the experimental results of TA-HLP are obviously better than other algorithms.
- In addition, the Hyper-Atten model has the best performance among all baseline methods. This may be because the Hyper-Atten model additionally applies an attention module to the incidence matrix to update the degree of association between nodes in real-time. It can be seen that more attention to important content is effective. However, compared with the Hyper-Atten model, our model can distinguish the importance of different levels in a more fine-grained way. It measures the impact of different components on network embedding from the perspectives of nodes and hyperedges, respectively, so that the embedded representation of the network can more truly restore the connotation of structure and semantics, which is also an important reason for the significant improvement of our model performance.
5.5. Ablation Experiment
5.6. Attention Mechanism Analysis
5.7. Parameter Sensitivity Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoon, S.E.; Song, H.; Shin, K.; Yi, Y. How Much and When Do We Need Higher-order Information in Hypergraphs? A Case Study on Hyperedge Prediction. arXiv 2020, arXiv:2001.11181. [Google Scholar]
- Zhang, M.; Cui, Z.; Jiang, S.; Chen, Y. Beyond Link Prediction: Predicting Hyperlinks in Adjacency Space. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Karantaidis, G.; Sarridis, I.; Kotropoulos, C. Adaptive hypergraph learning with multi-stage optimizations for image and tag recommendation. Signal Process. Image Commun. 2021, 97, 116367. [Google Scholar] [CrossRef]
- Fatemi, B.; Taslakian, P.; Vazquez, D.; Poole, D. Knowledge Hypergraphs: Prediction Beyond Binary Relations. arXiv 2019, arXiv:1906.00137. [Google Scholar]
- Guo, Z.; Zhao, J.; Jiao, L.; Liu, X.; Liu, F. A universal quaternion hypergraph network for multimodal video question answering. IEEE Trans. Multimed. 2021, 97, 116367. [Google Scholar] [CrossRef]
- Lande, D.; Fu, M.; Guo, W.; Balagura, I.; Gorbov, I.; Yang, H. Link prediction of scientific collaboration networks based on information retrieval. World Wide Web 2020, 23, 2239–2257. [Google Scholar] [CrossRef]
- Nasiri, E.; Berahmand, K.; Rostami, M.; Dabiri, M. A novel link prediction algorithm for protein-protein interaction networks by attributed graph embedding. Comput. Biol. Med. 2021, 137, 104772. [Google Scholar] [CrossRef] [PubMed]
- Greibe, P. Accident prediction models for urban roads. Accid. Anal. Prev. 2003, 35, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Hou, C.; Yao, X. Learning topological representation for networks via hierarchical sampling. In Proceedings of the International Joint Conference on Neural Network, Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Wang, X.; Chai, Y.; Li, H.; Wu, D. Link prediction in heterogeneous information networks: An improved deep graph convolution approach. Decis. Support Syst. 2021, 141, 113448. [Google Scholar] [CrossRef]
- Chen, H.; Yin, H.; Wang, W.; Wang, H.; Nguyen, Q.V.H.; Li, X. PME: Projected metric embedding on heterogeneous networks for link prediction. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery &Data Mining, London, UK, 19–23 August 2018; pp. 1177–1186. [Google Scholar]
- Zhang, M.; Cui, Z.; Jiang, S.; Chen, Y. Hyper2vec: Biased random walk for hyper-network embedding. In Proceedings of the International Conference on Database Systems for Advanced Applications, Chiang Mai, Thailand, 22–25 April 2019; pp. 273–277. [Google Scholar]
- Tu, K.; Cui, P.; Wang, X.; Wang, F.; Zhu, W. Structural Deep Embedding for Hyper-Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Huang, J.; Chen, C.; Ye, F.; Wu, J.; Zheng, Z.; Ling, G. Modeling multi-way relations with hypergraph embedding. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, New York, NY, USA, 22–26 October 2018. [Google Scholar]
- Li, D.; Xu, Z.; Li, S.; Sun, X. Link prediction in social networks based on hypergraph. In Proceedings of the 22nd International Conference on World Wide Web, New York, NY, USA, 13–17 May 2013. [Google Scholar]
- Vaida, M.; Purcell, K. Hypergraph link prediction: Learning drug interaction networks embeddings. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 16–19 December 2019; pp. 1860–1865. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge discovery and data mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Sharma, G.; Patil, P.; Murty, M.N. C3MM: Clique-Closure based Hyperlink Prediction. In Proceedings of the International Joint Conference on Artificial Intelligence, Yokohame, Japan, 7–15 January 2021. [Google Scholar]
- Yadati, N.; Nitin, V.; Nimishakavi, M.; Yadav, P.; Louis, A.; Talukdar, P. Link prediction in hypergraphs using graph convolutional networks. In Proceedings of the International Conference on Learning Representations, Ernest, New Orleans, LA, USA, 6–9 November 2019; pp. 449–458. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 27–28 January 2015; pp. 3558–3565. [Google Scholar]
- Yadati, N.; Nimishakavi, M.; Yadav, P.; Nitin, V.; Louis, A.; Talukdar, P. HyperGCN: A New Method For Training Graph Convolutional Networks on Hypergraphs. arXiv 2018, arXiv:1809.02589. [Google Scholar]
- Zhang, R.; Zou, Y.; Ma, J. Hyper-SAGNN: A self-attention based graph neural network for hypergraphs. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26 April–1 May 2020. [Google Scholar]
- Bai, S.; Zhang, F.; Torr, P. Hypergraph convolution and hypergraph attention. Pattern Recognit. 2021, 110, 107637. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. The link prediction problem for social networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, New Orleans, LA, USA, 3–8 November 2003; pp. 556–559. [Google Scholar]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef] [Green Version]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Davidson, T.R.; Falorsi, L.; De Cao, N.; Kipf, T.; Tomczak, J.M. Hyperspherical variational auto-encoders. arXiv 2016, arXiv:1804.00891. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
- Huang, J.; Liu, X.; Song, Y. Hyper-path-based representation learning for hyper-networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 449–458. [Google Scholar]
- Luo, X.; Peng, J.; Liang, J. Directed hypergraph attention network for traffic forecasting. IET Intell. Transp. Syst. 2022, 16, 85–98. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, C.; Hu, L.; Liu, Z. TRHINE: Relation Structure-Aware Heterogeneous Information Network Embedding. IEEE Trans. Knowl. Data Eng. 2022, 34, 433–447. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Gallagher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]




| Notation | Description |
|---|---|
| Attribute hypernetwork. | |
| V | A set of nodes. |
| E | A set of hyperedges. |
| X | An attribute characteristic matrix. |
| m | The number of nodes. |
| n | The number of hyperedges. |
| d | The dimension of node attributes. |
| Structure incidence matrix. | |
| Attribute incidence matrix. | |
| Structural embedding of nodes. | |
| Attribute embedding of nodes. | |
| Embedding of nodes after fusion. | |
| Embedding of hyperedges. |
| Node | Hyperedge | Attribute | |
|---|---|---|---|
| CC | 2708 | 1072 | 1433 |
| CD | 41,302 | 22,363 | 1425 |
| CCI | 3327 | 1079 | 3703 |
| CP | 19,717 | 7963 | 500 |
| OR | 16,293 | 11,433 | 298 |
| YR | 50,758 | 679,302 | 1862 |
| CC | CD | CCI | CP | OR | YR | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC | R@k | AUC | R@k | AUC | R@k | AUC | R@k | AUC | R@k | AUC | R@k | |
| DeepWalk | 0.53 | 0.23 | 0.57 | 0.23 | 0.54 | 0.21 | 0.54 | 0.24 | 0.56 | 0.26 | 0.55 | 0.26 |
| LINE | 0.56 | 0.25 | 0.52 | 0.25 | 0.55 | 0.24 | 0.58 | 0.22 | 0.61 | 0.24 | 0.54 | 0.25 |
| Node2vec | 0.55 | 0.25 | 0.58 | 0.25 | 0.58 | 0.23 | 0.62 | 0.26 | 0.57 | 0.27 | 0.58 | 0.28 |
| CMM | 0.64 | 0.22 | 0.67 | 0.27 | 0.64 | 0.31 | 0.63 | 0.29 | 0.66 | 0.33 | 0.68 | 0.29 |
| C3MM | 0.66 | 0.26 | 0.68 | 0.26 | 0.64 | 0.32 | 0.67 | 0.32 | 0.68 | 0.27 | 0.71 | 0.32 |
| DHNE | 0.62 | 0.29 | 0.65 | 0.26 | 0.61 | 0.31 | 0.63 | 0.30 | 0.62 | 0.31 | 0.64 | 0.30 |
| NHP-U | 0.69 | 0.28 | 0.68 | 0.29 | 0.71 | 0.32 | 0.68 | 0.31 | 0.70 | 0.29 | 0.73 | 0.33 |
| HGNN | 0.68 | 0.27 | 0.69 | 0.23 | 0.69 | 0.29 | 0.69 | 0.32 | 0.71 | 0.27 | 0.71 | 0.33 |
| HyperGCN | 0.66 | 0.28 | 0.70 | 0.28 | 0.67 | 0.30 | 0.70 | 0.31 | 0.69 | 0.31 | 0.66 | 0.32 |
| Hyper-SAGNN | 0.63 | 0.26 | 0.68 | 0.24 | 0.64 | 0.28 | 0.68 | 0.30 | 0.65 | 0.28 | 0.65 | 0.31 |
| Hyper-Atten | 0.68 | 0.30 | 0.70 | 0.31 | 0.71 | 0.34 | 0.70 | 0.31 | 0.71 | 0.32 | 0.73 | 0.35 |
| TA-HLP | 0.78 | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Ma, H.; Liu, S.; Wang, K. Hypernetwork Link Prediction Method Based on Fusion of Topology and Attribute Features. Entropy 2023, 25, 89. https://doi.org/10.3390/e25010089
Ren Y, Ma H, Liu S, Wang K. Hypernetwork Link Prediction Method Based on Fusion of Topology and Attribute Features. Entropy. 2023; 25(1):89. https://doi.org/10.3390/e25010089
Chicago/Turabian StyleRen, Yuyuan, Hong Ma, Shuxin Liu, and Kai Wang. 2023. "Hypernetwork Link Prediction Method Based on Fusion of Topology and Attribute Features" Entropy 25, no. 1: 89. https://doi.org/10.3390/e25010089
APA StyleRen, Y., Ma, H., Liu, S., & Wang, K. (2023). Hypernetwork Link Prediction Method Based on Fusion of Topology and Attribute Features. Entropy, 25(1), 89. https://doi.org/10.3390/e25010089






