Security Risk Assessment Approach for Distribution Network Cyber Physical Systems Considering Cyber Attack Vulnerabilities
Abstract
:1. Introduction
- Based on the information transfer structure model of the distribution network CPS, the probability of exploiting the vulnerabilities existing in the cyber layer of the distribution network is calculated by using the common vulnerability scoring system (CVSS), and then the Bayesian network model under cyber attack vulnerabilities can be derived.
- Different evaluation metrics are given in this paper to consider attack selection from the attacker’s perspective, not only considering the objective existence of indicator weights, but also incorporating the subjective opinions of several experts who undertake different professional works. Finally, a combination of subjective and objective approaches is used to determine the selection tendency of the attacker, and the practicality of expert experience and the informational variability of objective data are taken into account.
- Multiple scenarios where vulnerabilities in a distribution network cyber system are exploited by attackers are designed and simulated in a dynamic Bayesian network. The dynamic Bayesian network simulation is able to reflect the risk value after an attack vulnerability or under normal conditions, which can reflect whether the system is under attack vulnerability and thus effectively avoid the risk.
2. Background of the Study
2.1. Structure of Distribution Network CPS
- The control layer is an important part of the CPS, whose function is to unify and integrate the data transmitted from different communication networks and generate control commands in response, which guarantees the safe and stable operation of the power system;
- The control layer and the physical layer are connected through the network layer which is responsible for information data transmission during system operation.
- The physical layer mainly consists of power devices and corresponding network components, such as distributed generation units and their controllers, loads and their measurement units, circuit breakers and their devices, and substations and their communication systems.
2.2. Cyber Security of Distribution Network CPS
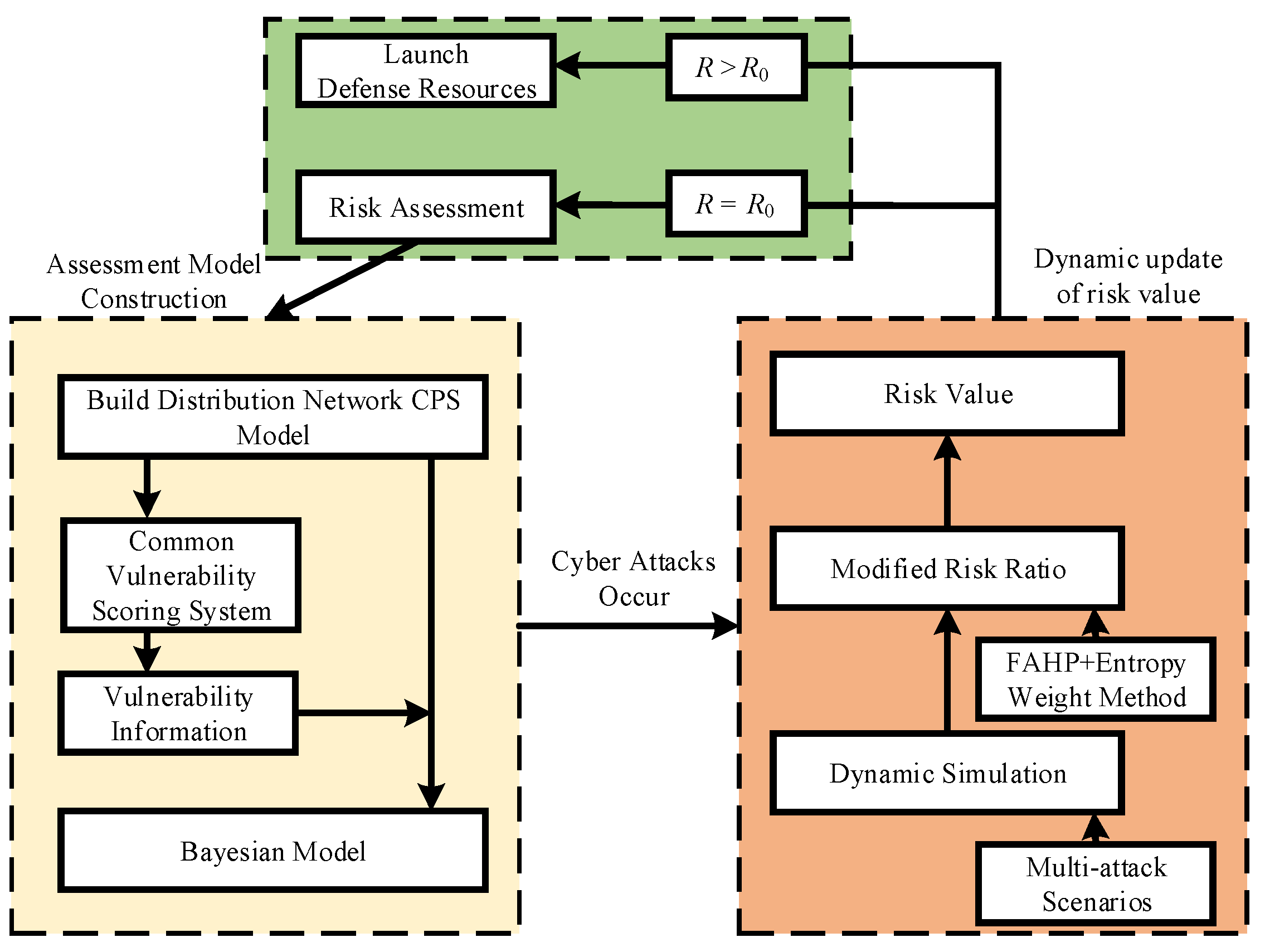
2.3. Risk Assessment Process for Distribution Network CPS
3. Risk Delivery Model
3.1. Common Vulnerability Scoring Systems
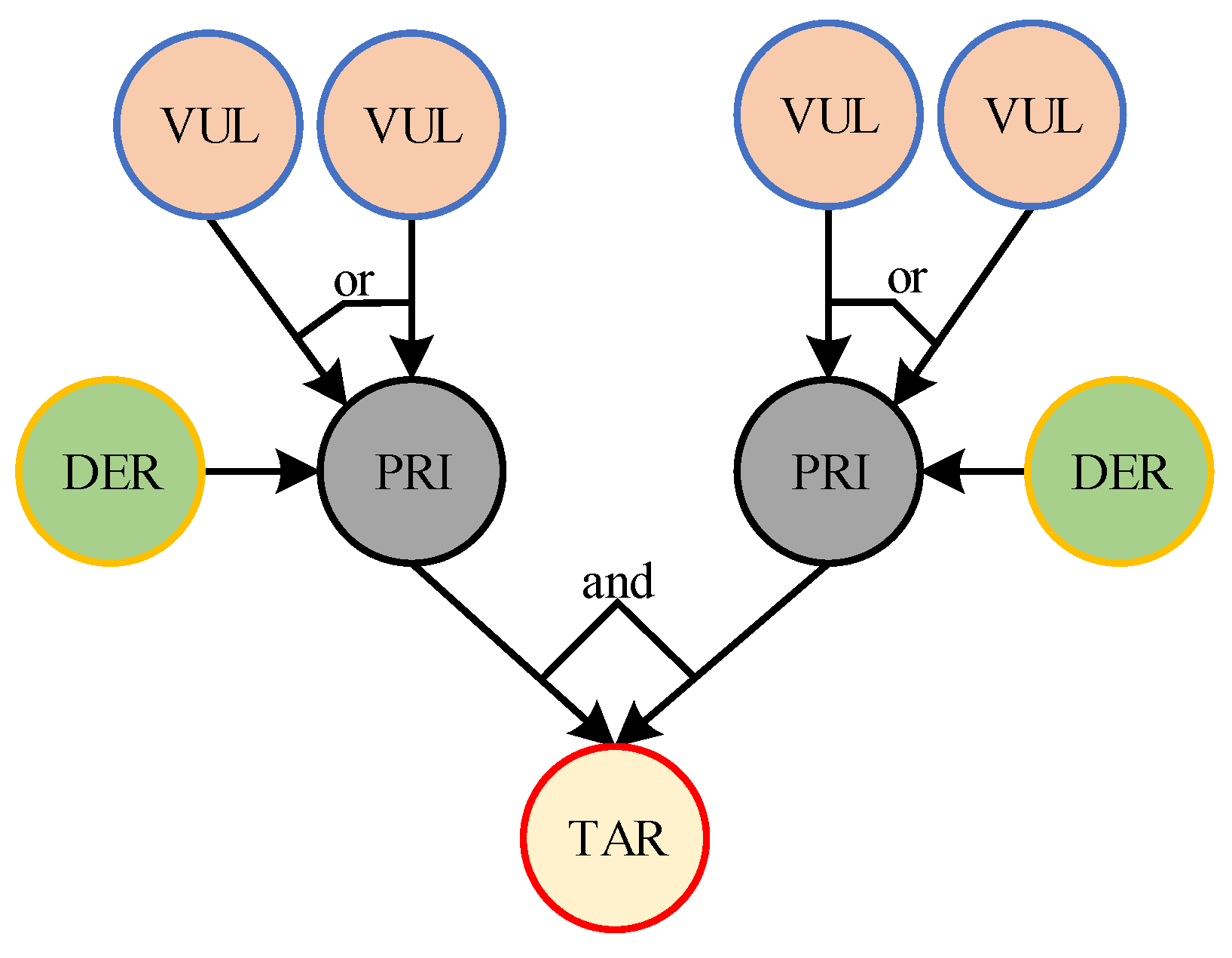
3.2. Bayesian Network Model of Distribution Network CPS
- Attribute Nodes
- Directed Edges
- Logical Structure
- Prior Probability
- Posterior Probability
3.3. Calculation of Prior Probabilities
3.3.1. Calculate the Probability of Vulnerability Being Exploited
3.3.2. Calculation of the Prior Probability
3.4. Calculation of the Posterior Probability
4. Quantitative Risk Assessment of Distribution Network CPS
4.1. Portfolio Empowerment Method
4.1.1. Indicator Definition
4.1.2. Subjective Weight Based on FAHP
- Calculation Steps
- Build Fuzzy Complementary Judgment Matrix
- Weight Calculation
- Consistency Test
- Subjective Empowerment
- Set the matrix ;
- Calculate the characteristic root matrix and the eigenvector matrix of the matrix ;
- Find the largest characteristic root and its corresponding eigenvector ;
- Normalize the eigenvector θ to obtain the subjective weight vector , , given by the k experts.
4.1.3. Objective Weight Based on the Entropy Weight Method
4.1.4. Combined Weight
4.1.5. Attacker’s Selective Probability of Attacking Target Node
4.2. Risk Quantification Model
4.3. Risk Assessment Flow
5. Example Analysis
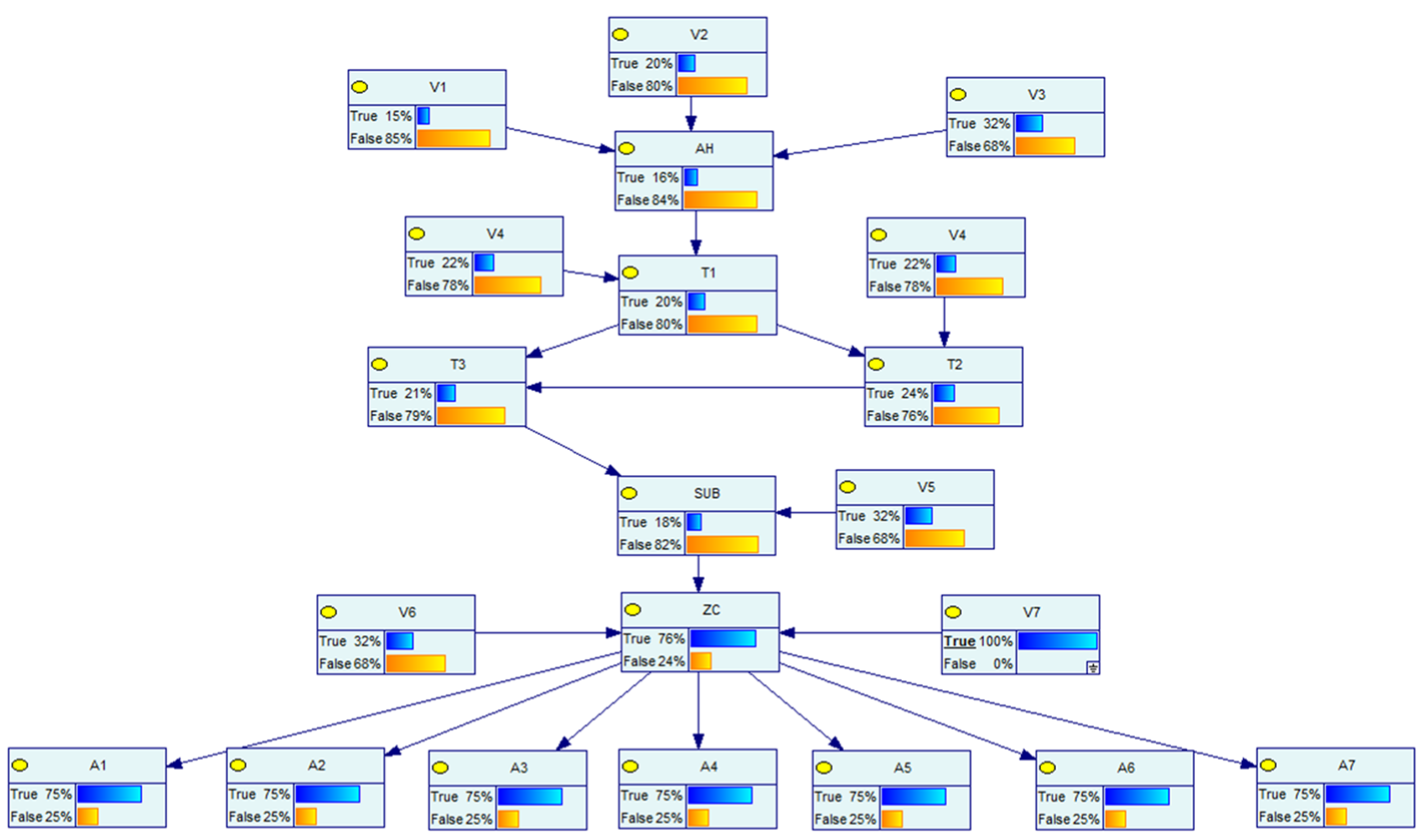
5.1. Bayesian Modeling of CPS in Distribution Networks
5.2. Simulation Test
5.2.1. Scenario Setting for Different Network Attacks
- The vulnerability has been exploited by the attacker, and its dynamic probability is shown in Figure 9, set as scene 1;
- The vulnerability has been exploited by the attacker, and its dynamic probability is shown in Figure 10, set as scene 2;
- The vulnerability , has been exploited by the attacker, and its dynamic probability is shown in Figure 11, set as scene 3.
5.2.2. Risk Rate Correction by Defense Resources
5.2.3. Correction of the Selective Strike Target by the Attacker
- Subjective Weight
- Objective Weight
- Combined Weight
- Ideal intervals for indicators
5.2.4. Quantification of Risk
5.2.5. Classification of Risk Level
5.2.6. Comparative Analysis of Weight Methods and Defense Resources
5.2.7. Base Risk Value Update after Fixing Vulnerability
5.2.8. Selectivity of Target Nodes without Considering the Attacker’s Perspective
6. Conclusions
- Dynamic Bayesian networks that portray cyber attack vulnerabilities in the form of probabilistic transmission are superior in distribution network CPS security risk assessment. It can quantify the risk value of the system when different cyber attack vulnerabilities occur according to different attack scenarios and dynamically calculate the risk value. Based on the size of the risk value, the corresponding defense resources are invested to reduce the impact of cyber attack vulnerabilities.
- From the perspective of the attacker, when it controls the corresponding equipment, there is a certain bias in choosing different strike targets. Using the method of combined assignment to correct this preference can combine the advantages of the subjective assignment method and the objective assignment method to obtain a relatively accurate corrected risk value.
- Risk passive defense resources are an integral part of distribution network CPS. As much as possible, more resources are allocated to nodes with higher risk values in the case of limited resources. The comparison experiments were set up to reflect the role of defense resources in this paper, which demonstrates the need for the defense role to be taken into account in the assessment of security risks in distribution network CPS.
- The magnitude of the static risk value under stable operation of a distribution network CPS depends on the vulnerability information in the system. A system with a high static risk value indicates a greater degree of adverse impact from an attack; however, a system with a low static risk may have a greater increase in risk value from the same attack than the former. Therefore, whenever there is any risk of cyber attack vulnerability in a distribution network CPS, a risk assessment should be carried out.
- As the focus of this paper is to propose a risk assessment method for distribution network CPS that considers the attacker’s perspective and the allocation of defense resources, the uncertainty introduced in Bayesian network modeling and its propagation is not considered. The ways to eliminate uncertainty problems are mentioned in the literature [30]. The physical model in this paper uses a simple distribution network system. In fact, the physical system can be replaced with a more complex distribution network system, such as a distributed generation distribution network, and the method in this paper is equally applicable after replacing the node importance evaluation metric and asset model. Meanwhile, the research can also be extended in subsequent studies to study the optimal allocation of defense resources based on the simulation results, and this series of issues should be considered in further studies.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Sheng, W.; Wang, Y.; Lu, Y. Key Technologies and Their Progress in Cyber Physics System of Power Grid. Proc. CSEE 2015, 35, 3522–3531. [Google Scholar]
- Liu, W.; Lin, Z.; Wang, L.; Wang, Z.; Wang, H.; Gong, Q. Analytical Reliability Evaluation of Active Distribution Systems Considering Information Link Failures. IEEE Trans. Power Syst. 2020, 35, 4167–4179. [Google Scholar] [CrossRef]
- Pahwa, A.; DeLoach, S.A.; Natarajan, B.; Das, S.; Malekpour, A.R.; Shafiul Alam, S.M.; Case, D.M. Goal-Based Holonic Multiagent System for Operation of Power Distribution Systems. IEEE Trans. Smart Grid 2015, 6, 2510–2518. [Google Scholar] [CrossRef]
- Zhuang, P.; Liang, H. False Data Injection Attacks Against State-of-Charge Estimation of Battery Energy Storage Systems in Smart Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 2566–2577. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, S.; Ma, W.; Qu, J. Research on Attack Detection of Cyber Physical Systems Based on Improved Support Vector Machine. Mathematics 2022, 10, 2713. [Google Scholar] [CrossRef]
- Guo, Q.; Xin, S.; Sun, H. Integrated Security Assessment of Information Energy Systems from the Ukraine Power Outage. Autom. Electr. Power Syst. 2016, 40, 145–147. [Google Scholar]
- Sridhar, S.; Hahn, A.; Govindarasu, M. Cyber–Physical System Security for the Electric Power Grid. Proc. IEEE 2012, 100, 210–224. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, L.; Wang, X.; Zhang, C.; Zhu, H.; Tan, Y. A Packet-Reordering Covert Channel over VoLTE Voice and Video Traffics. J. Netw. Comput. Appl. 2019, 126, 29–38. [Google Scholar] [CrossRef]
- Du, X.; Guizani, M.; Xiao, Y.; Chen, H.-H. Transactions Papers a Routing-Driven Elliptic Curve Cryptography Based Key Management Scheme for Heterogeneous Sensor Networks. IEEE Trans. Wirel. Commun. 2009, 8, 1223–1229. [Google Scholar] [CrossRef]
- Dai, Q.; Shi, L.; Ni, Y. Risk Assessment for Cyberattack in Active Distribution Systems Considering the Role of Feeder Automation. IEEE Trans. Power Syst. 2019, 34, 3230–3240. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, Z.; Ni, M.; Lin, H.; Li, M.; Tang, Y. Analysis of the Impact of Combined Information-Physical-Failure on Distribution Network CPS. IEEE Access 2020, 8, 44140–44152. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, C.; Xiong, N.; Qin, Y.; Li, X.; Huang, S. Multimodel-Based Incident Prediction and Risk Assessment in Dynamic Cybersecurity Protection for Industrial Control Systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1429–1444. [Google Scholar] [CrossRef]
- Lee, C.-J.; Lee, K.J. Application of Bayesian Network to the Probabilistic Risk Assessment of Nuclear Waste Disposal. Reliab. Eng. Syst. Saf. 2006, 91, 515–532. [Google Scholar] [CrossRef]
- Qin, H.; Liu, D. Risk Assessment in Distribution Networks Considering Cyber Coupling. Int. J. Electr. Power Energy Syst. 2023, 145, 108650. [Google Scholar] [CrossRef]
- Yazdi, M.; Zarei, E.; Adumene, S.; Abbassi, R.; Rahnamayiezekavat, P. Chapter Eleven—Uncertainty Modeling in Risk Assessment of Digitalized Process Systems. Methods Assess Manag. Process Saf. Digit. Process Syst. 2022, 6, 389–416. [Google Scholar]
- Song, F.; Ai, Z.; Zhang, H.; You, I.; Li, S. Smart Collaborative Balancing for Dependable Network Components in Cyber-Physical Systems. IEEE Trans. Ind. Inform. 2021, 17, 6916–6924. [Google Scholar] [CrossRef]
- Cao, G.; Gu, W.; Li, P.; Sheng, W.; Liu, K.; Sun, L.; Cao, Z.; Pan, J. Operational Risk Evaluation of Active Distribution Networks Considering Cyber Contingencies. IEEE Trans. Ind. Inform. 2020, 16, 3849–3861. [Google Scholar] [CrossRef]
- Wei, L.; Sarwat, A.I.; Saad, W.; Biswas, S. Stochastic Games for Power Grid Protection Against Coordinated Cyber-Physical Attacks. IEEE Trans. Smart Grid 2018, 9, 684–694. [Google Scholar] [CrossRef]
- Pal, A.; Jolfaei, A.; Kant, K. A Fast Prekeying-Based Integrity Protection for Smart Grid Communications. IEEE Trans. Ind. Inform. 2021, 17, 5751–5758. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Xiang, Y.; Ten, C.-W. Power System Reliability Evaluation With SCADA Cybersecurity Considerations. IEEE Trans. Smart Grid 2015, 6, 1707–1721. [Google Scholar] [CrossRef]
- Mell, P.; Scarfone, K.; Romanosky, S. Common Vulnerability Scoring System. IEEE Secur. Priv. 2006, 4, 85–89. [Google Scholar] [CrossRef]
- Johnson, P.; Lagerström, R.; Ekstedt, M.; Franke, U. Can the Common Vulnerability Scoring System Be Trusted? A Bayesian Analysis. IEEE Trans. Dependable Secur. Comput. 2018, 15, 1002–1015. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G. Quantitative Assessment Model for Dynamic Performance Analysis of Security Risks in Industrial Cyber Physical Systems. Control Decis. 2021, 36, 1939–1946. [Google Scholar]
- Poolsappasit, N.; Dewri, R.; Ray, I. Dynamic Security Risk Management Using Bayesian Attack Graphs. IEEE Trans. Dependable Secur. Comput. 2012, 9, 61–74. [Google Scholar] [CrossRef]
- Muñoz-González, L.; Sgandurra, D.; Barrère, M.; Lupu, E.C. Exact Inference Techniques for the Analysis of Bayesian Attack Graphs. IEEE Trans. Dependable Secur. Comput. 2019, 16, 231–244. [Google Scholar] [CrossRef] [Green Version]
- Laitila, P.; Virtanen, K. On Theoretical Principle and Practical Applicability of Ranked Nodes Method for Constructing Conditional Probability Tables of Bayesian Networks. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1943–1955. [Google Scholar] [CrossRef]
- Zhang, B.; Li, C.-C.; Dong, Y.; Pedrycz, W. A Comparative Study Between Analytic Hierarchy Process and Its Fuzzy Variants: A Perspective Based on Two Linguistic Models. IEEE Trans. Fuzzy Syst. 2021, 29, 3270–3279. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, K.; Yao, Y.; Yang, J.; Zheng, G.; Li, Q. Capture and Prediction of Rainfall-Induced Landslide Warning Signals Using an Attention-Based Temporal Convolutional Neural Network and Entropy Weight Methods. Sensors 2022, 22, 6240. [Google Scholar] [CrossRef]
- Chen, B.; Lu, Z.; Li, B. Distribution Network Reliability Assessment with Multiple Types of Information Disturbances. Autom. Electr. Power Syst. 2019, 43, 103–110. [Google Scholar]
- Yazdi, M.; Kabir, S.; Walker, M. Uncertainty Handling in Fault Tree Based Risk Assessment: State of the Art and Future Perspectives. Process. Saf. Environ. Prot. 2019, 131, 89–104. [Google Scholar] [CrossRef]














| Vulnerability Number | Vulnerability Location | CVE Number | Vulnerability Description |
|---|---|---|---|
| Control Center | CVE-2021-20106 | The vulnerability could allow an administrator user to upload specially crafted files and thus gain administrator privileges on the control center. | |
| Control Center | CVE-2021-20135 | The vulnerability could allow an authenticated local administrator to run specific executable files on the host. | |
| Control Center | CVE-2021-41619 | A malicious actor with unmanaged user access on the host could exploit this vulnerability to escalate privileges. | |
| Switch | CVE-2022-20864 | Enables an unauthenticated, local attacker to recover the configuration or reset the enable password. | |
| Sub-server | CVE-2020-12142 | Users with knowledge of the system can use the material to decrypt ongoing communications. | |
| Zone Controller | CVE-2021-33523 | Allows remote upload of a new driver that can execute arbitrary commands on the underlying host. | |
| Zone Controller | CVE-2020-5237 | Allow remote attackers to upload, copy and modify files on the file system with certain parameters. |
| Metric | Metric Value | Numerical Value |
|---|---|---|
| Attack Vector | N | 0.85 |
| A | 0.62 | |
| L | 0.55 | |
| P | 0.20 | |
| Attack Complexity | L | 0.77 |
| H | 0.44 | |
| Privilege Required | N | 0.85 |
| L | 0.62 | |
| H | 0.27 | |
| User Interaction | N | 0.85 |
| R | 0.62 |
| Scale | Definition | Description |
|---|---|---|
| 0.5 | Comparing two elements | Equally important |
| 0.6 | Comparing two elements | Slightly more important |
| 0.7 | Comparing two elements | Obviously important |
| 0.8 | Comparing two elements | Much more important |
| 0.9 | Comparing two elements | Extremely important |
| 0.1, 0.2, 0.3, 0.4 | Inverse comparison of two elements | On the contrary |
| Target Node | |||||||
|---|---|---|---|---|---|---|---|
| Node Power /MVA | 4544.08 | 3904.53 | 3346.96 | 2403.10 | 1991.01 | 859.19 | 632.46 |
| Vulnerability Number | CVE Number | ||||||
|---|---|---|---|---|---|---|---|
| CVE-2021-20106 | L | L | H | R | U | 0.1489 | |
| CVE-2021-20135 | L | L | H | N | U | 0.2041 | |
| CVE-2021-41619 | N | L | H | N | U | 0.3154 | |
| CVE-2022-20864 | P | L | N | N | U | 0.2337 | |
| CVE-2020-12142 | N | L | H | N | U | 0.3154 | |
| CVE-2021-33523 | N | L | N | N | U | 0.9930 | |
| CVE-2020-5237 | N | L | L | N | U | 0.7243 |
| Risk Status | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.7 | 0.6 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 |
| 1 | 0.3 | 0.4 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| Meric | |||||||
|---|---|---|---|---|---|---|---|
| A | 4544.084 | 3904.529 | 3346.964 | 2403.096 | 1991.011 | 859.190 | 632.456 |
| B | 33 | 27 | 22 | 12 | 8 | 4 | 0 |
| C | 4/32 | 6/32 | 2/32 | 4/32 | 2/32 | 2/32 | 2/32 |
| Indicator Node | |||
|---|---|---|---|
| 0.3834 | 0.3333 | 0.2833 | |
| 0.3834 | 0.3333 | 0.2833 | |
| 0.4000 | 0.3167 | 0.2833 | |
| 0.4000 | 0.3333 | 0.2667 | |
| 0.3667 | 0.3333 | 0.3000 | |
| 0.3833 | 0.3167 | 0.3000 |
| Expert Number | ||||||
|---|---|---|---|---|---|---|
| Compatibility Index I | 0.0554 | 0.0666 | 0.0730 | 0.0664 | 0.0444 | 0.0455 |
| Node Metric | |||
|---|---|---|---|
| Feature Algorithm Value | 0.3862 | 0.3281 | 0.2857 |
| Indicator | |||||||
|---|---|---|---|---|---|---|---|
| A | 1 | 0.8365 | 0.6940 | 0.4527 | 0.3473 | 0.0580 | 0 |
| B | 1 | 0.8182 | 0.6667 | 0.3636 | 0.2424 | 0.1212 | 0 |
| C | 0.5 | 1 | 0 | 0.5 | 0 | 0 | 0 |
| Indicator | A | B | C |
|---|---|---|---|
| Entropy Value | 0.8234 | 0.8239 | 0.5343 |
| Objective Weight | 0.2158 | 0.2151 | 0.5691 |
| Indicator | A | B | C |
|---|---|---|---|
| Objective Weight | 0.2158 | 0.2151 | 0.5691 |
| Subjective Weight | 0.3862 | 0.3281 | 0.2857 |
| Combined Weight | 0.2633 | 0.2230 | 0.5137 |
| Node | |||||||
|---|---|---|---|---|---|---|---|
| A | 1.0000 | 0.8593 | 0.7366 | 0.5288 | 0.4382 | 0.1891 | 0.1392 |
| B | 1.0000 | 0.8182 | 0.6667 | 0.3636 | 0.2424 | 0.1212 | 0.0000 |
| C | 1.0000 | 0.7500 | 0.5000 | 0.2500 | 0.2500 | 0.2500 | 0.2500 |
| Objective Correction | 1.0000 | 0.7883 | 0.5869 | 0.3346 | 0.2890 | 0.2092 | 0.1723 |
| Subjective Correction | 1.0000 | 0.8146 | 0.6461 | 0.3949 | 0.3202 | 0.1842 | 0.1252 |
| Combined Correction | 1.0000 | 0.7942 | 0.6000 | 0.3493 | 0.2981 | 0.2049 | 0.1645 |
| Scene | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.1740 | 0.1842 | 0.1391 | 0.1012 | 0.1036 | 0.0833 | 0.0766 |
| 1 | 0.2040 | 0.2160 | 0.1631 | 0.1186 | 0.1215 | 0.0976 | 0.0898 |
| 2 | 0.2250 | 0.2382 | 0.1799 | 0.1308 | 0.1340 | 0.1077 | 0.0991 |
| 3 | 0.2310 | 0.2446 | 0.1846 | 0.1342 | 0.1375 | 0.1105 | 0.1017 |
| Scene | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 790.7 | 719.2 | 465.6 | 243.2 | 206.3 | 71.6 | 48.4 |
| 1 | 927.0 | 843.4 | 545.9 | 285.0 | 241.9 | 83.9 | 56.8 |
| 2 | 1022.4 | 930.1 | 602.1 | 314.3 | 266.8 | 92.5 | 62.7 |
| 3 | 1036.1 | 942.6 | 609.8 | 318.4 | 270.4 | 93.7 | 63.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Sun, B.; Zang, T.; Cai, Y.; Wu, J.; Luo, H. Security Risk Assessment Approach for Distribution Network Cyber Physical Systems Considering Cyber Attack Vulnerabilities. Entropy 2023, 25, 47. https://doi.org/10.3390/e25010047
Zhou B, Sun B, Zang T, Cai Y, Wu J, Luo H. Security Risk Assessment Approach for Distribution Network Cyber Physical Systems Considering Cyber Attack Vulnerabilities. Entropy. 2023; 25(1):47. https://doi.org/10.3390/e25010047
Chicago/Turabian StyleZhou, Buxiang, Binjie Sun, Tianlei Zang, Yating Cai, Jiale Wu, and Huan Luo. 2023. "Security Risk Assessment Approach for Distribution Network Cyber Physical Systems Considering Cyber Attack Vulnerabilities" Entropy 25, no. 1: 47. https://doi.org/10.3390/e25010047






