Synchronization Transition of the Second-Order Kuramoto Model on Lattices
Abstract
1. Introduction
2. Models and Methods
2.1. The Second-Order Kuramoto Model
2.2. Linear Approximation for the Frequency Entrainment
3. Synchronization Transition in 2D
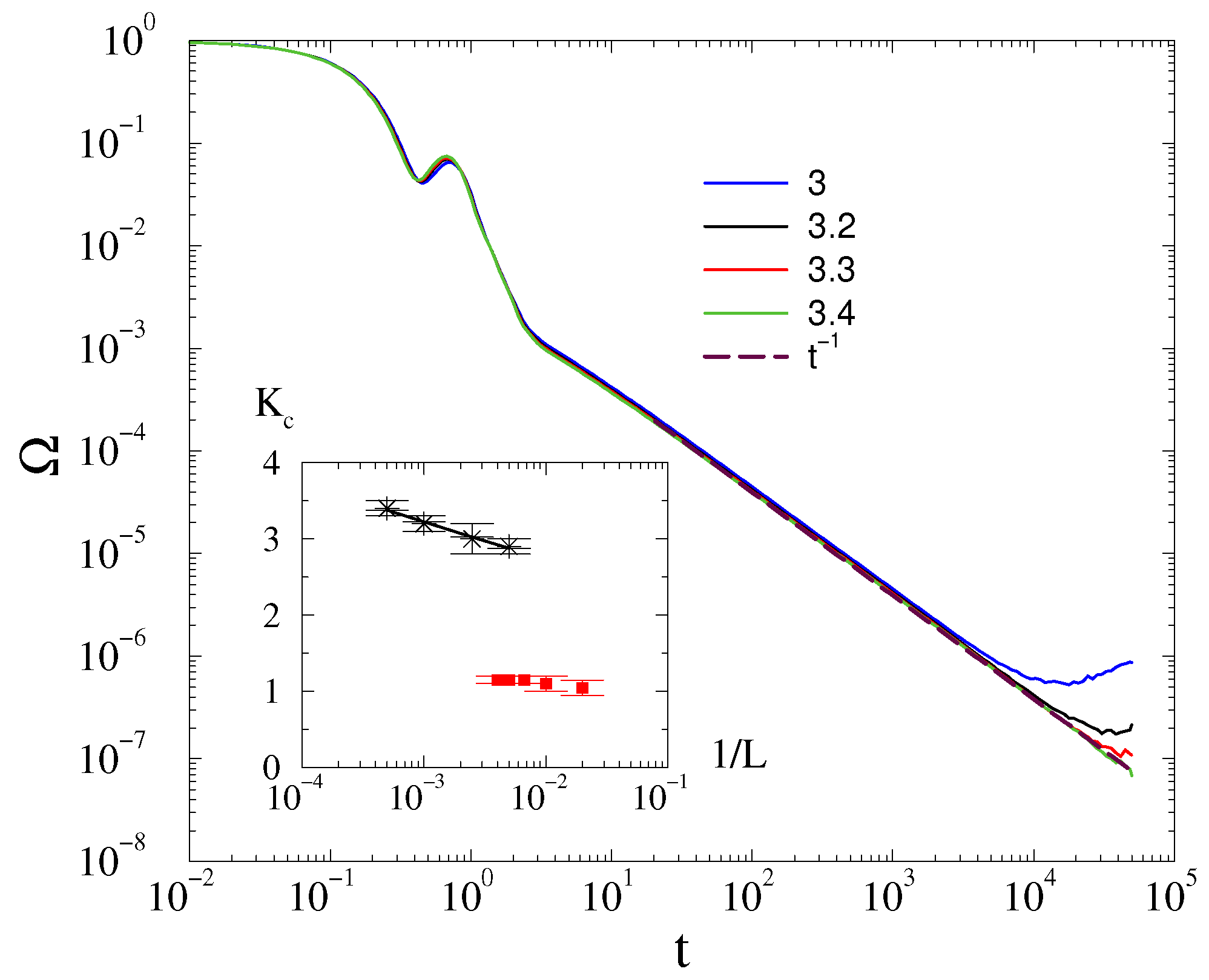
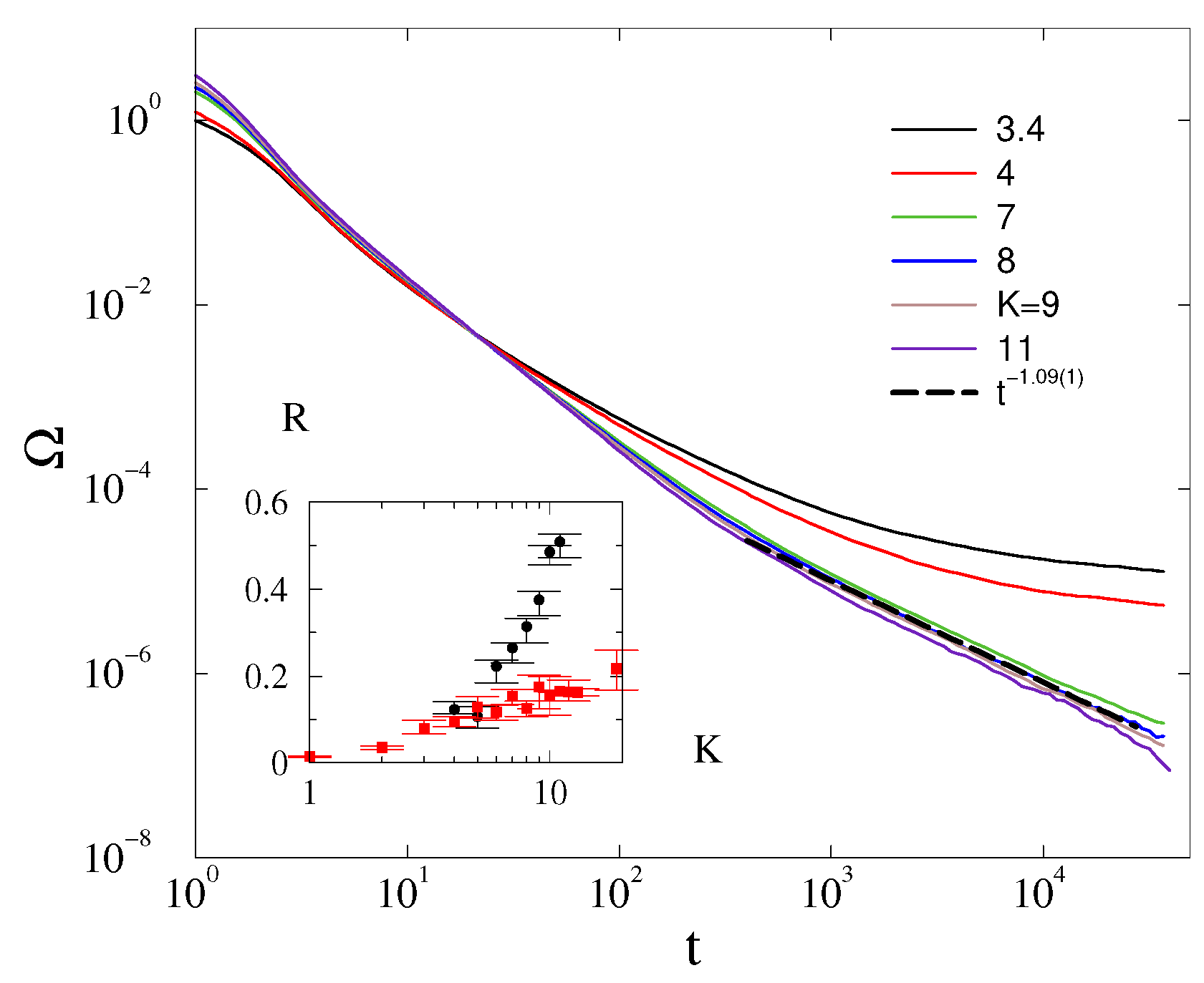
3.1. Frequency Entrainment Phase Transition
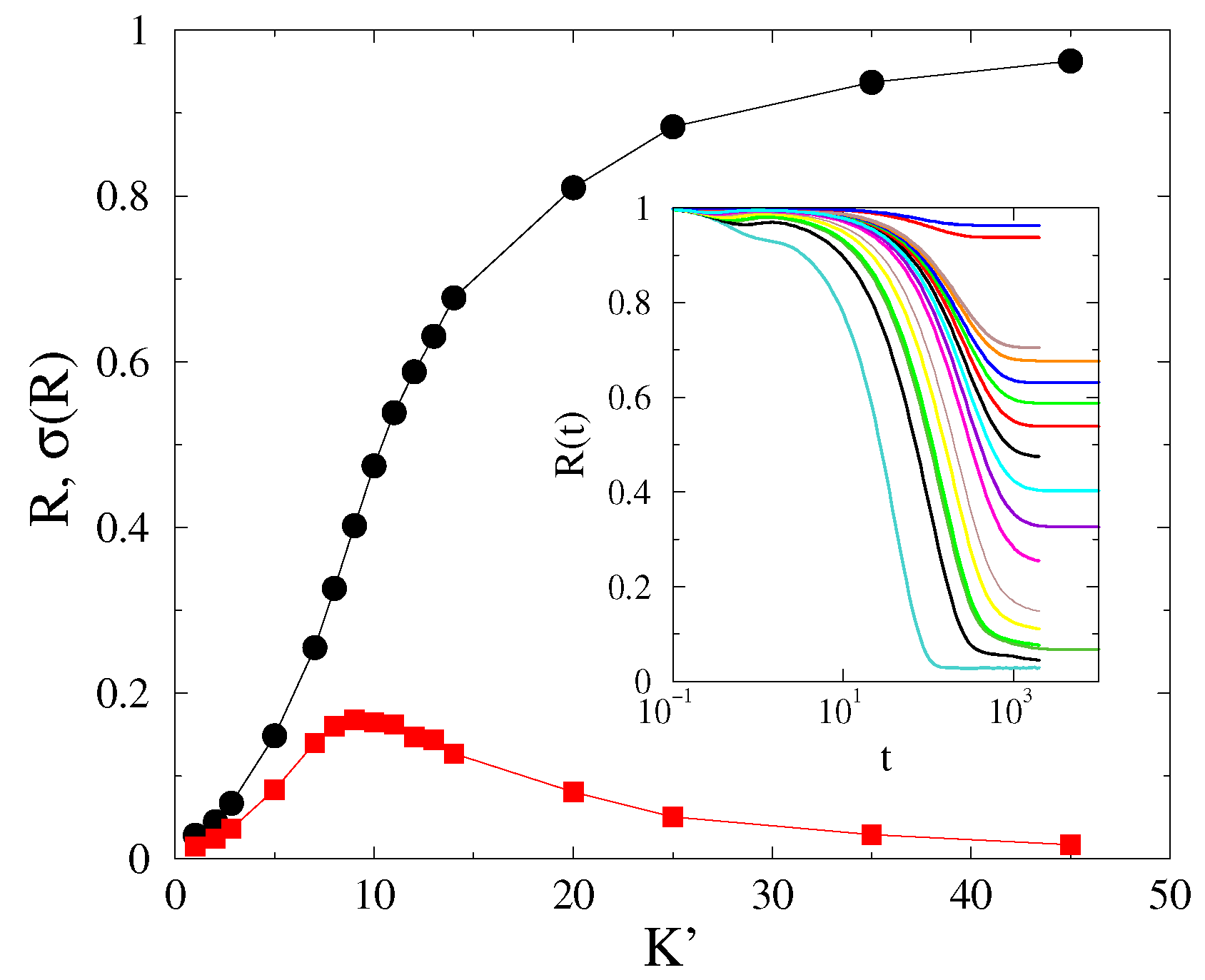
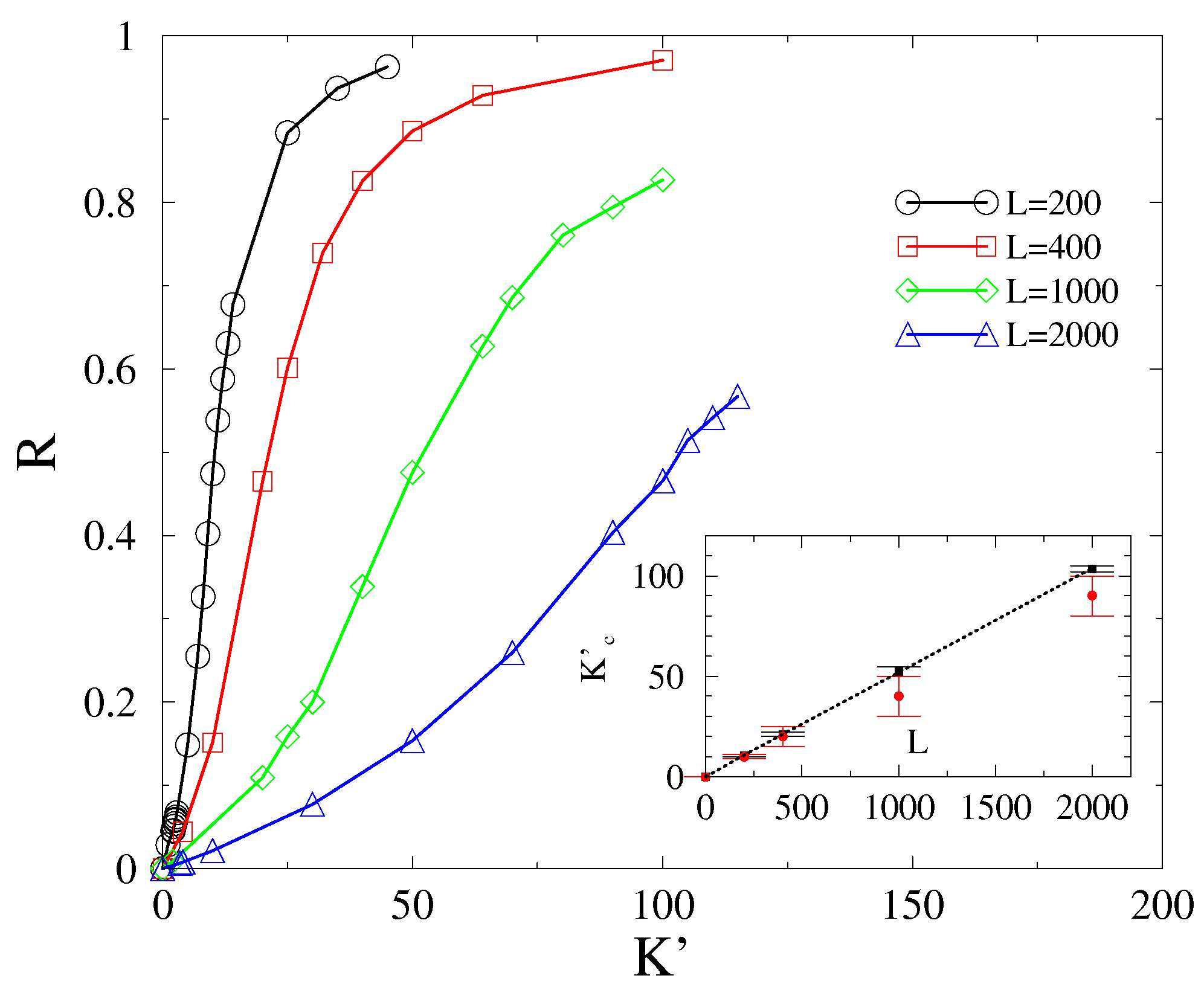
3.2. Phase-Order Parameter Transition
4. Synchronization Transition in 3D
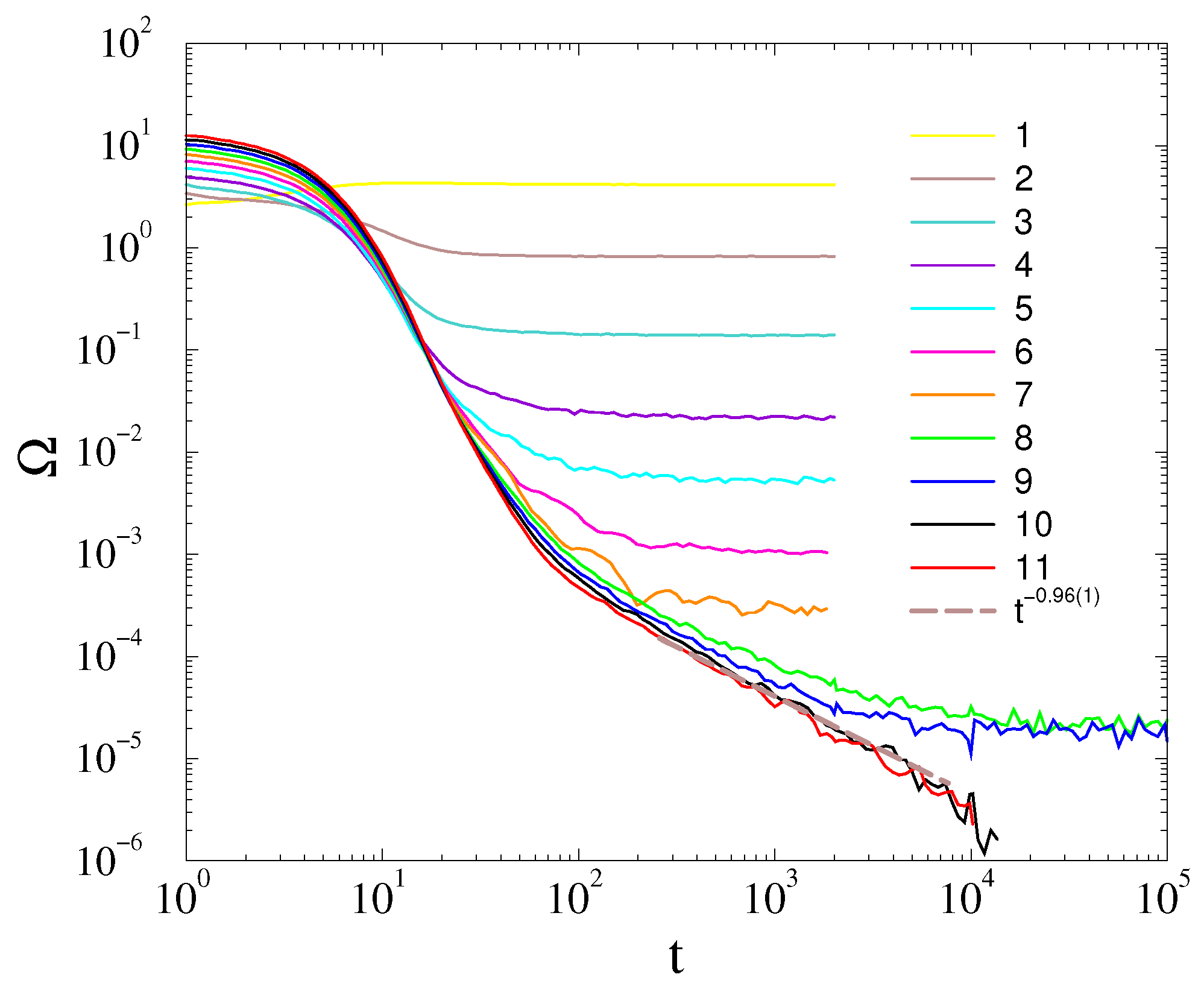
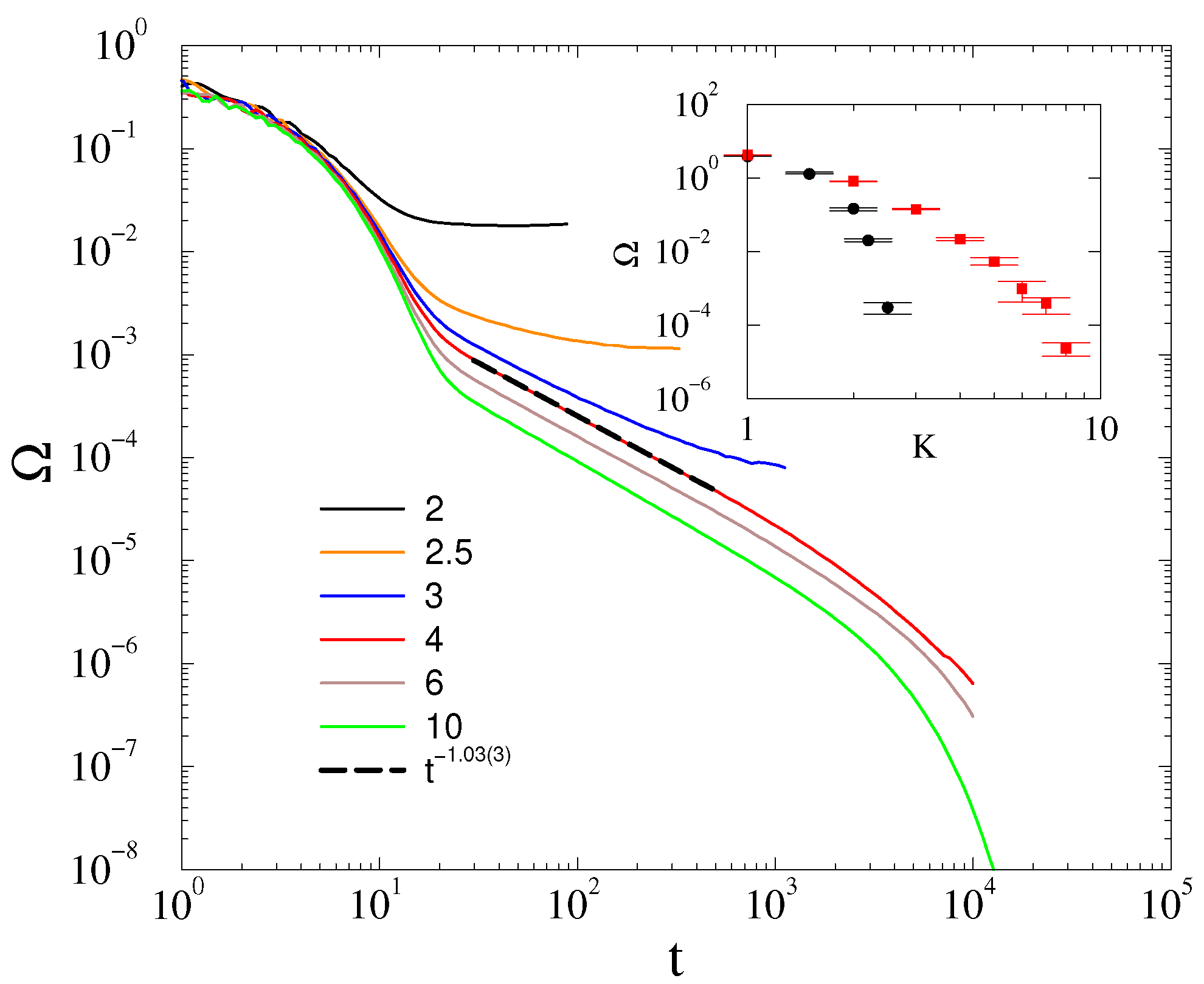
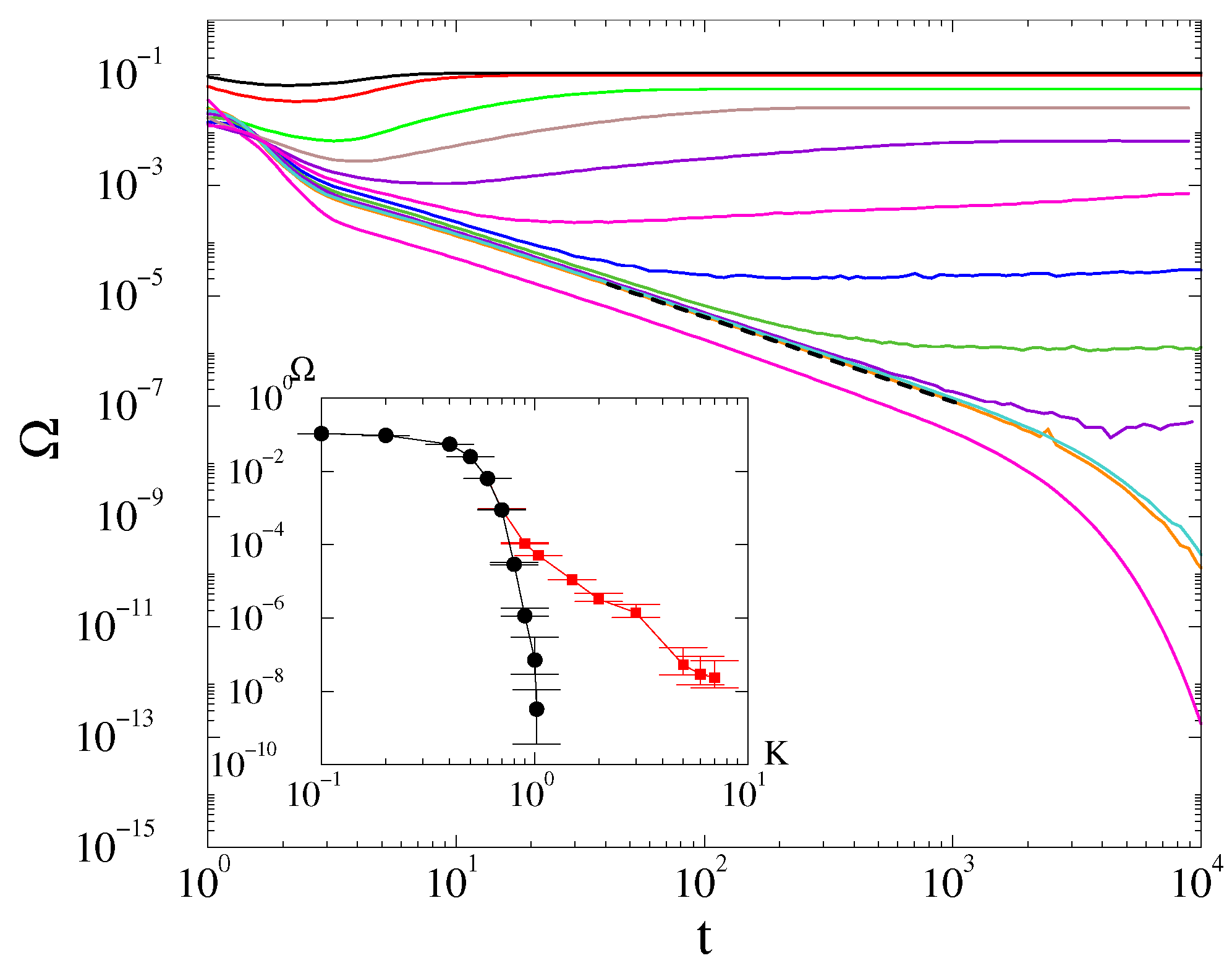
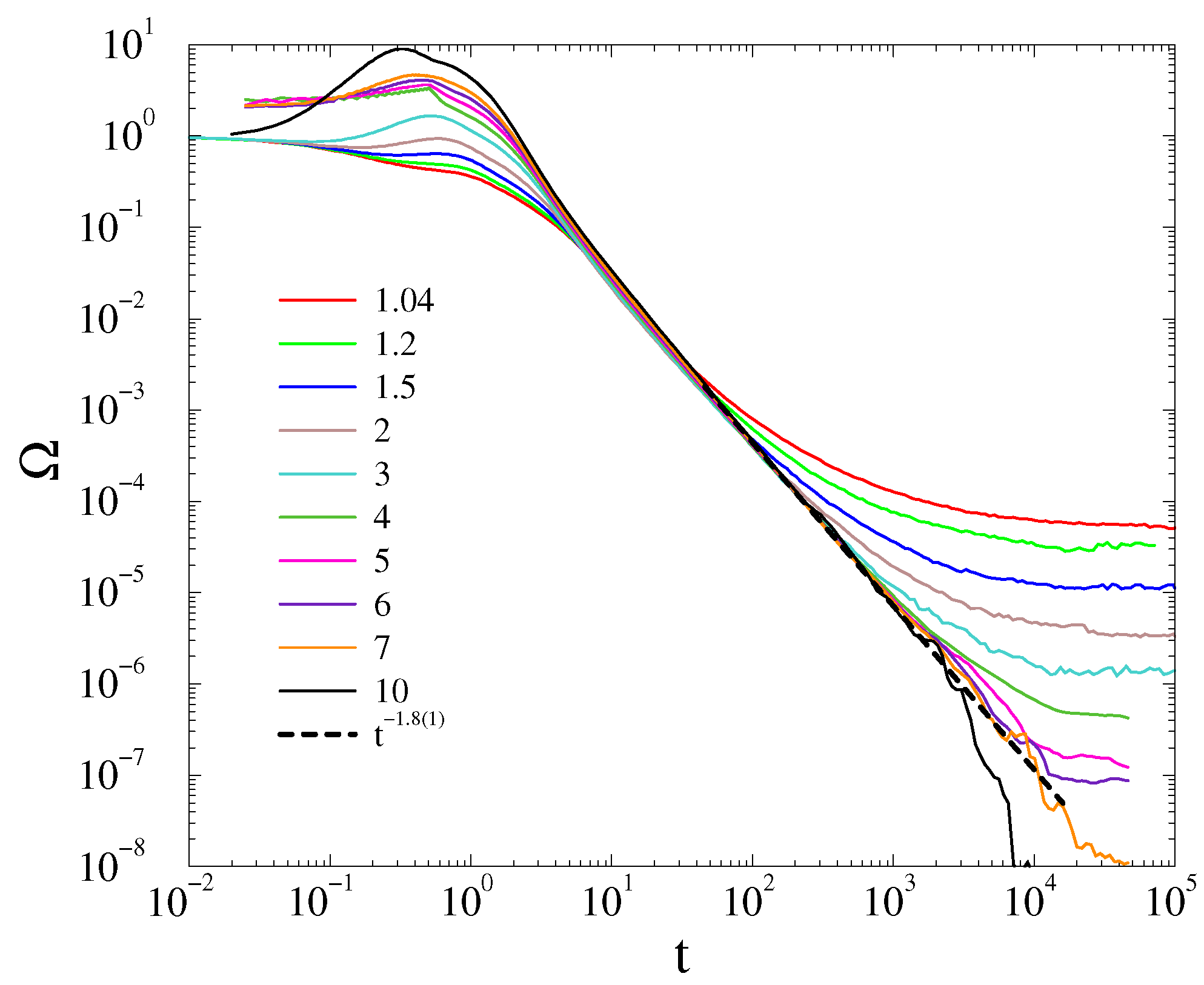
4.1. Frequency Entrainment Phase Transition
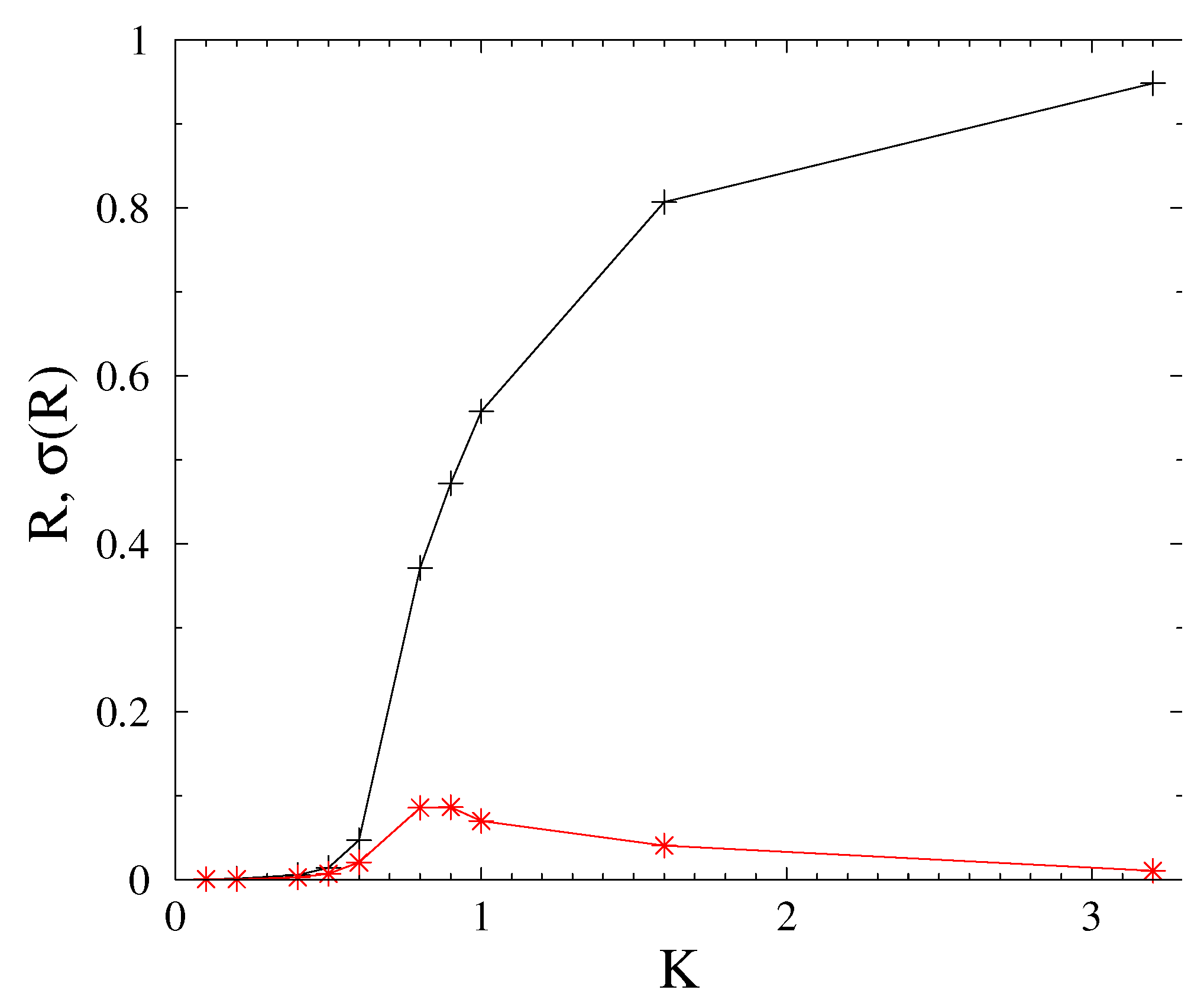
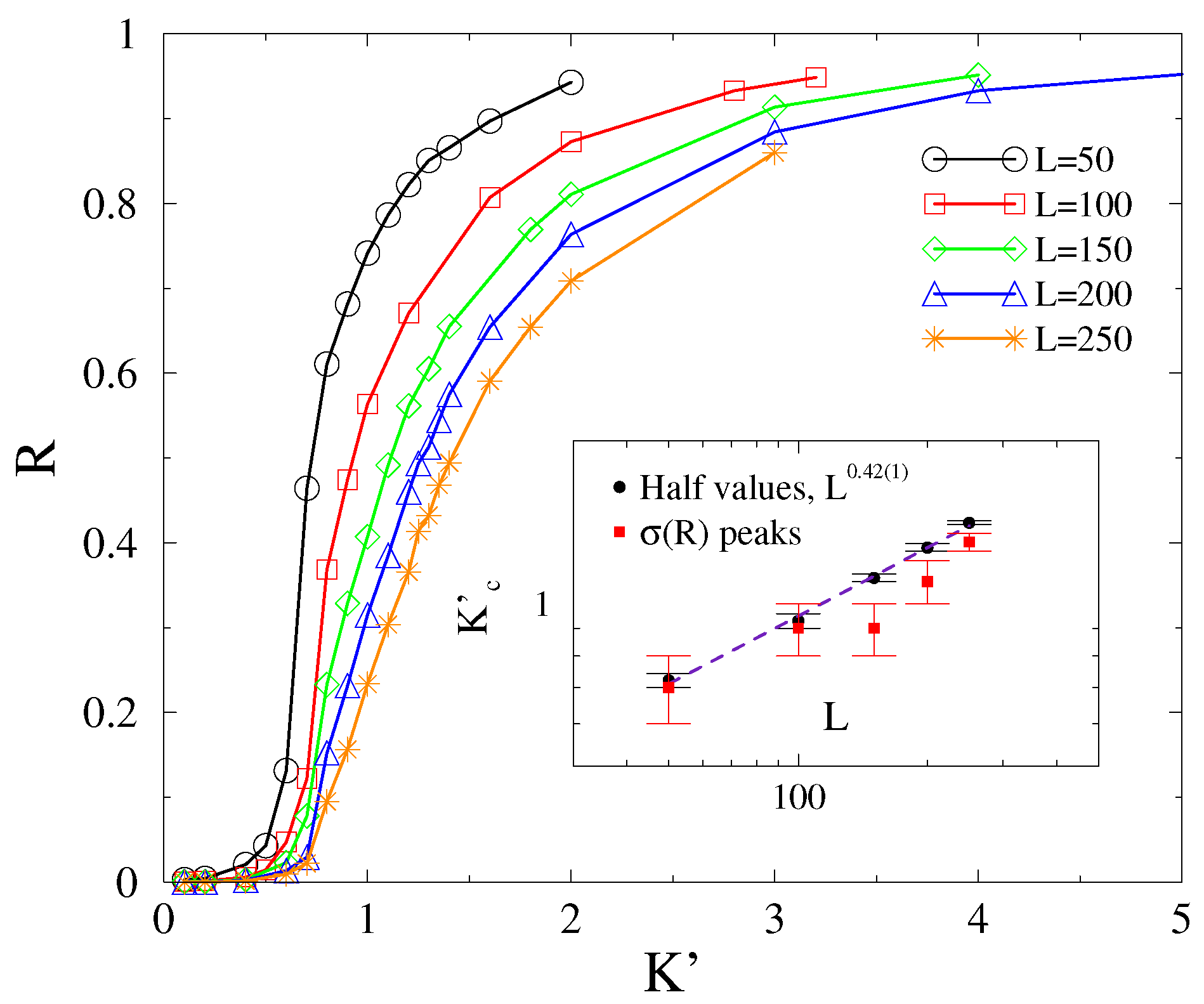
4.2. Phase-Order Parameter Transition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Pikovsky, A.; Kurths, J.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence. In Proceedings of the International Symposium on Mathematical Problems in Theoretical Physics, Kyoto, Japan, 23–29 January 1975. [Google Scholar]
- Ott, E.; Antonsen, T.M. Low dimensional behavior of large systems of globally coupled oscillators. Chaos 2008, 18, 037113. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Chaté, H.; Park, H.; Tang, L.H. Entrainment transition in populations of random frequency oscillators. Phys. Rev. Lett. 2007, 99, 184101. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.; Ha, M.; Kahng, B. Extended finite-size scaling of synchronized coupled oscillators. Phys. Rev. 2013, 88, 032126. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Shinomoto, S.; Kuramoto, Y. Local and grobal self-entrainments in oscillator lattices. Prog. Theor. Phys. 1987, 77, 1005. [Google Scholar] [CrossRef]
- Hong, H.; Park, H.; Choi, M. Collective synchronization in spatially extended systems of coupled oscillators with random frequencies. Phys. Rev. E 2005, 72, 036217. [Google Scholar] [CrossRef]
- Juhász, R.; Kelling, J.; Ódor, G. Critical dynamics of the Kuramoto model on sparse random networks. J. Stat. Mech. Theory Exp. 2019, 2019, 053403. [Google Scholar] [CrossRef]
- Filatrella, G.; Nielsen, A.H.; Pedersen, N.F. Analysis of a power grid using a Kuramoto-like model. Eur. Phys. J. B 2008, 61, 485–491. [Google Scholar] [CrossRef]
- Tanaka, H.A.; Lichtenberg, A.J.; Oishi, S. First order phase transition resulting from finite inertia in coupled oscillator systems. Phys. Rev. Lett. 1997, 78, 2104–2107. [Google Scholar] [CrossRef]
- Ódor, G.; Hartmann, B. Heterogeneity effects in power grid network models. Phys. Rev. E 2018, 98, 022305. [Google Scholar] [CrossRef] [PubMed]
- Villegas, P.; Moretti, P.; Munoz, M.A. Frustrated hierarchical synchronization and emergent complexity in the human connectome network. Sci. Rep. 2014, 4, 5990. [Google Scholar] [CrossRef]
- Millán, A.P.; Torres, J.J.; Bianconi, G. Complex network geometry and frustrated synchronization. Sci. Rep. 2018, 8, 9910. [Google Scholar] [CrossRef] [PubMed]
- Ódor, G.; Deng, S.; Hartmann, B.; Kelling, J. Synchronization dynamics on power grids in Europe and the United States. Phys. Rev. E 2022, 106, 034311. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Ódor, G.; Hartmann, B. Power-law distributions of dynamic cascade failures in power-grid models. Entropy 2020, 22, 666. [Google Scholar] [CrossRef]
- Cardy, J.L. One-dimensional models with 1/r2interactions. J. Phys. A Math. Gen. 1981, 14, 1407–1415. [Google Scholar] [CrossRef]
- Janssen, H.K.; Müller, M.; Stenull, O. Generalized epidemic process and tricritical dynamic percolation. Phys. Rev. E 2004, 70, 026114. [Google Scholar] [CrossRef]
- Chan, W.; Ghanbarnejad, F.; Grassberger, P. Avalanche outbreaks emerging in cooperative contagions. Nat. Phys. 2015, 11, 936–940. [Google Scholar]
- Gómez-Gardeñes, J.; Gómez, S.; Arenas, A.; Moreno, Y. Explosive Synchronization Transitions in Scale-Free Networks. Phys. Rev. Lett. 2011, 106, 128701. [Google Scholar] [CrossRef]
- Coutinho, B.C.; Goltsev, A.V.; Dorogovtsev, S.N.; Mendes, J.F.F. Kuramoto model with frequency-degree correlations on complex networks. Phys. Rev. E 2013, 87, 032106. [Google Scholar] [CrossRef]
- Ódor, G.; de Simoni, B. Heterogeneous excitable systems exhibit Griffiths phases below hybrid phase transitions. Phys. Rev. Res. 2021, 3, 013106. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Ahnert, K.; Mulansky, M. Boost::odeint. Available online: https://odeint.com (accessed on 1 December 2022).
- Jeffrey, K.; Deng, S.; Barancsuk, L.; Hartmann, B.; Ódor, G. Solving the Kuramoto Equation by GPUs; Centre for Energy Research: Budapest, Hungary, to be published.
- Ódor, G.; Deco, G.; Kelling, J. Differences in the critical dynamics underlying the human and fruit-fly connectome. Phys. Rev. Res. 2022, 4, 023057. [Google Scholar] [CrossRef]
- Ódor, G.; Kelling, J.; Deco, G. The effect of noise on the synchronization dynamics of the Kuramoto model on a large human connectome graph. J. Neurocomput. 2021, 461, 696–704. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ódor, G.; Deng, S. Synchronization Transition of the Second-Order Kuramoto Model on Lattices. Entropy 2023, 25, 164. https://doi.org/10.3390/e25010164
Ódor G, Deng S. Synchronization Transition of the Second-Order Kuramoto Model on Lattices. Entropy. 2023; 25(1):164. https://doi.org/10.3390/e25010164
Chicago/Turabian StyleÓdor, Géza, and Shengfeng Deng. 2023. "Synchronization Transition of the Second-Order Kuramoto Model on Lattices" Entropy 25, no. 1: 164. https://doi.org/10.3390/e25010164
APA StyleÓdor, G., & Deng, S. (2023). Synchronization Transition of the Second-Order Kuramoto Model on Lattices. Entropy, 25(1), 164. https://doi.org/10.3390/e25010164







