1. Introduction
Causal confirmation is the expansion of Bayesian confirmation. It is also a task of causal inference. The Existing Causal Inference Theory (ECIT), including Rubin’s (or Neyman-Rubin) potential outcomes model [
1,
2] and Pearl’s causal graph [
3,
4], has achieved great success. However, causal confirmation is rarely mentioned.
Bayesian confirmation theories are also called confirmation theories, which can be divided into incremental and inductive schools. The incremental school affirms that the confirmation measures the supporting strength of evidence
e to hypothesis
h, as explained by Fitelson [
5]. Following Carnap [
6], the incremental school’s researchers often use the increment of a hypothesis’ probability or logical probability,
P(
h|e) −
P(
h), as a confirmation measure. Fitelson [
5] discussed causal confirmation with this measure and obtained some conclusions incompatible with the ECIT. On the other hand, the inductive school [
7,
8] considers confirmation as induction’s modern form, whose task is to measure a major premise’s creditability supported by a sample or sampling distribution.
We use e→h to denote a major premise. Variable e takes one of two possible values e1 and its negation e0. Variable h takes one of two possible values h1 and its negation h0. Then a sample includes four examples (e1, h1), (e1, h0), (e0, h1), and (e0, h0) with different proportions. The inductive school’s researchers often use positive examples and counterexamples’ proportions (P(e1|h1) and P(e1|h0)) or likelihood ratio (P(e1|h1)/P(e1|h0)) to express confirmation measures.
A confirmation measure is often denoted by
C(
e, h) or
C(
h, e). The author (of this paper) agrees with the inductive school and suggests using
C(
e→
h) to express a confirmation measure so that the task is evident [
8]. In this paper, we use “
x=>
y” to denote “Cause
x leads to outcome
y”.
Although the two schools understand confirmation differently, both use sampling distribution
P(
e,
h) to construct confirmation measures. There have been many confirmation measures [
8,
9]. Most researchers agree that an ideal confirmation measure should have the following two desired properties:
normalizing property [
9,
10], which means
C(
e,
h) should change between −1 and 1 so that the difference between a rule
e→
h and the best or the worst rule is clear;
hypothesis symmetry [
11] or consequent symmetry [
8], which means
C(
e1→
h1) = −
C(
e1→
h0). For example,
C(raven→black) = −
C(raven→non-black).
The author in [
8] distinguished channels’ confirmation and predictions’ confirmation and provided channels’ confirmation measure
b*(
e→h) and predictions’ confirmation measure
c*(
e→
h). Both have the above two desired properties and can be used for the probability predictions of
h according to
e.
Bayesian confirmation confirms associated relationships, which are different from causal relationships. Association includes causality, but many associated relationships are not causal relationships. One reason is that the existence of association is symmetrical (if P(h|e) ≠ 0, then P(e|h) ≠ 0), whereas the existence of causality is asymmetrical. For example, in medical tests, P(positive|infected) reflects both association and causality. However, inversely, P(infected|positive) only indicates association. Another reason is that two associated events, A and B, such as electric fans’ easy selling and air conditioners’ easy selling, are the outcomes caused by the third event (hot weather). Neither P(A|B) nor P(B|A) indicates causality.
Causal inference only deals with uncertain causal relationships in nature and human society without considering those in mathematics, such as (x + 1)(x − 1) < x2 because (x + 1)(x − 1) = x2 − 1. We know that Kant distinguishes analytic judgments and synthetic judgments. Although causal inference is a mathematical method, it is used for synthetic judgments to obtain uncertain rules in biology, psychology, economics, etc. In addition, causal confirmation only deals with binary causality.
Although causal confirmation was rarely mentioned in the ECIT, the researchers of causal inference and epidemiology have provided many measures (without using the term “confirmation measure”) to indicate the strength of causation. These measures include risk difference [
12]:
relative risk difference or the risk ratio (like the likelihood ratio for medical tests):
and the probability of causation
Pd (used by Rubin and Greenland [
13]) or the probability of necessity
PN (used by Pearl [
3]). There is:
Pd is also called Relative Risk Reduction (RRR) [
12]. In the above formula, max(0, ∙) means its minimum is 0. This function is to make
Pd more like a probability. Measure
b* proposed by the author in [
8] is like
Pd, but
b* changes between −1 and 1. The above risk measures can measure not only risk or relative risk but also success or relative success raised by the cause.
The risk measures in Equations (1)–(3) are significant; however, they do not possess the two desired properties and hence are improper as causal confirmation measures.
We will encounter Simpson’s Paradox if we only use sampling distributions for the above measures. Simpson’s Paradox has been accompanying the study of causal inference, as the Raven Paradox has been going with the study of Bayesian confirmation. Simpson proposed the paradox [
14] using the following example.
Example 1 [
15]
. The admission data of the graduate school of the University of California, Berkeley (UCB), for the fall of 1973 showed that 44% of male applicants were accepted, whereas only 35% of female applicants were accepted. There was probably gender bias present. However, in most departments, female applicants’ acceptance rates were higher than male applicants.
Was there a gender bias? Should we accept the overall conclusion or the grouping conclusion (i.e., that from every department)? If we take the overall conclusion, we can think that the admission had a bias against the female. On the other hand, if we accept the grouping conclusion, we can say that the female applicants were priorly accepted. Therefore, we say there exists a paradox.
Example 1 is a little complicated and easy to raise arguments against. To simplify the problem, we use Example 2, which the researchers of causal inference often mentioned, to explain Simpson’s Paradox quantitatively.
We use x1 to denote a new cause (or treatment) and x0 to denote a default cause or no cause. If we need to compare two causes, we may use x1 and x2, or xi and xj, to represent them. In these cases, we may assume that one is default like x0.
Example 2 [
16,
17]
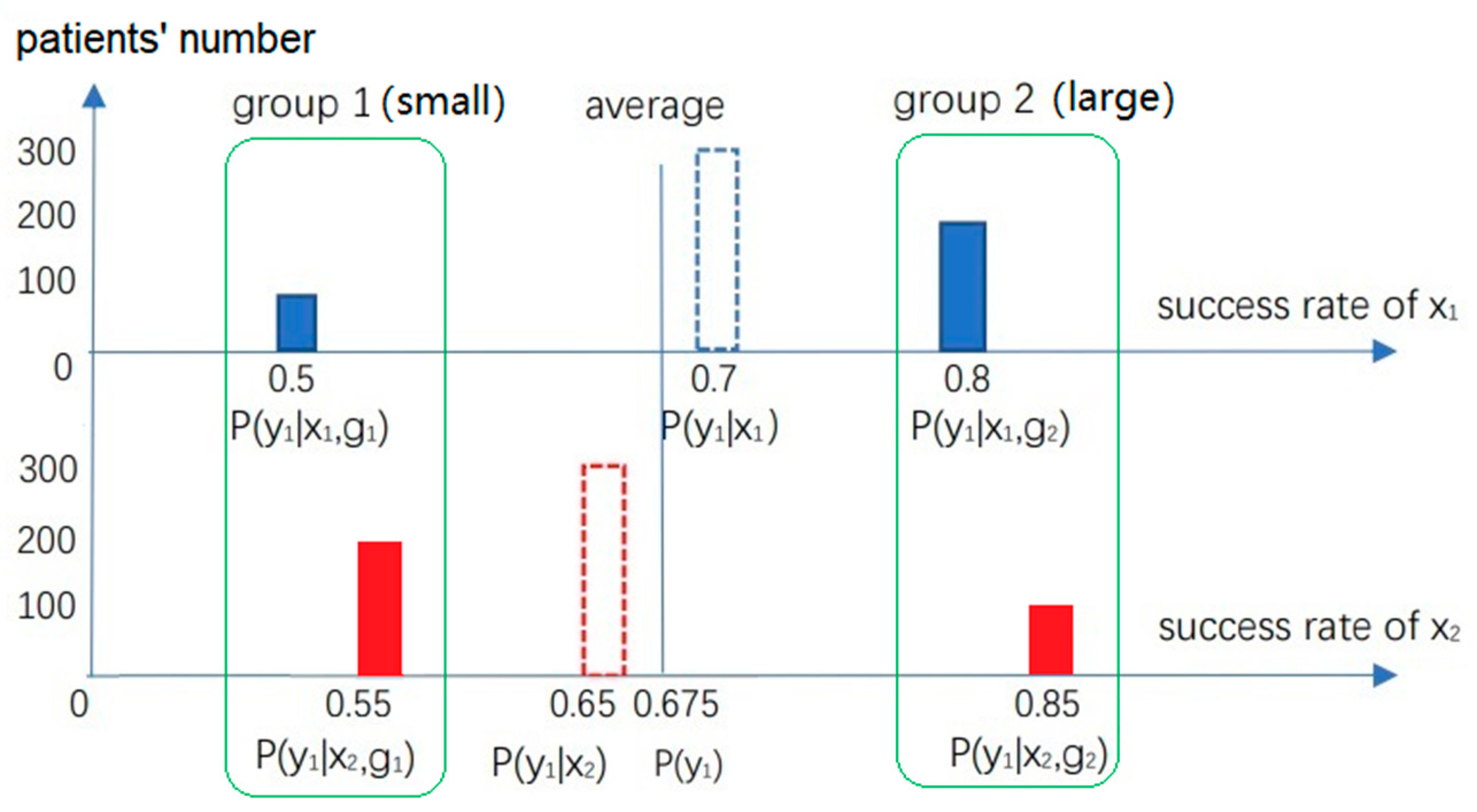
. Suppose there are two treatments, x1 and x2, for patients with kidney stones. Patients are divided into two groups according to their size of stones. Group g1 includes patients with small stones, and group g2 has large ones. Outcome y1 represents the treatment’s success. Success rates shown in Figure 1 are possible. In each group, the success rate of x2 is higher than that of x1; however, the overall conclusion is the opposite.
According to Rubin’s potential outcomes model [
1], we should accept the grouping conclusion:
x2 is better than
x1. The reason is that the stones’ size is a confounder, and the overall conclusion is affected by the confounder. We should eliminate this influence. The method is to imagine the patients’ numbers in each group are unchanged whether we use
x1 or
x2. Then we replace weighting coefficients
P(
gi|
x1) and
P(
gi|x2) with
P(
gi) (
i = 1, 2) to obtain two new overall success rates. Rubin [
1] expresses them as
P(
y1x1) and
P(
y1x2); whereas Pearl [
3] expresses them as
P(
y1|do(
x1)) and
P(
y1|do(
x2)). Then, the overall conclusion is consistent with the grouping conclusion.
Should we always accept the grouping conclusion when the two conclusions are inconsistent? It is not sure! Example 3 is a counterexample.
Example 3 (from [
18])
. Treatment x1 denotes taking a kind of antihypertensive drug, and treatment x0 means taking nothing. Outcome y1 denotes recovering health, and y0 means not. Patients are divided into group g1 (with high blood pressure) and group g0 (with low blood pressure). It is very possible that in each group g, P(y1|g, x1) < P(y1|g, x0) (which means x0 is better than x1); whereas overall result is P(y1|x1) > P(y1|x0) (which means x1 is better than x0). The ECIT tells us that we should accept the overall conclusion that x1 is better than x0 because blood pressure is a mediator, which is also affected by x1. We expect that x1 can move a patient from g1 to g0; hence we need not change the weighting coefficients from P(g|x) to P(g). The grouping conclusion, P(y1|g, x1) < P(y1|g, x0), exists because the drug has a side effect.
There are also some examples where the grouping conclusion is acceptable from one perspective, and the overall conclusion is acceptable from another.
Example 4 [
19]
. The United States statistical data about COVID-19 in June 2020 show that COVID-19 led to a higher Case Fatality Rate (CFR) of non-Hispanic whites than others (overall conclusion). We can find that only 35.3% of the infected people were non-Hispanic whites, whereas 49.5% of the infected people who died from COVID-19 were non-Hispanic whites. It seems that COVID-19 is more dangerous to non-Hispanic whites. However, Dana Mackenzie pointed out [
19]
that we will obtain the opposite conclusion from every age group because the CFR of non-Hispanic whites is lower than that of other people in every age group. So, there exists Simpson’s Paradox. The reason is that non-Hispanic whites have longer lifespans and a relatively large proportion of the elderly, while COVID-19 is more dangerous to the elderly.
Kügelgen et al. [
20] also pointed out the existence of Simpson’s Paradox after they compared the CFRs of COVID-19 (reported in 2020) in China and Italy. Although the overall conclusion was that the CFR in Italy was higher than in China, the CFR of every age group in China was higher than in Italy. The reason is that the proportion of the elderly in Italy is larger than in China.
According to Rubin’s potential outcomes model or Pearl’s causal graph, if we think that the reason for non-Hispanic whites’ longevity is good medical conditions or other elements instead of their race, then the lifespan is a confounder. Therefore, we should accept the grouping conclusion. On the other hand, if we believe that non-Hispanic whites are longevous because they are whites, then the lifespan is a mediator, so we should accept the overall conclusion.
Example 1 is similar to Example 4, but the former is not easy to understand. The data show that the female applicants tended to choose majors with low admission rates (perhaps because lower thresholds resulted in more intense competition). This tendency is like the lifespan of the white. If we regard lifespan as a confounder, Berkeley University had no gender bias against the female. On the other hand, if we believe the female is the cause of this tendency, the overall conclusion is acceptable, and gender bias should have existed. Deciding which of the two judgments is right depends on one’s perspective.
Pearl’s causal graph [
3] makes it clear that for the same data, if supposed causal relationships are different, conclusions are also different. So, it is not enough to have data only. We also need the structural causal model.
However, the incremental school’s philosopher Fitelson argues that from the perspective of Bayesian confirmation, we should accept the overall conclusion according to the data without considering causation; Simpson’s Paradox does not exist according to his rational explanation. His reason is that we can use the measure [
5]:
to measure causality. Fitelson proves (see Fact 3 of Appendix in [
5]) that if there is:
then there must be
P(
y1|
x1) >
P(
y1). The result is the same when “>“ is replaced with “<“. Therefore, Fitelson affirms that, unlike
RD and
Pd,
measure i does not result in the paradox.
However, Equation (5) expresses a rigorous condition, which excludes all examples with joint distributions P(y, x, g) that cause the paradox, including Fitelson’s simplified example about the admissions of the UCB.
One cannot help asking:
For Example 2 about kidney stones, is it reasonable to accept the overall conclusion without considering the difficulties of treatments?
Is it necessary to extend or apply a Bayesian confirmation measure incompatible with the ECIT and medical practices to causal confirmation?
Except for the incompatible confirmation measures, are there no compatible confirmation measures?
In addition to the incremental school’s confirmation measures, there are also the inductive school’s confirmation measures, such as F proposed by Kemeny and Oppenheim in 1952 and b* provided by the author in 2020.
This paper mainly aims at:
combining the ECIT to deduce causal confirmation measure Cc(x1 => y1) (“C” stands for confirmation and “c” for the cause), which is similar to Pd but can measure negative causal relationships, such as “vaccine => infection”;
explaining that measures Cc and Pd are more suitable for causal confirmation than measure i by using some examples with Simpson’s Paradox;
supporting the inductive school of Bayesian confirmation in turn.
When the author proposed measure
b*, he also provided measure
c* for eliminating the Raven Paradox [
8]. For extending
c* to causal confirmation, this paper presents measure
Ce(
x1 =>
y1), which indicates the outcome’s inevitability or the cause’s sufficiency.
2. Background
2.1. Bayesian Confirmation: Incremental School and Inductive School
A universal judgment is equivalent to a hypothetical judgment or a rule, such as “All ravens are black” is equivalent to “For every x, if x is a raven, then x is black”. Both can be used as a major premise for a syllogism. Due to the criticism of Hume and Popper, most philosophers no longer expect to obtain absolutely correct universal judgments or major premises by induction but hope to obtain their degrees of belief. A degree of belief supported by a sample or sampling distribution is the degree of confirmation.
It is worth noting that a proposition does not need confirmation. Its truth value comes from its usage or definition [
8]. For example, “People over 18 are adults” does not need confirmation; whether it is correct depends on the government’s definition. Only major premises (such as “All ravens are black” and “If a person’s Nucleic Acid Test is positive, he is likely to be infected with COVID-19”) need confirmation.
A natural idea is to use conditional probability
P(
h|e) to confirm a major premise or rule denoted with
e→
h. This measure is also recommended by Fitelson [
5], and called
confirm f. There is [
5,
6]:
However, P(h|e) depends very much on the prior probability P(h) of h. For example, where COVID-19 is prevalent, P(h) is large, and P(h|e) is also large. Therefore, P(h|e) cannot reflect the necessity of e. An extreme example is that h and e are independent of each other, but if P(h) is large, P(h|e) = P(h, e)/P(e) = P(h) is also large. At this time, P(h|e) does not reflect the creditability of the causal relationship. For example, h = “There will be no earthquake tomorrow”, P(h) = 0.999, and e = “Grapes are ripe”. Although e and h are irrelative, P(h|e) = P(h) = 0.999 is very large. However, we cannot say that the ripe grape supports no earthquake happening.
For this reason, the incremental school’s researchers use posterior (or conditional) probability minus prior probability to express the degree of confirmation. These confirmation measures include [
6,
10,
21,
22]:
In the above measures,
D(
e1,
h1) is
measure i recommended by Fitelson in [
5].
R(
e1,
h1) is an information measure. It can be written as log
P(
h1|
e1) − log
P(
h1). Since log
P(
h1|
e1) − log
P(
h1) = log
P(
e1|
h1) − log
P(
e1) = log
P(
h1,
e1) − log[
P(
h1)
P(
e1)],
D,
M, and
C increase with
R and hence can be replaced with each other.
Z is the normalization of
D for having the two desired properties [
10]. Therefore, we can also call the incremental school the information school.
On the other hand, the inductive school’s researchers use the difference (or likelihood ratio) between two conditional probabilities representing the proportions of positive and negative examples to express confirmation measures. These measures include [
7,
8,
23,
24,
25]:
They are all positively related to the Likelihood Ratio (
LR+ =
P(
e1|
h1)/
P(
e1|
h0)). For example,
L = log
LR+ and
F = (
LR+ − 1)/(
LR+ + 1) [
7]. Therefore, these measures are compatible with risk (or reliability) measures, such as
Pd, used in medical tests and disease control. Although the author has studied semantic information theory for a long time [
26,
27,
28] and believe both schools have made important contributions to Bayesian confirmation, he is on the side of the inductive school. The reason is that information evaluation occurs before classification, whereas confirmation is needed after classification [
8].
Although the researchers understand confirmation differently, they all agree to use a sample including four types of examples (
e1,
h1), (
e0,
h1), (
e1,
h0), and (
e0,
h0) with different proportions as the evidence to construct confirmation measures [
8,
10]. The main problem with the incremental school is that they do not distinguish the evidence of a major premise and that of the consequent of the major premise well. When they use the four examples’ proportions to construct confirmation measures,
e is regarded as the major premise’s antecedent, whose negation
e0 is meaningful. However, when they say “to evaluate the supporting strength of
e to
h”,
e is understood as a sample, whose negation
e0 is meaningless. It is more meaningless to put a sample
e or
e0 in an example (
e1,
h1) or (
e0,
h1).
We compare
D (i.e.,
measure i) and
S to show the main difference between the two schools’ measures. Since:
we can find that
D changes with
P(
e0) or
P(
e1), but
S does not.
P(
e) means the source and
P(
h|e) means the channel.
D is related to the source and the channel, but
S is only related to the channel. Measures
F and
b* are also only related to channel
P(
e|h). Therefore, the author calls
b* the channels’ confirmation measure.
2.2. The P-T Probability Framework and the Methods of Semantic Information and Cross-Entropy for Channels’ Confirmation Measure b*(e→h)
In the P-T probability framework [
28] proposed by the author, there are both statistical probability
P and logical probability (or truth value)
T; the truth function of a predicate is also a membership function of a fuzzy set [
29]. Therefore, the truth function also changes between 0 and 1. The purpose of proposing this probability framework is to set up the bridge between statistics and fuzzy logic.
Let X be a random variable representing an instance, taking a value x∈A = {x0,x1,…}, and Y be a random variable representing a label or hypothesis, taking a value y∈B = { y0,y1,…}. The Shannon channel is a conditional probability matrix P(yj|xi) (i = 1,2,...; j = 1,2,…) or a set of transition probability functions P(yj|x) (j = 1,2,…). The semantic channel is a truth value matrix T(yj|xi) (i = 1,2,…; j = 1,2,…) or a set of truth functions T(yj|x) (j = 0,1,…). Let the elements in A that make yj true form a fuzzy subset θj. The membership function T(θj|x) of θj is also the truth function T(yj|x) of yj, i.e., T(θj|x) = T(yj|x).
The logical probability of
yj is:
Zadeh calls it the fuzzy event’s probability [
30]. When
yj is true, the conditional probability of
x is:
Fuzzy set θj can also be understood as a model parameter; hence P(x|θj) is a likelihood function.
The differences between logical probability and statistical probability are:
The statistical probability is normalized (the sum is 1), whereas the logical probability is not. Generally, we have T(θ0) + T(θ1) + … > 1.
The maximum value of T(θj|x) is 1 for different x, whereas P(y0|x) + P(y1|x) + … = 1 for a given x.
We can use the sample distribution to optimize the model parameters. For example, we use x to represent the age, use a logistic function as the truth function of the elderly: T(“elderly”|x) = 1/[1 + exp (− bx + a)], and use a sampling distribution to optimize a and b.
The (amount of) semantic information about
xi conveyed by
yj is:
For different
x, the average semantic information conveyed by
yj is:
In the above formula,
H(X|θj) is a cross-entropy:
The cross-entropy has an important property: when we change
P(
x|
θj) so that
P(
x|
θj) =
P(
x|yj),
H(X|θj) reaches its minimum. It is easy to find from Equation (10) that
I(X;
θj) reaches its maximum as
H(X|θj) reaches its minimum. The author has proved that if
P(
x|
θj) =
P(
x|yj), then
T(
θj|
x)∝
P(
yj|
x) [
27]. If for all
j,
T(
θj|
x)∝
P(
yj|
x), we say that the semantic channel matches the Shannon channel.
We use the medical test as an example to deduce the channels’ conformation measure b*. We define h∈{h0, h1} = {infected, uninfected} and e∈{e0, e1} = {positive, negative}. The Shannon channel is P(e|h), and the semantic channel is T(e|h). The major premise to be confirmed is e1→h1, which means “If one’s test is positive, then he is infected”.
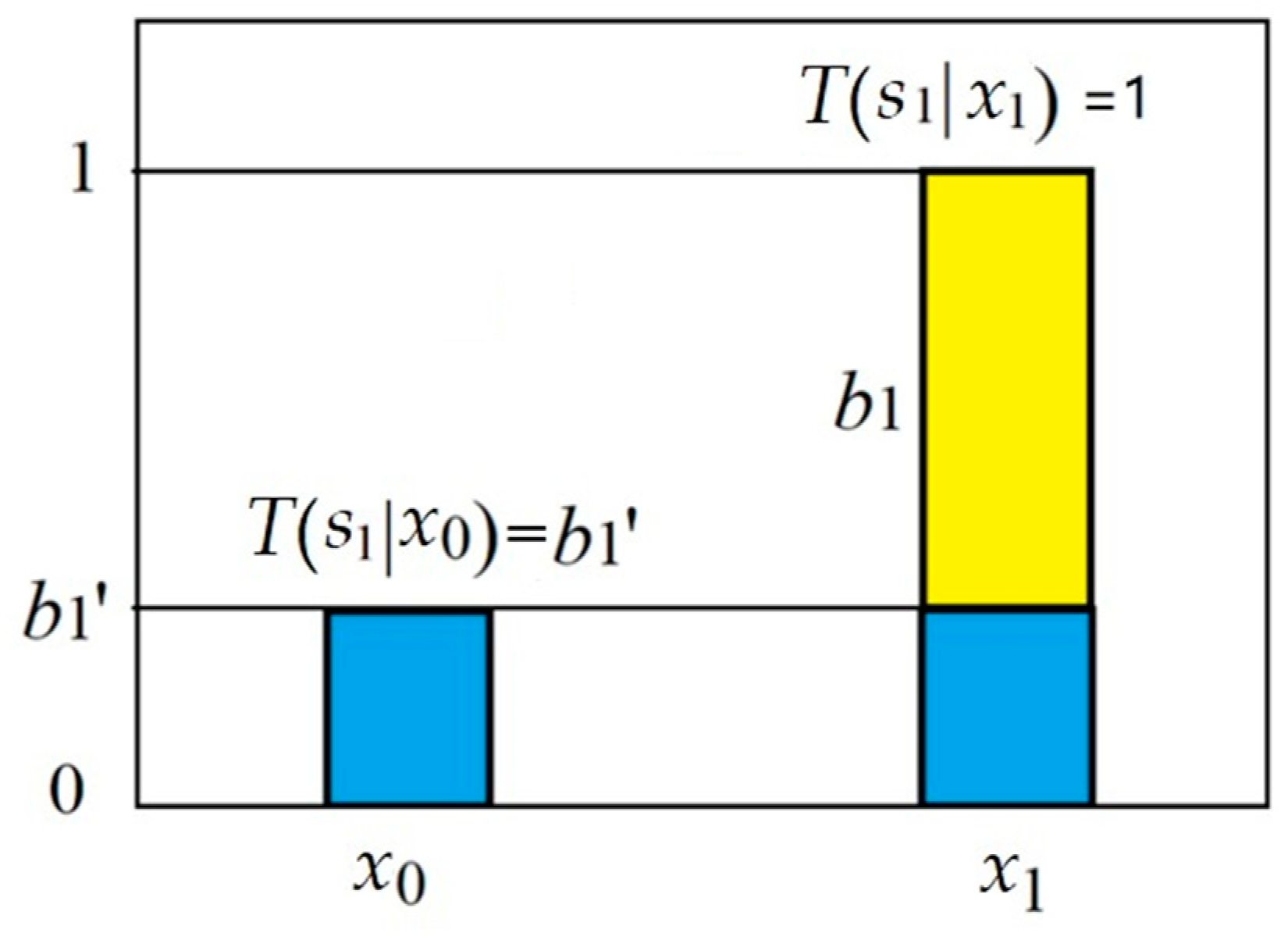
We regard a fuzzy predicate
e1(
h) as the linear combination of a clear predicate (whose truth value is 0 or 1) and a tautology (whose truth value is always 1). Let the tautology’s proportion be
b1′ and the clear predicate’s proportion be 1 −
b1′. Then we have:
The
b1′ is also called the degree of disbelief of rule
e1→
h1. The degree of disbelief optimized by a sample, denoted by
b1′*, is the degree of disconfirmation. Let
b1* denote the degree of confirmation; we have
b1′* = 1 − |
b1*|. By maximizing average semantic information
I(
H;
θ1) or minimizing cross-entropy
H(H|θj), we can deduce (see
Section 3.2 in [
8]):
Suppose that likelihood function
P(
h|
e1) is decomposed into an equiprobable part and a part with 0 and 1. Then, we can deduce the predictions’ confirmation measure
c*:
Measure
b* is compatible with the likelihood ratio and suitable for evaluating medical tests. In contrast, measure
c* is appropriate to assess the consequent inevitability of a rule and can be used to clarify the Raven Paradox [
8]. Moreover, both measures have the normalizing property and symmetry mentioned above.
2.3. Causal Inference: Talking from Simpson’s Paradox
According to the ECIT, the grouping conclusion is acceptable for Example 2 (about kidney stones), whereas the overall conclusion is acceptable for Example 3 (about blood pressure). The reason is that
P(
y1|
x1) and
P(
y1|
x0) may not reflect causality well; in addition to the observed data or joint probability distribution
P(
y,
x,
g), we also need to suppose the causal structure behind the data [
3].
Suppose there is the third variable,
u.
Figure 2 shows the causal relationships in Examples 2, 3, and 4.
Figure 2a shows the causal structure of Example 2, where
u (kidney stones’ size) is a confounder that affects both
x and
y.
Figure 2b describes the causal structure of Example 3, where
u (blood pressure) is a mediator that affects
y but is affected by
x. In
Figure 2c,
u can be interpreted as either a confounder or a mediator. The causality will differ from different perspectives, and
P(
y1|do(
x)) will also differ. In all cases, we should replace
P(
y|
x) with
P(
y|do(
x)) (if they are different) to get
RD,
RR, and
Pd.
We should accept the overall conclusion for the example where
u is a mediator. However, for the example where
u is a confounder, how do we obtain a suitable
P(
y|do(
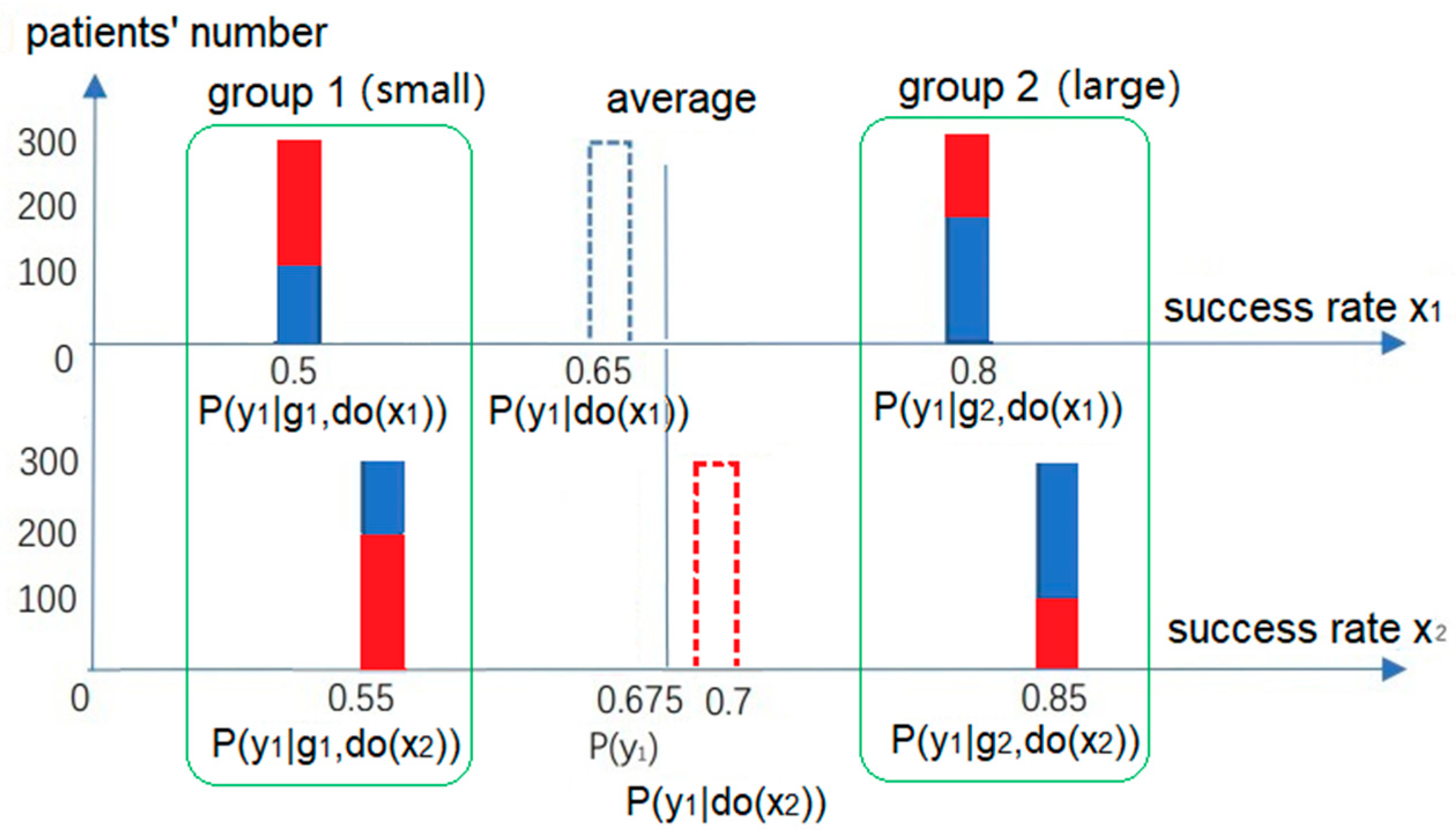
x))? According to Rubin’s potential outcomes model, we use
Figure 3 to explain the difference between
P(
y|do(
x)) and
P(
y|
x).
To find the difference in the outcomes caused by
x1 and
x2, we should compare the two outcomes in the same background. However, there is often no situation where other conditions remain unchanged except for the cause. For this reason, we need to replace
x1 with
x2 in our imagination and see the shift in
y1 or its probability. If
u is a confounder and not affected by
x, the number of members in
g1 and
g2 should be unchanged with
x, as shown in
Figure 3. The solution is to use
P(
g) instead of
P(
g|
x) for the weighting operation so that the overall conclusion is consistent with the grouping conclusion. Hence, the paradox no longer exists.
Although P(x0) + P(x1) = 1 is tenable, P(do (x1)) + P(do (x0)) = 1 is meaningless. That is why Rubin emphasizes that P(yx), i.e., P(y|do(x)), is still a marginal probability instead of a conditional probability, in essence.
Rubin’s reason [
2] for replacing
P(
g|
x) with
P(
g) is that for each group, such as
g1, the two subgroups’ members (patients) treated by
x1 and
x2 are interchangeable (i.e., Pearl’s causal independence assumption mentioned in [
5]). If a member is divided into the subgroup with
x1, its success rate should be
P(
y1|
g,
x1); if it is divided into the subgroup with
x2, the success rate should be
P(
y1|
g,
x2).
P(
g|
x1) and
P(
g|x2) are different only because half of the data are missing. However, we can fill in the missing data using our imagination.
If
u is a mediator, as shown in
Figure 2b, a member in
g1 may enter
g2 because of
x, and vice versa.
P(
g|
x0) and
P(
g|
x1) are hence different without needing to be replaced with
P(
g). We can let
P(
y1|do (
x)) =
P(
y1|
x) directly and accept the overall conclusion.
2.4. Probability Measures for Causation
In Rubin and Greenland’s article [
13]:
is explained as the probability of causation, where
t is one’s age of exposure to some harmful environment.
R(
t) is the age-specific infection rate (infected population divided by uninfected population). Let
y1 stand for the infection,
x1 for the exposure, and
x0 for no exposure. Then there is
R(
t) =
P(
y1|do(
x1),
t)/
P(
y1|do(
x0),
t). Its lower limit is 0 because the probability cannot be negative. When the change of
t is neglected, considering the lower limit, we can write the probability of causation as:
Pearl uses
PN to represent
Pd and explains
PN as the probability of necessity [
3].
Pd is very similar to confirmation measure
b* [
8]. The main difference is that
b* changes between −1 and 1.
Robert van Rooij and Katrin Schulz [
31] argue that conditionals of the form “If
x, then
y” are assertable only if:
is high. This measure is similar to confirmation measure
Z. The difference between
Pd and Δ*
Pxy is that
Pd, like
b*, is sensitive to counterexamples’ proportion
P(
y1|
x0), whereas Δ*
Pxy is not.
Table 1 shows their differences.
David E. Over et al. [
32] support the Ramsey test hypothesis, implying that the subjective probability of a natural language conditional,
P(if
p then
q), is the conditional subjective probability,
P(
q|p). This measure is
confirm f in [
5].
The author [
8] suggests that we should distinguish two types of confirmation measures for
x=>y or
e→
h. One is to stand for the necessity of
x compared with
x0; the other is for the inevitability of
y.
P(
y|
x) may be good for the latter but not for the former. The former should be independent of
P(
x) and
P(
y).
Pd is such a one.
However, there is a problem with Pd. If Pd is 0 when y is uncorrelated to x, then Pd should be negative instead of 0 when x inversely affects y (e.g., vaccine affects infection). Therefore, we need a confirmation measure between −1 and 1 instead of a probability measure between 0 and 1.
6. Conclusions
Fitelson, a representative of the incremental school of Bayesian confirmation, used D(x1, y1) = P(y1|x1) − P(y1) to denote the supporting strength of the evidence to the consequence and extended this measure for causal confirmation without considering the confounder. This paper has shown that measure D is incompatible with the ECIT and popular risk measures, such as Pd = max(0, (R − 1)/R). Using D, one can only avoid Simpson’s Paradox but he cannot eliminate it or provide a reasonable explanation as the ECIT does.
On the other hand, Rubin et al. used Pd as the probability of causation. Pd is better than D, but it is improper to call Pd a probability measure and use the probability measure to measure causation. If we use Pd as a causal confirmation measure, it lacks the normalizing property and symmetry that an ideal confirmation measure should have.
This paper has deduced causal confirmation measure Cc(x1 => y1) = (R – 1) / max(R, 1) by the semantic information method with the minimum cross-entropy criterion. Cc is similar to the inductive school’s confirmation measure b* proposed by the author earlier. However, the positive examples’ proportion P(y1|x1) and the counterexamples’ proportion P(y1|x0) are replaced with P(y1|do(x1)) and P(y1|do(x0)) so that Cc is an improved Pd. Compared with Pd, Cc has the normalizing property (it changes between –1 and 1) and the cause symmetry (Cc(x0/x1 => y1) = −Cc (x1/x0 => y1)). Since Cc may be negative, it is also suitable for evaluating the inhibition relationship between cause and outcome, such as between vaccine and infection.
This paper has provided some examples with Simpson’s Paradox for calculating the degrees of causal confirmation. The calculation results show that Pd and Cc are more reasonable and meaningful than D, and Cc is better than Pd mainly because Cc may be less than zero. In addition, this paper has also provided a causal confirmation measure Ce(x1 => y1) that indicates the inevitability of the outcome y1.
Since measure Cc and the ECIT support each other, the inductive school of Bayesian confirmation are also supported by the ECIT and the epidemical risk theory.
However, like all Bayesian confirmation measures, causal confirmation measure Cc and Ce also use size-limited samples, hence, the degrees of causal confirmation are not strictly reliable. Therefore, replacing a degree of causal confirmation with a degree interval is necessary to retain the inevitable uncertainty. This work needs further studies by combining existing theories.