Smartphone Camera Identification from Low-Mid Frequency DCT Coefficients of Dark Images
Abstract
:1. Introduction and Motivation
2. Related Work
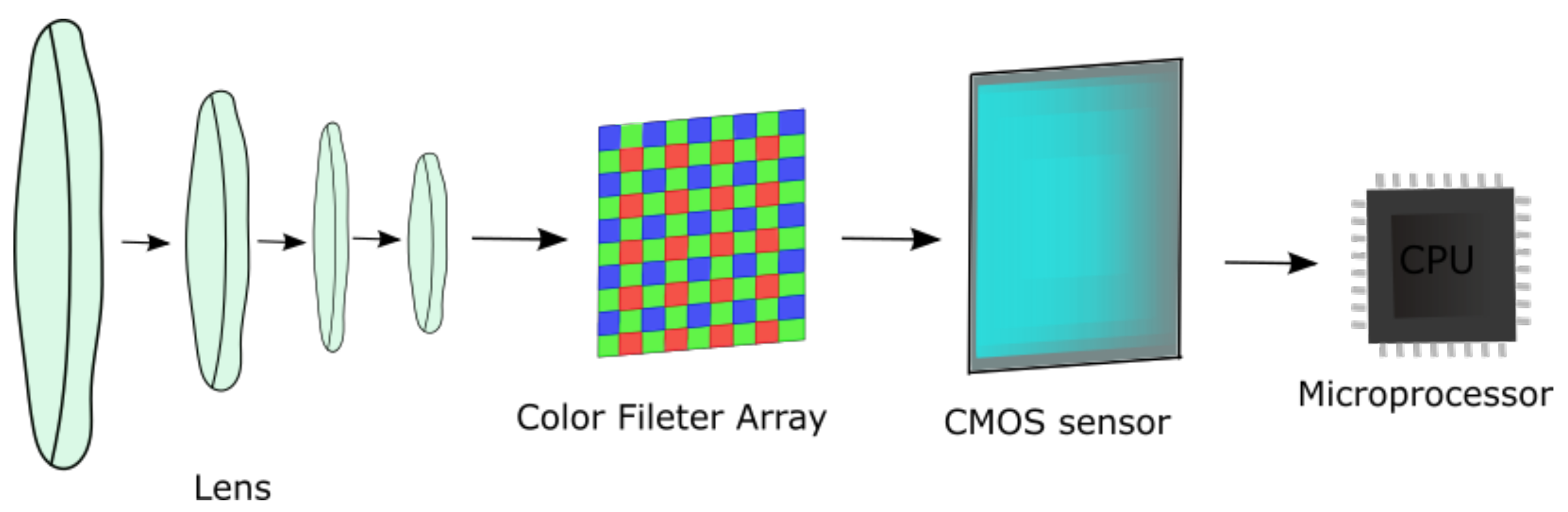
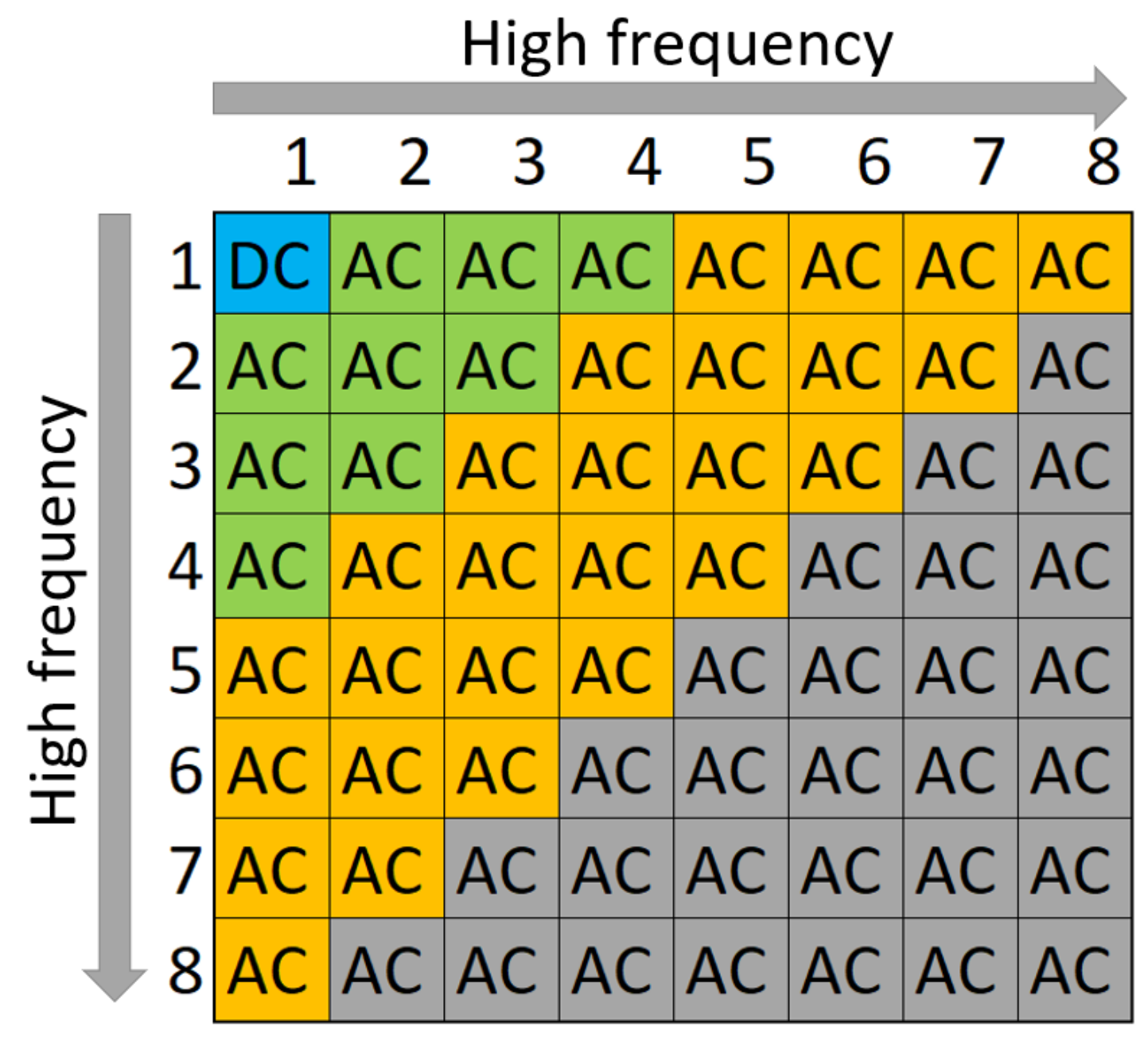
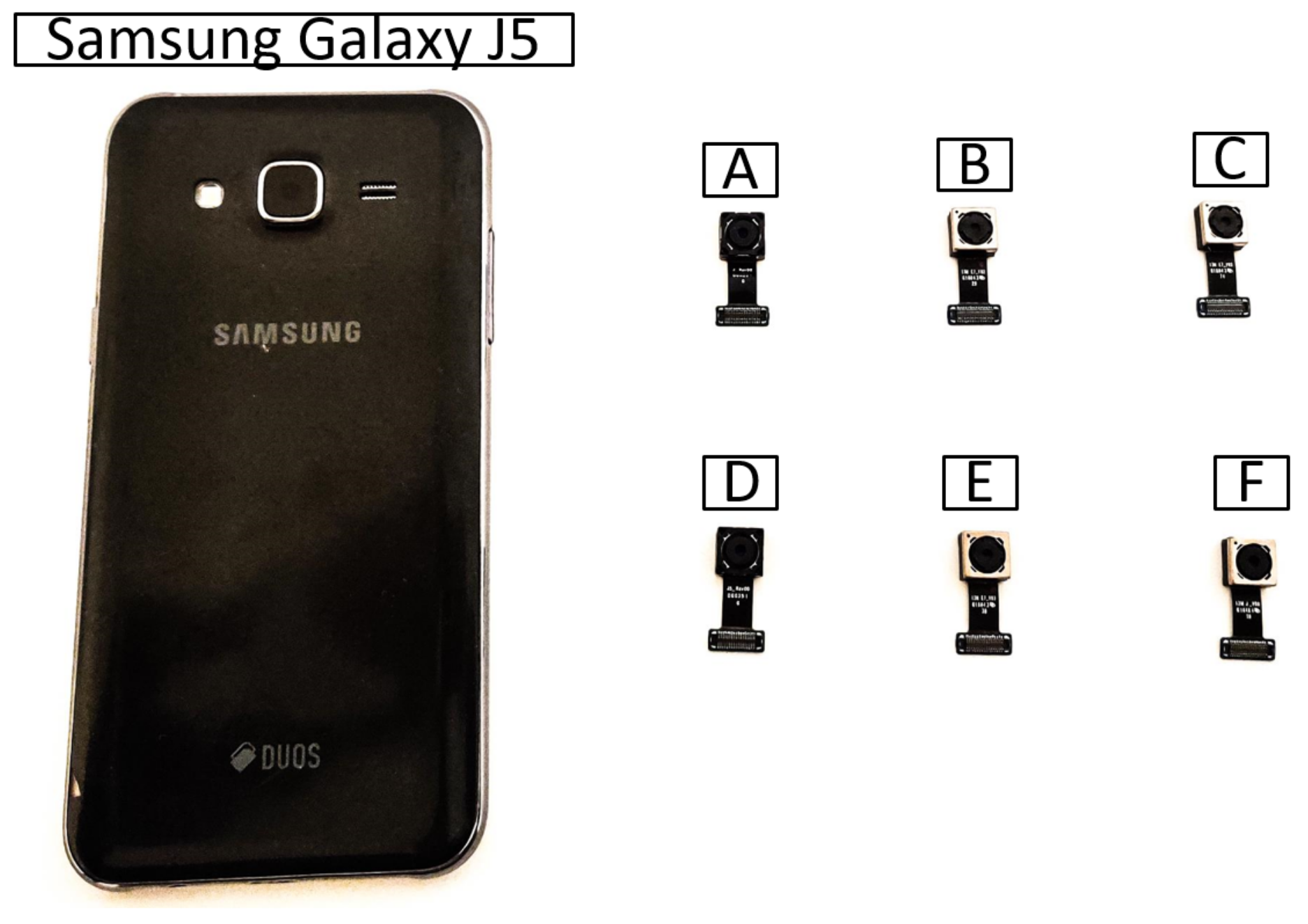
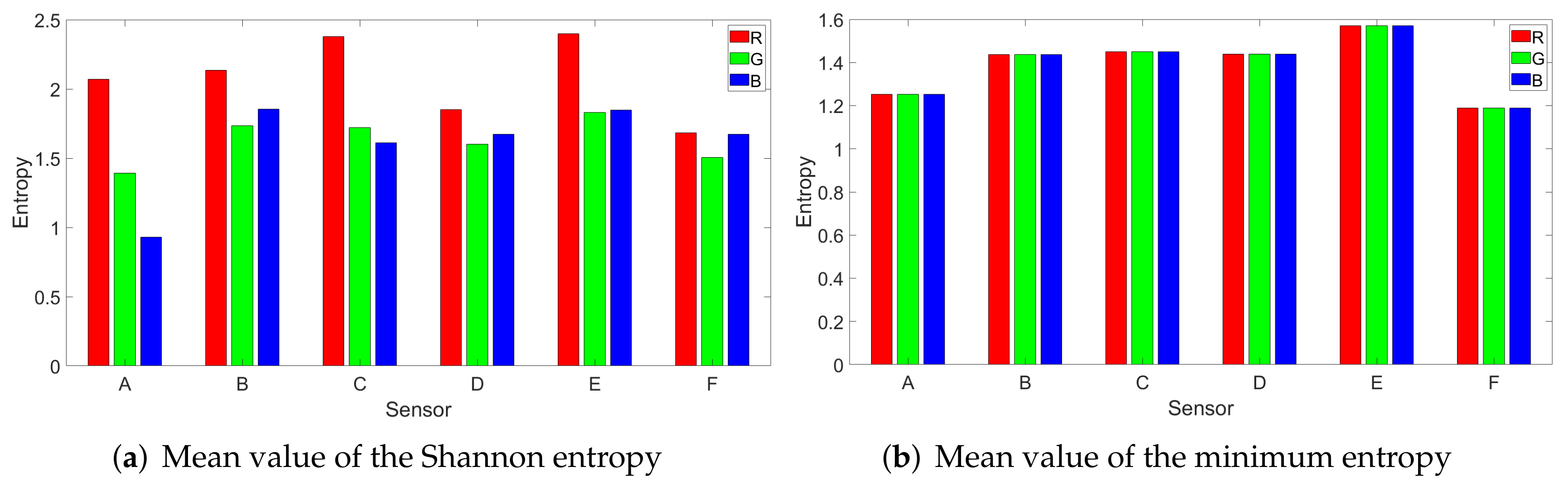
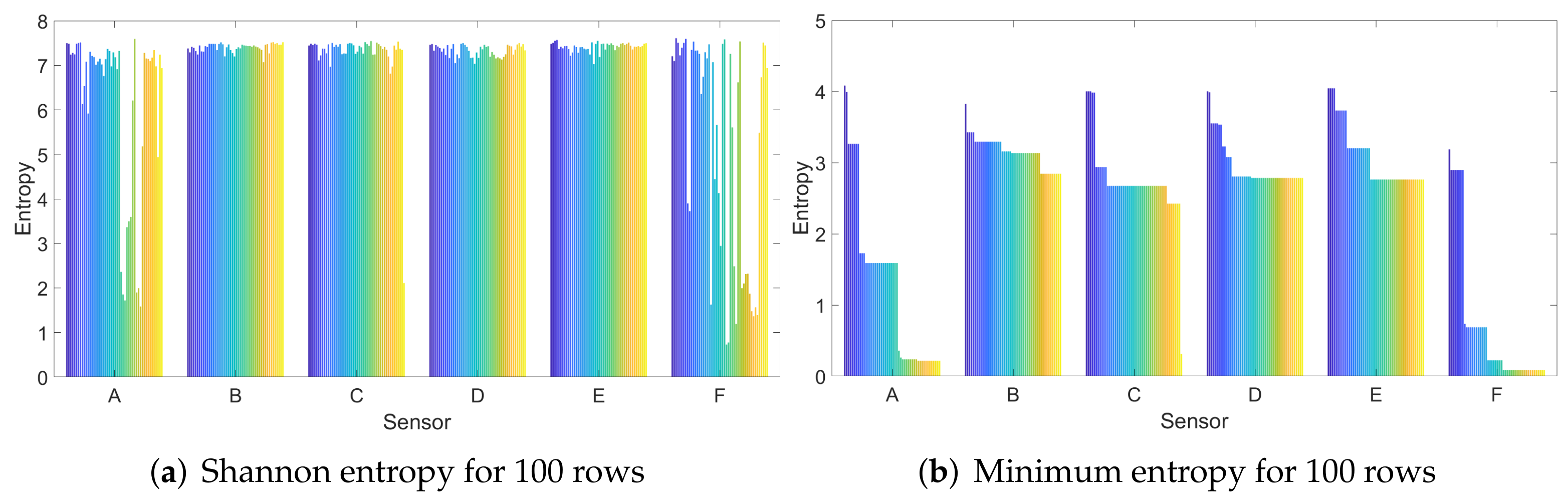
3. Setup and Methodology
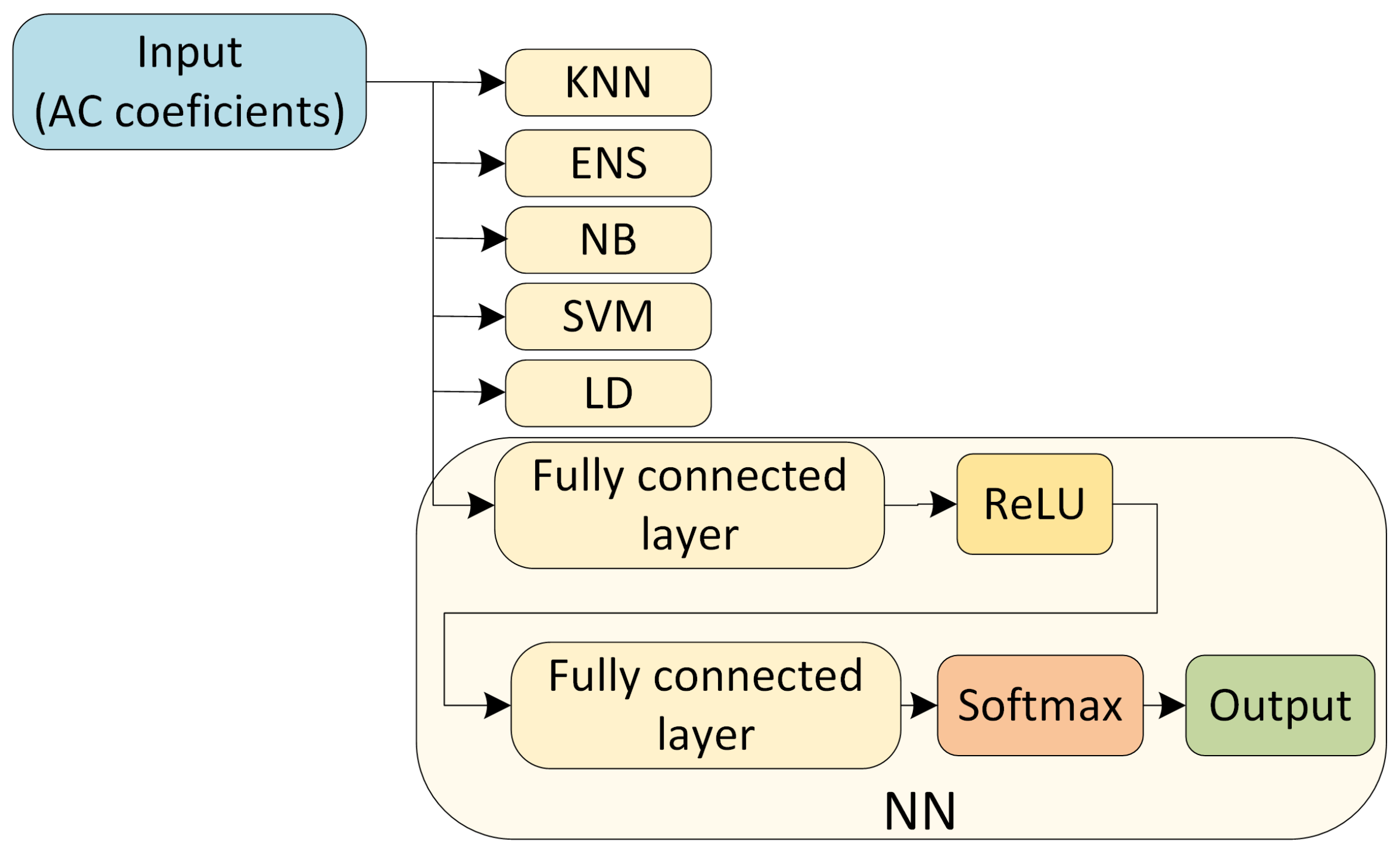
4. CMOS Sensor Identification with Machine Learning Algorithms
4.1. Selected Classifiers
4.1.1. Wide Neural Network Structure (WNN)
4.1.2. Fine KNN (KNN)
4.1.3. Ensemble—Subspace Discriminant (Ensemble)
4.1.4. Naive Bayes (NB)
4.1.5. Linear SVM (SVM)
4.1.6. Linear Discriminant (LD)
4.2. Performance Metrics
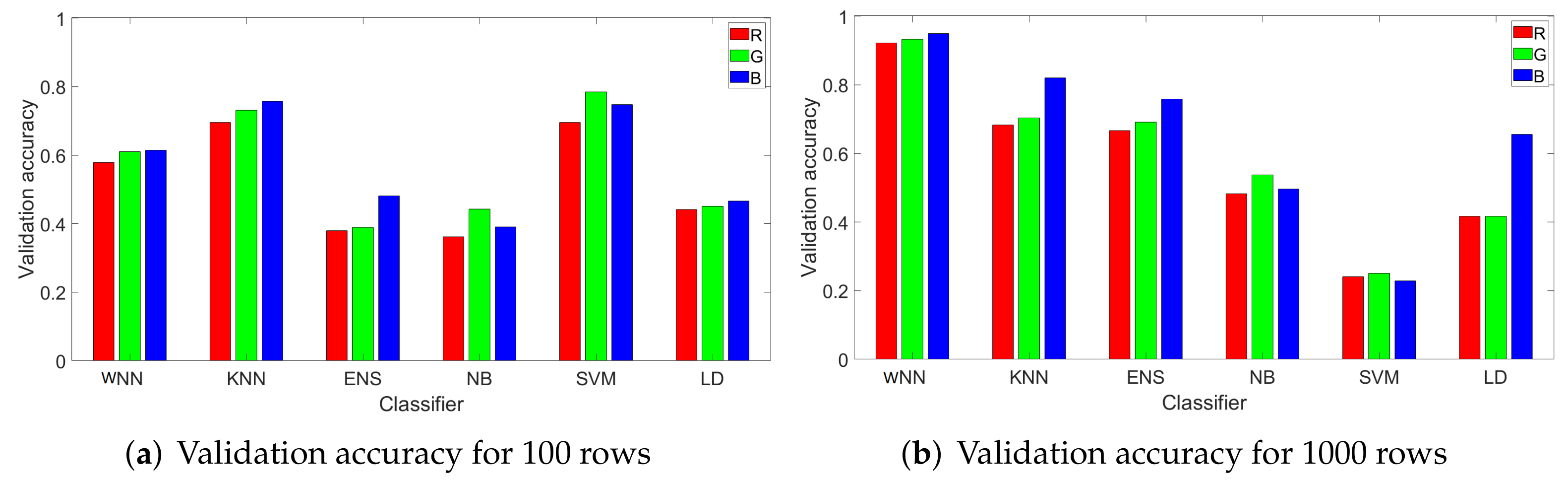
4.3. Results for 100 Randomly Selected Rows from Each Image
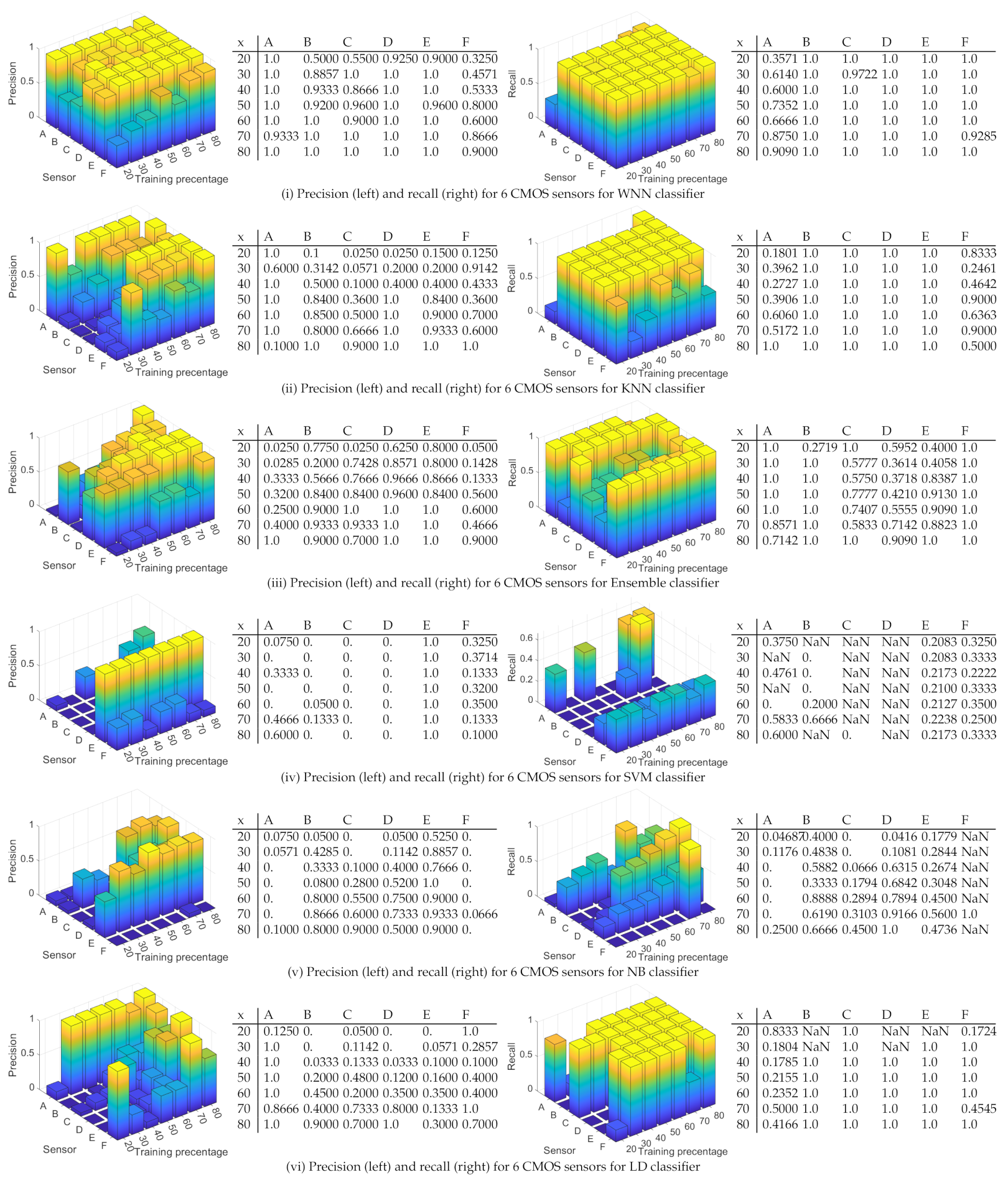
- (i)
- WNN: For a training percentage below 60%, the values for the precision are below 50% for most of sensors, while for a training percentage of 80%, the lowest precision is 60% for sensors C, 80% for sensors B, D, and F, 90% for sensor E, and 100% for sensor A. In terms of recall, sensor D reached the recall 100% regardless of training percentage. The recall of sensor E is close to 100% for all training percentages. The worst recall was obtained for sensors A and F, but in this case, the results are generally increasing with the training percentage until reaching 66% for sensor A at 80% training and 61% for sensor F.
- (ii)
- KNN: The precision is similar with the results obtained with WNN. For a training percentage below 60%, the results for precision are poor, while for a training percentage of 70%, the lowest precision is increasing to 66% for sensor C. For recall, sensor B is around 100% regardless of training percentage. Sensors C, D, and E reach a recall close to 100% for all training percentages, while sensors A and F have a recall below 70%.
- (iii)
- ENS: The precision and recall are lower that in case of KNN and WNN for all tested training percentages. In case of 20% training for sensor A, the recall value is marked with NaN since the result was not a real number due to a division by zero (there were no true positives and false negatives).
- (iv)
- SVM: For all training percentages, the precision is highest, even close to 100% in many cases for sensors A, B, C, D, and E, while sensor F reaches the maximum value of 30% at 40% training, which is not good. Regarding the recall, for all training percentages, the recall is above 53% for sensors A, B, C, and D, which proves an average performance. At higher training set sizes, sensor E has a recall of around 60–70%, which is again average, and sensor F is between 0–66%, which is not good at all.
- (v)
- NB: The precision and recall are worse than for the rest of the classifiers. For all training percentages, sensors A–F have a precision between 0–90%, which is a mixed result, only for sensor E to be more consistent at around 80%. For all sensors and all training percentages, the recall is below 81%, generally staying at around 30–50%, which is again not good.
- (vi)
- LD: For all training percentages, sensors B, C, D, and E generally have a precision below 50%, which is not good (with a few exceptions), while sensor A and F have a higher precision between 46% and 100%. Concerning the recall, the situation, however, reverses, and sensors A and F, which had better precision now have the worse recall at around 23–42%. While sensors B to E have a recall of 100%, this seems of little use as long as most of the samples for A and F are rejected.
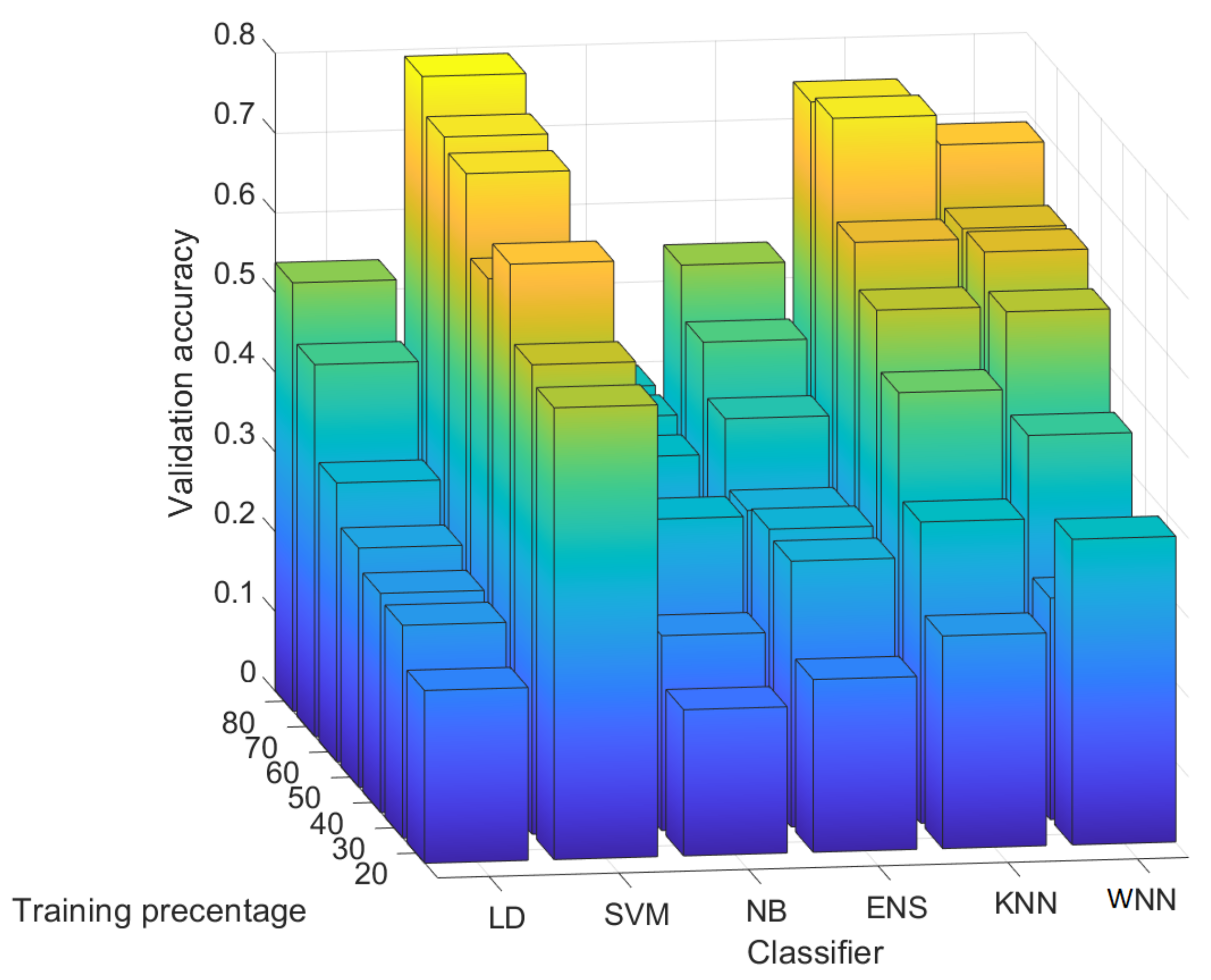
4.4. Results for 1000 Randomly Selected Rows from Each Image
- (i)
- WNN: For a training percentage above 30%, sensors A–E are identified with a precision above 86%, which is good, while sensor F is identified with a precision between 45% and 90%. For 80% training, sensors A–F are identified with a precision between 90% and 100%, which is very good. Concerning the recall, for all training percentages, the recall for sensors B–F is close or equal to 100%. For sensor A, the recall increases with the training percentage from 35% at 20% training to 90% at 80% training. These results seem satisfactory for all sensors.
- (ii)
- KNN: The results are poorer than the ones obtained with the WNN. For a training percentage below 60%, the precision is poor, while for a training percentage of 60–70%, the precision ranges from 50% to 100%. For 80% training, sensor A has only 10% precision, which is very bad, sensor C has 90% precision, and sensors B, D, E, and F reach a precision of 100%. In terms of recall, for all training percentages, the recall for sensors B–E is 100%, while sensors A and F have a mixed recall between 18% and 100%. Overall, the results with the KNN are not bad, but they are not very stable, e.g., for sensor A, the precision dropped from 100% to 10%.
- (iii)
- ENS: The precision is comparable with the precision obtained in case of the KNN. For a training percentage below 70%, the precision is lowest for sensors A and F, while for sensors B, C, D, and E, it reaches 100%. For 80% training, the precision is 100% for sensors A, D, and E and 90% for B and F, while for C, it is only 70%. For the recall, on sensor F, the recall is 100% for all training percentages and the same 100% is reached for sensor B (except in the case of 20% training, which does not seem enough). For A, C, D, and E, at 80% training, the recall is between 71–100%; below this, the results are poor for D and E, reaching under 50%.
- (iv)
- SVM: For all training percentages, the precision for sensors C and D is zero, which immediately discards this classifier. Sensors A and B similarly lead to 0% precision in some training sets, while sensor F has the precision below 35%. Even if sensor E reaches 100% precision, this is because all sensors are wrongly identified as sensor E. Finally, all sensors have a recall below 66%, which is not good.
- (v)
- NB: The results are comparable with the results in case of SVM. For all training percentages, sensors A and F are identified with a precision close to 0%, while sensors B–E are identified with a precision between 0% and 93%. In terms of recall, the values are generally between 0% and 60%, with a few exceptions, which is not great.
- (vi)
- LD: For all training percentages, sensors B–F generally give a precision below 40%, which is not good, while sensor A reaches 100% precision in most circumstances. Concerning the recall, the situation, however, reverses, and sensor A, which had better precision, now has the worse recall, generally around 20% with some exceptions. While sensors B–F have a recall of 100%, this seems of little use as long as most of the samples for A are rejected, and the precision for B–F was not great either.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Litwiller, D. Ccd vs. cmos. Photonics Spectra 2001, 35, 154–158. [Google Scholar]
- Lofstrom, K.; Daasch, W.R.; Taylor, D. IC identification circuit using device mismatch. In Proceedings of the IEEE International Solid-State Circuits Conference. Digest of Technical Papers (Cat. No. 00CH37056), San Francisco, CA, USA, 9 February 2000; pp. 72–373. [Google Scholar]
- Gassend, B.; Clarke, D.; Van Dijk, M.; Devadas, S. Silicon physical random functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 148–160. [Google Scholar]
- Kim, Y.; Lee, Y. CamPUF: Physically unclonable function based on CMOS image sensor fixed pattern noise. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–29 June 2018; pp. 1–6. [Google Scholar]
- Cao, Y.; Zalivaka, S.S.; Zhang, L.; Chang, C.H.; Chen, S. CMOS image sensor based physical unclonable function for smart phone security applications. In Proceedings of the 2014 International Symposium on Integrated Circuits (ISIC), Singapore, 10–12 December 2014; pp. 392–395. [Google Scholar]
- Cao, Y.; Zhang, L.; Zalivaka, S.S.; Chang, C.H.; Chen, S. CMOS image sensor based physical unclonable function for coherent sensor-level authentication. IEEE Trans. Circuits Syst. Regul. Pap. 2015, 62, 2629–2640. [Google Scholar] [CrossRef]
- ISO/IEC 10918-1:1994; Information Technology-Digital Compression and Coding of Continuous-Tone Still Images: Requirements and Guidelines. ISO IEC, 1994. Available online: https://www.iso.org/standard/18902.html (accessed on 5 March 2022).
- Shullani, D.; Fontani, M.; Iuliani, M.; Al Shaya, O.; Piva, A. VISION: A video and image dataset for source identification. EURASIP J. Inf. Secur. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Gloe, T.; Böhme, R. The’Dresden Image Database’for benchmarking digital image forensics. In Proceedings of the 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010; pp. 1584–1590. [Google Scholar]
- Costa, F.d.O.; Silva, E.; Eckmann, M.; Scheirer, W.J.; Rocha, A. Open set source camera attribution and device linking. Pattern Recognit. Lett. 2014, 39, 92–101. [Google Scholar] [CrossRef]
- Yao, H.; Qiao, T.; Xu, M.; Zheng, N. Robust multi-classifier for camera model identification based on convolution neural network. IEEE Access 2018, 6, 24973–24982. [Google Scholar] [CrossRef]
- Tuama, A.; Comby, F.; Chaumont, M. Camera model identification with the use of deep convolutional neural networks. In Proceedings of the IEEE International workshop on information forensics and security (WIFS), Dhabi, United Arab Emirates, 4–7 December 2016; pp. 1–6. [Google Scholar]
- Roy, A.; Chakraborty, R.S.; Sameer, U.; Naskar, R. Camera source identification using discrete cosine transform residue features and ensemble classifier. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1848–1854. [Google Scholar]
- Huang, Y.; Cao, L.; Zhang, J.; Pan, L.; Liu, Y. Exploring feature coupling and model coupling for image source identification. IEEE Trans. Inf. Forensics Secur. 2018, 13, 3108–3121. [Google Scholar] [CrossRef]
- Sameer, V.U.; Dali, I.; Naskar, R. A Deep Learning Based Digital Forensic Solution to Blind Source Identification of Facebook Images. In Proceedings of the International Conference on Information Systems Security, Maderia, Portugal, 22–24 January 2022; Springer: Berlin/Heidelberg, Germany, 2018; pp. 291–303. [Google Scholar]
- Júnior, P.R.M.; Bondi, L.; Bestagini, P.; Tubaro, S.; Rocha, A. An in-depth study on open-set camera model identification. IEEE Access 2019, 7, 180713–180726. [Google Scholar] [CrossRef]
- Cozzolino, D.; Marra, F.; Gragnaniello, D.; Poggi, G.; Verdoliva, L. Combining PRNU and noiseprint for robust and efficient device source identification. EURASIP J. Inf. Secur. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Mandelli, S.; Cozzolino, D.; Bestagini, P.; Verdoliva, L.; Tubaro, S. CNN-based fast source device identification. arXiv 2020, arXiv:2001.11847. [Google Scholar] [CrossRef]
- Chuang, K.H.; Bury, E.; Degraeve, R.; Kaczer, B.; Groeseneken, G.; Verbauwhede, I.; Linten, D. Physically unclonable function using CMOS breakdown position. In Proceedings of the IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 2–6 April 2017; p. 4C-1. [Google Scholar]
- Okura, S.; Nakura, Y.; Shirahata, M.; Shiozaki, M.; Kubota, T.; Ishikawa, K.; Takayanagi, I.; Fujino, T. P01 A Proposal of PUF Utilizing Pixel Variations in the CMOS Image Sensor. Available online: https://www.imagesensors.org/Past%20Workshops/2017%20Workshop/2017%20Papers/P01.pdf (accessed on 10 June 2022).
- Lu, X.; Hong, L.; Sengupta, K. CMOS Optical PUFs Using Noise-Immune Process-Sensitive Photonic Crystals Incorporating Passive Variations for Robustness. IEEE J. Solid-State Circuits 2018, 53, 2709–2721. [Google Scholar] [CrossRef]
- Zheng, Y.; Cao, Y.; Chang, C.H. A PUF-based data-device hash for tampered image detection and source camera identification. IEEE Trans. Inf. Forensics Secur. 2019, 15, 620–634. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhao, X.; Sato, T.; Cao, Y.; Chang, C.H. Ed-PUF: Event-Driven Physical Unclonable Function for Camera Authentication in Reactive Monitoring System. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2824–2839. [Google Scholar] [CrossRef]
- Arjona, R.; Prada-Delgado, M.A.; Arcenegui, J.; Baturone, I. Using Physical Unclonable Functions for Internet-of-Thing Security Cameras. In Interoperability, Safety and Security in IoT; Springer: Berlin/Heidelberg, Germany, 2017; pp. 144–153. [Google Scholar]
- Maes, R.; Rozic, V.; Verbauwhede, I.; Koeberl, P.; Van der Sluis, E.; van der Leest, V. Experimental evaluation of physically unclonable functions in 65 nm CMOS. In Proceedings of the ESSCIRC (ESSCIRC), Bordeaux, France, 17–21 September 2012; pp. 486–489. [Google Scholar]
- Wali, A.; Dodda, A.; Wu, Y.; Pannone, A.; Usthili, L.K.R.; Ozdemir, S.K.; Ozbolat, I.T.; Das, S. Biological physically unclonable function. Commun. Phys. 2019, 2, 1–10. [Google Scholar] [CrossRef]
- Valsesia, D.; Coluccia, G.; Bianchi, T.; Magli, E. User authentication via PRNU-based physical unclonable functions. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1941–1956. [Google Scholar] [CrossRef]
- Lukas, J.; Fridrich, J.; Goljan, M. Digital camera identification from sensor pattern noise. IEEE Trans. Inf. Forensics Secur. 2006, 1, 205–214. [Google Scholar] [CrossRef]
- Chen, M.; Fridrich, J.; Goljan, M.; Lukás, J. Determining image origin and integrity using sensor noise. IEEE Trans. Inf. Forensics Secur. 2008, 3, 74–90. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, B. Efficient prnu extraction using joint edge-preserving filtering for source camera identification and verification. In Proceedings of the 2018 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 December 2018; pp. 14–18. [Google Scholar]
- Behare, M.S.; Bhalchandra, A.; Kumar, R. Source camera identification using photo response noise uniformity. In Proceedings of the 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 731–734. [Google Scholar]
- Valsesia, D.; Coluccia, G.; Bianchi, T.; Magli, E. Large-scale image retrieval based on compressed camera identification. IEEE Trans. Multimed. 2015, 17, 1439–1449. [Google Scholar] [CrossRef]
- Marra, F.; Poggi, G.; Sansone, C.; Verdoliva, L. Blind PRNU-based image clustering for source identification. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2197–2211. [Google Scholar] [CrossRef]
- Darvish Morshedi Hosseini, M.; Goljan, M. Camera identification from HDR images. In Proceedings of the ACM Workshop on Information Hiding and Multimedia Security, Paris, France, 3–5 July 2019; pp. 69–76. [Google Scholar]
- Debiasi, L.; Leitet, E.; Norell, K.; Tachos, T.; Uhl, A. Blind Source Camera Clustering of Criminal Case Data. In Proceedings of the IWBF, Wałbrzych, Poland, 28 August–9 September 2019; pp. 1–6. [Google Scholar]
- Lawgaly, A.; Khelifi, F. Sensor pattern noise estimation based on improved locally adaptive DCT filtering and weighted averaging for source camera identification and verification. IEEE Trans. Inf. Forensics Secur. 2016, 12, 392–404. [Google Scholar] [CrossRef]
- Deka, R.; Galdi, C.; Dugelay, J.L. Hybrid G-PRNU: Optimal parameter selection for scale-invariant asymmetric source smartphone identification. Electron. Imaging 2019, 2019, 546-1. [Google Scholar] [CrossRef]
- Lawgaly, A.; Khelifi, F.; Bouridane, A. Image sharpening for efficient source camera identification based on sensor pattern noise estimation. In Proceedings of the Fourth International Conference on Emerging Security Technologies, Cambridge, UK, 9–11 September 2013; pp. 113–116. [Google Scholar]
- Taspinar, S.; Mohanty, M.; Memon, N. Camera Fingerprint Extraction via Spatial Domain Averaged Frames. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3270–3282. [Google Scholar] [CrossRef]
- Zeng, H.; Wan, Y.; Deng, K.; Peng, A. Source Camera Identification With Dual-Tree Complex Wavelet Transform. IEEE Access 2020, 8, 18874–18883. [Google Scholar] [CrossRef]
- Gupta, B.; Tiwari, M. Improving performance of source-camera identification by suppressing peaks and eliminating low-frequency defects of reference SPN. IEEE Signal Process. Lett. 2018, 25, 1340–1343. [Google Scholar] [CrossRef]
- Thai, T.H.; Retraint, F.; Cogranne, R. Camera model identification based on DCT coefficient statistics. Digit. Signal Process. 2015, 40, 88–100. [Google Scholar] [CrossRef]
- Ding, X.; Chen, Y.; Tang, Z.; Huang, Y. Camera identification based on domain knowledge-driven deep multi-task learning. IEEE Access 2019, 7, 25878–25890. [Google Scholar] [CrossRef]
- Sameer, V.U.; Sarkar, A.; Naskar, R. Source camera identification model: Classifier learning, role of learning curves and their interpretation. In Proceedings of the International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 22–24 March 2017; pp. 2660–2666. [Google Scholar]
- Chen, C.; Stamm, M.C. Robust camera model identification using demosaicing residual features. Multimed. Tools Appl. 2021, 80, 11365–11393. [Google Scholar] [CrossRef]
- Al Banna, M.H.; Haider, M.A.; Al Nahian, M.J.; Islam, M.M.; Taher, K.A.; Kaiser, M.S. Camera Model Identification using Deep CNN and Transfer Learning Approach. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; pp. 626–630. [Google Scholar]
- El-Yamany, A.; Fouad, H.; Raffat, Y. A Generic Approach CNN-Based Camera Identification for Manipulated Images. In Proceedings of the IEEE International Conference on Electro/Information Technology, Rochester, MI, USA, 3–5 May 2018; pp. 0165–0169. [Google Scholar]
- Liu, Y.; Zou, Z.; Yang, Y.; Law, N.F.B.; Bharath, A.A. Efficient Source Camera Identification with Diversity-Enhanced Patch Selection and Deep Residual Prediction. Sensors 2021, 21, 4701. [Google Scholar] [CrossRef]
- Rafi, A.M.; Tonmoy, T.I.; Kamal, U.; Wu, Q.J.; Hasan, M.K. RemNet: Remnant convolutional neural network for camera model identification. Neural Comput. Appl. 2021, 33, 3655–3670. [Google Scholar] [CrossRef]
- Yang, P.; Ni, R.; Zhao, Y.; Zhao, W. Source camera identification based on content-adaptive fusion residual networks. Pattern Recognit. Lett. 2019, 119, 195–204. [Google Scholar] [CrossRef]
- You, C.; Zheng, H.; Guo, Z.; Wang, T.; Wu, X. Multiscale Content-Independent Feature Fusion Network for Source Camera Identification. Appl. Sci. 2021, 11, 6752. [Google Scholar] [CrossRef]
- Dal Cortivo, D.; Mandelli, S.; Bestagini, P.; Tubaro, S. CNN-Based Multi-Modal Camera Model Identification on Video Sequences. J. Imaging 2021, 7, 135. [Google Scholar] [CrossRef] [PubMed]
- Freire-Obregón, D.; Narducci, F.; Barra, S.; Castrillón-Santana, M. Deep learning for source camera identification on mobile devices. Pattern Recognit. Lett. 2019, 126, 86–91. [Google Scholar] [CrossRef]
- Cozzolino, D.; Verdoliva, L. Noiseprint: A CNN-based camera model fingerprint. IEEE Trans. Inf. Forensics Secur. 2019, 15, 144–159. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, B.; Wei, F.; Zhu, M.; Sui, X. Source camera identification based on coupling coding and adaptive filter. IEEE Access 2019, 8, 54431–54440. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Zhou, X.; Xi, J.; Wang, S. Source camera identification from image texture features. Neurocomputing 2016, 207, 131–140. [Google Scholar] [CrossRef]
- Rashidi, A.; Razzazi, F. Single image camera identification using I-vectors. In Proceedings of the 7th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 26–27 October 2017; pp. 406–410. [Google Scholar]
- Bernacki, J. On robustness of camera identification algorithms. Multimed. Tools Appl. 2021, 80, 921–942. [Google Scholar] [CrossRef]
- Baldini, G.; Amerini, I.; Gentile, C. Microphone identification using convolutional neural networks. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Qamhan, M.A.; Altaheri, H.; Meftah, A.H.; Muhammad, G.; Alotaibi, Y.A. Digital Audio Forensics: Microphone and Environment Classification Using Deep Learning. IEEE Access 2021, 9, 62719–62733. [Google Scholar] [CrossRef]
- Berdich, A.; Groza, B.; Mayrhofer, R.; Levy, E.; Shabtai, A.; Elovici, Y. Sweep-to-Unlock: Fingerprinting Smartphones based on Loudspeaker Roll-off Characteristics. IEEE Trans. Mob. Comput. 2021. [Google Scholar] [CrossRef]
- Zhou, Z.; Diao, W.; Liu, X.; Zhang, K. Acoustic fingerprinting revisited: Generate stable device id stealthily with inaudible sound. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 429–440. [Google Scholar]
- Das, A.; Borisov, N.; Caesar, M. Do you hear what i hear? Fingerprinting smart devices through embedded acoustic components. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 441–452. [Google Scholar]
- Tian, J.; Zhang, J.; Li, X.; Zhou, C.; Wu, R.; Wang, Y.; Huang, S. Mobile Device Fingerprint Identification using Gyroscope Resonance. IEEE Access 2021. [Google Scholar] [CrossRef]
- Chen, J.; He, K.; Chen, J.; Fang, Y.; Du, R. PowerPrint: Identifying Smartphones through Power Consumption of the Battery. Secur. Commun. Netw. 2020, 2020, 3893106. [Google Scholar] [CrossRef]
- Ding, Z.; Ming, M. Accelerometer-based mobile device identification system for the realistic environment. IEEE Access 2019, 7, 131435–131447. [Google Scholar] [CrossRef]
- Groza, B.; Berdich, A.; Jichici, C.; Mayrhofer, R. Secure Accelerometer-Based Pairing of Mobile Devices in Multi-Modal Transport. IEEE Access 2020, 8, 9246–9259. [Google Scholar] [CrossRef]
- NIST. Recommendation for the Entropy Sources Used for Random Bit Generation. Available online: https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-90B.pdf (accessed on 1 July 2022).
- Mathworks. Choose Classifier Options. Available online: https://www.mathworks.com/help/stats/choose-a-classifier.html (accessed on 1 December 2021).
- Han, H.; Jiang, X. Overcome support vector machine diagnosis overfitting. Cancer Inform. 2014, 13, CIN-S13875. [Google Scholar] [CrossRef]
- Ahmad, I.; Basheri, M.; Iqbal, M.J.; Rahim, A. Performance comparison of support vector machine, random forest, and extreme learning machine for intrusion detection. IEEE Access 2018, 6, 33789–33795. [Google Scholar] [CrossRef]






| Work | Feature | Classifier | Max. Accuracy |
|---|---|---|---|
| [12] | highpass filter | CNN, AlexNet, and GoogleNet | 94.5% |
| [13] | DCT + PCA | RF based ENS | 99.1% |
| [14] | Prb. Repr. and thresholding | SVM | 87.6 |
| [15] | social network | ResNet50 | 96% |
| [11] | split image | CNN | 100% |
| [16] | Supervised pipeline (rich features, CFA features, and CNN-derived features) | PISVM, ET, and SSVM classifier and CNN | 98.68% |
| [17] | PRNU and noiseprint | CNN + SVM, LRT, and r-LRT | 95.5% |
| [18] | PRNU | CNN | 80% |
| This work | DSNU | WNN, KNN, ENS, SVM, NB, and LD | 97% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berdich, A.; Groza, B. Smartphone Camera Identification from Low-Mid Frequency DCT Coefficients of Dark Images. Entropy 2022, 24, 1158. https://doi.org/10.3390/e24081158
Berdich A, Groza B. Smartphone Camera Identification from Low-Mid Frequency DCT Coefficients of Dark Images. Entropy. 2022; 24(8):1158. https://doi.org/10.3390/e24081158
Chicago/Turabian StyleBerdich, Adriana, and Bogdan Groza. 2022. "Smartphone Camera Identification from Low-Mid Frequency DCT Coefficients of Dark Images" Entropy 24, no. 8: 1158. https://doi.org/10.3390/e24081158
APA StyleBerdich, A., & Groza, B. (2022). Smartphone Camera Identification from Low-Mid Frequency DCT Coefficients of Dark Images. Entropy, 24(8), 1158. https://doi.org/10.3390/e24081158






