Modeling Dual-Drive Gantry Stages with Heavy-Load and Optimal Synchronous Controls with Force-Feed-Forward Decoupling
Abstract
:1. Introduction
2. Materials and Methods
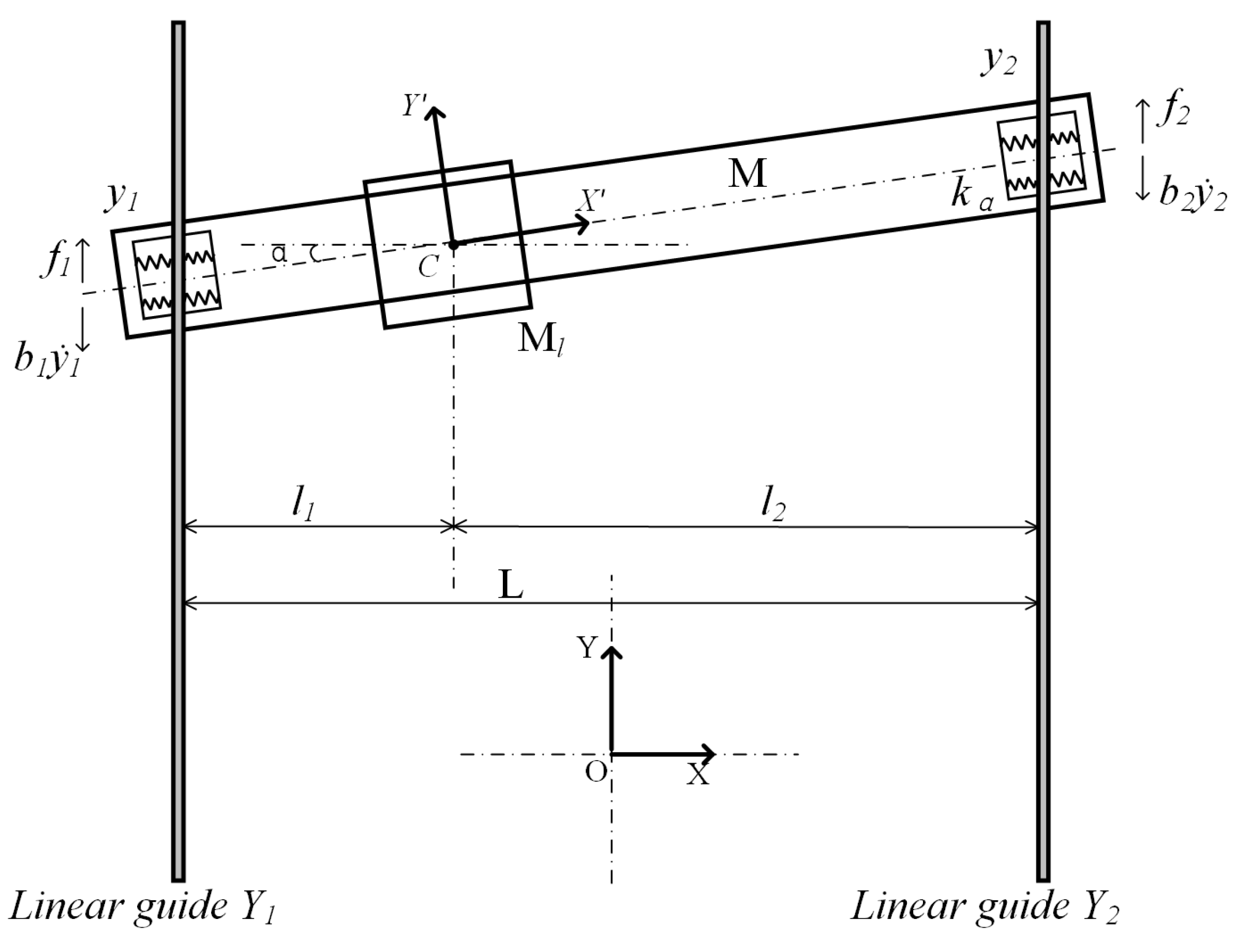
2.1. Physical Modeling of Heavy-Load Dual-Drive Gantry System
2.1.1. Equivalent Dynamic Model of the System
2.1.2. Full State-Space Equation of the System
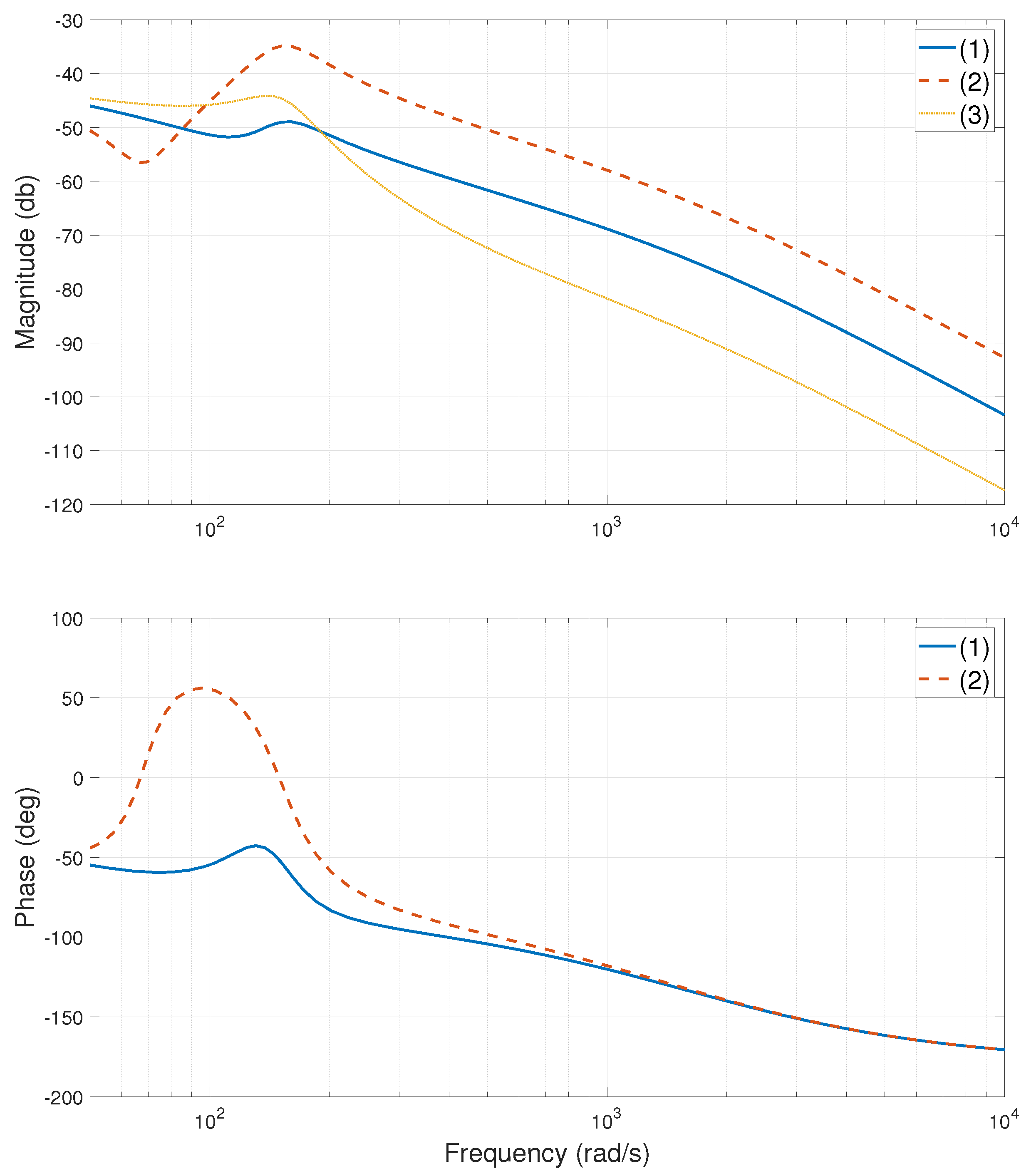
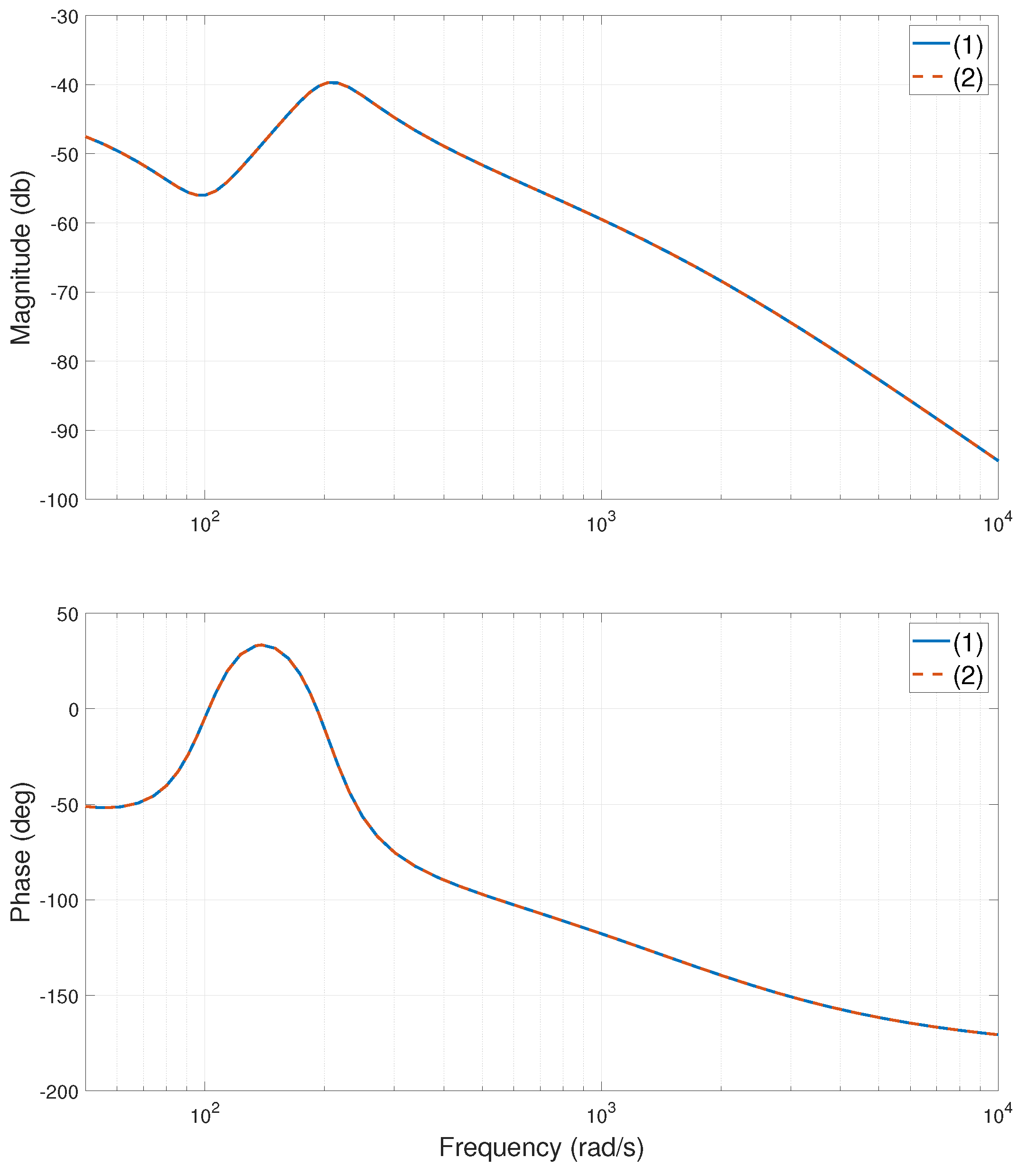
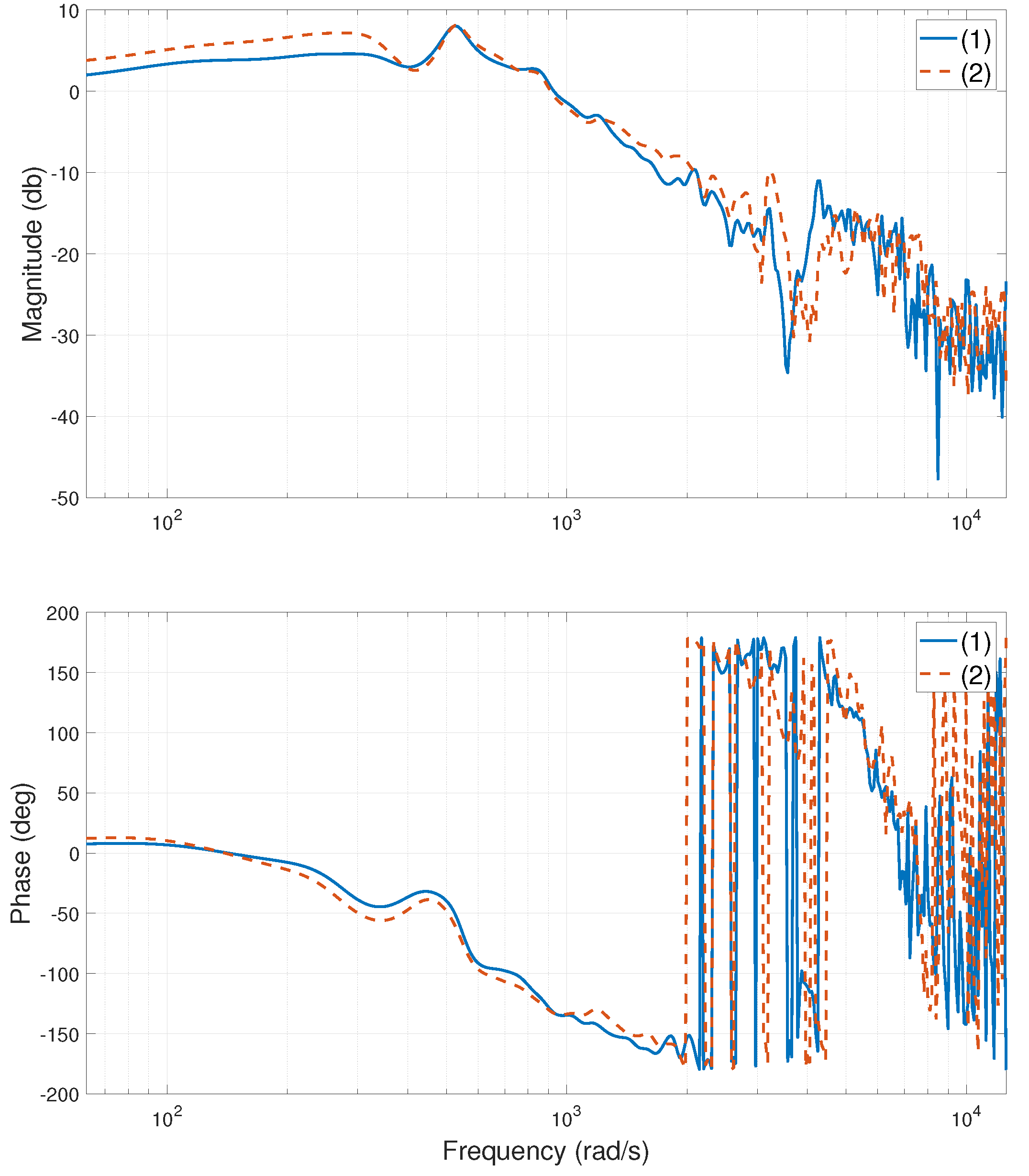
2.1.3. Validity of the Established Model
2.2. Virtual-Centroid-Based GSLQR Optimal Control and Force-FF Decoupling Control Algorithm Design
2.2.1. GSLQR Optimal Control Algorithm Design
2.2.2. Virtual-Centroid-Based Force-FF Decoupling Control Algorithm Design
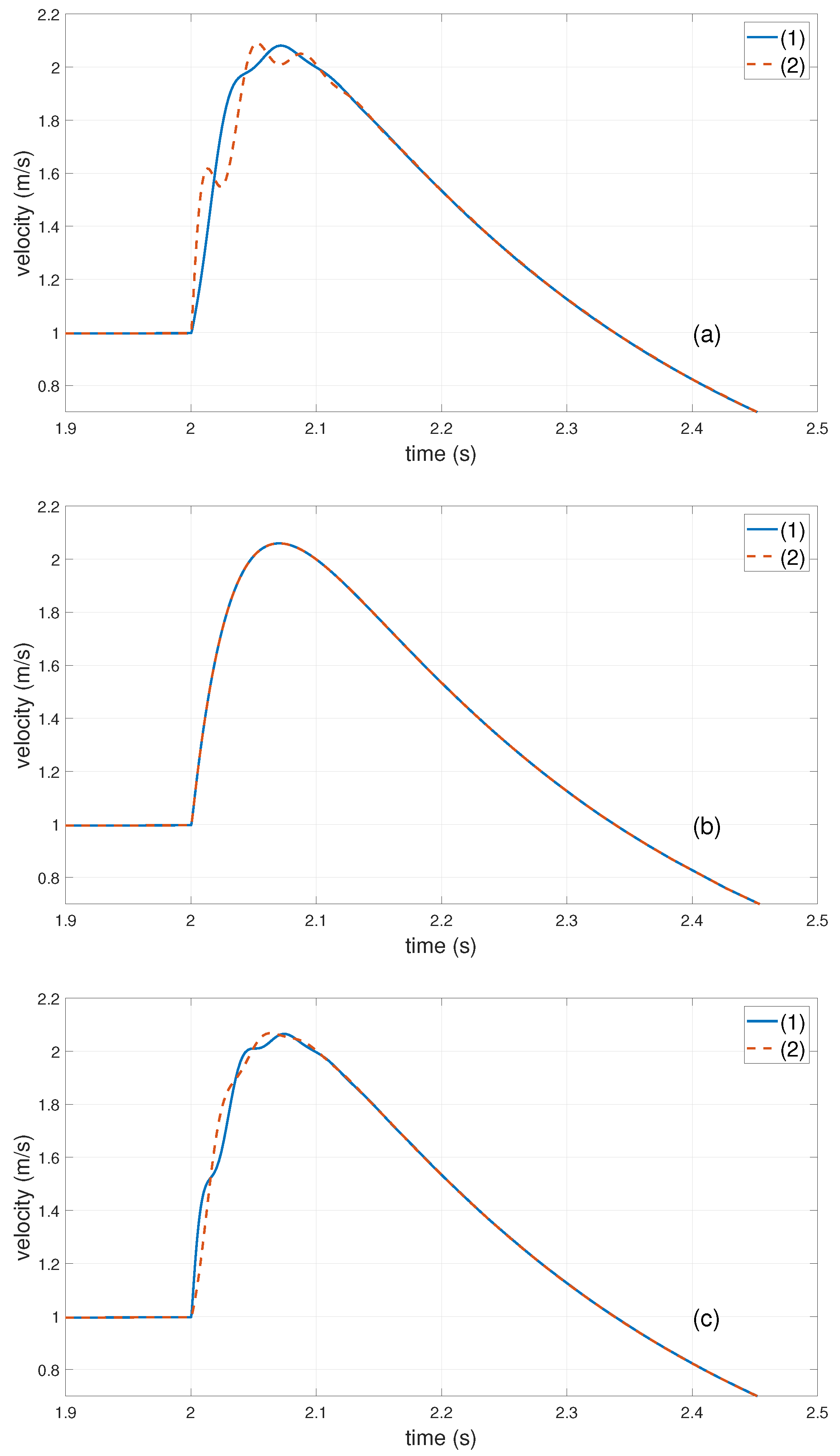
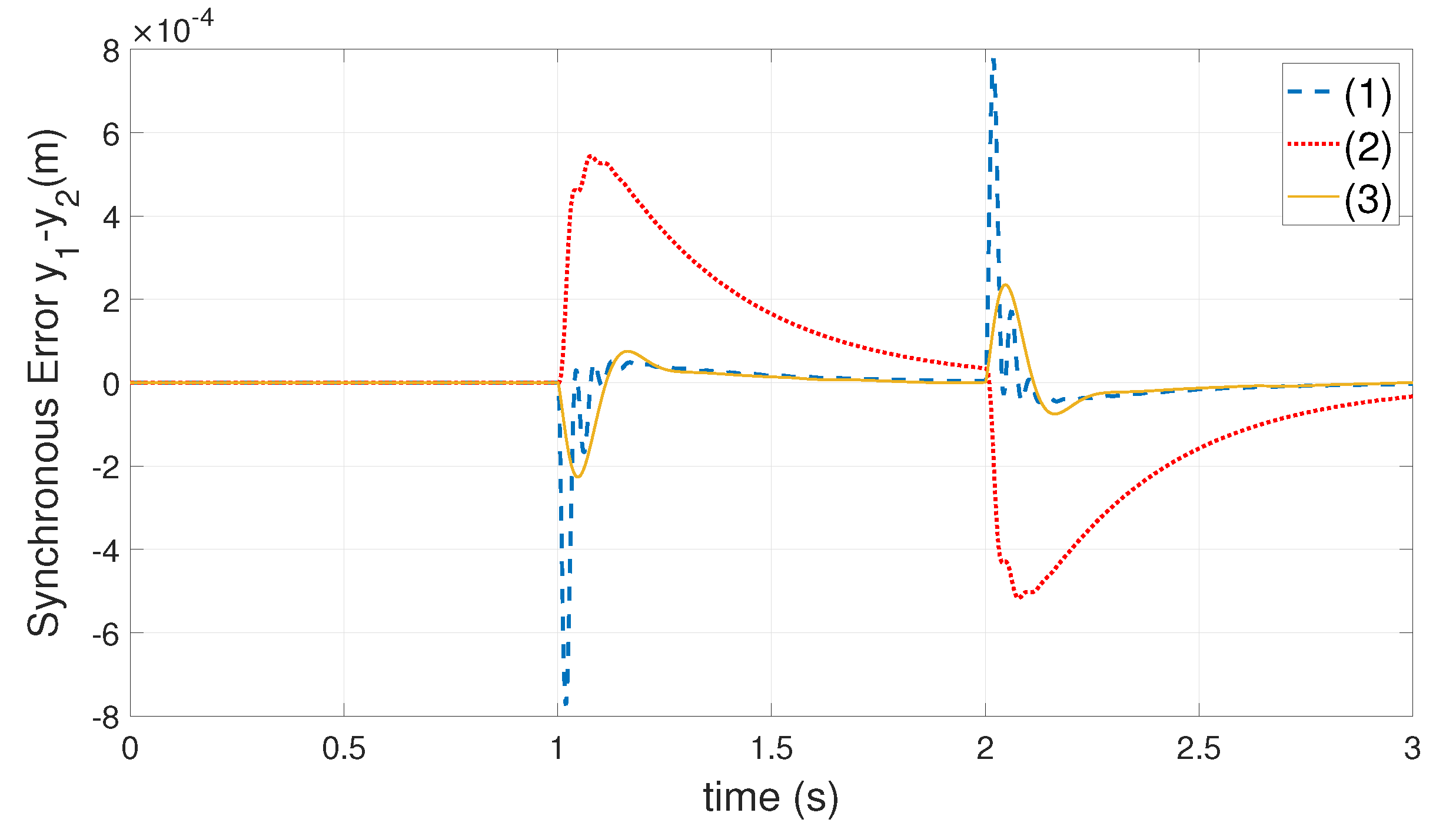
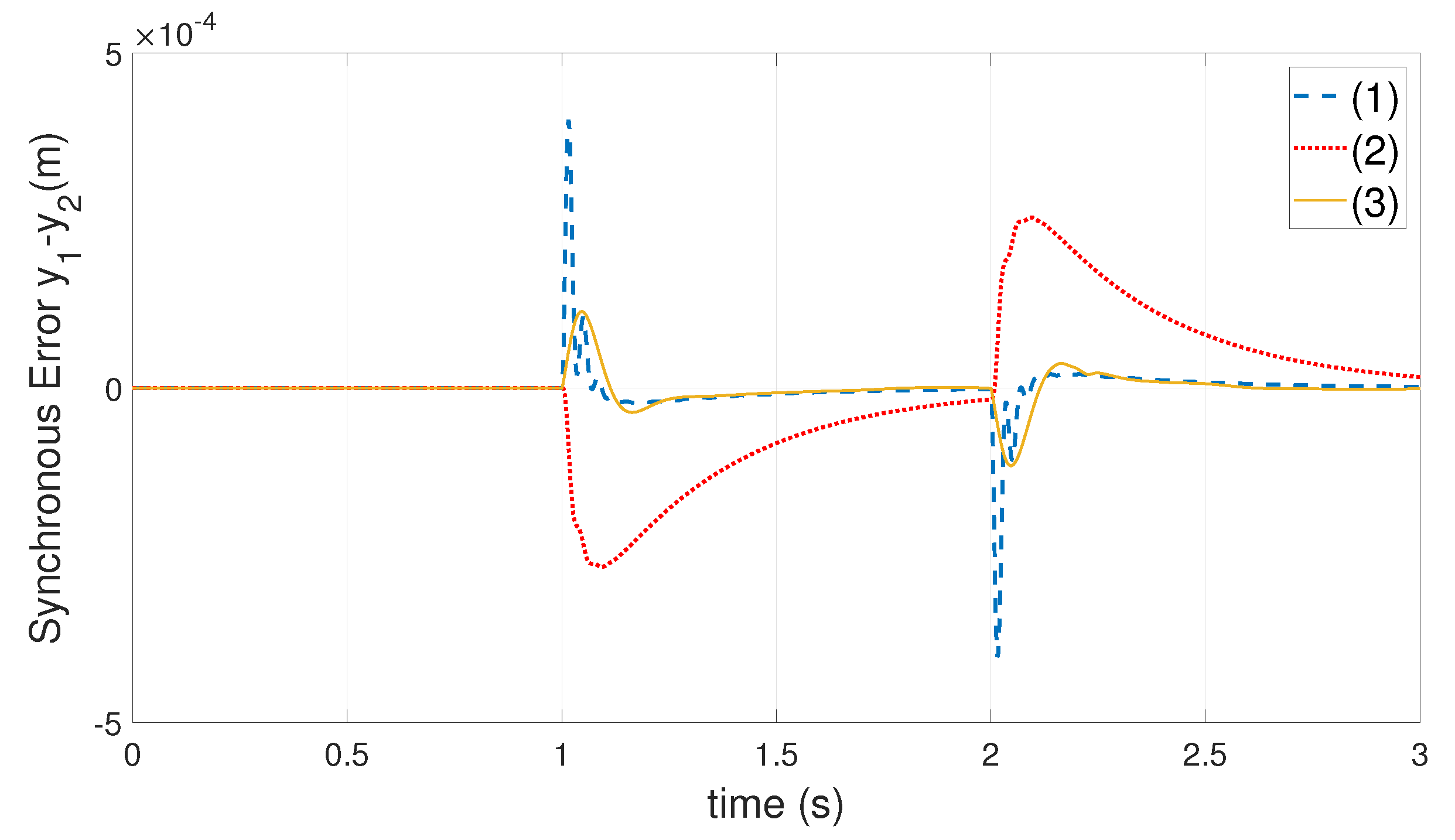
3. Simulation Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Yao, B.; Wang, Q. Modeling and Synchronization Control of a Dual Drive Industrial Gantry Stage. IEEE/ASME Trans. Mechatron. 2018, 23, 2940–2951. [Google Scholar] [CrossRef]
- Li, C.; Sun, Y.; Pu, S. Accurate physical modeling and synchronization control of dual-linear-motor-driven gantry with dynamic load. AIP Adv. 2021, 11, 025133. [Google Scholar] [CrossRef]
- Chen, R.; Yan, L.; Jiao, Z.; Shang, Y. Dynamic modeling and analysis of flexible H-type gantry stage. J. Sound Vib. 2019, 439, 144–155. [Google Scholar] [CrossRef]
- Meng, Y.; Manzie, C.; Lu, G.; Good, M.; Shames, I. Modelling and Contouring Error Bounded Control of a Biaxial Industrial Gantry Machine. In Proceedings of the 3rd Conference on Control Technology and Applications (CCTA 2019), Hong Kong, China, 19–21 August 2019. [Google Scholar]
- Yunbo, H.; Wentao, Y.; Jian, G.; Chengqiang, C.; Xun, C.; Xin, C.; Zhijun, Y.; Kai, Z.; Yun, C.; Yu, Z. Research on Dual-Linear Motor Synchronous Control in the High-Precision Gantry Motion Platform. In Proceedings of the 2017 IEEE 19th Electronics Packaging Technology Conference (EPTC), Singapore, 6–9 December 2017; pp. 1–5. [Google Scholar]
- Ishizaki, K.; Sencer, B.; Shamoto, E. Cross Coupling Controller for Accurate Motion Synchronization of Dual Servo Systems. Int. J. Autom. Technol. 2013, 7, 514–522. [Google Scholar] [CrossRef]
- Wang, S.M.; Wang, R.J.; Tsooj, S. A new synchronous error control method for CNC machine tools with dual-driving systems. Int. J. Precis. Eng. Manuf. 2013, 14, 1415–1419. [Google Scholar] [CrossRef]
- Dongmei, Y.; Dan, L.; Qing, H. Synchronous control for a dual linear motor of moving gantry machining centers based on improved sliding mode variable structure and decoupling control. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 2525–2528. [Google Scholar]
- Utkin, V.I. Sliding mode control design principles and applications to electric drives. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, H.; Man, Z.; Jin, J.; Fu, M. Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode. IEEE/ASME Trans. Mechatron. 2014, 20, 1743–1752. [Google Scholar] [CrossRef]
- Kim, S.; Chu, B.; Hong, D.; Park, H.K.; Park, J.M.; Cho, T.Y. Synchronizing dual-drive gantry of chip mounter with LQR approach. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. 838–843. [Google Scholar]
- Li, X. Model Decoupled Synchronization Control Design with Fractional Order Filter for H-Type Air Floating Motion Platform. Entropy 2021, 23, 633. [Google Scholar] [CrossRef]
- Caiyan, Q.; Chaoning, Z.; Haiyan, L. H-Shaped Multiple Linear Motor Drive Platform Control System Design Based on an Inverse System Method. Energies 2017, 10, 1990. [Google Scholar] [CrossRef]
- Li, P.; Zhu, G.; Gong, S.; Huang, Y.; Yue, L. Synchronization control of dual-drive system in gantry-type machine tools based on disturbance observer. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–7. [Google Scholar]
- García-Herreros, I.; Kestelyn, X.; Gomand, J.; Coleman, R.; Barre, P.J. Model-based decoupling control method for dual-drive gantry stages: A case study with experimental validations. Control Eng. Pract. 2013, 21, 298–307. [Google Scholar] [CrossRef]
- Tan, K.K.; Lim, S.Y.; Huang, S.; Dou, H.; Giam, T.S. Coordinated motion control of moving gantry stages for precision applications based on an observer-augmented composite controller. IEEE Trans. Control Syst. Technol. 2004, 12, 984–991. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Li, C.; Li, C.; Chen, Z.; Yao, B. Advanced synchronization control of a dual-linear-motor-driven gantry with rotational dynamics. IEEE Trans. Ind. Electron. 2018, 65, 7526–7535. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Yao, B. Adaptive robust synchronization control of a dual-linear-motor-driven gantry with rotational dynamics and accurate online parameter estimation. IEEE Trans. Ind. Inform. 2017, 14, 3013–3022. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. μ-Synthesis-Based Adaptive Robust Control of Linear Motor Driven Stages With High-Frequency Dynamics: A Case Study. IEEE/ASME Trans. Mechatron. 2014, 20, 1482–1490. [Google Scholar] [CrossRef]
- Landau, I.D.; Lozano, R.; M’Saad, M.; Karimi, A. Adaptive Control: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jianzhou, Q. Modeling and Synchronous Control of H-Shaped Truss Positioning Platform under High-Speed Conditions. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2010. [Google Scholar]
- Gomand, J.; Kestelyn, X.; Bearee, R.; Barre, P.J. Dual-drive gantry stage decoupling control based on a coupling model. ElectroMotion 2008, 15, 94–98. [Google Scholar]
- Hrcek, S.; Brumercik, F.; Smetanka, L.; Lukac, M.; Patin, B.; Glowacz, A. Global Sensitivity Analysis of Chosen Harmonic Drive Parameters Affecting Its Lost Motion. Materials 2021, 14, 5057. [Google Scholar] [CrossRef] [PubMed]
- Hibbeler, R. Engineering Mechanics: Dynamics; Pearson Educación: London, UK, 2004. [Google Scholar]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Triantafyllou, M.S.; Hover, F.S. Maneuvering and Control of Marine Vehicles; Citeseer: Princeton, NJ, USA, 2003. [Google Scholar]
- Zhang, C.; Fu, M. A revisit to the gain and phase margins of linear quadratic regulators. IEEE Trans. Autom. Control 1996, 41, 1527–1530. [Google Scholar] [CrossRef]
- Cheema, M.A.M.; Fletcher, J.E.; Rahman, M.F.; Xiao, D. Optimal, combined speed, and direct thrust control of linear permanent magnet synchronous motors. IEEE Trans. Energy Convers. 2016, 31, 947–958. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Luo, Y.; Chen, X.; Zeng, L. Iterative Tuning of Feedforward Controller with Precise Time-Delay Compensation for Precision Motion System. Math. Probl. Eng. 2020, 2020, 9391526. [Google Scholar] [CrossRef]
- Geyer, T.; Beccuti, G.A.; Papafotiou, G.; Morari, M. Model predictive direct torque control of permanent magnet synchronous motors. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 199–206. [Google Scholar]
- Béarée, R.; Barre, P.J.; Hautier, J.P. Control structure synthesis for electromechanical systems based on the concept of inverse model using Causal Ordering Graph. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 5289–5294. [Google Scholar]





| Name | Symbol | Value |
|---|---|---|
| midrule mass of crossbeam (including load ) | M | 25 kg |
| mass of load | 10 kg | |
| length of crossbeam | L | 0.8 m |
| damping of rotor | 5 N·m·s | |
| damping of rotor | 5 N·m·s | |
| stiffness of joint between crossbeam and rails | 52,520 N/m | |
| thrust constant of Motor | 61.0 N/A | |
| thrust constant of Motor | 61.0 N/A | |
| back EMF constant of motor | 49.6 V/M/S | |
| back EMF constant of motor | 49.6 V/M/S | |
| inductance of Motor | H | |
| inductance of Motor | H | |
| resistance of Motor | 8.4 | |
| resistance of Motor | 8.4 |
| Index | Algo (1) | Algo (2) | Algo (3) |
|---|---|---|---|
| , mm | 0.76 | 0.54 | 0.22 |
| Index | Algo (1) | Algo (2) | Algo (3) |
|---|---|---|---|
| , mm | 0.39 | 0.26 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Wang, Q. Modeling Dual-Drive Gantry Stages with Heavy-Load and Optimal Synchronous Controls with Force-Feed-Forward Decoupling. Entropy 2022, 24, 1153. https://doi.org/10.3390/e24081153
Xie H, Wang Q. Modeling Dual-Drive Gantry Stages with Heavy-Load and Optimal Synchronous Controls with Force-Feed-Forward Decoupling. Entropy. 2022; 24(8):1153. https://doi.org/10.3390/e24081153
Chicago/Turabian StyleXie, Hanjun, and Qinruo Wang. 2022. "Modeling Dual-Drive Gantry Stages with Heavy-Load and Optimal Synchronous Controls with Force-Feed-Forward Decoupling" Entropy 24, no. 8: 1153. https://doi.org/10.3390/e24081153
APA StyleXie, H., & Wang, Q. (2022). Modeling Dual-Drive Gantry Stages with Heavy-Load and Optimal Synchronous Controls with Force-Feed-Forward Decoupling. Entropy, 24(8), 1153. https://doi.org/10.3390/e24081153






