A Novel Image Encryption Algorithm Based on Improved Arnold Transform and Chaotic Pulse-Coupled Neural Network
Abstract
:1. Introduction
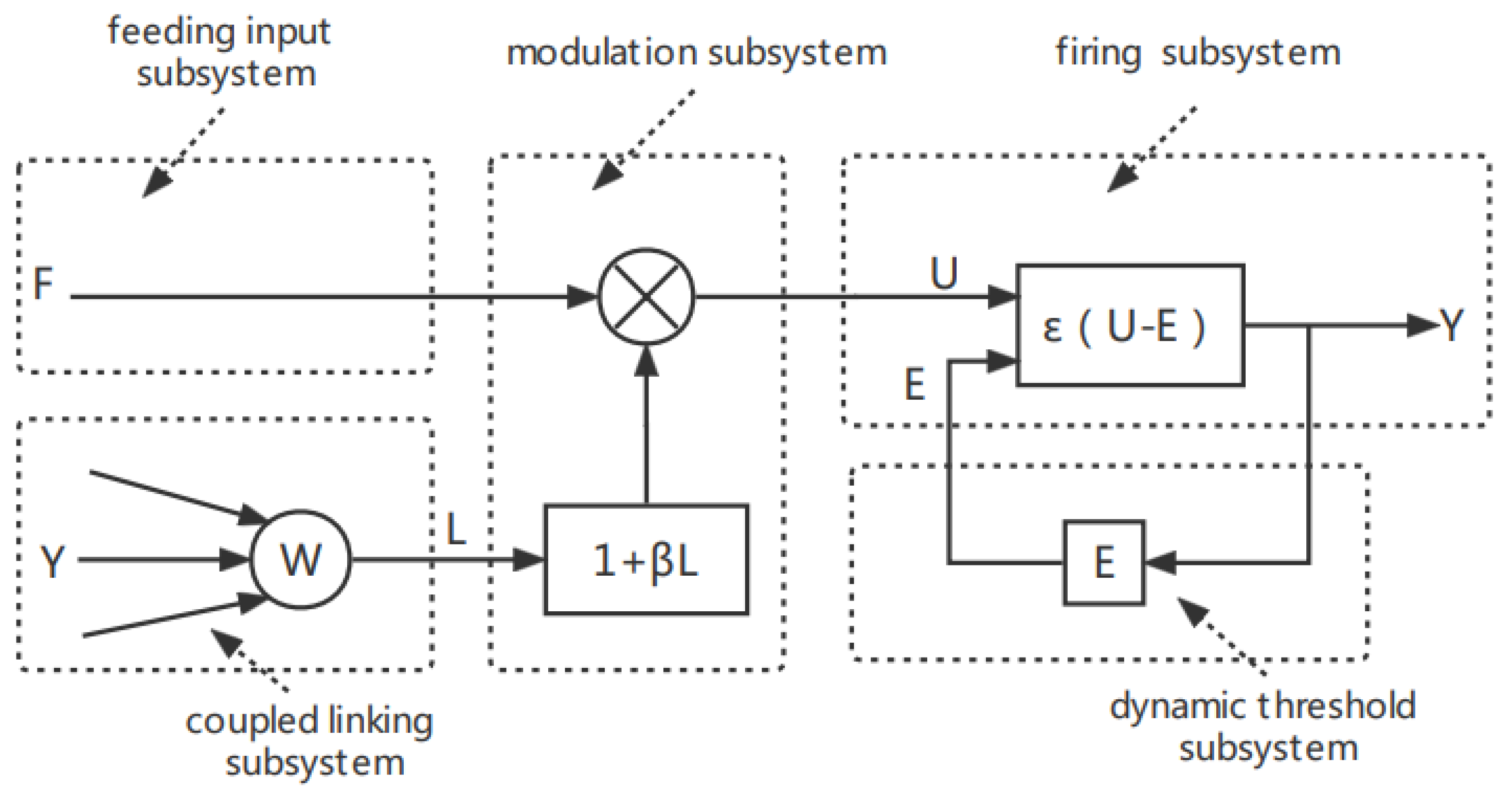
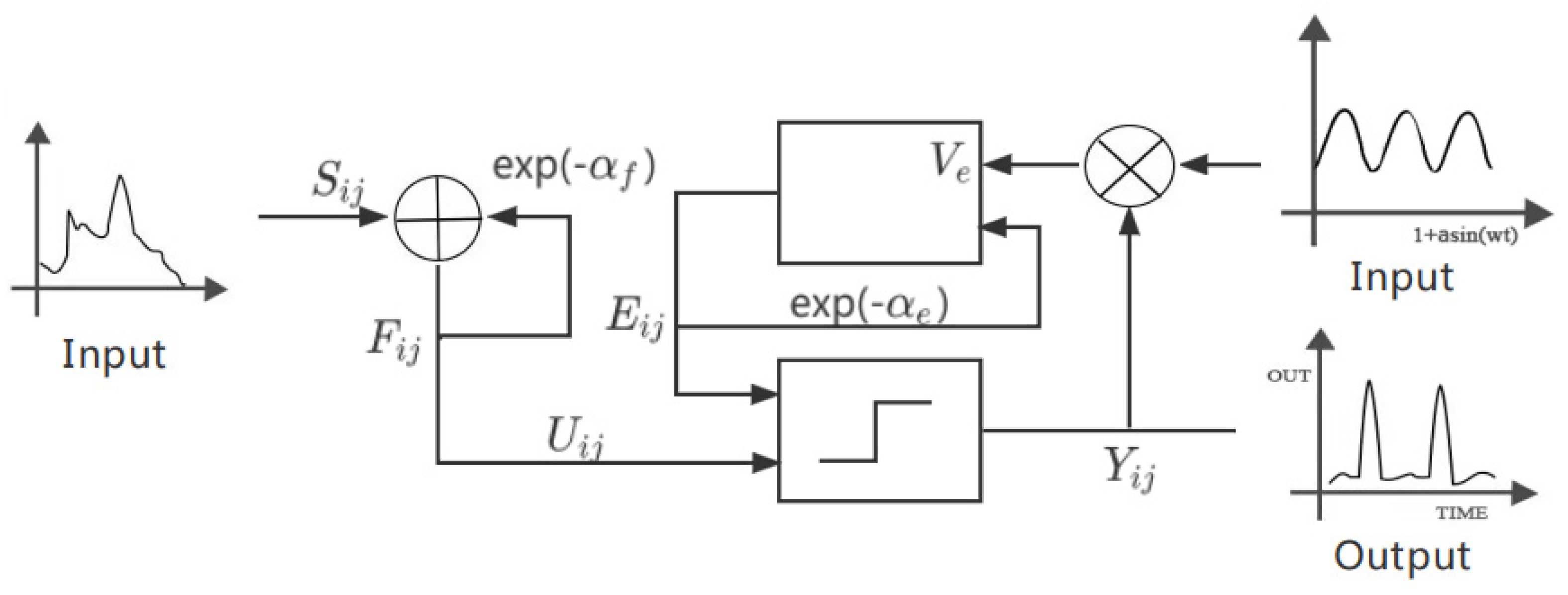
2. Theoretical Analysis of Chaotic PCNN Model
2.1. Uncoupled Linking PCNN Model
2.1.1. Firing Period Analysis of Uncoupled Linking PCNN
- (1)
- When n = 0, which is the initial stage, , , , neurons fire for the first time;
- (2)
- When n = 1, , , , neurons extinguish;
- (3)
- When n = 2, , , .
2.2. Uncoupled Linking Chaotic PCNN
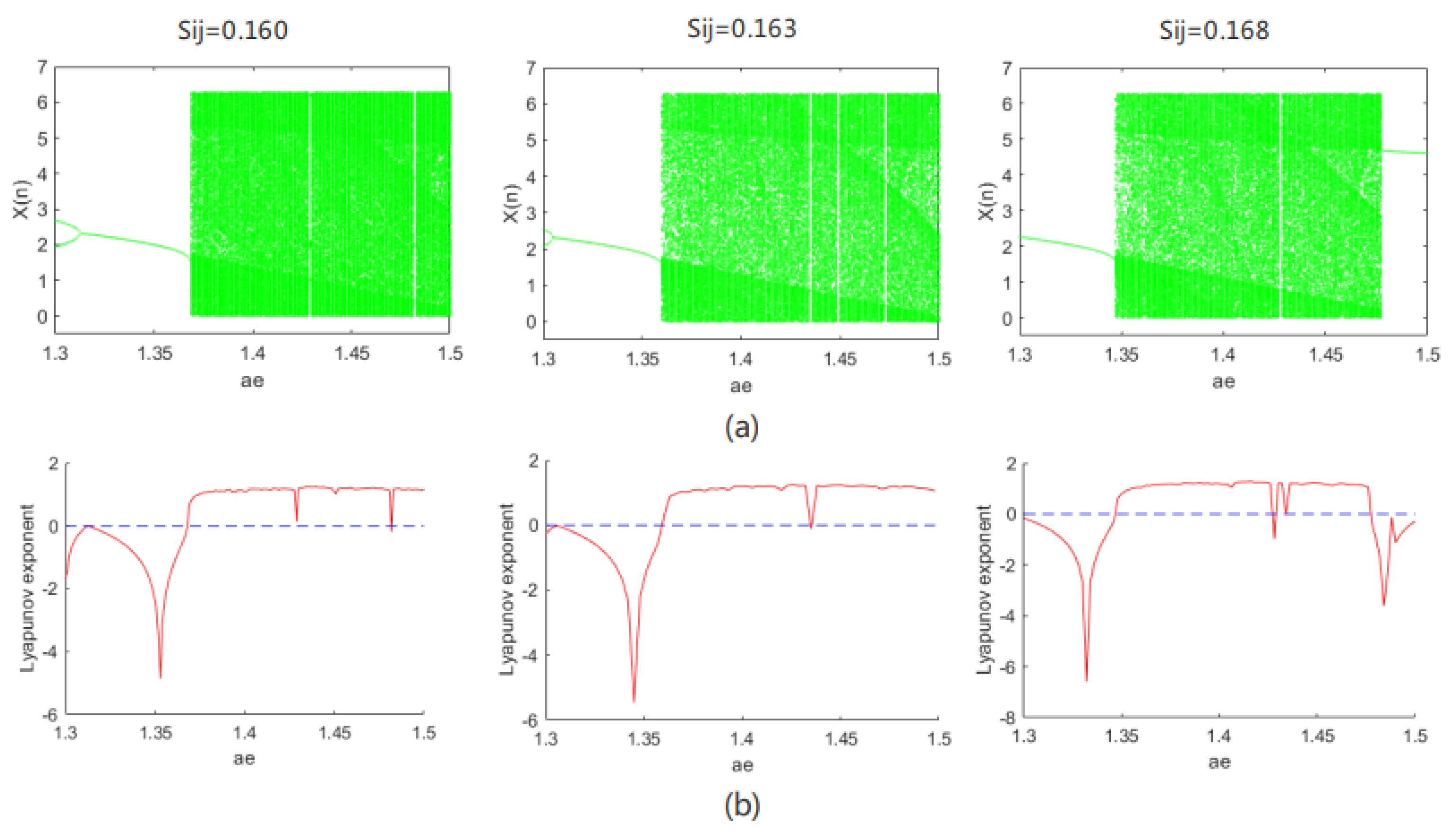
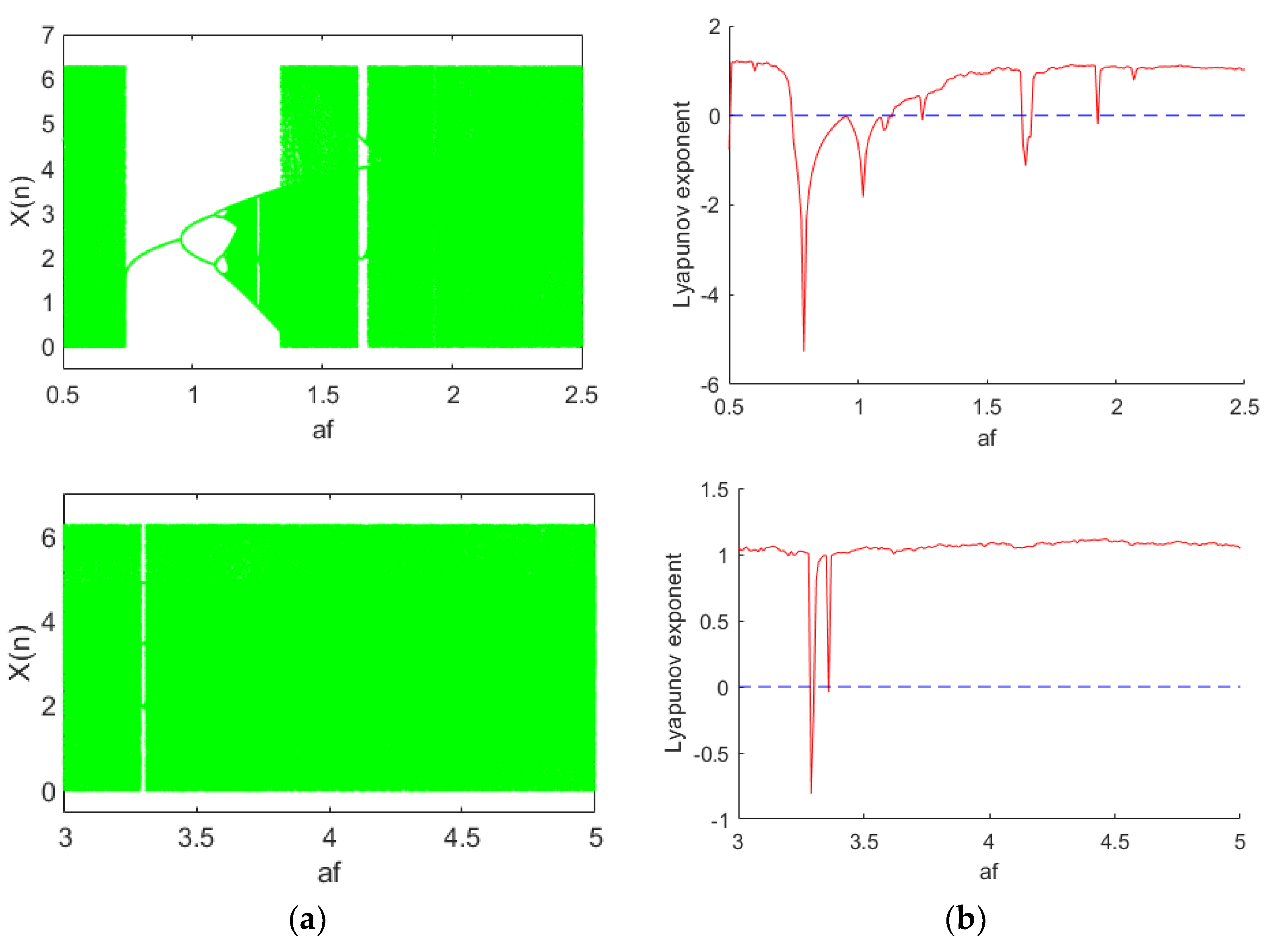
2.2.1. Basic Bifurcation Behavior Analysis of Chaotic PCNN
2.2.2. Non-Periodicity Analysis of Sequence
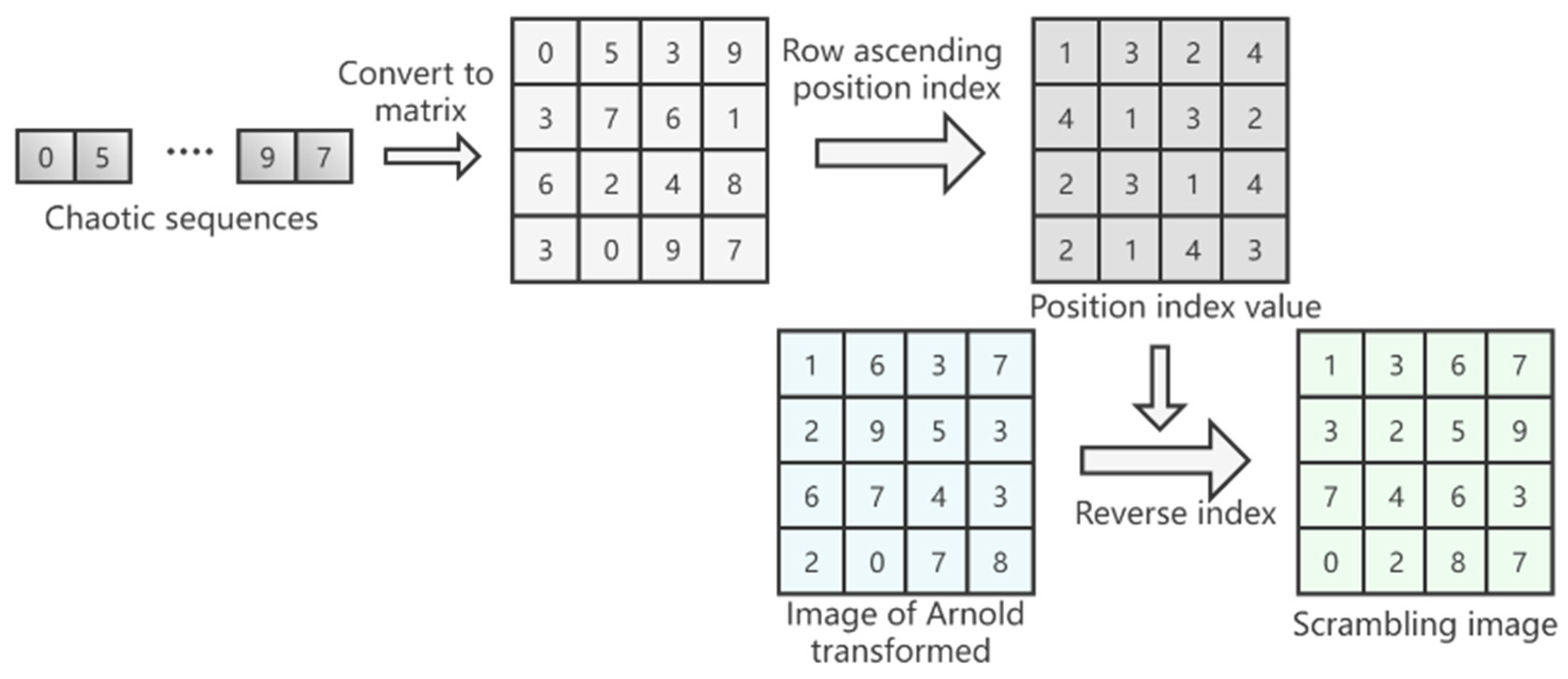
2.3. Improved Arnold Transform Image Scrambling Method
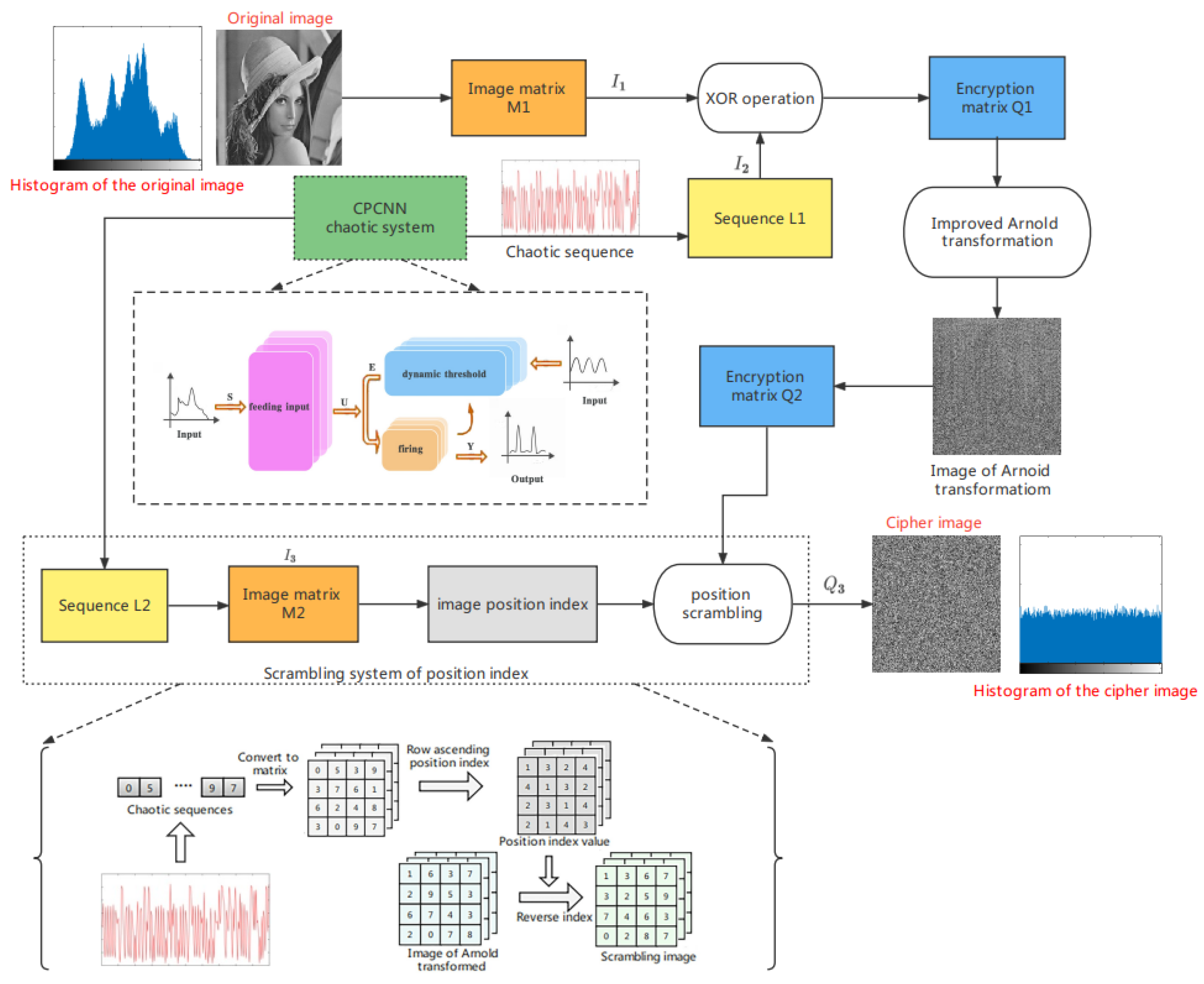
3. Scheme and Process of Image Encryption and Decryption
| Algorithm 1: Proposed decryption algorithm. |
| Input: Image M1 of size W × H. Output: Encryption result Q3. 1: Set the initial parameter value of the chaotic system, set fixed parameters , , ; controlling parameters , , , ; initial value ; |
| 2: Generate chaotic sequence L1 and L2 using proposed CPCNN map; 3: sum = sum(M1); 4: = reshape (M1, 1, W × H); |
| 5: for i = 1 to L1 do 6: ; 7: if sum 0 then 8: ; 9: else 10: ; 11: end if 12: end for 13: Q2 = reshape (, W, H); 14: Using a 100 × 100 square sliding window and setting the step size to 30, the pre-encrypted image is traversed, and the entire pre-encrypted image is Arnold transformed to obtain a new scrambled image Q2; 15: M2 = reshape (L2, W, H); 16: index = zeros (W, H); 17: for i = 1 to W do 18: [~, index (i, :)] =sort (M2 (i, :)); 19: end for |
| 20: count = W; 21: for i = 1 to W do 22: for j = 1 to H do 23: Q3 (i, j) = Q2 (index (i, j), count); 24: end for 25: count = count − 1; |
| 26: end for |
4. Experiment Environment and Results
4.1. Experiment Environment
4.2. Experiment Parameter Setting and Result
5. Security Analysis
5.1. Statistical Characteristic Analysis of Ciphertext
5.1.1. Histogram Statistical Analysis
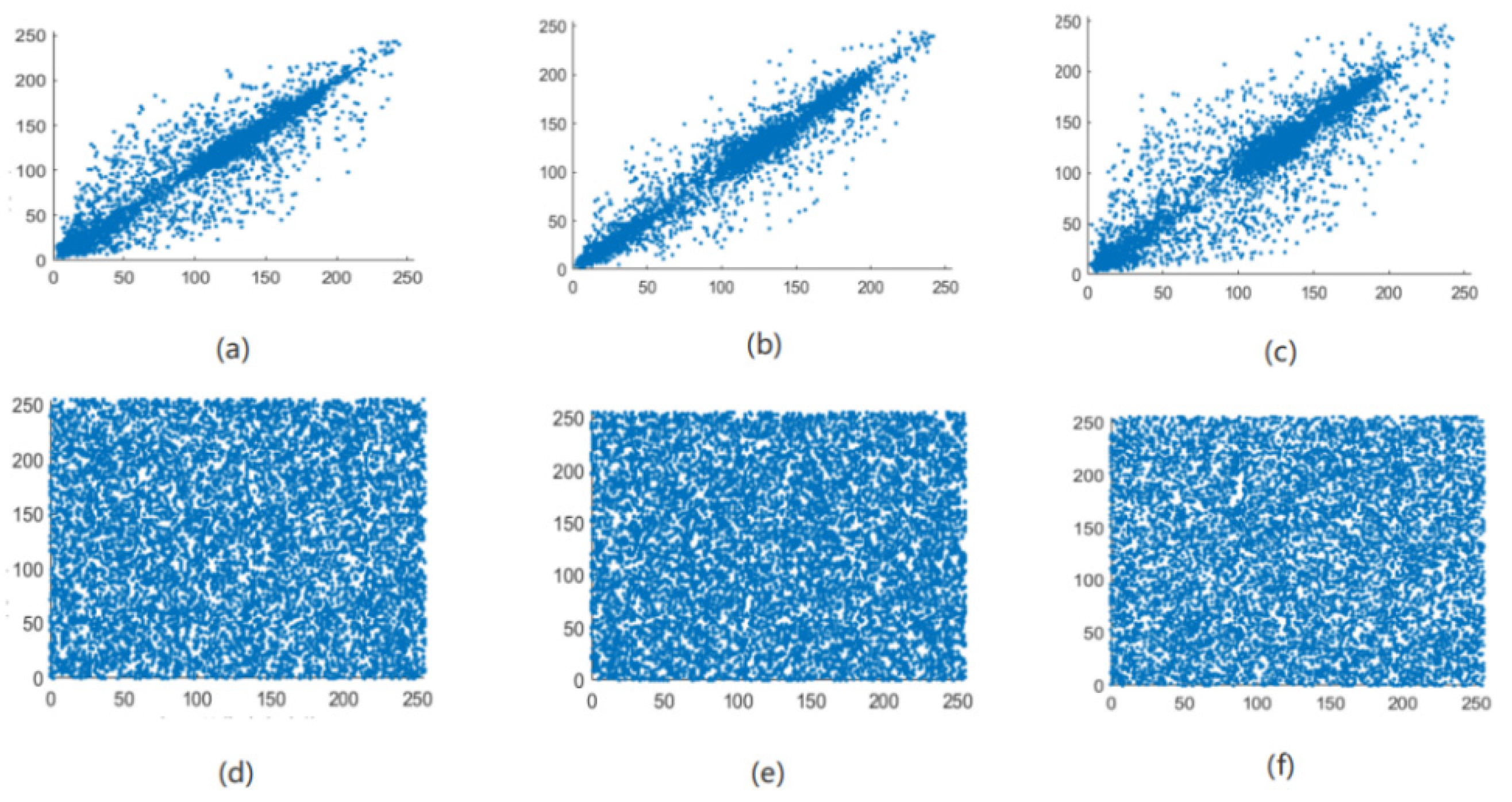
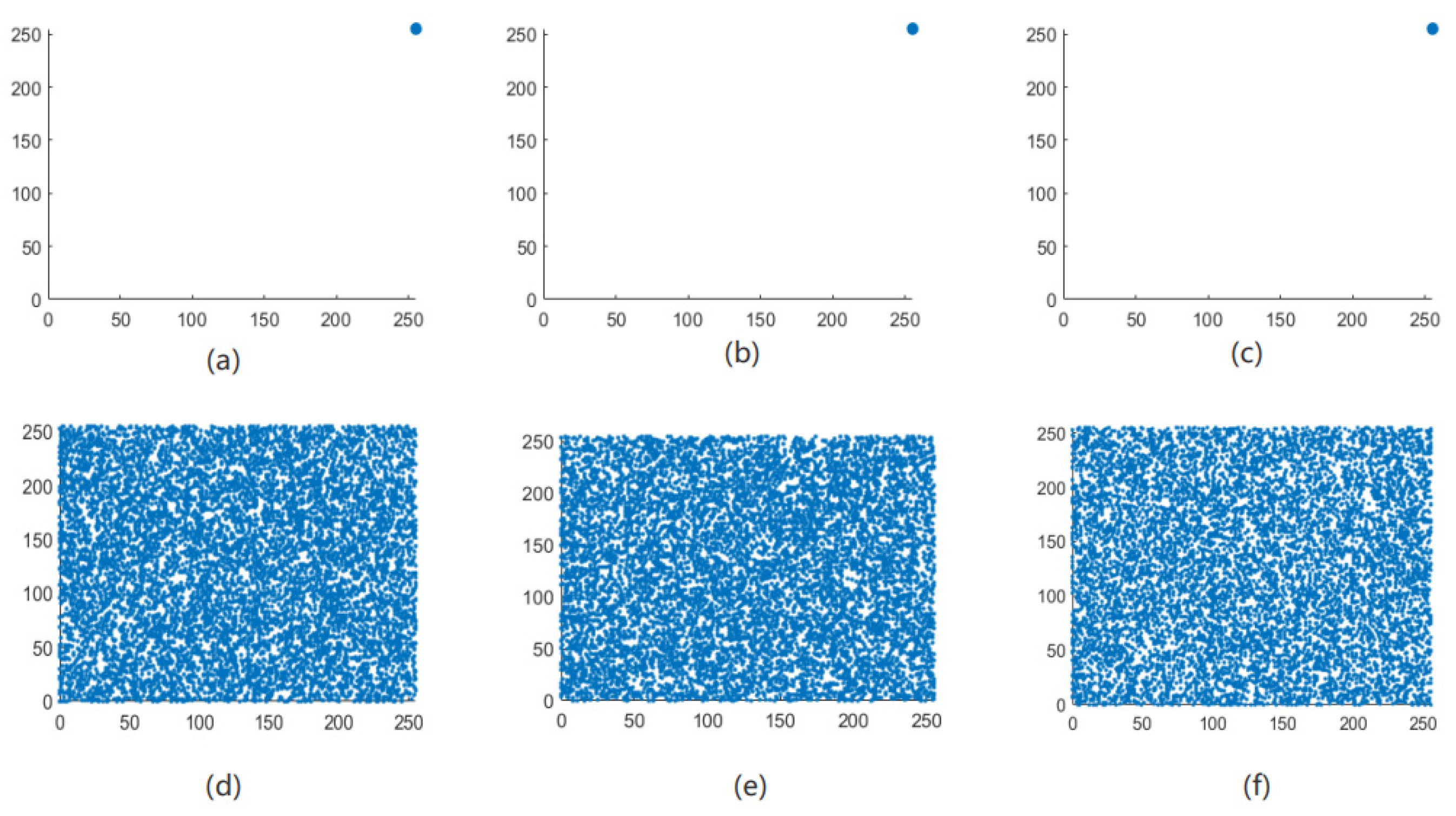
5.1.2. Correlation Analysis of Adjacent Pixels
5.2. Information Entropy Analysis
5.3. Tests for Randomness
5.4. Key Space Analysis
5.5. Key Sensitivity Analysis
5.6. Anti-Attack Ability Analysis
5.6.1. Anti-Differential Attack Analysis
5.6.2. Anti-Salt and Pepper, Gaussian Noise Attack Analysis
5.6.3. Analysis of Anti-Shearing Attack Ability
5.6.4. Noise Processing of Decrypted Images
5.7. Analysis of Speed
5.8. Algorithm Comparative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghai, D.; Tiwari, S.; Das, N.N. Bottom-boosting differential evolution based digital image security analysis. J. Inf. Secur. Appl. 2021, 61, 102811. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. A Comprehensive Review on Image Encryption Techniques. Arch. Comput. Methods Eng. State Art Rev. 2020, 27, 15–43. [Google Scholar] [CrossRef]
- Liang, R.; Qin, Y.; Zhang, C.; Lai, J.; Liu, M.; Chen, M. An Improved Arnold Image Scrambling Algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 042020. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X. An image encryption algorithm based on dynamic row scrambling and Zigzag transformation. Chaos Solitons Fractals 2021, 147, 110962. [Google Scholar] [CrossRef]
- Li, C.L.; Zhou, Y.; Li, H.M.; Feng, W.; Du, J.R. Image encryption scheme with bit-level scrambling and multiplication diffusion. Multimed. Tools Appl. 2021, 80, 18479–18501. [Google Scholar] [CrossRef]
- Khalil, N.; Sarhan, A.; Alshewimy, M.A. An efficient color/grayscale image encryption scheme based on hybrid chaotic maps. Opt. Laser Technol. 2021, 143, 107326. [Google Scholar] [CrossRef]
- Gao, X. Image encryption algorithm based on 2D hyperchaotic map. Opt. Laser Technol. 2021, 142, 107252. [Google Scholar] [CrossRef]
- Ghosh, G.; Anand, D.; Verma, S.; Rawat, D.B.; Shafi, J.; Marszałek, Z.; Woźniak, M. Secure Surveillance Systems Using Partial-Regeneration-Based Non-Dominated Optimization and 5D-Chaotic Map. Symmetry 2021, 13, 1447. [Google Scholar] [CrossRef]
- Hussain, R.; Karbhari, Y.; Ijaz, M.F.; Woźniak, M.; Singh, P.K.; Sarkar, R. Revise-Net: Exploiting Reverse Attention Mechanism for Salient Object Detection. Remote Sens. 2021, 13, 4941. [Google Scholar] [CrossRef]
- Etoundi, C.M.L.; Nkapkop, J.D.D.; Tsafack, N.; Ngono, J.M.; Ele, P.; Wozniak, M.; Shafi, J.; Ijaz, M.F. A Novel Compound-Coupled Hyperchaotic Map for Image Encryption. Symmetry 2022, 14, 493. [Google Scholar] [CrossRef]
- Joshi, A.B.; Kumar, D.; Mishra, D.C.; Guleria, V. Colour-image encryption based on 2D discrete wavelet transform and 3D logistic chaotic map. J. Mod. Opt. 2020, 67, 933–949. [Google Scholar] [CrossRef]
- Deng, X.; Ma, Y. PCNN model analysis and its automatic parameters determination in image segmentation and edge detection. Chin. J. Electron. 2014, 23, 97–103. [Google Scholar]
- Eckhorn, R.; Reitboeck, H.J.; Arndt, M.T.; Dicke, P. Feature linking via synchronization among distributed assemblies: Simulations of results from cat visual cortex. Neural Comput. 1990, 2, 293–307. [Google Scholar] [CrossRef]
- Johnson, J.L.; Padgett, M.L. PCNN models and applications. IEEE Trans. Neural Netw. 1999, 10, 480–498. [Google Scholar] [CrossRef]
- Deng, X.; Ye, J. A retinal blood vessel segmentation based on improved D-MNet and pulse-coupled neural network. Biomed. Signal Process. Control 2022, 73, 103467. [Google Scholar] [CrossRef]
- De, Y.M.; Xin, W. Signal tracking of the chaotic system of pulse coupled neural network. J. Lanzhou Univ. (Nat. Sci.) 2010, 46, 133–136, 142. [Google Scholar] [CrossRef]
- Qu, G.; Meng, X.; Yin, Y.; Wu, H.; Yang, X.; Peng, X.; He, W. Optical color image encryption based on Hadamard single-pixel imaging and Arnold transformation. Opt. Lasers Eng. 2021, 137, 106392. [Google Scholar] [CrossRef]
- Joshi, A.B.; Kumar, D.; Gaffar, A.; Mishra, D.C. Triple color image encryption based on 2D multiple parameter fractional discrete Fourier transform and 3D Arnold transform. Opt. Lasers Eng. 2020, 133, 106139. [Google Scholar] [CrossRef]
- Sehra, K.; Raut, S.; Mishra, A.; Kasturi, P.; Wadhera, S.; Saxena, G.J.; Saxena, M. Robust and Secure Digital Image Watermarking Technique Using Arnold Transform and Memristive Chaotic Oscillators. IEEE Access 2021, 11, 72465–72483. [Google Scholar] [CrossRef]
- Selvi, C.T.; Amudha, J.; Sudhakar, R. A modified salp swarm algorithm (SSA) combined with a chaotic coupled map lattices (CML) approach for the secured encryption and compression of medical images during data transmission. Biomed. Signal Process. Control 2021, 66, 102465. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, S.; Zhang, J. A Hybrid Domain Image Encryption Algorithm Based on Improved Henon Map. Entropy 2022, 24, 287. [Google Scholar] [CrossRef] [PubMed]
- Hosny, K.M.; Kamal, S.T.; Darwish, M.M.; Papakostas, G.A. New Image Encryption Algorithm Using Hyperchaotic System and Fibonacci Q-Matrix. Electronics 2021, 10, 1066. [Google Scholar] [CrossRef]
- Akhshani, A.; Akhavan, A.; Mobaraki, A.; Lim, S.C.; Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 101–111. [Google Scholar] [CrossRef]
- Hmg, A.; An, A.; Re, B. An overview of encryption algorithms in color images. Signal Process. 2019, 164, 163–185. [Google Scholar]
- Wang, Y.; Chen, L.; Yu, K.; Gao, Y.; Ma, Y. An Image Encryption Scheme Based on Logistic Quantum Chaos. Entropy 2022, 24, 251. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Huang, X.; Mei, Q. An efficient pixel-level chaotic image encryption algorithm. Nonlinear Dyn. 2018, 94, 745–756. [Google Scholar] [CrossRef]
- Li, R.; Liu, Q.; Liu, L. Novel image encryption algorithm based on improved logistic map. IET Image Process. 2019, 13, 125–134. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Zhang, Y. A chaotic image encryption algorithm based on random dynamic mixing. Opt. Laser Technol. 2021, 138, 106837. [Google Scholar] [CrossRef]
- Xiang, H.; Liu, L. A novel image encryption algorithm based on improved key selection and digital chaotic map. Multimed. Tools Appl. 2021, 80, 22135–22162. [Google Scholar] [CrossRef]
- Ye, G.; Jiao, K.; Huang, X. Quantum logistic image encryption algorithm based on SHA-3 and RSA. Nonlinear Dyn. 2021, 104, 2807–2827. [Google Scholar] [CrossRef]
- Muoz-Guillermo, M. Image encryption using q-deformed logistic map–ScienceDirect. Inf. Sci. 2020, 552, 352–364. [Google Scholar] [CrossRef]
- Jiang, X.; Xiao, Y.; Xie, Y.; Liu, B.; Ye, Y.; Song, T.; Chai, J.; Liu, Y. Exploiting optical chaos for double images encryption with compressive sensing and double random phase encoding. Opt. Commun. 2021, 484, 126683. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, P.; Sun, C.; Zhao, B. Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm. Entropy 2021, 23, 1159. [Google Scholar] [CrossRef]
- Deng, X.; Ma, Y.; Dong, M. A new adaptive filtering method for removing salt and pepper noise based on multilayered PCNN. Pattern Recognit. Lett. 2016, 79, 8–17. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, M.; Tong, X.; Wang, Z. Image compression and encryption algorithm based on compressive sensing and nonlinear diffusion. Multimed. Tools Appl. 2021, 80, 25433–25452. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y. Image encryption based on compressed sensing and DNA encoding. Signal Process. Image Commun. 2021, 95, 116246. [Google Scholar] [CrossRef]
- Wen, W.; Hong, Y.; Fang, Y.; Li, M.; Li, M. A visually secure image encryption scheme based on semi-tensor product compressed sensing-ScienceDirect. Signal Process. 2020, 173, 107580. [Google Scholar] [CrossRef]
- Farah, M.A.; Guesmi, R.; Kachouri, A.; Samet, M. A new design of cryptosystem based on S-box and chaotic permutation. Multimed. Tools Appl. 2020, 79, 19129–19150. [Google Scholar] [CrossRef]
- Artiles, J.A.; Chaves, D.P.; Pimentel, C. Image encryption using block cipher and chaotic sequences-ScienceDirect. Signal Process. Image Commun. 2019, 79, 24–31. [Google Scholar] [CrossRef]
- Li, T.; Du, B.; Liang, X. Image Encryption Algorithm Based on Logistic and Two-Dimensional Lorenz. IEEE Access 2020, 8, 13792–13805. [Google Scholar] [CrossRef]
- Wang, X.; Sun, H. A chaotic image encryption algorithm based on improved Joseph traversal and cyclic shift function. Opt. Laser Technol. 2020, 122, 105854. [Google Scholar] [CrossRef]
- Kamrani, A.; Zenkouar, K.; Najah, S. A new set of image encryption algorithms based on discrete orthogonal moments and Chaos theory. Multimed. Tools Appl. 2020, 79, 20263–20279. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L. A novel image encryption algorithm based on SPWLCM and DNA coding. Math. Comput. Simul. 2021, 190, 723–744. [Google Scholar] [CrossRef]
- Musanna, F.; Dangwal, D.; Kumar, S. Novel image encryption algorithm using fractional chaos and cellular neural network. J. Ambient. Intell. Humaniz. Comput. 2021, prepublish. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, X. Image Encryption Algorithm of Based on Variable Step Length Josephus Traversing and DNA Dynamic Coding. J. Electron. Inf. Technol. 2020, 42, 9. [Google Scholar]
- Wu, J.; Xia, W.; Zhu, G.; Liu, H.; Ma, L.; Xiong, J. Image encryption based on adversarial neural cryptography and SHA controlled chaos. J. Mod. Opt. 2021, 68, 409–418. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, C. A novel image encryption scheme based on conservative hyperchaotic system and closed-loop diffusion between blocks. Signal Process. 2020, 171, 107484. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Image encryption using 2D Hénon-Sine map and DNA approach. Signal Process. 2018, 153, 11–23. [Google Scholar] [CrossRef]
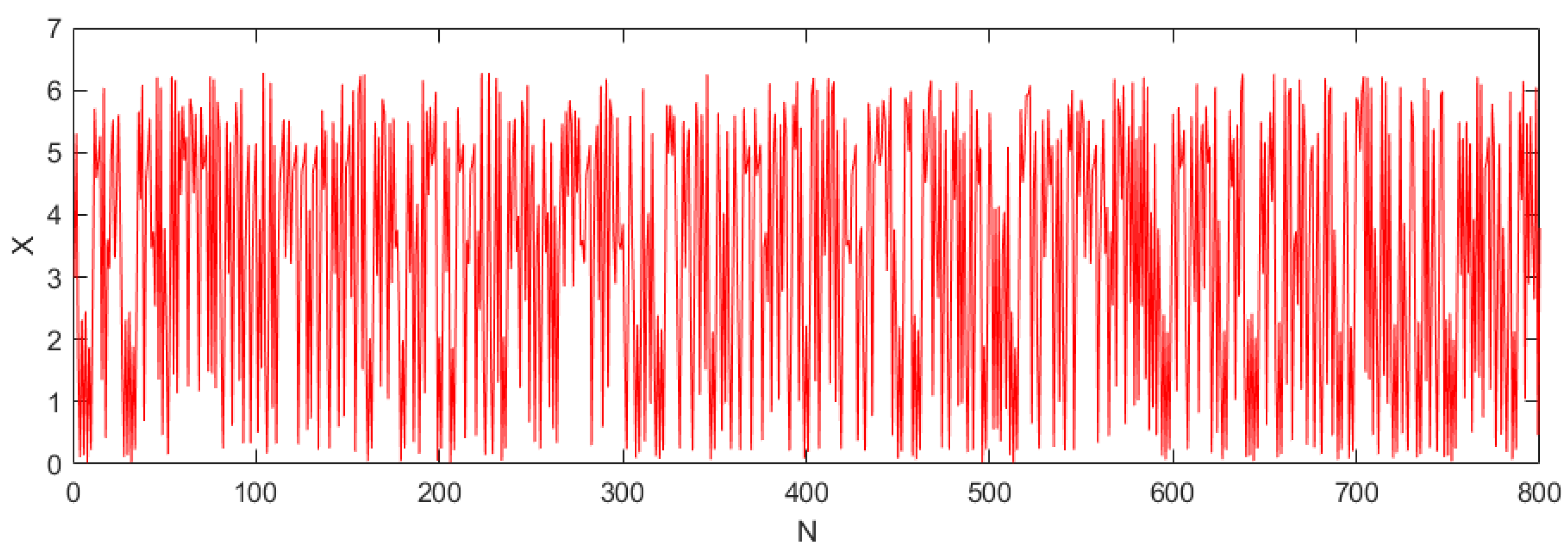
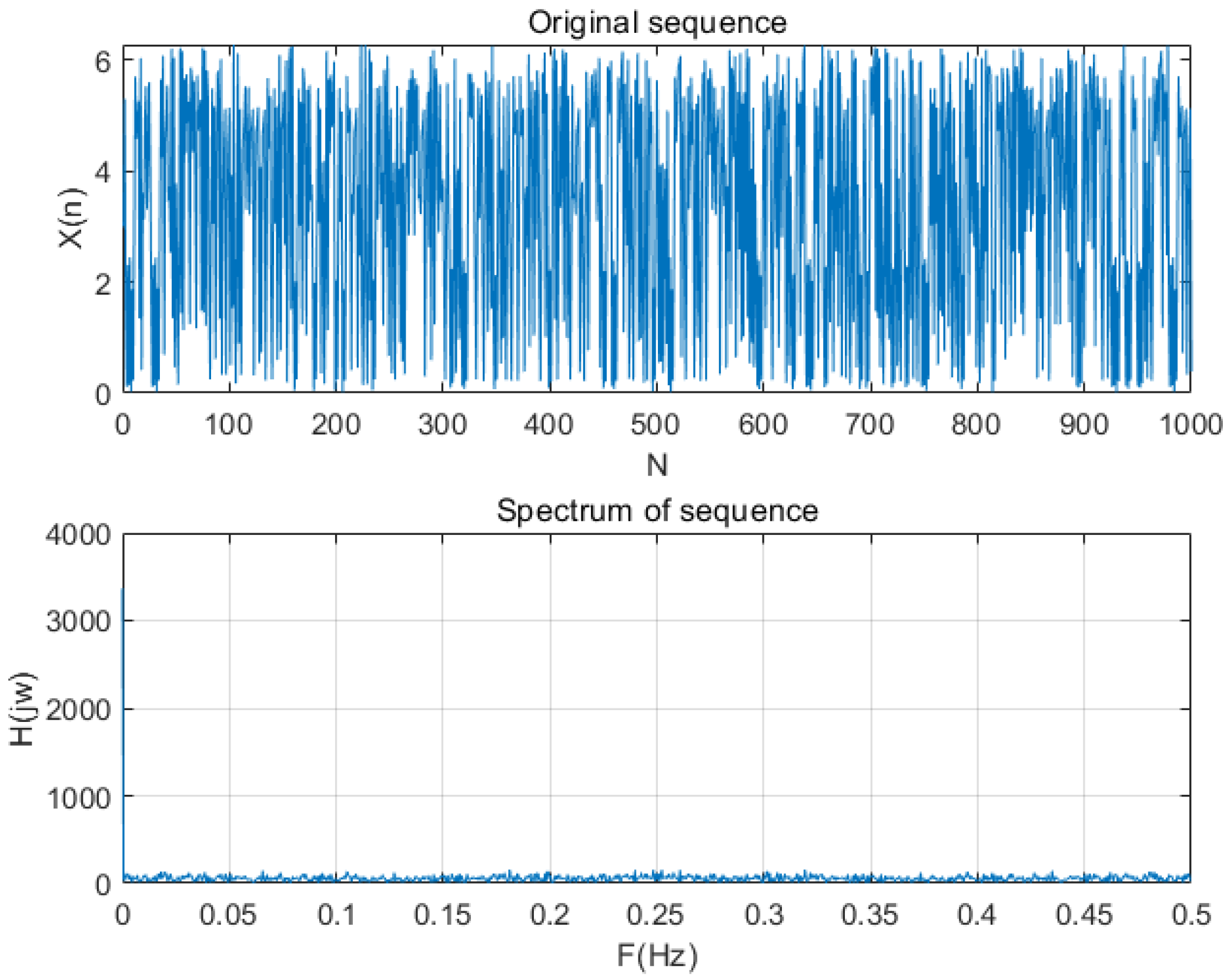













| Image Size N | Scrambling Period T | Image Size N | Scrambling Period T |
|---|---|---|---|
| 10 | 30 | 32 | 24 |
| 14 | 24 | 64 | 48 |
| 16 | 12 | 128 | 96 |
| 18 | 12 | 256 | 192 |
| 25 | 50 | 512 | 384 |
| Image (256 × 256) | Original Original | Encrypted Image | Result |
|---|---|---|---|
| Lena | 4.2981 × 105 | 232.6328 | pass |
| Cameraman | 1.5196 × 106 | 211.2109 | pass |
| White | 1.6712 × 107 | 209.8203 | pass |
| Black | 1.6711 × 107 | 259.1016 | pass |
| Peppers | 3.1639 × 104 | 246.3125 | pass |
| Plane | 1.7322 × 105 | 219.4922 | pass |
| Image (256 × 256) | Correlation Coefficient | |||||
|---|---|---|---|---|---|---|
| Unencrypted | Encrypted | |||||
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal | |
| Lena | 0.9204 | 0.9546 | 0.8944 | 0.0035 | 5.3876 × 10−4 | 3.2753 × 10−4 |
| Cameraman | 0.9756 | 0.9851 | 0.9601 | −0.0020 | 0.0016 | 0.0013 |
| White | -- | -- | -- | 0.0037 | −7.5285 × 10−4 | −7.6476 × 10−4 |
| Black | -- | -- | -- | −1.4710 × 10−5 | 0.0065 | −0.0042 |
| Peppers | 0.9648 | 0.9697 | 0.9388 | 0.0015 | 0.0029 | 0.0019 |
| Plane | 0.9387 | 0.9320 | 0.8832 | 0.0018 | −0.0057 | −1.1486 × 10−4 |
| Image (256 × 256) | Information Entropy | |
|---|---|---|
| Original | Encrypted | |
| Lena | 7.7758 | 7.9974 |
| Cameraman | 6.9749 | 7.9977 |
| White | 0 | 7.9977 |
| Black | 0 | 7.9972 |
| Peppers | 7.5798 | 7.9973 |
| Plane | 6.7334 | 7.9976 |
| Battery | Parameters | Number of Statistics | Result |
|---|---|---|---|
| SmallCrush | Standard | 15 | Pass |
| Alphabit | Standard | 17 | Pass |
| Rabbit | Standard | 40 | Pass |
| FIPS_140_2 | Standard | 16 | Pass |
| BlockAlphabit | Standard | 17 | Pass |
| Image | GVD Score | Image | GVD Score |
|---|---|---|---|
| Lena | 0.9415 | Peppers | 0.9674 |
| Cameraman | 0.9700 | Plane | 0.9512 |
| White | 1.000 | Black | 1.000 |
| Method | Year | Key Space |
|---|---|---|
| C.H. et al. [26] | 2018 | 2106 |
| G.D. et al. [27] | 2018 | 2186 |
| R.Z. et al. [28] | 2019 | 2199 |
| Xiaohong et al. [7] | 2021 | 2212 |
| Xw et al. [29] | 2021 | 2100 |
| Xiang H et al. [30] | 2021 | 2128 |
| Khalil Noura et al. [6] | 2021 | 2262 |
| Wang X et al. [4] | 2021 | 2420 |
| Our algorithm | 2022 | 2430 |
| Image (256 × 256) | Initial Value | NPCR | UACI | Different Pixel Proportions |
|---|---|---|---|---|
| Lena | 99.6368 | 33.3494 | 99.64 | |
| 99.6170 | 33.4318 | 99.62 | ||
| 99.6002 | 33.3646 | 99.60 | ||
| 99.6063 | 33.5540 | 99.61 | ||
| 99.6231 | 33.3861 | 99.62 | ||
| Cameraman | 99.6445 | 33.3839 | 99.64 | |
| 99.5956 | 33.5159 | 99.60 | ||
| 99.6078 | 33.4547 | 99.61 | ||
| 99.6109 | 33.4457 | 99.61 | ||
| 99.6445 | 33.4119 | 99.64 | ||
| White | 99.6429 | 33.6027 | 99.64 | |
| 99.6689 | 33.5871 | 99.67 | ||
| 99.5865 | 33.5613 | 99.59 | ||
| 99.6262 | 33.5986 | 99.63 | ||
| 99.5895 | 33.2934 | 99.62 | ||
| Black | 99.6078 | 33.6249 | 99.61 | |
| 99.6063 | 33.5503 | 99.61 | ||
| 99.5712 | 33.4333 | 99.57 | ||
| 99.6048 | 33.4588 | 99.60 | ||
| 99.5895 | 33.4558 | 99.59 | ||
| Average | -- | 99.614015 | 33.4841 | 99.6145 |
| Image | Different Pixel Proportions | Image | Different Pixel Proportions |
|---|---|---|---|
| Lena | 99.65 | Cameraman | 99.59 |
| White | 99.62 | Black | 99.58 |
| Peppers | 99.65 | Plane | 99.61 |
| Original Image (256 × 256) | NPCR | UACI |
|---|---|---|
| Lena | 99.6460 | 33.4397 |
| Cameraman | 99.5880 | 33.5050 |
| White | 99.6170 | 33.4276 |
| Black | 99.5758 | 33.5291 |
| Peppers | 99.6506 | 33.4559 |
| Plane | 99.6063 | 33.4554 |
| Average | 99.61395 | 33.468783 |
| Ideal value | 99.609375 | 33.463542 |
| Image | Year | Image Size | Time (s) |
|---|---|---|---|
| Lena (Our method) | 2022 | 256 × 256 | 0.1690 |
| Cameraman (Our method) | 2022 | 256 × 256 | 0.1740 |
| JinLong et al. [36] | 2021 | 256 × 256 | 0.6563 |
| Wang et al. [37] | 2021 | 256 × 256 | 0.2523 |
| Wenying Wen et al. [38] | 2020 | 256 × 256 | 2.1328 |
| Farah M et al. [39] | 2020 | 256 × 256 | 1.1202 |
| Lena (Our method) | 2022 | 512 × 512 | 0.7080 |
| Cameraman (Our method) | 2022 | 512 × 512 | 0.6640 |
| Wenying Wen et al. [38] | 2020 | 512 × 512 | 18.1354 |
| José, A. et al. [40] | 2019 | 512 × 512 | 10.4200 |
| Lena (Our method) | 2022 | 1024 × 1024 | 2.2990 |
| Cameraman (Our method) | 2022 | 1024 × 1024 | 2.1700 |
| Image (256 × 256) | Method | Year | Info Entropy | Correlation Coefficient | ||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | ||||
| Lena | Li et al. [41] | 2020 | 7.9894 | 0.0044 | 0.0015 | 0.0019 |
| Wang et al. [42] | 2020 | 7.9969 | 0.0006 | 0.0082 | 0.0032 | |
| Kamrani et al. [43] | 2020 | 7.9945 | -- | -- | -- | |
| Hosny et al. [22] | 2021 | 7.9972 | 0.0069 | 0.0479 | 0.0075 | |
| Xw et al. [29] | 2021 | 7.9971 | −0.0017 | −0.0132 | 0.0084 | |
| Zhang et al. [44] | 2021 | 7.9969 | 0.0040 | −0.0012 | −0.0021 | |
| Farhan et al. [45] | 2021 | 7.9971 | −0.0004 | −0.0028 | 0.0040 | |
| Wang et al. [37] | 2021 | 7.9960 | 0.0023 | 0.0020 | 0.0073 | |
| Xiang et al. [30] | 2021 | 7.9972 | 0.0013 | -0.0041 | −0.0044 | |
| JinLong et al. [36] | 2021 | 7.9858 | 0.0031 | 0.0076 | −0.0026 | |
| Proposed | 2022 | 7.9974 | −0.0035 | 5.3876 × 10−4 | 3.2753 × 10−4 | |
| Cameraman | Niu et al. [46] | 2020 | 7.9971 | −0.0070 | 0.0083 | 0.0013 |
| Kamrani et al. [43] | 2020 | 7.9947 | -- | -- | -- | |
| Wu et al. [47] | 2021 | 7.9935 | −0.0036 | 0.0048 | 0.0073 | |
| JinLong et al. [36] | 2021 | 7.9868 | −0.0252 | −0.0060 | −0.0078 | |
| Proposed | 2022 | 7.9977 | 0.0020 | 0.0016 | 0.0013 | |
| Peppers | Hua, Z. et al. [48] | 2019 | 7.9971 | 0.0196 | 0.0165 | 0.0210 |
| Minjun et al. [49] | 2020 | 7.9970 | 0.00476 | −0.009531 | 0.007338 | |
| Wang et al. [37] | 2021 | 7.9964 | −0.0037 | 0.0035 | −0.0057 | |
| Xw et al. [29] | 2021 | 7.9971 | −0.0062 | −0.0236 | −0.0047 | |
| Wu et al. [47] | 2021 | 7.9941 | −0.0170 | −0.0334 | −0.0073 | |
| Hosny et al. [22] | 2021 | 7.9970 | 0.0211 | 0.0129 | 0.0013 | |
| Proposed | 2022 | 7.9973 | 0.0015 | 0.0029 | −0.0019 | |
| Plane | Wu et al. [50] | 2018 | 7.9970 | 0.0028 | 0.0041 | 0.0010 |
| Hua, Z. et al. [48] | 2019 | 7.9971 | 0.0055 | 0.0014 | 0.0083 | |
| Xw et al. [29] | 2021 | 7.9972 | −0.0043 | −0.0236 | −0.0047 | |
| Hosny et al. [22] | 2021 | 7.9972 | 0.0229 | 0.0103 | 0.0100 | |
| Wang et al. [37] | 2021 | 7.9959 | 0.0054 | 0.0027 | 0.0028 | |
| Proposed | 2022 | 7.9976 | −0.0018 | −0.0057 | −1.1486 × 10−4 | |
| Image (256 × 256) | Method | Year | NPCR (%) | UACI (%) | |
|---|---|---|---|---|---|
| Ideal value | 99.609375 | 33.463542 | Minimum | ||
| Lena | Kamrani et al. [43] | 2020 | 99.7864 | 30.3256 | -- |
| Li et al. [41] | 2020 | 99.66 | 33.42 | -- | |
| Minjun et al. [49] | 2020 | 99.6114 | 33.4523 | -- | |
| Hosny et al. [22] | 2021 | 99.6246 | 33.4226 | 264.8750 | |
| Zhang et al. [44] | 2021 | 99.62 | 33.50 | -- | |
| Wang et al. [37] | 2021 | 99.5894 | 33.4629 | -- | |
| Xw et al. [29] | 2021 | -- | -- | 266.6797 | |
| Proposed | 2022 | 99.6460 | 33.4397 | 232.6328 | |
| Cameraman | Kamrani et al. [43] | 2020 | 99.791 | 27.6376 | -- |
| Zhang et al. [44] | 2021 | 99.63 | 33.56 | -- | |
| Wang et al. [37] | 2021 | 99.5879 | 33.4553 | -- | |
| Proposed | 2022 | 99.5880 | 33.5050 | 211.2109 | |
| Peppers | Minjun et al. [49] | 2020 | 99.6115 | 33.4245 | -- |
| Hosny et al. [22] | 2021 | 99.6033 | 33.4274 | 268.4766 | |
| Xw et al. [29] | 2021 | -- | -- | 260.3906 | |
| Proposed | 2022 | 99.6506 | 33.4559 | 246.3125 | |
| Plane | Minjun et al. [49] | 2020 | 99.6043 | 33.2875 | -- |
| Xw et al. [29] | 2021 | -- | -- | 252.1172 | |
| Proposed | 2022 | 99.6063 | 33.4554 | 219.4922 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Deng, X.; Zhang, A.; Yu, H. A Novel Image Encryption Algorithm Based on Improved Arnold Transform and Chaotic Pulse-Coupled Neural Network. Entropy 2022, 24, 1103. https://doi.org/10.3390/e24081103
Ye J, Deng X, Zhang A, Yu H. A Novel Image Encryption Algorithm Based on Improved Arnold Transform and Chaotic Pulse-Coupled Neural Network. Entropy. 2022; 24(8):1103. https://doi.org/10.3390/e24081103
Chicago/Turabian StyleYe, Jinhong, Xiangyu Deng, Aijia Zhang, and Haiyue Yu. 2022. "A Novel Image Encryption Algorithm Based on Improved Arnold Transform and Chaotic Pulse-Coupled Neural Network" Entropy 24, no. 8: 1103. https://doi.org/10.3390/e24081103
APA StyleYe, J., Deng, X., Zhang, A., & Yu, H. (2022). A Novel Image Encryption Algorithm Based on Improved Arnold Transform and Chaotic Pulse-Coupled Neural Network. Entropy, 24(8), 1103. https://doi.org/10.3390/e24081103





