A Pattern Dictionary Method for Anomaly Detection
Abstract
:1. Introduction
2. Related Works
3. Framework and Notation
Notation
- All logarithms are base 2 unless otherwise is indicated.
- In the encoding process, we always adhere to lossless compression and strict decodability at the decoder.
- While adhering to strict decodability, we only care about the codelength, not the codes themselves.
4. Pattern Dictionary: Design and Properties
4.1. A Special Case
4.2. The General Case
4.3. Pattern Dictionary for Detection (PDD)
| Algorithm 1 Pattern Dictionary (PD) Parser |
|
5. Pattern Dictionary-Based Atypicality (PDA)
5.1. Lempel–Ziv Parser
5.2. Pattern Dictionary Parser versus LZ78 Parser
5.3. Atypicality Criterion for Detection of Anomalous Subsequences
6. Experiment
6.1. Anomaly Detection in Mackey–Glass Time Series
- Pattern Dictionary for Detection (PDD)
- Pattern Dictionary Based Atypicality (PDA)
- Ziv–Merhav Method (ZM) [48]
- Nearest Neighbors-Based Similarity (NNS) [7]
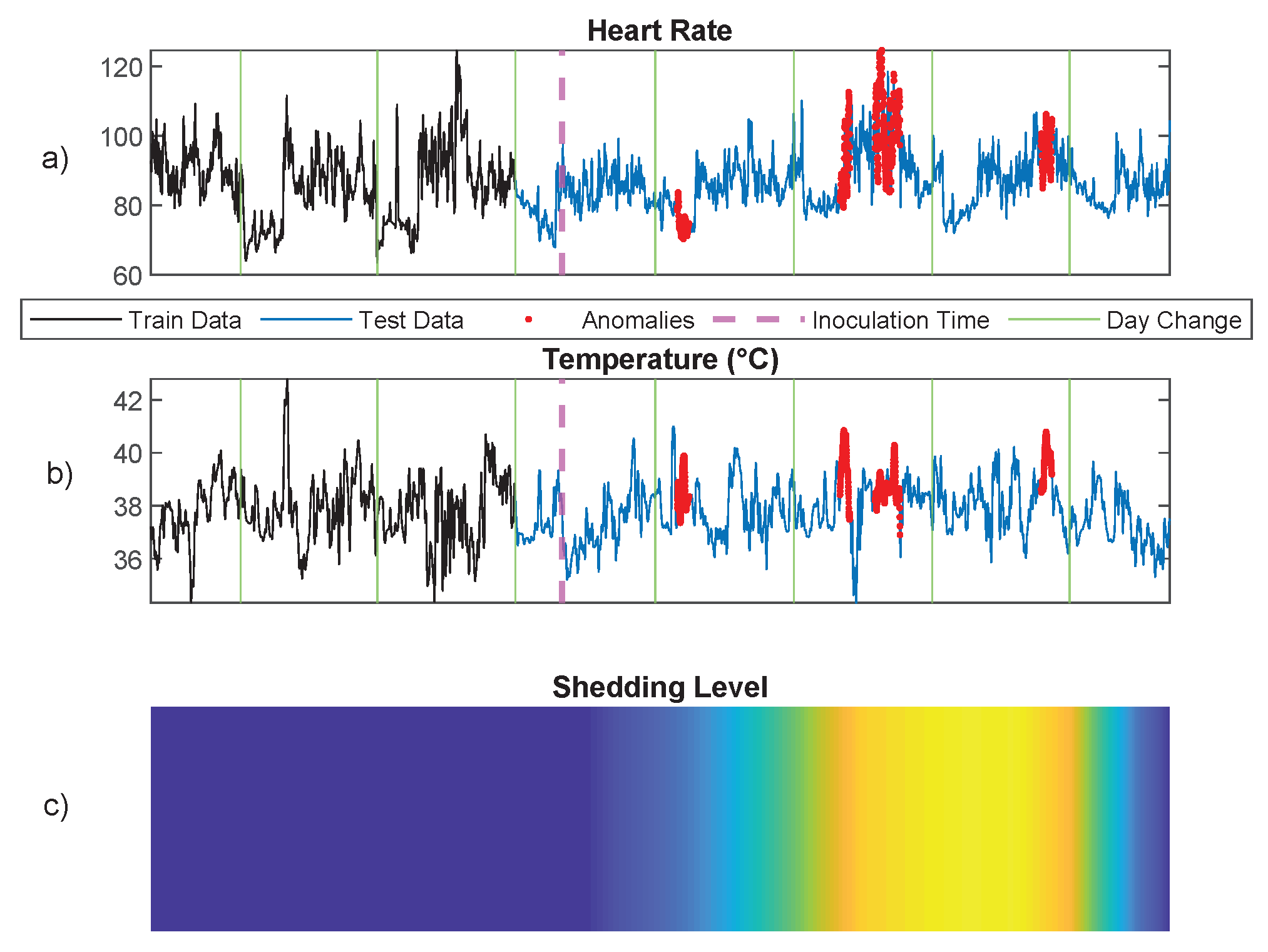
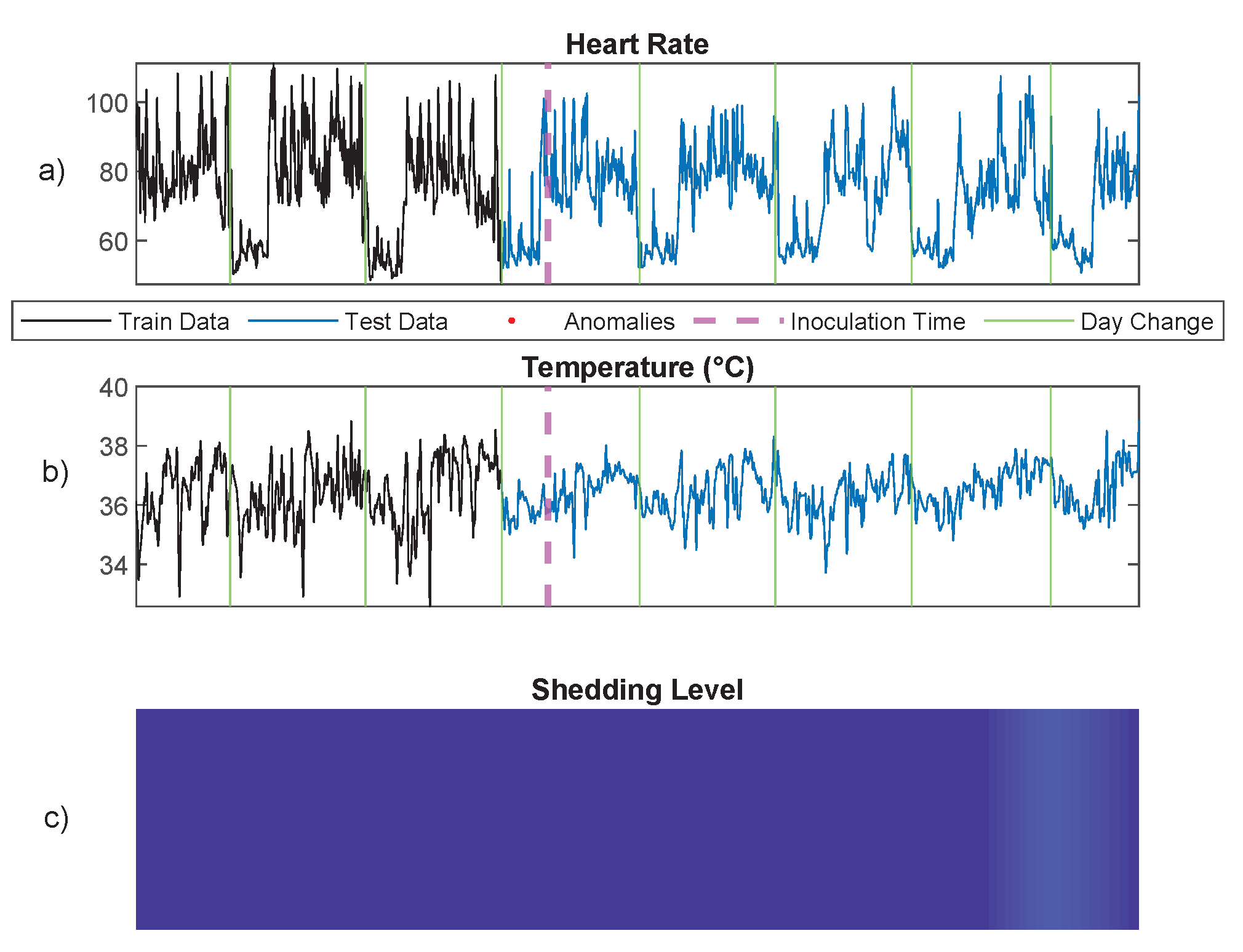
6.2. Infection Detection Using Physiological Signals
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 15. [Google Scholar] [CrossRef]
- Høst-Madsen, A.; Sabeti, E.; Walton, C. Data discovery and anomaly detection using atypicality: Theory. IEEE Trans. Inf. Theory 2019, 65, 5302–5322. [Google Scholar] [CrossRef]
- Sabeti, E.; Høst-Madsen, A. Data Discovery and Anomaly Detection Using Atypicality for Real-Valued Data. Entropy 2019, 21, 219. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Thomas, J. Information Theory, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. Inf. Theory IEEE Trans. 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the LambertW function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Chandola, V.; Mithal, V.; Kumar, V. Comparative evaluation of anomaly detection techniques for sequence data. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 743–748. [Google Scholar]
- Cabrera, J.B.; Lewis, L.; Mehra, R.K. Detection and classification of intrusions and faults using sequences of system calls. ACM SIGMOD Rec. 2001, 30, 25–34. [Google Scholar] [CrossRef]
- Hofmeyr, S.A.; Forrest, S.; Somayaji, A. Intrusion detection using sequences of system calls. J. Comput. Secur. 1998, 6, 151–180. [Google Scholar] [CrossRef]
- Lane, T.; Brodley, C.E. Temporal sequence learning and data reduction for anomaly detection. ACM Trans. Inf. Syst. Secur. (TISSEC) 1999, 2, 295–331. [Google Scholar] [CrossRef]
- Warrender, C.; Forrest, S.; Pearlmutter, B. Detecting intrusions using system calls: Alternative data models. In Proceedings of the 1999 IEEE Symposium on Security and Privacy (Cat. No. 99CB36344), Oakland, CA, USA, 14 May 1999; pp. 133–145. [Google Scholar]
- Keogh, E.; Lonardi, S.; Ratanamahatana, C.A. Towards parameter-free data mining. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 206–215. [Google Scholar]
- Keogh, E.; Lonardi, S.; Ratanamahatana, C.A.; Wei, L.; Lee, S.H.; Handley, J. Compression-based data mining of sequential data. Data Min. Knowl. Discov. 2007, 14, 99–129. [Google Scholar] [CrossRef]
- Keogh, E.; Keogh, L.; Handley, J.C. Compression-based data mining. In Encyclopedia of Data Warehousing and Mining, 2nd ed.; IGI Global: Pennsylvania, PA, USA, 2009; pp. 278–285. [Google Scholar]
- Keogh, E.; Lonardi, S.; Chiu, B.C. Finding surprising patterns in a time series database in linear time and space. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 550–556. [Google Scholar]
- Keogh, E.; Lin, J.; Lee, S.H.; Van Herle, H. Finding the most unusual time series subsequence: Algorithms and applications. Knowl. Inf. Syst. 2007, 11, 1–27. [Google Scholar] [CrossRef]
- Ferguson, T.S. Mathematical Statistics: A decision Theoretic Approach; Academic Press: Cambridge, MA, USA, 2014; Volume 1. [Google Scholar]
- Siegmund, D.; Venkatraman, E. Using the generalized likelihood ratio statistic for sequential detection of a change-point. Ann. Stat. 1995, 23, 255–271. [Google Scholar] [CrossRef]
- Hirai, S.; Yamanishi, K. Detecting changes of clustering structures using normalized maximum likelihood coding. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 343–351. [Google Scholar]
- Yamanishi, K.; Miyaguchi, K. Detecting gradual changes from data stream using MDL-change statistics. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 156–163. [Google Scholar]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal detection of changepoints with a linear computational cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. (CSUR) 2014, 46, 44. [Google Scholar] [CrossRef]
- Chernoff, H. Sequential design of experiments. Ann. Math. Stat. 1959, 30, 755–770. [Google Scholar] [CrossRef]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall Englewood Cliffs: Hoboken, NJ, USA, 1993; Volume 104. [Google Scholar]
- Veeravalli, V.V.; Banerjee, T. Quickest change detection. Acad. Press Libr. Signal Process. Array Stat. Signal Process. 2013, 3, 209–256. [Google Scholar]
- Han, C.; Willett, P.; Chen, B.; Abraham, D. A detection optimal min-max test for transient signals. Inf. Theory IEEE Trans. 1998, 44, 866–869. [Google Scholar] [CrossRef]
- Wang, Z.; Willett, P. A performance study of some transient detectors. Signal Process. IEEE Trans. 2000, 48, 2682–2685. [Google Scholar] [CrossRef]
- Wang, Z.; Willett, P.K. All-purpose and plug-in power-law detectors for transient signals. Signal Process. IEEE Trans. 2001, 49, 2454–2466. [Google Scholar] [CrossRef]
- Wang, Z.J.; Willett, P. A variable threshold page procedure for detection of transient signals. IEEE Trans. Signal Process. 2005, 53, 4397–4402. [Google Scholar] [CrossRef]
- Hero, A.O. Geometric entropy minimization (GEM) for anomaly detection and localization. NIPS 2006, 19, 585–592. [Google Scholar]
- Sricharan, K.; Hero, A. Efficient anomaly detection using bipartite k-nn graphs. Adv. Neural Inf. Process. Syst. 2011, 24, 478–486. [Google Scholar]
- Sen, P.K. Theory and Applications of Sequential Nonparametrics; SIAM: Philadelphia, PA, USA, 1985. [Google Scholar]
- Balsubramani, A.; Ramdas, A. Sequential Nonparametric Testing with the Law of the Iterated Logarithm. In Proceedings of the Thirty-Second Conference on Uncertainty in Artificial Intelligence, Jersey City, NJ, USA, 25–29 June 2016; AUAI Press: Arlington, VA, USA, 2016; pp. 42–51. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection for Discrete Sequences: A Survey. Knowl. Data Eng. IEEE Trans. 2012, 24, 823–839. [Google Scholar] [CrossRef]
- Evans, S.; Barnett, B.; Bush, S.; Saulnier, G. Minimum description length principles for detection and classification of FTP exploits. In Proceedings of the Military Communications Conference, Monterey, CA, USA, 31 October–3 November 2004; Volume 1, pp. 473–479. [Google Scholar] [CrossRef]
- Wang, N.; Han, J.; Fang, J. An Anomaly Detection Algorithm Based on Lossless Compression. In Proceedings of the 2012 IEEE 7th International Conference on Networking, Architecture and Storage (NAS), Xiamen, China, 28–30 June 2012; pp. 31–38. [Google Scholar] [CrossRef]
- Lee, W.; Xiang, D. Information-theoretic measures for anomaly detection. In Proceedings of the 2001 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 14–16 May 2001; pp. 130–143. [Google Scholar] [CrossRef]
- Paschalidis, I.; Smaragdakis, G. Spatio-Temporal Network Anomaly Detection by Assessing Deviations of Empirical Measures. Netw. IEEE/ACM Trans. 2009, 17, 685–697. [Google Scholar] [CrossRef]
- Han, C.K.; Choi, H.K. Effective discovery of attacks using entropy of packet dynamics. Netw. IEEE 2009, 23, 4–12. [Google Scholar] [CrossRef]
- Baliga, P.; Lin, T. Kolmogorov complexity based automata modeling for intrusion detection. In Proceedings of the 2005 IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; Volume 2, pp. 387–392. [Google Scholar] [CrossRef]
- Shahriar, H.; Zulkernine, M. Information-Theoretic Detection of SQL Injection Attacks. In Proceedings of the 2012 IEEE 14th International Symposium on High-Assurance Systems Engineering (HASE), Omaha, NE, USA, 25–27 October 2012; pp. 40–47. [Google Scholar] [CrossRef]
- Xiang, Y.; Li, K.; Zhou, W. Low-Rate DDoS Attacks Detection and Traceback by Using New Information Metrics. Inf. Forensics Secur. IEEE Trans. 2011, 6, 426–437. [Google Scholar] [CrossRef]
- Pan, F.; Wang, W. Anomaly detection based-on the regularity of normal behaviors. In Proceedings of the 1st International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, 19–21 January 2006. [Google Scholar] [CrossRef]
- Eiland, E.; Liebrock, L. An application of information theory to intrusion detection. In Proceedings of the Fourth IEEE International Workshop on Information Assurance, London, UK, 13–14 April 2006. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitanyi, P. The similarity metric. Inf. Theory IEEE Trans. 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Li, Y.; Nitinawarat, S.; Veeravalli, V.V. Universal outlier hypothesis testing. IEEE Trans. Inf. Theory 2014, 60, 4066–4082. [Google Scholar] [CrossRef]
- Li, Y.; Nitinawarat, S.; Veeravalli, V.V. Universal outlier detection. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 10–15 February 2013; pp. 1–5. [Google Scholar]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Chandola, V. Anomaly Detection for Symbolic Sequences and Time Series Data. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2009. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 589. [Google Scholar]
- Wu, Q.; Shao, Z. Network anomaly detection using time series analysis. In Proceedings of the Joint International Conference on Autonomic and Autonomous Systems and International Conference on Networking And Services-(icas-isns’ 05), Papeete, France, 23–28 October 2005; p. 42. [Google Scholar]
- Pincombe, B. Anomaly detection in time series of graphs using arma processes. Asor Bull. 2005, 24, 2. [Google Scholar]
- Moayedi, H.Z.; Masnadi-Shirazi, M. Arima model for network traffic prediction and anomaly detection. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; Volume 4, pp. 1–6. [Google Scholar]
- Ma, J.; Perkins, S. Online novelty detection on temporal sequences. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 613–618. [Google Scholar]
- Knorn, F.; Leith, D.J. Adaptive kalman filtering for anomaly detection in software appliances. In Proceedings of the IEEE INFOCOM Workshops, Phoenix, AZ, USA, 13–18 April 2008; pp. 1–6. [Google Scholar]
- Gusfield, D. Algorithms on stings, trees, and sequences: Computer science and computational biology. Acm Sigact News 1997, 28, 41–60. [Google Scholar] [CrossRef]
- Thottan, M.; Ji, C. Anomaly detection in IP networks. Signal Process. IEEE Trans. 2003, 51, 2191–2204. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Sarawagi, S.; Dom, B. Mining surprising patterns using temporal description length. In Proceedings of the VLDB’98, 24rd International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 606–617. [Google Scholar]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef]
- Ranshous, S.; Shen, S.; Koutra, D.; Harenberg, S.; Faloutsos, C.; Samatova, N.F. Anomaly detection in dynamic networks: A survey. Wiley Interdiscip. Rev. Comput. Stat. 2015, 7, 223–247. [Google Scholar] [CrossRef]
- Yu, R.; Qiu, H.; Wen, Z.; Lin, C.; Liu, Y. A survey on social media anomaly detection. ACM SIGKDD Explor. Newsl. 2016, 18, 1–14. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Philip, S.Y. An effective and efficient algorithm for high-dimensional outlier detection. VLDB J. 2005, 14, 211–221. [Google Scholar] [CrossRef]
- Goldstein, M.; Dengel, A. Histogram-based outlier score (hbos): A fast unsupervised anomaly detection algorithm. In Proceedings of the KI-2012: Poster and Demo Track, Saarbrücken, Germany, 24-27 September 2012; 2012; pp. 59–63. [Google Scholar]
- Foorthuis, R. SECODA: Segmentation-and combination-based detection of anomalies. In Proceedings of the 2017 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 755–764. [Google Scholar]
- Foorthuis, R. The Impact of Discretization Method on the Detection of Six Types of Anomalies in Datasets. arXiv 2020, arXiv:2008.12330. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer vision with the OpenCV Library; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2008. [Google Scholar]
- Tung, S. On lower and upper bounds of the difference between the arithmetic and the geometric mean. Math. Comput. 1975, 29, 834–836. [Google Scholar] [CrossRef]
- Willems, F. The context-tree weighting method: Extensions. Inf. Theory IEEE Trans. 1998, 44, 792–798. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.; Tjalkens, T. The context-tree weighting method: Basic properties. Inf. Theory IEEE Trans. 1995, 41, 653–664. [Google Scholar] [CrossRef]
- Willems, F.; Shtarkov, Y.; Tjalkens, T. Reflections on “The Context Tree Weighting Method: Basic properties”. Newsl. IEEE Inf. Theory Soc. 1997, 47. [Google Scholar]
- Hoorfar, A.; Hassani, M. Inequalities on the Lambert W function and hyperpower function. J. Inequal. Pure Appl. Math 2008, 9, 5–9. [Google Scholar]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. Inf. Theory IEEE Trans. 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Jacquet, P.; Szpankowski, W. Limiting Distribution of Lempel Ziv’78 Redundancy. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings (ISIT), St. Petersburg, Russia, 31 July–5 August 2011; pp. 1509–1513. [Google Scholar]
- Yang, E.H.; Meng, J. Non-asymptotic equipartition properties for independent and identically distributed sources. In Proceedings of the 2012 Information Theory and Applications Workshop, San Diego, CA, USA, 5–10 February 2012; pp. 39–46. [Google Scholar]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 159. [Google Scholar]
- Grzesiak, E.; Bent, B.; McClain, M.T.; Woods, C.W.; Tsalik, E.L.; Nicholson, B.P.; Veldman, T.; Burke, T.W.; Gardener, Z.; Bergstrom, E.; et al. Assessment of the Feasibility of Using Noninvasive Wearable Biometric Monitoring Sensors to Detect Influenza and the Common Cold Before Symptom Onset. JAMA Netw. Open 2021, 4, e2128534. [Google Scholar] [CrossRef] [PubMed]
- She, X.; Zhai, Y.; Henao, R.; Woods, C.; Chiu, C.; Ginsburg, G.S.; Song, P.X.; Hero, A.O. Adaptive multi-channel event segmentation and feature extraction for monitoring health outcomes. IEEE Trans. Biomed. Eng. 2020, 68, 2377–2388. [Google Scholar] [CrossRef]
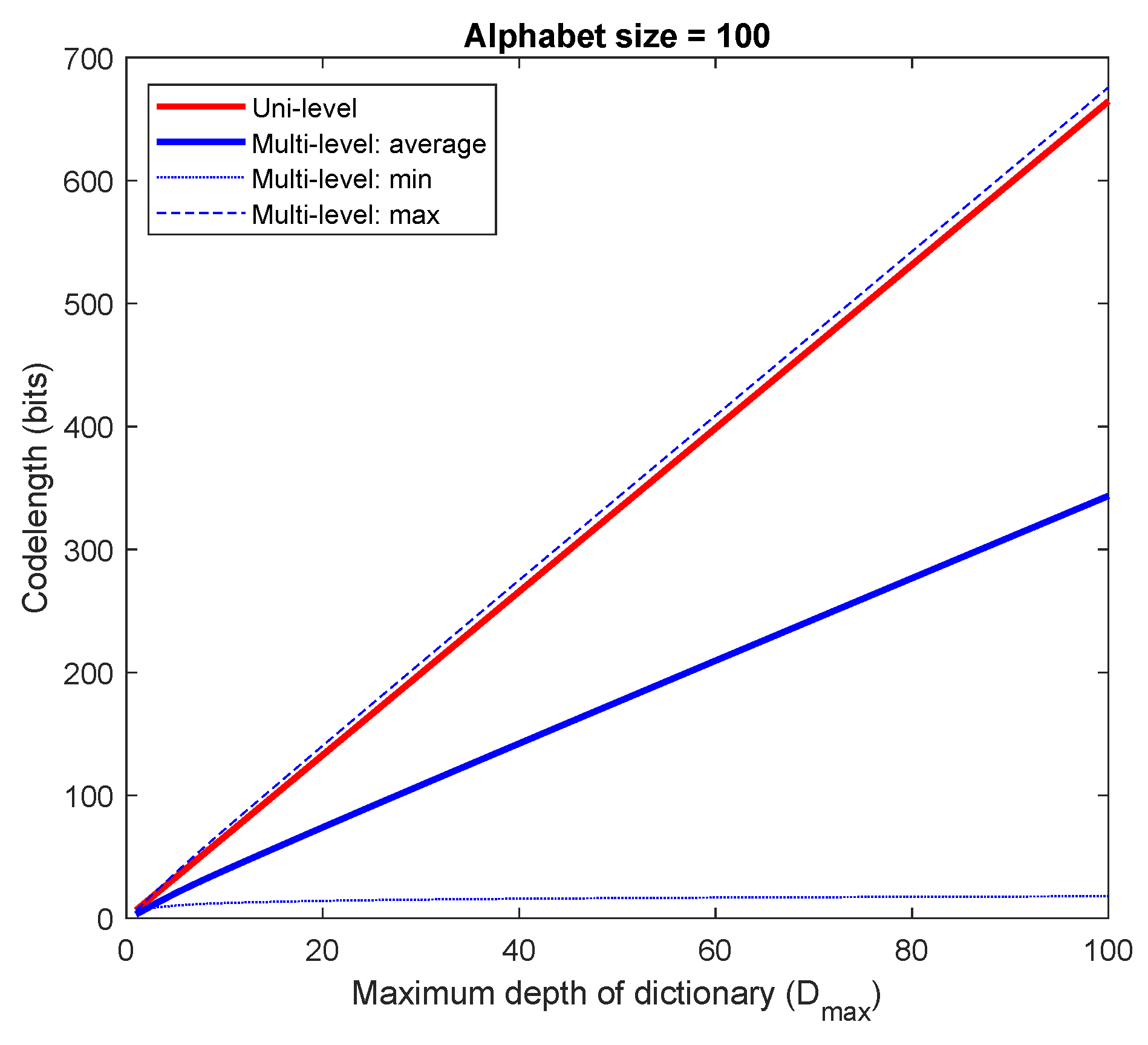


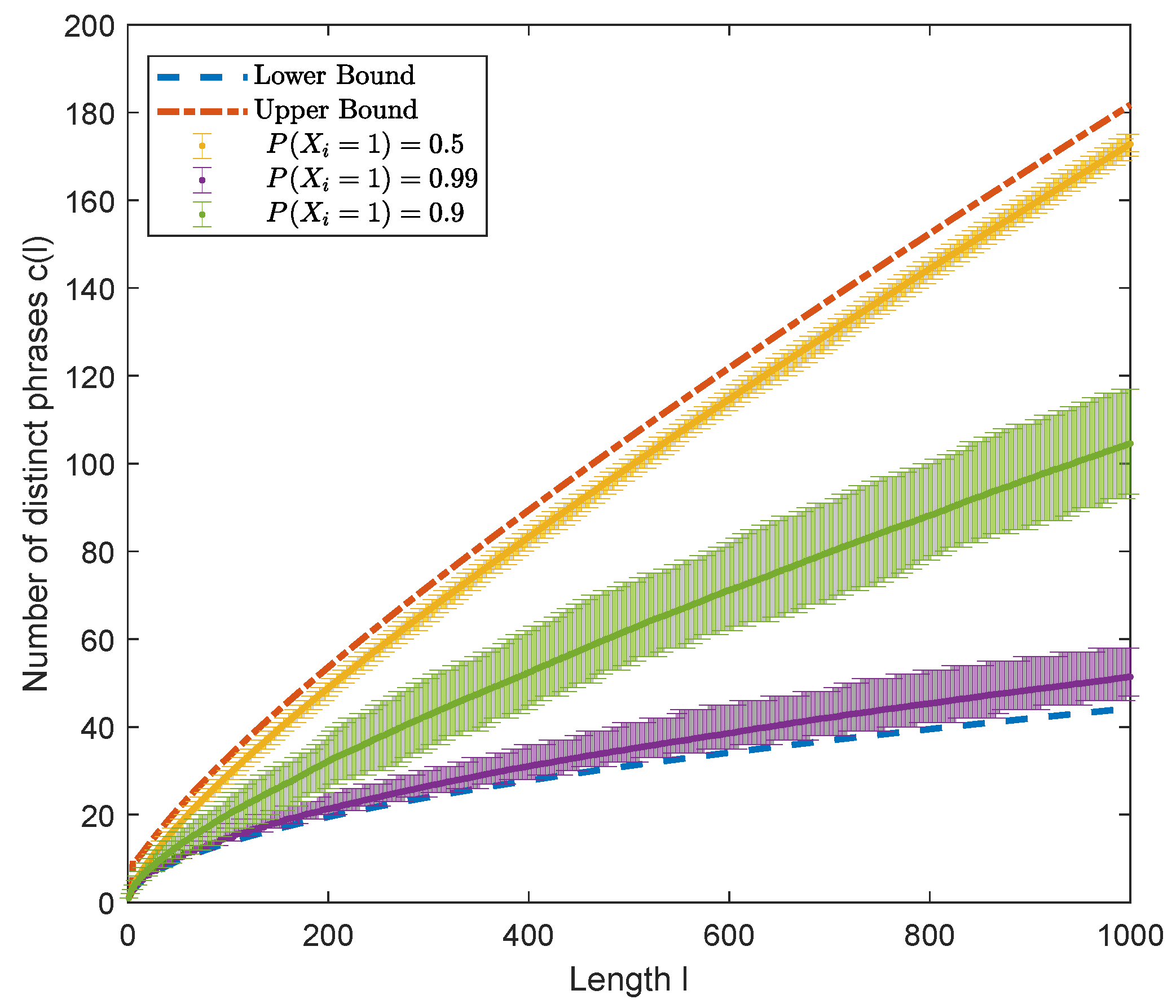

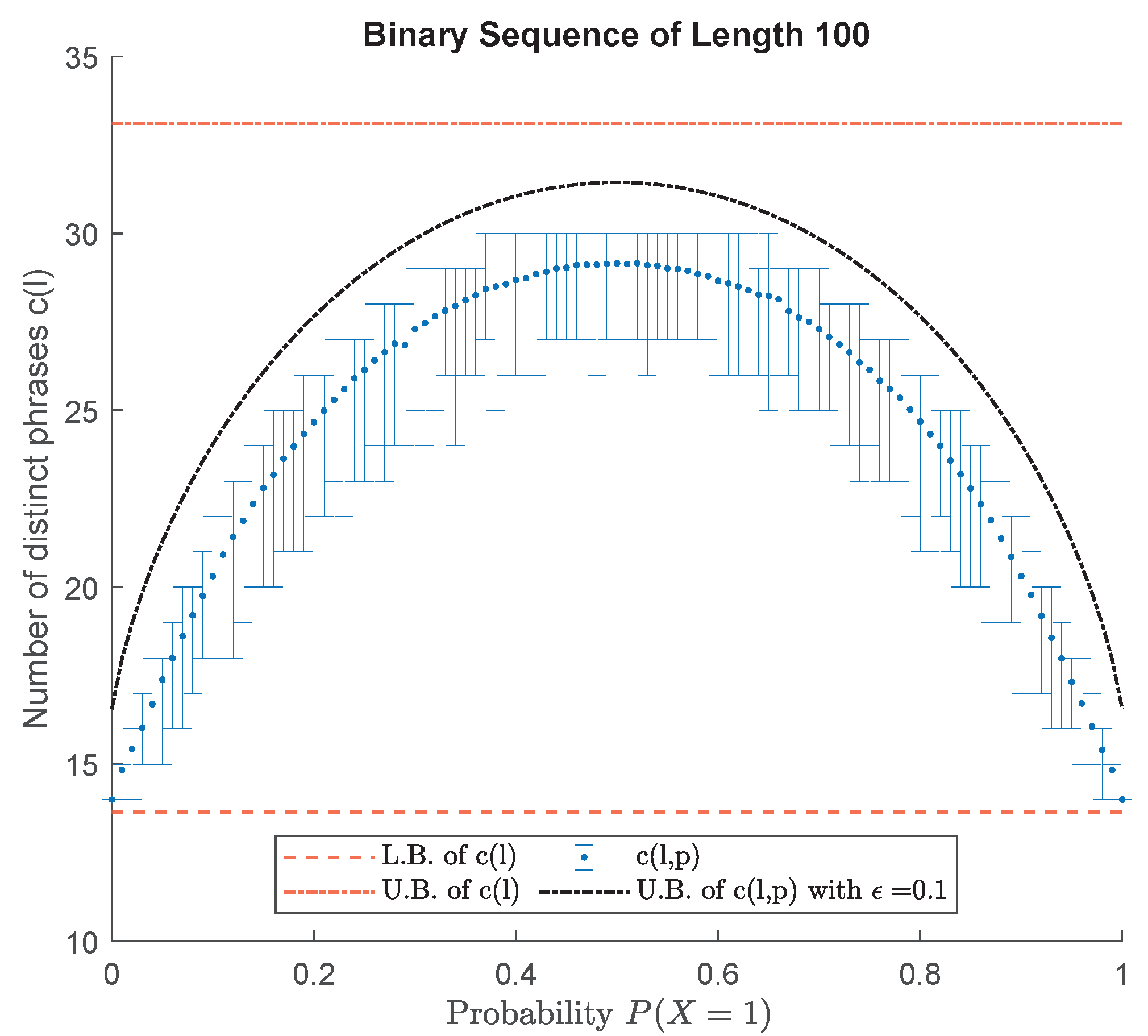


| Depth 1 | Depth 2 | Depth 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Pr | Pr | Pr | ||||||
| A | 0.44 | 1 | AB | 0.2083 | 2 | ABA | 0.1304 | 3 |
| B | 0.24 | 2 | BA | 0.1667 | 3 | BAC | 0.1304 | 3 |
| C | 0.16 | 3 | AC | 0.1250 | 3 | CAD | 0.1304 | 3 |
| D | 0.16 | 3 | CA | 0.1250 | 3 | DAB | 0.1304 | 3 |
| AD | 0.1250 | 3 | ACA | 0.0870 | 4 | |||
| DA | 0.1250 | 3 | ADA | 0.0870 | 4 | |||
| BB | 0.0417 | 4 | ABB | 0.0435 | 4 | |||
| CC | 0.0417 | 5 | BBA | 0.0435 | 4 | |||
| DD | 0.0417 | 5 | ACC | 0.0435 | 4 | |||
| CCA | 0.0435 | 4 | ||||||
| ADD | 0.0435 | 4 | ||||||
| DDA | 0.0435 | 5 | ||||||
| BAB | 0.0435 | 5 | ||||||
| ROC AUC | PR AUC | |
|---|---|---|
| PDA | ||
| PDD | ||
| ZM | ||
| CDM | ||
| NNS | ||
| t-STIDE |
| Resolution | PDA | PDD | ZM | CDM | NNS | t-STIDE | |
|---|---|---|---|---|---|---|---|
| ROC AUC | Low | 0.948 ±0.011 | 0.930 ±0.013 | 0.943 ±0.014 | 0.787 ±0.017 | 0.901 ±0.027 | 0.725 ±0.025 |
| Medium | 0.955 ±0.010 | 0.943 ±0.011 | 0.954 ±0.011 | 0.940 ±0.014 | 0.918 ±0.022 | 0.881 ±0.017 | |
| High | 0.963 ±0.009 | 0.959 ±0.009 | 0.959 ±0.009 | 0.957 ±0.012 | 0.920 ±0.021 | 0.897 ±0.013 | |
| PR AUC | Low | 0.876 ±0.050 | 0.871 ±0.052 | 0.826 ±0.071 | 0.669 ±0.067 | 0.719 ±0.098 | 0.678 ±0.067 |
| Medium | 0.885 ±0.046 | 0.882 ±0.047 | 0.881 ±0.053 | 0.880 ±0.060 | 0.777 ±0.093 | 0.828 ±0.050 | |
| High | 0.909 ±0.044 | 0.907 ±0.044 | 0.895 ± 0.044 | 0.907 ±0.057 | 0.777 ±0.091 | 0.857 ±0.044 |
| Resolution | PD-Based | ZM-Codebook | ZM | |
|---|---|---|---|---|
| dictionary generation | Low | 6.80 | 29.98 | N/A |
| Medium | 13.12 | 39.01 | N/A | |
| High | 15.46 | 40.80 | N/A | |
| parsing procedure | Low | 6.07 | 9.23 | 142.77 |
| Medium | 10.81 | 11.10 | 433.55 | |
| High | 14.83 | 16.70 | 670.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabeti, E.; Oh, S.; Song, P.X.K.; Hero, A.O. A Pattern Dictionary Method for Anomaly Detection. Entropy 2022, 24, 1095. https://doi.org/10.3390/e24081095
Sabeti E, Oh S, Song PXK, Hero AO. A Pattern Dictionary Method for Anomaly Detection. Entropy. 2022; 24(8):1095. https://doi.org/10.3390/e24081095
Chicago/Turabian StyleSabeti, Elyas, Sehong Oh, Peter X. K. Song, and Alfred O. Hero. 2022. "A Pattern Dictionary Method for Anomaly Detection" Entropy 24, no. 8: 1095. https://doi.org/10.3390/e24081095
APA StyleSabeti, E., Oh, S., Song, P. X. K., & Hero, A. O. (2022). A Pattern Dictionary Method for Anomaly Detection. Entropy, 24(8), 1095. https://doi.org/10.3390/e24081095







