The Structural Role of Smart Contracts and Exchanges in the Centralisation of Ethereum-Based Cryptoassets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Four Tokens Used as DeFi Collateral
2.2. Transaction Networks in Blockchain
2.3. Deep Dive: Network Construction
2.4. Preferential Attachment
2.5. Deep Dive Methodology
- We extract from a fully synchronised archive Ethereum node all transactions from the Ethereum blockchain involving transfers of tokens.
- We build the corresponding directed transaction networks for four DeFi-relevant tokens: Ampleforth (AMP), Basic Attention Token (BAT), DAI and Uniswap.
- We calculate the correlation between in- and out-degree distributions both for all nodes in the network and for high-degree nodes to see whether high-degree nodes are more correlated.
- We compare in- and out-degree distributions with potential best fit functions for the degree distributions.
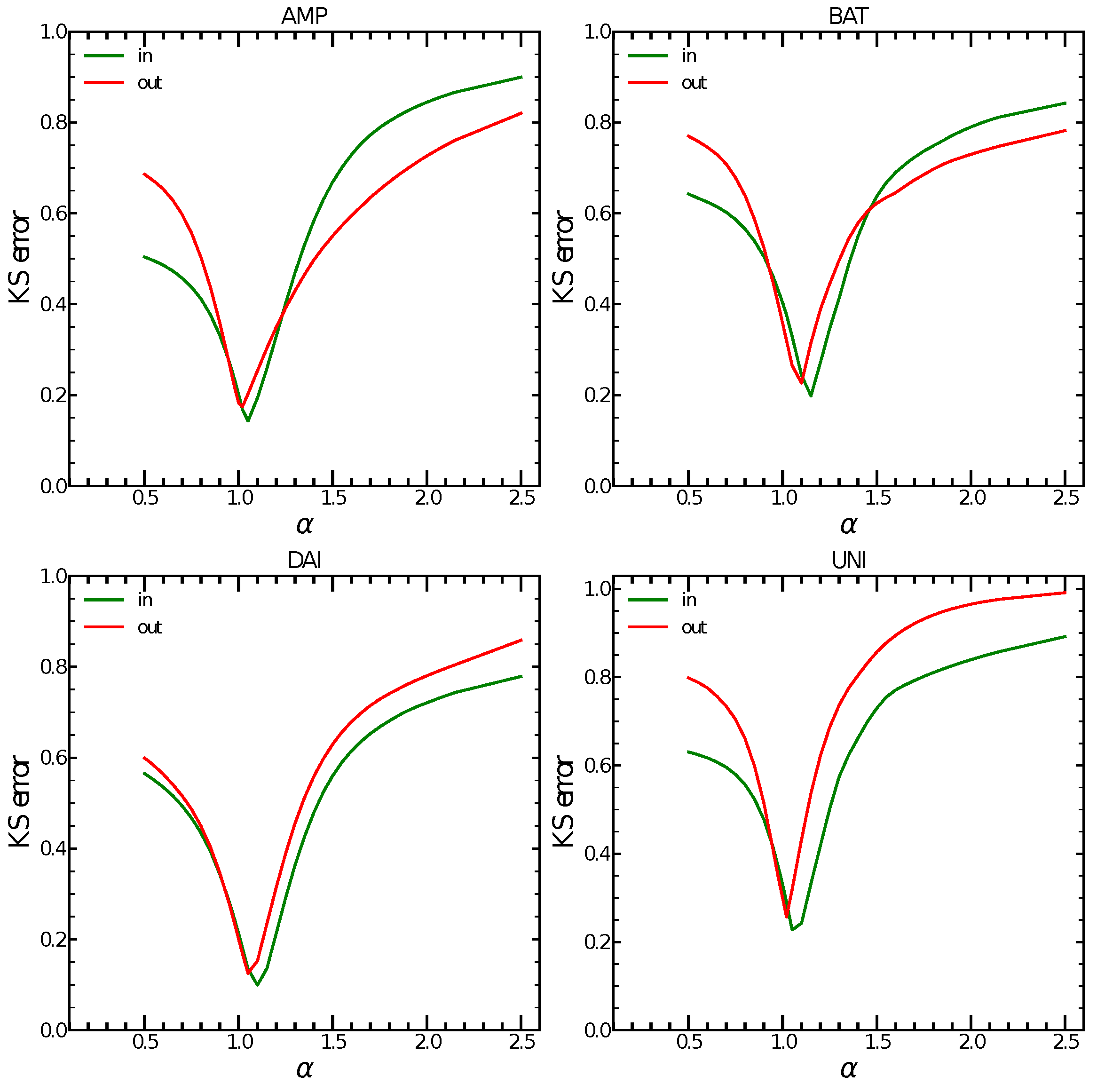
- We study the centralisation of the network, analysing the preferential attachment to identify the role of hubs. We use the K–S distance between the empirical degree distributions and a power law degree distribution in the range [0, 2.5] for all tokens using the rank function to identify the K–S distance between the empirical cumulative distribution function (ECDF) and the theoretical CDF function.
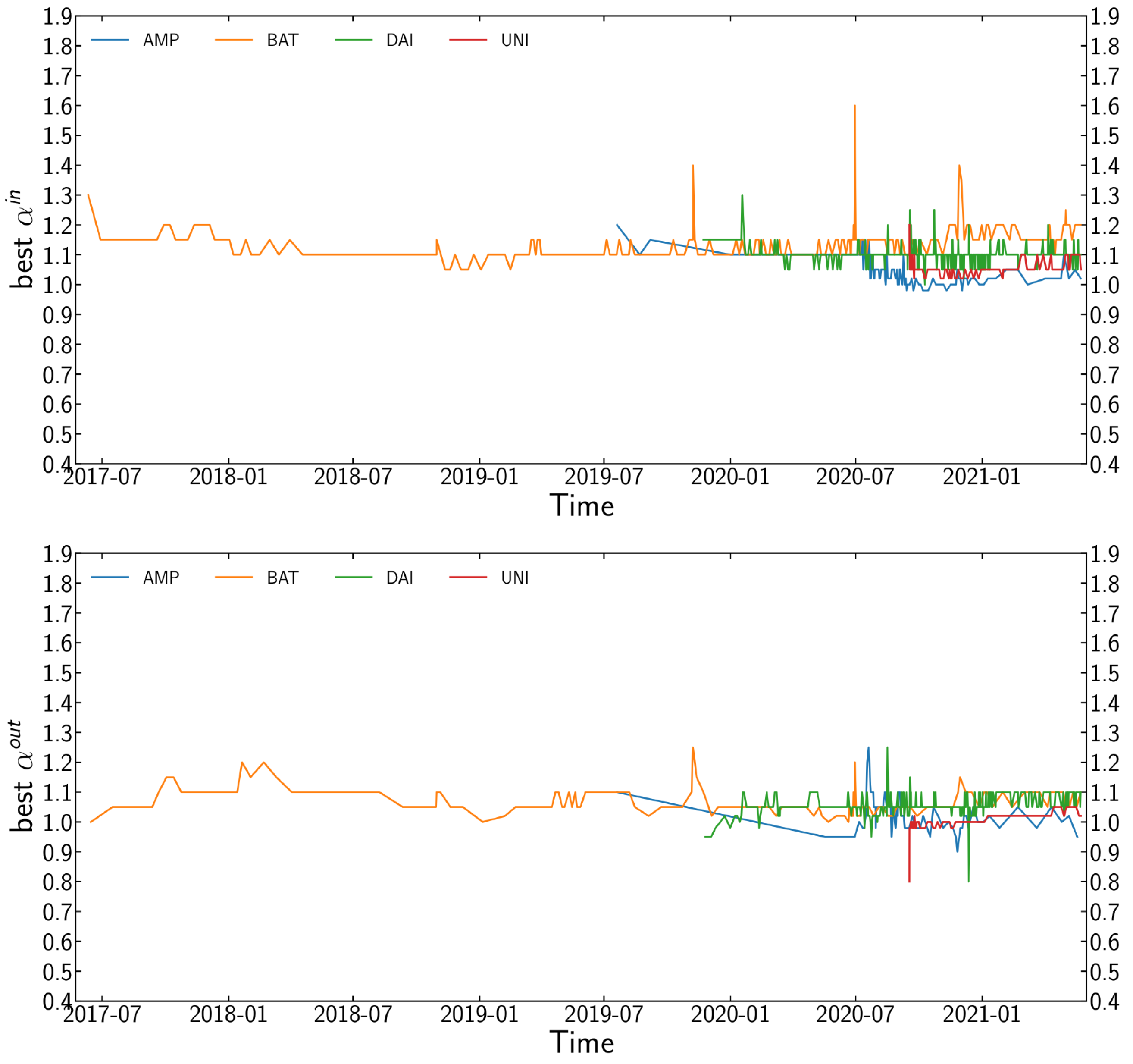
- We explore the evolution throughout time of the of the value of in the rank function to confirm the super-linear attachment in the transaction networks.
- We calculate how the density, i.e., the number of edges, grows with the growth in size of the network to confirm our preferential attachment study.
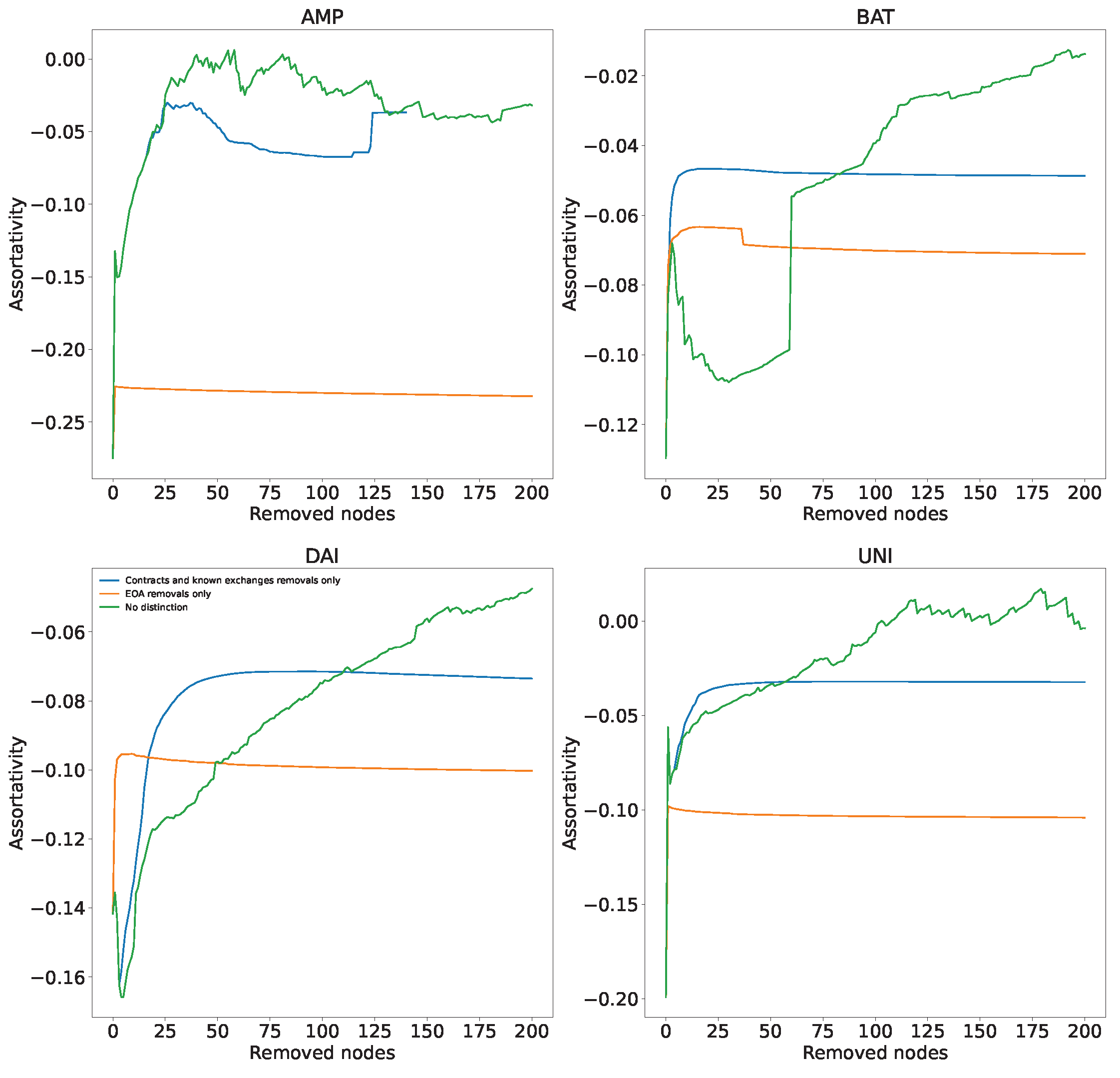
- We study network dismantling by removing up to 200 addresses (represented as nodes in the network) with the highest degree, and we observe how the network is impacted via the Largest Strongly Connected Component (LSCC) over network size ratio. For this, we use three strategies based on the type of node to remove.
- We study the evolution of the scalar assortativity of the transaction networks during dismantling.
2.6. Multilayer Network-Based Methodology
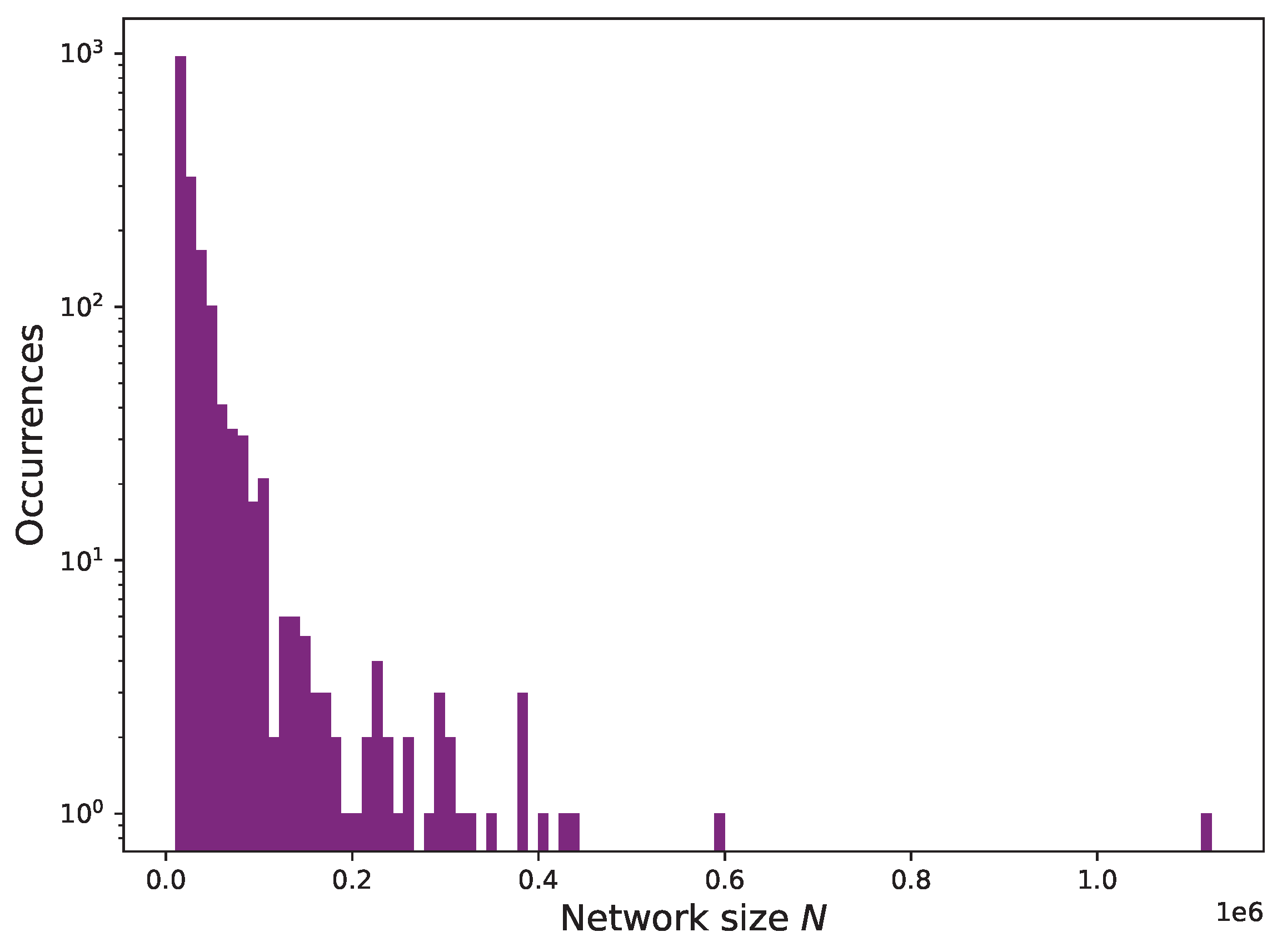
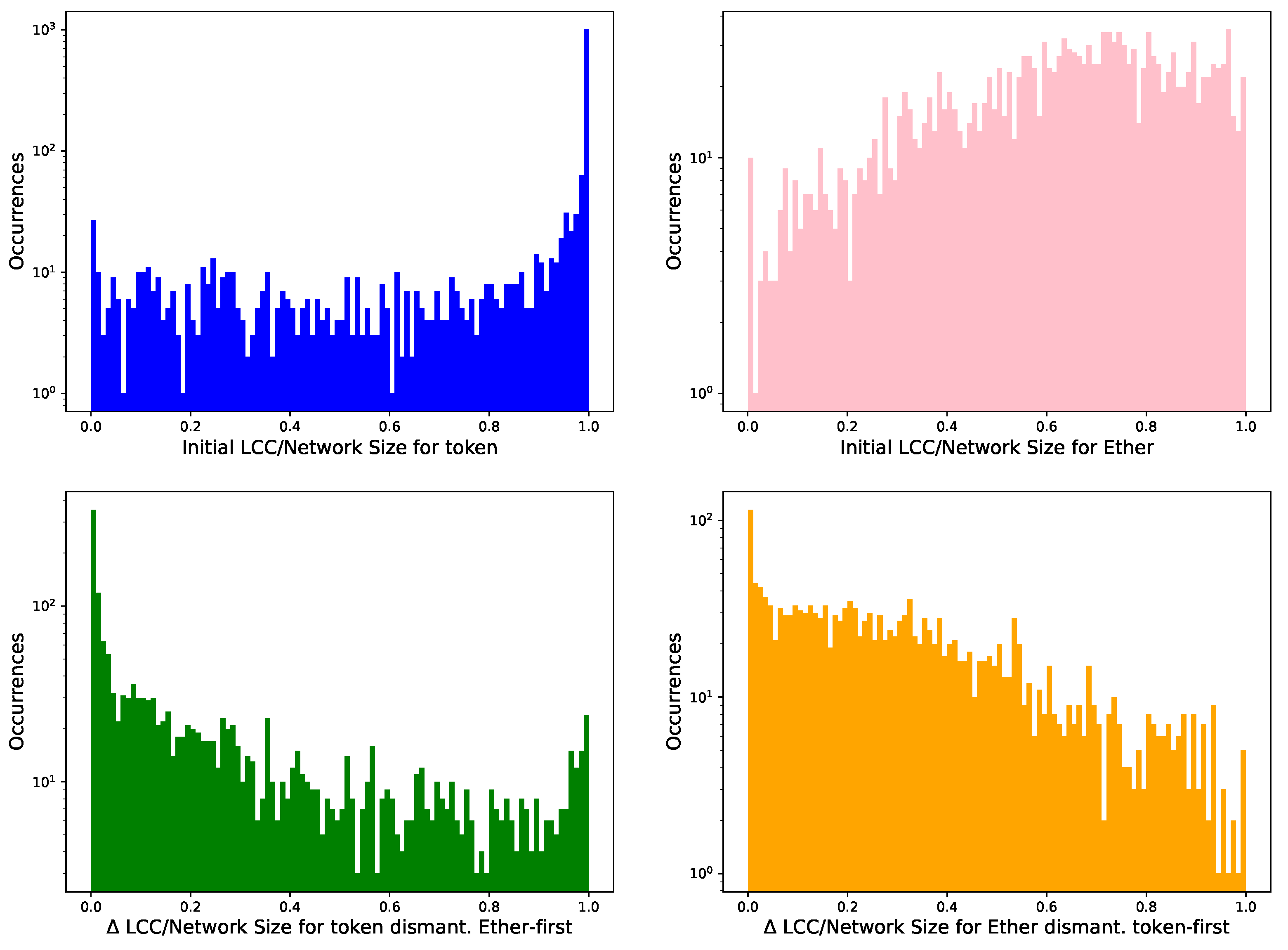
- We measure the initial size of the resulting networks in terms of number of nodes and plot the histograms of its distribution.
- We calculate the distribution of the initial LCC over network size ratio for and to characterize the different networks.
- We perform a similar exercise in each layer after 100 highest degree iterative node removals in the other layer to observe how dismantling takes place in each network.
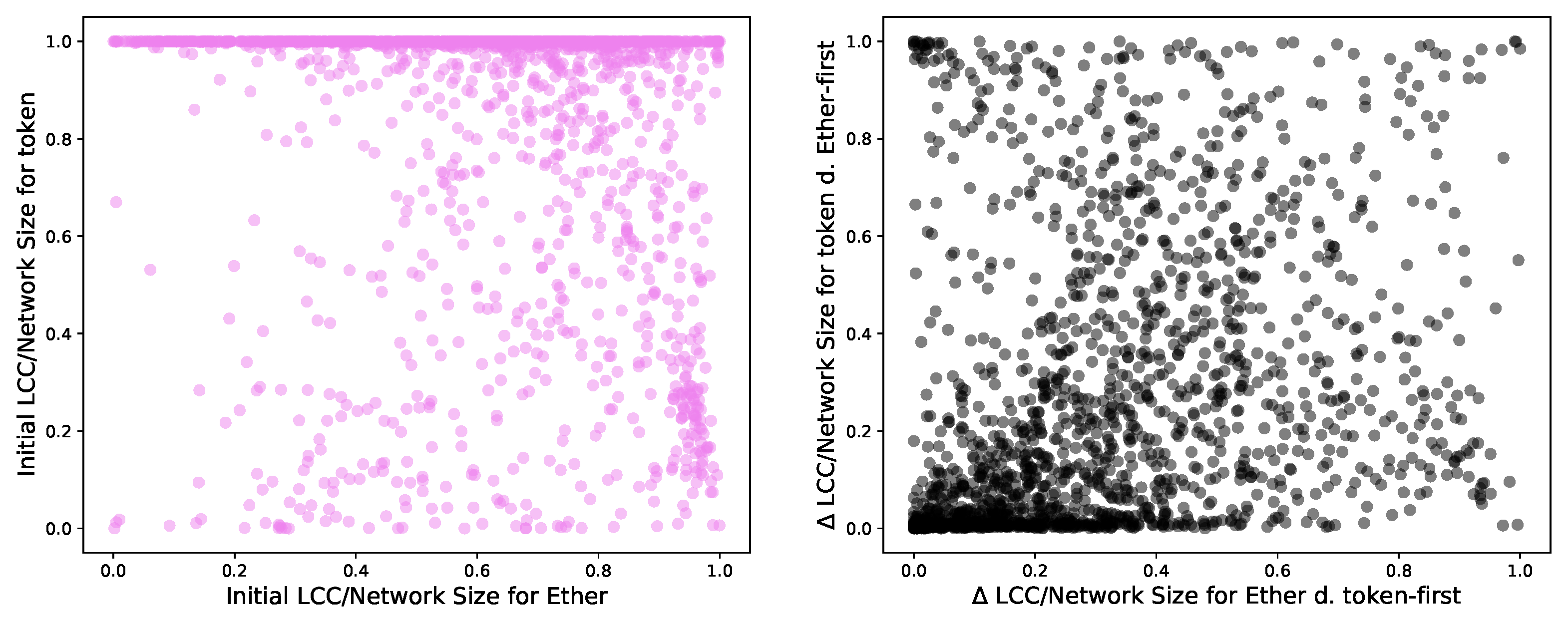
- We explore the relation between the LCC over network size ratio reached after dismantling in the Ether and the token network.
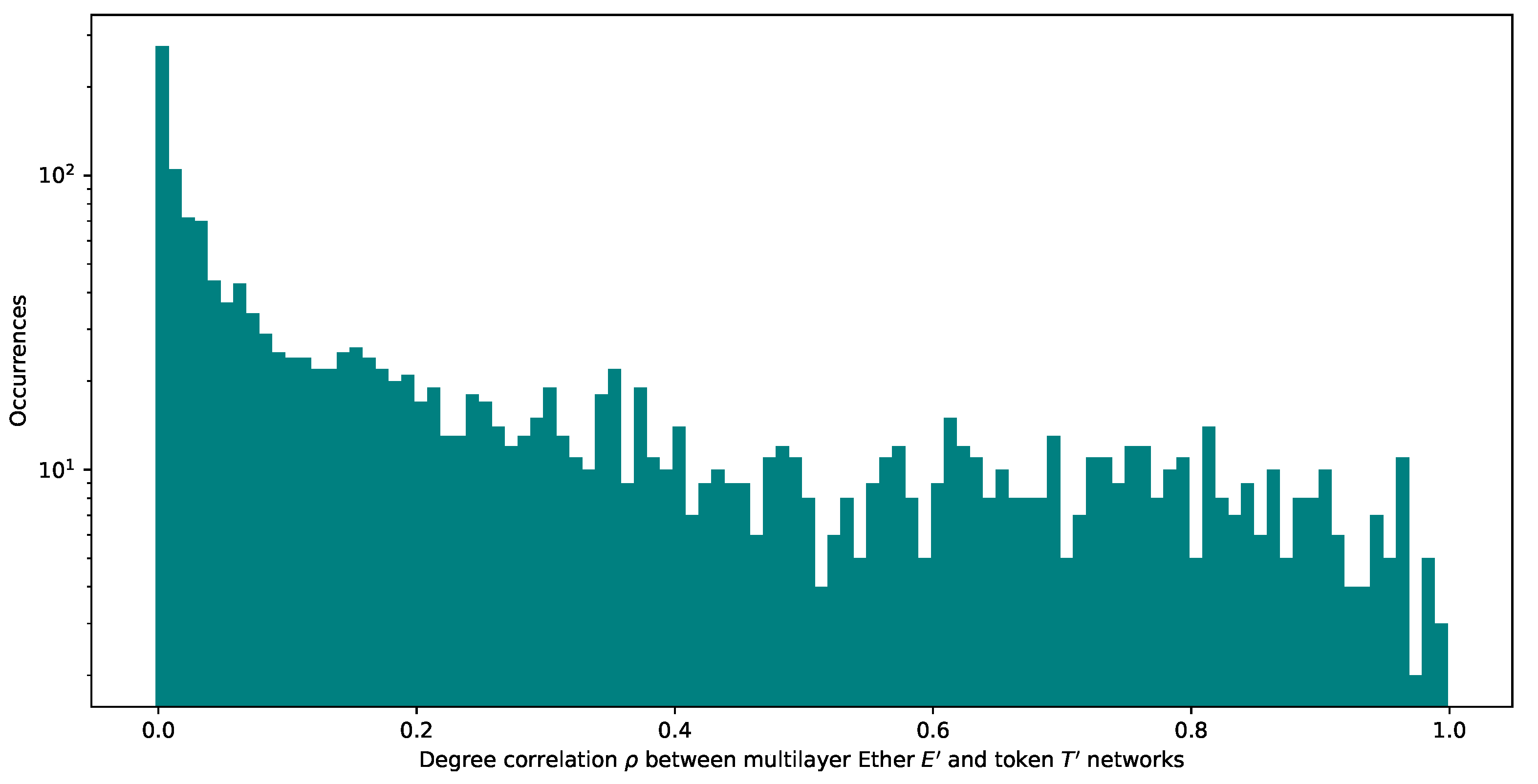
- We study the relation between the degrees of a node in different layers.
2.7. Bird’s Eye Methodology
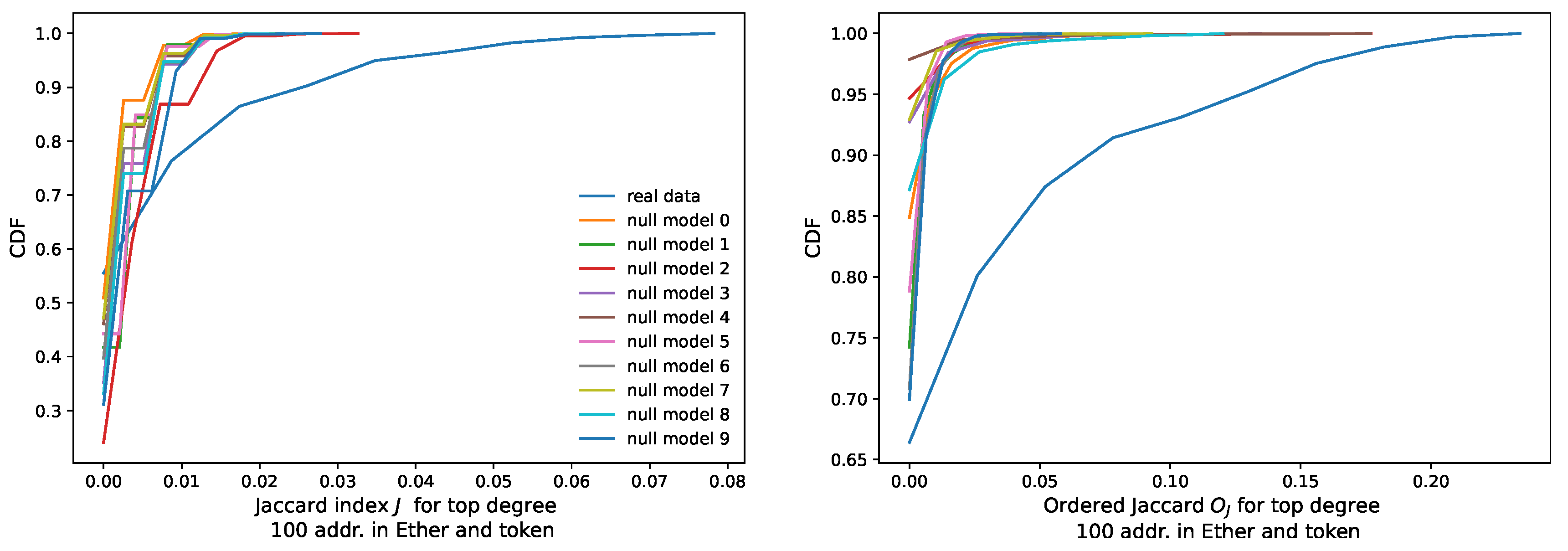
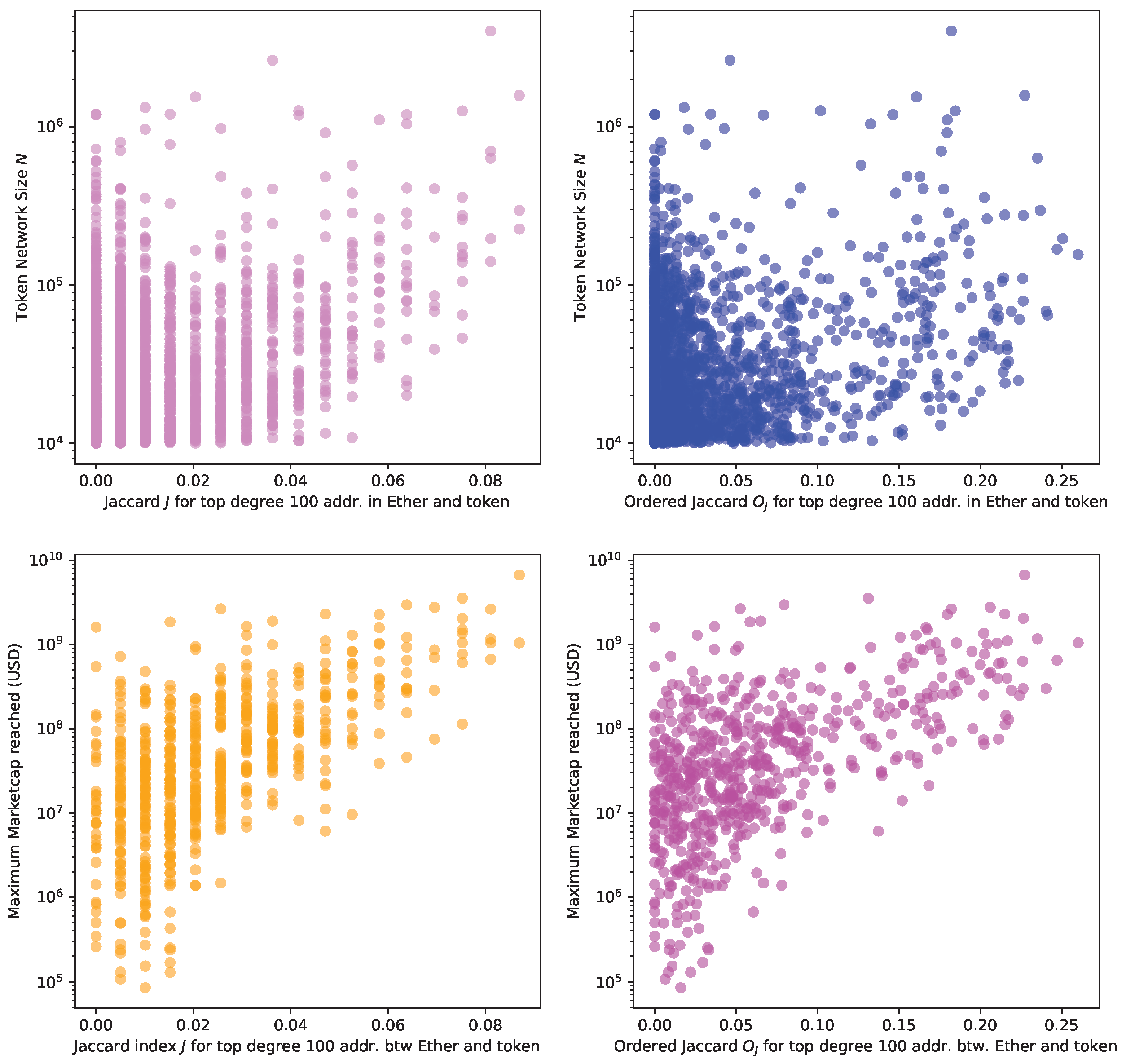
- We plot the Jaccard Index between every token network T and the one of Ether E. We do this pairwise for every one of our tokens.
- We analyse the in-degrees of the 2432 token networks using the model selection for power law fits proposed by Alstott et al. [35]) in 2014.
- We propose a novel similarity measure that is order-sensitive and potentially useful for our case of networks with very different sizes, and we test its meaningfulness using a set of randomized null models.
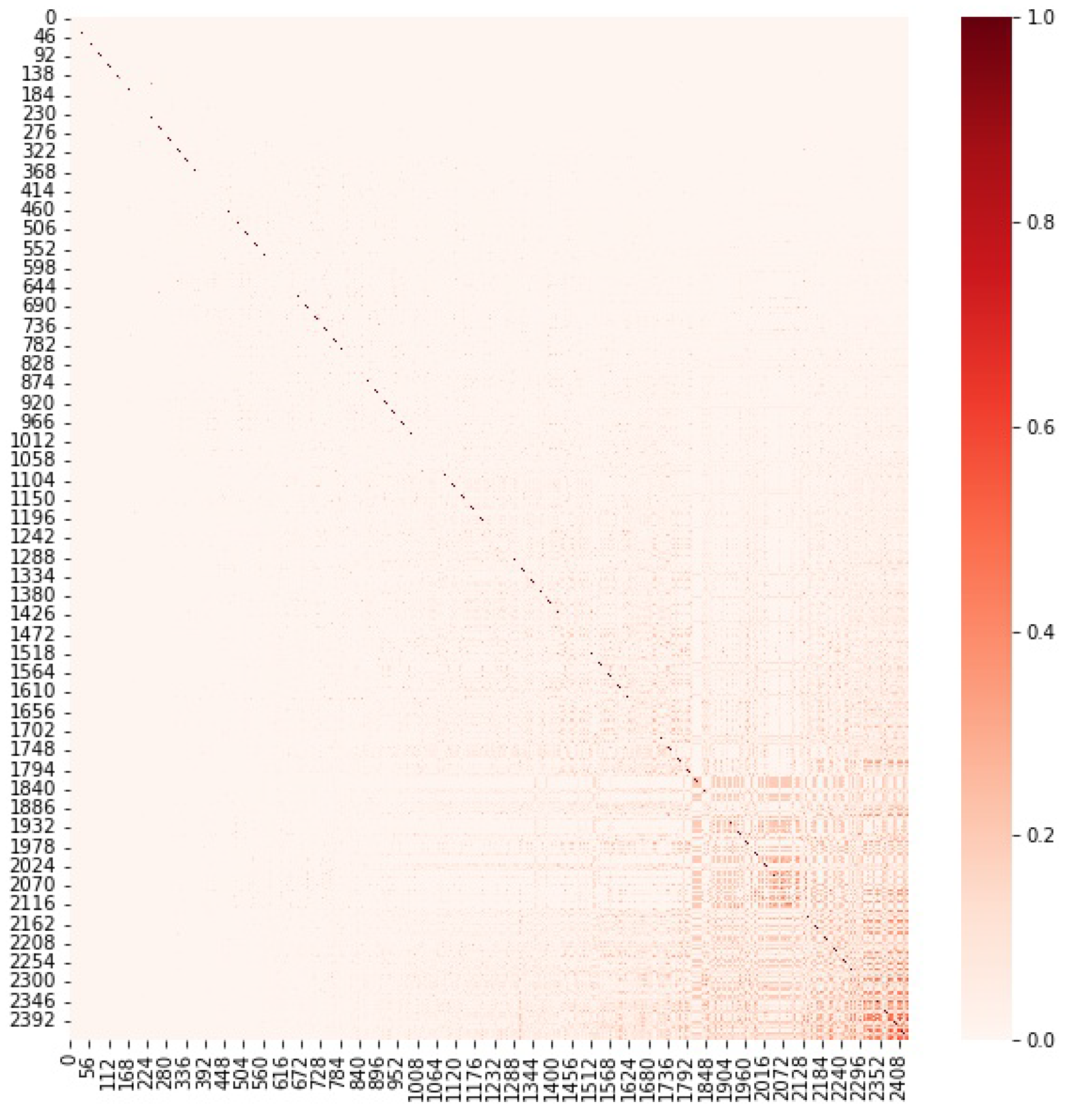
- We draw a heat map with this new similarity measure between all analysed tokens.
- We plot the histograms of the distributions of both the Jaccard Index and our new similarity metric, called Ordered Jaccard, measured between every individual token and Ether, and we calculate their correlation.
- We research potential similarity drivers: network size and market capitalisation. We calculate their correlation.
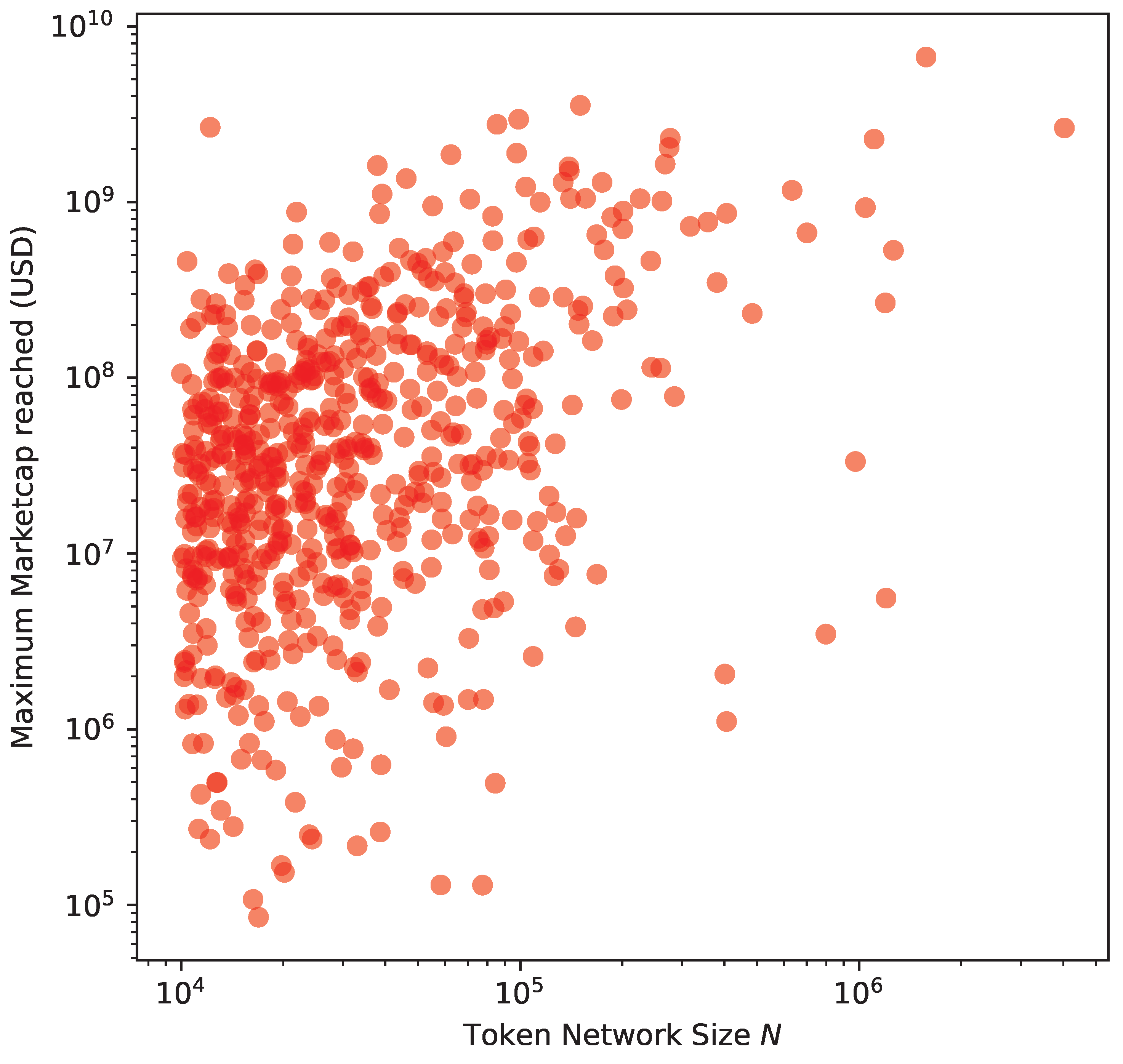
- We plot network size and the Jaccard and Ordered Jaccard Indexes between the Ether and token networks to identify any potential correlation. Here we start to detect a pattern.
- We perform a similar exercise with the maximum market capitalisation reached by every token network.
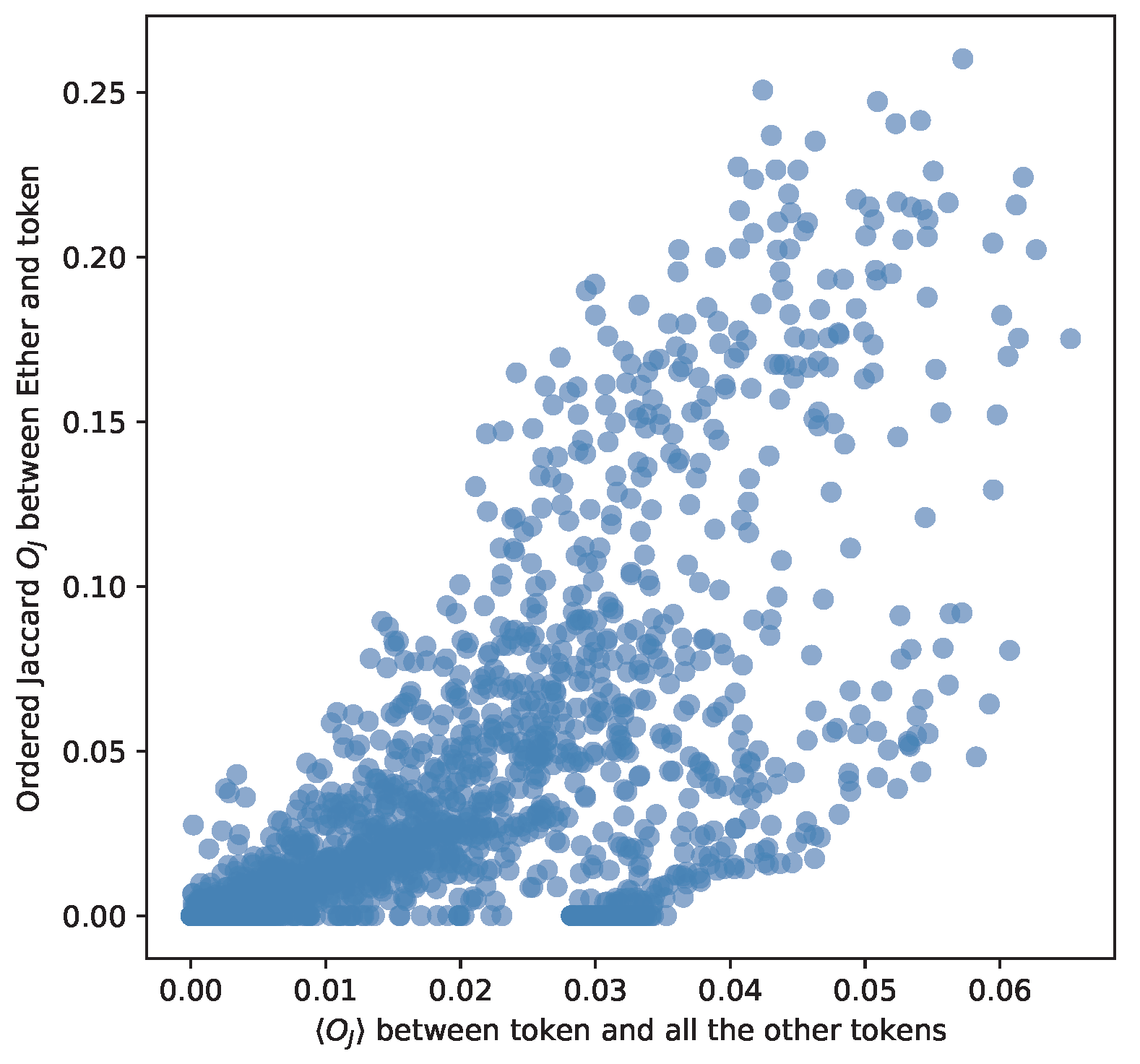
- We study the relation between Ether and a specific token and that token with all other Ethereum-based tokens via the Ordered Jaccard Index.
- We explain the methods that we follow to identify addresses belonging to exchanges and smart contracts.
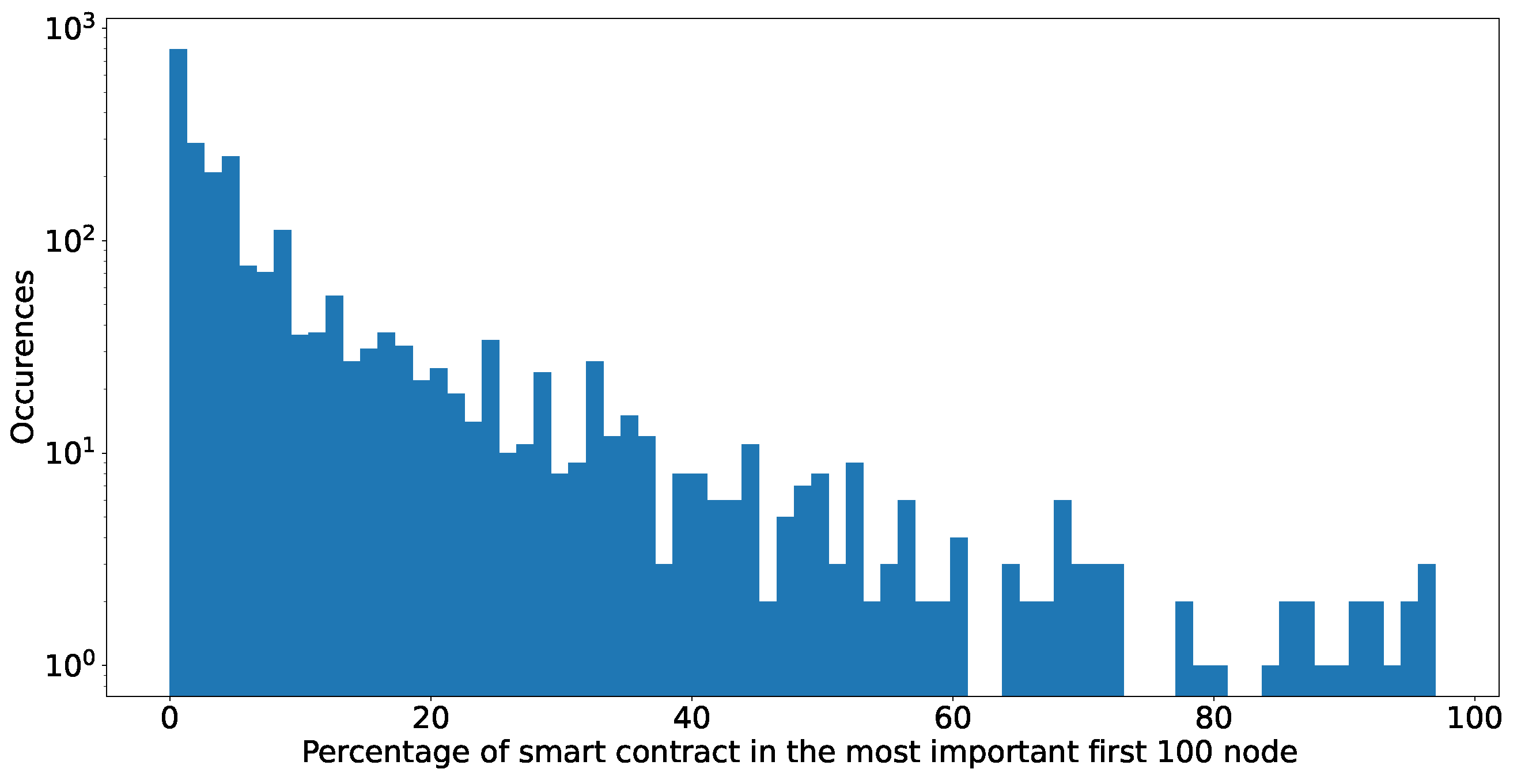
- We plot the percentage of exchanges and smart contracts in the top 100 high-degree nodes.
- Finally, we plot a histogram with the reappearance frequency of dismantled nodes across networks.
3. Results
3.1. In- and Out-Degree Correlation
3.2. Power Law Fit
3.3. Preferential Attachment
3.4. Network Dismantling
3.5. Assortativity
3.6. Multilayer Network Dismantling
3.7. Bird’s Eye View of Ethereum-Based Tokens
4. Discussion
- First, in our deep dive, we observed a slightly super-linear preferential attachment coefficient (), that is persistent throughout time. This implies that few nodes attract a majority of connections from new nodes. This resembles a form of “winner takes all” effect, commonly observed in social systems as well [48]. We identified the relevance of smart contracts and exchanges when we dismantled the resulting transaction networks following selective strategies with a special focus on SC and exchanges.
- Second, we studied a larger set of tokens and focused only on non-zero Ether and token transactions in networks that share at least 10k addresses with the Ether network. We used a multilayer network approach and tried to dismantle a specific layer (aspect) based on selective node-related information coming from a different layer (aspect). Although we confirmed again the relevance hubs when dismantling the layers, we abandoned this research path due to the big size difference between token networks and the Ether transaction network.
- Third, we broadened our lens and study similarities in all transaction networks with at least 10k addresses. For this, we came up with a new index, the Ordered Jaccard Index, that facilitated and confirmed our findings regarding the structural role of SC and exchanges in these networks. We completed our analysis by identifying a degree of correlation between this new index and network size and even market capitalisation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SC | smart contracts |
| EOA | Externally Owned Accounts |
References
- Tasca, P.; Tessone, C.J. A Taxonomy of Blockchain Technologies: Principles of Identification and Classification. Ledger 2020, 4. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System, Nakamotoinstitute.org. October 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 5 May 2022).
- Buterin, V. ETH whitepaper. Available online: https://ethereum.org/en/whitepaper/ (accessed on 5 May 2022).
- ERC-20 Specification. Available online: https://ethereum.org/en/developers/docs/standards/tokens/erc-20/ (accessed on 5 May 2022).
- Etherscan ERC-20 Token Tracker. Available online: https://etherscan.io/tokens (accessed on 5 May 2022).
- Polkadot White Paper. Available online: https://polkadot.network/PolkaDotPaper.pdf (accessed on 5 May 2022).
- Antonopoulos, A.; Wood, G. Mastering Ethereum, Building Smart Contracts and Dapps; O’Reilly Media: Newton, MA, USA, 2019. [Google Scholar]
- Bai, Q.; Zhang, C.; Liu, N.; Chen, X.; Xu, Y.; Wang, X. Evolution of Transaction Pattern in Ethereum: A Temporal Graph Perspective. IEEE Trans. Comput. Soc. Syst. 2022, 9, 851–866. [Google Scholar] [CrossRef]
- Kondor, D.; Bulatovic, N.; Stéger, J.; Csabai, I.; Vattay, G. The Rich Still Get Richer: Empirical Comparison of Preferential Attachment via Linking Statistics in Bitcoin and Ethereum. Front. Blockchain 2021, 4. Available online: https://www.frontiersin.org/article/10.3389/fbloc.2021.668510 (accessed on 11 October 2021). [CrossRef]
- Campajola, C.; Cristodaro, R.; De Collibus, F.; Yan, T.; Vallarano, N.; Tessone, C.J. The Evolution Of Centralisation on Cryptocurrency Platforms. arXiv 2022, arXiv:2206.05081. [Google Scholar] [CrossRef]
- Somin, S.; Gordon, G.; Pentland, A.; Shmueli, E.; Altshuler, Y. ERC20 Transactions over Ethereum Blockchain: Network Analysis and Predictions. arXiv 2020, arXiv:2004.08201. [Google Scholar] [CrossRef]
- Victor, F.; Lüders, B. Measuring Ethereum-Based ERC20 Token Networks. In Financial Cryptography And Data Security; Springer: Berlin/Heidelberg, Germany, 2019; pp. 113–129. [Google Scholar]
- Chen, W.; Zhang, T.; Chen, Z.; Zheng, Z.; Lu, Y. Traveling the Token World: A Graph Analysis of Ethereum ERC20 Token Ecosystem. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 1411–1421. [Google Scholar] [CrossRef]
- De Collibus, F.M.; Partida, A.; Piškorec, M.; Tessone, C.J. Heterogeneous Preferential Attachment in Key Ethereum-Based Cryptoassets. Front. Phys. 2021, 9, 720708. [Google Scholar] [CrossRef]
- Partida, A.; Gerassis, S.; Criado, R.; Romance, M.; Giráldez, E.; Taboada, J. Modeling Bitcoin plus Ethereum as an Open System of Systems of Public Blockchains to Improve Their Resilience against Intentional Risk. Electronics 2022, 11, 241. [Google Scholar] [CrossRef]
- Ampleforth Whitepaper. Available online: https://bit.ly/3lkxsAP (accessed on 11 September 2021).
- CoinMarketCap. Cryptocurrencies Market Capitalisation in Real Time. Available online: https://coinmarketcap.com/all/views/all/ (accessed on 11 September 2021).
- BAT Whitepaper. Available online: https://basicattentiontoken.org/static-assets/documents/BasicAttentionTokenWhitePaper-4.eps (accessed on 11 September 2021).
- DAI Whitepaper. Available online: https://makerdao.com/en/whitepaper/ (accessed on 11 September 2021).
- Uniswap Whitepaper. Available online: https://uniswap.org/whitepaper.eps (accessed on 11 September 2021).
- Kondor, D.; Pósfai, M.; Csabai, I.; Vattay, G. Do the Rich Get Richer? An Empirical Analysis of the Bitcoin Transaction Network. PLoS ONE 2014, 9, e86197. [Google Scholar] [CrossRef]
- Liang, J.; Li, L.; Zeng, D. Evolutionary dynamics of cryptocurrency transaction networks: An empirical study. PLoS ONE 2018, 13, e0202202. [Google Scholar] [CrossRef]
- Bovet, A.; Campajola, C.; Mottes, F.; Restocchi, V.; Vallarano, N.; Squartini, T.; Tessone, C.J. The evolving liaisons between the transaction networks of Bitcoin and its price dynamics. arXiv 2019, arXiv:1907.03577. [Google Scholar]
- Vallarano, N.; Tessone, C.J.; Squartini, T. Bitcoin Transaction Networks: An Overview of Recent Results. Front. Phys. 2020, 8, 286. [Google Scholar] [CrossRef]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–257. [Google Scholar] [CrossRef]
- Collibus, F.M.D.; Partida, A.; Piškorec, M. The Role of Smart Contracts in the Transaction Networks of Four Key DeFi-Collateral Ethereum-Based Tokens. In International Conference on Complex Networks and Their Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 792–804. [Google Scholar] [CrossRef]
- Costa, L.D.F.; Oliveira, O.N., Jr.; Travieso, G.; Rodrigues, F.A.; Villas Boas, P.R.; Antiqueira, L.; Viana, M.P.; Correa Rocha, L.E. Analyzing and modeling real-world phenomena with complex networks: A survey of applications. Adv. Phys. 2011, 60, 329–412. [Google Scholar] [CrossRef]
- Ren, X.L.; Gleinig, N.; Helbing, D.; Antulov-Fantulin, N. Generalized network dismantling. Proc. Natl. Acad. Sci. USA 2019, 116, 6554–6559. [Google Scholar] [CrossRef]
- Braunstein, A.; Dall’Asta, L.; Semerjian, G.; Zdeborová, L. Network dismantling. Proc. Natl. Acad. Sci. USA 2016, 113, 12368–12373. [Google Scholar] [CrossRef] [PubMed]
- Janson, S.; Thomason, A. Dismantling sparse random graphs. Comb. Probab. Comput. 2008, 17, 259–264. [Google Scholar] [CrossRef]
- Gallotti, R.; Barthelemy, M. The multilayer temporal network of public transport in Great Britain. Sci. Data 2015, 2, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kinsley, A.C.; Rossi, G.; Silk, M.J.; VanderWaal, K. Multilayer and multiplex networks: An introduction to their use in veterinary epidemiology. Front. Vet. Sci. 2020, 7, 596. [Google Scholar] [CrossRef] [PubMed]
- De Domenico, M.; Solé-Ribalta, A.; Cozzo, E.; Kivelä, M.; Moreno, Y.; Porter, M.A.; Gómez, S.; Arenas, A. Mathematical formulation of multilayer networks. Phys. Rev. X 2013, 3, 041022. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef] [PubMed]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Barabási, A. Network Science. 2014-09-05. Creative Commons: CC BY-NC-SA 2.0. Available online: http://barabasi.com/book/network-science (accessed on 29 December 2020).
- Broido, A.D.; Clauset, A. Scale-free networks are rare. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Chapela, V.; Criado, R.; Moral, M.; Romance, R. Intentional Risk Management through Complex Networks Analysis; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Partida, A.; Criado, R.; Romance, M. Identity and Access Management Resilience against Intentional Risk for Blockchain-Based IOT Platforms. Electronics 2021, 10, 378. [Google Scholar] [CrossRef]
- Partida, A.; Criado, R.; Romance, M. Visibility Graph Analysis of IOTA and IoTeX Price Series: An Intentional Risk-Based Strategy to Use 5G for IoT. Electronics 2021, 10, 2282. [Google Scholar] [CrossRef]
- Newman, M.E.J. Mixing patterns in networks. Phys. Rev. E 2003, 67, 026126. [Google Scholar] [CrossRef] [PubMed]
- Clauset, A.; Shalizi, C.; Newman, M. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Coingecko. Cryptocurrencies Market Aggregator, with API. Available online: https://www.coingecko.com/en/api (accessed on 15 July 2022).
- Chainanalysis.com. Richest Addresses in Ethereum. Cryptocurrency Exchanges in 2021: A Competitive Analysis. Available online: https://go.chainalysis.com/2021-crypto-exchange-landscape-report.html (accessed on 4 May 2022).
- Etherscan.io. Richest Addresses in Ethereum. Available online: https://etherscan.io/accounts (accessed on 4 May 2022).
- Total value locked in DeFi. Available online: https://defillama.com/ (accessed on 28 June 2022).
- Salganik, M.J.; Dodds, P.S.; Watts, D.J. Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market. Science 2006, 311, 854–856. [Google Scholar] [CrossRef]
- Costa, L. Further Generalizations of the Jaccard Index. arXiv 2021, arXiv:2110.09619. [Google Scholar] [CrossRef]
- Chierichetti, F.; Kumar, R.; Pandey, S.; Vassilvitskii, S. Finding the Jaccard Median. In Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, Austin, TX, USA, 17–19 January 2010; pp. 293–311. [Google Scholar]
- Kosub, S. A note on the triangle inequality for the Jaccard distance. Pattern Recognit. Lett. 2019, 120, 36–38. [Google Scholar] [CrossRef]
- Ethereum-etl Data in Google Cloud by Evgeny Medvedev. Available online: https://console.cloud.google.com/bigquery?p=bigquery-public-data&d=crypto_ethereum&t=transactions&page=table (accessed on 27 June 2022).
- Ethereum-etl in Google Cloud Deep Dive by Evgeny Medvedev. Available online: https://cloud.google.com/blog/products/data-analytics/ethereum-bigquery-how-we-built-dataset (accessed on 27 June 2022).
- Etherscan API Documentation. Available online: https://etherscan.io/apis (accessed on 4 May 2022).







| Token | Tx | Nodes | Edges | Blocks | Time Span |
|---|---|---|---|---|---|
| AMP | 755,827 | 83,050 | 201,456 | 7,953,823–12,500,000 | 14 June 2019–25 May 2021 |
| BAT | 3,046,615 | 1,105,958 | 1,702,429 | 3,788,601–12,500,000 | 29 May 2017–25 May 2021 |
| DAI | 8,422,158 | 1,042,638 | 2,523,076 | 8,928,674–12,500,000 | 13 November 2019–25 May 2021 |
| UNI | 2,079,132 | 701,054 | 1,271,933 | 10,861,674–12,500,000 | 14 September 2020–25 May 2021 |
| Token | p-Value | Where | p-Value | |
|---|---|---|---|---|
| AMP | 0.5201 | 0 | 0.6772 | 1.2470 |
| BAT | 0.1523 | 0 | 0.4119 | 2.6450 |
| DAI | 0.4842 | 0 | 0.4874 | 5.112 |
| UNI | 0.2710 | 0 | 0.5094 | 1.3512 |
| Token | k | d | Best Fit | |||
|---|---|---|---|---|---|---|
| AMP | 3.0 | 2.9254 | 0.0169 | 0.0362 | Power Law | |
| AMP | 13.0 | 1.6150 | 0.0409 | 0.0395 | Power Law | |
| BAT | 44.0 | 1.7677 | 0.0330 | 0.0292 | Power Law | |
| BAT | 58.0 | 1.6580 | 0.0326 | 0.0304 | Truncated Power Law | |
| DAI | 57.0 | 1.8552 | 0.0240 | 0.0115 | Power Law | |
| DAI | 4.0 | 2.5021 | 0.0055 | 0.0121 | Lognormal | |
| UNI | 51.0 | 1.7812 | 0.0409 | 0.0271 | Power Law | |
| UNI | 29.0 | 1.6591 | 0.0299 | 0.0300 | Power Law |
| Token | Error | Error | ||
|---|---|---|---|---|
| AMP | 1.05 | 0.143 | 1.02 | 0.174 |
| BAT | 1.15 | 0.198 | 1.1 | 0.226 |
| DAI | 1.1 | 0.099 | 1.05 | 0.126 |
| UNI | 1.05 | 0.227 | 1.02 | 0.257 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Collibus, F.M.; Piškorec, M.; Partida, A.; Tessone, C.J. The Structural Role of Smart Contracts and Exchanges in the Centralisation of Ethereum-Based Cryptoassets. Entropy 2022, 24, 1048. https://doi.org/10.3390/e24081048
De Collibus FM, Piškorec M, Partida A, Tessone CJ. The Structural Role of Smart Contracts and Exchanges in the Centralisation of Ethereum-Based Cryptoassets. Entropy. 2022; 24(8):1048. https://doi.org/10.3390/e24081048
Chicago/Turabian StyleDe Collibus, Francesco Maria, Matija Piškorec, Alberto Partida, and Claudio J. Tessone. 2022. "The Structural Role of Smart Contracts and Exchanges in the Centralisation of Ethereum-Based Cryptoassets" Entropy 24, no. 8: 1048. https://doi.org/10.3390/e24081048
APA StyleDe Collibus, F. M., Piškorec, M., Partida, A., & Tessone, C. J. (2022). The Structural Role of Smart Contracts and Exchanges in the Centralisation of Ethereum-Based Cryptoassets. Entropy, 24(8), 1048. https://doi.org/10.3390/e24081048






