A Calculation Method of Passenger Flow Distribution in Large-Scale Subway Network Based on Passenger–Train Matching Probability
Abstract
:1. Introduction
- (1)
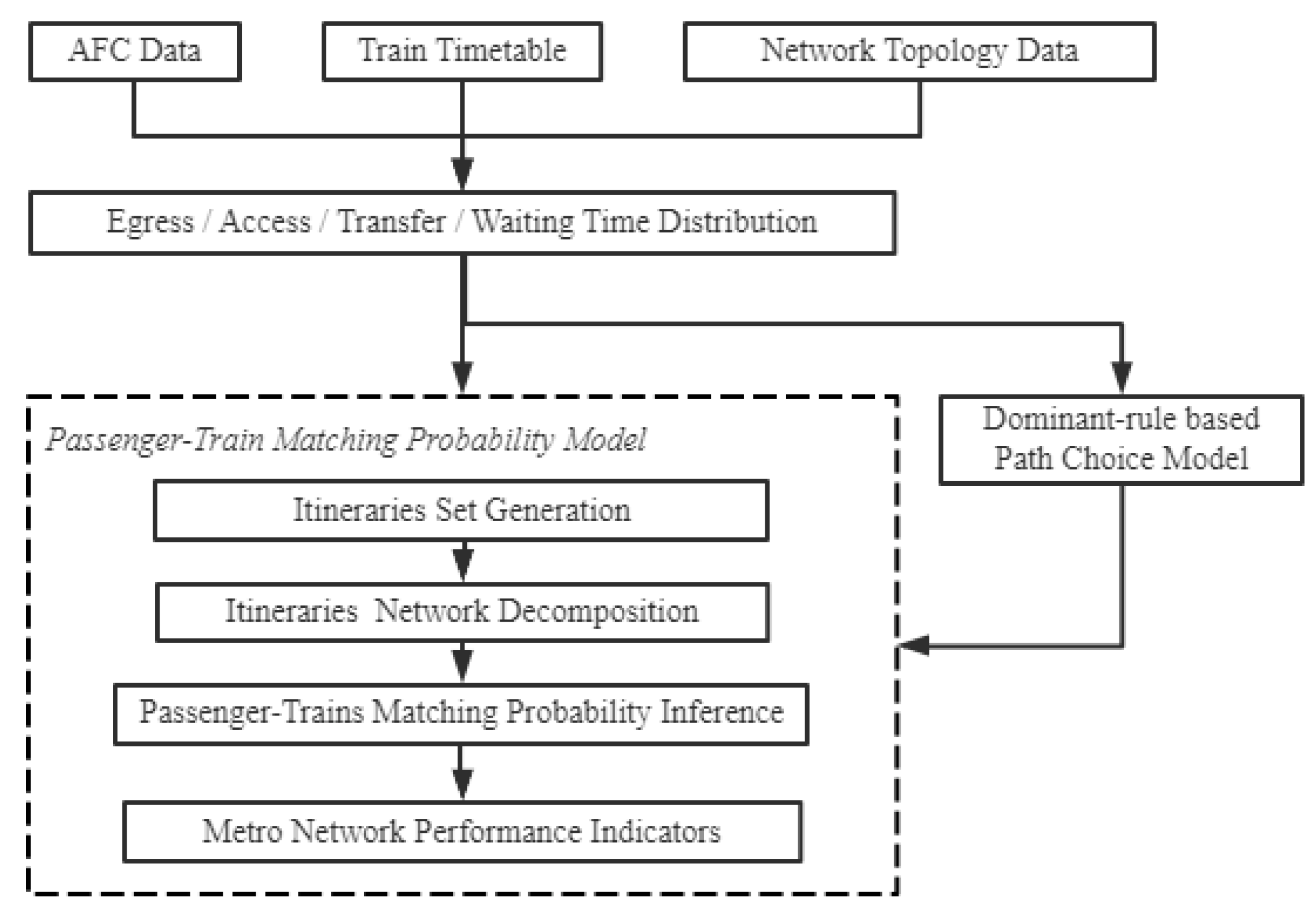
- A data-driven passenger–train matching probability model is proposed. In this model, the dynamic time–space trajectory of each individual passenger is explicitly characterized by mining AFC data, train timetables and network topology.
- (2)
- According to the consistency characteristics of passenger travel behavior [10,23] and the topology data of the subway network, a reverse derivation method is proposed to decompose the passenger itinerary network into multiple small subnets. This method can reduce the scale of passenger itineraries without affecting the accuracy of the model to avoid many unnecessary calculations and improve the computational efficiency. Therefore, the model can be applied to calculate the passenger flow distribution in a large-scale network.
- (3)
- Based on the Beijing subway network, two case studies are conducted to explore the effectiveness and efficiency of the proposed method. In the first case, a simulation-based passenger flow loading model is designed with fixed capacity and strict boarding priorities (FCFS) to illustrate the accuracy of the suggested model. In the second case, the proposed model is used for the actual AFC data, and the result shows that the model has a good accuracy and computational efficiency in a large-scale subway network.
2. Problem Description
2.1. Notations
2.2. Passenger’s Trajectory
- Trip refers to the travel record of a passenger’s journey from the origin to the destination, including the tap-in time, tap-in station, tap-out time and tap-out station.
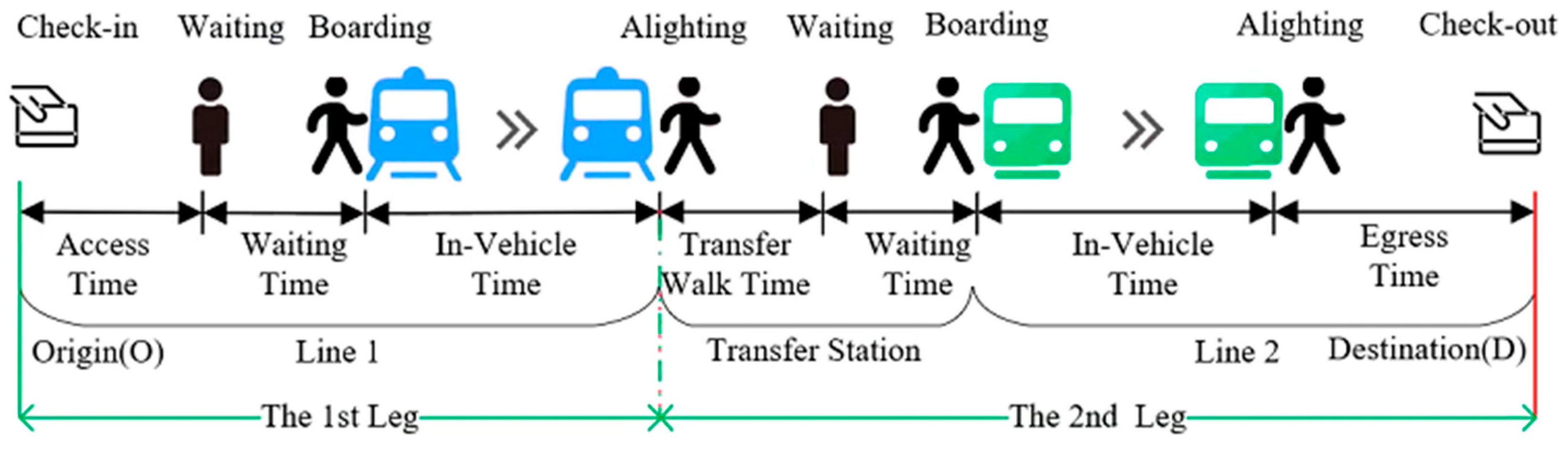
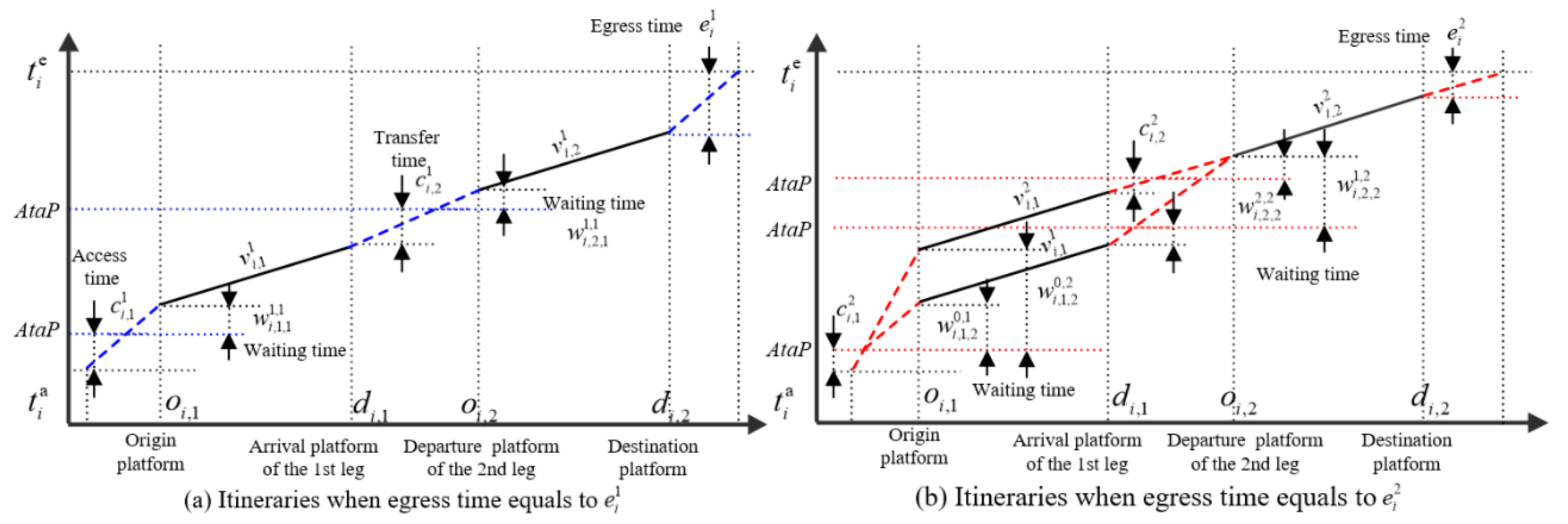
- Leg describes the movement of a passenger on a single train. As shown in Figure 1, the leg begins from the platform where the passenger boards and ends at the platform where the passenger alights. Obviously, there is at least one leg in a passenger journey.
- Itinerary refers to the combination of trains/services that a passenger may take on each trip. Each combination includes one or more trains/services sorted in chronological order. It is worth noting that there is only one train/service for each leg in each combination.
2.3. The Passenger–Train Matching Probability
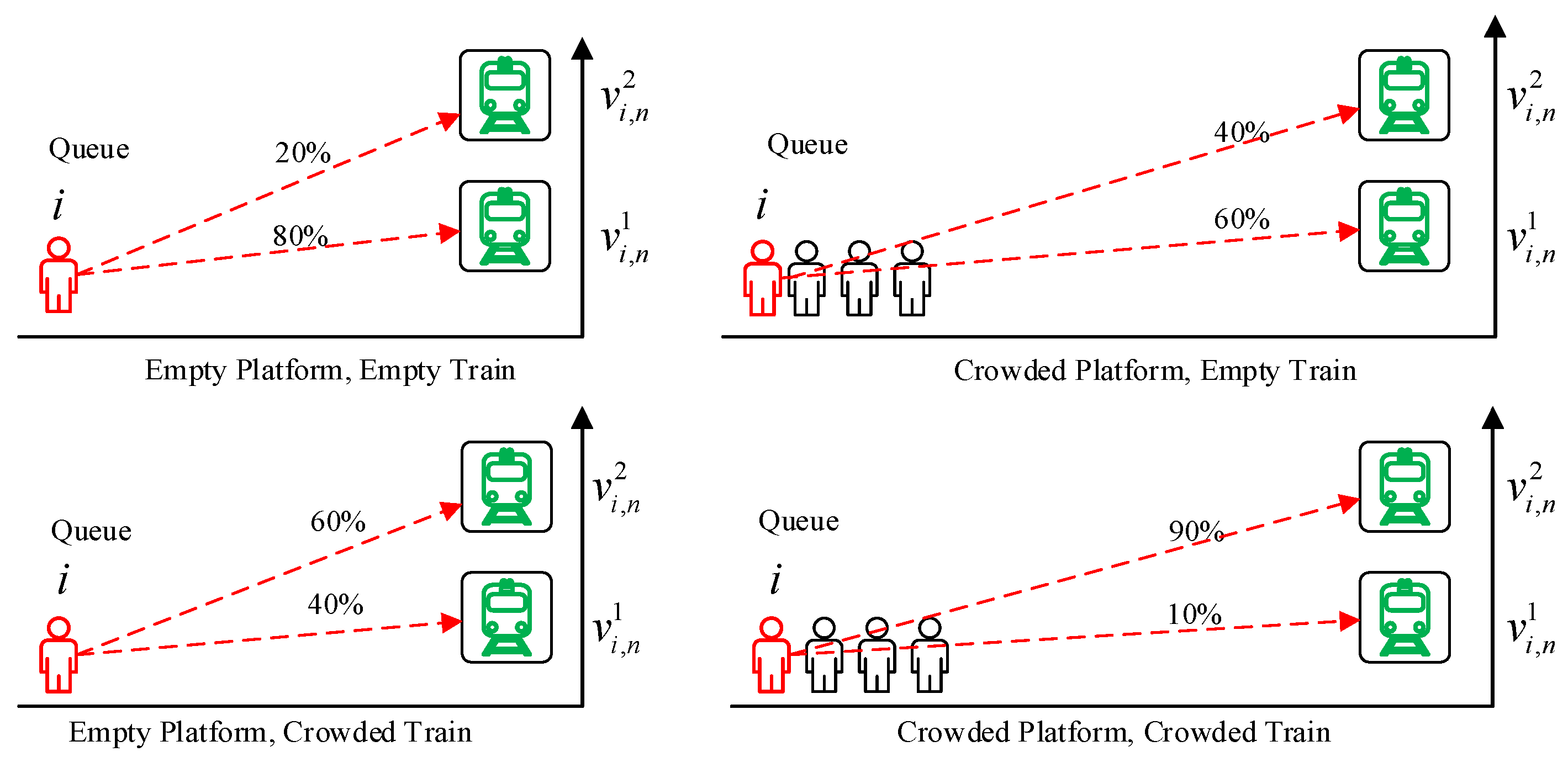
2.3.1. Passenger Preference
2.3.2. Passenger Retention
2.3.3. Interdependence of Legs
2.3.4. Heterogeneity of Passengers
3. Assumptions
4. Modeling Framework
4.1. Feasible Train Set
4.2. The Calculation of Passenger–Train Probability
4.3. The Calculation of Passenger Flow Distribution
5. Case Study
5.1. Experimental Design
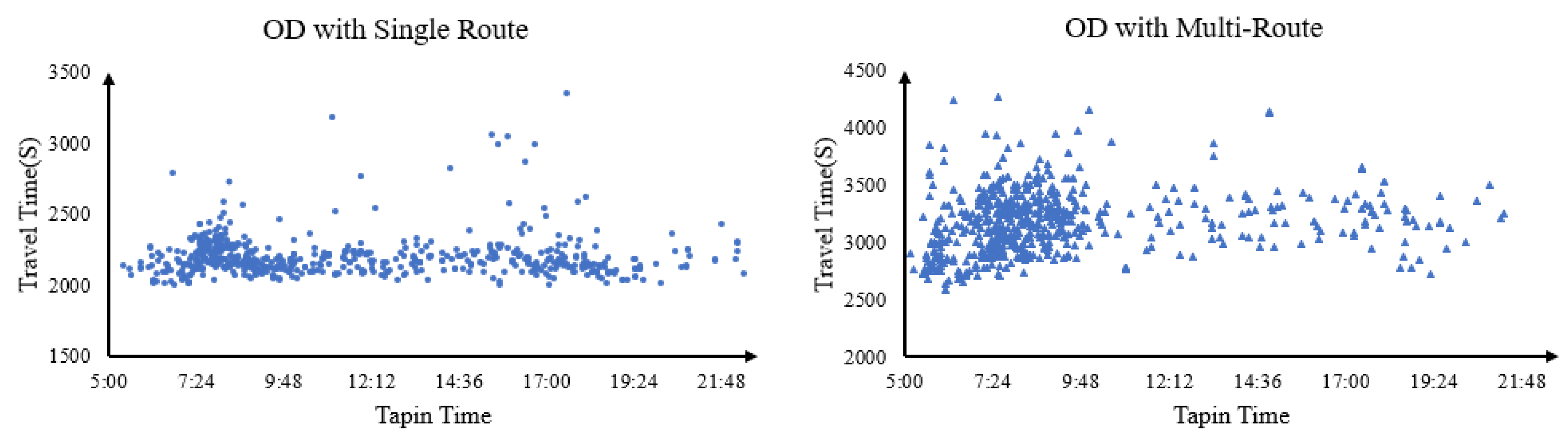
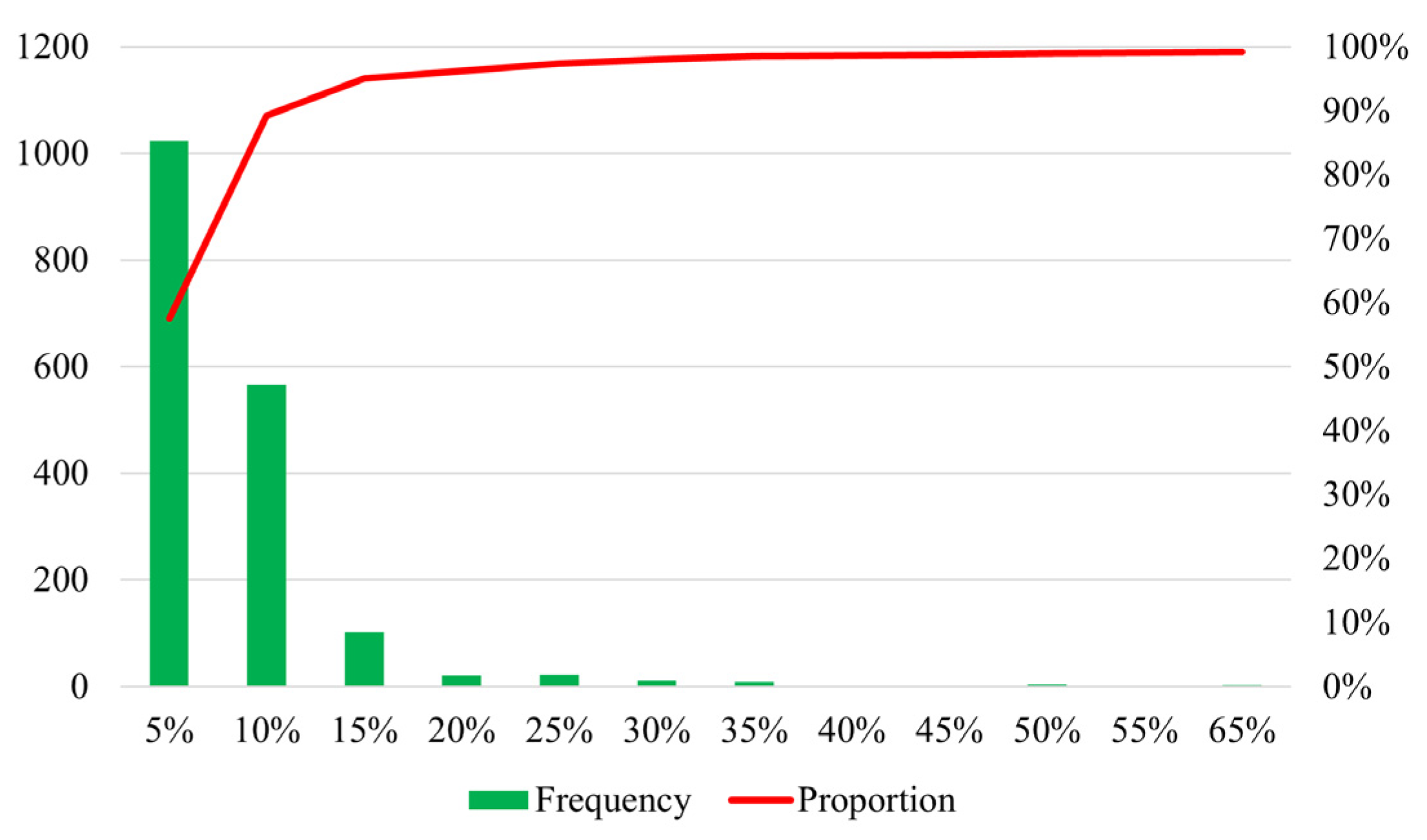
5.2. Comparison of Boarding the “Actual” Train
5.3. Comparison of Passenger Flow
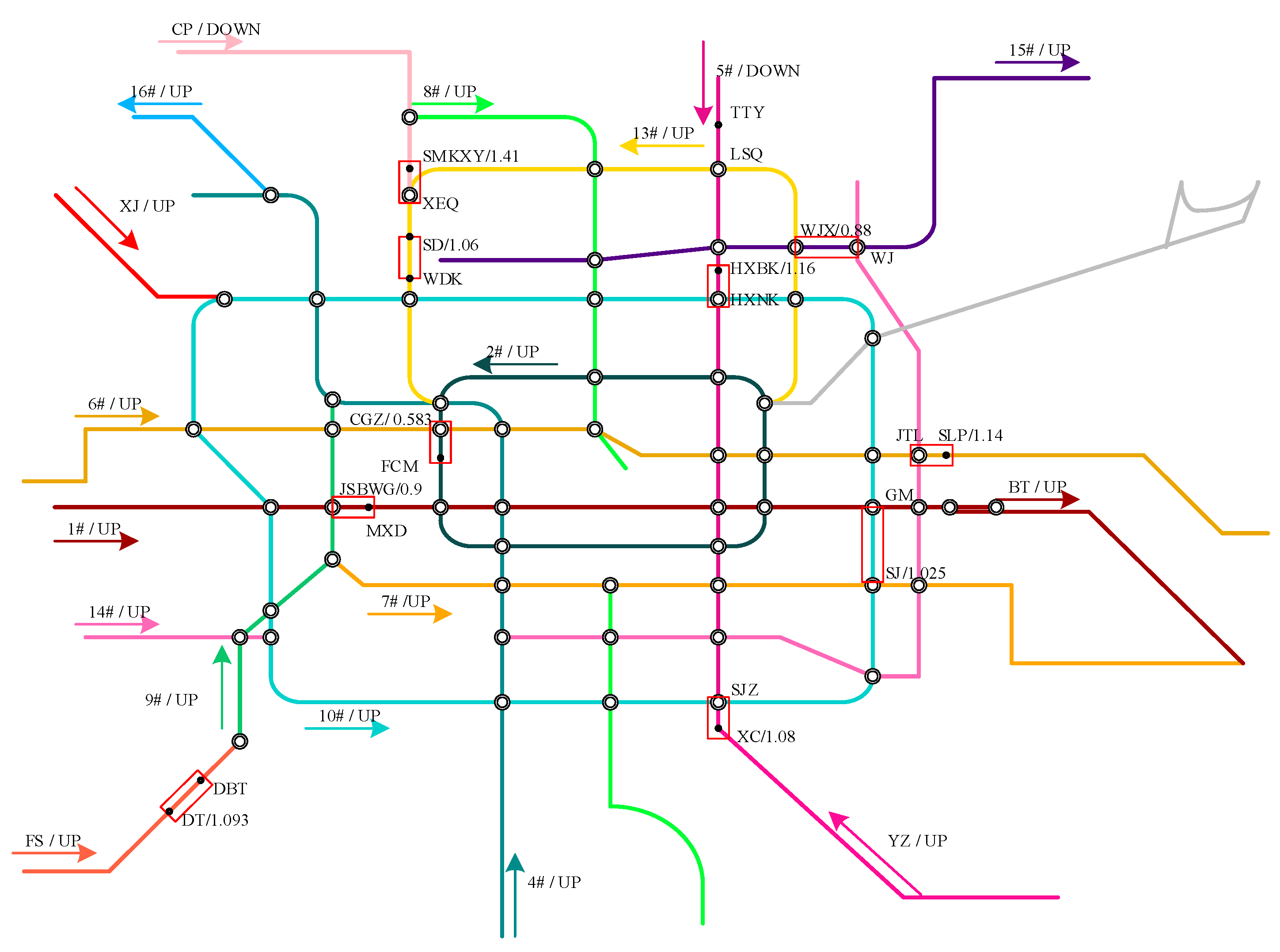
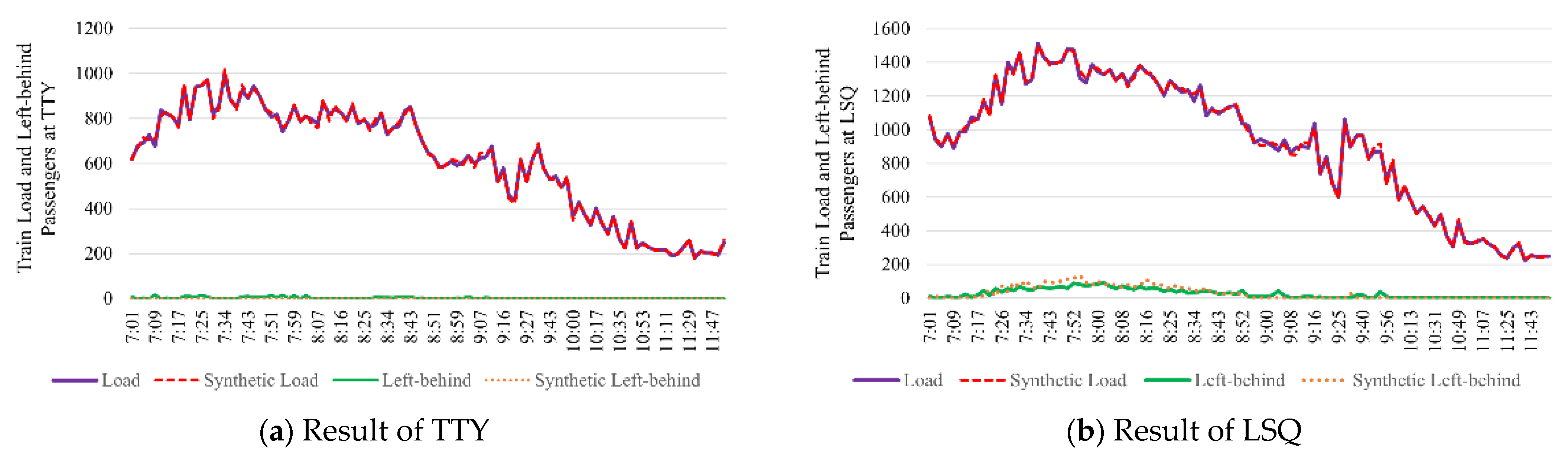
5.4. Practical Application for Beijing Subway Network
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mo, P.; D’Ariano, A.; Yang, L.; Veelenturf, L.P.; Gao, Z. An Exact Method for the Integrated Optimization of Subway Lines Operation Strategies with Asymmetric Passenger Demand and Operating Costs. Transp. Res. Part B Methodol. 2021, 149, 283–321. [Google Scholar] [CrossRef]
- Jin, J.G.; Tang, L.C.; Sun, L.; Lee, D.H. Enhancing Metro Network Resilience via Localized Integration with Bus Services. Transp. Res. Part E Logist. Transp. Rev. 2014, 63, 17–30. [Google Scholar] [CrossRef]
- Poon, M.H.; Wong, S.C.; Tong, C.O. A Dynamic Schedule-Based Model for Congested Transit Networks. Transp. Res. Part B Methodol. 2004, 38, 343–368. [Google Scholar] [CrossRef]
- Yao, X.; Han, B.; Yu, D.; Ren, H. Simulation-Based Dynamic Passenger Flow Assignment Modelling for a Schedule-Based Transit Network. Discret. Dyn. Nat. Soc. 2017, 2017, 2890814. [Google Scholar] [CrossRef]
- Mo, B.; Ma, Z.; Koutsopoulos, H.N.; Zhao, J. Capacity-Constrained Network Performance Model for Urban Rail Systems. Transp. Res. Rec. 2020, 2674, 59–69. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Crisalli, U.; Rosati, L. A Schedule-Based Assignment Model with Explicit Capacity Constraints for Congested Transit Networks. Transp. Res. Part C Emerg. Technol. 2012, 20, 16–33. [Google Scholar] [CrossRef]
- Hamdouch, Y.; Ho, H.W.; Sumalee, A.; Wang, G. Schedule-Based Transit Assignment Model with Vehicle Capacity and Seat Availability. Transp. Res. Part B Methodol. 2011, 45, 1805–1830. [Google Scholar] [CrossRef]
- Codina, E.; Rosell, F. A Heuristic Method for a Congested Capacitated Transit Assignment Model with Strategies. Transp. Res. Part B Methodol. 2017, 106, 293–320. [Google Scholar] [CrossRef]
- Cepeda, M.; Cominetti, R.; Florian, M. A Frequency-Based Assignment Model for Congested Transit Networks with Strict Capacity Constraints: Characterization and Computation of Equilibria. Transp. Res. Part B Methodol. 2006, 40, 437–459. [Google Scholar] [CrossRef]
- Paul, E.C. Estimating Train Passenger Load from Automated Data Systems: Application to London Underground. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Schmöcker, J.D.; Fonzone, A.; Shimamoto, H.; Kurauchi, F.; Bell, M.G.H. Frequency-Based Transit Assignment Considering Seat Capacities. Transp. Res. Part B Methodol. 2011, 45, 392–408. [Google Scholar] [CrossRef]
- Sun, L.; Axhausen, K.W. Understanding Urban Mobility Patterns with a Probabilistic Tensor Factorization Framework. Transp. Res. Part B Methodol. 2016, 91, 511–524. [Google Scholar] [CrossRef]
- Hörcher, D.; Graham, D.J.; Anderson, R.J. Crowding Cost Estimation with Large Scale Smart Card and Vehicle Location Data. Transp. Res. Part B Methodol. 2017, 95, 105–125. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Chen, W.; Zheng, Y. Willingness to Board: A Novel Concept for Modeling Queuing up Passengers. Transp. Res. Part B Methodol. 2016, 90, 70–82. [Google Scholar] [CrossRef]
- Lee, E.H.; Kim, K.; Kho, S.Y.; Kim, D.K.; Cho, S.H. Exploring for Route Preferences of Subway Passengers Using Smart Card and Train Log Data. J. Adv. Transp. 2022, 2022, 6657486. [Google Scholar] [CrossRef]
- Pelletier, M.P.; Trépanier, M.; Morency, C. Smart Card Data Use in Public Transit: A Literature Review. Transp. Res. Part C Emerg. Technol. 2011, 19, 557–568. [Google Scholar] [CrossRef]
- Mo, B.; Ma, Z.; Koutsopoulos, H.N.; Zhao, J. Calibrating Path Choices and Train Capacities for Urban Rail Transit Simulation Models Using Smart Card and Train Movement Data. J. Adv. Transp. 2021, 2021, 5597130. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Yang, L.; Ma, W.; Jin, G.; Gao, Z. Network-Wide Link Travel Time and Station Waiting Time Estimation Using Automatic Fare Collection Data: A Computational Graph Approach. IEEE Trans. Intell. Transp. Syst. 2022, 1–16. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, L.; Bai, Z.; Yue, Y.; Guo, B.; Zhou, H. Data-Driven Approaches to Mining Passenger Travel Patterns: “Left-Behinds” in a Congested Urban Rail Transit Network. J. Adv. Transp. 2019, 2019, 6830450. [Google Scholar] [CrossRef]
- Yu, C.; Li, H.; Xu, X.; Liu, J. Data-Driven Approach for Solving the Route Choice Problem with Traveling Backward Behavior in Congested Metro Systems. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102037. [Google Scholar] [CrossRef]
- Su, G.; Si, B.; Zhao, F.; Li, H. Data-Driven Method for Passenger Path Choice Inference in Congested Subway Network. Complexity 2022, 2022, 5451017. [Google Scholar] [CrossRef]
- Kusakabe, T.; Iryo, T.; Asakura, Y. Estimation Method for Railway Passengers’ Train Choice Behavior with Smart Card Transaction Data. Transportation 2010, 37, 731–749. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, R.H. Model of Passenger Flow Assignment for Urban Rail Transit Based on Entry and Exit Time Constraints. Transp. Res. Rec. 2012, 2284, 57–61. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, F.; Tu, L.; Xu, C.; Shen, D.; Tian, C.; Li, X.Y.; Li, Z. Estimation of Passenger Route Choice Pattern Using Smart Card Data for Complex Metro Systems. IEEE Trans. Intell. Transp. Syst. 2017, 18, 790–801. [Google Scholar] [CrossRef]
- Zhu, Y.; Koutsopoulos, H.N.; Wilson, N.H.M. A Probabilistic Passenger-to-Train Assignment Model Based on Automated Data. Transp. Res. Part B Methodol. 2017, 104, 522–542. [Google Scholar] [CrossRef]
- Zhu, Y.; Koutsopoulos, H.N.; Wilson, N.H.M. Passenger Itinerary Inference Model for Congested Urban Rail Networks. Transp. Res. Part C Emerg. Technol. 2021, 123, 102896. [Google Scholar] [CrossRef]
- Preston, J.; Pritchard, J.; Waterson, B. Train Overcrowding: Investigation of the Provision of Better Information to Mitigate the Issues. Transp. Res. Rec. 2017, 2649, 1–10. [Google Scholar] [CrossRef]
- Si, B.; Zhong, M.; Liu, J.; Gao, Z.; Wu, J. Development of a Transfer-Cost-Based Logit Assignment Model for the Beijing Rail Transit Network Using Automated Fare Collection Data. J. Adv. Transp. 2013, 47, 297–318. [Google Scholar] [CrossRef]
- Abedi, N.; Bhaskar, A.; Chung, E.; Miska, M. Assessment of Antenna Characteristic Effects on Pedestrian and Cyclists Travel-Time Estimation Based on Bluetooth and WiFi MAC Addresses. Transp. Res. Part C Emerg. Technol. 2015, 60, 124–141. [Google Scholar] [CrossRef]
- Gu, J.; Jiang, Z.; Sun, Y.; Zhou, M.; Liao, S.; Chen, J. Spatio-Temporal Trajectory Estimation Based on Incomplete Wi-Fi Probe Data in Urban Rail Transit Network. Knowledge-Based Syst. 2021, 211, 106528. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Song, W. A Radar-Nearest-Neighbor Based Data-Driven Approach for Crowd Simulation. Transp. Res. Part C Emerg. Technol. 2021, 129, 103260. [Google Scholar] [CrossRef]


| Set | Description |
|---|---|
| the set of passengers, . | |
| the set of train/service id in the train timetable, ; | |
| the set of platforms, ; | |
| the set of train, ; | |
| the leg number of passenger i’s journey, ; | |
| the train j of passenger i on the leg n of his/her journey, the variable as a whole corresponds to the train id in the timetable; | |
| the train’s subnet index, ; | |
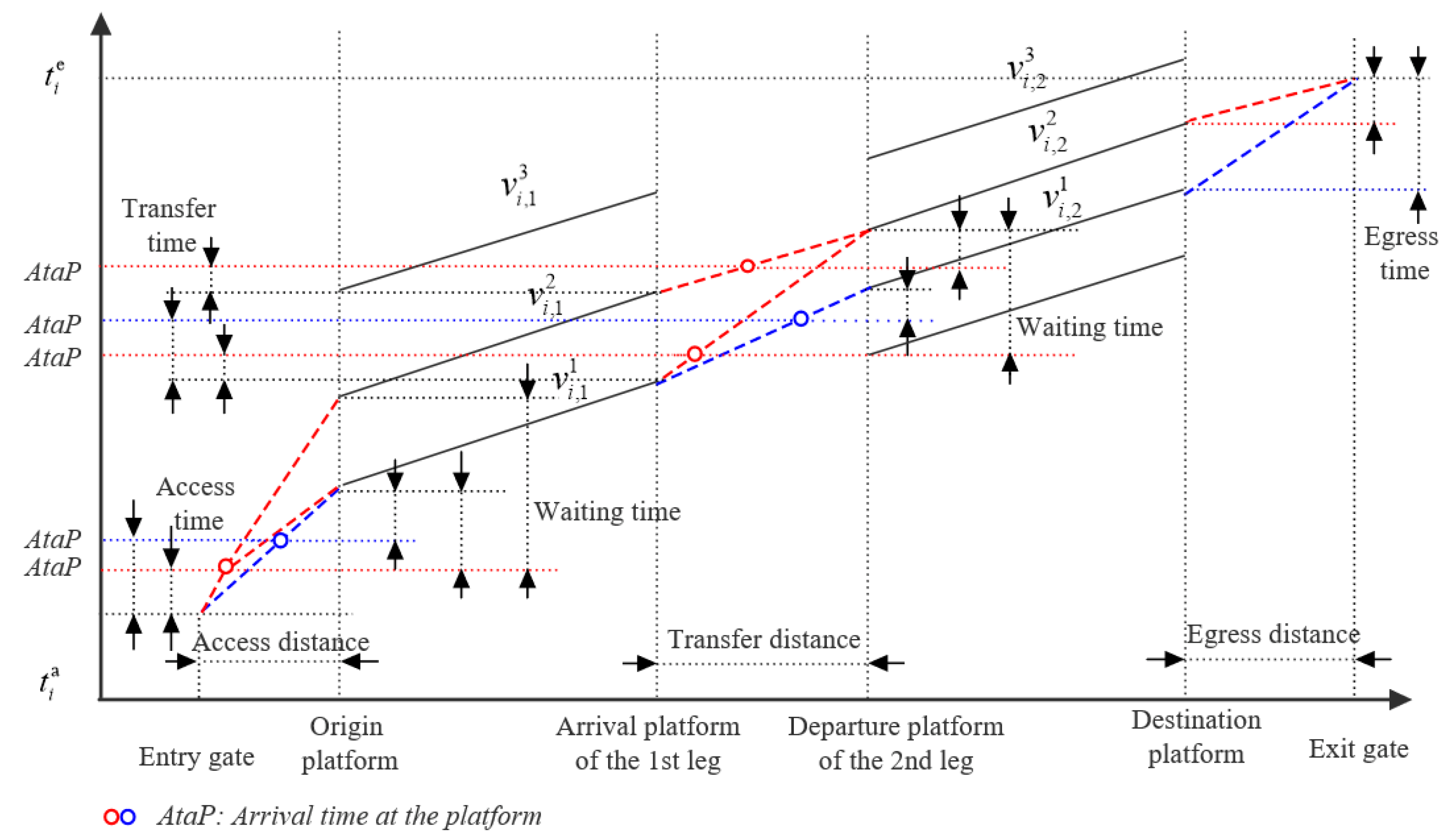
| the tap-in time of passenger i; | |
| the tap-out time of passenger i; | |
| the origin/departure platform of passenger i on leg n; | |
| the destination/arrival platform of passenger i on leg n; | |
| the departure time of train from the origin platform; | |
| the arrival time of train to the destination platform; | |
| the egress time of passenger i in the subnet g; | |
| the ratio of access distance or transfer distance to egress distance ; | |
| the transfer time of passenger i between the arrival platform of leg and the departure platform of leg n in the subnet g, is the access time; | |
| the waiting time of passenger i at the departure platform of leg n in subnet g when the passenger boards train k on leg and boards train j on leg n. It equals the departure time of train minus the arrival time of train , and then minus the transfer time between the two legs, that is ; | |
| the train set of passenger i on the leg n of his/her journey | |
| the train set of passenger i on leg n of subnet g, | |
| the egress time probability density of platform u; | |
| the waiting time probability density of platform u at time t; | |
| the transfer time probability density from platform to platform u, when , it is the access time probability density. |
| ID | Origin Station | Destination Station | Tap-In Time | Tap-Out Time |
|---|---|---|---|---|
| 20036058711 | TTY | SYJ | 17 October 2017 08:22:00 | 17 October 2017 08:57:18 |
| … | … | … | … | … |
| Our Model | Simulation Method | Data-I | ||||
| Capacity Constraint | 1.0 | 1.1 | 1.2 | 1.3 | ||
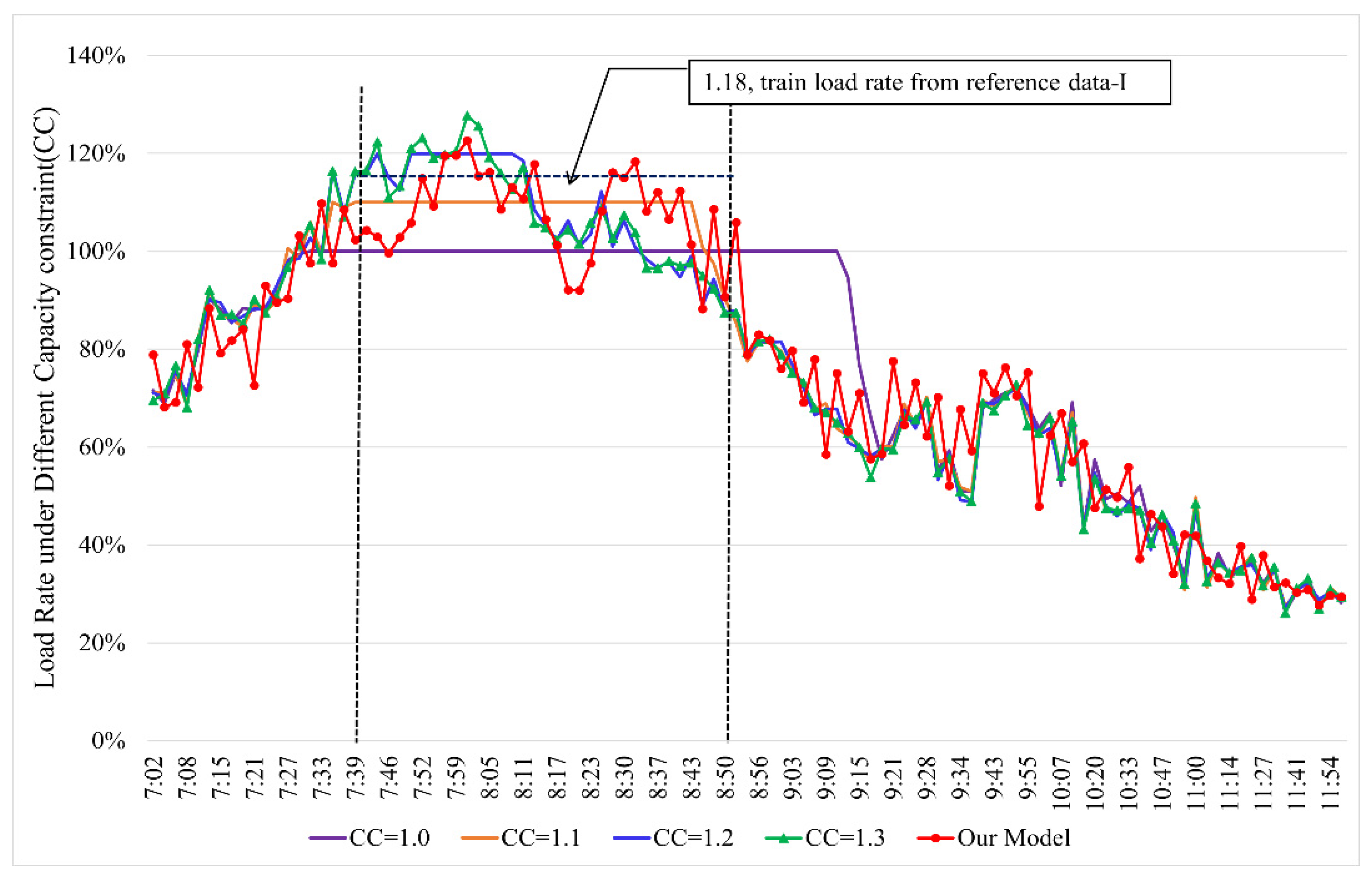
| Train Load Rate in Average | 1.16 | 1.0 | 1.096 | 1.09 | 1.09 | 1.18 |
| Number/Percentage of Train Load Rate Reaches the CC | - | 28/100% | 25/89% | 10/36% | 0/0% | - |
| Line | 1 | 2 | 6 | 10 | 13 | 15 | CP | FS | YZ |
|---|---|---|---|---|---|---|---|---|---|
| Period | 7:35~8:35 | 7:50~8:50 | 7:35~8:35 | 7:50~8:50 | 7:35~8:35 | 8:25~9:25 | 7:45~8:45 | 7:20~8:20 | 7:20~8:20 |
| Direction/Station | UP/JSBWG | UP/CGZ | DN/SLP | UP/SJ | UP/SD | UP/WJX | DOWN/SMKXY | UP/DT | UP/XC |
| Data-I | 0.95 | 0.62 | 1.21 | 0.95 | 1.1 | 0.88 | 1.24 | 1.1 | 1.14 |
| Our Model/Errors | 0.9 | 0.583 | 1.14 | 1.025 | 1.061 | 0.88 | 1.41 | 1.093 | 1.08 |
| 5.14% | 6.03% | 5.47% | 7.89% | 3.55% | 0% | 13.71% | 0.64% | 5.26% | |
| OCC | 1.2 | 1.4 | 1.3 | 1.0 | 1.5 | 1.1 | 1.2 | 1.1 | 1.2 |
| MTR | Beijing Subway | |
|---|---|---|
| Lines | 11 1 | 19 |
| Stations | 154 1 | 370 |
| Transfer stations | 20 1 | 56 |
| AFC data | 5 M~7 M 2 | 5.4 M |
| Candidate paths | 2 (Maximum) 2 | 4 (Maximum), 2.45 (In average) |
| PC | 3.40 GHz CPU, 16 GB RAM 2 | 3.80 GHZ CPU, 16 G RAM |
| With Parallel computing | Unknown | No |
| Computational time | About 2880 min 2 | About 82 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, G.; Si, B.; Zhi, K.; Li, H. A Calculation Method of Passenger Flow Distribution in Large-Scale Subway Network Based on Passenger–Train Matching Probability. Entropy 2022, 24, 1026. https://doi.org/10.3390/e24081026
Su G, Si B, Zhi K, Li H. A Calculation Method of Passenger Flow Distribution in Large-Scale Subway Network Based on Passenger–Train Matching Probability. Entropy. 2022; 24(8):1026. https://doi.org/10.3390/e24081026
Chicago/Turabian StyleSu, Guanghui, Bingfeng Si, Kun Zhi, and He Li. 2022. "A Calculation Method of Passenger Flow Distribution in Large-Scale Subway Network Based on Passenger–Train Matching Probability" Entropy 24, no. 8: 1026. https://doi.org/10.3390/e24081026
APA StyleSu, G., Si, B., Zhi, K., & Li, H. (2022). A Calculation Method of Passenger Flow Distribution in Large-Scale Subway Network Based on Passenger–Train Matching Probability. Entropy, 24(8), 1026. https://doi.org/10.3390/e24081026






