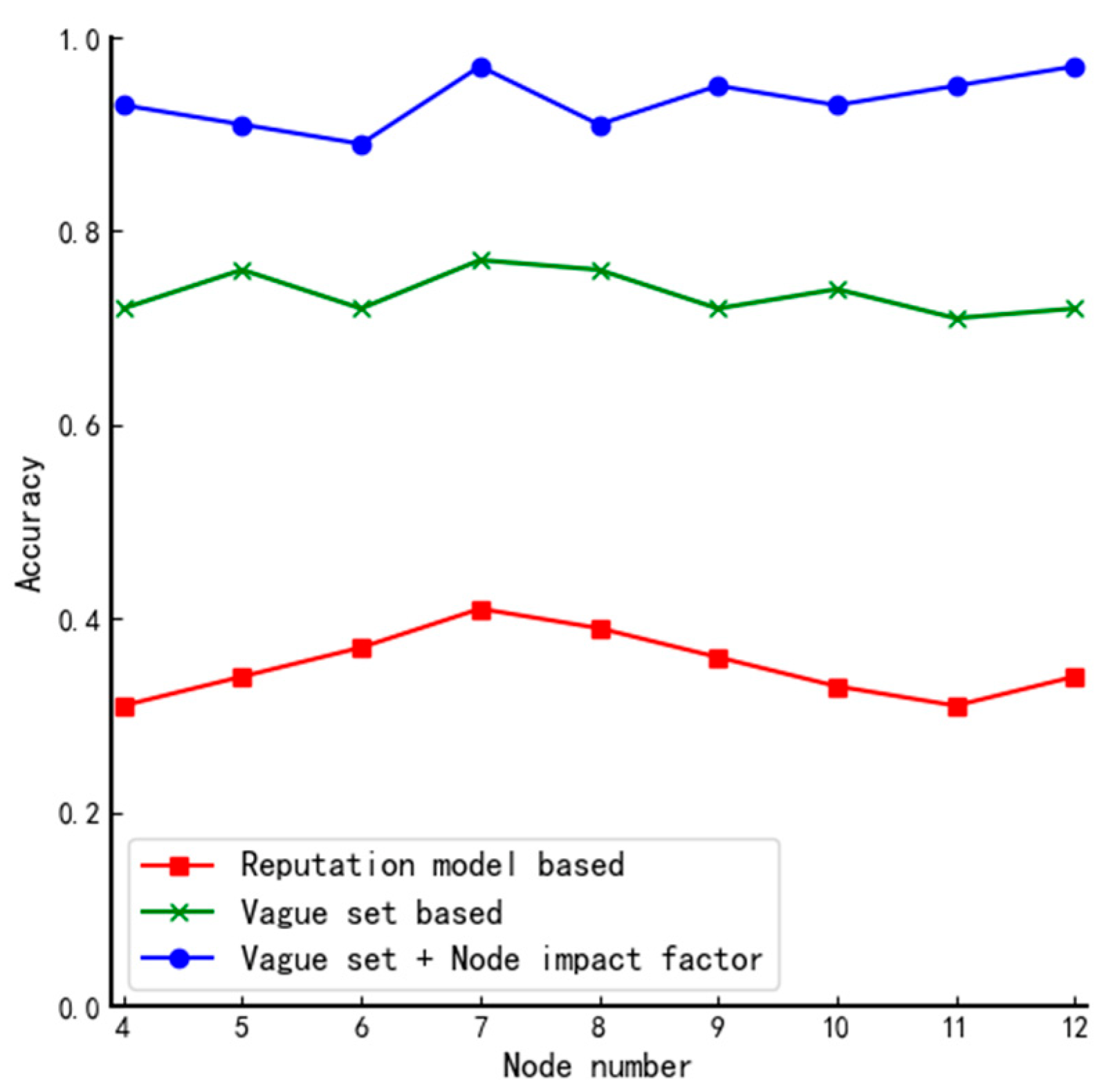
3.1. Fuzzy Value and Its Threshold
Define
as the voting matrix,
represents the vote from node
to node
, where:
All nodes can vote for, abstain from, or oppose other nodes during the voting process, and by default, all nodes will vote for themselves. Here is one of the voting matrices:
Assuming that the total number of nodes in the system is
, we improve Equation (2) in this paper, and the equation for calculating the fuzzy value is as follows.
Compared with Equations (2) and (3) does not consider the node’s own favorable votes. Here are the reasons: firstly, counting the votes of nodes without considering the node’s own favorable votes can improve the objectivity of the voting result; secondly, we need to calculate the impact factor of each node in this paper, and counting the node’s own favorable votes will make the screening results more biased towards those with higher impact factor so that fairness cannot be guaranteed.
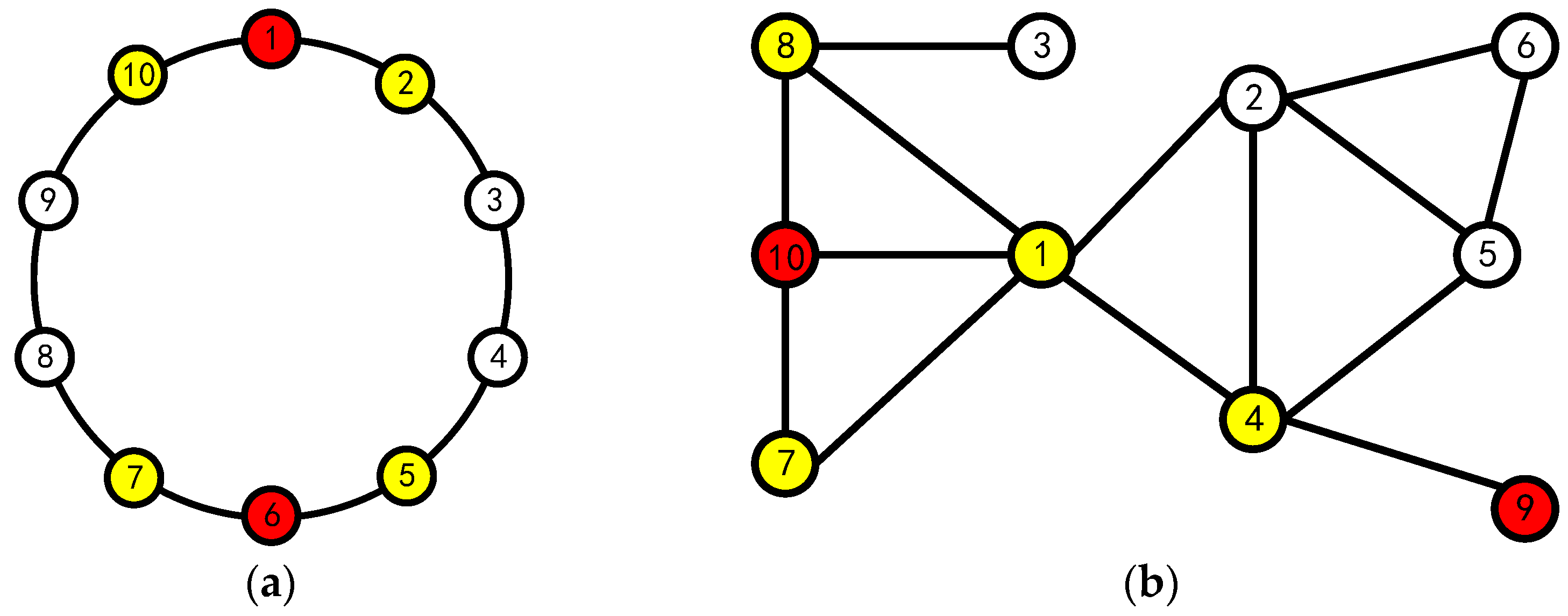
Taking node 2 as an example, the second row of the matrix shows that node 2 received a total of 7 favor votes, 4 abstention votes and 1 against vote. Therefore, according to the definition of fuzziness, we can calculate: , , so .
After using the method above to calculate the fuzzy value corresponding to all nodes, the nodes are first arranged in descending order according to their fuzzy value, and in the case of the same fuzzy value, the nodes are arranged in descending order according to the number of favorable votes they received, with results shown in
Table 1.
From
Table 1, we can see that using fuzzy values to calculate the votes of nodes has a more intuitive differentiation of nodes’ voting situation than the traditional method of counting the number of votes. Meanwhile, adding the abstention vote makes the voting results more objective and closer to reality and can filter out the nodes corresponding to the conditions more effectively.
Next, we will discuss how to determine the committee node. Most of the traditional algorithms select them one by one according to one specific index, and this will lead to a high possibility that some of the agent nodes only obtain less than half the support rate, which will bring risks to the whole system. In real-life voting activities, not only the number of votes received is considered, but sometimes additional provisions are made for the vote percentage to ensure the reliability of the results. Therefore, we set a threshold value on their fuzzy value to conduct first-round screening. It must satisfy the following two conditions:
- (1)
Against votes must be less than one-third of the total votes (excluding its own vote);
- (2)
The number of favor votes received by a node (excluding its own vote) must be higher than the number of against votes.
Therefore, if a system has
nodes,
can be calculated according to Equation (4).
In this paper,
, so
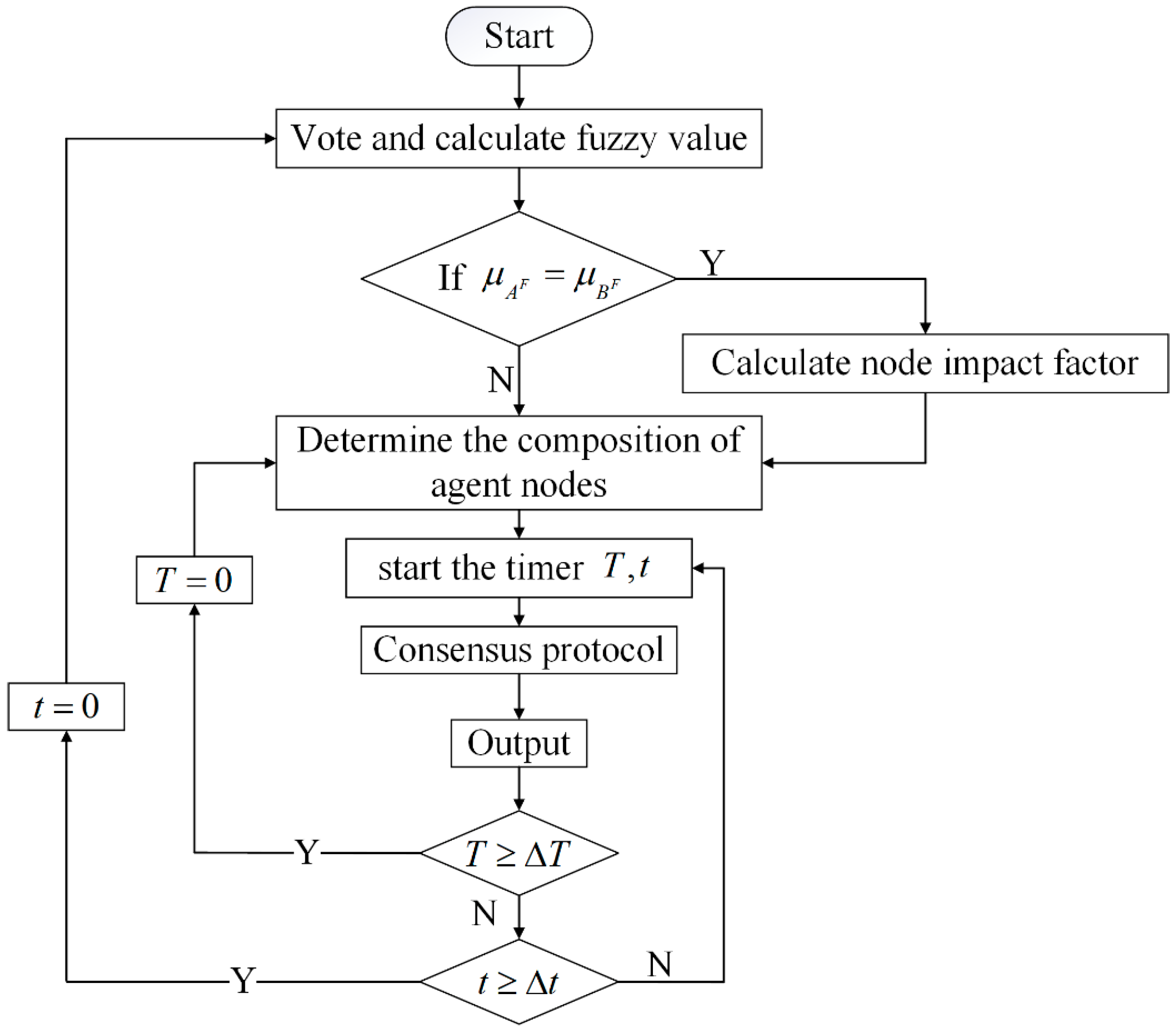
. Compared with the traditional algorithms, the threshold setting may increase the complexity of the whole algorithm. However, it can ensure that all screened nodes have a high support rate so that the system’s security can be enhanced. The flow of the first round of screening is shown in Algorithm 1.
| Algorithm 1: First-round screening |
| Input: node , fuzzy value , threshold |
| Output: alternative set |
| 1: sort by in descending order |
| 2: if then |
| 3: add to |
| 4: end if |
| 5: return |
Since all nodes in the system will vote based on the historical behavior of the destination node, we can roughly think that the vote rate is the reliability of the node. In addition, in the algorithm proposed in this paper, all non-member nodes can only perform the operation of receiving member node information. Therefore, once a node has an information mismatch, we can default it to a malicious node.
When the following situations occur, the entire voting process is invalid and a new vote is required:
Abstaining from voting contains more than half of the total number of votes. In general, the votes of all nodes are based on the good or bad historical behavior of other nodes. Therefore, in this case, taking any node in the system as an example, the final votes of the node may only have the following two situations: in favor votes more than abstentions and negative votes, and negative votes more than votes in favor and abstentions votes. Therefore, under normal circumstances, it is almost impossible for the abstention votes cast by nodes in the system to exceed more than half of the total votes. Once it happens, we first need to observe not only the vote type of each node but also the vote type of each node to preliminarily determine the malicious nodes in the system, and then, after determining the malicious nodes, we need to re-vote.
Allare smaller than the threshold value. Through simulation experiments and calculations, we found that this situation is often accompanied by the above-mentioned situations. Therefore, the response to this situation is the same as above.
3.2. Node Impact Factor
In measuring the importance of nodes in the system, Zhu used a way to determine the degree centrality of nodes based on node itself and its neighbor layer information [
25]. Similar to this, we propose an easier method to determine the impact factor of different nodes in the network. We count the number of first-order and second-order neighboring nodes, and then assign the parameter 1, 0, 5 according to the relevant rules of information transmission.
Define
represents the node number,
is the first-order centrality of the node, the union of all nodes constituted by
, the set of all first-order neighboring node numbers is
, the set of all second-order neighboring node numbers is
, and the impact factor of the node
is:
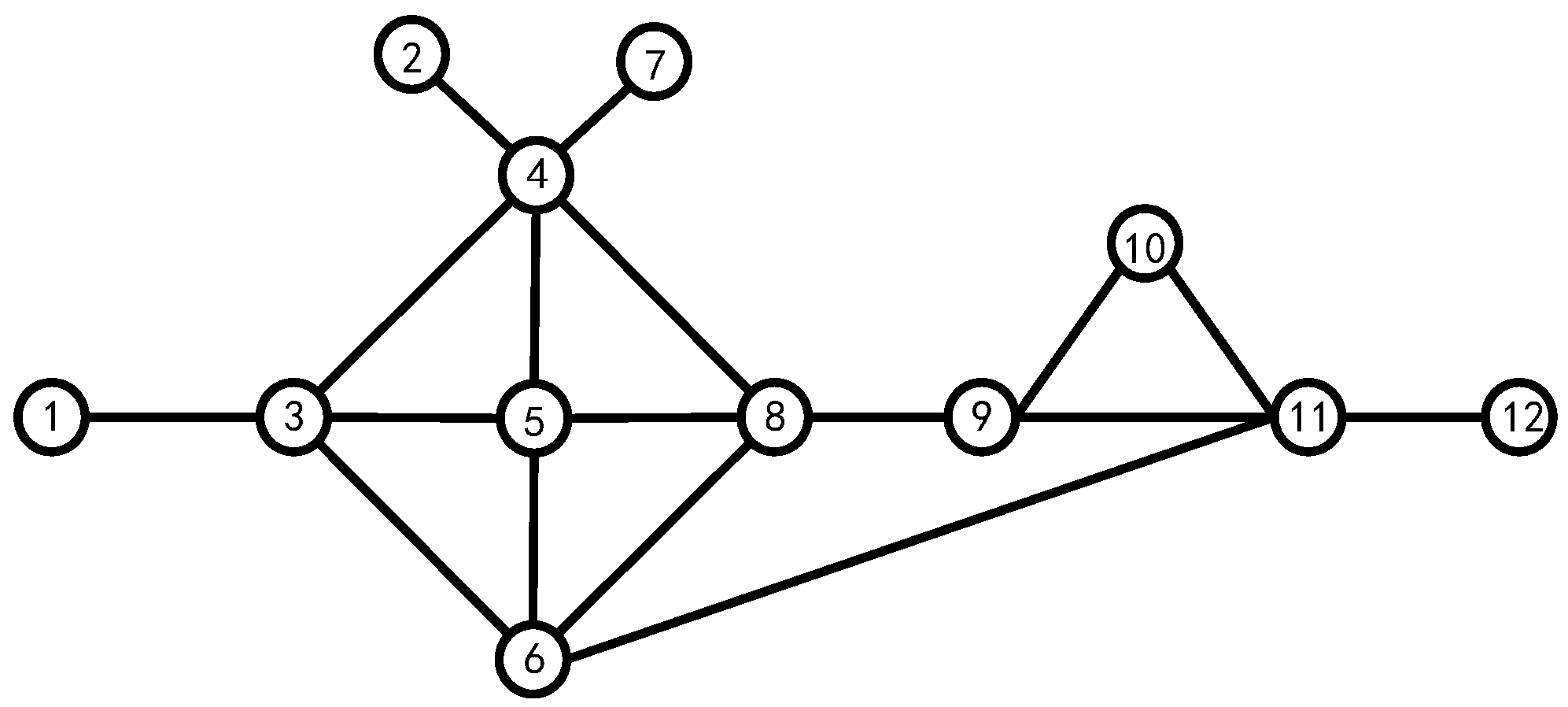
From
Figure 3, we can easily calculate the first-order centrality of all nodes, which is shown in
Table 2.
Taking node 5 as an example, , , so we can calculate .
All nodes’ impact factor is shown in
Table 3.
From
Table 2, we can see that when judging the impact factor of a node only from its first-order centrality, nodes 3, 4, 5, 6, 8, and 11 have higher impact factors; if we consider the first-order and the second-order centrality of the node, nodes 3, 4, 5, 6, 8, and 9 have higher impact factors in the system. Comparing node 9 with 11 in
Figure 3, we can reach the conclusion that the later method is closer to reality. Therefore, evaluating the influence of a node in the system cannot only consider the number of its neighboring nodes but should also consider the magnitude of its neighboring nodes’ influence in the system.
3.3. Second-Round Screening
When there is a tie vote among multiple nodes, most algorithms often use the traditional coin toss method to randomly determine the winning node. Although this algorithm can greatly reduce the communication complexity, the random election of the winning node not only lacks a certain theoretical basis, but also may increase the risk of the system. The new method proposed in this paper can solve the above problems very well. We consider that blockchain is a complex system. The position of different nodes, the number of their adjacent nodes and their roles are different to a certain extent. Meanwhile, from the point of information transmission, the evaluation of a node’s adjacent nodes is often more valuable. Therefore, we comprehensively consider the influence factor of the node and the adjacent nodes when conducting the second-round screening. Here are the details:
When comparing the number of elements in with the actual number of nodes in agent set , there exists the following three circumstances:
Circumstance 1:
In this circumstance, . There is no need to make further judgments.
Circumstance 2:
In this case, we need to do further screening of the elements in . If , we can get by comparing their fuzzy value; if , since the nodes numbered 6, 9 have the same fuzzy value, it is necessary to consider the impact factors of these two nodes and their first-order and second-order adjacency nodes votes for further screening. The specific process is as follows:
According to
Figure 2 and the voting matrix
, the neighboring votes of nodes numbered 6,9 can be derived as shown in the following table:
Define node support rate
, first-order neighboring node support rate
, and the second-order neighboring node support rate
. The calculation formula is as follows:
where:
Take node 6 as an example, and we can calculate from the data in
Table 4 to get
,
so that
, and similarly
. Therefore, we can get
.
Circumstance 3:
In this case, most traditional algorithms select the nodes with the higher fuzzy value among the remaining nodes to fill the vacant slots. These methods are simple, but since the fuzzy value of the remaining nodes does not reach the threshold, even if they are selected, it still makes the subsequent consensus protocols riskier and more unreliable. To address this problem, we propose a new judgment method divided into two main steps.
Step1: Determine whether all the remaining nodes get more than 1/3 of the total votes (excluding the nodes’ votes); if so, turn to Step2;
Step2: Finalize the remaining elements of the agent node-set based on the votes of the nodes in set for all nodes that satisfy the conditions of Step 1.
If
, we need to select 2 nodes from the remaining nodes to the fill set
, and according to Step1, we first find the nodes that satisfy the condition, which are
; then, we calculate the vote percentage of each node according to Equation (9) based on the vote of the nodes above, and the results are shown in the following table.
From
Table 5, we can find that
. Therefore, when
,
. In addition, no matter what
is, we can only find one corresponding
. The flow of the second-round screening is shown in Algorithm 2.
| Algorithm 2: Second-round screening |
| Input: node , alternative set , fuzzy value , total number , impact factor , voting matrix |
| Output: member node-set |
| 1: if the number of elements in larger than then |
| 2: sort all in descending order and find the largest values |
| 3: if all these are not the same then |
| 4: add the corresponding to |
| 5: else |
| 6: make further comparison |
| 6: add all corresponding to |
| 7: else |
| 8: combined with for further comparison of some of the remaining nodes |
| 9: add all corresponding to |
| 10: return |
3.4. Dynamic Change of Agent Node-Set
The dynamic change in set includes two aspects: the dynamic change in the composition of the agent node-set and the dynamic change in the size of the agent node-set according to the total number of nodes in the network.
3.4.1. Dynamic Changes in the Composition of the Agent Node-Set
The DPoS consensus mechanism specifies that all nodes in the system will be recounted at regular intervals based on the running time of its consensus protocol, which means that the set of agent nodes will be replaced at regular intervals. In this paper, we develop personalized dynamic adjustment rules based on the characteristics of member nodes:
- (1)
If all in are larger than , we use the method of half replacement to replace half the number of nodes in randomly.
- (2)
If there are in smaller than , all the nodes which will be replaced, and the remaining nodes are still replaced by the method of half replacement.
Although the half-replacement method increases the centralization tendency of the system to some extent, the nodes retained before and after the replacement can maintain the consistency of the system and the stability of the system operation at the early stage of the next phase and avoid the possible disorder of information timing caused by the replacement of all nodes.
3.4.2. Dynamic Changes in the Size of the Agent Node-Set
The DPoS consensus mechanism always decides the size according to the application environment. For example, the EOS system with the DPoS + BFT consensus algorithm has 21 members, and the Asch system with the DPoS + PBFT consensus algorithm has 101 members. The total number of nodes in the system for public and coalition chains changes a lot. If the number of agent nodes is fixed, it will inevitably increase the workload of these nodes. Based on this, this paper defines as the ratio of the number of agent nodes to the total number of nodes . It has the following properties:
- (1)
represents the absence of an agent node in the network, and accordingly, the entire blockchain system will lack nodes for packaging transactions or information. In this circumstance, the blockchain will not function properly.
- (2)
represents that all nodes in the whole system are member nodes, so the blockchain system is a public chain, which is truly decentralized. A more typical one is the PBFT consensus algorithm.
- (3)
represents that there is only one agent node in the whole system, which means that this node handles all transactions or data packaging and block generation. It is a typical centralized system and contradicts the decentralized nature of blockchain.
In general, we have
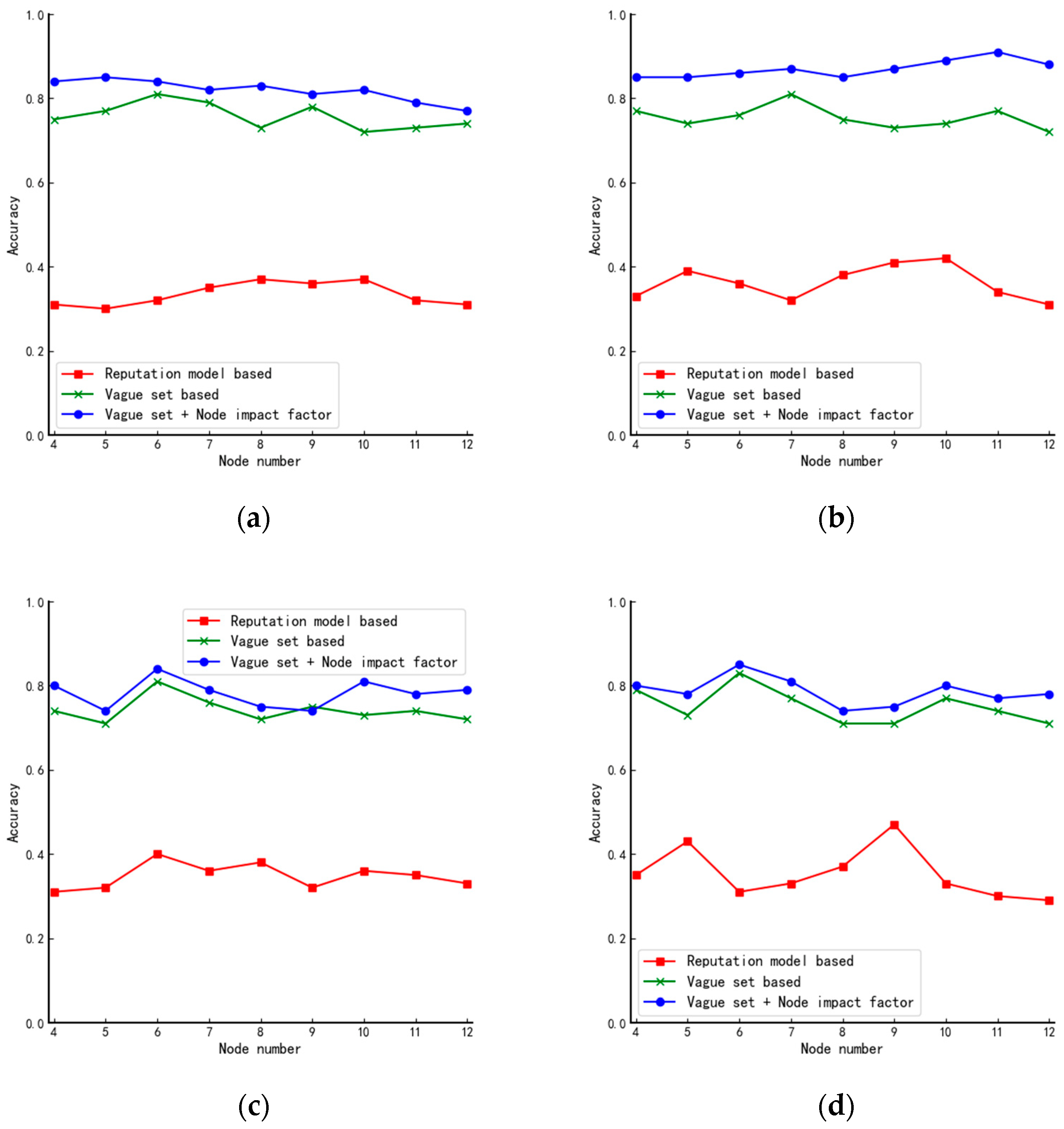
and the specific value should be determined by the size of the corresponding blockchain system which will be analyzed experimentally in
Section 4.