Privacy-Preserving Design of Scalar LQG Control
Abstract
:1. Related Work
1.1. Research on Active Adversarial Attacks
1.2. Research on Privacy Problems
2. Introduction
2.1. Motivation
2.2. Content and Contribution
2.3. Notation
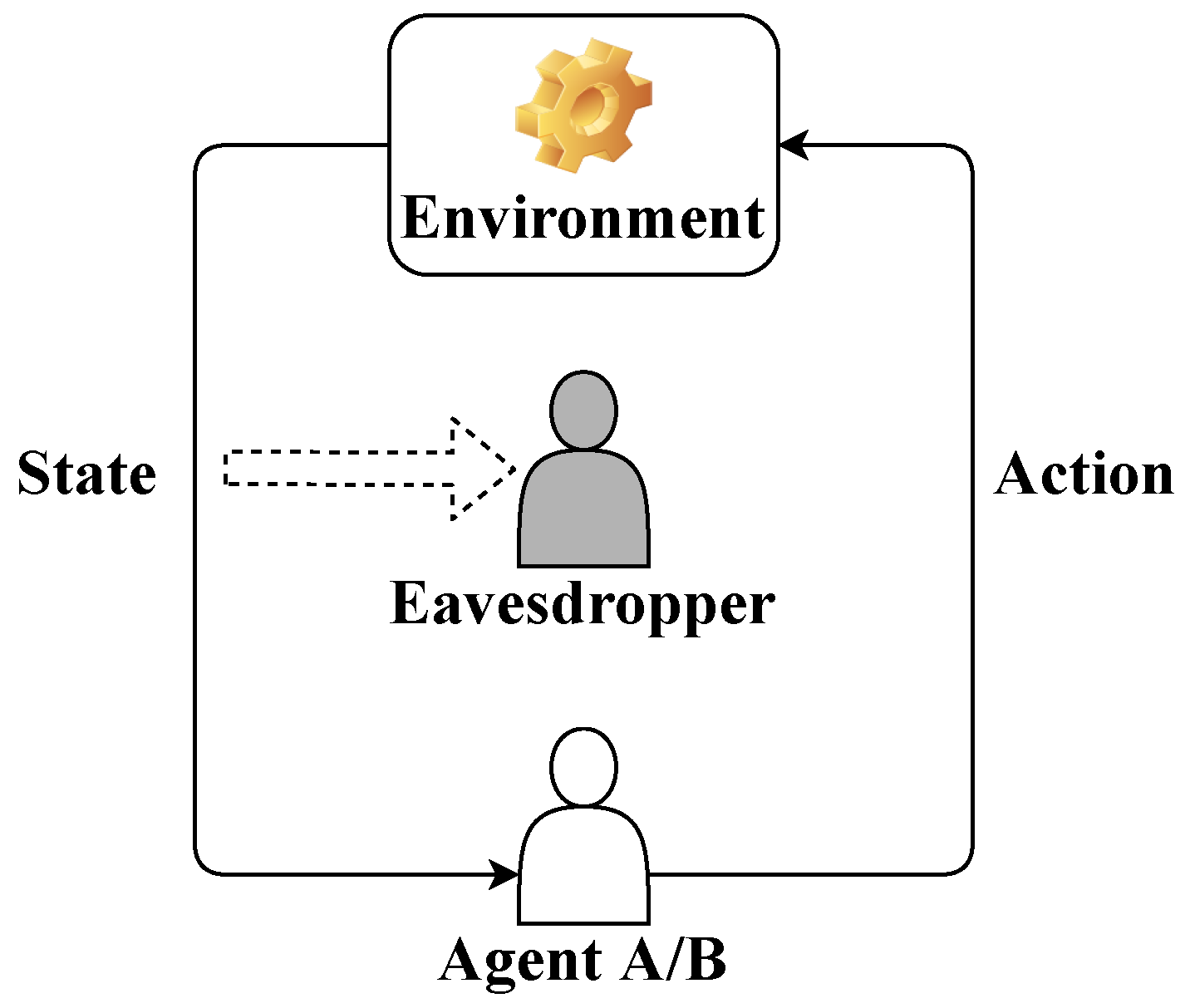
3. Agent Identity Privacy Problem in LQG Control
4. Deterministic Privacy-Preserving LQG Policy
5. Random Privacy-Preserving LQG Policy
6. Numerical Experiments
6.1. Convergence of the Sequence
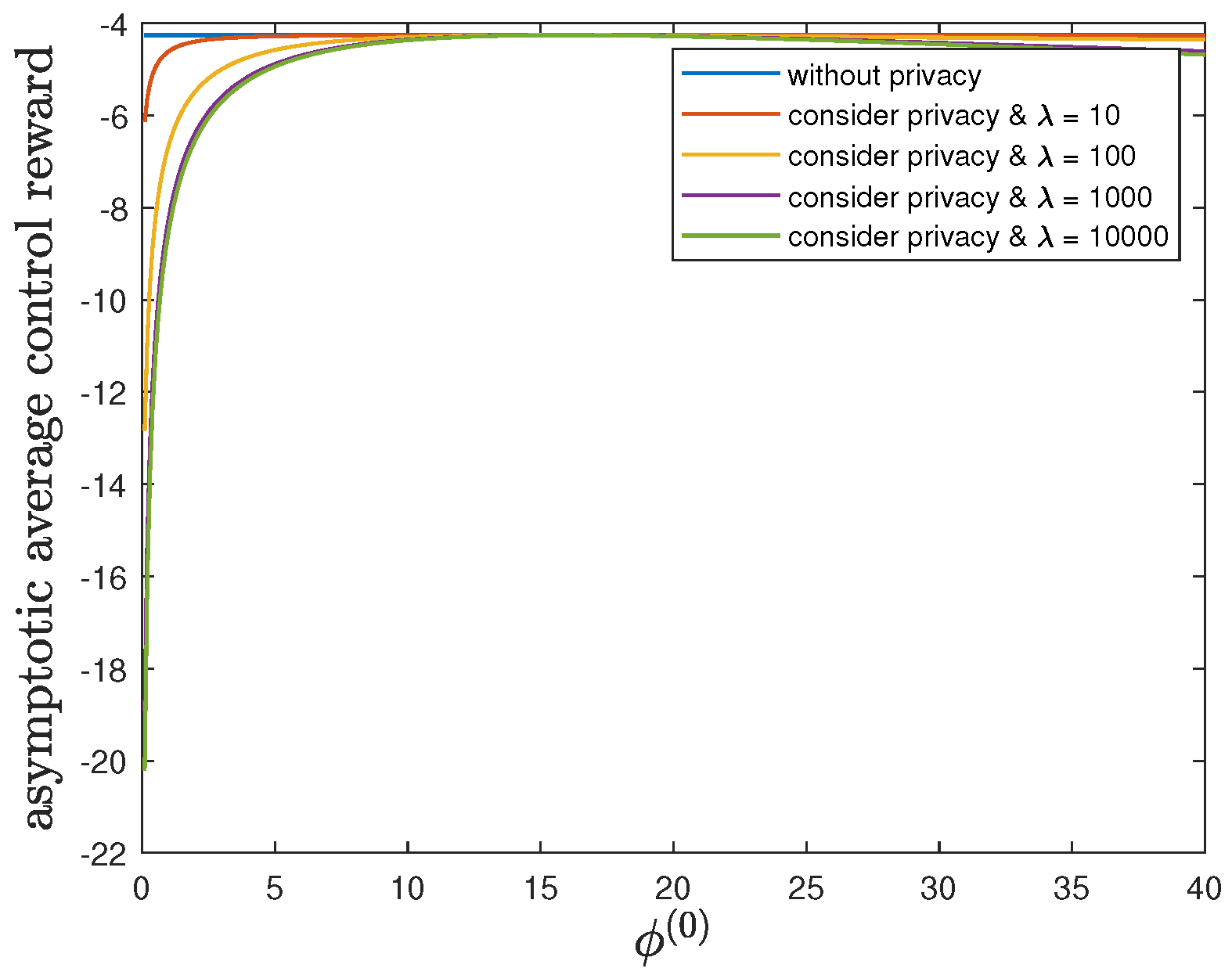
6.2. Impact of the Privacy-Preserving Design Weight
6.3. Impact of Parameter
6.4. Impact of Parameter
6.5. Impact of Parameter
6.6. Impact of Parameter
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Papernot, N.; Goodfellow, I.; Duan, Y.; Abbeel, P. Adversarial attacks on neural network policies. arXiv 2016, arXiv:1702.02284. [Google Scholar]
- Lin, Y.C.; Hong, Z.W.; Liao, Y.H.; Shih, M.L.; Liu, M.Y.; Min, S. Tactics of adversarial attack on deep reinforcement learning agents. In Proceedings of the 2017 International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3756–3762. [Google Scholar]
- Behzadan, V.; Munir, A. Vulnerability of deep reinforcement learning to policy induction attacks. In Proceedings of the MLDM 2017, New York, NY, USA, 15–20 July 2017; pp. 262–275. [Google Scholar]
- Russo, A.; Proutiere, A. Optimal attacks on reinforcement learning policies. arXiv 2019, arXiv:1907.13548. [Google Scholar]
- Goodfellow, I.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Tramer, F.; Kurakin, A.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. Ensemble adversarial training: Attacks and defenses. In Proceedings of the ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Sinha, A.; Namkoong, H.; Duchi, J. Certifying some distributional robustness with principled adversarial training. In Proceedings of the ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Zheng, S.; Song, Y.; Leung, T.; Goodfellow, I. Improving the robustness of deep neural networks via stability training. In Proceedings of the CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Yan, Z.; Guo, Y.; Zhang, C. Deep defense: Training DNNs with improved adversarial robustness. In Proceedings of the NIPS 2018, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Shapley, L. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gleave, A.; Dennis, M.; Wild, C.; Kant, N.; Levine, S.; Russell, S. Adversarial policies: Attacking deep reinforcement learning. In Proceedings of the ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Pinto, L.; Davidson, J.; Sukthankar, R.; Gupta, A. Robust adversarial reinforcement learning. In Proceedings of the ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; pp. 2817–2826. [Google Scholar]
- Horak, K.; Zhu, Q.; Bosansky, B. Manipulating adversary’s belief: A dynamic game approach to deception by design for proactive network security. In Proceedings of the GameSec 2017, Vienna, Austria, 23–25 October 2017; pp. 273–294. [Google Scholar]
- Crawford, V.P.; Sobel, J. Strategic information transmission. Econometrica 1982, 50, 1431–1451. [Google Scholar] [CrossRef]
- Saritas, S.; Yuksel, S.; Gezici, S. Nash and Stackelberg equilibria for dynamic cheap talk and signaling games. In Proceedings of the ACC 2017, Seattle, WA, USA, 24–26 May 2017; pp. 3644–3649. [Google Scholar]
- Saritas, S.; Shereen, E.; Sandberg, H.; Dán, G. Adversarial attacks on continuous authentication security: A dynamic game approach. In Proceedings of the GameSec 2019, Stockholm, Sweden, 30 October–1 November 2019; pp. 439–458. [Google Scholar]
- Li, Z.; Dán, G. Dynamic cheap talk for robust adversarial learning. In Proceedings of the GameSec 2019, Stockholm, Sweden, 30 October–1 November 2019; pp. 297–309. [Google Scholar]
- Li, Z.; Dán, G.; Liu, D. A game theoretic analysis of LQG control under adversarial attack. In Proceedings of the IEEE CDC 2020, Jeju Island, Korea, 14–18 December 2020; pp. 1632–1639. [Google Scholar]
- Osogami, T. Robust partially observable Markov decision process. In Proceedings of the ICML 2015, Lille, France, 6–11 July 2015. [Google Scholar]
- Sayin, M.O.; Basar, T. Secure sensor design for cyber-physical systems against advanced persistent threats. In Proceedings of the GameSec 2017, Vienna, Austria, 23–25 October 2017; pp. 91–111. [Google Scholar]
- Sayin, M.O.; Akyol, E.; Basar, T. Hierarchical multistage Gaussian signaling games in noncooperative communication and control systems. Automatica 2019, 107, 9–20. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Li, Z.; Wang, C. Adversarial linear quadratic regulator under falsified actions. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022. [Google Scholar]
- Zhang, R.; Venkitasubramaniam, P. Stealthy control signal attacks in linear quadratic Gaussian control systems: Detectability reward tradeoff. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1555–1570. [Google Scholar] [CrossRef]
- Ren, X.X.; Yang, G.H. Kullback-Leibler divergence-based optimal stealthy sensor attack against networked linear quadratic Gaussian systems. IEEE Trans. Cybern. 2021, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Venkitasubramaniam, P. Privacy in stochastic control: A Markov decision process perspective. In Proceedings of the Allerton 2013, Monticello, IL, USA, 2–4 October 2013; pp. 381–388. [Google Scholar]
- Ny, J.L.; Pappas, G.J. Differentially private filtering. IEEE Trans. Autom. Control. 2013, 59, 341–354. [Google Scholar]
- Hale, M.T.; Egerstedt, M. Cloud-enabled differentially private multiagent optimization with constraints. IEEE Trans. Control. Netw. Syst. 2017, 5, 1693–1706. [Google Scholar] [CrossRef] [Green Version]
- Hale, M.; Jones, A.; Leahy, K. Privacy in feedback: The differentially private LQG. In Proceedings of the ACC 2018, Milwaukee, WI, USA, 27–29 June 2018; pp. 3386–3391. [Google Scholar]
- Hawkins, C.; Hale, M. Differentially private formation control. In Proceedings of the IEEE CDC 2020, Jeju Island, Korea, 14–18 December 2020; pp. 6260–6265. [Google Scholar]
- Dwork, C. Differential privacy. In Proceedings of the ICALP 2006, Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Wang, B.; Hegde, N. Privacy-preserving Q-learning with functional noise in continuous spaces. In Proceedings of the NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Alexandru, A.B.; Pappas, G.J. Encrypted LQG using labeled homomorphic encryption. In Proceedings of the ACM/IEEE ICCPS 2019, Montreal, QC, Canada, 16–18 April 2019. [Google Scholar]
- Arora, S.; Doshi, P. A survey of inverse reinforcement learning: Challenges, methods and progress. Artif. Intell. 2021, 297, 103500. [Google Scholar] [CrossRef]
- Soderstrom, T. Discrete-Time Stochastic Systems; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Baranga, A. The contraction principle as a particular case of Kleene’s fixed point theorem. Discret. Math. 1991, 98, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE ICASSP 2007, Honolulu, HI, USA, 15–20 April 2007. [Google Scholar]
- Durrieu, J.; Thiran, J.; Kelly, F. Lower and upper bounds for approximation of the Kullback-Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE ICASSP 2012, Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Cui, S.; Datcu, M. Comparison of Kullback-Leibler divergence approximation methods between Gaussian mixture models for satellite image retrieval. In Proceedings of the IEEE IGARSS 2015, Milan, Italy, 26–31 July 2015. [Google Scholar]










| Private Information | Privacy Model/Measure | Privacy Mechanism | |
|---|---|---|---|
| [26] | State | Equivocation | Privacy-preserving policy design |
| [27,28,29,30] | State | Differential privacy | Adding privacy noise to state |
| [32] | Reward function | Differential privacy | Adding privacy noise to value function |
| [33] | The whole LQG system | Computational secrecy | Labeled homomorphic encryption |
| This work | Agent identity | Kullback–Leibler divergence | Privacy-preserving policy design |
| Parameter | Meaning | Parameter | Meaning |
|---|---|---|---|
| N | Number of steps | H | Agent identity binary hypothesis |
| , | Time-invariant linear coefficients in the linear Gaussian dynamic model | , | Independent zero-mean Gaussian-distributed disturbance noise in the i-th step and its variance |
| State of the agent in the i-th step | Action of the agent in the i-th step | ||
| Policy of the agent in the i-th step | State feedback gain of a linear policy of the agent in the i-th step | ||
| Instantaneous control reward of the agent in the i-th step | , , | Time-invariant instantaneous quadratic control reward function of the agent and its coefficients | |
| , | Mean and variance of the Gaussian-distributed initial state | Privacy-preserving design weight |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value | 1 | 1 | 1 | 1 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari, E.; Tian, Y.; Sun, C.; Li, Z.; Wang, C. Privacy-Preserving Design of Scalar LQG Control. Entropy 2022, 24, 856. https://doi.org/10.3390/e24070856
Ferrari E, Tian Y, Sun C, Li Z, Wang C. Privacy-Preserving Design of Scalar LQG Control. Entropy. 2022; 24(7):856. https://doi.org/10.3390/e24070856
Chicago/Turabian StyleFerrari, Edoardo, Yue Tian, Chenglong Sun, Zuxing Li, and Chao Wang. 2022. "Privacy-Preserving Design of Scalar LQG Control" Entropy 24, no. 7: 856. https://doi.org/10.3390/e24070856
APA StyleFerrari, E., Tian, Y., Sun, C., Li, Z., & Wang, C. (2022). Privacy-Preserving Design of Scalar LQG Control. Entropy, 24(7), 856. https://doi.org/10.3390/e24070856






