Robust Self-Testing of Four-Qubit Symmetric States
Abstract
:1. Introduction
2. Basic Definitions and Preliminaries
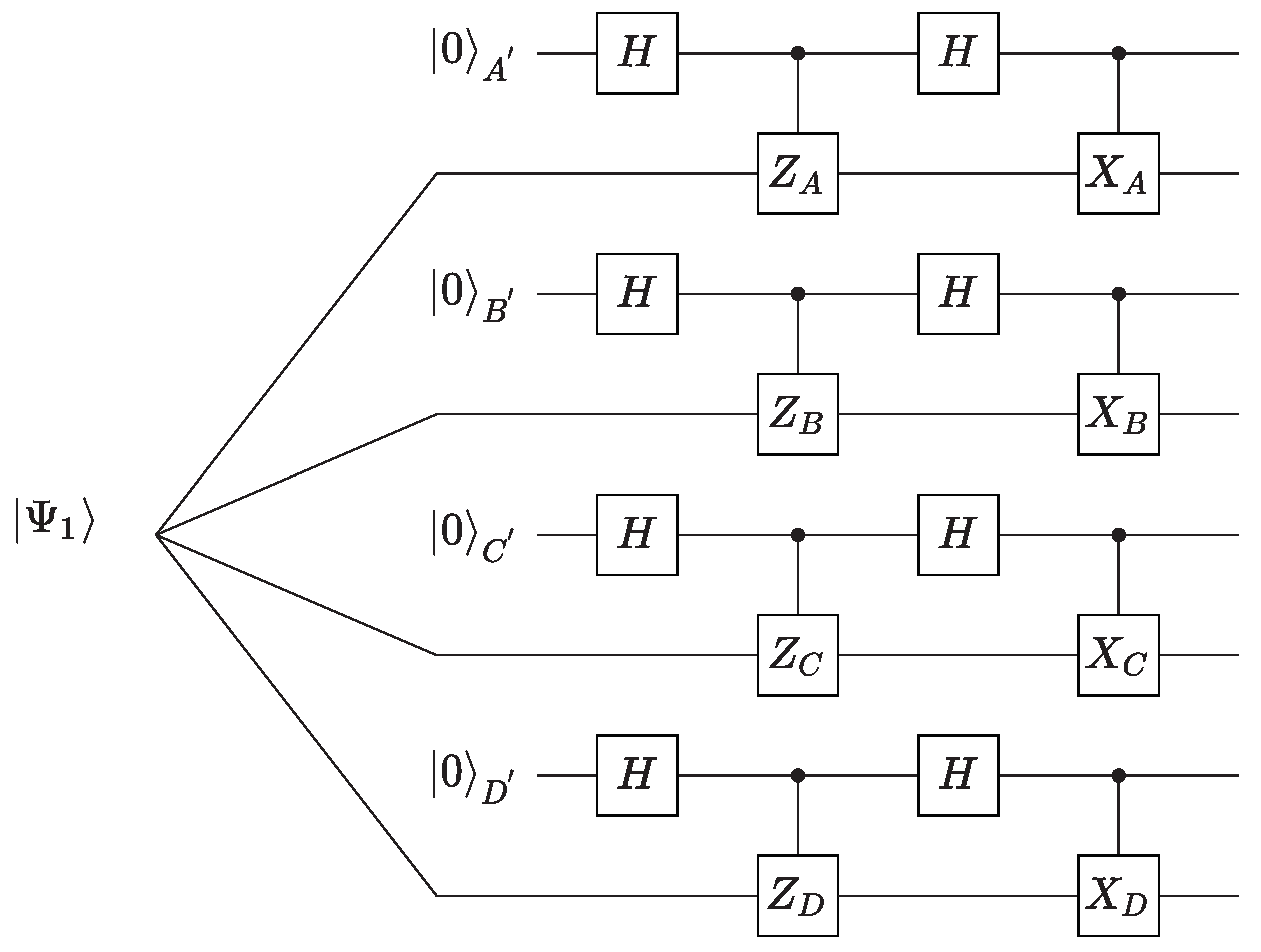
3. Self-Testing of a Four-Qubit Symmetric State
3.1. Self-Testing of a Specific Four-Qubit Symmetric State
3.2. Robustness Analysis Based on the Norm
4. Self-Testing of a Family of Parameterized Four-Qubit Symmetric States
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Appendix A. Proof of the Robustness
Appendix B. Proof of the Self-Testing of a Family of Parameterized Four-Qubit Symmetric States
Appendix C. Relations between Pauli Operators and the Unknown Measurements
References
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. A 2003, 361, 1655–1674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photon. 2007, 1, 165–171. [Google Scholar] [CrossRef] [Green Version]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.H.; Gao, F.; Liu, C.; Huynh, D.; Reynolds, M.; Wang, J. Quantum algorithm for visual tracking. Phys. Rev. A 2019, 99, 022301. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wu, Y.; Wan, L.; Pan, S.; Qin, S.; Gao, F.; Wen, Q. Variational quantum algorithm for Poisson equation. Phys. Rev. A 2021, 104, 022418. [Google Scholar] [CrossRef]
- Eisert, J.; Hangleiter, D.; Walk, N.; Roth, I.; Markham, D.; Parekh, R.; Chabaud, U.; Kashefi, E. Quantum certification and benchmarking. Nat. Rev. Phys. 2020, 2, 382–390. [Google Scholar] [CrossRef]
- Cramer, M.; Plenio, M.B.; Flammia, S.T.; Somma, R.; Gross, D.; Bartlett, S.D.; Landon-Cardinal, O.; Poulin, D.; Liu, Y.-K. Efficient quantum state tomography. Nat. Commun. 2010, 1, 149. [Google Scholar] [CrossRef] [Green Version]
- Mayers, D.; Yao, A. Self testing quantum apparatus. Quant. Inf. Comput. 2004, 4, 273–286. [Google Scholar] [CrossRef]
- Gallego, R.; Brunner, N.; Hadley, C.; Acín, A. Device-independent tests of classical and quantum dimensions. Phys. Rev. Lett. 2010, 105, 230501. [Google Scholar] [CrossRef] [Green Version]
- Long, G.; Liu, X. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef] [Green Version]
- Kwek, L.; Cao, L.; Luo, W.; Wang, Y.; Sun, S.; Wang, X.; Liu, A. Chip-based quantum key distribution. Assoc. Asia Pac. Phys. Soc. Bull. 2021, 31, 15. [Google Scholar] [CrossRef]
- Pironio, S.; Acín, A.; Massar, S.; de la Giroday, A.B.; Matsukevich, D.N.; Maunz, P.; Olmschenk, S.; Hayes, D.; Luo, L.; Manning, T.A.; et al. Random numbers certified by Bell’s theorem. Nature 2010, 464, 1021–1024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bancal, J. Device-independent witnesses of genuine multipartite entanglement. Phys. Rev. Lett. 2011, 106, 250404. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bancal, J.-D.; Navascués, M.; Scarani, V.; Vértesi, T.; Yang, T.H. Physical characterization of quantum devices from nonlocal correlations. Phys. Rev. A 2015, 91, 022115. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.; Rohrlich, D. Generic quantum nonlocality. Phys. Rev. A 1992, 166, 293–297. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef] [Green Version]
- Fannes, M.; Lewis, J.T.; Verbeure, A. Symmetric states of composite systems. Lett. Math. Phys. 1988, 15, 255–260. [Google Scholar] [CrossRef]
- Briegel, H.J.; Browne, D.E.; Dür, W.; Raussendorf, R.; Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 2009, 5, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Šupić, I.; Coladangelo, A.; Augusiak, R.; Acín, A. Self-testing multipartite entangled states through projections onto two systems. New J. Phys. 2018, 20, 083041. [Google Scholar] [CrossRef]
- Coladangelo, A.; Goh, K.T.; Scarani, V. All pure bipartite entangled states can be self-tested. Nat. Commun. 2017, 8, 15485. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.H.; Navascués, M. Robust self-testing of unknown quantum systems into any entangled two-qubit states. Phys. Rev. A 2013, 87, 050102. [Google Scholar] [CrossRef] [Green Version]
- Bamps, C.; Pironio, S. Sum-of-squares decompositions for a family of Clauser-Horne-Shimony-Holt-like inequalities and their application to self-testing. Phys. Rev. A 2015, 91, 052111. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wu, X.; Scarani, V. All the self-testings of the singlet for two binary measurements. New J. Phys. 2016, 18, 025021. [Google Scholar] [CrossRef]
- Navascues, M.; Pironio, S.; Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys. 2008, 10, 073013. [Google Scholar] [CrossRef] [Green Version]
- Acín, A.; Massar, S.; Pironio, S. Randomness versus nonlocality and entanglement. Phys. Rev. Lett. 2012, 108, 100402. [Google Scholar] [CrossRef] [Green Version]
- Carteret, H.A.; Higuchi, A.; Sudbery, A. Multipartite generalization of the Schmidt decomposition. J. Math. Phys. 2000, 41, 7932–7939. [Google Scholar] [CrossRef] [Green Version]
- Long, G. Collapse-in and collapse-out in partial measurement in quantum mechanics and its wise interpretation. Sci. China Phys. Mech. Astron. 2021, 64, 280321. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, R.; Chang, Z.; Quan, Q.; Gao, H.; Li, F.; Zhang, P. A geometrical framework for quantum incompatibility resources. Assoc. Asia Pac. Phys. Soc. Bull. 2022, 32, 17. [Google Scholar] [CrossRef]
- Wu, X.; Cai, Y.; Yang, T.H.; Le, H.N.; Bancal, J.-D.; Scarani, V. Robust self-testing of the three-qubit W state. Phys. Rev. A 2014, 90, 042339. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, Y.; Han, Y.; Qin, S.; Gao, F.; Wen, Q. Self-Testing of Symmetric Three-Qubit States. IEEE J. Sel. Areas Commun. 2020, 38, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Bhatia, R.; Davis, C. A Cauchy-Schwarz inequality for operators with applications. Linear Algebra Appl. 1995, 223–224, 119–129. [Google Scholar] [CrossRef] [Green Version]
- McKague, M.; Yang, T.H.; Scarani, V. Robust self-testing of the singlet. J. Phys. A Math. Theor. 2012, 45, 455304. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, D.; Tan, X.; Xu, Q.; Wang, H.; Huang, R. Robust Self-Testing of Four-Qubit Symmetric States. Entropy 2022, 24, 1003. https://doi.org/10.3390/e24071003
Bao D, Tan X, Xu Q, Wang H, Huang R. Robust Self-Testing of Four-Qubit Symmetric States. Entropy. 2022; 24(7):1003. https://doi.org/10.3390/e24071003
Chicago/Turabian StyleBao, Daipengwei, Xiaoqing Tan, Qingshan Xu, Haozhen Wang, and Rui Huang. 2022. "Robust Self-Testing of Four-Qubit Symmetric States" Entropy 24, no. 7: 1003. https://doi.org/10.3390/e24071003
APA StyleBao, D., Tan, X., Xu, Q., Wang, H., & Huang, R. (2022). Robust Self-Testing of Four-Qubit Symmetric States. Entropy, 24(7), 1003. https://doi.org/10.3390/e24071003





