Axisymmetric Fractional Diffusion with Mass Absorption in a Circle under Time-Harmonic Impact
Abstract
:1. Introduction
2. Integer Order of Time-Derivative
2.1. Diffusion Equation with Mass Absorption ()
2.2. Klein–Gordon Equation ()
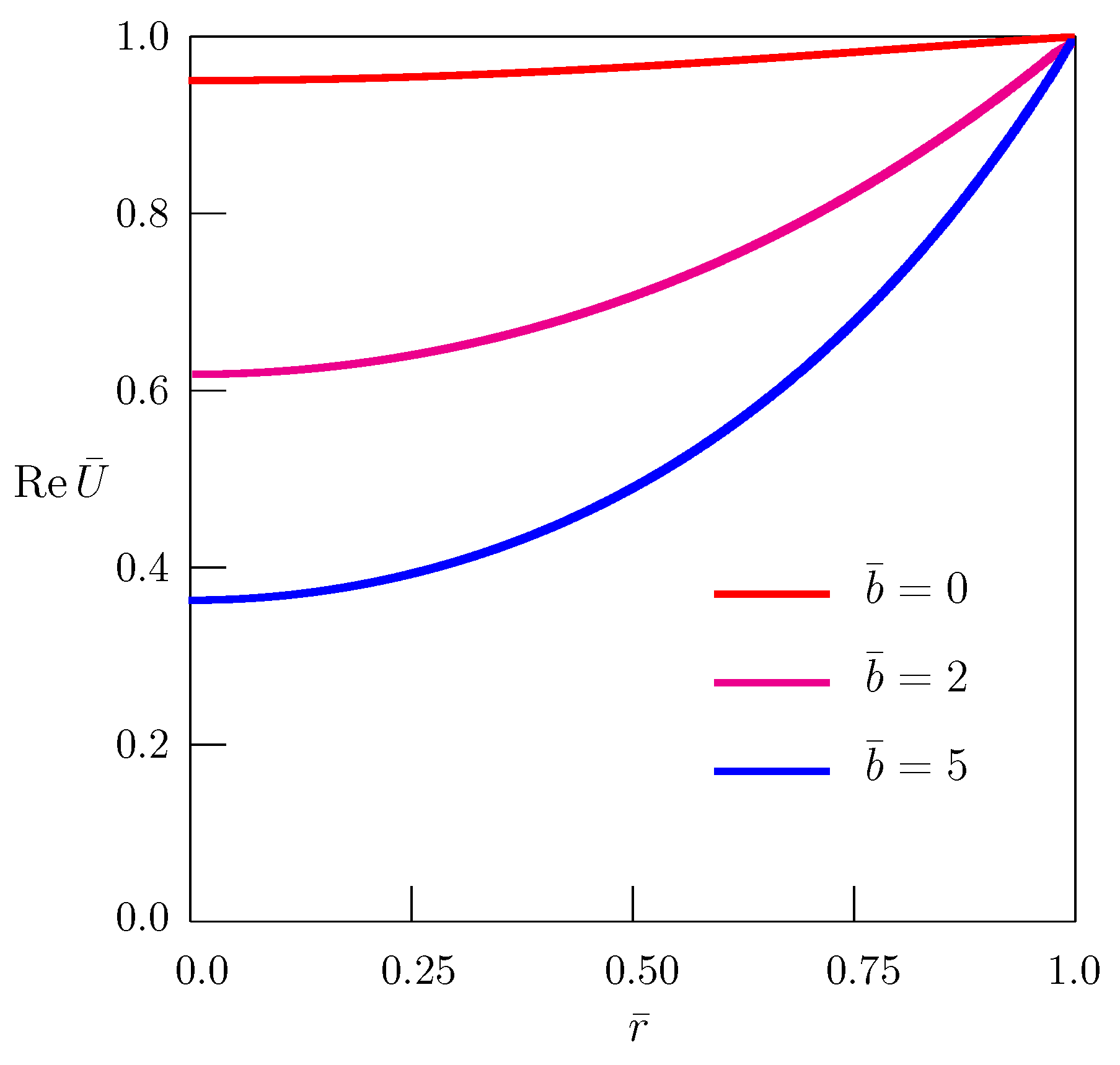
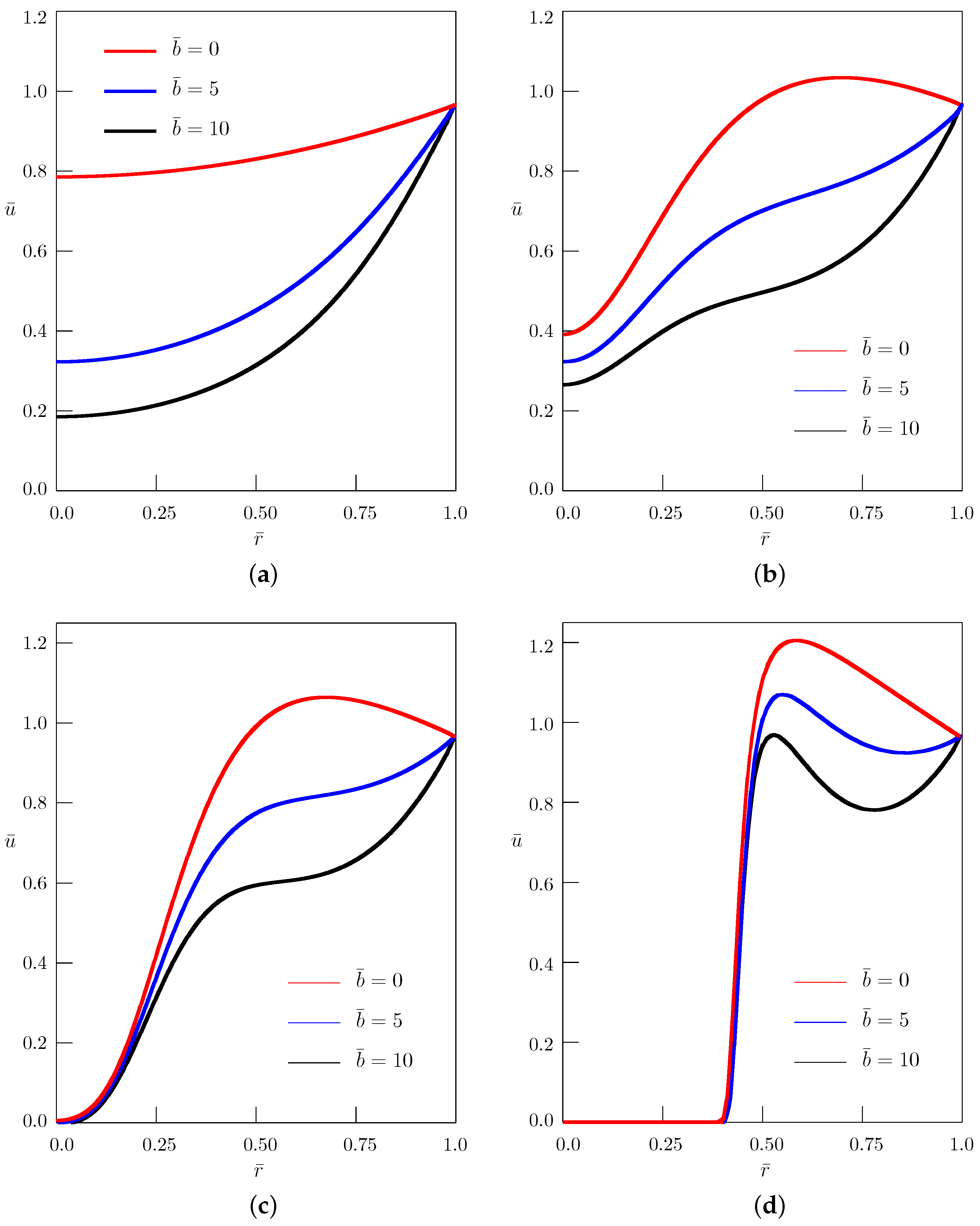
3. Time-Fractional Diffusion-Wave Equation
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Atanacković, T.M.; Pilipovć, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Pinto, C.M.A.; Carvalho, A.R.M. Analysis of a non-integer order model for the coinfection of HIV and HSV-2. Int. J. Nonlinear Sci. Numer. Simulat. 2020, 21, 291–302. [Google Scholar] [CrossRef]
- Carvalho, A.R.M.; Pinto, C.M.A.; de Carvalho, J.M. Fractional model for type 1 diabetes. In Mathematical Modelling and Optimization of Engineering Problems; Machado, J., Özdemir, N., Baleanu, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 175–185. [Google Scholar]
- Su, N. Fractional Calculus for Hydrology, Soli Science and Geomechanics; Taylor & Francis: Boca Raton, FL, USA, 2021. [Google Scholar]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Tenreiro Machado, J.A.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Fourier, J.B.J. Théorie Analytique de la Chaleur; Firmin Didot: Paris, France, 1822. [Google Scholar]
- Fick, A. Ueber Diffusion. Ann. Phys. 1855, 94, 59–86. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Pipkin, A.C. A general theory of heat conduction with finite wave speeds. Arch. Ration. Mech. Anal. 1968, 31, 113–126. [Google Scholar] [CrossRef]
- Day, W. The Thermodynamics of Simple Materials with Fading Memory; Springer: Berlin, Germany, 1972. [Google Scholar]
- Moodi, T.B.; Tait, R.J. On thermal transients with finite wave speeds. Acta Mech. 1983, 50, 97–104. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Stat. Sol. B 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional heat conduction equation and associated thermal stresses. J. Thermal Stresses 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Povstenko, Y. Theory of thermoelasticity based on the space-time-fractional heat conduction equation. Phys. Scr. 2009, 136, 014017. [Google Scholar] [CrossRef]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Absorption by simultaneous diffusion and chemical reaction into particles of various shapes and into falling drops. Trans. Faraday Soc. 1951, 47, 1014–1023. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Carslaw, H.C.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Podstrigach, Y.S.; Kolyano, Y.M. Unsteady Temperature Fields and Stresses in Thin Plates; Naukova Dumka: Kiev, Ukraine, 1972. (In Russian) [Google Scholar]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Fasano, A.; Sequeira, A. Hemomath. The Mathematics of Blood; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Wazwaz, A.-M. Partial Differential Equations and Solitary Waves Theory; Higher Education Press: Beijing, China; Springer: Berlin, Germany, 2009. [Google Scholar]
- Gravel, P.; Gauthier, C. Classical applications of the Klein-Gordon equation. Am. J. Phys. 2011, 79, 447–453. [Google Scholar] [CrossRef]
- Ångström, A.J. Neue Methode, das Wärmeleitungs vermögen der Körper zu bestimmen. Ann. Phys. Chem. 1861, 114, 513–530. [Google Scholar]
- Mandelis, A. Diffusion waves and their uses. Phys. Today 2000, 53, 29–33. [Google Scholar] [CrossRef] [Green Version]
- Mandelis, A. Diffusion-Wave Fields: Mathematical Methods and Green Functions; Springer: New York, NY, USA, 2001. [Google Scholar]
- Nowacki, W. State of stress in an elastic space due to a source of heat varying harmonically as function of time. Bull. Acad. Polon. Sci. Sér. Sci. Technol. 1957, 5, 145–154. [Google Scholar]
- Nowacki, W. Thermoelasticity, 2nd ed.; PWN-Polish Scientic Publishers: Warsaw, Poland; Pergamon Press: Oxford, UK, 1986. [Google Scholar]
- Vrentas, J.S.; Vrentas, C.M. Diffusion and Mass Transfer; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Povstenko, Y. Fractional heat conduction in a space with a source varying harmonically in time and associated thermal stresses. J. Thermal Stresses 2016, 39, 1442–1450. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Time-fractional diffusion with mass absorption under harmonic impact. Fract. Calc. Appl. Anal. 2018, 21, 118–133. [Google Scholar] [CrossRef] [Green Version]
- Datsko, B.; Podlubny, I.; Povstenko, Y. Time-fractional diffusion-wave equation with mass absorption in a sphere under harmonic impact. Mathematics 2019, 7, 433. [Google Scholar] [CrossRef] [Green Version]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Vol. 2: Special Functions; Gordon & Breach Science Publishers: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Povstenko, Y. Fractional radial diffusion in a cylinder. J. Mol. Liq. 2008, 135, 46–50. [Google Scholar] [CrossRef]
- Olver, F.W.J. (Ed.) Bessel Functions, Part III: Zeros and Associated Values; Cambridge University Press: Cambridge, UK, 1960. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Podlubny, I. Mittag-Leffler Function; Calculates the Mittag-Leffler Function with Desired Accuracy, MATLAB Central File Exchange, File ID 8738. Available online: www.mathworks.com/matlabcentral/fileexchange/8738 (accessed on 17 April 2019).
- Sneddon, I.N. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Doetsch, G. Anleitung zum praktischer Gebrauch der Laplace-Transformation und der Z-Transformation; Springer: München, Germany, 1967. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 1. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Kyrylych, T. Axisymmetric Fractional Diffusion with Mass Absorption in a Circle under Time-Harmonic Impact. Entropy 2022, 24, 1002. https://doi.org/10.3390/e24071002
Povstenko Y, Kyrylych T. Axisymmetric Fractional Diffusion with Mass Absorption in a Circle under Time-Harmonic Impact. Entropy. 2022; 24(7):1002. https://doi.org/10.3390/e24071002
Chicago/Turabian StylePovstenko, Yuriy, and Tamara Kyrylych. 2022. "Axisymmetric Fractional Diffusion with Mass Absorption in a Circle under Time-Harmonic Impact" Entropy 24, no. 7: 1002. https://doi.org/10.3390/e24071002
APA StylePovstenko, Y., & Kyrylych, T. (2022). Axisymmetric Fractional Diffusion with Mass Absorption in a Circle under Time-Harmonic Impact. Entropy, 24(7), 1002. https://doi.org/10.3390/e24071002





