Supernovae and the Arrow of Time
Abstract
1. Introduction
2. Fluid Instabilities and Interfacial Mixing
3. Results
3.1. Group Theory
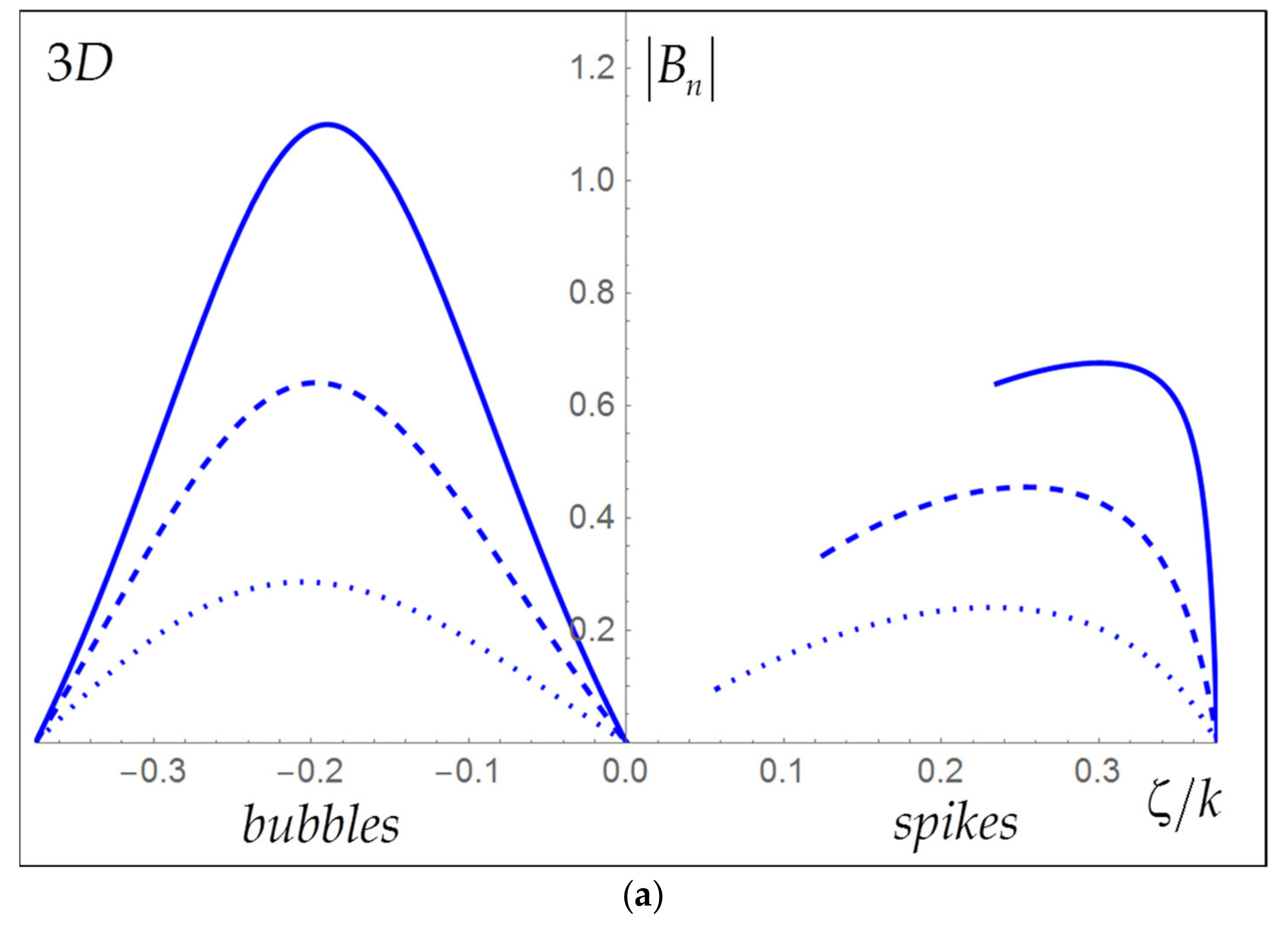
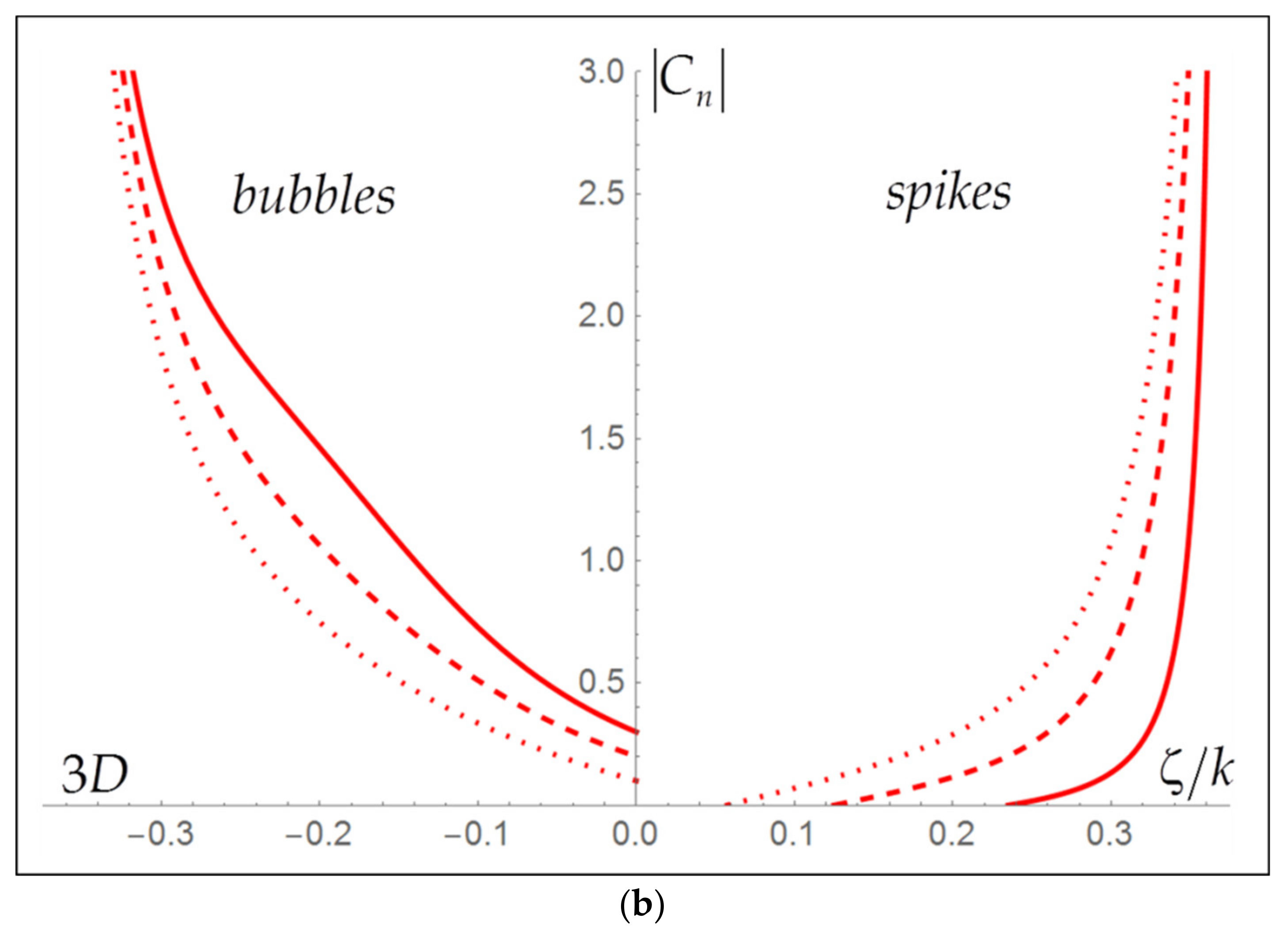
3.2. Scale-Dependent Linear Dynamics
3.3. Scale-Dependent Nonlinear Dynamics
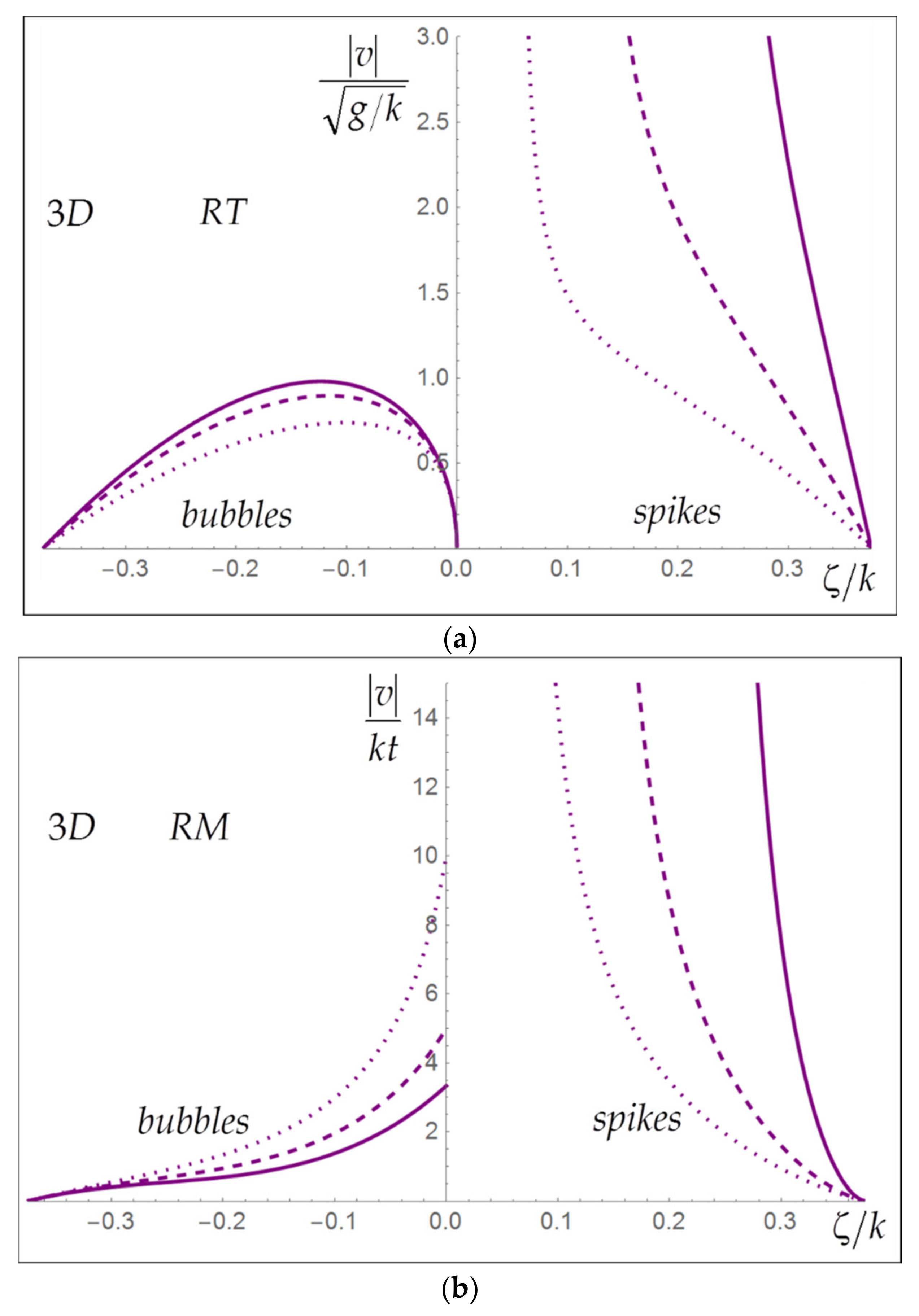
3.4. Transition to Self-Similar Mixing
3.5. Self-Similar Mixing
3.6. Properties of Self-Similar Mixing
4. Outcome of the Theory
4.1. Fundamental Aspects
4.2. Astrophysical Aspects
4.3. Scaled Laboratory Experiments
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abarzhi, S.I.; Bhowmick, A.K.; Naveh, A.; Pandian, A.; Swisher, N.C.; Stellingwerf, R.F.; Arnett, W.D. Supernova, nuclear synthesis, fluid instabilities and mixing. Proc. Natl. Acad. Sci. USA 2019, 116, 18184. [Google Scholar] [CrossRef] [PubMed]
- Arnett, D. Supernovae and Nucleosynthesis; Princeton University Press: Princeton, NJ, USA, 1996; ISBN 9780691011479. [Google Scholar]
- Arnett, W.D. Pulsars and neutron star formation. Nature 1969, 222, 359. [Google Scholar] [CrossRef]
- Arnett, W.D. A possible model of supernovae: Detonation of 12C. Astroph. Space Sci. 1969, 5, 180. [Google Scholar] [CrossRef]
- Fryxell, B.; Arnett, W.D.; Mueller, E. Instabilities and clumping in SN 1987A. Astroph. J. 1991, 367, 619. [Google Scholar] [CrossRef]
- Bazan, G.; Arnett, W.D. Convection, nucleosynthesis, and core collapse. Astroph. J. 1994, 433, 41. [Google Scholar] [CrossRef]
- Arnett, W.D.; Meakin, C.; Young, P.A. Turbulent convection in stellar interiors. Astroph. J. 2009, 690, 1729. [Google Scholar] [CrossRef]
- Supernova Remnant Cassiopeia A December 2004. Available online: http://www.hubblesite.org; http://www.nasa.gov/; (accessed on 23 January 2022).
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and γ-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Abarzhi, S.I.; Goddard, W.A. Interfaces and mixing: Non-equilibrium transport across the scales. Proc. Natl. Acad. Sci. USA 2019, 116, 18171. [Google Scholar] [CrossRef] [PubMed]
- Abarzhi, S.I.; Gauthier, S.; Sreenivasan, K.R. Turbulent Mixing and Beyond: Non-Equilibrium Processes from Atomistic to Astrophysical Scales. I; Royal Society Publishing: London, UK, 2013; ISBN 1782520384. [Google Scholar]
- Rayleigh Lord Strutt, J.W. Investigations of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 1883, 14, 170–177. [Google Scholar]
- Davies, R.M.; Taylor, G.I. The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. A 1950, 200, 375–390. [Google Scholar]
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun Pure Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Meshkov, E.E. Instability of the interface of two gases accelerated by a shock. Sov. Fluid Dyn. 1969, 4, 101–104. [Google Scholar] [CrossRef]
- Abarzhi, S.I.; Gauthier, S.; Sreenivasan, K.R. Turbulent Mixing and Beyond: Non-Equilibrium Processes from Atomistic to Astrophysical Scales. II; Royal Society Publishing: London, UK, 2013; ISBN 0854039864. [Google Scholar]
- Drake, R.P. Perspectives on high-energy-density physics. Phys. Plasmas 2009, 16, 055501. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory Course I–X; Pergamon Press: New York, NY, USA, 1987. [Google Scholar]
- Kolmogorov, A.N. Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 1941, 30, 299–303, Erratum in Energy dissipation in locally isotropic turbulence. Dokl. Akad. Nauk. SSSR 1941, 32, 19–21. [Google Scholar]
- Boltzmann, L. 1895 & 1897 Lectures on Gas Theory; Brush, S.G., Translator; University of California Press: Berkeley, CA, USA, 1964. [Google Scholar]
- Klimenko, A.Y. On the effect of decoherence on quantum tunneling. Springer Nat. Appl. Sci. 2021, 3, 710. [Google Scholar]
- Penrose, R. Road to Reality: A Complete Guide to the Laws of the Universe; A. Knopf Inc.: New York, NY, USA, 2005. [Google Scholar]
- Albert David, Z. Time and Chance; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Reichenbach, H. The Direction of Time; 1971 Reprint; University of California Press: Berkeley, CA, USA, 1956. [Google Scholar]
- Davies, P.C.W. The Physics of Time Asymmetry; University of California Press: Berkeley, CA, USA, 1977. [Google Scholar]
- Anisimov, S.I.; Drake, R.P.; Gauthier, S.; Meshkov, E.E.; Abarzhi, S.I. What is certain and what is not so certain in our knowledge of Rayleigh–Taylor mixing? Phil. Trans. R. Soc. A 2013, 371, 20130266. [Google Scholar] [CrossRef]
- Remington, B.A.; Park, H.; Casey, D.T.; Cavallo, R.M.; Clark, D.S.; Huntington, C.M.; Kuranz, C.C.; Miles, A.R.; Nagel, S.R.; Raman, K.S.; et al. Rayleigh–Taylor instabilities in high-energy density settings on the National Ignition Facility. Proc. Natl. Acad. Sci. USA 2019, 116, 18233. [Google Scholar] [CrossRef]
- Robey, H.F.; Zhou, Y.; Buckingham, A.C.; Keiter, P.; Remington, B.A.; Drake, R.P. The time scale for the transition to turbulence in a high Reynolds number, accelerated flow. Phys. Plasmas 2003, 10, 614. [Google Scholar] [CrossRef]
- Swisher, N.C.; Kuranz, C.C.; Arnett, D.; Hurricane, O.; Remington, B.A.; Robey, H.F.; Abarzhi, S.I. Rayleigh-Taylor mixing in supernova experiments. Phys. Plasmas 2015, 22, 102707. [Google Scholar] [CrossRef]
- Lugomer, S. Laser-matter interactions: Inhomogeneous Richtmyer–Meshkov and Rayleigh–Taylor instabilities. Laser Part Beams 2016, 34, 123. [Google Scholar] [CrossRef]
- Sedov, L. Similarity and Dimensional Methods in Mechanics, 10th ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Taylor, G.I. The Formation of a Blast Wave by a Very Intense Explosion. Phil. Trans. R. Soc. A 1950, 201, 175. [Google Scholar]
- Guderley, G. Starke Kugelige und Zylindrische Verdichtungsstosse in der Nahe des Kugelmitterpunktes bnw. der Zylinderachse. Luftfahrtforschung 1942, 19, 302. (In German) [Google Scholar]
- Stanyukovich, K.P. Non-Steady Motion of Continuous Media; Oxford University Press: Oxford, UK, 1960. [Google Scholar]
- Kadau, K.; Barber, J.L.; Germann, T.C.; Holian, B.L.; Alder, B.J. Atomistic methods in fluid simulation. Phil. Trans. R. Soc. A 2010, 368, 1547. [Google Scholar] [CrossRef] [PubMed]
- Abarzhi, S.I. Special class of self-similar dynamics for Rayleigh-Taylor mixing with variable acceleration. arXiv 2019, arXiv:1901.04563Erratum in Phys. Fluids 2021, 33, 122110. 33, 122110. [Google Scholar]
- Abarzhi, S.I. Review of theoretical modeling approaches of Rayleigh-Taylor instabilities and turbulent mixing. Phil. Trans. R. Soc. A 2010, 368, 1809–1828. [Google Scholar] [CrossRef]
- Meshkov, E.E.; Abarzhi, S.I. On Rayleigh-Taylor interfacial mixing. Fluid Dyn. Res. 2019, 51, 065502. [Google Scholar] [CrossRef]
- Betti, R.; Hurricane, O.A. Inertial-confinement fusion with lasers. Nat. Phys. 2006, 12, 435. [Google Scholar] [CrossRef]
- Meshkov, E.E. Some peculiar features of hydrodynamic instability development. Phil. Trans. R. Soc. A 2013, 371, 20120288. [Google Scholar] [CrossRef]
- Taylor, G.I. The criterion for turbulence in curved pipes. Proc. R. Soc. A 1929, 124, 243–249. [Google Scholar]
- Narasimha, R.; Sreenivasan, K.R. Relaminarization in highly accelerated turbulent boundary layers. J. Fluid Mech. 1979, 61, 417. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. Turbulent mixing: A perspective. Proc. Natl. Acad. Sci. USA 2019, 116, 18175–18183. [Google Scholar] [CrossRef]
- Pfefferle, D.; Abarzhi, S.I. Whittle maximum likelihood estimate of spectral properties of Rayleigh-Taylor interfacial mixing using hot-wire anemometry experimental data. Phys. Rev. E 2020, 102, 053107. [Google Scholar] [CrossRef]
- Abarzhi, S.I. Review of nonlinear dynamics of the unstable fluid interface: Conservation laws and group theory. Phys. Scr. 2008, 2008, 014012. [Google Scholar] [CrossRef]
- Glimm, J.; Sharp, D.H.; Kaman, T.; Lim, H. New directions for Rayleigh–Taylor mixing. Phil. Trans. R. Soc. A 2013, 371, 20120183. [Google Scholar] [CrossRef][Green Version]
- Youngs, D.L. The density ratio dependence of self-similar Rayleigh–Taylor mixing. Phil. Trans. R. Soc. A 2013, 371, 20120173. [Google Scholar] [CrossRef]
- Thornber, B.; Griffond, J.; Poujade, O.; Attal, N.; Varshochi, H.; Bigdelou, P.; Ramaprabhu, P.; Olson, B.; Greenough, J.; Zhou, Y.; et al. Late-time growth rate, mixing, and anisotropy in the multimode narrowband Richtmyer–Meshkov instability: The θ-group collaboration. Phys. Fluids 2017, 29, 105107. [Google Scholar] [CrossRef]
- Stanic, M.; Stellingwerf, R.F.; Cassibry, J.T.; Abarzhi, S.I. Scale coupling in Richtmyer-Meshkov flows induced by strong shocks. Phys. Plasmas 2012, 19, 082706. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: London, UK, 1961. [Google Scholar]
- Abarzhi, S.I. Stable steady flows in Rayleigh–Taylor instability. Phys. Rev. Lett. 1998, 81, 337–340. [Google Scholar] [CrossRef]
- Abarzhi, S.I.; Williams, K.C. Scale-dependent Rayleigh-Taylor dynamics with variable acceleration by group theory approach. Phys. Plasmas 2020, 27, 072107. [Google Scholar] [CrossRef]
- Abarzhi, S.I. On fundamentals of Rayleigh-Taylor turbulent mixing. Europhys. Lett. 2010, 91, 12867. [Google Scholar] [CrossRef]
- Abarzhi, S.I.; Gorobets, A.; Sreenivasan, K.R. Turbulent mixing in immiscible, miscible and stratified media. Phys. Fluids 2005, 17, 081705. [Google Scholar] [CrossRef]
- Abarzhi, S.I. Coherent structures and pattern formation in the Rayleigh-Taylor turbulent mixing. Phys. Scr. 2008, 78, 015401. [Google Scholar] [CrossRef]
- Alon, U.; Hecht, J.; Offer, D.; Shvarts, D. Power-laws and similarity of Rayleigh-Taylor and Richtmyer-Meshkov mixing fronts at all density ratios. Phys. Rev. Lett. 1995, 74, 534. [Google Scholar] [CrossRef] [PubMed]
- Glimm, J.; Sharp, D.H. Chaotic mixing as a renormalization-group fixed-point. Phys. Rev. Lett. 1990, 64, 2137–2139. [Google Scholar] [CrossRef]
- Abarzhi, S.I.; Rosner, R. Comparative study of approaches for modeling Rayleigh-Taylor turbulent mixing. Phys. Scr. 2010, T142, 014012. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, L.; Zhai, Z.; Ding, J.; Si, T.; Luo, X. Richtmyer–Meshkov instability on two-dimensional multi-mode interface. J. Fluid Mech. 2021, 928, A37. [Google Scholar] [CrossRef]

| Buoyancy | |
| Drag | |
| Quantities | |
| Range |
| Buoyancy | |
| Drag | |
| Quantities | |
| Range |
| Buoyancy | |
| Drag | |
| Quantities | |
| Range |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abarzhi, S.I.; Hill, D.L.; Naveh, A.; Williams, K.C.; Wright, C.E. Supernovae and the Arrow of Time. Entropy 2022, 24, 829. https://doi.org/10.3390/e24060829
Abarzhi SI, Hill DL, Naveh A, Williams KC, Wright CE. Supernovae and the Arrow of Time. Entropy. 2022; 24(6):829. https://doi.org/10.3390/e24060829
Chicago/Turabian StyleAbarzhi, Snezhana I., Desmon L. Hill, Annie Naveh, Kurt C. Williams, and Cameron E. Wright. 2022. "Supernovae and the Arrow of Time" Entropy 24, no. 6: 829. https://doi.org/10.3390/e24060829
APA StyleAbarzhi, S. I., Hill, D. L., Naveh, A., Williams, K. C., & Wright, C. E. (2022). Supernovae and the Arrow of Time. Entropy, 24(6), 829. https://doi.org/10.3390/e24060829







